Adjustment of Rates
Asst Prof Dr. Ahmed Samir Al-Naaimi - MBChB, MSc epi, PhD
Dep .of Community Medicine-Baghdad College of medicine
Email:
info@topmedresearch.com

Learning Objectives
1.
Define adjusted rate.
2.
Value the role of adjusted rates in comparison.
3.
Discuss the advantages and disadvantages of adjusted rate.
4.
Compare adjusted rate to crude and specific rates.
5.
List two methods of rate adjustment.
6.
Master the calculation of direct and indirect method of
rate adjustment.
7.
Define the standard population.
8.
Interpret the value of SMR.

Definition
Adjusted rates:
are summary rates that have undergone statistical
transformation to permit fair comparison between groups differing
in some characteristic that may affect risk of disease. They are
useful in comparison between two (or more) populations or the
same population over time.
Two types of commonly used adjusted rates are:
Adjusted (standardized) death rate:
takes into account the
population structure (age, or gender) and its effect on overall death
rate.
Standardized fertility rate
(age adjusted general fertility rate):
The age structure of the female population affects the general
fertility rate, therefore it is better to control for the confounding
effect of age before making comparisons between populations.
Advantages / Disadvantages
Advantages:
adjusted rates provide the advantage of crude rates in being
summary measures (single figure), overcoming at the same time the
crude rate inherent property of unfairness in comparison. It also
provide the advantage of specific rates in permitting fair
comparisons between 2 groups of homogenous structure,
overcoming at the same time the difficulty in comparing two
populations by using multiple specific rates for comparison.
Disadvantages:
adjusted rates are not real figures. In this context they are
absolutely useless when used outside the comparison for which
they were calculated.

Methods of rate adjustment
There are essentially two methods for adjusting rates, the
direct
method and the
indirect
one. The age is the most
common factor adjusted for, and it will be used in the coming
examples. Other confounding factors may be used in the same
context when needed.
Direct method of rate adjustment:
The actual age specific rates observed in two or more studied
populations are applied to an arbitrarily chosen population of
known age structure referred to as "standard population".

Choices for a standard population
There are 3 options for selecting a standard population:
Any of the two compared populations.
The sum of the two compared populations.
The US population for the year 2000 (the last decennial
census). To simplify the calculations the total of the
population is forced to a sum of one million and the
resulting standard population is called the
standard million
.
To calculate this standard million the relative frequency of
each age group in the US population is multiplied by one
million.
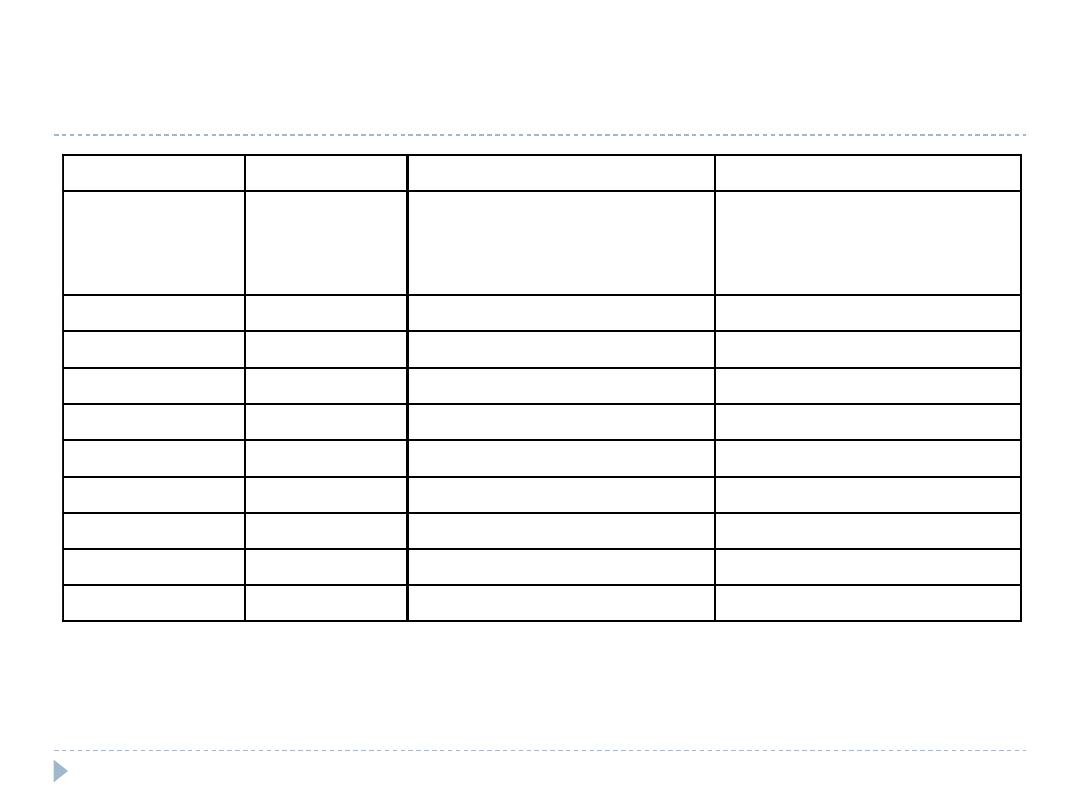
Calculation of million standard population
D
E
E
Age group
(years)
US
population
(year 2000)
Standard million
population based on year
2001
Standard million
population based on year
2000
=(D / total D) x 1,000,000 =(D x (total E / total D))
(0-4)
19,175,798
68,139
68,139
(5-9)
20,549,505
73,020
73,020
(10-14)
20,528,072
72,944
72,944
(15-19)
20,219,890
71,849
71,849
(20-44)
104,004,252
369,567
369,567
(45-64)
61,952,636
220,141
220,141
(65 and over)
34,991,753
124,339
124,339
Total
281,421,906
1,000,000
1,000,000
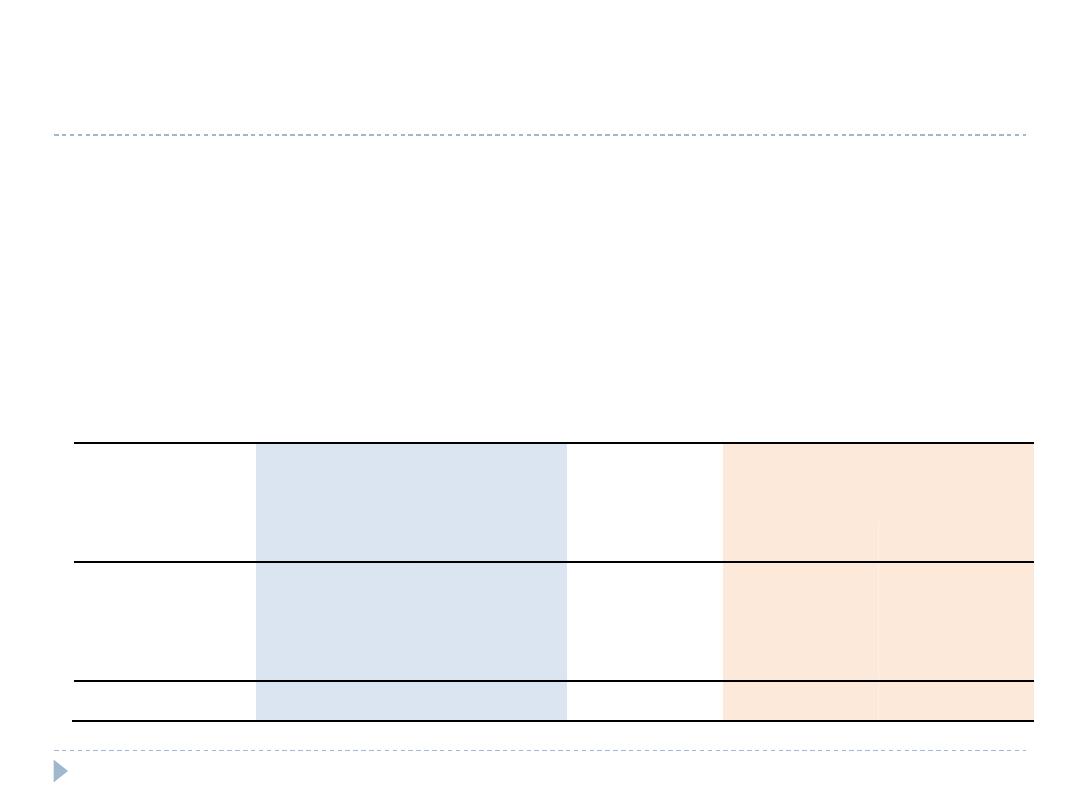
Hypothetical Example
The population size by age groups and observed number of
deaths in each age group were provided for a certain
population at year 1990 and repeated at year 2000. Calculate
the crude and age adjusted death rates and comment on
comparing the death between the 2 points of time.
at year 1990
at year 2000
Age group
(years)
Population
Observed
Deaths
Population
Observed
Deaths
<50
500,000
60
300,000
30
50-69
300,000
396
400,000
400
70+
100,000
406
200,000
700
Total
900,000
862
900,000
1,130
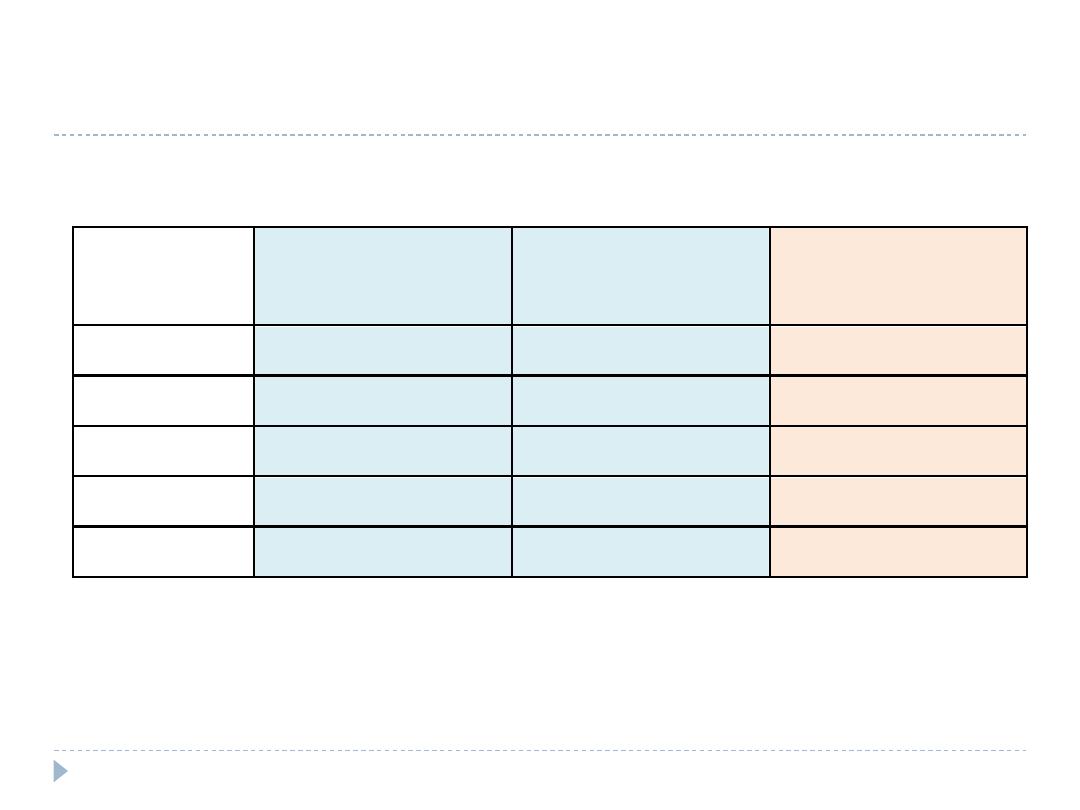
Answer
First calculate the standard population
Age group
(years)
Population at year
1990
Population at year
2000
Standard
population
A
B
=A+B
<50
500,000
300,000
800,000
50-69
300,000
400,000
700,000
70+
100,000
200,000
300,000
Total
900,000
900,000
1,800,000
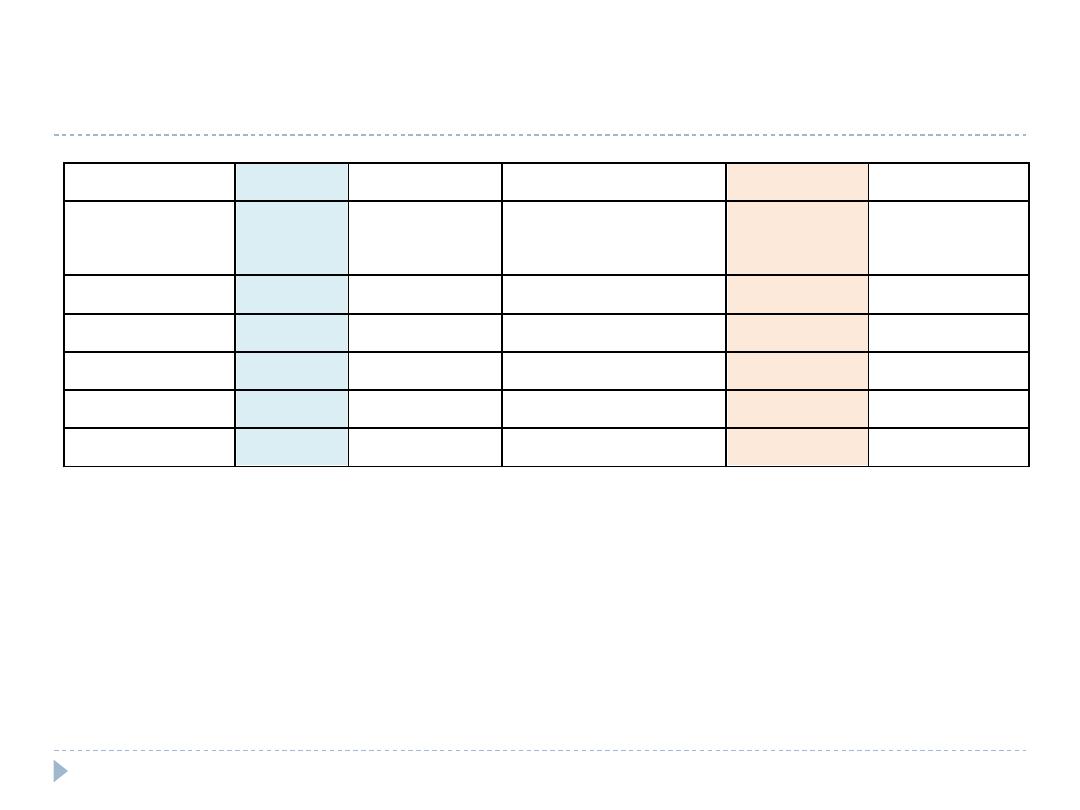
Answer
At 1990
A
B
C
D
E
Age group
(years)
Total
N
Observed
Deaths
Age specific
death rate (/10
5
)
Standard
population
Expected
deaths
=(B/A) x 100,000
=((CxD)/10
5
)
<50
500,000
60
12.0
800,000
96
50-69
300,000
396
132.0
700,000
924
70+
100,000
406
406.0
300,000
1,218
Total
900,000
862
1,800,000
2,238
Crude Death rate = 862 / 900,000 = 95.8 per 100,000
Age adjusted death rate at 1990 = 2,238 /1,800,000
= 124.3 per 100,000
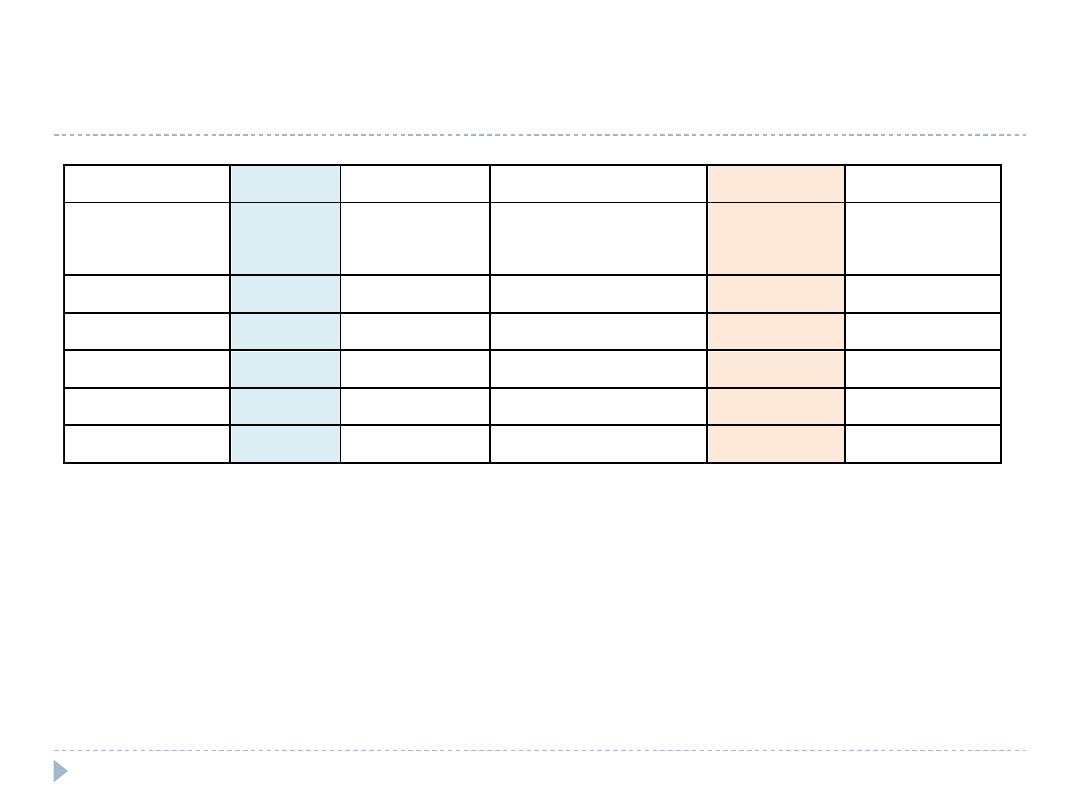
Answer
At 2000
A
B
C
D
E
Age group
(years)
Total
N
Observed
Deaths
Age specific
death rate (/10
5
)
Standard
population
Expected
deaths
=(B/A) x 100,000
=((CxD)/10
5
)
<50
300,000
30
10.0
800,000
80
50-69
400,000
400
100.0
700,000
700
70+
200,000
700
350.0
300,000
1,050
Total
900,000
1,130
1,800,000
1,830
Crude Death rate = 1,130 / 900,000= 125.6 per 100,000
Age adjusted death rate = 1,830 /1,800,000
= 101.7 per 100,000

Interpretation / Conclusion
The crude death rate in year 2000 is higher than that in the
previous decade (year 1990), i.e. in general the risk of death
has increased over time, but the question is how to
interpret this finding.
“Is there a deterioration in health status
for the population over time which explains this increase in
crude death rate?”
A comparison of age adjusted death rates reflects a
reduction in death rate over time (from 124.3 to 101.7 per
100,000 population), i.e. improvement in health status of the
population. The change in population structure overtime
towards an older population explain the increase in crude
death rates over time.
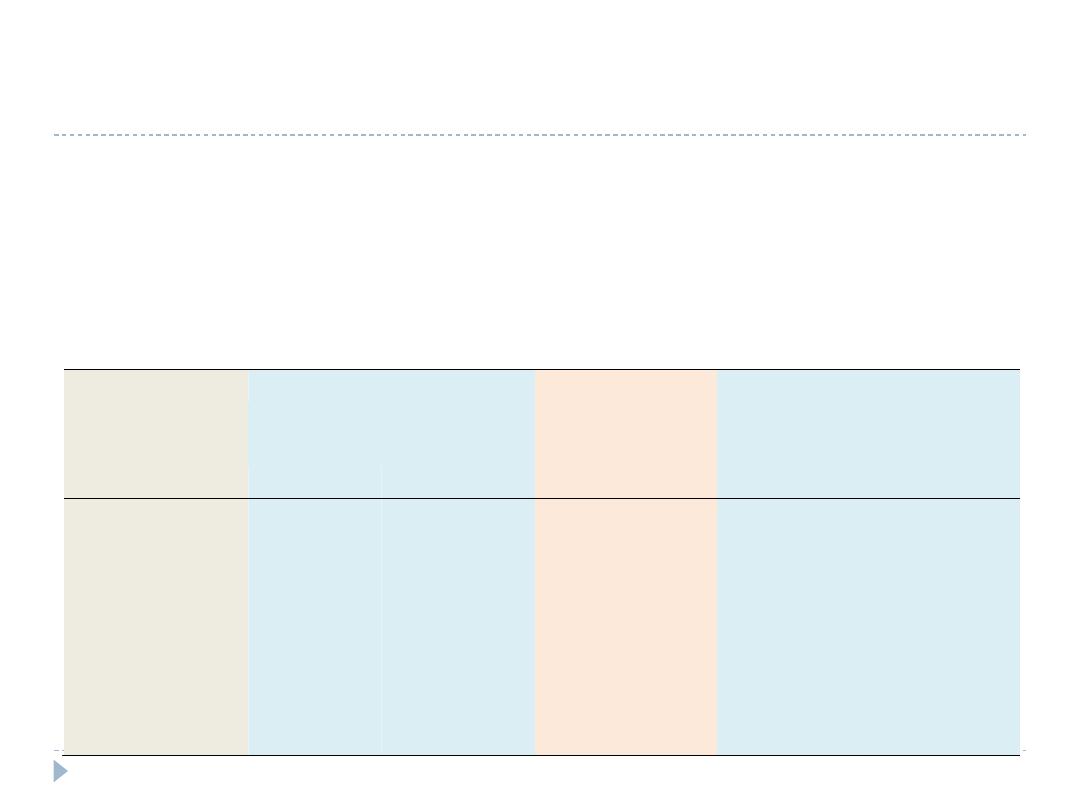
Exercise: (home work)
The population size by age groups and observed number of deaths
in each age group are provided for the population of Georgia at
year 1999 and 2000. Calculate the crude and age adjusted death
rates and comment on comparing the death between the 2 points
of time.
Georgia, 1999 population
Georgia, 2000 population
Age group (years) Population
Observed
Deaths
Standard million
population based
on year 2000
Population
Observed
Deaths
(0-4)
580,222
1,197
68,139
595,150
1,299
(5-9)
577,151
126
73,020
615,584
101
(10-14)
563,293
153
72,944
607,759
136
(15-19)
570,547
460
71,849
596,277
447
(20-44)
3,083,521
4,989
369,567
3,244,960
5,185
(45-64)
1,653,515
12,633
220,141
1,741,448
13,092
(65 and over)
761,457
42,076
124,339
785,275
43,397
Total
7,789,706
61,634
1,000,000
8,186,453
63,657

Indirect method of rate adjustment (SMR)
Here one or more populations are compared to a reference
population. The age specific rates of the studied populations
are either unknown or are excessively variable (unstable)
because of small number.
The more stable rates of the reference population are applied
to the studied population to calculate the expected number
of deaths.
The standardized mortality ratio (SMR) is a comparison of the
actually observed to expected number of deaths.
SMR =
Observed deaths
Expected deaths

Interpretation of SMR
An SMR equal to 1 indicates that the risk of death in the
studied population is equal to the reference population. This
is the null value for SMR, which is similar to that of RR and
OR.
An SMR in excess of 1 indicates a higher risk of death in the
studied population
An SMR <1 indicates a lower risk of death in the studied
population.
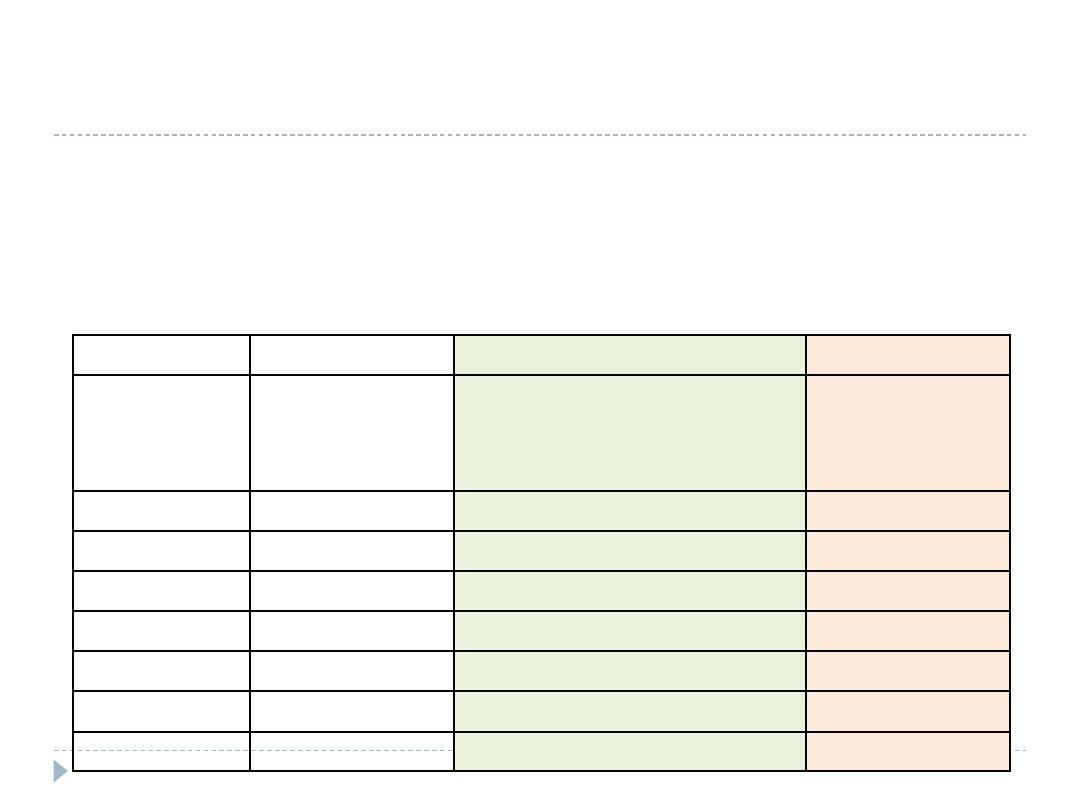
Exercise
The table below contains data for deaths from TB in White Miners
of US 1950. The age specific death rates from TB of males in the
general US population are also provided. Calculate the SMR for
White Miners compared to general male population.
A
B
C
Age group
(years)
Population of
white miners
(Males)
Age specific death rate from
TB (/100,000) in males in the
general population
Observed
Deaths from TB
in white miners
20-24
74,598
12.26
10
25-29
85,077
16.12
20
30-34
80,845
21.54
22
35-44
148,870
33.96
98
45-54
102,649
56.82
174
55-59
42,494
75.23
112
Total
534,533
436
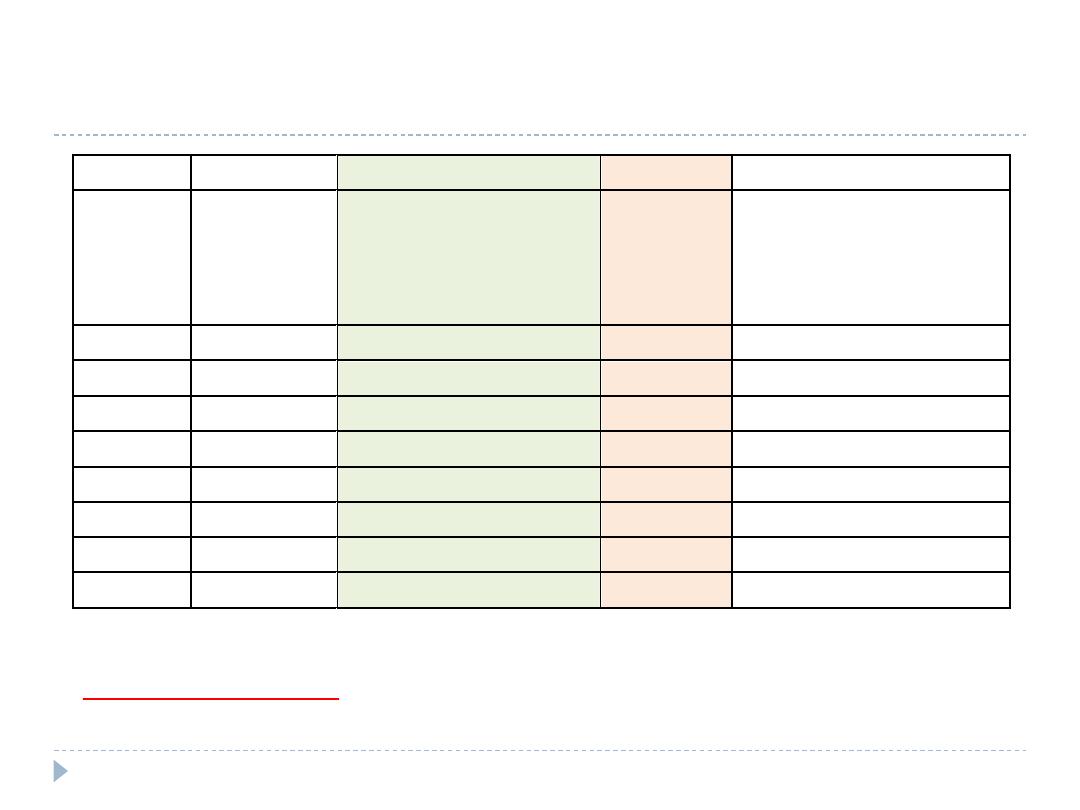
Answer-calculations of SMR
A
B
C
D
Age group
(years)
Population of
white miners
(Males)
Age specific death rate
from TB (/100,000) in
males in the general
population
Observed
Deaths from
TB in white
miners
Expected Deaths from TB
in White Miners if they
had the same risk as the
general population
=(A x B) / 100,000
20-24
74,598
12.26
10
9
25-29
85,077
16.12
20
14
30-34
80,845
21.54
22
17
35-44
148,870
33.96
98
51
45-54
102,649
56.82
174
58
55-59
42,494
75.23
112
32
Total
534,533
436
181
SMR = 436 / 181 = 2.4
Interpretation:
Being a miner increase the risk of death from
TB by 2.4 times compared to general population of white males
