
Chapter I
CRYSTAL STRUCTURE AND CRYSTALLOGRAPHY
1.0 What is meant by Crystallography and why to study the structure of crystalline solids?
Crystallography is the experimental science of determining the arrangement of atoms in the
crystalline solids. The properties of some materials are directly related to their crystal structures. For
example, pure and undeformed magnesium and beryllium, having one crystal structure, are much
more brittle (i.e., fracture at lower degrees of deformation) than pure and undeformed metals such as
gold and silver that have yet another crystal structure. Furthermore, significant property differences
exist between crystalline and non-crystalline materials having the same composition. For example,
non-crystalline ceramics and polymers normally are optically transparent; the same materials in
crystalline (or semi-crystalline) form tend to be opaque or, at best, translucent.
An important reason to have an understanding of interatomic bonding in solids is that, in some
instances, the type of bond allows us to explain a material’s properties. For example, consider
carbon, which may exist as both graphite and diamond. Whereas graphite is relatively soft and has a
“greasy” feel to it, diamond is the hardest known material. This dramatic disparity in properties is
directly attributable to a type of interatomic bonding found in graphite that does not exist in
diamond.
Thus by studying the crystal structure and bonding nature of different materials, we can
investigate the reasons for the similar or dissimilar nature of the selected materials in terms of
different properties or different parameters. The crystal structure and symmetry of a material play a
vital role in determining many of its physical properties, such as cleavage, electronic band structure,
and optical transparency, etc.
1.1 Introduction
Based on the atomic arrangement in a substance, solids can be broadly classified as either
crystalline or non-crystalline. In a crystalline solid, all the atoms are arranged in a periodic manner in
all three dimensions where as in a non-crystalline solid the atomic arrangement is random or non-
periodic in nature. A crystalline solid can either be a single crystalline or a polycrystalline. In the
case of single crystal the entire solid consists of only one crystal and hence, periodic arrangement of
atoms continues throughout the entire material. A polycrystalline material is an aggregate of many
small crystals separated by well-defined grain boundaries and hence periodic arrangement of atoms
is limited to small regions of the material called as grain boundaries as shown in Fig. 1.1. The non-
crystalline substances are also called as amorphous substances materials. Single crystalline materials

exhibit long range as well as short range periodicities while long range periodicity is absent in case
of poly-crystalline materials and non-crystalline materials.
Some more differences between crystalline solids and amorphous solids is listed in Table 1.1.

In this chapter, as we are studying about crystal structures of materials, we restrict our
discussion to crystalline solids. As already mentioned in table 1.1, a crystal has regular shape and
when it is broken all broken pieces have the same regular shape. A crystal has sharp melting point.
Since the crystals may have different periodic arrangements in all three dimensions, the physical
properties vary with direction and therefore they are called anisotropic substances. Crystalline solids
may be made up of metallic crystals or non metallic crystals. Copper, Silver, aluminum, tungsten and
magnesium are examples of metallic crystals while carbon, crystallized polymers and plastics are
examples of nonmetallic crystals. Let us now discuss the elementary concepts of crystallography.
1.1.1 Space Lattice or Crystal Lattice:
In a solid crystalline material, the atoms or molecules are arranged regularly and periodically
in all three dimensions. The atomic arrangement in a crystal is called crystal structure. To explain
crystal symmetries easily, it is convenient to represent an atom or a group of atoms that repeats in
three dimensions in the crystal as a unit. If each such atom or unit of atoms in a crystal is replaced by
a point in space, then the resultant points in space are called space lattice. Each point in a space
lattice is called a lattice point and each atom or unit of atoms is called basis or pattern. A space
lattice represents the geometrical pattern of crystal in which the surroundings of each lattice point is
the same. If the surroundings of each lattice point is same or if the atom or all the atoms at lattice
points are identical, then such a lattice is called Bravais lattice. On the other hand, if the atom or the
atoms at lattice points are not same, then it is said to be a non-Bravais lattice. Figure 1.2 shows a
two- dimensional lattice.

In the same manner, it is very convenient to imagine periodic arrangement of points in space in 3-
dimensions about which these atoms are located. “A space lattice or a crystal lattice is defined as a
three dimensional infinite array of points in space in which every point has surroundings identical
to that of every other point in the array”.
1.1.2 Basis and Crystal Structure
The atomic arrangement in a crystal is called crystal structure. The crystal structure is formed
by associating every lattice point with an atom or an assembly of atoms or molecules or ions, which
are identical in composition, arrangement and orientation, called the basis. i.e. an atom, or a group of
atoms or molecules identical in composition is called the basis or the pattern. The basis provides the
number of atoms per lattice point, their types, mutual orientations and distances of separation
between the atoms. If the basis is substituted for the lattice points, then the resulting structure is
called crystal structure as shown in Fig. 1.3. Thus lattice + basis = crystal structure. The basis shown
in Fig. 1.3 contains three different atoms. In copper and sodium crystals the basis is single atoms; in
NaCl, the basis is diatomic and in CaF
2
the basis is triatomic. A lattice is an imaginary assumption
while the crystal structure is a real concept.

1.1.3 Unit Cell and
Lattice Parameters
Unit cells for most of the crystals are parallelopipeds or cubes having three sets of parallel
faces. A unit cell is the basic structural unit or building block of the crystal. A unit cell is defined as
the smallest parallelopiped volume in the crystal, which on repetition along the crystallographic axes
gives the actual crystal structure or the smallest geometric figure, which on repetition in three-
dimensional space, gives the actual crystal structure is called a unit cell. The choice of a unit cell is
not unique but it can be constructed in a number of ways; Fig. 1.4 shows different ways of
representing unit cells in a two-dimensional lattice. A unit cell can be represented as ABCD or
A′B′C′D′ or A″B″C″D″, etc.
To define the unit cell parameters or lattice parameters, first we define crystallographic axes.
These axes are obtained by the intersection of the three non-coplanar faces of the unit cell. The angle
between these faces or crystallographic axes are known as interfacial or interaxial angles. The angles
between the axes Y and Z is α, between Z and X is β and between X and Y is γ. The translational
vectors or primitives a, b, c of a unit cell along X, Y, Z axes and interaxial angles α, β, γ are called
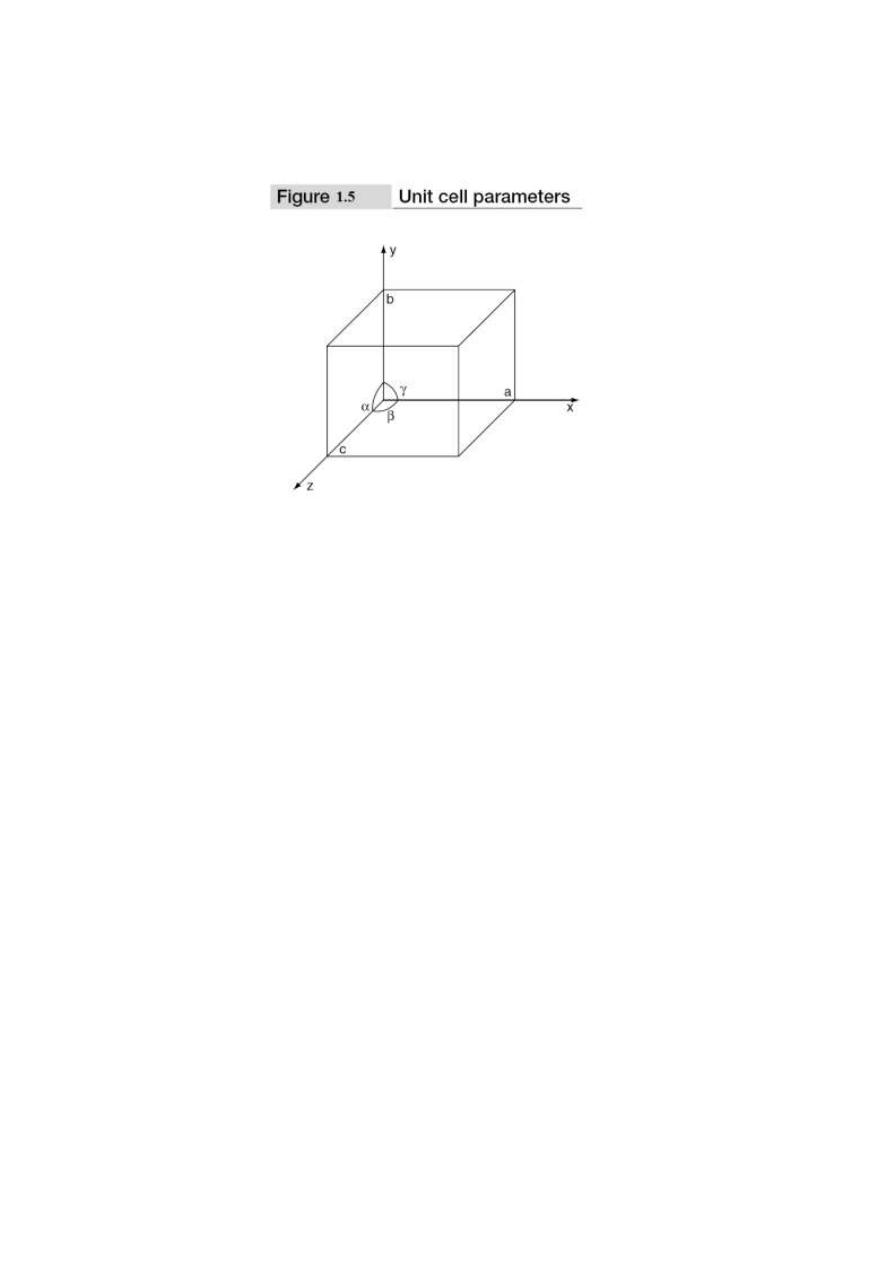
cell parameters. These cell parameters are shown in Fig. 1.5. The cell parameters determine the
actual size and shape of the unit cell.
1.1.4 Primitive and non-primitive unit cells: The unit cell formed by primitives is called a simple
or a primitive unit cell. A primitive unit cell contains only one lattice point. If a unit cell contains
more than one lattice point, then it is called a non-primitive unit cell or a multiple unit cell. Most of
the unit cells of various crystal lattices contain two or more lattice points and hence it is not
necessary that unit cell should be a primitive unit cell. For example, BCC and FCC are non-primitive
unit cells.
1.1.5 Bravais Lattice: If the surroundings of each lattice point is same or if the atom or all the atoms
at lattice points are identical, then such a lattice is called Bravais lattice. Based on the number of
lattice points present per unit cell and stacking sequence of base atoms in a crystal structure, the
Bravais lattices are classified into Simple or Primitive (P), Body Centered (I), Face Centered (F) and
Base Centered (C) lattices. In simple or primitive lattice, 8 lattice points or 8 atoms are present at the
8 corners of the unit cell, each contributing 1/8
th
to the unit cell and hence there will be 8 x 1/8 = 1
lattice point per unit cell. In body-centered lattice, in addition to the 8 atoms at 8 corners each
contributing 1/8
th
to the unit cell, there will be one complete atom at the center of the unit cell.
Therefore number of atoms or lattice points in a body centered unit cell becomes 8 x 1/8 + 1 x 1 = 2.
In case of face-centered lattice, in addition to the 8 atoms at 8 corners each contributing 1/8
th
to the
unit cell, six atoms will be present at the center of six faces of the cell each contributing 1/2
nd
to the
unit cell. Therefore number of atoms or lattice points in a face centered unit cell becomes 8 x 1/8 + 6
x 1/2 = 4. Similarly, in case of base-centered lattice, in addition to the 8 atoms at 8 corners each
contributing 1/8
th
to the unit cell, two atoms will be present at the center of upper and lower faces of

the unit cell each contributing 1/2
nd
to the unit cell and hence the number of atoms or lattice points in
a base centered unit cell becomes 8 x 1/8 + 2 x 1/2 = 2.
1.2 Crystal Systems and Bravais Lattices:
For representing the type of distribution of lattice points in space, seven different co-ordinate
systems are required. These co-ordinate systems are called crystal systems. The crystal systems are
named on the basis of geometrical shape and symmetry. The seven crystal systems are: (1) Cubic (2)
Tetragonal (3) Orthorhombic (4) Monoclinic (5) Triclinic (6) Trigonal (or Rhombohedral) and (7)
Hexagonal. Space lattices are classified according to their symmetry. In 1948, Bravais showed that
14 lattices are sufficient to describe all crystals. These 14 lattices are known as Bravais lattices and
are classified into 7 crystal systems based on cell parameters. The Bravais lattices are categorized as
primitive lattice (P); body-centered lattice (I); face-centered lattice (F) and base-centered lattice (C).
These seven crystal systems and Bravais lattices are described below.
1. Cubic crystal system: In this crystal system, all the unit cell edge lengths are equal and
are at right angles to one another i.e., a = b = c and α = β = γ = 90°. In cubic system, there
are three Bravais lattices; they are simple (primitive); body-centered and face-centered.
Examples for cubic system are Au, Cu, Ag, NaCl, diamond, etc. In simple cubic lattice,
lattice points or atoms are present at the corners of the cube. In body-centered cube,
atoms are present at the corners and one atom is completely present at the center of the
cube. In the case of face-centered cube, atoms are present at corners and at the centers of
all faces of cube.
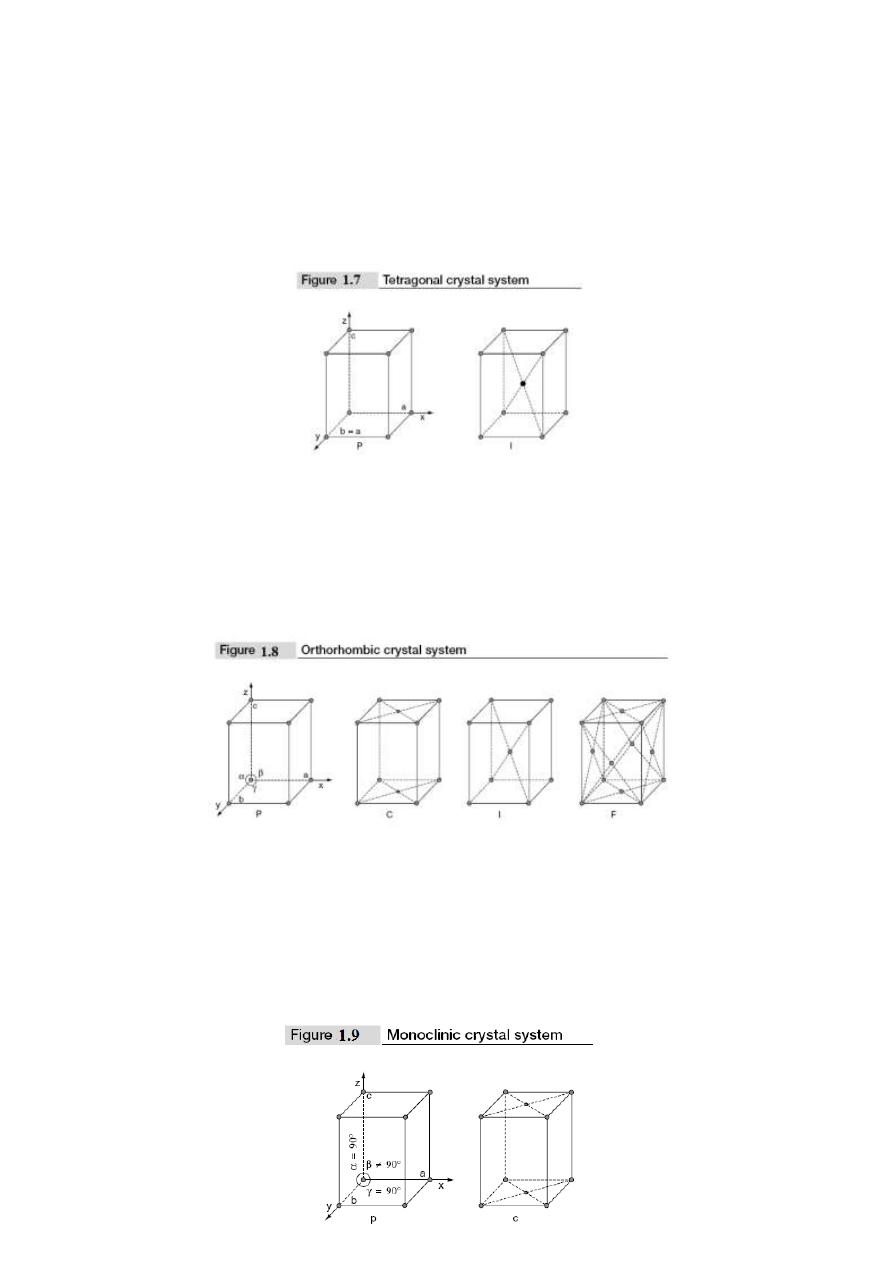
2. Tetragonal crystal system: In this crystal system, two lengths of the unit cell edges are
equal whereas the third length is different. The three edges are perpendicular to one
another i.e., a = b ≠ c and α = β = γ = 90°. In tetragonal system, there are two Bravais
lattices; they are simple and body-centered. These are shown in Fig. 1.7. Examples for
tetragonal crystal systems are TiO
2
, SnO
2
, etc.
3. Orthorhombic crystal system: In this crystal system, unit cell edge lengths are different
and they are perpendicular to one another i.e., a ≠ b ≠ c and α = β = γ = 90°. There are
four Bravais lattices in this system. They are simple, face centered, body centered and
base centered. These are shown in Fig. 1.8. Examples for orthorhombic crystal system are
BaSO
4
, K
2
SO
4
, SnSO
4
, etc.
4. Monoclinic crystal system: In this crystal system, the unit cell edge lengths are different.
Two unit cell edges are not perpendicular, but they are perpendicular to the third edge i.e.,
a ≠ b ≠ c; α = γ = 90° ≠ β. This crystal system has two Bravais lattices; they are simple
and base centered. These are shown in Fig. 1.9. Examples for Monoclinic crystal system
are CaSO
4
.2H
2
O (gypsum), Na
3
AlF
6
(cryolite), etc.

5. Triclinic crystal system: In this crystal system, the unit cell edge lengths are different
and are not perpendicular i.e., a ≠ b ≠ c and α ≠ β ≠ γ ≠ 90° and all the angles are
different. This crystal exists in primitive cell only. This is shown in Fig. 1.10. Examples
for triclinic crystal system are K
2
Cr
2
O
7
, CuSO4. 5H
2
O, etc.
6. Trigonal or Rhombohedral crystal system: In this crystal system, all the lengths of unit
cell edges are equal. The angles between the axes are equal but other than 90° i.e., a = b =
c and α = β = γ ≠ 90°. The Bravais lattice is simple only as shown in Fig. 1.11. Examples
for Rhombohedral crystal system are As, Bi, Sb, etc.
7. Hexagonal crystal system: In this crystal system, two sides of the unit cell edge lengths
are equal and the angle between these edges is 120°. These two edges are perpendicular to
the third edge, and not equal in length i.e., a = b ≠ c and α = β = 90°; γ = 120°. The
Bravais lattice is primitive only. This is shown in Fig. 1.12. The atoms in this crystal
system are arranged in the form of a hexagonal close pack.
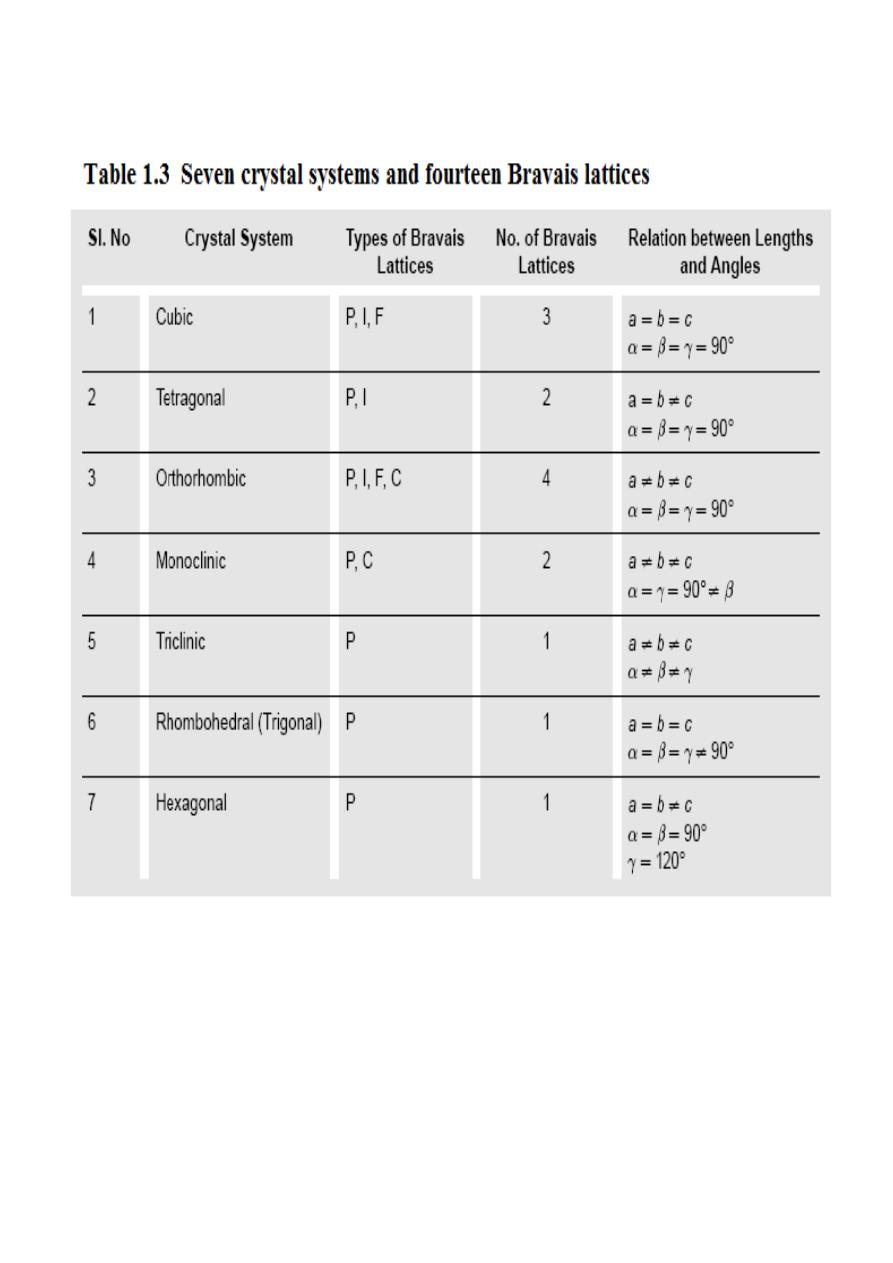
The fourteen Bravais lattices of seven crystal systems are summarized in Table 1.3.
1.3 Crystal structures of cubic lattices:
There are three different types of cubical crystal lattice systems namely Simple Cubic (SC), Body-
Centered Cubic (BCC) and the Face Centered Cubic (FCC).

Atomic packing factor is defined as the fraction of the space occupied by atoms in the unit cell or it
is the ratio of the volume occupied by atoms in the unit cell to the unit cell volume. An example for
simple cubic structure is polonium crystal.


Therefore, based on the above packing fractions information, FCC is the most closely packed
structure among all the three cubic crystal lattices SC, BCC and FCC.
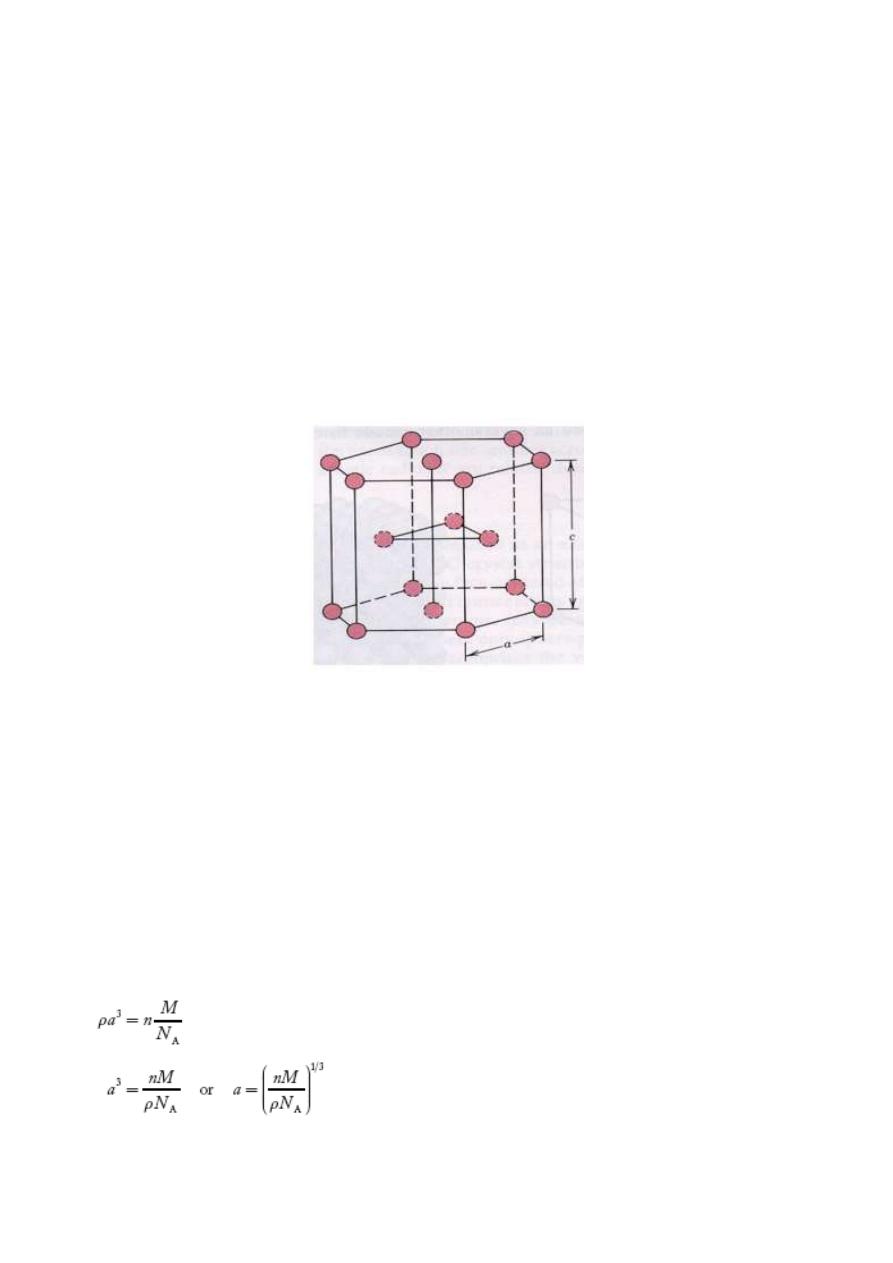
1.3.4 Hexagonal Closed Packed structure ( HCP) :
The top and bottom faces of the unit cell consist of six atoms that form regular hexagons and
surround a single atom in the center. Another plane that provides three additional atoms to the unit
cell is situated between the top and bottom planes. The atoms in this mid-plane have as nearest
neighbors atoms in both of the adjacent two planes. The equivalent of six atoms is contained in each
unit cell; one-sixth of each of the 12 top and bottom face corner atoms, one-half of each of the 2
center face atoms, and all 3 mid-plane interior atoms. If a and c represent, respectively, the short(
basal) and long 9 height) parameters of unit cell dimensions of Fig a, the c_a ratio should be 1.633 .
The coordination number and the atomic packing factor for the HCP crystal structure are the same as
for FCC: 12 and 0.74, respectively
Fig 1.16: Structure of HCP
1.4. Calculation of lattice constant
The unit cell edge length of a cubic system is calculated using the density of the crystal. Let ‘a’ be
the edge length (or primitive) of a cubic unit cell and ‘ρ’ be the density of the crystal.
The mass of the unit cell = ρa
3
___________ (1)
Let ‘M ’ be the molecular weight and N
A
be the Avogadro number (i.e., number of molecules per kg
mole of the substance) of the crystal. Then, mass of each molecule
= M/N
A
If each unit cell contains
n molecules (or lattice points), Then the mass of unit cell
=n M/N
A
___________ (2)
From Equation (1) and (2), we have:
