THE LOGARITHIM FUNCTIONS
LEC : 4
22
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
الدوال المتسامية
Trancendental Functions
. ثيثٞح اىعنسٞحَىا هاٗذىاٗ حٞثيثَىا,حٞسلاا , حَٞرٝساغ٘يىا هاٗذىا لىر ٚيع حيثٍاٗ حٍٞاسرٍ حىاد َٚسذ حٝشثج دسٞى حىاد وم
دالة اللوغاريتيم
الطبيعي
The Natural Logarithim
is the function define as :
1
1
( )
,
0
x
Ln x
dt
x
t
its domain is the set of all positive number.
مشتقة دالة اللوغاريتم الطبيعي
if f(x)=Ln(x) then :
1
( )
d
Ln x
dx
x
1
( )
d
du
Ln u
dx
u dx
and in general form
THEOREM : if a&b are positive number and n is any rational number then :
1
1
0
2
1
,
2.718...
3
.
4
. . ...
...
1
5
6
7
.
8
:
n
Ln
Lne
e
Lna b
Lna
Lnb
Lna b c z
Lna
Lnb
Lnz
a
Ln
Lna
Lnb
Ln
Lna
Lnx
n Lnx
b
a
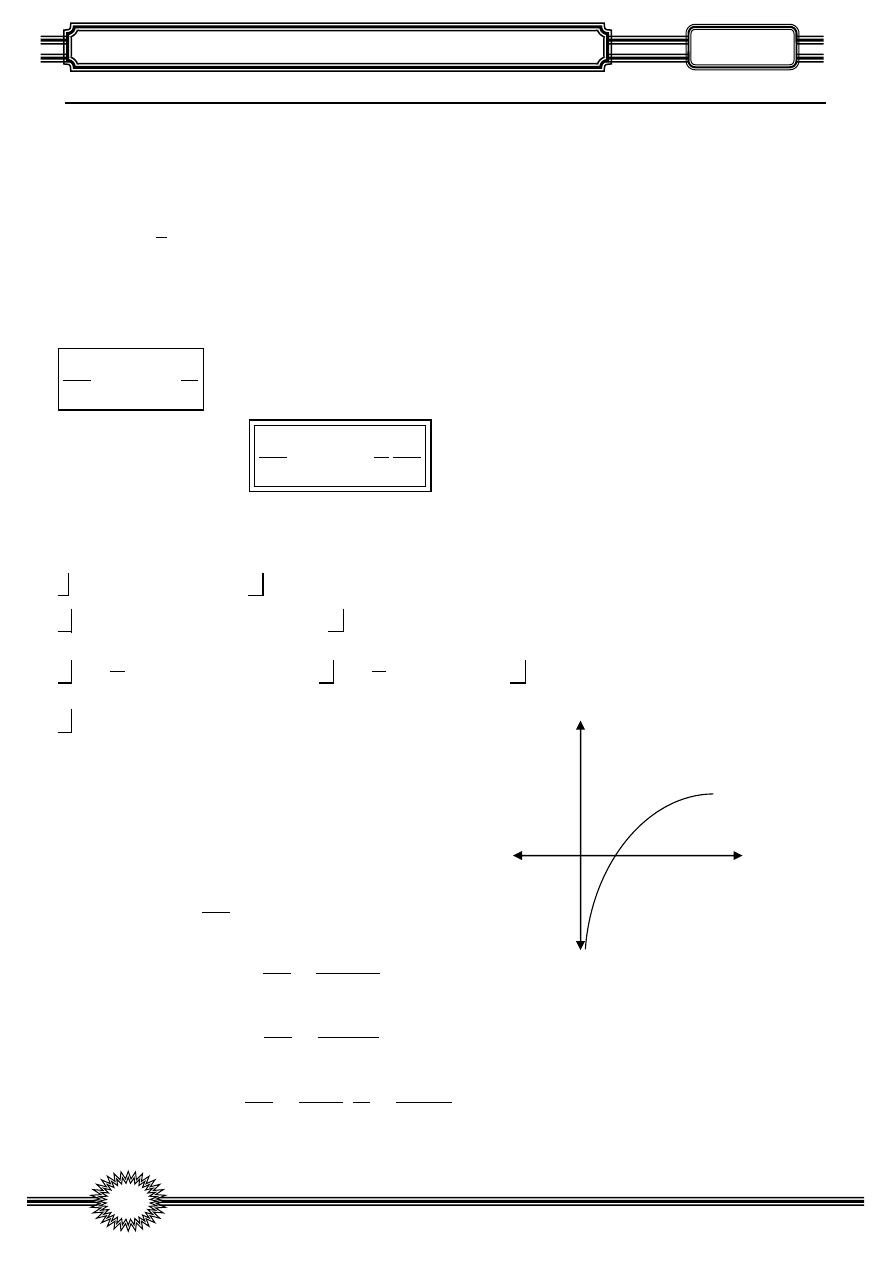
graph of y
Lnx
is
EXAM : Find
dy
dx
to
2
2
2
1)
(2
7)
2
7
2
2)
(
8)
8
1
1
1
3)
(
)
.
dy
y
Ln
x
dx
x
dy
x
y
Ln x
dx
x
dy
y
Ln Lnx
dx
Lnx x
xLnx
y=Ln(x)

THE LOGARITHIM FUNCTIONS
LEC : 4
22
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
تكامالت دوال اللوغارتيم الطبيعي
1
dx
Ln x
C
x
and in general form
1 du
Ln u
C
u dx
EXAM : Find
3
1
2
1
(2
1)
2
1
2 2
1
2
4
1
dx
dx
Ln
x
C
x
x
x
x
dx
x
. وٍانّ ٌث ًلاٗا ٌسقّ ًاقَىا حجسد ٍِ ٚيعا طسثىا حجسد ُ٘نذ اٍذْع
3
3
2
4
1
1
4
4
3
x
x
dx
dx
dx
x
x
x
x
x dx
dx
dx
x
Ln x
C
x
2
2
2
3
2
3
2
3
1
1 (
1)
(
1)
2 (
1)
2
2
2
(
1)
x
x
dx
x x
dx
x x
dx
C
x
االشتقاق اللوغاريتمي
Logarithim Diff.
ٓزٕ ًذخرسذ اٍ جداعٗ حقتاسىا قشطىات جاطعَىا حىاذىا قاقرشا اْرعاطرسا ًذع حىاح ٜف َٜرٝساغ٘يىا قاقرشلاا ًذخرسٝ
اىطشٝق
: ضشٗتح تثعضٖا ٗذح٘ٛ عيٚ حذٗد مثٞشج ٗذريخض اىطشٝقح ماالذَٜىا هاٗذىاٗ حٝشسنىا هاٗذىا ٜف ح
1
ٌ) اخز ى٘غاسٝر
Ln
. ِاىطشفٞ
2
. اخَرٝساغ٘يىا صا٘خ ًاذخرسات حىاذىا طسثّ )
3
ـــسثح ىْىات ًاَْٞض ِٞفشطىا قرشّ )
x
.
4
ــــ تِٞفشطىا بشض )
y
.
5
حَٞق ضٝ٘عذ )
y
ا َٝت
رغٞشَىات اٖىداع
x
.
EXAM : Find
dy
dx
to
1)
1
1
(1) 1
(1
)
(1
)
x
x
x
y
x
Lny
Lnx
xLnx
dy
x
Lnx
Lnx
y dx
x
dy
y
Lnx
x
Lnx
dx
THE LOGARITHIM FUNCTIONS
LEC : 4
22
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
1
2
1
2
1
2
1
2
2
5
4
2
3
2
5
2
5
4
2
3
4
2
3
2
5
4
2
3
2
4
3
2
4
(
3) (2
1)
2)
(
1)
(
3) (2
1)
(
3) (2
1)
(
1)
(
1)
(
3)
(2
1)
(
1)
1
(
3) 5
(2
1)
2
(
1) 3
2
1
1 2
2
4
3
5
2
2
2
1
3
1
x
x
y
x
x
x
x
Lny
Ln
Ln x
x
Ln x
x
x
x
Ln x
Ln
x
Ln x
Lnx
Ln x
Ln
x
Ln x
Lnx
dy
x
x
y dx
x
x
x
x
dy
y
dx
1
2
3
2
4
2
5
3
4
2
3
2
4
10
8
3
2
1
3
1
(
3) (2
1)
10
8
3
2
1
(
1)
3
1
x
x
x
x
x
x
dy
x
x
x
x
dx
x
x
x
x
x
x
2
3
3
2
2
3
3
2
2
3
3
2
2
3
2
2
2
3
2
2
2
3
2
3)
(5
1)(
2)
1
(5
1)(
2)
1
(5
1)
(
2)
1
1
(5
1) 3
(
2)
(
1)
2
1
10
1
3
1 2
3
2
5
1
2
1
10
1
9
5
1
2
1
(5
y
x
x
x
x
Lny
Ln
x
x
x
x
Lny
Ln
x
x
Ln x
Ln x
Lny
Ln
x
x
Ln x
Ln x
dy
x
x
x
y dx
x
x
x
x
dy
x
x
x
y
dx
x
x
x
x
dy
dx
2
2
3
3
2
2
3
2
10
1
9
1)(
2)
1
5
1
2
1
x
x
x
x
x
x
x
x
x
x
x
اللوغاريتم االعتيادي ذو االساس
a
Logarithim with base a
ٕ٘ ٔساسا ٛزىا ٌرٝساغ٘يىا ٕ٘ ٜعٞثطىا ٌرٝساغ٘يىا
e
ٜٕ ٙشخا حغٞصت ةرنٝ ُا ِنَٝٗ
e
Lnx
Log x
ىٞسٔساسا ٛزىا ٌرٝساغ٘يىا ٖ٘ف ٛداٞرعلاا ٌرٝساغ٘يىا اٍا
e
ٔ اىزٛ اساسٌرٝساغ٘يىاٗ ٛششعىا ٌرٝساغ٘يىا وثٍ
a
ح ذشتظ اىي٘غٍَٖ حقلاع كإْٗ
: ٜٕٗ ٜعٞثطىا ٌرٝساغ٘يىات ٛداٞرعلاا ٌرٝسا
,
1
a
Lnx
Log x
a
Lna

THE LOGARITHIM FUNCTIONS
LEC : 4
22
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
: مشتقة دالة اللوغاريتم االعتيادي
1
1
a
a
d
d Lnx
Log x
dx
dx Lna
x Lna
d
Log x
dx
x Lna
and in general form :
a
d
du
Log u
dx
u Lna
EXAM : Find
dy
dx
to
2
y= Log(3
1)
x
(3
1)
3
1)
2
(3
1)
2
3
2)
(3
1)
2
Ln
x
dy
y
Ln
dx
x
Ln
dy
dx
x
Ln
EXAM : Find
dy
dx
to
2
3
y=LnLnx+ Log(
5)
x
2
1
2
(
5)
3
dy
x
dx
xLnx
x
Ln
2
3
2
1
3
2
2
3
2
2
2
3
3
5
2
2
1)
(
1)
(2
) ,
(
) ,
(
1
) ,
3
5 ,
(
1)
2
1
,
(
(
2 ))
,
1
(2
1)
1
2)
.
.(
1) .
1.
3)
2
,
3
,
4 ,
9 ,
6 ,
1.5 ,
8
2
4)
x
x
dy
Find
to
y
dx
Ln x
Ln
x
Ln
Ln
x
x
x Ln
x
Ln x
Log x
x
x Log x
x
Log x
Ln
x
dy
Find
to y
Sinx Lnx x
x
dx
x
if Ln
a
Ln
b
find Ln
Ln
Ln
Ln
Ln
x
x
Find
3
2
4
8
18
,
(2
1)(
5)
3
12
10
x
dx
dx
x
x
x
x
x
MOHAMED SABAH AL TAEE
M.SC / MATHEMATICS
E-MAIL : msmt_80@yahoo.com
2013 -2014
