
Chapter Three
Equilibrium of a Particle
Asst.Lecturer:
M
ohanad
N
ihad

M
ohanad N Noaman
E
lectronic
E
ngineering
C
ollege
N
inevah University
2
Condition for the Equilibrium of a Particle

M
ohanad N Noaman
E
lectronic
E
ngineering
C
ollege
N
inevah University
3

M
ohanad N Noaman
E
lectronic
E
ngineering
C
ollege
N
inevah University
4
2.
Cables and Pulleys
All cables (or cords) will be assumed to have negligible weight
and they cannot stretch.
A cable can support only a tension or “pulling” force, and this
force always acts in the direction of the cable.
The tension force developed in a continuous cable which
passes over a
frictionless pulley
.
Hence,
for any angle Ɵ, shown in Fig, the cable is subjected to a
constant tension
T
throughout its length.

M
ohanad N Noaman
E
lectronic
E
ngineering
C
ollege
N
inevah University
5
Procedure for Drawing a Free-Body Diagram
Draw Outlined Shape.
Imagine the particle to be
isolated
or cut “free” from its
surroundings by drawing its outlined shape.
Show All Forces.
Indicate on this sketch
all
the forces that act
on the
particle
.
Active forces: which tend to set the particle in motion.
Reactive forces: which are the result of the constraints or
supports that tend to prevent motion.
Identify Each Force.
The forces that are
known
should be labelled with their
proper magnitudes and directions. Letters are used to
represent the magnitudes and directions of forces that
are unknown.
M
ohanad N Noaman
E
lectronic
E
ngineering
C
ollege
N
inevah University
6
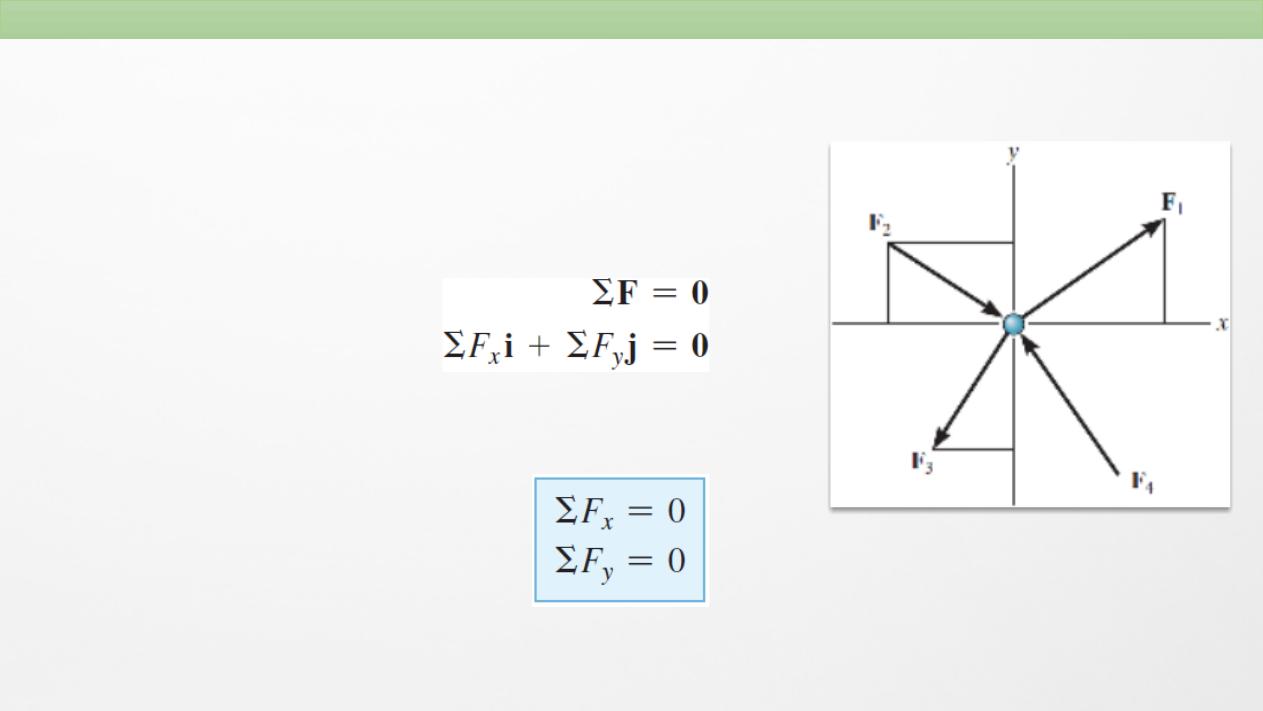
Coplanar Force Systems
If a particle is subjected to a system of coplanar forces that
lie in the
x–y
plane, as in Fig, then each force can be
resolved into its
i
and
j
components. For equilibrium, these
forces must sum to produce a zero force resultant, i.e.,
For this vector equation to be satisfied, the resultant force’s
x
and y components must both be equal to zero. Hence,

M
ohanad N Noaman
E
lectronic
E
ngineering
C
ollege
N
inevah University
7
Notes
These two equations can be solved for at most two unknowns, generally represented as
angles and magnitudes of forces.
we must account for the sense of direction of any component by using an algebraic sign
which corresponds to the arrowhead direction of the component along the x or y axis. if
the solution yields a positive scalar , this indicates that the sense of the force is in
direction of what we assumed. if the solution yields a negative scalar , this indicates that
the sense of the force is opposite to that which was assumed.
It is important to note that if a force has an
unknown magnitude
, then the arrowhead
sense of the force on the free-body diagram can be
assumed
. If the final result indicate
what we assumed, the assumption is correct otherwise the assumption was in correct
and the right result is opposite direction.
