
1
Chapter three
Derivatives
Let y = f ( x ) be a function of x . If the limit :
x
y
lim
x
)
x
(
f
)
x
x
(
f
lim
)
x
(
'
f
dx
dy
o
x
0
x
exists and is finite , we call this limit the derivative of f at x and say
that f is differentiable at x .
EX-1 – Find the derivative of the function :
3
x
2
1
)
x
(
f
Sol.:
3
0
x
0
x
0
x
0
x
)
3
x
2
(
1
)
3
x
2
3
x
2
)(
3
x
2
(
2
)
3
)
x
x
(
2
3
x
2
(
3
x
2
3
)
x
x
(
2
.
x
)
3
)
x
x
(
2
(
)
3
x
2
(
lim
3
)
x
x
(
2
3
x
2
3
)
x
x
(
2
3
x
2
.
3
x
2
3
)
x
x
(
2
.
x
3
)
x
x
(
2
3
x
2
lim
x
3
x
2
1
3
)
x
x
(
2
1
lim
x
)
x
(
f
)
x
x
(
f
lim
)
x
(
'
f
Rules of derivatives :
Let c and n are constants, u , v and w are
differentiable functions of x :
1.
0
c
dx
d
2.
dx
du
u
1
u
1
dx
d
dx
du
nu
u
dx
d
2
1
n
n
3.
dx
du
c
cu
dx
d
4.
dx
dv
dx
du
)
v
u
(
dx
d
;
dx
dw
dx
dv
dx
du
)
w
v
u
(
dx
d
5.
dx
du
v
dx
dv
.
u
)
v
.
u
(
dx
d

2
and
dx
du
w
.
v
dx
dv
w
.
u
dx
dw
v
.
u
)
w
.
v
.
u
(
dx
d
6.
0
v
where
v
dx
dv
u
dx
du
v
v
u
dx
d
2
EX-2- Find
dx
dy
for the following functions :
2
x
x
1
x
y
)
f
x
)
1
x
x
)(
x
x
(
y
)
e
x
3
x
4
x
12
y
)
d
)
x
6
x
3
x
2
(
y
)
c
)
x
2
4
)(
x
5
(
y
)
b
)
1
x
(
y
)
a
2
2
3
2
2
4
3
5
2
3
2
5
2
Sol.-
)
7
x
2
)(
x
2
)(
x
5
(
8
)
x
2
4
(
)
x
5
(
2
)
x
2
4
)(
x
5
(
2
dx
dy
)
b
)
1
x
(
x
10
x
2
.
)
1
x
(
5
dx
dy
)
a
4
2
4
2
5
4
2
5
4
2
4
3
1
2
6
2
3
2
6
2
3
x
12
x
12
x
12
dx
dy
x
12
x
12
x
12
dx
dy
x
3
x
4
x
12
y
)
d
)
1
x
x
(
)
x
6
x
3
x
2
(
30
)
6
x
6
x
6
(
)
x
6
x
3
x
2
(
5
dx
dy
)
c
4
6
2
2
2
3
3
2
x
3
x
)
1
x
x
)(
1
x
(
x
3
)
1
x
2
)(
1
x
(
)
1
x
x
(
x
dx
dy
x
)
1
x
x
)(
1
x
(
y
)
e
2
2
2
2
2
2
2
)
2
x
x
(
1
x
2
x
)
2
x
x
(
)
1
x
2
)(
1
x
(
)
2
x
x
(
x
2
dx
dy
)
f

3
The Chain Rule:
1. Suppose that h = g
o
f is the composite of the differentiable
functions y = g( t ) and x = f( t ) , then h is a differentiable
functions of x whose derivative at each value of x is :
2. If y is a differentiable function of t and t is differentiable
function of x , then y is a differentiable function of x :
EX-3 – Use the chain rule to express dy / dx in terms of x and y :
2
x
at
x
1
1
t
and
t
1
1
y
)
d
2
t
at
1
t
1
x
and
1
t
1
t
y
)
c
1
t
4
x
and
1
t
1
y
)
b
1
x
2
t
and
1
t
t
y
)
a
2
2
2
2
2
Sol.-
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
2
)
1
x
(
2
1
1
x
2
1
.
)
1
)
1
x
2
((
1
x
2
2
1
x
2
1
.
)
1
t
(
t
2
dx
dt
.
dt
dy
dx
dy
1
x
2
1
2
.
)
1
x
2
.(
2
1
dx
dt
)
1
x
2
(
t
)
1
t
(
t
2
)
1
t
(
t.
t
2
)
1
t
(
t
2
dt
dy
1
t
t
y
)
a
dt
dx
dt
dy
dx
dy
dx
dt
*
dt
dy
dx
dy
)
x
(
f
t
and
)
t
(
g
y

4
y
1
1
t
1
t
1
y
where
4
1
x
t
1
t
4
x
where
4
)
1
x
(
xy
y
1
x
.
4
1
x
)
1
t
(
1
t
4
t
1
t
4
2
)
1
t
(
t
2
dt
dx
dt
dy
dx
dy
1
t
4
2
4
.
)
1
t
4
(
2
1
dt
dx
)
1
t
4
(
x
)
1
t
(
t
2
)
1
t
(
t
2
dx
dy
)
1
t
(
y
)
b
2
2
2
2
2
2
2
2
2
2
2
2
1
2
1
2
2
2
2
1
2
27
16
4
1
27
4
dt
dx
dt
dy
dx
dy
4
1
2
2
dt
dx
t
2
dt
dx
1
t
1
x
27
4
)
1
2
(
)
1
2
(
4
dt
dy
)
1
t
(
)
1
t
(
4
)
1
t
(
)
1
t
(
1
t
1
t
1
t
2
dt
dy
1
t
1
t
y
)
c
2
t
2
t
3
2
t
3
2
3
2
t
3
2
2
1
1
*
1
dx
dt
.
dt
dy
dx
dy
1
)
2
1
(
1
dx
dt
)
x
1
(
1
)
1
(
)
x
1
(
dx
dt
)
x
1
(
t
1
)
1
(
1
dt
dy
t
1
dt
dy
t
1
1
y
2
x
at
1
2
1
1
x
1
1
t
)
d
2
x
2
x
2
x
2
2
x
2
2
1
2
1
t
2
Higher derivatives : If a function y = f( x ) possesses a derivative at every
point of some interval , we may form the function f '(x) and talk
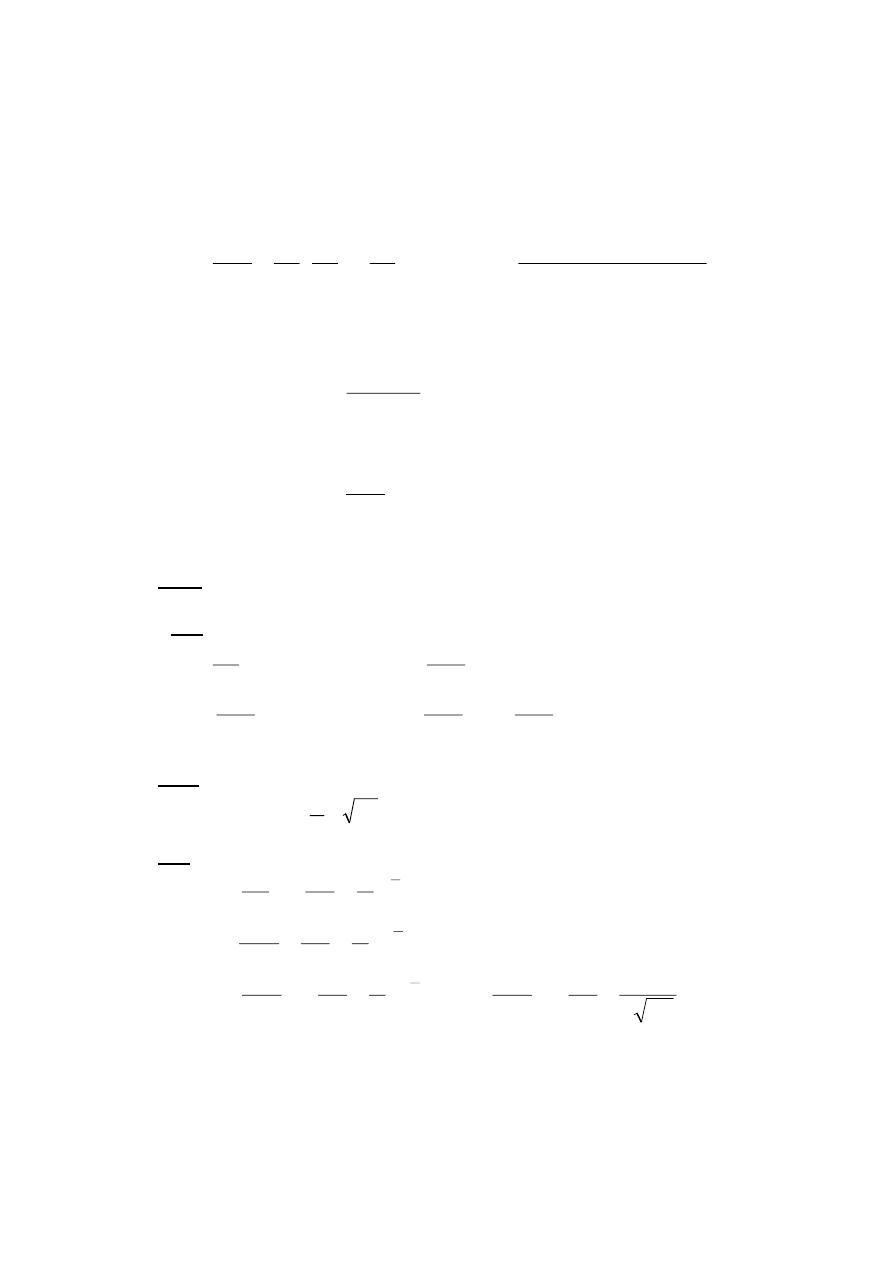
5
about its derivate , if it has one . The procedure is formally identical
with that used before , that is :
x
)
x
(
f
)
x
x
(
f
lim
)
x
(
f
dx
d
dx
dy
dx
d
dx
y
d
0
x
2
2
if the limit exists .
This derivative is called the second derivative of y with respect to x .
It is written in a number of ways , for example,
y'' , f ''(x) , or
2
2
dx
)
x
(
f
d
.
In the same manner we may define third and higher derivatives ,
using similar notations . The nth derivative may be written :
n
n
)
n
(
)
n
(
dx
y
d
,
)
x
(
f
,
y
.
EX-4- Find all derivatives of the following function :
y = 3x
3
- 4x
2
+ 7x + 10
Sol.-
....
dx
y
d
0
dx
y
d
,
18
dx
y
d
8
x
18
dx
y
d
,
7
x
8
x
9
dx
dy
5
5
4
4
3
3
2
2
2
Ex-5 – Find the third derivative of the following function :
3
x
x
1
y
Sol.-
3
4
3
3
2
3
4
3
3
2
1
3
2
2
2
1
2
x
8
3
x
6
dx
y
d
x
8
3
x
6
dx
y
d
x
4
3
x
2
dx
y
d
x
2
3
x
1
dx
dy

6
Implicit Differentiation: If the formula for f is an algebraic combination
of powers of x and y . To calculate the derivatives of these implicitly
defined functions , we simply differentiate both sides of the defining
equation with respect to x .
EX-6- Find
dx
dy
for the following functions:
P(3,2)
at
2
5y
-
2x
xy
d)
P(3,1)
at
2
y
2
x
y
x
)
c
y
x
)
y
x
(
y)
(x
)
b
y
x
y
.
x
)
a
4
4
3
3
2
2
2
2
Sol.
3
2
2
3
3
2
2
2
2
3
3
3
2
2
2
2
2
2
y
2
xy
6
y
3
x
3
x
2
dx
dy
y
4
)
y
x
(
3
)
y
x
(
3
)
y
x
(
3
)
y
x
(
3
x
4
dx
dy
dx
dy
y
4
x
4
)
dx
dy
1
(
)
y
x
(
3
)
dx
dy
1
(
y)
3(x
)
b
y
y
x
xy
x
dx
dy
dx
dy
y
2
x
2
)
x
2
(
y
)
dx
dy
y
2
(
x
)
a
2
3
5
2
2
dx
dy
x
5
2
y
dx
dy
0
dx
dy
5
2
y
dx
dy
x
)
d
3
1
dx
dy
x
y
dx
dy
0
)
y
2
x
(
)
dx
dy
2
1
)(
y
x
(
)
dx
dy
-
2y)(1
-
(x
)
c
)
2
,
3
(
)
1
,
3
(
2
Exponential functions : If u is any differentiable function of x , then :
dx
du
.
e
e
dx
d
and
dx
du
.
a
.ln
a
a
dx
d
)
7
u
u
u
u

7
EX-7 –Find
dx
dy
for the following functions :
2
2
5x
1
x
2
x
x
x
3x
e
y
)
f
e
y
e)
x.2
y
)
d
)
2
(
y
c)
.3
2
y
b)
2
y
)
a
)
e
(x
5x
Sol.-
2
x
5
1
2
1
2
)
5x
(1
)
5x
(1
x
5
)
e
(x
)
e
(x
2
x
x
x
x
1
x
2
x
2
x
2
2
x
x
x
x
x
x
3
3x
x
5
1
x
5
e
x
10
.
)
x
5
1
(
2
1
e
dx
dy
e
y
)
f
)
e
5
1
(
e
dx
dy
e
y
)
e
1)
ln2
(2x
2
2
ln2.2x
x.2
dx
dy
x.2
y
)
d
2
ln
2
2
.
2
ln
2
dx
dy
2
y
)
(2
y
)
c
6
ln
.
6
dx
dy
6
y
3
.
2
y
)
b
2
ln
3
*
2
dx
dy
2
y
)
a
2
2
1
2
2
1
2
5x
5x
2
2
2
2
Logarithm functions : If u is any differentiable function of x , then :
dx
du
.
u
1
u
ln
dx
d
and
dx
du
.
a
.ln
u
1
u
log
dx
d
)
8
a
EX-8 – Find
dx
dy
for the following functions :
2
3
2
5
2
3
2
3
3
2
2
3
2
2
2
5
x
10
)
3
x
4
x
7
(
)
3
x
2
.(
)
4
(2x
y
f)
1
ln(xy)
y
)
e
)
2
ln(x
y
)
d
)
1
x
3
(
log
y
)
c
)
1
x
(
log
y
)
b
e
log
y
)
a
Sol. –

8
2
x
)
2
x
ln(
x
48
x
2
.
2
x
2
)
2
x
ln(
2
3
dx
dy
d)
2
ln
)
1
x
3
(
x
18
2
ln
x
6
.
1
x
3
3
dx
dy
)
1
x
3
(
log
3
y
)
c
5
ln
)
1
x
(
2
dx
dy
)
1
x
(
log
2
)
1
x
(
log
y
)
b
10
ln
1
10
ln
e
ln
e
log
dx
dy
e
log
x
y
e
log
y
)
a
2
2
2
2
2
2
2
2
2
2
5
2
5
10
10
x
10
3
x
4
x
7
4
x
21
3
x
2
x
5
4
x
2
x
2
y
2
dx
dy
3
x
4
x
7
4
x
21
.
2
3
x
2
x
4
.
2
5
4
x
2
x
6
.
3
2
dx
dy
.
y
1
)
3
x
4
x
7
ln(
2
)
3
x
2
ln(
2
5
)
4
x
2
ln(
3
2
lny
)
f
)
1
y
(
x
y
dx
dy
0
dx
dy
.
y
1
x
1
dx
dy
1
lny
lnx
y
)
e
3
2
2
3
2
3
2
2
3
2
3
2
3
Trigonometric functions : If u is any differentiable function of x , then :
dx
du
scu.cotu.
c
cscu
dx
d
)
14
dx
du
secu.tanu.
secu
dx
d
)
13
dx
du
u.
sc
c
cotu
dx
d
)
12
dx
du
u.
sec
tanu
dx
d
)
11
dx
du
u.
sin
cosu
dx
d
)
10
dx
du
cosu.
inu
s
dx
d
)
9
2
2
EX-9- Find
dx
dy
for the following functions :

9
x
tan
x
sec
y
f)
0
tan(xy)
x
)
e
)
x
(cos
tan
y
)
d
2
x
xCos
2
x
2sin
y
c)
cotx)
(cscx
y
b)
)
tan(3x
y
)
a
4
4
2
2
2
Sol.-
2
x
sin
.
2
x
2
x
cos
2
1
).
2
x
sin
(
x
2
1
.
2
x
cos
2
dx
dy
)
c
)
x
cot
x
.(csc
x
csc
2
)
x
csc
x
cot
.
x
csc
)(
x
cot
x
(csc
2
dx
dy
)
b
)
x
3
(
sec
.
x
6
x
6
).
x
3
(
sec
dx
dy
)
a
2
2
2
2
2
2
x
sec
.
x
tan
4
x
sec
.
x
tan
.
4
x
tan
.
x
sec
.
x
sec
4
dx
dy
)
f
x
y
)
xy
(
cos
)
xy
(
sec
.
x
)
xy
(
sec
.
y
1
dx
dy
0
)
y
dx
dy
x
).(
xy
(
sec
1
)
e
)
x
(cos
sec
).
x
tan(cos
.
x
sin
.
2
)
x
sin
).(
x
(cos
sec
).
x
tan(cos
.
2
dx
dy
)
d
2
2
3
3
2
2
2
2
2
2
EX-10- Prove that :
dx
du
.
u
tan
.
u
sec
u
sec
dx
d
)
b
dx
du
.
u
sec
u
tan
dx
d
)
a
2
Proof :
.
S
.
H
.
R
dx
du
.
u
tan
.
u
sec
dx
du
.
u
cos
u
sin
.
u
cos
1
dx
du
)
u
sin
(
u
cos
1
u
cos
1
dx
d
u
sec
dx
d
.
S
.
H
.
L
)
b
.
S
.
H
.
R
dx
du
.
u
sec
dx
du
.
u
cos
1
dx
du
.
u
cos
u
sin
u
cos
u
cos
dx
du
)
u
sin
.(
u
sin
dx
du
.
u
cos
.
u
cos
u
cos
u
sin
dx
d
u
tan
dx
d
.
S
.
H
.
L
)
a
2
2
2
2
2
2
2
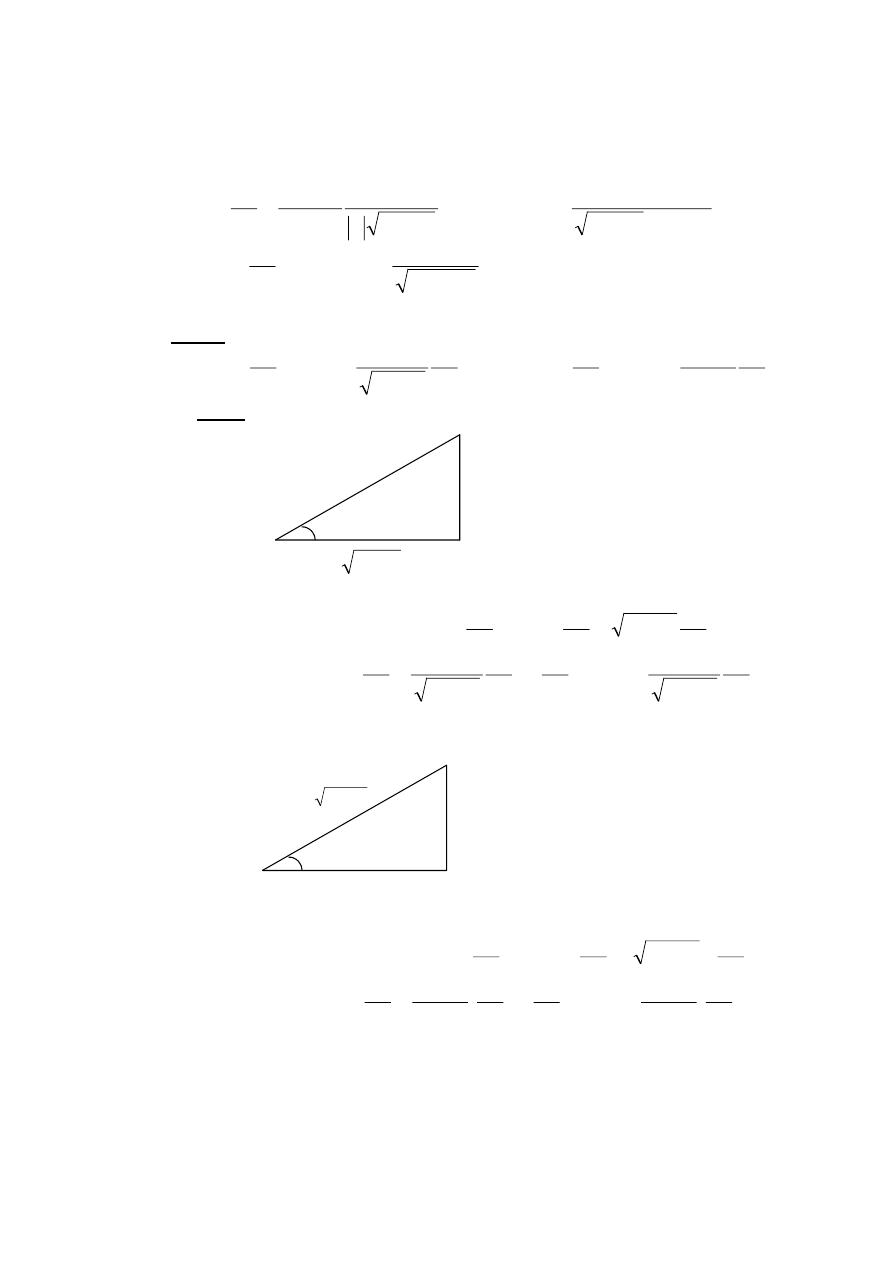
The inverse trigonometric functions : If u is any differentiable function

10
of x , then :
EX-11- Find
dx
dy
in each of the following functions :
Sol. –
x
)
1
x
(
1
)
1
x
(
1
).
1
x
(
1
).
1
x
(
.
1
x
1
x
1
1
dx
dy
)
b
x
4
4
2
1
.
2
x
1
1
x
1
.
2
x
2
1
1
dx
dy
)
a
2
2
2
2
2
2
1
x
25
x
1
1
x
25
x
5
5
dx
dy
)
d
x
2
cos
x
4
1
x
8
.
4
1
x
2
cos
x
4
1
2
x
dx
dy
)
c
2
2
1
2
1
2
1
u
dx
du
1
u
u
1
u
csc
dx
d
)
20
1
u
dx
du
1
u
u
1
u
sec
dx
d
)
19
dx
du
u
1
1
u
cot
dx
d
)
18
dx
du
u
1
1
u
tan
dx
d
)
17
1
u
1
dx
du
u
1
1
u
cos
dx
d
)
16
1
u
1
dx
du
u
1
1
u
sin
dx
d
)
15
2
1
2
1
2
1
2
1
2
1
2
1
3
y
)
f
)
x
x.ln(sec
y
)
e
x
5
sec
y
)
d
x
4
1
2
1
x
2
x.cos
y
)
c
1
x
1
x
in
s
y
)
b
2
x
tan
x
2
cot
y
)
a
x
2
sin
1
-
1
-
2
1
-
1
-
1
1
-
1
-
11
x
4
1
2
.
3
ln
.
3
dx
dy
)
f
)
x
ln(sec
x
sec
.
1
x
1
)
x
ln(sec
1
x
x
1
x
sec
x
dx
dy
)
e
2
x
2
sin
1
1
2
1
2
1
1
EX-12- Prove that :
dx
du
u
1
1
u
tan
dx
d
)
b
dx
du
u
1
1
u
sin
dx
d
)
a
2
1
2
1
Proof : a)
dx
du
u
1
1
u
sin
dx
d
dx
du
u
1
1
dx
dy
dx
dy
u
1
dx
dy
.
y
cos
dx
du
y
sin
u
u
sin
y
Let
2
1
2
2
1
-
b)
dx
du
.
u
1
1
u
tan
dx
d
dx
du
.
u
1
1
dx
dy
dx
dy
u
1
dx
du
.
y
sec
dx
du
tany
u
u
tan
y
Let
2
1
2
2
2
2
1
-
y
u
1
2
u
1
y
u
2
u
-
1
1

12
Hyperbolic functions : If u is any differentiable function of x , then :
dx
du
.
u
coth
.
u
h
csc
hu
csc
dx
d
)
26
dx
du
.
u
tanh
.
u
h
sec
hu
sec
dx
d
)
25
dx
du
.
u
h
csc
u
coth
dx
d
)
24
dx
du
.
u
h
sec
u
tanh
dx
d
)
23
dx
du
.
u
sinh
u
cosh
dx
d
)
22
dx
du
.
u
cosh
u
sinh
dx
d
)
21
2
2
EX-13 - Find
dx
dy
for the following functions :
x
csch
y
)
f
x
sech
y
)
e
x
2
cosh
.
2
1
-
x.sinh2x
y
)
d
2
x
tanh
ln
y
)
c
)
x
(tanh
sin
y
)
b
coth(tanx)
y
)
a
2
3
-1
Sol. -
x
h
csc
x
sinh
1
2
x
cosh
.
2
x
sinh
2
1
2
x
cosh
2
x
sinh
.
2
2
x
cosh
1
2
1
.
2
x
h
sec
2
x
tanh
1
dx
dy
)
c
x
h
sec
x
h
sec
x
h
sec
x
tanh
1
x
h
sec
dx
dy
)
b
x
sec
).
x
(tan
h
csc
dx
dy
)
a
2
2
2
2
2
2
2
2

13
x
coth
.
x
h
csc
2
)
x
coth
.
x
h
csc
(
x
h
csc
2
dx
dy
)
f
x
tanh
.
x
h
sec
3
)
x
tanh
.
x
h
sec
(
x
h
sec
3
dx
dy
)
e
x
2
cosh
x
2
2
.
x
2
sinh
2
1
x
2
sinh
2
.
x
2
cosh
x
dx
dy
)
d
2
3
2
EX-14- Show that the functions :
3
t
cosh
3
t
sinh
3
1
y
and
3
t
sinh
3
2
x
Taken together , satisfy the differential equations :
0
y
dt
dy
dt
dx
)
ii
and
0
x
dt
dy
2
dt
dx
)
i
Proof -
3
t
sinh
3
1
3
t
cosh
3
1
dt
dy
3
t
cosh
3
t
sinh
3
1
y
3
t
cosh
3
2
dt
dx
3
t
sinh
3
2
x
0
3
t
cosh
3
t
sinh
3
1
3
t
sinh
3
1
3
t
cosh
3
1
3
t
cosh
3
2
y
dt
dy
dt
dx
)
ii
0
3
t
sinh
3
2
3
t
sinh
3
2
3
t
cosh
3
2
3
t
cosh
3
2
x
dt
dy
2
dt
dx
)
i
EX-15 - Prove that :
dx
du
.
u
tanh
.
u
h
sec
u
h
sec
dx
d
)
b
and
dx
du
.
u
h
sec
u
tanh
dx
d
)
a
2
Proof-
dx
du
.
u
tanh
.
u
h
sec
dx
du
.
u
sinh
.
u
cosh
1
u
cosh
1
dx
d
)
b
dx
du
.
u
h
sec
dx
du
.
u
cosh
1
u
cosh
dx
du
)
u
sinh
u
(cosh
u
cosh
dx
du
.
u
sinh
.
u
sinh
dx
du
.
u
cosh
.
u
cosh
u
cosh
u
sinh
dx
d
u
tanh
dx
d
)
a
2
2
2
2
2
2
2

14
The inverse hyperbolic functions : If u is any differentiable function of x ,
then :
EX-16 - Find
dx
dy
for the following functions :
)
x
2
(sin
sech
y
)
d
)
x
(sec
coth
y
)
c
)
x
(cos
tanh
y
)
b
)
x
(sec
cosh
y
)
a
1
-
1
-
-1
-1
Sol.-
0
x
tan
where
x
sec
x
tan
x
tan
.
x
sec
1
x
sec
x
tan
.
x
sec
dx
dy
)
a
2
2
x
csc
x
sin
x
sin
x
cos
1
x
sin
dx
dy
)
b
2
2
x
csc
x
tan
x
tan
.
x
sec
x
sec
1
x
tan
.
x
sec
dx
dy
)
c
2
2
0
x
2
cos
where
x
2
csc
2
x
2
sin
1
.
x
2
sin
x
2
cos
.
2
dx
dy
)
d
2
EX-17 – Verify the following formulas :
1
u
dx
du
.
u
1
1
u
tanh
dx
d
)
b
dx
du
.
1
u
1
u
cosh
dx
d
)
a
2
1
2
1
dx
du
u
1
u
1
u
h
csc
dx
d
)
32
dx
du
u
1
u
1
u
h
sec
dx
d
)
31
1
u
dx
du
u
1
1
u
coth
dx
d
)
30
1
u
dx
du
u
1
1
u
tanh
dx
d
)
29
dx
du
1
u
1
u
cosh
dx
d
)
28
dx
du
u
1
1
u
sinh
dx
d
)
27
2
1
2
1
2
1
2
1
2
1
2
1

15
Proof
dx
du
.
1
u
1
u
cosh
dx
d
dx
du
.
1
u
1
dx
dy
1
u
y
sinh
1
y
sinh
u
1
y
sinh
y
cosh
dx
du
.
y
sinh
1
dx
dy
dx
dy
.
y
sinh
dx
du
y
cosh
u
u
cosh
y
Let
)
a
2
1
2
2
2
2
2
2
-1
dx
du
.
u
1
1
u
tanh
dx
d
dx
du
.
u
1
1
dx
dy
u
1
y
h
sec
1
u
y
h
sec
1
y
tanh
y
h
sec
dx
du
.
y
h
sec
1
dx
dy
dx
dy
.
y
h
sec
dx
du
y
tanh
u
u
tanh
y
Let
)
b
2
1
2
2
2
2
2
2
2
2
2
1
The derivatives of functions like u
v
: Where u and v are differentiable
functions of x , are found by logarithmic differentiation :
dx
dv
.
u
ln
dx
du
.
u
v
y
dx
dy
dx
dv
.
u
ln
dx
du
.
u
v
dx
dy
.
y
1
u
ln
.
v
y
ln
u
y
Let
v
dx
dv
.
u
ln
dx
du
.
u
v
.
u
u
dx
d
)
33
v
v
EX-18- Find
dx
dy
for :
tanx
cosx
x)
(lnx
y
b)
x
y
)
a
Sol. -
x
ln
.
x
sin
x
x
cos
y
dx
dy
osx
c
v
and
x
u
where
,
formula
by
or
x
ln
.
x
sin
x
x
cos
y
dx
dy
)
x
sin
.(
x
ln
x
x
cos
dx
dy
.
y
1
x
ln
.
x
cos
y
ln
x
y
)
a
x
cos

16
x
sec
).
x
x
ln(ln
)
x
x
(ln
x
x
tan
).
1
x
(
.
y
x
sec
).
x
x
ln(ln
)
1
x
1
(
x
x
ln
x
tan
.
y
dx
dy
tanx
v
and
x
lnx
u
where
,
formula
by
or
x
sec
).
x
x
ln(ln
)
x
x
(ln
x
x
tan
).
1
x
(
y
dx
dy
x
sec
).
x
x
ln(ln
)
1
x
1
.(
x
x
ln
x
tan
dx
dy
.
y
1
)
x
x
ln(ln
.
x
tan
y
ln
)
x
x
(ln
y
)
b
2
2
2
2
x
tan

17
Problems -3
1. Find
dx
dy
for the following functions :
)
x
)
1
x
(
3
:
.
ans
(
x
1
x
y
)
5
)
x
10
x
1
x
9
:
.
ans
(
x
5
x
2
x
3
y
)
4
)
)
3
x
2
(
1
:
.
ans
(
3
x
2
4
x
3
y
)
3
)
x
b
:
.
ans
(
x
b
ax
y
)
2
)
x
2
4
:
.
ans
(
)
x
1
)(
3
x
(
y
)
1
4
6
2
3
3
3
2
2
3
2
2
)
)
4
x
5
(
Cos
)
4
x
5
(
Sin
.
x
30
:
.
ans
(
)
2
x
5
(
Cos
y
)
10
)
Cosx
.
x
3
:
.
ans
(
Sinx
y
)
9
)
x
tan
:
.
ans
(
)
Cosx
ln(
y
)
8
)
x
ln
.
x
1
:
.
ans
(
)
x
ln(ln
y
)
7
)
2
x
(
1
)
2
x
3
(
)
1
x
2
(
y
)
6
2
4
2
2
3
3
2
3
2
2
3
2
)
3
)
2
x
(
2
)
1
x
30
(
)
2
x
3
)(
1
x
2
(
:
.
ans
(
)
7
x
2
tan
7
x
2
2
7
x
2
Sec
:
.
ans
(
7
x
2
tan
y
)
15
)
x
Cosx
Sinx
.
x
:
.
ans
(
x
Cosx
y
)
14
)
1
x
1
x
Csc
.
1
x
1
x
Cot
.
)
1
x
(
6
:
.
ans
(
1
x
1
x
Cot
y
)
13
)
x
tan
.
Secx
).
Secx
(
Sec
:
.
ans
(
)
Secx
tan(
y
)
12
)
Secx
.
x
tan
Sinx
:
.
ans
(
x
sin
.
x
tan
y
)
11
2
2
2
2
2
3
2
)
)
x
(ln
Cos
.
2
:
.
ans
(
)
x
(ln
Cos
)
x
(ln
Sin
x
y
)
18
)
x
5
Csc
x
5
Cot
.
x
5
3
5
:
.
ans
(
x
5
Csc
y
)
17
)
Sinx
.
x
2
Cosx
.
x
:
.
ans
(
Sinx
.
x
y
)
16
3
2
3
2
2
2

18
)
x
25
1
x
10
:
.
ans
(
)
x
5
(
Sin
y
)
19
4
2
1
)
x
1
1
:
.
ans
(
x
1
x
1
Cot
y
)
20
2
1
)
3
x
2
2
1
x
x
2
2
x
1
1
x
1
x
1
3
y
:
.
ans
(
)
2
x
Sec
.
x
2
4
x
x
2
x
)
x
2
(
)
x
2
(
x
x
4
:
.
ans
(
2
3
2
2
1
1
1
1
1
2
4
2
2
1
2
2
1
6
2
2
3
2
1
3
3
2
3
1
)
3
x
2
)(
1
x
(
)
2
x
)(
1
x
(
x
y
)
25
)
x
4
1
)
x
2
Sin
x
2
Cos
(
2
:
.
ans
(
x
2
Cos
.
x
2
Sin
y
)
24
2
x
Sec
.
x
x
2
x
Sin
y
)
23
)
1
)
1
x
3
(
1
x
3
x
18
:
.
ans
(
)
1
x
3
(
Sec
y
)
22
)
2
x
4
)
1
x
4
(
x
6
:
.
ans
(
2
x
4
tan
y
)
21
))
x
tan
.
x
2
x
cos
(ln
x
2
y
:
.
ans
(
)
x
(cos
y
)
30
)
1
e
2
:
.
ans
(
e
sec
y
)
29
))
x
2
3
2
x
tan
).
x
1
(
1
x
3
14
(
y
2
:
.
ans
(
x
).
x
2
3
(
x
tan
.
x
y
)
28
))
)
x
ln
2
1
(
x
2
2
x
tan
2
x
cot
(
4
y
3
:
.
ans
(
x
ln
.
2
1
x
cos
.
x
sin
y
)
27
)
)
)
x
(ln
1
(
x
1
:
.
ans
(
)
x
(ln
tan
y
)
26
x
x
4
x
2
1
1
2
3
1
5
3
4
2
1
))
x
tanh
2
x
h
sec
x
(
x
tanh
.
x
:
.
ans
(
x
tanh
.
x
y
)
35
)
x
1
coth
.
x
1
h
csc
.
x
1
:
.
ans
(
x
1
h
csc
y
)
34
))
x
2
cosh(cos
.
x
2
sin
2
:
.
ans
(
)
x
2
sinh(cos
y
)
33
)
)
x
5
(
cosh
x
2
)
x
5
sinh(
).
x
5
cosh(
5
x
2
:
.
ans
(
)
x
5
(
cosh
x
2
y
)
32
))
x
sin
ln
.
x
sec
1
(
y
:
.
ans
(
)
x
(sin
y
)
31
2
2
.
2
2
2
2
2
2
2
x
tan

19
)
3
x
2
cot
.
3
x
2
csc
3
x
2
7
ln
3
x
2
csc
7
:
.
ans
(
)
x
2
1
x
tan
x
cos
.
x
sin
x
sec
.
x
tan
3
x
sin
x
cos
:
.
ans
(
7
y
)
40
)
e
)
x
tan
x
2
x
sec
x
(
:
.
ans
(
e
y
)
39
)
e
)
e
5
x
2
(
:
.
ans
(
e
y
)
38
)
4
ln
x
cot
:
.
ans
(
x
sin
log
y
)
37
x
x
tan
x
cos
.
x
sin
ln
y
)
36
3
x
2
csc
x
tan
x
2
2
x
tan
x
)
e
x
(
x
5
)
e
x
(
4
3
2
2
2
2
3
2
2
2
2
x
5
x
5
)
4
x
x
:
.
ans
(
4
x
2
x
2
x
cosh
2
y
)
46
)
2
ln
)
x
2
3
(
x
2
)
x
2
3
(
log
x
3
:
.
ans
(
)
x
2
3
(
log
x
y
)
45
)
)
x
(ln
x
)
1
x
ln
x
(
e
:
.
ans
(
x
ln
e
y
)
44
)
)
x
(ln
1
x
x
ln
:
.
ans
(
)
x
(ln
1
y
)
43
)
x
sec
:
.
ans
(
)
x
(tan
sinh
y
)
42
)
x
sin
)
2
x
ln(
2
2
x
x
cos
.
x
4
:
.
ans
(
x
cos
)
2
x
ln(
y
)
41
2
2
2
1
3
2
2
2
3
2
x
x
2
2
1
2
2
2
2
2. Verify the following derivatives :
)
c
bx
3
ax
5
(
x
2
1
)
c
bx
ax
(
x
dx
d
)
b
x
1
6
)
x
1
x
(
x
5
dx
d
)
a
2
2
2
2
3. Find the derivative of y with respect to x in the following functions :
)
x
4
3
x
x
:
.
ans
(
3
x
u
and
u
2
u
y
)
b
)
)
2
x
3
(
y
x
18
:
.
ans
(
2
3x
u
and
1
u
u
y
)
a
2
2
3
3
2
2
3
2
2

20
4. Find the second derivative for the following functions :
)
x
:
.
ans
(
0
x
16
y
xy
2
x
)
c
)
4
1
:
(ans.
2
x
at
x
2
2
x
2
)
x
(
f
)
b
)
x
12
x
6
x
6
:
.
ans
(
)
x
1
x
(
y
)
a
2
3
2
2
5
3
3
5. Find the third derivative of the function :
)
8y
3
-
:
(ans.
x
y
3
6. Show for
v
u
y
that
3
v
)
'
uv
'
vu
(
'
v
2
)
'
'
uv
'
'
vu
(
v
'
'
y
.
7. Show for y = u.v that y''' = uv''' + 3u' v'' + 3u'' v' + u''' v .
8. Show that
3
x
30
x
35
y
2
4
satisfies
0
y
20
'
xy
2
'
'
y
)
x
1
(
2
.
9. Find
dx
dy
for the following implicit functions :

21
)
y
cosh
x
sec
.
x
tan
.
2
:
.
ans
(
x
tan
y
sinh
)
g
)
)
xy
cos(
.
xy
)
xy
sin(
.
y
2
)
xy
cos(
.
y
x
sec
:
.
ans
(
x
tan
)
xy
sin(
.
y
)
f
)
)
y
x
(
1
x
)
xy
(
1
)
xy
(
1
)
y
x
(
1
y
:
.
ans
(
)
y
x
(
cos
)
xy
(
sin
)
e
)
x
y
1
)
y
tan
x
3
)(
y
1
(
:
.
ans
(
y
y
tan
.
x
x
)
d
)
y
x
y
3
x
2
y
2
y
x
x
3
:
.
ans
(
)
y
x
(
xy
3
)
c
)
x
xy
2
y
:
.
ans
(
y
1
xy
)
b
)
y
x
2
y
x
10
y
4
x
y
5
x
3
:
.
ans
(
3
x
y
5
y
x
4
x
)
a
2
2
2
3
2
2
2
2
2
2
1
1
2
1
2
2
1
3
3
3
2
3
3
2
2
3
3
3
1
2
2
2
2
3
10. Prove the following formulas :
dx
du
.
u
1
u
1
u
h
sec
dx
d
)
h
dx
du
.
u
1
1
u
sinh
dx
d
)
g
dx
du
.
u
coth
.
u
h
csc
u
h
csc
dx
d
)
f
dx
du
.
u
cosh
u
sinh
dx
d
)
e
dx
du
.
1
u
u
1
u
sec
dx
d
)
d
dx
du
.
u
1
1
u
cos
dx
d
)
c
dx
du
.
u
cot
.
u
csc
u
csc
dx
d
)
b
dx
du
.
u
csc
u
cot
dx
d
)
a
2
1
2
1
2
1
2
1
2
11. Show that the tangent to the hyperbola x
2
- y
2
= 1 at the point
P(coshu, sinhu) , cuts the x-axis at the point ( sechu , 0 ) and
except when vertical , cuts the y-axis at the point ( 0 , -cschu ) .
