١
Chapter – one
The Rate of Change of a Function
:
Coordinates for the plane
-
1
-
1
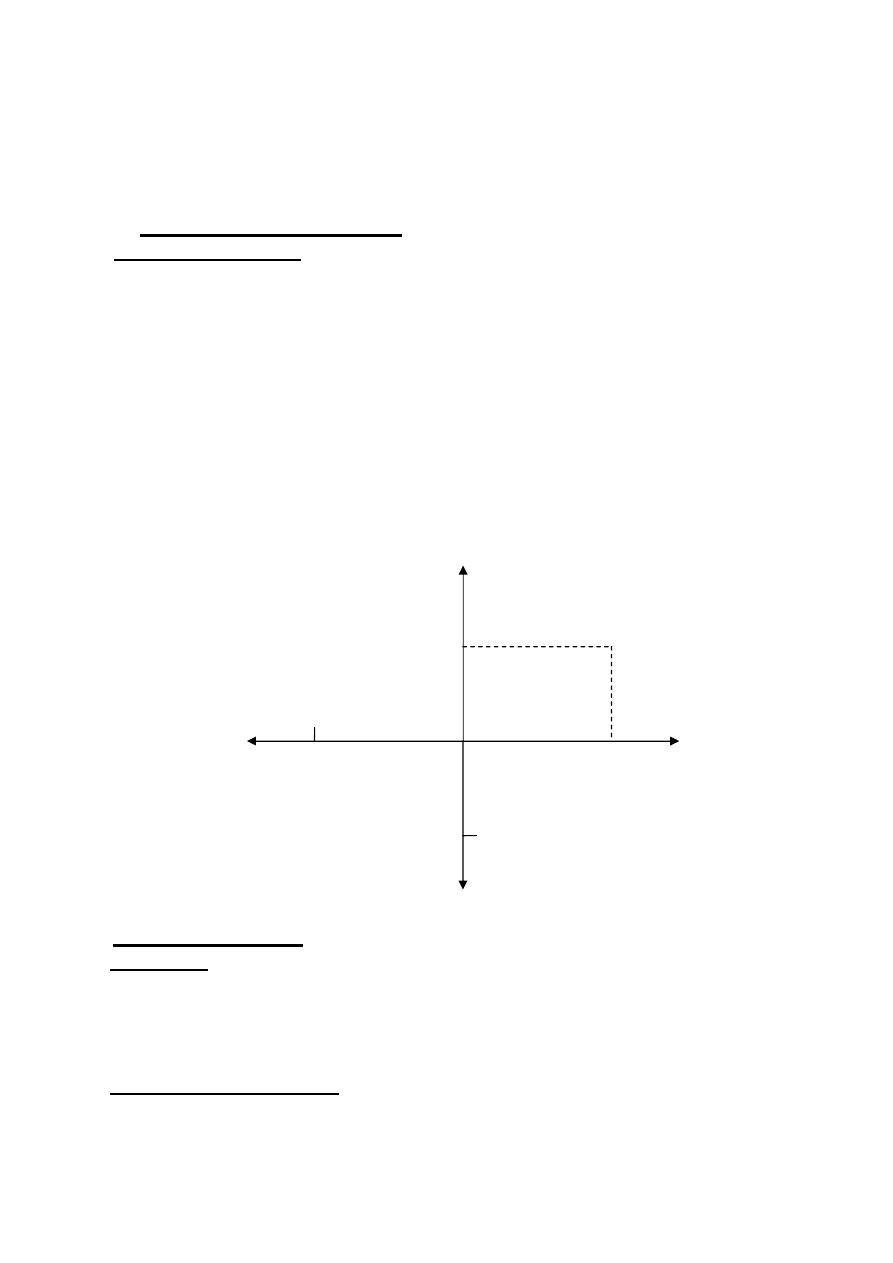
Cartesian Coordinate- Two number lines , one of them horizontal (called
x-axis ) and the other vertical ( called y-axis ). The point where the
lines cross is the origin . Each line is assumed to represent the real
number .
On the x-axis , the positive number a lies a units to the right of
the origin , and the negative number –a lies a units to the left of the
origin . On the y-axis , the positive number b lies b units above the
origin while the negative where –b lies b units below the origin .
With the axes in place , we assign a pair (a,b) of real number to
each point P in the plane . The number a is the number at the foot
of the perpendicular from P to the x-axis (called x-coordinate of P).
The number b is the number at the foot of the perpendicular from
P to the y-axis ( called y-coordinate of P ).
1-2- The Slope of a line :
Increments – When a particle moves from one position in the plane to
another , the net changes in the particle's coordinates are calculated
by subtracting the coordinates of the starting point ( x
1
, y
1
) from
the coordinates of the stopping point (x
2
, y
2
) ,
i.e.
∆x = x
2
–x
1
, ∆y = y
2
– y
1
.
Slopes of nonvertical lines :
Let L be a nonvertical line in the plane ,
Let P
1
(x
1
, y
1
) and P
2
( x
2
, y
2
) be two points on L.
Then the slope m is :
x-axis
0
a
P(a,b)
-b
b
-a
y-axis
٢
0
x
where
x
x
y
y
x
y
m
1
2
1
2
- A line that goes uphill as x increases has a positive slope . A line that
goes downhill as x increases has a negative slope .
- A horizontal line has slope zero because ∆y = 0 .
- The slope of a vertical line is undefined because ∆x = 0 .
- Parallel lines have same slope .
- If neither of two perpendicular lines L
1
and L
2
is vertical , their slopes
m
1
and m
2
are related by the equation : m
1
. m
2
= -1 .
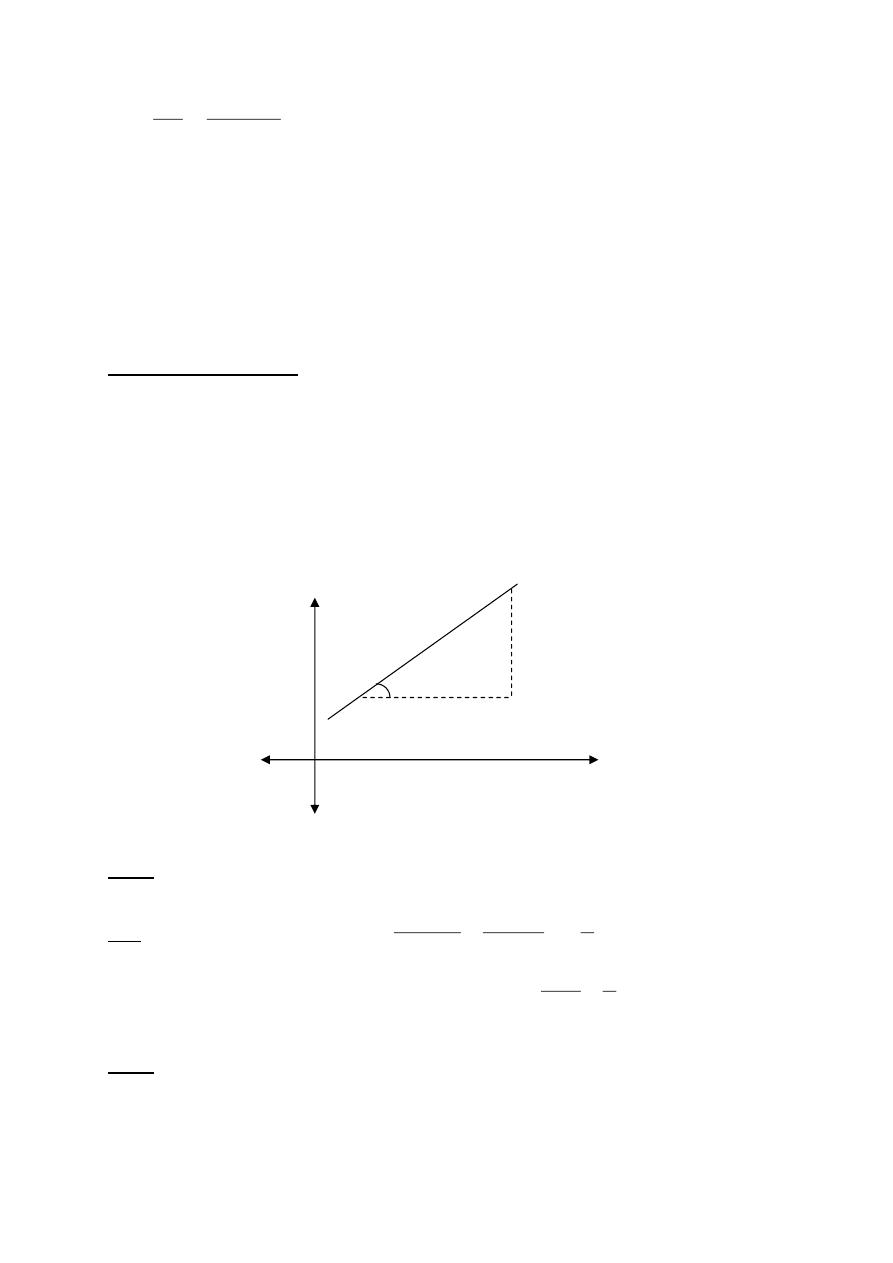
Angles of Inclination: The angle of inclination of a line that crosses the x-
axis is the smallest angle we get when we measure counter clock from the
x-axis around the point of intersection .
The slope of a line is the tangent of the line angle of inclination .
m = tan Ф
where Ф is the angle of inclination .
- The angle of inclination of a horizontal line is taken to be 0
o
.
- Parallel lines have equal angle of inclination .
EX-1- Find the slope of the line determined by two points A(2,1) and B(-1,3)
and find the common slope of the line perpendicular to AB.
Sol.- Slope of AB is:
3
2
2
1
1
3
x
x
y
y
m
1
2
1
2
AB
Slope of line perpendicular to AB is :
2
3
m
1
AB
EX-2- Use slopes to determine in each case whether the points are collinear
(lie on a common straight line ) :
a) A(1,0) , B(0,1) , C(2,1) .
b) A(-3,-2) , B(-2,0) , C(-1,2) , D(1,6) .
y-axis
P
1
(x
1
,y
1)
L
Ф
y
∆
P
2
(x
2
,y
2
)
Q(x
2
,y
1)
x
∆
x-axis

٣
Sol. –
a)
AB
BC
AB
m
0
0
2
1
1
m
and
1
1
0
0
1
m
The points A , B and C are not lie on a common straight line .
b)
2
)
1
(
1
2
6
m
,
2
)
2
(
1
0
2
m
,
2
)
3
(
2
)
2
(
0
m
CD
BC
AB
Since m
AB
= m
BC
= m
CD
Hence the points A , B , C , and D are collinear .
1-3- Equations for lines :
An equation for a line is an equation that is satisfied
by the coordinates of the points that lies on the line and is not satisfied by the
coordinates of the points that lie elsewhere .
Vertical lines : Every vertical line L has to cross the x-axis at some point
(a,0). The other points on L lie directly above or below (a,0) . This mean
that :
)
y
,
x
(
a
x
Nonvertical lines : That point – slope equation of the line through the point
( x
1
, y
1
) with slope m is :
y – y
1
= m ( x – x
1
)
Horizontal lines : The standard equation for the horizontal line through the
point ( a , b ) is : y = b .
The distance from a point to a line : To calculate the distance d between the
point P(x
1
, y
1
) and Q( x
2
, y
2
) is :
2
1
2
2
1
2
)
y
y
(
)
x
x
(
d
We use this formula when the coordinate axes are scaled in a common
unit .
To find the distance from the point P( x
1
, y
1
) to the line L , we follow :
1. Find an equation for the line L' through P perpendicular to L :
y – y
1
= m' ( x – x
1
)
where
m' = -1 / m
2
.
Find the point Q( x
2
, y
2
) by solving the equation for L and L'
simultaneously .
3. Calculate the distance between P and Q .
The general linear equation :
Ax + By = C
where A and B not both zero.
EX-3 – Write an equation for the line that passes through point :
a) P( -1 , 3 ) with slope m = -2 .
b) P
1
( -2 , 0 ) and P
2
( 2 , -2 ).
Sol. - a) y – y
1
= m ( x – x
1
) → y – 3 = -2 ( x – (-1)) → y + 2x = 1
b)
0
2
x
y
2
))
2
(
x
(
2
1
0
y
)
x
x
(
m
y
y
2
1
)
2
(
2
0
2
x
x
y
y
m
1
1
1
2
1
2
٤
EX-4 - Find the slope of the line : 3x + 4y = 12 .
Sol. -
4
3
m
is
slope
the
3
x
4
3
y
EX-5- Find :
a) an equation for the line through P( 2 ,1 ) parallel to L: y = x + 2 .
b) an equation for the line through P perpendicular to L .
c) the distance from P to L .
Sol.-
a)
1
x
y
)
2
x
(
1
1
y
1
m
m
L
//
L
ce
sin
1
L
2
L
1
2
b) Since L
1
and L
3
are perpendicular lines then :
3
x
y
)
2
x
(
1
y
1
m
3
L
c)
5
.
4
)
y
y
(
)
x
x
(
d
2
5
,
2
1
Q
and
)
1
,
2
(
P
2
5
y
and
2
1
x
3
x
y
2
x
y
2
P
Q
2
P
Q
EX-6 – Find the angle of inclination of the line :
3
y
x
3
Sol.-
o
120
3
tan
m
3
m
3
x
3
y
EX-7- Find the line through the point P(1, 4) with the angle of inclination
Ф=60
o
.
Sol.-
3
4
x
3
y
)
1
x
(
3
4
y
3
60
tan
tan
m
EX-8- The pressure P experienced by a diver under water is related to the
diver's depth d by an equation of the form P = k d + 1 where k a
constant . When d = 0 meters , the pressure is 1 atmosphere . The
pressure at 100 meters is about 10.94 atmosphere . Find the pressure
at 50 meters.
Sol.- At P = 10.94 and d = 100
→ 10.94 = k(100)+1 → k = 0.0994
P = 0.0994 d + 1 , at d = 50 → P = 0.0994 * 50 + 1 = 5.97 atmo.
٥
1-4- Functions :
Function is any rule that assigns to each element in one set
some element from another set :
y = f( x )
The inputs make up the domain of the function , and the outputs make up
the function's range.
The variable x is called independent variable of the function , and the
variable y whose value depends on x is called the dependent variable of the
function .
We must keep two restrictions in mind when we define functions :
1. We never divide by zero .
2. We will deal with real – valued functions only.
Intervals :
-
The open interval is the set of all real numbers that be strictly between
two fixed numbers a and b :
b
x
a
)
b
,
a
(
-
The closed interval is the set of all real numbers that contain both
endpoints :
b
x
a
]
b
,
a
[
-
Half open interval is the set of all real numbers that contain one
endpoint but not both :
b
x
a
]
b
,
a
(
b
x
a
)
b
,
a
[
Composition of functions : suppose that the outputs of a function f can be
used as inputs of a function g . We can then hook f and g together to
form a new function whose inputs are the inputs of f and whose outputs
are the numbers :
))
x
(
f
(
g
)
x
)(
f
o
g
(
EX-9- Find the domain and range of each function :
x
2
y
)
d
,
x
9
y
)
c
2
x
1
y
)
b
,
4
x
y
)
a
2
Sol. -
0
y
:
R
,
4
x
:
D
4
x
0
4
x
)
a
y
x
0
y
:
R
2
y
1
x
2
x
1
y
2
x
:
D
2
x
0
2
x
)
b
y
x
3
y
0
:
R
0
y
ce
sin
3
y
3
0
y
9
ce
sin
y
9
x
x
9
y
3
x
3
:
D
3
x
3
0
x
9
)
c
y
2
2
2
x
2

٦
2
y
0
:
R
0
y
4
x
if
2
y
0
x
if
4
x
0
:
D
4
x
0
0
x
2
)
d
y
x
EX-10- Let
x
1
1
)
x
(
g
and
1
x
x
)
x
(
f
.
Find (g
o
f)(x) and (f
o
g)(x) .
Sol.-
1
x
1
x
1
1
x
1
1
x
1
1
f
))
x
(
g
(
f
)
x
)(
g
f
(
x
1
x
2
1
x
x
1
1
1
x
x
g
))
x
(
f
(
g
)
x
)(
f
g
(
o
o
EX-11- Let
x
1
)
x
(
f
and
x
)
x
)(
f
g
(
o
. Find g(x).
Sol.-
x
1
)
x
(
g
x
x
1
g
)
x
)(
f
g
(
o
1-5- Limits and continuity :
Limits : The limit of F( t ) as t approaches C is the number L if :
Given any radius ε > 0 about L there exists a radius δ > 0 about
C such that for all t ,
C
t
0
implies
L
)
t
(
F
and we
can write it as :
L
)
t
(
F
lim
C
t
The limit of a function F( t ) as t→C never depend on what
happens when t = C .
Right hand limit :
L
)
t
(
F
lim
C
t
The limit of the function F( t ) as t →C from the right equals L if :
Given any ε > 0 ( radius about L ) there exists a δ > 0 ( radius to
the right of C ) such that for all t :
L
)
t
(
F
C
t
C
Left hand limit :
L
)
t
(
F
lim
C
t
The limit of the function F( t ) as t →C from the left equal L if :
Given any ε > 0 there exists a δ > 0 such that for all t :
L
)
t
(
F
C
t
C

٧
Note that – A function F( t ) has a limit at point C if and only if the right
hand and the left hand limits at C exist and equal . In symbols :
L
)
t
(
F
lim
and
L
)
t
(
F
lim
L
)
t
(
F
lim
C
t
C
t
C
t
The limit combinations theorems :
radius
in
measured
is
that
provided
1
Sin
lim
)
5
k
)
t
(
F
lim
*
k
)
t
(
F
*
k
lim
)
4
0
)
t
(
F
lim
where
)
t
(
F
lim
)
t
(
F
lim
)
t
(
F
)
t
(
F
lim
)
3
)
t
(
F
lim
*
)
t
(
F
lim
)
t
(
F
*
)
t
(
F
lim
)
2
)
t
(
F
lim
)
t
(
F
lim
)
t
(
F
)
t
(
F
lim
)
1
0
1
1
2
2
1
2
1
2
1
2
1
2
1
2
1
The limits ( in 1 – 4 ) are all to be taken as t→C and F
1
( t ) and F
2
( t ) are
to be real functions .
Thm. -1 : The sandwich theorem : Suppose that
)
t
(
h
)
t
(
g
)
t
(
f
for all
C
t
in some interval about C and that f( t ) and h( t ) approaches the
same limit L as t→C , then :
L
)
t
(
g
lim
C
t
Infinity as a limit :
1.The limit of the function f( x ) as x approaches infinity is the number L:
L
)
x
(
f
lim
x
. If , given any ε > 0 there exists a number M such that
for all x :
L
)
x
(
f
x
M
.
2. The limit of f( x ) as x approaches negative infinity is the number L :
L
)
x
(
f
lim
x
. If , given any ε > 0 there exists a number N such that
for all x :
L
)
x
(
f
N
x
.
The following facts are some times abbreviated by saying :
a) As x approaches 0 from the right , 1/x tends to ∞ .
b) As x approaches 0 from the left , 1/x tends to -∞ .
c) As x tends to ∞ , 1/x approaches 0 .
d) As x tends to -∞ , 1/x approaches 0 .
Continuity :
Continuity at an interior point : A function y = f( x ) is continuous at an
interior point C of its domain if :
)
C
(
f
)
x
(
f
lim
C
x
.
Continuity at an endpoint : A function y = f( x ) is continuous at a left
endpoint a of its domain if :
)
a
(
f
)
x
(
f
lim
a
x
.
A function y = f( x ) is continuous at a right endpoint b of its domain
if:
)
b
(
f
)
x
(
f
lim
b
t
.

٨
Continuous function : A function is continuous if it is continuous at
each point of its domain .
Discontinuity at a point : If a function f is not continuous at a point C ,
we say that f is discontinuous at C ,
and call C a point of
discontinuity of f .
The continuity test : The function y = f ( x ) is continuous at x = C if
and only if all three of the following statements are true :
1)
f ( C ) exist ( C is in the domain of f ) .
2)
)
x
(
f
lim
C
x
exists ( f has a limit as x→C ) .
3)
)
C
(
f
)
x
(
f
lim
C
x
( the limit equals the function value ) .
Thm.-2 : The limit combination theorem for continuous function :
If the function f and g are continuous at x = C , then all of the
following combinations are continuous at x = C :
0
)
C
(
g
provided
g
/
f
)
5
g
f
,
f
g
)
4
k
g
.
k
)
3
g
.
f
)
2
g
f
)
1
o
o
Thm.-3 : A function is continuous at every point at which it has a
derivative . That is , if y = f ( x ) has a derivative f ' ( C ) at x = C ,
then f is continuous at x = C .
EX-12
– Find :
)
x
(tan
Cos
2
Sin
lim
)
12
,
x
Sinx
1
Cos
lim
)
11
1
x
1
lim
)
10
,
5
x
7
x
2
1
x
lim
)
9
2
y
7
y
3
lim
)
8
,
5
x
11
x
10
7
x
5
x
3
lim
)
7
x
1
Cos
1
lim
)
6
,
x
x
2
x
2
Sin
lim
)
5
y
3
y
2
tan
lim
)
4
,
x
3
Sin
x
5
Sin
lim
)
3
a
x
a
x
lim
)
2
,
x
16
x
3
x
8
x
5
lim
)
1
0
x
0
x
1
x
2
3
x
2
y
3
2
3
x
x
2
0
x
0
y
0
x
4
4
3
3
a
x
2
4
2
3
0
x
S0l.-
2
1
16
0
8
0
16
x
3
8
x
5
lim
x
16
x
3
x
8
x
5
lim
)
1
2
0
x
2
4
2
3
0
x
a
4
3
)
a
a
)(
a
a
(
a
a
a
)
a
x
)(
a
x
)(
a
x
(
)
a
ax
x
)(
a
x
(
lim
a
x
a
x
lim
)
2
2
2
2
2
2
2
2
2
2
a
x
4
4
3
3
a
x
3
5
x
3
x
3
Sin
lim
x
5
x
5
Sin
lim
.
3
5
x
3
x
3
Sin
3
x
5
x
5
Sin
5
lim
)
3
0
x
3
0
x
5
0
x
٩
3
2
y
2
Cos
1
lim
.
y
2
y
2
Sin
lim
.
3
2
y
3
y
2
tan
lim
)
4
0
y
0
y
2
0
y
2
1
x
2
1
lim
.
x
2
x
2
Sin
lim
2
x
x
2
x
2
Sin
lim
)
5
0
x
0
x
2
2
0
x
2
0
Cos
1
x
1
Cos
1
lim
)
6
x
10
3
x
5
x
11
10
x
7
x
5
3
lim
5
x
11
x
10
7
x
5
x
3
lim
)
7
3
2
3
x
3
2
3
x
0
1
0
y
2
1
y
7
y
3
lim
2
y
7
y
3
lim
)
8
2
2
y
2
y
0
1
x
5
x
7
x
2
x
1
1
lim
5
x
7
x
2
1
x
lim
)
9
3
2
3
x
2
3
x
1
1
1
1
x
1
lim
)
10
1
x
1
0
Cos
x
Sinx
lim
1
Cos
x
Sinx
1
Cos
lim
)
11
0
x
0
x
1
2
Sin
0
Cos
2
Sin
)
0
(tan
Cos
2
Sin
)
x
(tan
Cos
2
Sin
lim
)
12
0
x
EX-13- Test continuity for the following function :
3
x
2
0
2
x
1
4
x
2
1
x
1
1
x
0
x
2
0
x
1
1
x
)
x
(
f
2
Sol.- We test the continuity at midpoints x = 0 , 1 , 2 and endpoints x = -1 , 3 .
0
x
at
ous
discontinu
function
the
Hence
exist
t
'
doesn
)
x
(
f
lim
Since
)
x
(
f
lim
0
x
2
lim
)
x
(
f
lim
1
)
1
x
(
lim
)
x
(
f
lim
0
0
*
2
)
0
(
f
0
x
At
0
x
0
x
0
x
0
x
2
0
x
0
x

٠١
1
x
at
ous
discontinu
is
function
the
Hence
)
1
(
f
)
x
(
f
lim
Since
)
x
(
f
lim
)
x
(
f
lim
2
)
4
x
2
(
lim
)
x
(
f
lim
2
x
2
lim
)
x
(
f
lim
1
)
1
(
f
1
x
At
1
x
1
x
1
x
1
x
1
x
1
x
1
x
2
x
at
continuous
is
function
the
Hence
0
)
2
(
f
)
x
(
f
lim
Since
)
x
(
f
lim
)
x
(
f
lim
0
0
lim
)
x
(
f
lim
0
)
4
x
2
(
lim
)
x
(
f
lim
0
4
2
*
2
)
2
(
f
2
x
At
2
x
2
x
2
x
2
x
2
x
2
x
2
x
1
x
at
continuous
is
function
the
Hence
)
1
(
f
0
)
1
x
(
lim
)
x
(
f
lim
0
1
)
1
(
)
1
(
f
1
x
At
2
1
x
1
x
2
3
x
at
continuous
is
function
the
Hence
)
3
(
f
0
0
lim
)
x
(
f
lim
0
)
3
(
f
3
x
At
3
x
3
x
EX-14- What value should be assigned to a to make the function :
3
x
ax
2
3
x
1
x
)
x
(
f
2
continuous at x = 3 ?
Sol. –
3
4
a
a
6
8
ax
2
lim
)
1
x
(
lim
)
x
(
f
lim
)
x
(
f
lim
3
x
2
3
x
3
x
3
x

١١
Problems – 1
1. The steel in railroad track expands when heated . For the track
temperature encountered in normal outdoor use , the length S of a piece
of track is related to its temperature t by a linear equation . An
experiment with a piece of track gave the following measurements :
ft
16
.
35
S
,
F
135
t
ft
35
S
,
F
65
t
2
o
2
1
o
1
Write a linear equation for the relation between S and t .
(ans.: S=0.0023t+34.85)
2. Three of the following four points lie on a circle center the origin . Which
are they , and what is the radius of the circle ?
A(-1.7) , B(5,-5) , C(-7,5) and D(7,-1). (ans.: A,B,D;√50)
3. A and B are the points (3,4) and (7,1) respectively . Use Pythagoras
theorem to prove that OA is perpendicular to AB . Calculate the slopes of
OA and AB , and find their product . (ans.: 4/3, -3/4;-1)
4. P(-2,-4) , Q(-5,-2) , R(2,1) and S are the vertices of a parallelogram . Find
the coordinates of M , the point of intersection of the diagonals and of S.
(ans.: M(0,-3/2) , S(5,-1))
5. Calculate the area of the triangle formed by the line 3x-7y+4 =0 , and the
axes . (ans.: 8/21)
6. Find the equation of the straight line through P(7,5) perpendicular to the
straight line AB whose equation is 3x + 4y -16 = 0 . Calculate the length of
the perpendicular from P and AB. (ans.: 3y-4x+13=0;5)
7. L(-1,0) , M(3,7) and N(5,-2) are the mid-points of the sides BC , CA and AB
respectively of the triangle ABC. Find the equation of AB. (ans.:4y=7x-43)
8. The straight line x – y – 6 = 0 cuts the curve y
2
= 8x at P and Q . Calculate
the length of PQ . (ans.:16√2)
9. A line is drawn through the point (2,3) making an angle of 45
o
with the
positive direction of the x-axis and it meets the line x = 6 at P . Find the
distance of P from the origin O , and the equation of the line through P
perpendicular to OP. (ans.: √85,7y+6x-85=0)
10. The vertices of a quadrilateral ABCD are A(4,0) , B(14,11) , C(0,6) and
D(-10,-5) . Prove that the diagonals AC and BD bisect each other at right
angles , and that the length of BD is four times that of AC .

٢١
11. The coordinates of the vertices A, B and C of the triangle ABC are (-3,7)
, (2,19) and (10,7) respectively :
a) Prove that the triangle is isosceles.
b) Calculate the length of the perpendicular from B to AC , and use it to
find the area of the triangle . (ans.:12,78)
12. Find the equations of the lines which pass through the point of
intersection of the lines x - 3y = 4 and 3x + y = 2 and are respectively
parallel and perpendicular to the line 3x + 4y = 0 .
(ans.:4y+3x+1=0;3y-4x+7=0)
13. Through the point A(1,5) is drawn a line parallel to the x-axis to meet at B
the line PQ whose equation is 3y = 2x - 5 . Find the length of AB and the
sine of the angle between PQ and AB ; hence show that the length of the
perpendicular from A to PQ is 18/√13 . Calculate the area of the triangle
formed by PQ and the axes . (ans.:9,2/√13,25/12)
14. Let
1
x
2
x
y
2
2
, express x in terms of y and find the values of y for
which x is real . (ans.:
)
1
y
or
2
y
;
1
y
2
y
x
15. Find the domain and range of each function :
x
3
1
y
)
c
,
x
1
1
y
)
b
,
x
1
1
y
)
a
2
)
0
y
,
3
x
)
c
;
0
y
,
0
x
)
b
;
1
y
0
,
x
)
a
:
.
ans
(
16. Find the points of intersection of x
2
= 4y and y = 4x . (ans.:(0,0),(16,64))
17. Find the coordinates of the points at which the curves cut the axes :
2
2
2
2
3
)
5
x
)(
1
x
(
y
)
c
,
)
9
x
)(
1
x
(
y
)
b
,
x
9
x
y
)
a
(ans.:a)(0,0);(0,0),(9,0);b)(0,9);(1,0),(-1,0),(3,0),(-3,0);c)(0,25);(-1,0),(5,0))
18. Let f(x) = ax + b and g(x) = cx + d . What condition must be satisfied by
the constants a , b , c and d to make f(g(x)) and g(f(x)) identical ?
(ans.:ad+b=bc+d)
19. A particle moves in the plane from (-2,5) to the y-axis in such away that
∆y = 3*∆x . Find its new coordinates . (ans.:(0,11),(0,-1))
20. If f(x) = 1/x and g(x)=1/√x , what are the domain of f , g , f+g , f-g , f.g ,
f/g , g/f , f
o
g and g
o
f ? What is the domain of h(x) = g(x+4) ?
)
4
x
;
0
x
,
0
x
,
0
x
,
0
x
,
0
x
,
0
x
,
0
x
,
0
x
,
0
x
:
.
ans
(

٣١
21. Discuss the continuity of :
2
x
for
0
2
x
for
1
2
x
1
for
1
1
x
0
for
x
0
x
for
x
1
x
)
x
(
f
3
(ans.: discontinuous at x=0,2 ; continuous at x=1)
22. Evaluate the following limits :
)
n
1
n
(
lim
)
g
x
x
x
2
1
x
lim
)
f
x
1
x
1
lim
)
e
)
Sinx
x
(
Sinx
.
x
lim
)
d
x
3
tan
x
lim
)
c
x
Sinx
1
lim
)
b
5
x
2
Sinx
x
lim
)
a
2
n
2
1
x
1
x
2
x
0
x
x
x
(ans.:a)1/2, b)0, c)1/3, d)0, e)1/2, f)-1/2√2, g)0)
23. Suppose that : f(x) = x
3
– 3x
2
-4x +12 and
3
x
for
k
3
x
for
3
x
)
x
(
f
)
x
(
h
.
Find : a) all zeros of f .
b) the value of k that makes h continuous at x=3 .
)
5
k
)
b
;
3
,
2
x
)
a
:
.
ans
(
