
ت س
ا
ﺍﻟﻔﺼﻞ
8
ﻧﻈﺮﻳﺔ ﺍﻟﺘﻘﺪﻳﺮ
................................
............................
2
أ ه
................................
................................
................................
................................
.
2
و
ار
................................
................................
................................
...........................
2
ل!" ا ل# $%ه
.
................................
................................
................................
..........................
3
آ ا ل
................................
................................
................................
................................
5
)! *+ ,-ل ا!
................................
................................
................................
..........................
5
)! . ,/012 ,-ل ا!
................................
................................
................................
........................
8
)! ير%ا فا 56و 7/2 ,-ا ل!
.%/8
................................
................................
.......................
9
7%! .1/ ,/01 ,-ت ا:!
................................
................................
................................
..............
11
,<6
................................
................................
................................
.........................
11
=2
.
)%!او قو 2 ,-ا ت:!
................................
................................
................................
.........
13
ق ا
ر
................................
................................
................................
.............................
14
موAا , 8
................................
................................
................................
.........................
14
BCا ,%ا , 8
)
8
/آFا ل#:ا ,
(
................................
................................
...........................
14

ا
VIII
.
ا , C5
2
ا
8
ا
أ ه
-
ق ا ل
-
ق ا ر
ﰲ ﺍﻟﻔﺼﻞ ﺍﻟﺴﺎﺑﻖ ﺩﺭﺳﻨﺎ
ﻣﻦ ﺧﻼﻝ
ﳎﻤﻮﻋﺔ ﻣﻦ ﺍﻟﻨﻈﺮﻳﺎﺕ ﺍﻟﻌﻼﻗﺔ ﺍﻟﺮﻳﺎﺿﻴﺔ ﺑﲔ
ﻣﻌﺎﱂ
ﺘﻤﻊﺍ ﰲ ﺎﳍ ﺓﺮﻇﺎﻨﳌﺍ ﱂﺎﻌﳌﺍﻭ ﺔﻨﻴﻌﻟﺍ
ﻣﺜﻞ ﺍﳌﺘ
ﺍﻟﻨﺴﺒﺔ،ﻦﻳﺎﺒﺘﻟﺍ ،ﻂﺳﻮ
...
ﺘﻤﻊ ﻭﺷﻜﻞ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﳌﻌﺎﱂ ﺍﻟﻌﻴﻨﺔﺍ ﻊﻳﺯﻮﺗ ﻞﻜﺷ ﲔﺑ ﺔﻗﻼﻌﻟﺍ ﺎﻨﺳﺭﺩ ﺎﻤﻛ
.
ﺗﻈﻬﺮ
،ﺔﺳﺍﺭﺪﻟﺍ ﻞﳏ ﻊﻤﺘﺍ ﱂﺎﻌﻣﻭ ﺺﺋﺎﺼﺧ ﺮﻳﺪﻘﺘﻟ ﺮﺜﻛﺃ ﻡﺪﺨﺘﺴﺗ ﺎﻬﻨﻜﻟﻭ ﺎﻬﳌﺎﻌﻣﻭ ﺔﻨﻴﻌﻟﺍ ﺺﺋﺎﺼﳋ ﻒﻴﺻﻮﺘﻛ ﺕﺎﻗﻼﻌﻟﺍ ﻩﺬﻫ
ﻭﻫﺬﺍ ﻣﺎ ﺳﻨﺘﻌﺮﻑ ﻋﻠﻴﻪ ﰲ ﻫﺬﺍ ﺍﻟﻔﺼﻞ
.
8
-
1
ه أ
و
ار
$%ه
ل!" ا ،.J1ا ا
8
-
1
-
1
! و#$
ا ر
:
ا،'(ا
$
و ارب
ﻗﺪ ﺗﺴﺘﺨﺪﻡ ﺍﻹﺣﺼﺎﺋﻴﺔ ﻟﺘﻘﺪﻳﺮ ﳌﻌﻠﻤﺔ،ﺔﻨﻴﻌﻟﺍ ﺕﺍﲑﻐﺘﻣ ﰲ ﺔﻟﺍﺩ ﺎﺄﺑ ﺔﻴﺋﺎﺼﺣﻹﺍ ﺎﻨﻓﺮﻋ ﻖﺑﺎﺴﻟﺍ ﻞﺼﻔﻟﺍ ﰲ
θ
ﻣﻦ ﻣﻌﺎﱂ ﳎﺘﻤﻊ
ﻭﺗﺴﻤﻰ ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ
"
ﻣﻘﺪﺭ
"
(estimateur)
ﻭﻧﺮﻣﺰ ﳍﺎ ﺏ
θ
)
.
ﺍﺧﺘﻴﺎﺭ ﺍﻹﺣﺼﺎﺋﻴﺔ ﺍﳌﻨﺎﺳﺒﺔ
ﻳﻜﻮﻥ ﺣﺴﺐ ﺧﺼﺎﺋﺼ
ﻬﺎ
.
8
-
1
-
1
-
1
ﺍﳌﻘﺪﺭ ﻏﲑ ﺍﳌﺘﺤﻴﺰ
ﺎ ﻣﻘﺪﺭ ﻏﲑ ﻣﺘﺤﻴﺰﺄﺑ ﺎﻣ ﺔﻴﺋﺎﺼﺣﺇ ﻦﻋ ﻝﻮﻘﻧ
(sans biais)
ﻲـﺿﺎﻳﺮﻟﺍ ﺎـﻬﻌﻗﻮﺗ ﻭﺃ ﺎﻬﻄﺳﻮﺘﻣ ﻥﺎﻛ ﺍﺫﺇ ﻊﻤﺘﺍ ﺔﻤﻠﻌﳌ
ﻣﺴﺎﻭﻳ
ﺎ
ﺘﻤﻊﺍ ﺔﻤﻠﻌﳌ
.
θ
θ
=
)
(
)
E
ﻣﺜﺎﻝ
:
•
ﻧﻘﻮﻝ ﻋﻦ ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ
M
ﺃﻧﻪ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﳌ ﺰﻴﺤﺘﻣ ﲑﻏ ﺭﺪﻘﻣ
µ
ﻷﻥ
E(M) = µ
.
•
ﻧﻘﻮﻝ ﻋﻦ
ﺍﻹﺣﺼﺎﺋﻴﺔ
S²
)
ﺗﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ
(
ﺎﺃ ﻉﺎﺟﺭﻹﺎﺑ ﺔﻨﻳﺎﻌﻣ ﰲ
ﻣﻘﺪﺭ ﻣﺘﺤﻴﺰ ﻝ
σ²
ﻷﻥ
:
E(S²) = σ² (n – 1)/n ≠ σ²
•
ﻧﻘﻮﻝ ﻋﻦ ﺍﻹﺣﺼﺎﺋﻴﺔ
= S²n/(n –1)
Ŝ²
ﰲ ﻣﻌﺎﻳﻨﺔ ﺑﺎﻹﺭﺟﺎﻉ
ﺎ ﻣﻘﺪﺭﺃ
ﻏﲑ ﻣﺘﺤﻴﺰ
ﻷﻥ
:
σ²
E(Ŝ²) =
8
-
1
-
1
-
2
ﺍﻟ
ﻔﻌﺎﻟﻴﺔ
ﺍﳌﻘﺪﺭ ﺍﻷﻛﺜﺮ
ﻓﻌﺎﻟﻴﺔ
(efficacité)
ﻫﻮ ﺍﳌﻘﺪﺭ
ﺍﻷﻗﻞ ﺗﺒﺎﻳﻨﺎ
.
ﻣﺜﺎﻝ
:
ﻛﻞ ﻣﻦ
ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﻭﺍﻟﻮﺳﻴﻂ ﰲ ﺍﻟﻌﻴﻨﺔ ﻫﻮ ﻣﻘﺪﺭ ﻏﲑ ﻣﺘﺤﻴﺰ ﻝ
µ
،
ﻟﻜﻦ
ﺗ
ﻌﺘﱪ
M
ﻣﻘﺪﺭﺍ ﺃﻛﺜﺮ
ﺔـﻴﻟﺎﻌﻓ
ﻦـﻣ
ﺍﻟﻮﺳﻴﻂ ﻷ
ﻥ ﳍ
ﺎ ﺧﻄﺄ ﻣﻌﺎﻳﻨﺔ ﺃﻗﻠ
ﻲ
:
σ²
m
= σ²/n
σ²
méd
= (σ²/n)(π/2) >
.
.P ا ء#Rا و ت:#:ا Bإ
–
ءA!ا
2
.
3
*(+, ر
9
-
1
$/
0$ ا12 345 6 ر ا
8
-
1
-
1
-
3
ﺍﻟﺘﻘﺎﺭﺏ
ﺍﳌ
ﻘﺪﺭ
ﺍﳌ
ﺘﻘﺎﺭﺏ
(convergeant)
ﻫﻮ ﺍﻟﺬﻱ
ﺔـﻳﺎ ﻻ ﺎﻣ ﱃﺇ ﺔﻨﻴﻌﻟﺍ ﻢﺠﺣ ﻝﻭﺆﻳ ﺎﻣﺪﻨﻋ ﺓﺭﺪﻘﳌﺍ ﺔﻤﻠﻌﳌﺍ ﺔﻤﻴﻗ ﱃﺇ ﻝﻭﺆﻳ
.
ﻳﺘﺤﻘﻖ ﺫﻟﻚ ﻣﺜﻼ
ﺑﺄﻥ ﻳﺆﻭﻝ ﺗﺒﺎﻳﻨﻪ ﺇﱃ ﺍﻟﺼﻔﺮ
.
ﻣﺜﺎﻝ
:
ﺘﻤﻊ ﻷﻥﺍ ﻂﺳﻮﺘﳌ ﺎﺑﺭﺎﻘﺘﻣ ﺍﺭﺪﻘﻣ ﺔﻨﻴﻌﻟﺍ ﻂﺳﻮﺘﻣ ﱪﺘﻌﻳ
:
.
0
²
)
(
,
)
(
→
=
=
∞
→
n
n
m
V
m
E
σ
µ
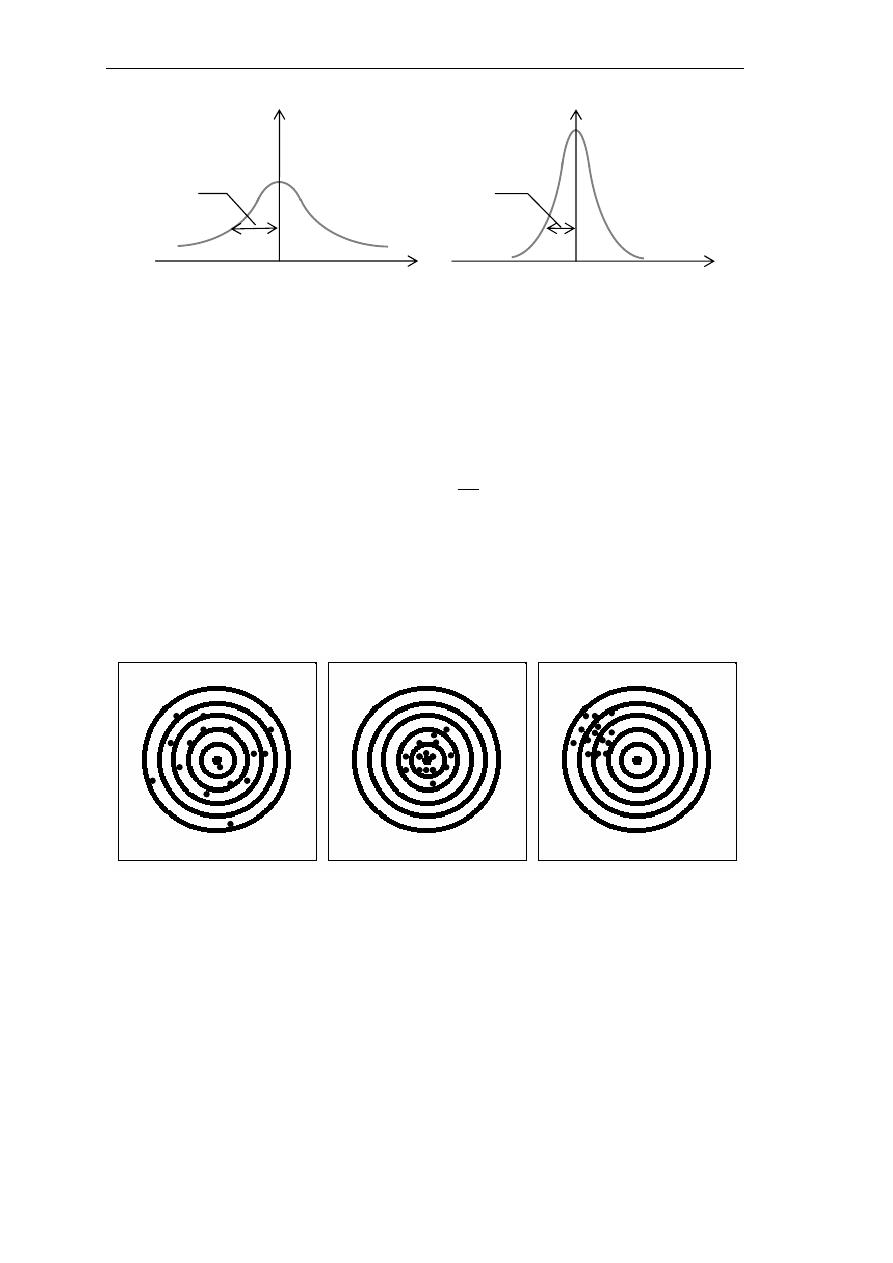
ﺎـﻣ ﻑﺪﻫ ﻰﻠﻋ ﻲﻣﺭ ﺞﺋﺎﺘﻨﻟ ﱄﺎﺘﻟﺍ ﻢﺳﺮﻟﺍ ﻝﻼﺧ ﻦﻣ ﺮﻳﺪﻘﺘﻟﺍ ﰲ ﺔﻴﻟﺎﻌﻔﻟﺍ ﻭ ﺰﻴﺤﺘﻟﺍ ﻢﻴﻫﺎﻔﻣ ﺢﻴﺿﻮﺗ ﺐﺳﺎﻨﳌﺍ ﻦﻣ ﻪﻠﻌﻟ
.
ﰲ
ﺍﻟﺮﺳﻢ ﺍﻷﻭﻝ
)
ﺇﱃ ﺍﻟﻴﻤﲔ
(
ﺍﻟﺮﻣﻴﺎﺕ ﻣﺘﻘﺎﺭﺑﺔ ﻟﻜﻦ ﻣﺮﻛﺰﻫﺎ ﻣﻨﺤﺮﻑ ﻋﻦ
ﺎﺕـﻴﻣﺮﻟﺍ ﺰﻛﺮﻤﻓ ﺚﻟﺎﺜﻟﺍ ﻢﺳﺮﻟﺍ ﰲ ﺎﻣﺃ ،ﻑﺪﳍﺍ
ﻳﻨﻄﺒﻖ ﻋﻠﻰ ﺍﳍﺪﻑ ﻟﻜﻦ ﺍﻟﺮﻣﻴﺎﺕ ﻣﺘﺒﺎﻋﺪﺓ
.
ﺍﳊﺎﻟﺔ ﺍﻷﻓﻀﻞ ﻫﻲ ﺃﻥ ﻳﻜﻮﻥ ﺍﻟﺮﻣﻲ ﺩﻗﻴﻘﺎ ﻭﻳﻜﻮﻥ ﻣﺮﻛﺰ
ﻩ
ﻣﻨﻄﺒﻘﺎ ﻋﻠﻰ ﺍﳍﺪﻑ
ﻭﻫﻮ ﻣﺎ ﻳﻌﻜﺴﻪ ﺍﻟﺮﺳﻢ ﺍﻷﻭﺳﻂ
.
ر
8
-
1
.
'(
.
م5
'(
.
$/ :; أو;د :;
.
8
-
1
-
2
ل,= ه
ا
و ا*10ا
ل
.
8
-
1
-
2
-
1
ﺍﻟ
ﺘﻘﺪﻳﺮ
ﺍﻟ
ﻨﻘﻄﻲ
ﻫﻮ ﺗﻘﺪﻳﺮ
ﻣﻌﻠﻤﺔ
ﺍ
ﺘﻤﻊ ﺑﻘﻴﻤﺔ ﻭﺍﺣﺪﺓ
ﻹﺣﺼﺎﺋﻴﺔ ﻣﺎ
،
ﻓﻨﻜﺘﺐ
θ
θ
=
ˆ
ﻭ ﻫﺬﺍ ﺇﺫﺍ ﻋﻠﻤﻨﺎ ﺃ
ﺎ ﻣﻘﺪﺭ ﻏﲑ ﻣﺘﺤﻴﺰ ﻟﻠﻤﻌﻠﻤﺔ
:
( )
θ
θ
=
ˆ
E
.
ﻣﺜﺎﻝ ﺫﻟﻚ
E(M) = µ
.
)
(
θ
)
E
θ
σ
)
)
(
θ
)
E
θ
σ
)

ا
VIII
.
ا , C5
4
8
-
1
-
2
-
2
ﺍﻟ
ﺘﻘﺪﻳﺮ ﲟﺠﺎﻝ
ﲢﺪﻳﺪ ﳎﺎﻝ
ﻣﻌﲔ ﺗﻨﺘﻤﻲ ﺇﻟﻴﻪ
ﺍﳌﻌﻠﻤﺔ ﺍﳌﻘﺪﺭﺓ ﺑﺎﺣﺘﻤﺎﻝ ﻣﺎ
،
ﻓﻨﻜﺘﺐ
:
[
]
2
1
; l
l
∈
θ
ﻭﻳﺴﻤﻰ
ﺎﻝﺍ ﺍﺬﻫ
ﳎﺎﻝ ﺍﻟﺜﻘﺔ
،
ﻛﺄﻥ
ﻧﻘﺪﺭ ﺍﻟﺪﺧﻞ
ﺍﻟﺸﻬﺮﻱ ﻟﻸﺳﺮﺓ
ﺑﺄﻧﻪ ﻳﻨﺘﻤﻲ
ﺎﻝﺍ ﱃﺇ
:
[16000 ; 24000]
ﲟﺴﺘﻮﻯ ﺛﻘﺔ
95
%
.
8
-
1
-
2
-
3
ﺩﺭﺟﺔ ﺍﻟﺘﺄﻛﺪ
ﺃﻭ ﻣﺴﺘﻮﻯ ﺍﻟﺜﻘﺔ
ﲢﺪﻳﺪ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻟﻠﻤﻌﻠﻤﺔ
ﻳﺮﻓﻖ ﺑﺘ
ﺤﺪ
ﻳ
ﺪ
ﺍﺣﺘﻤﺎﻝ
ﲢﻘﻘﻪ
،
ﺃﻱ
ﺑ
ﺎﺣﺘﻤﺎﻝ
ﺃﻥ
ﺗ
ﻨﺘﻤﻲ
ﺍﳌﻌﻠﻤﺔ
ﺎﻝ ﺍﳌﺬﻛﻮﺭﺍ ﱃﺇ
.
ﺬﺍـﳍ ﺰـﻣﺮﻳ
ﺍﻻﺣﺘﻤﺎﻝ ﺏ
(1 –
α
)
ﻭ
ﻳﺴﻤﻰ
ﺩﺭﺟﺔ
ﺍﻟﺘﺄﻛﺪ
ﺃﻭ
ﻣﺴﺘﻮﻯ ﺍﻟﺜﻘﺔ
.
ﺍﻻﺣﺘﻤﺎﻝ ﺍﳌﻌﺎﻛﺲ
α
1
ﻳﺴﻤﻰ
ﻣﺴﺘﻮﻯ
ﺔـﺟﺭﺩ ﻭﺃ
ﺍﳌﻌﻨﻮﻳﺔ
.
ﰲ ﺍﳊﻘﻴﻘﺔ ﳛ
ﺴﺐ
ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﺑﻨﺎﺀﺍ ﻋﻠﻰ ﻣﺴﺘﻮﻯ ﺛﻘﺔ
ﳏﺪﺩ ﻣﺴﺒﻘﺎ
.
ﻣﻼﺣﻈﺔ
:
-
ﻋ
ﺎﺩﺓ
ﻳﺴﺘﺨﺪﻡ ﺍﻹﺣﺼﺎﺋﻴﻮﻥ ﻣﺴﺘﻮﻯ ﺛ
ﻘﺔ
95
) %
ﺃﻱ ﻣﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
(
ﻭﺃﺣﻴﺎﻧﺎ،
90
%
ﺃﻭ،
99
%
.
-
ﺯﻳﺎﺩﺓ
ﺩﺭﺟﺔ ﺍﻟﺘﺄﻛﺪ
ﺗﺘﻄﻠﺐ
ﺗﻮﺳﻴﻊ ﳎﺎﻝ
ﺍﻟﺜﻘﺔ
)
ﻣﺎ ﻳﻌﲏ
ﺩﻗﺔ
ﺃﻗﻞ
(
ﺃﻭ
ﺯﻳﺎﺩﺓ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
.
8
-
1
-
2
-
4
ﻣﻌﺎﻣﻼﺕ
ﺍﻟﺜﻘﺔ
ﻣﻌﺎﻣﻼﺕ ﺍﻟﺜﻘﺔ ﻫﻲ ﺍﻟﻘﻴﻢ ﺍﳉﺪﻭﻟﻴﺔ ﻟﻠﻤﺘﻐﲑﺓ
z
ﺃﻭ
t
ﺃﻭ ﻙ
2
ﺣﺴﺐ ﺍﳊﺎﻟﺔ
.
ﻣﺜﻼ
ﺑﺎﻟﻨﺴﺒﺔ
ﻟﻠﻤﺘﻐﲑﺓ
z
ﻧﻌﻠﻢ ﺃﻥ
:
P(-1.64 < Z < 1.64) = 0.90, P(-1.96 < Z < 1.96) = 0.95, P(-2.58 < Z < 2.58) = 0.99
ﻟﺬﻟﻚ
ﰲ ﺣﺎﻟﺔ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﻟﻠﺘﻘﺪﻳﺮ ﺗﻜﻮﻥ
ﻣﻌﺎﻣﻼﺕ ﺍﻟﺜﻘﺔ ﻫﻲ
:
ﺍﻟﻘﻴﻤﺘﲔ
±
1.64
ﻣﻦ ﺃﺟﻞ ﻣﺴﺘﻮﻯ ﺛﻘﺔ
90
%
،
±
1.96
ﻣﻦ ﺃﺟﻞ ﻣﺴﺘﻮﻯ ﺛﻘﺔ
95
%
ﻭ
ﺍﻟﻘﻴﻤﺘﲔ
±2.58
ﻣﻦ ﺃﺟﻞ
ﻣﺴﺘﻮﻯ ﺛﻘﺔ
99
%
.
ﻣﺜﺎ
ﻝ
:
ﻟﻴﻜﻦ
µ
s
ﻭ
σ
s
ﻣﺘﻮﺳﻂ ﻭﺍﳓﺮﺍﻑ ﻣﻌﻴﺎﺭﻱ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻹﺣﺼﺎﺋﻴﺔ ﻣﺎ
s
ﺣﻴﺚ
µ
s
= µ
.
ﺇﺫﺍ ﻛﺎﻥ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻝ
s
ﻃﺒﻴﻌﻴﺎ
)
ﻛﻤﺎ ﻫﻮ ﺍﳊﺎﻝ ﺑﺎﻟﻨﺴﺒﺔ ﻷﻏﻠﺐ ﺍﻹﺣﺼﺎﺋﻴﺎﺕ ﻋﻨﺪﻣﺎ
(n ≥ 30)
(
ﻊـﻳﺯﻮﺗ ﱃﺇ ﺮﻈﻨﻟﺎـﺑﻭ ﻼﺜﻣ ﺭﺪﻘﻧ ﺎﻨﻧﺈﻓ
s
ﺃﻥ
ﺍﳌﺘﻐﲑﺓ ﺍﳌﻌﻴﺎﺭﻳﺔ ﻝ
µ
ﺃﻱ
z
µ
ﺗﺘﺮﺍﻭﺡ ﺑﲔ
± 1.96
ﺑ
ﺎﺣﺘﻤﺎﻝ
95
%
ﻭﻣﻨﻪ ﻓﺎﳌﺘﻮﺳﻂ
µ
ﺎﻝﺍ ﱃﺇ ﻲﻤﺘﻨﻳ
:
µ
s
±
z
1– (α/2) .
σ
s
µ
s
±
1.96
.
σ
s
1
آX" ءآ:ا 1ه 12Y
α
ب ةد^ _ A يXا %Fا اXه ،,1ا ى0 ةJ ,%a ,%ا . ه يXا
p
.
b2J مc+ا
,1ى ا0
(p-level)
ة لوF
.25وا " /a 7
(Brownlee)
.
1960
،
,%#Rا ,!%1ا ة %0d^ ا ef - و
(fiabilité du résultat)
7 /آأ ,1 ى0 6-
p = 0.05
)
1
/
20
(
,1ا 5ر آ _5أ .1
20
ةهiا j ة
)
,د
(
aFا B2^ ة#او ة
.
.P ا ء#Rا و ت:#:ا Bإ
–
ءA!ا
2
.
5
ر
9
-
2
@ا ل ج0ا تا,1!
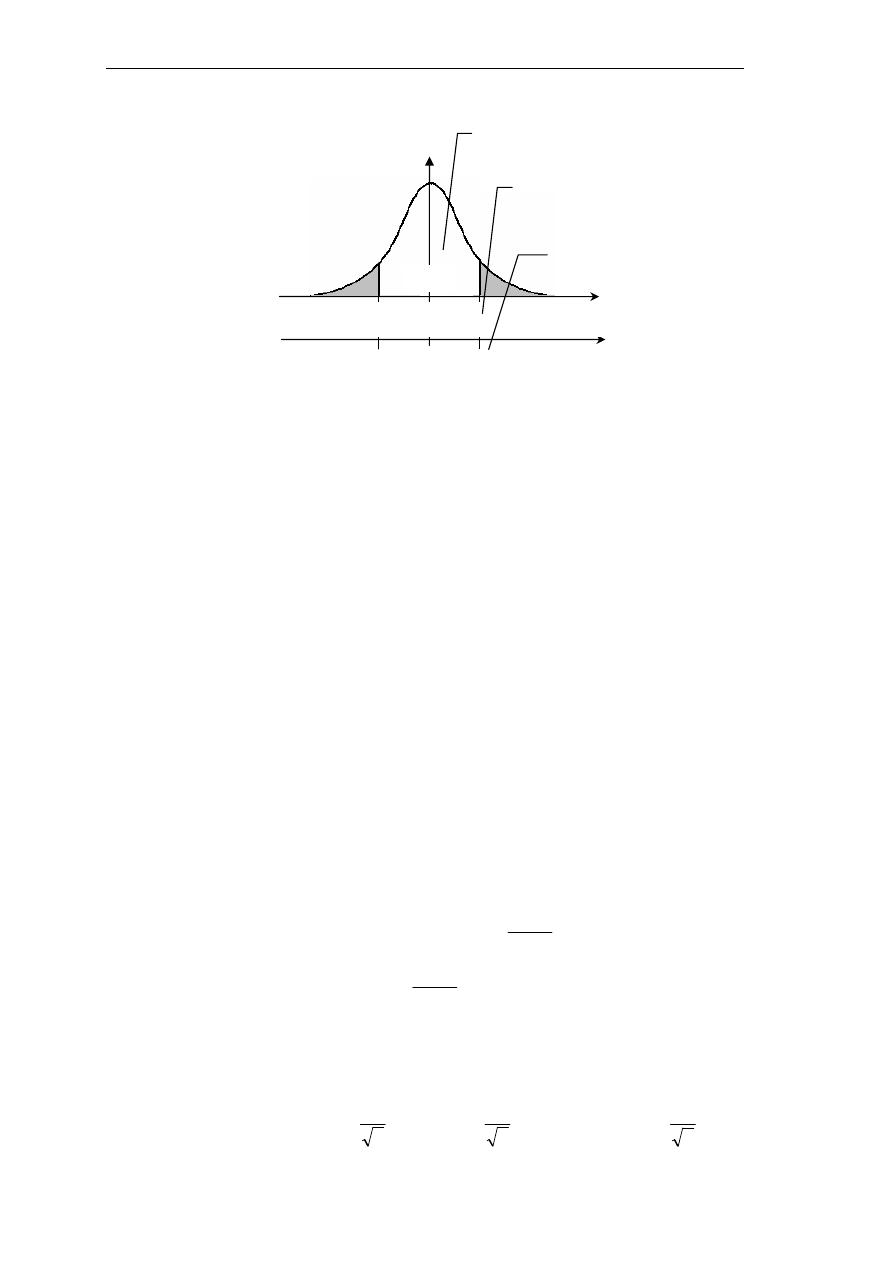
ﰲ ﺣﺎﻟﺔ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﻳﺮﻣﺰ
ﳌﻌﺎﻣﻼﺕ
ﺍﻟﺜﻘﺔ ﺏ
Z
c
ﺃﻭ
Z
1–α/2
)
ﺃﻧﻈﺮ ﺍﻟﺮﺳﻢ
(
ﻭﰲ ﺣﺎﻟﺔ ﺍﺳﺘﺨﺪﺍﻡ ﺗﻮﺯﻳﻊ ﺳﺘﻴﻮﺩﻧﺖ،
ﻳ
ﺮﻣﺰ
ﳌﻌﺎﻣﻼﺕ
ﺍﻟﺜﻘﺔ ﺏ
:
t
c
ﺃﻭ
t
1–α/2
ﻭ
ﻧﻜﺘﺐ
:
µ
s
±
t
1– (α/2) .
σ
s
8
-
2
ق
ا ل
7%% ,%%آ
*+ ,-ل ا!
)!
,/012 ,-ل ا!
)!. ا
7/ ,-ل ا!
)!
,-ل ا!
7%! .1/ ,/01
8
-
2
-
1
C, @ا ل
D
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ ﺭﺪﻘﻳ
µ
ﻣﻦ
ﺧﻼﻝ
ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ
M
ﺣﻴﺚ ﻧﻌﻠﻢ ﻣﻦ ﻧﻈﺮﻳﺎﺕ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﺃﻥ،
:
E(M) =
µ
m
= µ
.
ﻭ ﲝﺴﺐ ﻣﺴﺘﻮﻯ ﺍﻟﺜﻘﺔ
)
1 –
α
(
ﺗﺘﺤﺪﺩ ﻣﻌﺎﻣﻼﺕ ﺍﻟﺜﻘﺔ ﺍﻟﱵ ﲢﺴﺐ ﺇﻣﺎ ﺑﺎﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺃﻭ ﺗﻮﺯﻳﻊ ﺳﺘﻴﻮﺩﻧﺖ
.
8
-
2
-
1
-
1
ﺗﻘﺪﻳﺮ
ﻣﺘﻮﺳﻂ ﳎﺘﻤﻊ
µ
ﺑﺎﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
ﻣﺒﺪﺋﻴﺎ
ﻧﺴﺘﺨﺪﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
ﻟﺘﻘﺪﻳﺮ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ
ﲟﺠﺎﻝ
ﺘﻤﻊ ﺍﻟﺬﻱ ﺳﺤﺒﺖ ﻣﻨﻪ ﺍﻟﻌﻴﻨﺔﺍ ﻥﺃ ﺎﻨﻤﻠﻋ ﺍﺫﺇ
ﻳﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
)
ﺃﻧﻈﺮ ﻧﻈﺮﻳﺔ
4
ﻣﻦ ﻓﺼﻞ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ
(
.
⇒
−
=
⇒
⇒
→
)
1
,
0
(
~
)
,
(
~
)
,
(
N
m
z
N
M
N
X
m
m
m
σ
µ
σ
µ
σ
µ
(
)
(
)
(
)
m
c
m
c
m
c
m
c
m
c
m
c
c
m
c
z
m
z
m
P
z
m
z
m
P
z
m
z
P
z
m
z
P
σ
µ
σ
σ
µ
σ
σ
µ
σ
σ
µ
α
+
≤
≤
−
=
+
−
≤
−
≤
−
−
=
+
≤
−
≤
−
=
+
≤
−
≤
−
=
−
1
ﻭ
ﻟﺪﻳﻨﺎ
n
m
σ
σ
=
ﺇﺫﻥ
:
+
≤
≤
−
=
−
n
z
m
n
z
m
P
c
c
σ
µ
σ
α
1
µ
0
–
z
1
–
α/2
(σ
m
)
µ
0
µ
0
+z
1
–
α/2
(σ
m
) X
1
–
α
-z
1
–
α/2
0 z
1
–
α/2
Z
1
-
7%%
,-ى ا0
2
-
ج1+ا
,-ت ا6
3
-
ود# ج1+ا
,-ل ا!
α
/2
α
/2

ا
VIII
.
ا , C5
6
ﻓﺘﺼ
ﺒﺢ ﺣﺪﻭﺩ ﳎﺎﻝ ﺍﻟﺜﻘﺔ
ﻫﻲ
:
n
z
m
c
σ
±
ﻭ ﻧﻜﺘﺐ
:
+
−
∈
n
z
m
n
z
m
c
c
σ
σ
µ
;
ﲟﺴﺘﻮﻯ ﺛﻘﺔ
1 –
α
.
ر
9
-
2
@ا ل
ﳝﻜﻦ
،ﺃﻳﻀﺎ
ﺍﺳﺘﻨﺎﺩﺍ ﺇﱃ ﻗﺎﻧﻮﻥ
ﺍﻟﻨﻬﺎﻳﺔ ﺍﳌﺮﻛﺰﻳﺔ
1
،
ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﻟﺘﻘﺪﻳﺮ
M
ﺘﻤﻊ ﳎﻬﻮﻝﺍ ﻥﺎﻛ ﺍﺫﺇ ﱴﺣ
ﺍﻟﺘﻮﺯﻳﻊ ﺑﺸﺮﻁ ﺃﻥ ﺗﻜﻮﻥ
ﺍﻟﻌﻴﻨﺔ ﳑﺘﺪﺓ
(n ≥ 30)
)
ﺃﻧﻈﺮ ﺍﻟﻨﻈﺮﻳﺔ
5
ﻣﻦ ﺍﻟﻔﺼﻞ ﺍﻟﺴﺎﺑﻖ
(
.
ﺇﺫﺍ ﻛﺎﻥ ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﻠﻤﺠﺘﻤﻊ
σ
ﻣﻌﻠﻮﻣﺎ ﻟﻜﻦ
ﺘﻤﻊ ﳏﺪﻭﺩﺍ
)
ﺫﺍ ﺣﺠﻢ
N
(
ﻭﺍﳌﻌﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﺔ
ﻧﻜﺘﺐ
ﺣﺪﻭﺩ
ﺎﻝـﳎ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﳌ ﺔﻘﺜﻟﺍ
µ
ﻛﻤﺎ ﻳﻠﻲ
:
1
−
−
⋅
⋅
±
N
n
N
n
z
m
c
σ
ﺍﳉﺪﻭﻝ ﺍﻵﰐ ﻳﺒﲔ ﻗﻴﻢ
ﻣﻌﺎﻣﻼﺕ ﺍﻟﺜﻘ
ﺔ
z
c
)
ﺣﺪﻭﺩ ﳎﺎﻝ ﺍﻟﺜﻘﺔ
(
ﲝﺴﺐ ﻣﺴﺘﻮﻯ ﺍﻟﺜﻘﺔ
:
ولE
8
-
1
ا */ *$F1ا Dز,ا ما2ا = */ @ا تH $
ﻣﺴﺘﻮﻯ ﺍﻟﺜﻘﺔ
1– α
0.99
0.98
0.95
0.90
0.8
0.5
ﻣﺴﺘﻮﻯ ﺍﳌﻌﻨﻮﻳﺔ
α
0.01
0.02
0.05
0.10
0.2
0.5
1– α/2
0.995
0.99
0.975
0.95
0.9
0.75
Z
1–α/2
2.58
2.326
1.96
1.645
1.282
0.674
ﻣﺜﺎﻝ
:
ﻧﻘﺪﺭ ﺃﻥ
µ
ﻳﻮﺟﺪ
ﺎﻝﺍ ﻞﺧﺍﺩ
m ± 1.96σ
m
ﲟﺴﺘﻮﻯ ﺛﻘﺔ
95
%
)
0.95
(
ﺃﻱ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
)
0.05
(
،
ﺎﻝﺍ ﻞﺧﺍﺩﻭ
m ± 2.58σ
m
ﲟﺴﺘﻮﻯ ﺛﻘﺔ
99
%
ﺃﻱ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
0.01
...
8
-
2
-
1
-
2
ﺗﻘﺪﻳﺮ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ
µ
ﺑﺎﺳﺘﺨﺪﺍﻡ ﺍﻟ
ﺘﻮﺯﻳﻊ
t
ﺘﻤﻊ ﻃﺒﻴﻌﻴﺎﺍ ﻥﺎﻛ ﺍﺫﺇ ﻂﺳﻮﺘﻤﻠﻟ ﺔﻘﺜﻟﺍ ﻝﺎﳎ ﺪﻳﺪﺤﺘﻟ ﺖﻧﺩﻮﻴﺘﺳ ﻊﻳﺯﻮﺗ ﻡﺪﺨﺘﺴﻳ
)
ﺃﻭ ﻋﻠﻰ ﺍﻷ
ﻗ
ﻞ ﺟﺮﺳﻲ ﺍﻟﺸﻜﻞ
(
ﻭﺍ
ﻟﻌﻴﻨﺔ
ﺻﻐﲑﺓ
(n < 30)
ﻭ
σ
ﳎﻬﻮﻝ
)
ﻭﰲ ﺍﻟﻐﺎﻟﺐ ﻳﻜﻮﻥ ﻛﺬﻟﻚ
(
.
ﳝﻜﻦ ﺇﺛﺒﺎﺕ ﺫﻟﻚ ﻛﻤﺎ ﻳﻠﻲ
:
ﺘﻤﻊ ﻃﺒﻴﻌﻲ ﻓﺈﻥﺍ ﻥﺃ ﺎﲟ
ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﻫﻮ ﺍﻵﺧﺮ ﻃﺒﻴﻌﻲ ﻭ
ﻣﻨﻪ
)
1
,
0
(
~
N
m
m
σ
µ
−
ﻭ
ﻛﺬﻟﻚ
nS²/σ² ~
χ ²
(n–1)
.
ﺑﺎﻟﺘﻌﻮﻳﺾ ﰲ ﺗﻌﺮﻳﻒ
ﺍﳌﺘﻐﲑﺓ
ν
/
Z
Y
t
=
ﳒﺪ
:
1
! ) ز,%ا . c .ا
,1% ا$%a ع
-
,dا _% " ة %/آ ,1%ا نآ ,# .
-
*+ اo%و
.
m
–
z
1
–
α/2
(σ
m
)
µ m+z
1
–
α/2
(σ
m
)
1
–
α
α
/2
α
/2

.P ا ء#Rا و ت:#:ا Bإ
–
ءA!ا
2
.
7
1
1
~
1
)
(
/
1
/
~
)
1
(
/
²
²
/
−
−
−
=>
⋅
−
⋅
−
=
⋅
−
⋅
−
=>
−
−
n
n
t
S
n
n
m
n
S
n
n
n
m
t
n
nS
n
m
µ
σ
σ
µ
σ
σ
µ
σ
σ
µ
1
~
1
/
)
(
−
−
−
n
t
n
S
m
µ
ﻭ ﻣﻨﻪ ﳝﻜﻦ ﺍﺳﺘﺨﺪﺍﻡ
ﺗﻮﺯﻳﻊ ﺳﺘﻴﻮﺩﻧﺖ ﻟﺘ
ﻘﺪﻳﺮ
µ
ﲟﺠﺎﻝ ﻓﻨﻜﺘﺐ
ﺣﺪﻭﺩ
ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻛﻤﺎ ﻳﻠﻲ
:
−
+
−
−
∈
−
−
−
−
1
;
1
1
;
2
/
1
1
;
2
/
1
n
S
t
m
n
S
t
m
n
n
α
α
µ
ﻣﻼﺣﻈﺔ
:
ﰲ ﺣﺎﻟﺔ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﺍﳌﻌﺪﻝ ﻧﻜﺘﺐ
1
/
−
→
−
n
t
n
S
m
)
µ
ﻭﻧﻜﺘﺐ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻛﻤﺎ ﻳﻠﻲ
:
+
−
∈
−
−
−
−
n
S
t
m
n
S
t
m
n
n
)
)
1
;
2
/
1
1
;
2
/
1
;
α
α
µ
ﻣﺜﺎﻝ
2
.
ﲟﺴﺘﻮﻯ ﺛﻘﺔ،ﻲﻌﻴﺒﻃ ﻊﻤﺘﳎ ﻂﺳﻮﺘﻣ ﺮﻳﺪﻘﺗ ﺪﻳﺮﻧ
0.95
ﺍﻧﻄﻼﻗﺎ ﻣﻦ ﻋﻴﻨﺔ ﺣﺠﻤﻬﺎ،
10
ﻣﺘﻮﺳﻄﻬﺎ
15
ﻭ ﺍﳓﺮﺍﻓﻬﺎ
ﺍﳌﻌﻴﺎﺭﻱ
27
.
ﻟﺪﻳﻨﺎ
1
~
1
/
)
(
−
−
−
n
t
n
S
m
µ
ﺇﺫﻥ
:
[
]
[
]
687
.
21
;
214
.
8
)
3
(
262
,
2
15
;
)
3
(
262
,
2
15
1
10
27
15
;
1
10
27
15
1
;
1
1
10
,
975
.
0
1
10
,
975
.
0
1
,
2
/
1
1
,
2
/
1
∈
⇒
+
−
∈
⇒
−
+
−
−
∈
⇒
−
−
−
−
∈
−
−
−
−
−
−
µ
µ
µ
µ
α
α
t
t
n
S
t
m
n
S
t
m
n
n
ﻣﻼﺣﻈﺔ
:
ﰲ ﺣﺎﻟﺔ ﺍﻟﻌﻴﻨﺔ ﺍﳌﻤﺘﺪﺓ
)
ﺃﻛﱪ ﻣﻦ
30
(
ﻳﺆﻭﻝ ﺗﻮ
ﺯﻳﻊ ﺳﺘﻴﻮﺩﻧﺖ ﺇﱃ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
ﺍﳌﻌﻴﺎﺭﻱ ﻟﺬﻟﻚ ﻧﺴﺘﺨﺪﻡ ﻫﺬﺍ ﺍﻷﺧﲑ
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﺃﻳﻀﺎ ﻭ ﻧﻜﺘﺐ ﺑﺎﻟﺘﺎﱄ ﺣﺪﻭﺩ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻛﻤﺎ ﻳﻠﻲ
:
n
S
z
m
c
ˆ
±
ﺃﻭ
1
−
⋅
±
n
S
z
m
c
ﻭ ﻧﻜﺘﺐ
ﺑﺎﻟﺘﺎﱄ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻛﻤﺎ ﻳﻠﻲ
:
+
−
∈
n
S
z
m
n
S
z
m
c
c
ˆ
;
ˆ
µ
8
-
2
-
1
-
3
ﺗﻌﻴﲔ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﺍﳌﻨﺎﺳﺐ ﻟﺪﻗﺔ ﻣﻌﻴﻨﺔ
.
ﻗﺪ ﻧﺮﻏﺐ ﰲ ﲢﺪﻳﺪ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﺍ
ﻟﻼﺯﻡ ﻟﺘﺤﻘﻴﻖ
ﻣﻘﺪﺍﺭ ﺩﻗﺔ
ﻭ ﻣﺴﺘﻮﻯ ﺛﻘﺔ ﻣﻌﻴﻨﲔ
.
ﻳﻘﺼﺪ ﲟﻘﺪﺍﺭ ﺍﻟﺪﻗﺔ
m – µ
.
ﰲ ﺣﺎﻟﺔ
ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﰲ ﺍﻟﺘﻘﺪﻳﺮ ﻧﺴﺘﻨﺘﺞ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﺑﺪﻻﻟﺔ
ﻣﻘﺪﺍﺭ ﺩﻗﺔ
ﻭ ﻣﺴﺘﻮﻯ ﺛﻘﺔ ﻛﻤﺎ ﻳﻠﻲ
:
(
)
( )
2
/
1
)
(
−
=
⇒
−
=
⇒
=
−
⇒
=
−
⇒
+
=
µ
σ
µ
σ
σ
µ
σ
µ
σ
µ
m
z
n
m
z
n
n
z
m
n
z
m
n
z
m

ا
VIII
.
ا , C5
8
8
-
2
-
2
F30: @ا ل
D */
8
-
2
-
2
-
1
ﺘﻤﻊ ﻏﲑﺍ ﺔﻟﺎﺣ
ﺍﶈ
ﺪﻭﺩ ﺃﻭ
ﻛﻮﻥ
ﺍﳌﻌﺎ
ﻳﻨﺔ ﻏﲑ ﻧﻔﺎﺩﻳﺔ
ﻟﺘﻜﻦ
p’
ﲤﺜﻞ ﻧﺴﺒﺔ
"
ﳒﺎﺣﺎﺕ
"
ﰲ ﻋﻴﻨﺔ ﺫﺍﺕ ﺣﺠﻢ
n ≥ 30
ﻣﺴﺘﺨﺮﺟﺔ ﻣﻦ ﳎﺘﻤﻊ
ﻃﺒﻴﻌﻲ
،
ﺣﻴﺚ
p
ﻫﻲ ﻧﺴﺒﺔ
ﺍﻟﻨﺠﺎﺣﺎﺕ
ﺘﻤﻊﺍ ﰲ
.
ﻧﻌﻠﻢ ﻣﻦ ﻧﻈﺮﻳﺔ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﺃﻥ
p’~ N(p, σ
p’
)
.
ﺑﻨﻔﺲ ﺍﻟﻄﺮﻳﻘﺔ ﺍﳌﺴﺘﺨﺪﻣﺔ ﺑﺎﻟﻨﺴﺒﺔ ﻟﻠﻤﻌﻠﻤﺔ
µ
ﺃﻋﻼﻩ ﻧﺴﺘﻨﺘﺞ ﺃﻥ
p
ﺎﻝ ﺫﻱ ﺍﳊﺍ ﱃﺇ ﻲﻤﺘﻨﺗ
ﺪﻭﺩ
p’ ± z
c
σ
p’
.
ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﻏﲑ ﺍﻟﻨﻔﺎﺩﻳﺔ ﻧﻌﻠﻢ ﺃﻥ
n
pq
p
=
′
σ
ﻭﻣﻨﻪ ﳛﺪﺩ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻝ
p
ﺑﺎﳊﺪﻭﺩ
:
n
p
p
z
p
c
)
1
(
'
−
⋅
±
ﻟﻜﻦ
p
ﳎﻬﻮﻟﺔ ﻟﺬﻟﻚ ﻧﻌﻮﺽ
p
ﺏ
p’
ﻭ ﻧﻜﺘﺐ
ﺑﺎﻟﺘﺎﱄ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻟﻠﻨﺴﺒﺔ ﻛﻤﺎ ﻳﻠﻲ
:
′
′
⋅
±
′
′
⋅
−
∈
−
−
n
q
p
z
p
n
q
p
z
p
p
2
/
1
2
/
1
'
;
'
α
α
ﺘﻤﻊ ﳏﺪﻭﺩ ﺫﺍ ﺣﺠﻢﺍ ﻥﻮﻛ ﺔﻟﺎﺣ ﰲ
N
ﻭﺍﳌﻌﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﺔ
ﻧﺴﺘﺨﺪﻡ ﻣﻌﺎﻣﻞ ﺍﻹﺭﺟﺎﻉ ﻋﻨﺪ ﺣﺴﺎﺏ
σ
p’
:
1
)
1
(
'
−
−
⋅
′
−
′
=
N
n
N
n
p
p
p
σ
ﻣﺜﺎﻝ
.
ﺳﺤﺒﻨﺎ ﻋﻴﻨﺔ ﺣﺠﻤﻬﺎ
31
ﻣﻦ
ﻋﻼﻣﺎﺕ
ﺍﻟﻄﻠﺒﺔ ﰲ ﺍﻣﺘﺤﺎﻥ ﺍﻹﺣﺼﺎﺀ ﺍﻟﺮﻳﺎﺿﻲ ﻟ
ﺪﻓﻌﺔ
2008
ﻭ ﻋﺪﺩﻫﺎ
300
ﻓﻜﺎﻧﺖ
ﻛﺎﻟﺘﺎﱄ
:
3
،
18.5
،
10.5
،
19.5
،
11.5
،
14
،
11
،
16.5
،
18
،
7.5
،
3.5
،
2.5
،
2.5
،
8.5
،
10.5
،
8.5
،
2
،
5
،
12
،
1.5
،
5.5
،
8.5
،
6
،
15
،
6
،
6
،
10
،
2.5
،
1
،
2.5
،
3
.
ﻗﺪﺭ
ﻧﻘﻄﻴﺎ ﻭ
ﲟﺴﺘﻮﻯ ﺛﻘﺔ
0.90
ﻧﺴﺒﺔ ﺍﻟﻄﻠﺒﺔ ﺍﳊﺎﺻﻠﲔ ﻋﻠﻰ ﺍﻟﻌﻼﻣﺔ ﻋﺸﺮﺓ ﺃﻭ ﺃﻛﺜﺮ
ﰲ ﺍﻟﻜﻠﻴﺔ
.
ﻟﺪﻳﻨﺎ
12
ﻧﻘﻄﺔ ﺃﻛﱪ ﺃﻭ ﺗﺴﺎﻭﻱ ﺍﻟﻌﺸﺮﺓ
(n
a
= 12
)
ﺇﺫﻥ
:
p’ = 12/31 = 0.387
ﻭ ﻧﻜﺘﺐ
:
%
7
.
38
387
.
0
ˆ
=
=
′
=
p
p
ﺑﺎﻟﻨﻈﺮ ﳊﺠﻢ ﺍﻟﻌﻴﻨﺔ
ﳝﻜﻦ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﰲ ﺍﻟﺘﻘﺪﻳﺮ
.
ﺘﻤﻊ ﳏﺪﻭﺩ ﻭﺍﻟﻌﻴﻨﺔ ﻧﻔﺎﺩﻳﺔﺍ ﻥﺃ ﺎﲟ
)
ﻮﻥـﻜﺗ ﻥﺃ ﻞﺻﻷﺍ
ﻛﺬﻟﻚ
(
ﻧﺴﺘﺨﺪﻡ ﻣﻌﺎﻣﻞ ﺍﻹﺭﺟﺎﻉ
ﻭﺍﻟﺬﻱ ﻻ ﳝﻜﻦ ﺇﳘﺎﻟﻪ ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻷﻥ
n > 0.05N
.
ﳎﺎﻝ ﺍﻟﺜﻘﺔ
ﻳﻜﺘﺐ
ﻛﻤﺎ ﻳﻠﻲ
:
[
]
[
]
[
]
395
.
0
;
379
.
0
)
0048
.
0
(
64
.
1
387
.
0
;
)
0048
.
0
(
64
.
1
387
.
0
64
.
1
0048
.
0
1
300
31
300
31
)
387
.
0
1
(
387
.
0
1
'
;
'
95
.
0
2
/
1
.
0
1
2
/
1
'
'
2
/
1
2
/
1
∈
⇒
+
−
∈
=
=
=
=
−
−
−
=
−
−
′
′
=
⋅
+
⋅
−
∈
−
−
′
−
′
−
p
p
z
z
z
N
n
N
n
q
p
z
p
z
p
p
p
p
p
p
α
α
α
σ
σ
σ
σ
ﻣﺜﺎﻝ
2
.
ﺑ
ﺘﻔﺤﺺ
ﺍﳌ
ﻠﻔﺎﺕ ﺍﻟﻄﺒﻴﺔ
ﻟﻌﻴﻨﺔ ﻣﻦ
100
ﻣﺪﺧﻦ ﺗﺒﲔ ﺃﻥ
40
ﻣﻨﻬﻢ ﺃﺻﻴﺒﻮﺍ ﲟﺮﺽ ﻣﻌﲔ
.
ﻛﻴﻒ ﳝﻜﻦ
ﺗﻘﺪﻳﺮ ﻧﺴﺒﺔ
ﺍﻹﺻﺎﺑﺔ ﺑﺎﳌﺮﺽ ﻟﺪﻯ ﺍﳌﺪﺧﻨﲔ ﲟﺴﺘﻮﻯ ﺛﻘﺔ
90
ﺑﺎﳌﺎﺋﺔ
.
ﺍﳊﻞ
:
ﺍﻟﻌﻴﻨﺔ ﻛﺒﲑﺓ ﺇﺫﻥ ﳝﻜﻦ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﰲ ﺍﻟﺘﻘﺪﻳﺮ
.
ﻧﻔﺘﺮﺽ ﺃﻥ
N
ﻛﺒﲑ
)
ﻋﺪﺩ ﺍﳌﺪﺧﻨﲔ
(
ﺚـﻴﲝ
:
n/N < 0.05

.P ا ء#Rا و ت:#:ا Bإ
–
ءA!ا
2
.
9
[
]
[
]
[
]
48
.
0
;
32
.
0
)
049
.
0
(
64
.
1
4
.
0
;
)
049
.
0
(
64
.
1
4
.
0
64
.
1
049
.
0
100
)
4
.
0
1
(
4
.
0
'
;
'
95
.
0
2
/
1
.
0
1
2
/
1
'
2
/
1
2
/
1
∈
⇒
+
−
∈
=
=
=
=
−
=
′
′
=
⋅
+
⋅
−
∈
−
−
′
−
′
−
p
p
z
z
z
n
q
p
z
p
z
p
p
p
p
p
α
α
α
σ
σ
σ
8
-
2
-
2
-
2
ﲢﺪﻳﺪ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﻭﻓﻘﺎ ﳋ
ﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ
.
،ﻧﻌﻠﻢ ﺃﻥ ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ ﻣﺮﺗﺒﻂ ﲝﺠﻢ ﺍﻟﻌﻴﻨﺔ
ﻟﺬﻟﻚ
ﳝﻜﻦ ﲢﺪﻳﺪ
ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
ﺍﳌﻮﺍﻓﻖ ﻟﻘﻴﻤﺔ ﻣﻌﻴﻨﺔ ﻟﺘ
ﺒﺎﻳﻦ ﺍﳌﻘﺪﺭ
p’
ﻭﻳﻜﻮﻥ
ﺫﻟﻚ ﺣﺴﺐ ﺍﺳﺘﺨﺪﺍﻡ ﻣﻌﺎﻣﻞ ﺍﻹﺭﺟﺎﻉ ﺃﻭ ﻻ
.
-
ﰲ ﺣﺎﻟﺔ ﻋﺪﻡ ﺍﺳﺘﺨﺪﺍﻡ ﻣﻌﺎﻣﻞ ﺍﻹﺭﺟﺎﻉ ﺃﻱ
n
q
p
p
′
′
=
′
2
σ
ﳓﺴﺐ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﺍﳌﻨﺎﺳﺐ ﻛﻤﺎ ﻳﻠﻲ
:
2
'
2
'
p
p
q
p
n
n
q
p
σ
σ
′
′
=
⇒
′
′
=
-
ﺃﻣﺎ ﺇﺫﺍ ﺗﻮﺟﺐ ﺍﺳﺘﺨﺪﺍﻡ
ﻣﻌﺎﻣﻞ ﺍﻹﺭﺟﺎﻉ ﻓﺈﻥ ﺍﺳﺘﻨﺘﺎﺝ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﺍﳌﻨﺎﺳﺐ ﻳﻜﻮﻥ ﻛﺎﻟﺘﺎﱄ
:
+
′
′
−
=
⇒
+
′
′
−
=
⇒
=
+
′
′
−
⇒
−
−
′
′
=
−
′
′
−
−
′
′
=
−
′
′
−
′
′
=
−
−
′
′
=
′
′
′
′
1
1
1
1
1
1
1
1
1
1
1
)
1
(
)
1
(
1
2
2
2
2
q
p
N
N
n
q
p
N
N
n
n
N
q
p
N
n
N
N
q
p
N
q
p
N
n
N
q
p
N
n
n
q
p
N
q
p
N
n
N
n
q
p
p
p
p
p
σ
σ
σ
σ
8
-
2
-
3
@ا ل
وIF:
D ري$ ا فا(LH
*$F
ﻟﻴﻜﻦ ﻟﺪﻳﻨﺎ ﳎﺘﻤﻊ ﻳﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
N(
µ
, σ)
ﺑﺘﺒﺎﻳﻦ ﳎﻬﻮﻝ
.
ﻧﺮﻳﺪ ﺗﻘﺪﻳﺮ ﻫﺬﺍ ﺍﻟﺘﺒﺎﻳﻦ
.
ﲣﺘﻠﻒ ﻃﺮﻳﻘﺔ ﺍﻟﺘﻘﺪﻳﺮ ﺣﺴﺐ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ ﻥﻮﻛ
µ
ﻣﻌﻠﻮﻣﺎ ﺃﻭ ﻻ
.
8
-
2
-
3
-
1
ﰲ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ ﻥﻮﻛ ﺔﻟﺎﺣ
µµµµ
ﻣﻌﻠﻮﻣ
ﺎ
ﻧﻌﻠﻢ ﻣﻦ ﻧﻈ
ﺮ
ﻳﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺃﻥ
2
~
²
²
ˆ
n
n
χ
σ
σ
ﺣﻴﺚ
n
x
i
∑
−
=
i
)²
(
²
ˆ
µ
σ
ﻭ
x
i
ﺘﻤﻊﺍ ﻦﻣ ﺔﻄﻴﺴﺑ ﺔﻴﺋﺍﻮﺸﻋ ﺔﻨﻴﻋ ﺕﺍﺩﺮﻔﻣ
.
ﻧﺴﺘﻨﺘﺞ ﺃﻧﻪ ﻣﻦ ﺃﺟﻞ ﺃﻱ ﻣﺴﺘﻮﻯ ﺛﻘﺔ
1 –
α
:
α
χ
σ
σ
χ
α
α
−
=
≤
≤
−
1
²
²
ˆ
2
;
2
/
1
2
;
2
/
n
n
n
P
ﻣﺜﺎﻝ
:
ﺍﻻﺣﺘﻤﺎﻝ
= 0.95
1-α
ﺎﻝ ﺍﻹﺣﺼﺎﺋﻴﺔ
²
²
ˆ
σ
σ
n
ﻳﻜﺘﺐ ﻛﻤﺎ ﻳﻠﻲ
:
95
.
0
²
²
2
;
975
.
0
2
;
025
.
0
=
≤
≤
n
n
n
P
χ
σ
σ
χ
)
ا
VIII
.
ا , C5
10
ر
8
-
1
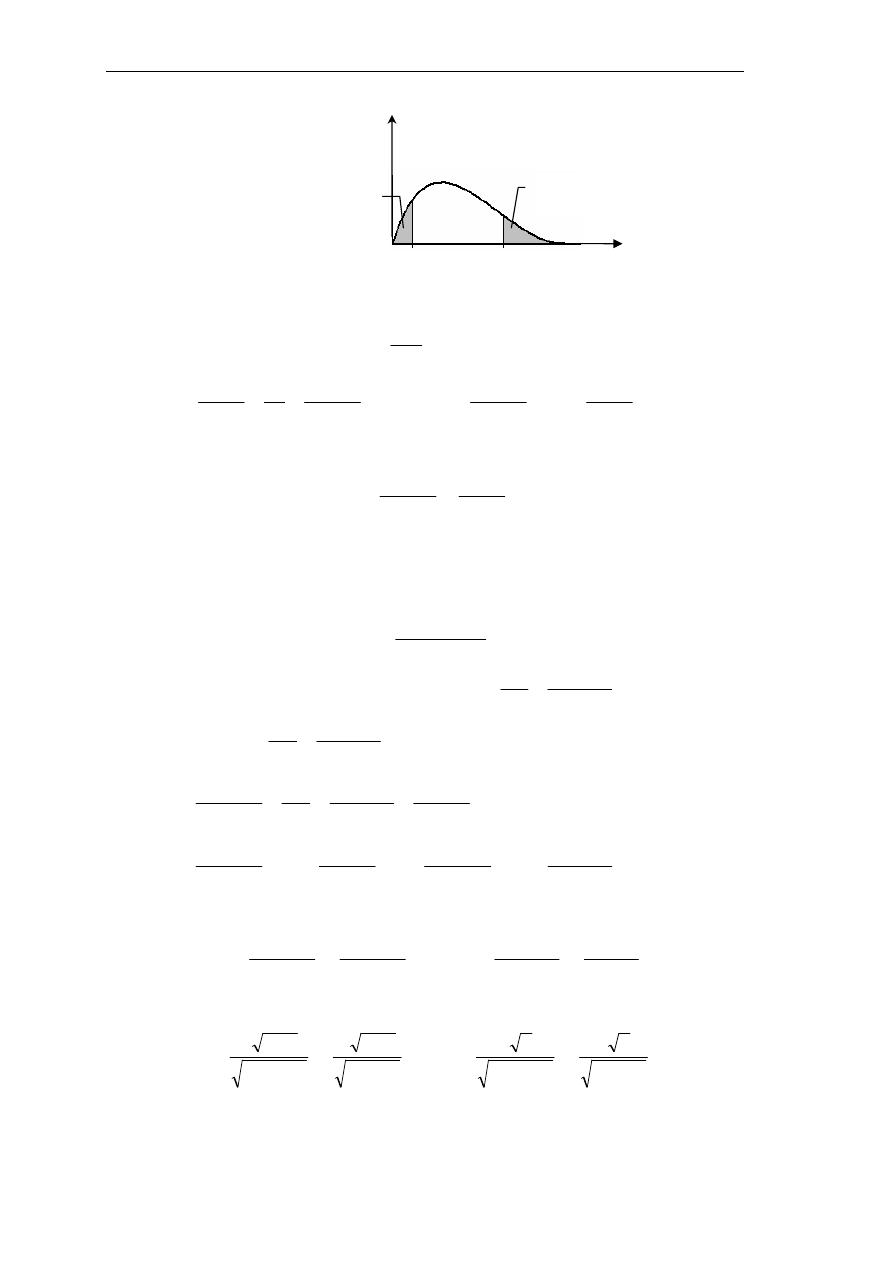
ﺤﺩﻭﺩ
ﻤﺠﺎل
ﻝﻤﺘﻐﻴﺭﺓ ﺘﺘﺒﻊ ﺘﻭﺯﻴﻊ ﻙ
2
ﻣﻦ ﺍﻟﺼﻴﻐﺔ ﺍﻟﻌﺎﻣﺔ
ﺎﻝ ﺍﻹﺣﺼﺎﺋﻴﺔ
α
χ
σ
σ
χ
α
α
−
=
≤
≤
−
1
²
²
ˆ
2
;
2
/
1
2
;
2
/
n
n
n
P
ﻧﺴﺘﻨﺘﺞ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﻟﻠﺘﺒﺎﻳﻦ ﻛﻤﺎ ﻳﻠﻲ
:
α
χ
σ
σ
χ
σ
α
σ
χ
σ
σ
χ
α
α
α
α
−
=
≤
≤
⇒
−
=
≤
≤
⇒
−
−
1
²
ˆ
²
ˆ
1
²
ˆ
²
1
²
ˆ
2
;
2
/
2
2
;
2
/
1
2
;
2
/
1
2
;
2
/
n
n
n
n
n
n
P
n
n
P
ﻭﻣﻨﻪ
:
∈
−
2
;
2
/
2
;
2
/
1
2
²
ˆ
,
²
ˆ
n
n
n
n
α
α
χ
σ
χ
σ
σ
8
-
2
-
3
-
2
ﰲ ﺣﺎﻟﺔ ﻛ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ ﻥﻮ
µµµµ
ﻏﲑ ﻣﻌﻠﻮﻡ
ﻧﺴﺘﻌﻤﻞ
ﺍﳌﺘﻮﺳﻂ ﺍﳊﺴﺎﰊ ﻟﻠﻌﻴﻨﺔ
M
ﻛﻤﻘﺪﺭ ﻝ
µ
:
1
)²
(
²
−
−
=
∑
n
m
x
S
i
i
)
ﻣﻦ
ﺍﳋﺎﺻﻴﺔ
:
1
²
~
²
²
ˆ
)
1
(
²
²
−
−
=
n
S
n
nS
χ
σ
σ
ﻧﺴﺘﻨﺘﺞ ﺃﻧﻪ ﻣﻦ ﺃﺟﻞ ﺃﻱ ﻣﺴﺘﻮﻯ ﺛﻘﺔ،
1–
α
:
α
χ
σ
χ
χ
σ
χ
α
χ
σ
σ
χ
α
χ
σ
σ
χ
α
α
α
α
α
α
α
α
−
=
−
≤
≤
−
=
≤
≤
⇒
−
=
≤
−
=
≤
⇒
−
=
≤
−
=
≤
−
−
−
−
−
−
−
−
−
−
−
−
1
²
)
1
(
²
²
)
1
(
²
²
²
1
1
²
)
1
(
²
²
²
1
1
²
²
)
1
(
²
²
2
1
;
2
/
2
1
;
2
/
1
2
1
;
2
/
2
1
;
2
/
1
2
1
;
2
/
2
1
;
2
/
1
2
1
;
2
/
1
2
1
;
2
/
n
n
n
n
n
n
n
n
S
n
S
n
P
nS
nS
P
S
n
nS
P
S
n
nS
P
)
)
)
)
ﻭ
ﻣﻨﻪ ﻧﺴﺘﻨﺘﺞ
ﳎﺎﻝ ﺍﻟﺜﻘﺔ
ﺘﻤﻊﺍ ﻦﻳﺎﺒﺘﻟ
:
∈
−
−
−
2
1
;
2
/
2
1
;
2
/
1
2
²
,
²
n
n
nS
nS
α
α
χ
χ
σ
ﺃﻭ
−
−
∈
−
−
−
2
1
;
2
/
2
1
;
2
/
1
2
²
)
1
(
,
²
)
1
(
n
n
S
n
S
n
α
α
χ
χ
σ
)
)
ﻭ
ﻛﺬﺍ
ﳎﺎﻝ
ﺍ
ﻟﺜﻘﺔ ﻝ
σ
ﻛﻤﺎ ﻳﻠﻲ
:
∈
−
−
−
2
1
;
2
/
2
1
;
2
/
1
,
n
n
n
S
n
S
α
α
χ
χ
σ
ﺃﻭ
−
−
∈
−
−
−
2
1
;
2
/
2
1
;
2
/
1
1
,
1
n
n
n
S
n
S
α
α
χ
χ
σ
)
)
ﻧﻈﺮﺍ ﻷﻥ ﺗﻮﺯﻳﻊ ﻙ
2
ﺇﺫ ﺗﻮﺟﺪ ﻃﺮﻳﻘﺔ ﻟﺘﻀﻴﻴﻖ ﳎﺎﻝ ﺍﻟﺜﻘﺔ ﺃﻛﺜﺮ ﺇﺫﺍ ﱂ ﻧﺸﺄ ﺃﻥ،ﻞﺜﻣﻷﺍ ﺲﻴﻟ ﻩﻼﻋﺃ ﻝﺎﺍ ﻥﺈﻓ ﻞﺛﺎﻤﺘﻣ ﲑﻏ
ﻭﻫﺬﺍ ﲞﻼﻑ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﺍﳌﺘﻤﺎﺛﻠﺔ ﻛﺎﻟﻄﺒﻴﻌﻲ ﻭﺳﺘﻴﻮﺩﻧﺖ،ﺔﻳﻭﺎﺴﺘﻣ ﲎﺤﻨﳌﺍ ﻑﺍﺮﻃﺃ ﻥﻮﻜﺗ
.
α
/2 =
0.025
α
/2 =
0.025
1-
α
=
0.95
0 χ²
0.025,n
χ
²
0.975,n
χ
²
f(χ²)
x)

.P ا ء#Rا و ت:#:ا Bإ
–
ءA!ا
2
.
11
8
-
2
-
4
F F30 @ا تN
*0
I$
ﺭﺃﻳﻨﺎ ﺳﺎﺑﻘﺎ
)
ﻓﺼﻞ
ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ
(
ﺃﻧﻪ ﺇﺫﺍ ﻛﺎﻥ ﻟﺪﻳﻨﺎ ﳎﺘﻤﻌﺎﻥ
ﻃﺒﻴﻌﻴﺎﻥ
ﺗﺒﺎﻳﻨﺎﳘﺎ
σ²
1
, σ²
2
ﻭﺳﺤﺒﻨﺎ ﻣﻨﻬﻤﺎ ﻋﻴﻨﺘ
ﺎ
ﻥ
ﻋﺸﻮﺍﺋﻴﺘ
ﺎ
ﻥ
ﺣﺠﻤﻴﻬﻤ
ﺎ
ﻋﻠﻰ ﺍﻟﺘﻮﺍﱄ
n
1
, n
2
ﻓﺈﻥ
:
1
;
1
2
2
2
2
2
1
2
1
2
1
/
ˆ
/
ˆ
−
−
→
n
n
F
S
S
σ
σ
α
σ
σ
α
α
−
=
≤
≤
⇒
−
−
−
−
−
1
/
/
1
,
1
,
2
/
1
2
2
2
2
2
1
2
1
1
,
1
,
2
/
2
1
2
1
n
n
n
n
F
S
S
F
P
)
)
ﻭﻣﻨﻪ ﳝﻜﻦ ﻛﺘﺎﺑﺔ ﳎﺎﻝ ﺍﻟﺜﻘﺔ
ﻋﻨﺪ ﻣﺴﺘﻮﻯ ﺛﻘﺔ
(1-α)
ﺘﻤﺍ ﻦﻳﺎﺒﺗ ﺔﺒﺴﻨﻟ
ﺘﻤﻊ ﺍﻟﺜﺎﱐﺍ ﻦﻳﺎﺒﺗ ﱃﺇ ﻝﻭﻷﺍ ﻊ
ﻛﻤﺎ ﻳﻠﻲ
:
1
,
1
,
2
/
2
2
2
1
2
2
2
1
1
,
1
,
2
/
1
2
2
2
1
2
1
2
1
/
/
−
−
−
−
−
≤
≤
n
n
n
n
F
S
S
F
S
S
α
α
σ
σ
)
)
)
)
ﻣﺜﻼ ﻋﻨﺪ ﻣﺴﺘﻮﻯ ﺛﻘﺔ
0.98
ﻧﻜﺘﺐ
:
1
,
1
,
01
.
0
2
2
2
1
2
2
2
1
1
,
1
,
99
.
0
2
2
2
1
2
1
2
1
/
/
−
−
−
−
≤
≤
n
n
n
n
F
S
S
F
S
S
)
)
)
)
σ
σ
8
-
2
-
5
OH!
ﻟﺘﻘﺪﻳﺮ ﺇﺣﺼﺎﺋﻴﺔ ﳎﺘﻤﻊ ﻧﺴﺘﺨﺪﻡ ﻧﻈﺮﻳﺎﺕ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ
.
ﺗﺘﻨﺎﻭﻝ ﻫﺬﻩ ﺍﻟﻨﻈﺮﻳﺎﺕ ﺧﺼﺎﺋﺺ ﺇﺣﺼﺎﺋﻴﺎﺕ ﺍﻟﻌﻴﻨﺔ ﻣﻦ ﻣﺘﻮﺳﻂ
، ﺍﻟﻨﺴﺒﺔ ﰲ ﺍﻟﻌﻴﻨﺔ،ﺔﻨﻴﻌﻟﺍ
...
ﺘﻤﻊﺍ ﰲ ﺎﳍ ﺓﺮﻇﺎﻨﳌﺍ ﺕﺎﻴﺋﺎﺼﺣﻹﺎﺑ ﺎﻬﺘﻗﻼﻋﻭ
.
ﻟﺘﻜﻮﻳﻦ ﳎﺎﻝ ﺛﻘﺔ ﳌﻌﻠﻤﺔ ﻣﺎ
θ
ﻟﻠﻤﺠﺘﻤﻊ ﲟﺴﺘﻮﻯ ﺛﻘﺔ ﻣﺎ
ﻧﺘﺒﻊ ﺍﳋﻄﻮﺍﺕ ﺍﻟﺘﺎﻟﻴﺔ
:
-
ﳓﺪﺩ ﻣﻘﺪﺭ
θ
)
ﻝ
θ
ﻣﻦ ﺧﻼﻝ ﻋﻴﻨﺔ ﻋﺸﻮﺍﺋﻴﺔ ﺑﺴﻴﻄﺔ
.
-
ﳓﺪﺩ ﺍﻟﻘﺎﻧﻮﻥ ﺍﻻﺣﺘﻤﺎﱄ ﻟﻠﻤﻘﺪﺭ
θ
)
)
M
ﻣﺜﻼ ﻗﺪ ﺗ
ﺘﺒﻊ ﺕ ﻁ ﺃﻭ ﺳﺘﻴﻮﺩﻧﺖ
(
ﺃﻭ ﳌﺘﻐﲑﺓ ﻣﺮﺗﺒﻄﺔ ﺑﻪ
)
ﺒﺔ ﻝـﺴﻨﻟﺎﺑ
σ
²
ﻧﻌﻠﻢ ﺃﻥ
nS²/σ² ~ χ²
n–1
.(
-
ﳓﺪﺩ ﺻﻴﻐﺔ ﺣﺪﻭﺩ ﳎﺎﻝ ﺍﻟﺜﻘﺔ
l
1
ﻭ
l
2
ﲝﻴﺚ ﳓﺼﻞ ﻋﻠﻰ ﺍﻟﻌﺒﺎﺭﺓ
:
P (l
1
≤ θ ≤ l
2
) = 1 –
α
-
ﳓﺪﺩ ﻣﻌﺎﻣﻼﺕ ﺍﻟﺜﻘﺔ
)
z
1–
α
/2
±
، ﰲ ﺣﺎﻟﺔ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
t
1–
α
/2
±
ﰲ ﺣﺎﻟﺔ ﺍﻟﺘﻮﺯﻳﻊ
T
...
(
ﰒ
ﺍﺣﺴ
ﺐ
l
1
ﻭ
l
2
.

ا
VIII
.
ا , C5
12
ولE
-8
2
0$ا =و IFا ,:$ ،D ا Dز, $F P3= C, : 0$ ا Dز,
.
ﻗﺎﻧﻮﻥ
M
ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ
σ
m
n
ﺗﺒﺎﻳﻦ
ﺘﻤﻊﺍ
)
σ²
(
ﻗﺎﻧﻮﻥ
ﺘﻤﻊﺍ
ﺍﳌﻌﻠﻤﺔ
ﺍﳌﻘﺪﺭﺓ
M ~ N(µ ; σ/√n)
σ
m
= σ/√n
n < 30
ﺃﻭ
n ≥ 30
ﻣﻌﻠﻮﻡ
1
~
/
1
/
−
−
=
−
−
n
t
n
S
m
n
S
m
)
µ
µ
n < 30
M ≈ N(µ ; Ŝ /√n)
1
−
=
=
n
S
n
S
m
)
)
σ
n ≥ 30
ﻏﲑ ﻣﻌﻠﻮﻡ
ﻃﺒﻴ
ﻌﻲ
M ≈ N(µ ; σ/√n)
σ
m
= σ/√n
n ≥ 30
ﻣﻌﻠﻮﻡ
M ≈ N(µ ; Ŝ /√n)
1
−
=
=
n
S
n
S
m
)
)
σ
n ≥ 100
ﻏﲑ ﻣﻌﻠﻮﻡ
ﻏﲑ
ﻣﻌﻠﻮﻡ
ﻣﺘﻮﺳﻂ
ﺘﻤﻊﺍ
µ

.P ا ء#Rا و ت:#:ا Bإ
–
ءA!ا
2
.
13
ولE
8
-
3
I0F I F30:و IF: ،F30: @ا ل (
ﺍﳌﻌﻠﻤﺔ
ﺍﳌﻘﺪﺭﺓ
ﺘﻤﻊﺍ
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﺍﳌﺴﺘﺨﺪﻡ
ﺣﺪﻭﺩ
ﳎﺎﻝ ﺍﻟﺜﻘﺔ
ﳎﺘﻤﻊ ﻏﲑ ﳏﺪﻭﺩ ﺃﻭ
ﻋﻴﻨﺔ
ﻏﲑ ﻧﻔﺎﺩﻳﺔ ﻭ ﳑﺘﺪﺓ
(n≥30)
p’
≈
N(p, σ
p’
)
n
p
p
z
p
c
)
1
(
'
−
⋅
±
ﺍﻟﻨﺴﺒﺔ ﰲ
ﺘﻤﻊﺍ
p
ﳎﺘﻤﻊ ﳏﺪﻭﺩ ﻣﻌ
ﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﺔ
1
)
1
(
'
−
−
⋅
−
⋅
±
N
n
N
n
p
p
z
p
c
ﳎﺘﻤﻊ ﻃﺒﻴﻌﻲ ﲟﺘﻮﺳﻂ ﻣﻌﻠﻮﻡ
2
~
²
²
ˆ
n
n
χ
σ
σ
∈
−
2
;
2
/
2
;
2
/
1
2
²
ˆ
,
²
ˆ
n
n
n
n
α
α
χ
σ
χ
σ
σ
ﺗﺒﺎﻳﻦ
ﺘﻤﻊﺍ
σ²
ﳎﺘﻤﻊ ﻃﺒﻴﻌﻲ ﲟﺘﻮﺳﻂ ﻏﲑ
ﻣﻌﻠﻮﻡ
1
²
~
²
²
ˆ
)
1
(
²
²
−
−
=
n
S
n
nS
χ
σ
σ
−
−
∈
−
−
−
2
1
;
2
/
2
1
;
2
/
1
2
²
)
1
(
,
²
)
1
(
n
n
S
n
S
n
α
α
χ
χ
σ
)
)
ﻧﺴﺒﺔ ﺗﺒﺎﻳﲏ
ﳎﺘﻤﻌﲔ
ﻋﻴﻨﺘﲔ ﻉ ﻣﻦ ﳎﺘﻤﻌﲔ ﻃﺒﻴﻌﻴﲔ
ﺃﻭ ﻣﻦ ﳎﺘﻤﻊ ﻃﺒﻴﻌﻲ ﻭﺍﺣﺪ
.
1
;
1
2
2
2
2
2
1
2
1
2
1
/
ˆ
/
ˆ
−
−
→
=
n
n
F
S
S
σ
σ
1
,
1
,
2
/
2
2
2
1
2
2
2
1
1
,
1
,
2
/
1
2
2
2
1
2
1
2
1
/
/
−
−
−
−
−
≤
≤
n
n
n
n
F
S
S
F
S
S
α
α
σ
σ
)
)
)
)
8
-
2
-
6
Q(:
.
D او قو : @ا تN
ﺇﺫﺍ ﻛﺎﻧﺖ
s
1
ﻭ
s
2
ﺗﻜﺘﺐ ﺣﺪﻭﺩ ﺍﻟﺜﻘﺔ،ﻥﺎﺘﻠﻘﺘﺴﻣ ﻥﺎﺘﻨﻴﻌﻟﺍﻭ ،ﻲﻌﻴﺒﻄﻟﺍ ﻊﻳﺯﻮﺘﻟﺍ ﻦﻣ ﺏﺮﺘﻘﻳ ﻊﻳﺯﻮﺗ ﺎﳍ ﺔﻨﻳﺎﻌﻣ ﺎﺘﻴﺋﺎﺼﺣﺇ
ﻟﻠﻔﺮﻭﻕ ﺑﲔ ﺍﳌﻌﺎﱂ ﺍﻟﱵ ﲤﺜﻠﻬﺎ ﺍﻹﺣﺼﺎﺋﻴﺘﲔ ﻛﻤﺎ ﻳﻠﻲ
:
2
1
2
1
²
²
2
1
2
1
S
S
c
S
S
c
z
S
S
z
S
S
σ
σ
σ
+
⋅
±
−
=
⋅
±
−
−
ﻤﻮﻉﺍ ﺔﻟﺎﺣ ﰲ
:
2
1
2
1
²
²
2
1
2
1
S
S
c
S
S
c
z
S
S
z
S
S
σ
σ
σ
+
⋅
±
+
=
⋅
±
+
−
ﻣﺜﺎﻝ
:
ﺇﺫﺍ ﻛﺎﻧﺖ ﺍﻹﺣﺼﺎﺋﻴﺘﺎﻥ ﳘﺎ
ﳓﺪﺩ ﳎﺎﻝ ﺍﻟﺜﻘﺔ،ﻦﻳﺩﻭﺪﳏ ﲑﻏ ﲔﻌﻤﺘﳎ ﻦﻣ ﲔﺘﺑﻮﺤﺴﻣ ،ﲔﺘﻠﻘﺘﺴﻣ ﲔﺘﻨﻴﻋ ﺎﻄﺳﻮﺘﻣ
ﻟﻠﻔﺮﻕ
)
ﻭ ﻟﻠﻤﺠﻤﻮﻉ
(
ﺘﻤﻌﲔﺍ ﻲﻄﺳﻮﺘﻣ ﲔﺑ
µ
1
– µ
2
ﻛﻤﺎ ﻳﻠﻲ
:
2
2
2
1
2
1
2
1
2
1
2
1
n
n
z
m
m
z
m
m
c
m
m
c
σ
σ
σ
+
⋅
±
−
=
⋅
±
−
−
ﻣﺜﺎﻝ
2
:
ﻣﺴﺤﻮﺑﺘﺎﻥ ﻣﻦ ﳎﺘﻤﻌﲔ ﻏﲑ ﳏﺪﻭﺩﻳﻦ،ﲔﺘﻠﻘﺘﺴﻣ ﲔﺘﻨﻴﻋ ﰲ ﻥﺎﺘﺒﺴﻧ ﺎﳘ ﻥﺎﺘﻴﺋﺎﺼﺣﻹﺍ ﺖﻧﺎﻛ ﺍﺫﺇ
:
2
2
1
1
2
1
'
'
2
1
'
'
'
'
2
1
n
pq
n
pq
z
p
p
z
p
p
c
p
p
c
+
⋅
±
−
=
⋅
±
−
−
σ

ا
VIII
.
ا , C5
14
8
-
3
ار&'( ق
1
, 8
ومAا
BCا ,%ا , 8
)
/آFا ل#:ا
(
ﻭﺇﺫﺍ ﻛﺎﻥ ﻫﺬﺍ ﺍﳌﻘﺪﺭ ﻻ ﻳﺘﺼﻒ،ﺔﻨﻴﻌﻟﺍ ﰲ ﺎﲑﻈﻧ ﺓﺮﺷﺎﺒﻣ ﺬﺧﺄﻧ ﻥﺃ ﻊﻤﺘﺠﻤﻠﻟ ﺎﻣ ﺔﻤﻠﻌﻣ ﺭﺪﻘﻣ ﺭﺎﻴﺘﺧﻻ ﻕﺮﻄﻟﺍ ﺪﺣﺃ
ﺑﺎﳋﺼﺎﺋﺺ ﺍﳌﻄﻠﻮﺑﺔ ﳒﺮﻱ ﻋﻠﻴﻪ ﺗﻌﺪﻳﻼ
)
ﺍﺳﺘﺨﺪﺍﻡ
Ŝ²
ﺑﺪﻻ ﻣﻦ
S²
ﻟﺘﻘﺪﻳﺮ
σ²
.(
ﺗﻮﺟﺪ ﻃﺮﻕ ﺃﺧﺮﻯ ﻟﺘﺤﺪﻳﺪ ﺍﳌﻘﺪﺭ ﺍﻷﻧﺴ
ﺐ
ﻣﻨﻬﺎ ﻃﺮﻳﻘﺔ ﺍﳌﻌﻘﻮﻟﻴﺔ ﺍﻟﻌﻈﻤﻰ ﻭﺍﻟﱵ ﺗﺪﻋﻰ ﺃﻳﻀﺎ ﻃﺮﻳﻘﺔ ﺍﻻﺣﺘﻤﺎﻝ ﺍﻷﻛﱪ ﻭﺍﻟﱵ ﺗﻨﺴﺐ ﺇﱃ ﺍﻟﻌﺎﱂ ﻓﻴﺸﺮ ﻭﻛﺬﺍ ﻃﺮﻳﻘﺔ ﺍﻟﻌﺰﻭﻡ
.
8
-
3
-
1
وم'$ا
ﻟﻴﻜﻦ ﺍﳌﻄﻠﻮﺏ ﺗﻘﺪﻳﺮ ﻋﺪﺩ
K
ﺘﻤﻊﺍ ﱂﺎﻌﻣ ﻦﻣ
:
θ
1
, θ
2
, . . , θ
k
.
ﻧﻜﻮﻥ ﲨﻠﺔ ﻣﻌﺎﺩﻻﺕ ﻋﺪﺩﻫﺎ
K
.
ﺗﺘﻀﻤﻦ ﻛﻞ
ﻣﻌﺎﺩﻟﺔ ﻣﺴﺎﻭﺍﺓ ﺍﻟﻌﺰﻡ ﺍﳌﺮﺗﺒﻂ ﺑﺎ
ﻷﺻﻞ ﻣﻦ ﺍﻟﺪﺭﺟﺔ
k
ﺘﻤﻊﺍ ﺓﲑﻐﺘﳌ
X
:
µ’
k
= E(X
k
)
ﺑﻨﻈﲑﻩ ﳌﺘﻐﲑﺓ ﺍﳌﻌﺎﻳﻨﺔ،
x
:
m’
k
= (1/n)∑
i
x
i
k
k = 1, 2, , K
ﻣﺜﺎﻝ
:
ﻟﻴﻜﻦ
X ~ B(20; p)
.
ﺗﻘﺪﻳﺮ
p
ﺑﻄﺮﻳﻘﺔ ﺍﻟﻌﺰﻭﻡ ﺍﻧﻄﻼﻗﺎ ﻣﻦ ﻋﻴﻨﺔ ﻳﺘﻢ ﻛﻤﺎ ﻳﻠﻲ
:
ﻟﺪﻳﻨﺎ ﻋﺪﺩ ﺍﳌﻌﺎﱂ ﺍﳌﺮﺍﺩ ﺗﻘﺪﻳﺮﻫﺎ
K = 1
ﺇﺫﺍ ﳓﺘﺎﺝ ﺇﱃ ﻣﻌﺎﺩﻟ
ﺔ ﻭﺍﺣﺪﺓ
:
µ = 20p
.
ﻭﻣﻨﻪ
p = 20/µ
ﻧﺄﺧﺬ ﺇﺫﺍ،
ﻛﻤﻘﺪﺭ ﻝ
p
ﺍﻟﻘﻴﻤﺔ
:
p’
ﻭﳓﺴﺒﻬﺎ ﻛﻤﺎ ﻳﻠﻲ
:
p’ = m/20
.
ﰲ ﺣﺎﻟﺔ ﺗﻘﺪﻳﺮ ﻣﻌﻠﻤﺘﲔ ﻟﻠﻤﺠﺘﻤﻊ ﳓﺘﺎﺝ ﺃﻥ ﻧﺴﺘﻌﻤﻞ ﲨﻠﺔ ﺍﳌﻌﺎﺩﻟﺘﲔ
:
µ = m , µ’
2
= m’
2
ﻣﺜﺎﻝ
2
:
ﻟﺘﻜﻦ
X ~ N(µ; σ²)
.
ﻧﺴﺤﺐ ﻋﻴﻨﺔ ﺫﺍﺕ ﻣﺘﻮﺳﻂ
m
،
ﻭﺗﺒﺎﻳﻦ
S²
.
ﻟﺘﻘﺪ
ﻳﺮ
µ
ﻭ
σ²
ﳓﺘﺎﺝ ﺇﱃ ﺣﻞ ﲨﻠﺔ
ﺍﳌﻌﺎﺩﻟﺘﲔ
:
'
'
2
2
=
=
m
m
µ
µ
ﺃﻭ
²
²
'
²
²
'
or
2
2
+
=
+
=
S
m
m
σ
µ
µ
ﺍﳊﻞ ﻫﻮ
:
²
²
ˆ
ˆ
est
=
=
S
m
σ
µ
ﻫﺬﻩ ﺍﻟﻄﺮﻳﻘﺔ ﻗﺪ ﺗﻌﻄﻲ ﻣﻘﺪﺭﺍﺕ
ﻏﲑ
ﻣﺘﺤﻴﺰﺓ ﻛﻤﺎ ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ
.
8
-
3
-
2
R S$ ا,$ ا
)
FآUا ل =Nا
(
ﺘﻤﻊ ﻣﺘﻘﻄﻌﺔﺍ ﺓﲑﻐﺘﻣ ﻥﻮﻛ ﺔﻟﺎﺣ
:
ﻧﺮﻳﺪ ﺗﻘﺪﻳﺮ ﻣﻌﻠﻤﺔ
θ
ﻭﻟﺪﻳﻨﺎ ﻋﻴﻨﺔ ﻏﲑ ﻧﻔﺎﺩ،ﻊﻤﺘﺠﻤﻠﻟ ﺓﺪﺣﺍﻭ
ﻳﺔ
)
ﺍﳌﺘﻐﲑﺍ ﺕ ﺍﻟﱵ ﲤﺜﻞ
ﻗﻴﻢ ﺍﶈﺼﻞ ﻋﻠﻴﻬﺎ ﰲ ﺍﻟﻌﻴﻨﺔ ﻣﺴﺘﻘﻠﺔ
(
ﳍﺎ ﻧﻔﺲ ﺍﻟﺘﻮﺯﻳﻊ ﻟﻠﻤﺠﺘﻤﻊ
.
ﺮﺗﺒﻂ ﺏـﻣ ﺎﺍﺬﺑ ﺔﻨﻴﻋ ﻖﻘﲢ ﻝﺎﻤﺘﺣﺍ ﻥﺃ ﻲﻬﻳﺪﺒﻟﺍ ﻦﻣ
ﻬﻮﻟﺔﺍ ﺔﻤﻠﻌﳌﺍ ﺔﻤﻴﻗ
:
P(x
1
, x
2
, …,x
n
) = L(
θ)
.
ﻫﻨﺎﻙ ﻗﻴﻤﺔ ﻝ
θ
ﻞـﺼﶈﺍ ﺔـﻨﻴﻌﻟﺍ ﻰﻠﻋ ﻝﻮﺼﳊﺍ ﻝﺎﻤﺘﺣﺍ ﻢﻈﻌﺗ
ﻭﻧﻔﺘﺮﺽ ﺃﻥ ﺗﻠﻚ ﺍﻟﻘﻴﻤ،ﺎﻬﻴﻠﻋ
ﺔ ﻫﻲ ﺍﻟﺼﺤﻴﺤﺔ ﲟﺎ ﺃﻥ ﺍﻟﻌﻴﻨﺔ ﺣﺼﻠﺖ ﺑﺎﻟﻔﻌﻞ
.
ﺗﺘﻤﺜﻞ ﻃﺮﻳﻘﺔ ﺍﳌﻌﻘﻮﻟﻴﺔ ﺍﻟﻌﻈﻤﻰ ﰲ ﺍﻟﺒﺤﺚ
ﻋﻦ ﻫﺬﻩ ﺍﻟﻘﻴﻤﺔ
.
ﺃﻱ ﺍﻟﺒﺤﺚ ﻋﻦ
θ
ﺍﻟﱵ ﺗﻌﻈﻢ
L(
θ)
ﺣﻴﺚ،
:
L(
θ) = f(x
1
, . . . , x
n
;
θ) = f(x
1
) . f(x
2
) . . . f(x
n
)
.
1
د
v%"راوز
،
1997
،
ص
. 308.
.P ا ء#Rا و ت:#:ا Bإ
–
ءA!ا
2
.
15
ﺗﻌﺘﻤﺪ ﻃﺮﻳﻘﺔ ﺍﳌﻌﻘﻮﻟﻴﺔ ﺍﻟﻌﻈﻤﻰ ﻋﻠﻰ ﺗﻌﻈﻴﻢ
ﺩﺍﻟﺔ ﺍﻻﺣﺘﻤﺎﻝ ﺍﳌﺸﺘﺮﻛﺔ
L(
θ)
.
ﻣﺜﺎﻝ
:
ﻟﻴﻜﻦ
X ~ B(p)
ﻮـﻫ ﺡﺎﺠﻨﻟﺍ ﺚﻴﺣ ،
ﻭﺟﻮﺩ ﺍﳋﺎﺻﻴﺔ
"
ﺃ
"
ﺤﻮﺏـﺴﻣ ﺩﺮـﻓ ﻯﺪﻟ
ﺘﻤﻊﺍ ﻦﻣ ﺎﻴﺋﺍﻮﺸﻋ
.
ﻧﺮﺩ ﺗﻘﺪﻳﺮ
p
ﻼﻝـﺧ ﻦﻣ
ﻋﻴﻨﺔ ﺣﺠﻤﻬﺎ
2
.
ﻣﺎ ﻫﻲ ﺍﻟﻘﻴﻤﺔ
p’
ﻝ
p
ﱵـﻟﺍ
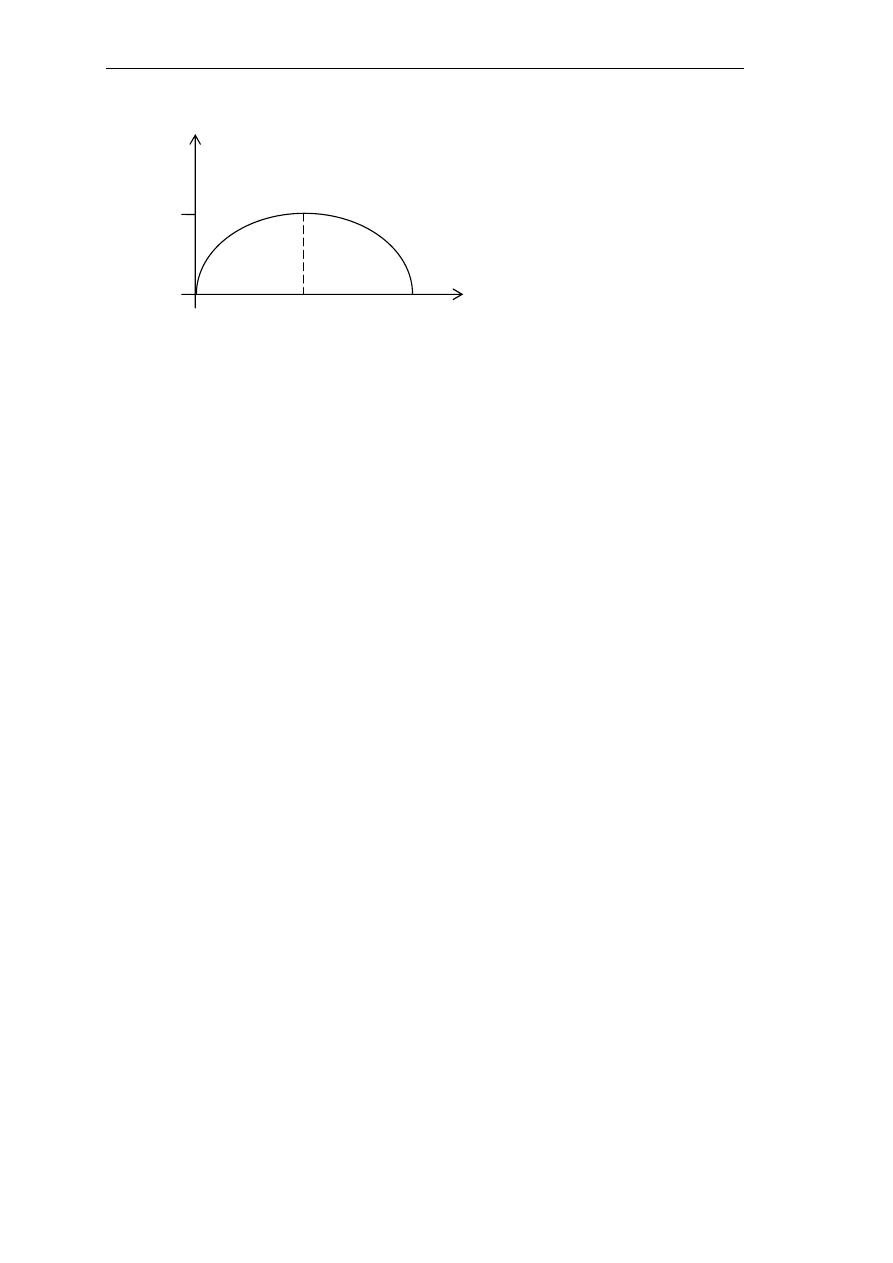
ﲡﻌﻞ ﺍﻟﻨﺘﻴﺠﺔ
1
،
0
ﺃﻱ ﻣﺎ؟ﻻﺎﻤﺘﺣﺍ ﺮﺜﻛﻷﺍ ﻲﻫ
ﻫﻲ
p’
ﺍﻟﱵ ﲡﻌﻞ
p(0.1) = pq
ﺎـﻣ ﱪﻛﺃ
؟ﳝﻜﻦ
ﻣﻦ ﺍﻟﻮﺍﺿﺢ ﺃ
ﻥ ﺃﻛﱪ ﻗﻴﻤﺔ ﻝ
p(0.1)
ﻫﻲ
¼
ﻭﺍﻟﻘﻴﻤﺔ ﺍﻟﱵ ﲢﻘﻘﻬﺎ ﻫﻲ
p’ = 1/2
ﺬﺍ ﳒﻴﺐ ﻋﻠﻰ ﺍﻟﺘﺴﺎﺅﻝﻭ ،
.
p
0
1/2
P(0.1)
1/4
ر
8
-
2
ل; R ;أ
P(0,1)
