
:
!
"# $
.
&'() !

4
..............................
4
!
................................
...
4
! "#$ %&
................................
............................
4
! "#$ %&
................................
.....................
5
' () %& *
................................
................................
...
5
" #+ %&
................................
................................
.............
6
" #+ %& , ! "#$ %& - .
................................
.
8
/ " #+ %&
)
1
(
................................
................
8
"#$ %&
................................
................................
9
%&
................................
................................
.............
9
%& - .
! "#$ %& ,
.........................
10
3 %& *
................................
................................
............
10
" #+ %& , 3 %& * - .
.
................................
......
12
3 %& " 4 5
................................
...............
13
.6
................................
................................
.........
14
# $!
................................
15
7. %& * ,8 "9 %&
:
7
................................
.........
15
3 (; <
................................
................................
.............
15
=> "9 %&
................................
........................
16
"9 %& ? 6
................................
.......................
16
" #+ %& , "9 %& - .
................................
......
18
3 %& *, "9 %& - .
................................
......
19
"@ %&
................................
................................
.............
19

- 3 -
3 (; <
%& 4A , B+ ,8 "@
.
.....................
19
"@ %& ? 6
................................
........................
20
%& *
................................
................................
.........
21
3 (; <
................................
................................
.............
21
%& * ? 6
................................
...........................
22
%& *
................................
................................
..
23
3 (; <
................................
................................
..
23
%& ? C
................................
...................
23
.6
................................
................................
..
25
DE
................................
................................
.........
26

4
%& '
.
FG& H 7>( 38 3I ##J '4K %& , L MN< OP #B) 38
G4K
MNOL
.
M>Q R, =>A, " # N 1S R T H TK R F& UVW 5*
.
UVW )+X8 H
Y F&
:
3 %& *, " #+ %&
G# "@ %& , "9 %& , [9; F& #
M)4 F&
.
4
-
1
Loi hyper géométrique
Loi Multi-
hypergéométrique
Loi Bernoulli
Loi Binomiale
)
(
Loi Binomiale négative
Loi géométrique
Loi
multinomiale
Loi de Poisson
.
4
-
1
-
1
!
(
.
\ ],#
6
O# F)X
4
, ^_
2
^)`
.
ab>c 3, /E(
3
F)X
.
-*)X d 1 e 14K /K
[H,_
3
, )X [^_ F)X
^_ )X , [^_ MK
.
F)X ],# H /E( #(8 f)P(
)*+, -./
W
n
d = g ],# 3X c [
N
O# )X
b
, ^_
r
^)`
(N = b + r)
- d 1 e 14K 3hB
x ≤ b
1.G6 H \ Ti 38 HJ ^_ F) H
F4K. ". 3 (;
)
4 . Fe
/
#4 Fe
(
F;B 5 k,
:
n
N
x
n
r
x
b
C
C
C
x
X
P
−
⋅
=
= )
(
< UVW d4*
:
/(, ! "#$ %& 3 (
b, p)
X ~ H(N,
lK
:
p = b/N
,
= 1– p
q = r/N
" 4X 1+ m8 d bQ 3I HJ
:
P(X = 2) = C
4
2
. C
2
3
/ C
1
6
= 12/20 , P(x = 3) = C
4
3
. C
2
0
/ C
6
3
= 1/5 , …
−
−
=
=
1
²
,
N
n
N
npq
np
σ
µ
01
:
N6@ V$ ])9( # W)XV# " #+ %& . ! "#$ %&
.

TP
IV
.
5 )+X@ 4K F&
5
4
-
1
-
2
!
! "
O HJ
n4*
3 (;
! "#$
-P# H )+X8 b, K d
)
k
o#
(
# o# TX H lK [
N
i
[)X
)
ΣN
i
= N
(
.+ p# A( 14K qe, [
2
^_ F)X
)
X
1
= 2
(
[
5
[^)`
1
[^>&
. . .
HJ
4X F;B 1.6 H #4, 4 . Fe qK
"
:
n
x
N
N
C
C
C
C
x
X
x
X
x
X
P
k
i
k
i
n
N
k
x
k
N
x
N
x
N
k
k
=
=
=
=
=
=
∑
∑
1
1
2
2
1
1
2
2
1
1
,
.
.
.
)
.
.
,.
,
(
i
i
i
np
N
N
n
X
E
=
=
)
(
01
:
N6@ V$ ])9( # W)XV# " #+ %& . ! "#$ %&
.
4
-
1
-
3
" !
1
$ ! "
r8 )s H 1 ;(
"
()
"
-A( T4u v(X c
)
-wK
(
-B#
A
,
A’
.
(
"4
A
, xy
A’
TLB
.
a MN< z(
X
T+{ |
345 67
V6}* [
X
4;
1
~e D;u #
A
,
0
X e R
.
q M !)(
p
"
xA# 14K
"
~e D;u 14K
A
,
q = 1– p
X ~e 14K
)
TLP
.(
%G& * -
" 4X ' ()
:
.
1
,
0
,
)
0
(
,
)
1
(
=
=
=
=
=
X
q
X
P
p
X
P
/(,
X ~ B(1, p)
= 1(p) + 0(q) = p => E(X) = p.
E(X) = Σx
i
p
i
V(X) = E(X²) – E(X)² = (1²p + 0²q) – p² = p – p² = p(1– p) = pq =>
V(X) = qp.
% & '(
M(t) = E(e
xt
) = e
0t
q + e
1t
p => M(t) = q + pe
t
.
1
' () b n
(Jacques Bernoulli)
3); )6,8 R %& VW 7> =V
17
.

") ^KQ , F4K c T6
–
^!
1
.
6
(
)
²)
²
(
)
1
(
)
0
(
)
(
3
3
3
3
3
3
p
q
qp
qp
pq
p
p
q
p
x
p
x
−
=
−
=
−
+
−
=
−
=
∑
µ
µ
qp
p
q
qp
qp
p
q
qp
²
²
²)
²
(
3
3
3
−
=
−
=
=
σ
µ
α
4
-
1
-
4
:
' () )s (>)X c
n
3hB M)
X
)
xA# F)
(
n; V6}*
:
X = 0, 1, 2, 3, . . . n
9 "> (z )A f)P#
M>) ;(
n
, [F) H
X
M> d 1 e F)
)
F
:(
K
:
n = 2
X = 0, 1, 2.
P(X = 0) = q.q = q², P(X=1) = P(FP) + P(PF) = p.q + q.p = 2p
1
q
1
K
:
n = 3
X = 0, 1, 2, 3.
P(X = 3) = P(FFF) = p.p.p = p
3
, P(X = 2) = P(FFP ∨ PFF ∨ FPF) = 3p
2
q
1
K
:
4
n =
X = 0, 1, 2, 3, 4.
P(X = 3) = P(FFFP ∨ PFFF ∨ FPFF ∨ FFPF) = 4 p
3
q
1
K.( MN6@ A# R
3
W
x
[
1
W
n - x
, [
4
~.Gw d 1 E 4 . ])9 W
- H FKy
(n = 4)
K HJ, [q>s
" 4X \
:
)!
(
!
!
x
n
x
n
C
x
n
−
=
14KB ',
x
- H FKA# H
n
" 4X /g () )s
:
.
.
..
,
3
,
2
,
1
,
,
.
.
..
,
3
,
2
,
1
,
0
,
)
(
=
=
=
=
−
n
n
x
q
p
C
x
X
P
x
n
x
x
n
lK
x
[xA# F)
p
xA# 14K
MK )A R
)
)A >)* # vw d;
(
[
q = 1 – p
14K
, TLP
n
q>A
.
o)*
"
" #+ %& 3 (
"
" 4X _8 /
:
x
n
x
x
n
p
p
C
x
X
P
−
−
=
=
)
1
(
)
(
8,
X ~ B(n, p)
.
- - )L )B * # 5 " #+ %& 38 _ D
:
F) H M>) () )s
[
vw )A R xA# 14K
)
; q>A
(
.

TP
IV
.
5 )+X@ 4K F&
7
npq
pq
6
1
3
4
−
+
=
α
:
(& ;( 9 "> # /K8
4
)
d 1 e 14K F
:
[-*) [MK, M) [M> M) ,
3
[F)
4
F)
.
P(X = x) = C
x
n
p
x
q
n –x
=> P(X = 0) = C
0
4
0.5
0
0.5
4
= 1/16
P(X = 1) = C
1
4
0.5
1
0.5
3
P(X = 2) = C
2
4
0.5
2
0.5
2
2
:
ab>Q /E(
3
= g ],# H F)X
5
F)X
O#
3
^)`
.
-*)X d 1 e 14K /K8
)`
H,
.
P(X = 2) = C
2
3
(3/5)
2
(2/5)
1
:
> HJ
X
() ; FN< a 4S
X = X
1
+ X
2
+ … X
i
+ … + X
n
GP( $
n
p
% P( ',
(E(X
i
) = p)
_8
.
c
y H, % ? 6 5
:
E(X) = E(X
1
+ X
2
+ … X
i
+ … + X
n
) = ΣE(X
i
) = Σp
i
= np => E(X) = np
V(X) = V(X
1
+ X
2
+ … X
i
+ … + X
n
),
X
i
3c ;
= ΣV(X
i
) = Σpq => V(X) = npq
:
D 1+4 H, % /K8
:
E(X) = np = 3(3/5) = 9/5 ; V(X) = npq = 3(3/5)(2/5) = 18/25
:
>
X
; () FN< a 4S
X = X
1
+ X
2
+ …X
i
+ … + X
n
GP( $
n
p
,! MA P(,
:
M
X
(t) = [q + pe
t
]
5,
-( ;
,! ;
:
"
Tb8 H
1
X
,
X
2
,! $ ; a
M
x1
(t)
M
x2
(t)
3hB
:
M
x1 + x2
(t) = M
x1
(t). M
x2
(t)
"
p
#(
:
M
X
(t) = M
x=x1+ x2 +…xn
(t) = M
x1
(t) . M
x2
(t) … M
xn
(t)
M
X
(t) = E(e
x1t
) . E(e
x2t
) … E(e
xnt
) => M
X
(t) =
[q + pe
t
]
n
(
)
(
)
∑
∑
−
=
=
−
=
−
=
=
)
(
.
.
.
)
(
)
(
.
3
3
3
3
3
3
p
q
npq
x
p
np
x
x
p
x
µ
µ
σ
µ
α
[
]
σ
α
p
npq
npq
p
p
npq
2
1
)
1
(
3
−
=
−
−
=
⇒
npq
p
q
−
=
3
:
# .w4 " #+ %& E# 3
α
3
= 0 => 2p = 1 => p = ½
%& E# 3
" #+
#
α
4
= 3 => qp = 1/6

") ^KQ , F4K c T6
–
^!
1
.
8
! !" #
K R
N
b NX
)
c 1,
∞
(
9
3,G /EG , ! "#$ %& H ) ( " #+ %& "
ab>Q /E );* ;9 ab>c
.
3@ " #+ %& H* H q); _8 H
)G
(N – n) / (N – 1)
c 1,
1
)
n
,
..(
4
-
1
-
5
)
(
$
:
:
d 1 e c ;( 9 "; (
3
M> F)
)
,8
.(
G k d Ti 38 14K /K8
5
[F>
4
[F>
3
H /K8, &. F) % * [F>
.
# 1+ VW R
() )s
)
TLB, xy -A(
(
UVW H [M>)
M)
! "# $ %&
)
r
(
)
*+,
.
X
"W e UVW R
-. / .01 * .
d 1 e c
r
xy
.
oX
/g
14K
n (
38
D;u
xA#
r
M)
\4K
p
r
14K,
TLP
(x – r)
M)G
=,G
q
x – r
.
c
14K
q 9
H4_
^b
HVW
-4K
p
r
q
x–r
.
H
#W
H
])9
.
4
D;E
r
xy
H
-
X
)s
%
n
38
)6
)s
"W
xy
.
38
)A
MN6@
A#
)
xy
(
4 . ])9 3hB [
=,
G
])9
4 .
>6
(r – 1)
xy
H
-
(x – 1)
)s
[
=8
C
r–1
x–1
c
:
∞
+
=
∞
+
+
+
=
=
=
−
−
−
,
.
.
.
,
3
,
2
,
1
,
...
,
2
,
1
,
,
)
(
1
1
r
r
r
r
X
q
p
C
x
X
P
r
x
r
r
x
/(, / " #+ ,8 1 %& * %& VW d4
:
X~BN (r, p)
" D 1+ m8 d bQ c HJ
:
P (X = 5) = C
3–1
5–1
p
3
q
5–3
= C
2
4
(½)
3
(½)
2
= 6 (1/8) (1/4) = 9/32
µ = r/p = 3/(1/2) = 6 , σ² = rq/p² = 3 (1/2) / (1/2)² = 12/2 = 6
$
(
)
r
t
t
qe
e
p
t
M
p
rq
p
r
−
=
=
=
1
)
(
,
²
²
,
σ
µ
nq
nq
q
q
q
)
1
(
3
)²
2
(
3
,
1
4
3
−
+
+
+
=
+
=
α
α

TP
IV
.
5 )+X@ 4K F&
9
4
-
1
-
6
.
.
!" #"$%
4
& '(
:
P(X = 4) = P(PPPF)
.
* +% %,& -
( ./ /.0
.1
2% 3
*%
45% 67
)
$%4 . 69
.(
(;% <% =>"+%
X
? @%
/.7"% %.1A '%. B
)
67*% C(D $ @% .+% C(D E
(
F*G% HI "% HJ"A
.
K 67*% #"$L M %
p
K <N% #"$L4
q
#O P"/"O Q1R #"$L% SD
:
P(X = 4) = q
3
p
/4
#( T #"$% SD N
X
#O P* U
:
.
.
.
,
3
,
2
,
1
,
)
(
1
=
=
=
−
X
p
q
x
X
P
x
(
)
t
t
qe
e
p
t
M
p
q
p
−
=
=
=
1
)
(
,
²
²
,
1
σ
µ
q
p
q
q
²
12
,
1
4
3
+
=
+
=
α
α
V($ 1F/ HI A Q W $ L & F*G% HI "%
r = 1
.
4
-
1
-
7
.
B.
7
'%.
.
2% #"$% X4
Y.% ZA.
6
Y.% ZA.4
1
4
3
Y.% '%.
5
.
[ B"+% HI "% #"\ ]^D Z"7(" JA /.0 $ - #"\ 45% #*(JD ];*% HI " Y(#A & B"+% HI "%
B /.7" 1 V($ %
k
*1#+% _;"*% Q
]
C`/ Q K7"% (a"F% H
.
K _;"*% b,G M.
A
1
, A
2
, .
. . A
k
K cL#"$L4
p
1
, p
2
, p
3
, . . . p
k
.
d%$5% E
)
_;"*%
(
A
i
SD (D*"
:
= 1
p
1
+ p
2
+ p
3
+ . . . + p
k
/.7"% b,& .O %
B _;"*%
n
d$ 1 * 1(\D '%.+% Q
)
7("
(
'%.e B ? (;% < =>"
P 4
.
K '%=>"+% b,G M.
X
1
, X
2
, . . . X
k
V($
X
1
+ X
2
+ . . . + X
k
= n
.
!O.+% d2% #"$% !\f
:
X
1
=
x
1
, X
2
= x
2
, . . ., X
k
= x
k
#O
:
k
x
k
x
x
k
k
k
p
p
p
x
x
x
n
x
X
x
X
x
X
P
.
.
.
!
.
.
.
!
!
!
)
,
.
.
.
,
,
(
2
1
2
1
2
1
2
2
1
1
=
=
=
=
E(X
1
) = np
1
, E(X
2
) = np
2
, . . . , E(X
k
) = np
k
V(X
1
) = np
1
q
1
, V(X
2
) = np
2
q
2
, . . . V(X
k
) = np
k
q
k

g.% h$i% 4 'L#"$L% W
–
hMk%
1
.
10
B"+% HI "%
_;" Q J. _;"
* ]B"+% ;%M% F*G% HI "%
:
N
∞, N
i
∞, N
i
/N
p
i
.
:
B. *( %
42
\$ ].
PA% Y.% H !F*" '%.+% Q B Y O .Cl #"$% !
)
Y.%
1
.eCl
Y.% ]ZA.
2
.Cl
4
Y.% ]'%.
3
.Cl
6
%,1&4 '%.
.(
( )
12
4
6
2
1
)
6
/
1
(
.
.
.
)
6
/
1
²(
6
/
1
!
12
.
.
.
!
6
!
4
!
2
!
42
)
12
.
.
.
,
4
,
2
(
=
=
=
=
X
X
X
P
2
.
P/ m4* Q ![\
5
Q #. '.O
1
5
m4*% CX. n .O o% "% '%. HJF
.
X4
#"$%
:
3
'% '.O
Y
1
Y '% Z".O ]
2
Y '% Z".O4
4
.
4
-
1
-
8
1
'%.+% Q ;pL 4 %X =JO B .1 ( ./ /.0 * Q1"
.
=>"+% (;J
X
HI "% HJ"A '$7*% B ? @%
%,& >( #"F/ #"$L% K\$ ! Q1 ];*%
1A * HI "%
n
=JO
.
a
#"$%
20
% 69
qO
n = 100
&
:
80
20
20
100
999
.
0
001
.
0
)
20
(
⋅
⋅
= C
P
.
l2 - d2% rs #"$% 14 ]QM/ F /.7"% %.1A '%. B tJ u%.#"F/ /.7"% .1"A *
%X %=>
.
2% b,& - v"
T ]
*
n
4w
∞
]
>( Bx
;*% HI "% >( BA
.
H`
λ
V(y q/z
p = λ/n
:
(
)
x
n
x
x
n
x
x
n
n
n
x
x
n
n
q
p
C
x
p
−
−
−
⋅
⋅
−
=
⋅
⋅
=
λ
λ
1
!
!
!
)
(
x
n
x
n
n
x
x
n
n
n
n
x
p
−
−
+
−
−
−
=
)
1
(
)
(
!
)
1
).....(
2
)(
1
(
)
(
λ
λ
x
n
n
x
n
x
n
n
n
n
n
n
n
x
p
x
−
−
+
−
−
−
=
)
1
(
!
)
1
(
.....
)
2
(
)
1
(
)
(
λ
λ
x
n
x
n
x
n
x
n
n
−
−
−
−
−
−
=
)
1
(
!
)
1
1
).....(
2
1
)(
1
1
(
1
λ
λ
x
n
λ
−
1
(Siméon-Denis Poisson) (1840-1781)
1837
! "# $% !
&' () ! *+ (, ! -./ (.
(Recherche sur la probabilité des jugements en matière criminelle et en matière
civile)
(- 0% 123 ".
4
.
67 8 $9 1: ; $ (8 ( 3 3 <7
1830
.
=.> 3 67 ?@AB @C
DEFE =G H ?IF- J/ K L23 0M K ! 1N
.
OP @ Q Q K 3
[1997]
.

1R
IV
.
M 4%/ .< S8P
11
x
n
x
x
n
x
n
n
x
n
x
x
p
n
n
n
−
−
−
−
=
−
=
⇒
=
=
=
⇒
∞
→
)
1
(
)
1
(
!
)
1
(
!
1
)
(
0
.
.
.
2
1
λ
λ
λ
λ
λ
T-
:
λ
λ
−
∞
→
=
−
e
n
n
n
1
lim
(
)
1
0
1
1
lim
=
−
=
−
−
−
∞
→
x
x
n
n
λ
V7
.
.
.
,
2
,
1
,
0
!
)
(
=
=
−
x
x
e
x
p
x
λ
λ
(.
x
". WPG =. ?. TMP ?. ! XY
λ > 0
.
=-
X~P(λ)
:
...
71828
.
2
1
1
lim
=
=
+
∞
→
e
n
n
n
[
]
λ
α
λ
α
λ
λ
1
3
,
1
,
)
1
(
exp
)
(
,
)
(
)
(
4
3
+
=
=
−
=
=
=
t
e
t
M
X
V
X
E
/ >Z [;J T\
] ;8' TF W^ ? M ]6
^_8
λ
λ
e
n
n
n
=
∑
∞
=0
!
:
(
)
(
)
∑
∑
∑
∑
∑
∞
=
−
−
∞
=
−
∞
=
−
∞
=
−
∞
=
−
=
−
=
=
=
=
1
1
1
1
0
0
!
1
!
1
!
!
)
(
)
(
x
x
x
x
x
x
x
x
x
x
e
x
e
x
e
x
x
e
x
x
xf
X
E
λ
λ
λ
λ
λ
λ
λ
λ
λ
W
n = x – 1
λ
λ
λ
λ
λ
λ
λ
=
=
=
−
∞
=
−
∑
e
e
n
e
X
E
x
n
0
!
)
(
(
)
(
)
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
=
−
+
=
+
=
+
=
+
=
+
=
−
=
−
=
=
−
=
∑
∑
∑
∑
∑
∑
∑
∞
=
∞
=
∞
=
−
−
∞
=
−
∞
=
−
−
∞
=
−
∞
=
−
²
²
)
(
²
)
(
)
(
!
!
!
)
1
(
!
1
!
1
!
²
)²
(
²)
(
)
(
0
0
0
0
1
1
1
0
2
X
V
n
P
X
E
n
e
n
e
n
n
e
n
x
e
x
x
e
x
x
e
x
X
E
X
E
X
V
n
n
n
n
n
n
n
x
x
x
x
x
x
t
.
t
λ
λt
:
( )
.
.
.
,
3
,
2
,
1
,
0
,
!
)
(
=
=
=
−
X
x
e
t
x
X
P
t
x
t
λ
λ
.
! "#$% "&'% ( )*%+, -. /0 1% 2 34*%+5 +6+76 .*!
λ=5
34+8 9
.
; +<' =>
7
?1 34+@ 9 +6+7
.
(
)
!
7
)
5
(
5
.
1
)
7
(
)
5
(
5
.
1
)
7
(
5
.
1
7
−
=
=
=
e
X
P
t
λ
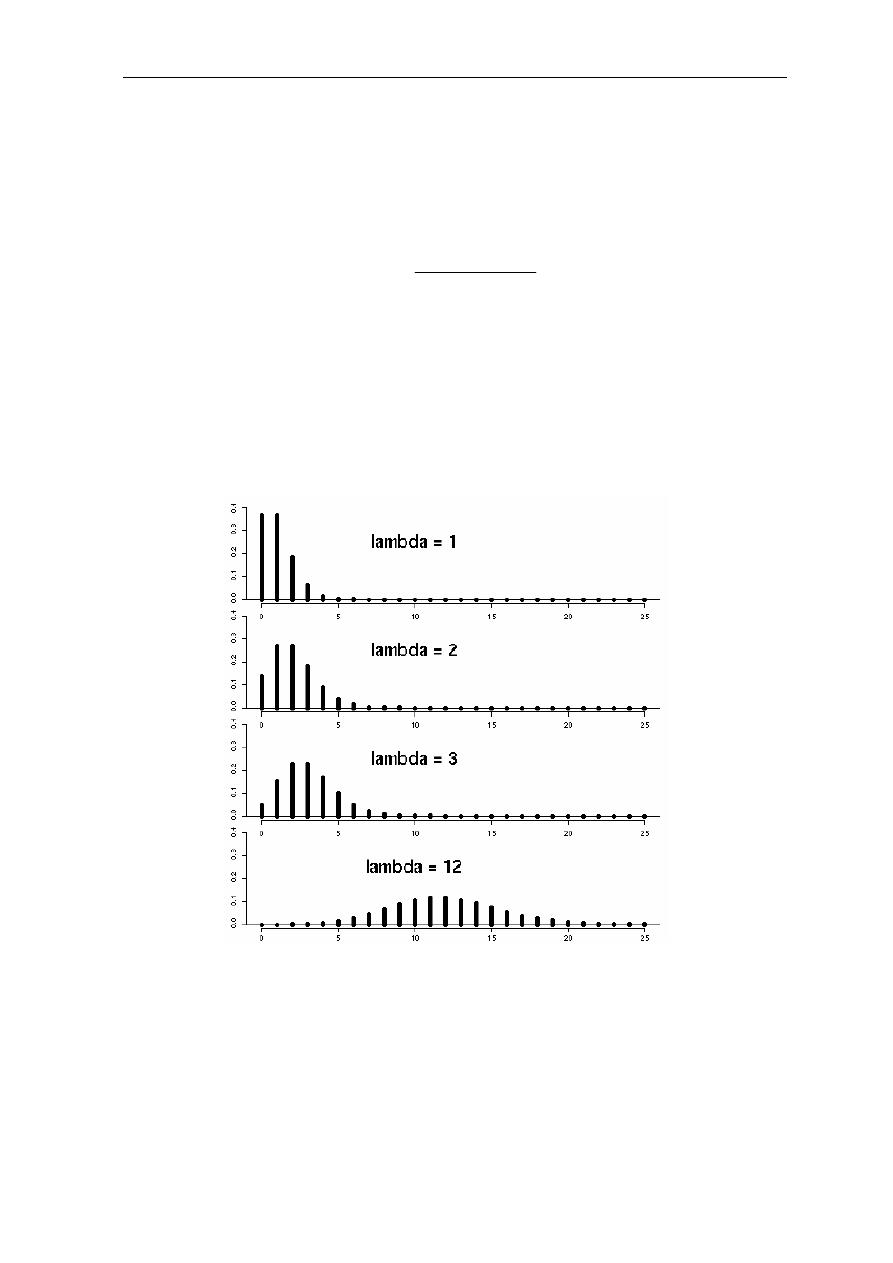
)A+#. B+1C D+<'D /0 E
–
BG
1
.
12
.
+- H0
X
! "#$% "&'#
λ
I J
Y= aX
! "#$% "&'# .EK ,
aλ
.
.
! "#$% "&'% ( )*%+, -. /0 1% 2 34*%+5 +6+76 .*!
λ=5
J34+@ 9
6
%
34 +6+7 ), +6+76 LM,
.
1% +<' =>
9
+6+7
34+@ 9 34
.
!
9
))
5
(
05
.
0
(
)
9
(
)
5
(
05
.
0
9
−
=
=
e
X
P
! "#$% N .#
O< P QE
(Diagramme en bâtons)
+R' +#$% S7
.
TU ! "#$'
)4&R "#$' V W+%
)
34+<'D +#$'U W+' TU> Y )4&R "#$' Y .Z
(
3<4\ O +#$
3<U6
λ
]H 3ZQ 7^ J
O#' N4\ ! "#$' 34+4& _ . 3+ QE
λ
.`Z# a4
)4&R "#$' +b4c +b4d .'# "#$'
+6
λ
3#+*7 S4 + e&-
.
]H (&% 34+' 34+4& _ .
.
4
1
! "##$ %!#& '#(
()
λλλλ
.
+
n
∞
! "#$' /0 )f+8 "#$' g# h!+@ i '6
.
"#$' 3&#.\ jf+' ! "#$% )R# +4U<
+6 )f+8
:

1*
IV
.
+k' .8-l 34+<'D +#$'
13
30
≥
n
5
<
np
*
5
<
nq
O+ (4f+1C m! _k'>#
34+'
1
:
n ≥ 25
p ≤ 0,1
:
=o>
+4fc
.c
0
?+' +` +'0 3&> 3p P+'
10
%
.
7# +<' =>
(!
3!o>6
+'*+% +%
.
P(X = 2) = C
2
10
(0.1)² (0.9)
8
= 0.1937
q
2
.
! "#$% +<' +!
:
3<U6 3<4\ D =>V
λ
)
! +\ 3<U
:(
λ = µ = np = 10(0,1) = 1
P(2) = λ
x
(e
–λ
/x!) = 1
2
(e
–1
/ 2 !) = 1/(2e) = 1,1839
4
-
1
-
8
-
1
O ' D+r 9 <'># _4 S7 JO + sl 48<' i <'># 3U#t O.'* ! "#$% u
.
+r 9
_U
34\ +4
4& 9 3c O
+ 38&6 +b#G
3 B+#4* 9 Q8 ! "#$% _k'># 34\
(microbiologie)
+v 9 +#e'7& .@+7% 3&\.6
J
. . .
9 ! "#$% _k'># e4>' +r 9
J+4f+10 O G 3&\.
)
+<' +>w
J3*+'
(...
+<-
3U' f+> 3 x+E 7c! _k'>#
"
+Z'D .,Z!
"
; .'*# + e8- Jf+>6 z M, )* {
! "#$% "&'# 3| +7 /0 f+!
.
]H 3U8
:
.E& J$ O 9 +R6 /0 1% 2 .f+R
2
2 34*%+5 +6+76 J$ O 9 }#.! ='7 /0 U1# #M f+! J$ O 9 B+4 /0 1%
J~*c'> /0 1% 2 34+' D D+w J)*%+, -. /0 1%
...
+Z'D *; 3#.Z 9 .,Z LM, ~<>%
"
; .,Z!
."
1
.
3 h4!
+4# ('@ + ! "#$% "&'# ( < 9 < s
.
( _# 9 s + } ># D +<'
.
_# 9 \l ~U s + +<'
:
P(X = 0) = λ
x
(e
–λ
/x!) = λ
0
(e
–λ
/0!) => P(X = 0) = e
–λ
= e
–2
P(X ≥ 1) = 1– P(0) = 1– [λ
0
(e
–λ
/0!)] => P(X ≥ 1) = 1 – e
–λ
= 1 – e
–2
2
.
3+> (! 34 #! 3R /0 1% 2 +4> 3!+ 34f+10 3 h4!
12:00
12:05
9 ,
i '6
3
! "#$% "&'# 3R /0 1% 2 +4> 3 h4! +<- J+4
.
1% +<'
4
(! +4
12:00
12:05
.
3+> 9 +4> i '
=
2
X
3
=
6
S
:
= 1296 (e
–6
/24) = 54 (e
–6
)
P(X = 4) = 6
4
(e
–6
/4!)
1
]4!$ .Z
1997
x J
262
.
)A+#. B+1C D+<'D /0 E
–
BG
1
.
14
)!
(
!
!
x
n
x
n
C
x
n
−
=
4
-
1
-
9
Oe`c 3R'6 +#$' q+ N, kU# oU6 G
.
+
1
,-(
- ./ 01) 2 !#3
%!#3
4-! 5
67(3 8) 13
9
! :3 %;#3
<=3 >?
X~H(N,
b, p)
z+ 0 ! =o
.
(*; +#.-
.
X = {0, 1, 2, …, b}
b ≤ b + r = N
n
N
x
n
r
x
b
C
C
C
x
X
P
−
⋅
=
= )
(
n
3!o>6 +#.7
N
)U7
+#.7U
b
B+4& +#.7
r
B.<w +#.7 z
µ
= np
−
−
=
1
²
N
n
N
npq
σ
p = b/N
q = r/N
!
.
Xi = {0, 1, 2,…,Ni}
Σx
i
= n,
ΣNi = N
P(X
1
=x
1
, X
2
=x
2
, …X
k
=x
k
) =
n
N
x k
N k
x
N
x
N
x
N
C
C
C
C
C
⋅
⋅
⋅
=
3
3
2
2
1
1
E[X
i
] = n (N
i
/N)
= np
i
# $
X~B(1, p)
% & '$(
)
*+
%,!
(
./0. 1234
.
X = {0, 1}
P(X = 1) = p,
P(X = 0) = 1 – p = q
µ = p, σ² = pq
X~B(n, p)
5'/0. '06 7,(
'83.9 %,!
)
p
:$6
.(
X = {0, 1, 2, …, n}
P(X = x) = C
x
n
p
x
q
n–x
µ= np, σ² = npq
)
(
X
:
7,/.
<
=8< >?@8 'AB
<
r
&/
'0 $ 7,( C
.
X = {r, r +1, r +2,
…, +∞}
P(X = x) = C
r–1
x–1
p
r
q
x–r
µ = r/p ,
σ² = rq/p²
X
:
7,/.
<
=8< >?@8 'AB
C >D E/
%,! '0 $ 7,(
.
X = {1, 2, …, +∞}
P(X = x) = q
x–1
p
µ = 1/p,
σ² = q/p²
A.8 F0GH4 I
'$( =8<
J. % H. %,!
.
∑
∑
=
=
≤
≤
∀
=
=
N
Ni
n
xi
Ni
xi
i
k
i
k
i
1
1
,
,
0
,
=
=
=
=
)
,
.
.
.
,
,
(
2
2
1
1
k
k
x
X
x
X
x
X
P
k
x
k
x
x
k
p
p
p
x
x
x
n
.
.
.
!
.
.
.
!
!
!
2
1
2
1
2
1
E(X
k
) = np
k
V(X
k
) = np
k
q
k
X~P(λ)
λ > 0
X
:
<
%.K C L
&D
A
5
& <
'@ C ' .
5MN
...
X ={0, 1, 2, …
+
∞}
!
)
(
x
e
x
X
P
x
λ
λ
−
=
=
P(X = 0) = e
–λ
P(X ≥ 1) = 1 – e
–λ
E(x) = V(x) = λ
1?
IV
.
O. D '0G.&P H A.
15
4
-
2
D. Normale ou D. de Laplace-Gausse
Distribution exponentielle
Distribution gamma
Distribution bêta
4
-
2
-
1
1
H
IQ %*2 '29 =8< R2S4 T?U V W X O.P 'H '0G.&P H A. FI H02S A.
' ?.YP '0<G.P '0H02S
.
, C ,W 'Z 'K ?$ .U 8K
%*2 '29 F[ 9Y \
'3 ,?Y '$,3 '29 '3 >[ '808Y '29 5 ]. '2 Y ^
.
MA_ '29$ `I 1
.
8
a 5>G.&P V0G9 M !b 5'29 1b c` d@W M! /. H. F8H C 02 e`I
1!
H02S A. I ].W >& 16G.
)
F Q
(
:
4
-
2
-
1
-
1
:
∞
<
<
−∞
−
−
=
x
x
e
x
f
2
2
/
1
2
1
)
(
σ
µ
π
σ
)
(
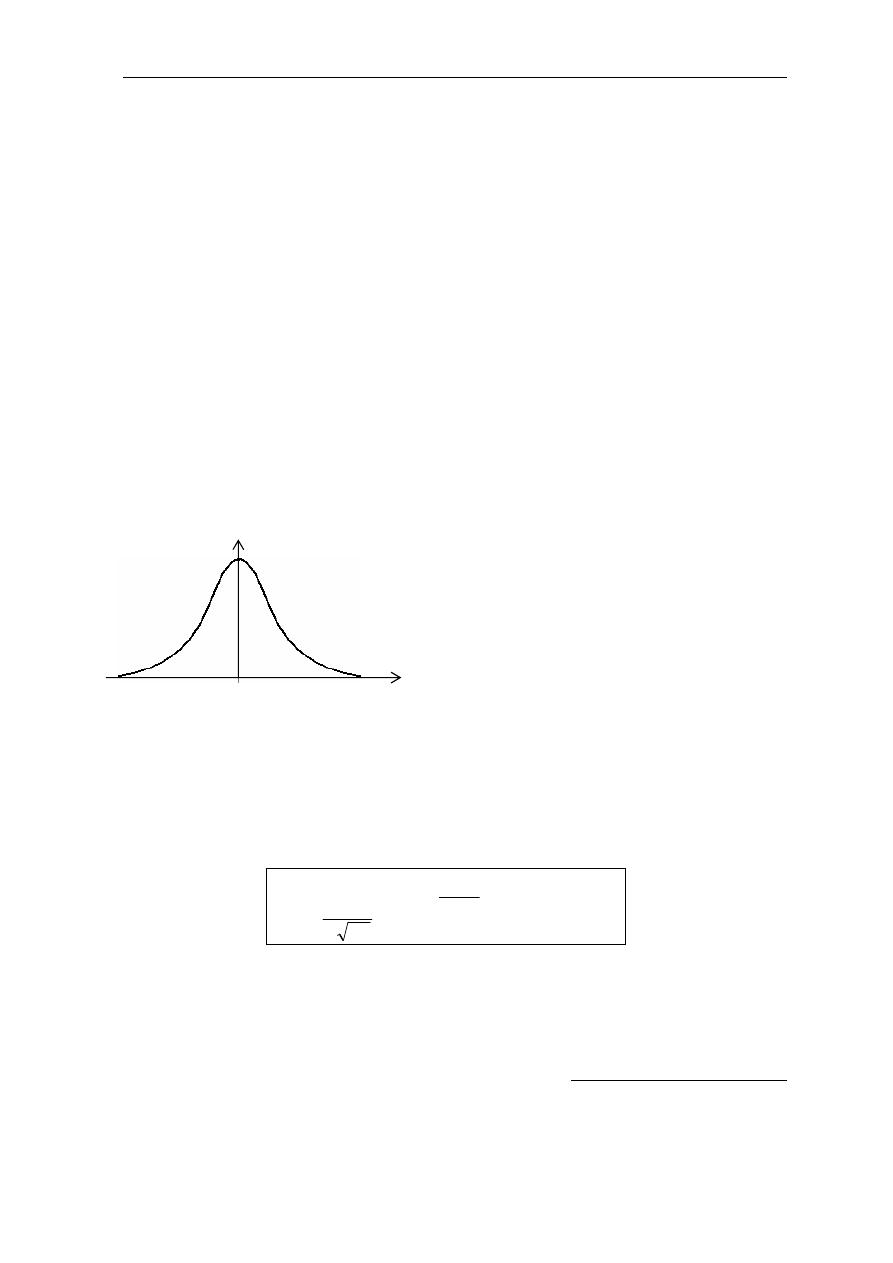
"# $%& # '(
1
% ) *+,
(-%. ) . / ) 01 . ) 2
34,5
(Pière Simon de Laplace 1749-1827)
36 78 /
(Carl Freidrich
Gauss 1777-1855)
)-9 :; <= "# >0 /? "# - ":
.
)+A, B ( CD? "# #?
(Pearson)
E
1893
.
%F-?
G ,/ H
(1997)
I J
329
.
4
2
f(x)
x
µ

2% KLMN / O5M5 PQ >R #
–
K1T
1
.
16
+
=
2
²
²
exp
)
(
µ
µ
t
t
t
M
x
∫
∞
−
−
−
=
≤
=
x
v
dv
e
x
X
P
x
F
2
2
/
1
2
1
)
(
)
(
σ
µ
π
σ
U M
µ
/
σ
V WD X
YH Z %[5 / 6
.
-/
X ~ N(µ, σ)
4
-
2
-
1
-
2
H $A\ ] ^(
Z = (X – µ)/σ
O5M4 0LMN _/ T "
:
P(0 ≤ Z ≤ z)
/?
F(z) = P(Z ≤ z)
J
,, `( U M
f
/
F
a 5 ,
M / _B
Z
"# 5 ,
3
a
> ;
x
/
µ
/
σ
Gb/
:
∞
<
<
∞
−
=
−
z
z
f
e
z
2
/
²
2
1
)
(
π
∫
∞
−
−
=
≤
=
z
u
du
e
z
Z
P
z
F
2
²
2
1
)
(
)
(
π
cA\ c, d 64 PQ %F,
X
/
Z
J
)e
Z
f.-
X
Y?
.
-/
)? *
:
E(Z) = 0, V(Z) = 1
:
Z ~ N(0, 1)
_9-/
:
Z
YH
.
4
-
2
-
1
-
3
]/1 $
$A\
:
5 # g h-? i0LR "#
J
`. >## g U M J.# 5/ , # 5
1
= 3)
4
(α
O _ D5 H #
.
h-? k? i0LR "#
6 9 _M >l#
0
3
3
3
=
=
σ
µ
α
# >lm
X
n+ _M
)
-?
%F
C-? *+%
(
>lm o
Z
_M
0
$A\ 6 Y? >p? "# h-? o q J
H
z > 0
:
1
`. >## \ r (M
α
4
= µ
4
/ σ
4
\ L ] ^( " (, #? J
α
4
= (µ
4
/ σ
4
)
- 3
Y/( `. ># J
0
.
>L.
IV
.
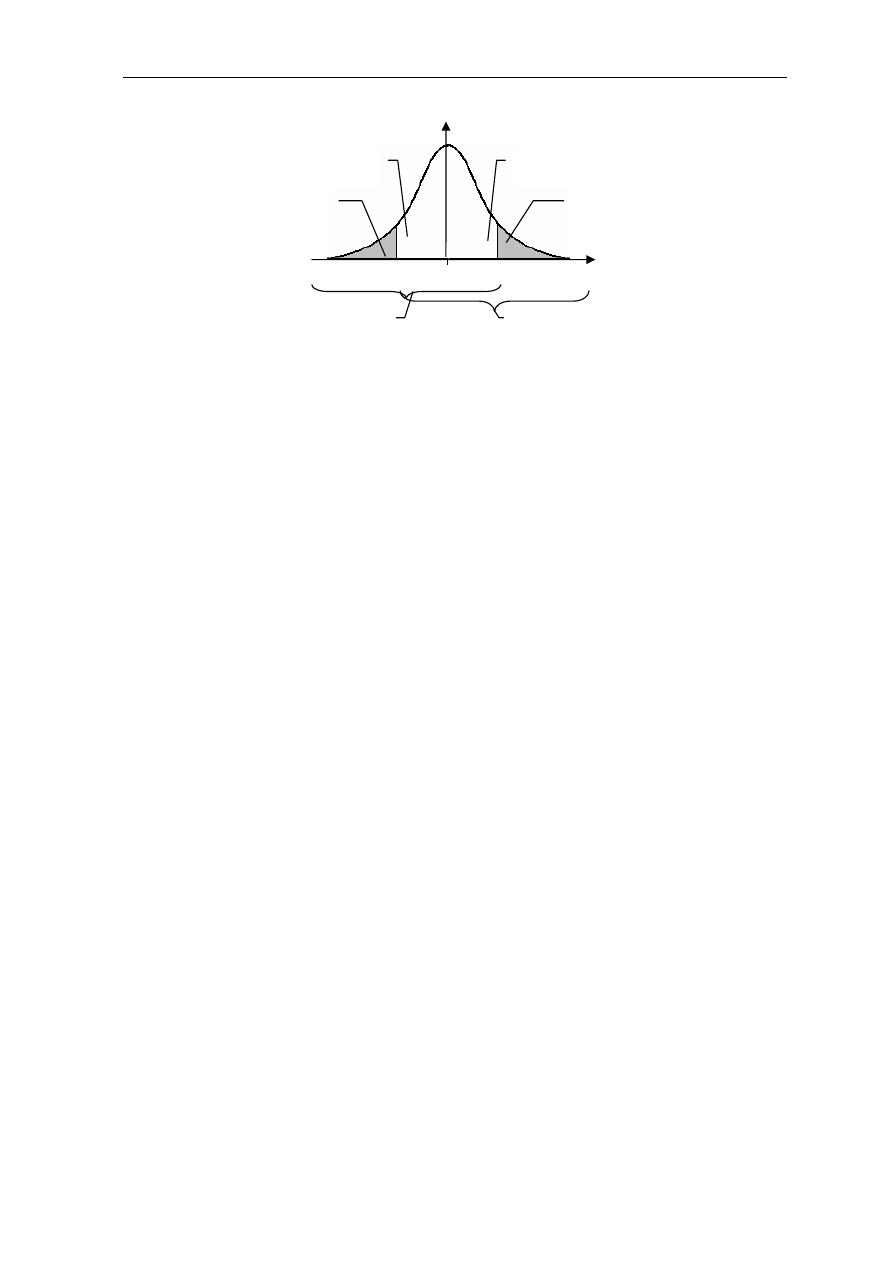
# ^+ %8 M5 O
17
P(0 ≤ Z ≤ z) = P(-z ≤ Z ≤ 0) = P(-z ≤ Z ≤ z) / 2
P(-
∞
≤ Z ≤ z) = P(-z ≤ Z ≤
∞
) = P(-z ≤ Z ≤ z)/2
P(Z ≤ -z) = 1– P(Z ≤ z) = P(Z ≥ z)
H $A\ ] ^+
Z
O5M5 s(t `u
)
OM(
(
rR B#/ vw
:
P(-σ ≤ X ≤ σ) = P(-σ ≤ Z ≤ σ) = 0.6837,
P(-2σ ≤ X ≤ 2σ) = P(-2 ≤ Z ≤ 2) = 0.9544,
P(-3σ ≤ X ≤ 3σ) = P(-3 ≤ Z ≤ 3) = 0.9973.
:;
p % "# A E ; x y 0LMN _/ T E $%# ;Az/ * 9 C
.
vw $A M(# )? {M5 J2% 6 s%9, O %. 1% k? i0LR "#
)
*+% %F-?
C-
(
_| E $HL}
(-3 σ ≤ X ≤ 3 σ)
O %. (- )? o # J
p ~2 _| :; "D % y
:
P(X ≤ -3σ) = P(X ≥ 3σ) = (1 – 0.9973) / 2 = 0.0027.
P(X ≤ -4σ) = P(X ≥ 4σ)
≅
0 , P(X ≤ 4σ) = P(X ≥ -4σ)
≅
1
-z 0 z Z
P(-z ≤ Z ≤ 0)
P(0 ≤ Z ≤ z)
P(-z ≤ Z ≤ z)
P(-
∞
≤ Z ≤ z)
P(-z ≤ Z ≤
∞
)
P(Z ≥ z)
P(Z ≤ -z)
4
3
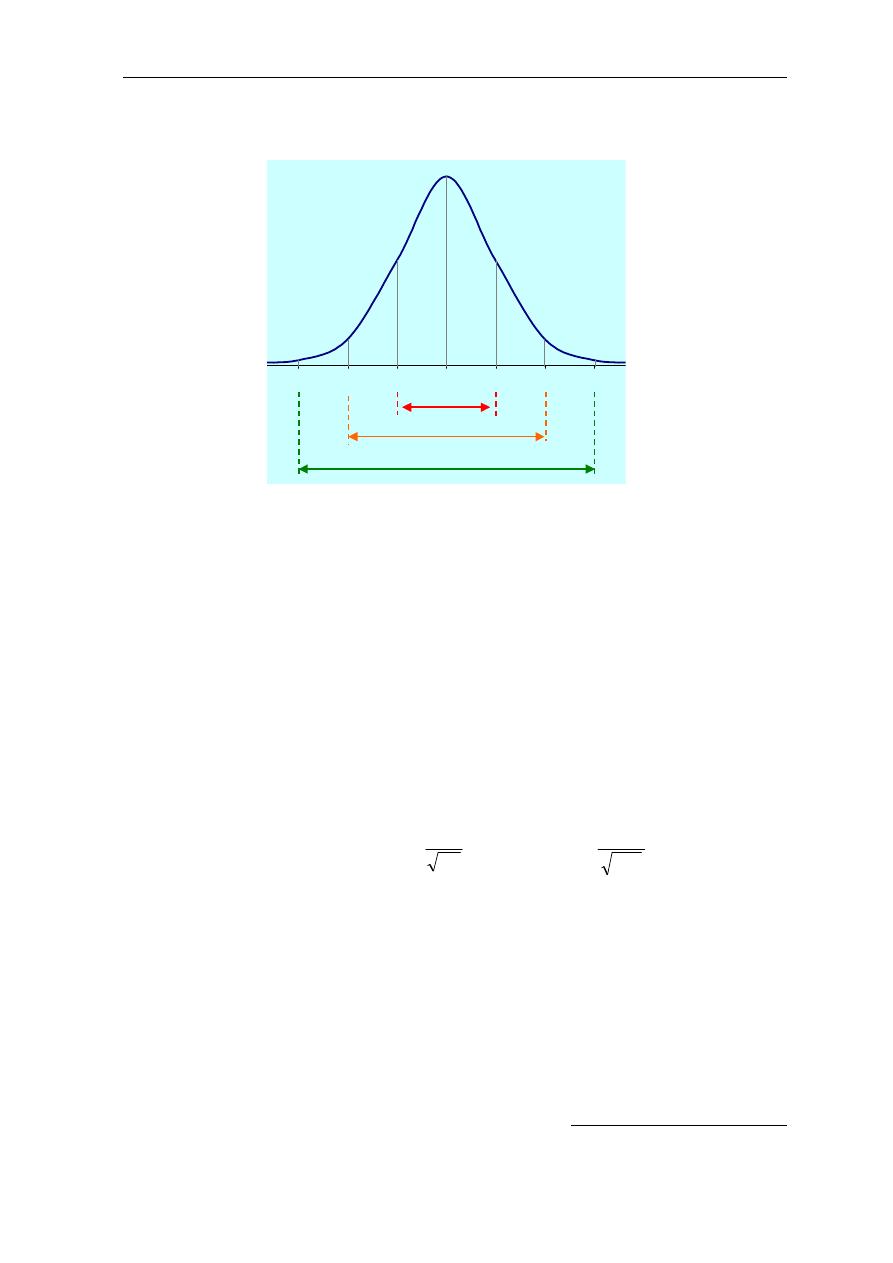
2% KLMN / O5M5 PQ >R #
–
K1T
1
.
18
µ - 4σ
µ - 3σ
µ - 2σ
µ -1σ
µ
µ +1σ
µ + 2σ
µ + 3σ
µ + 4σ
2σ = 68.26%
4σ = 95.44%
6σ = 99.73%
:
0LM5 _/ T _+,
1
(
(M?
:
P(0 ≤ Z ≤ z)
U M
z =1, 2, 3
2
(
(M?
P(-z ≤ Z ≤ z)
_ * 9 f.- >p? "#
z
.
1
(
0.3413
J
0.47725
J
0.49865
2
(
0.6827
J
0.9545
J
0.9973
4
-
2
-
1
-
4
M E
n
/ $A
p
"# %6 Az
0
p %9 0 H D "
.
%? '0- ) /
v- ,H9
n
%? $A
.
-/
:
npq
np
x
z
dz
e
b
z
a
P
b
a
z
n
−
=
=
≤
≤
∫
−
∞
→
,
2
1
)
(
lim
2
/
²
π
) "# 0 sH9 %(/
p
"# %6
0.5
.
!"# $%&
:
# D 04# 0 PQ %9 g- #D
np
/
nq
# g? X4
"
0.5
.
0LM5 , ] ^(
, "# >B+? Bk, %R? D 6 )
1
B#
:
npq9
n 20, np 10, nq 10
1
G ,/ H %F-?
1997
.
I
262
.
4
4
'( ) *
+,
- ./# 01
23(45#

>L.
IV
.
# ^+ %8 M5 O
19
4
-
2
-
1
-
5
# D
λ→ ∞
-/ 9,# '0- ) )+ ,/ c )e
:
∫
−
∞
→
=
≤
−
≤
b
a
z
dz
e
b
x
a
P
2
²
2
1
lim
π
λ
λ
λ
%9 $ D6
:
%9 )? g- #D
PQ )+ , "#
*04#
λ ≥ 15
c 0LMN "# D
1
%9 %=
λ ≥ 10
4 O '0- sH9 )? "/
#
:
$H: /%= (M / )+ , J0
.
4
-
2
-
2
.
" #$
% &'( )* %+ ,-.
%/ 0 1' %2. 3" 43&'
5 6 718 -9 : ;<=
...
9
>) ?;@ A BC
(atomes radioactives)
D E 6 - F <2 G + H A %#*&' :I -9
J CK L1=
.
) :ME % @( - NAI O9P :Q $ME %: 3.- 9R
:ME : - " Q3 ST 7JP :Q $T %#$ 6
7BCQ U -' VWA O9P V
: 7JP V X )
"I
"
-' Z) :P
.
:= [ J \X X 9R ]@( V-'
.
4
-
2
-
2
-
1
.
7^ : ' -' V C C NA :I ; _X
λ
NA
.
A ` :I 7CA aPI
9 6 N
)
3BQI PI NA
(
t
.
P(X ≥ 1) = 1 – e
–λt
P(X ≥ 1) =1– P(0) =1– [λ
0t
. e
–λt
/0!] =>
d 3X
T
)
(
VWA V
X :* :$T
f(t)
P %VWA V EB*
F(t) = P(T ≤ t)
7
T
.
e2X
7CA
P
:I
VWA V :*
9I PI
:
X
P = P(T ≤ t = 1)
:$T
:
)
1
............ (
P = F(t = 1)
g3"I A=
I
:
P
V NA 9 6 ` :I 7CAh 7 (
:
)
2
(
..........
P = P(X ≥ 1) = 1 – e
–λt
)
1
(
P
)
2
(
:I iX=
)
3
............ (
t
λ
–
e
–
1
=
)
t
(
F
jX P
f(t) = F(t)’ = (1 – e
–λt
)’
λ e
–λt
f(t) =
1
j&= a3)
.
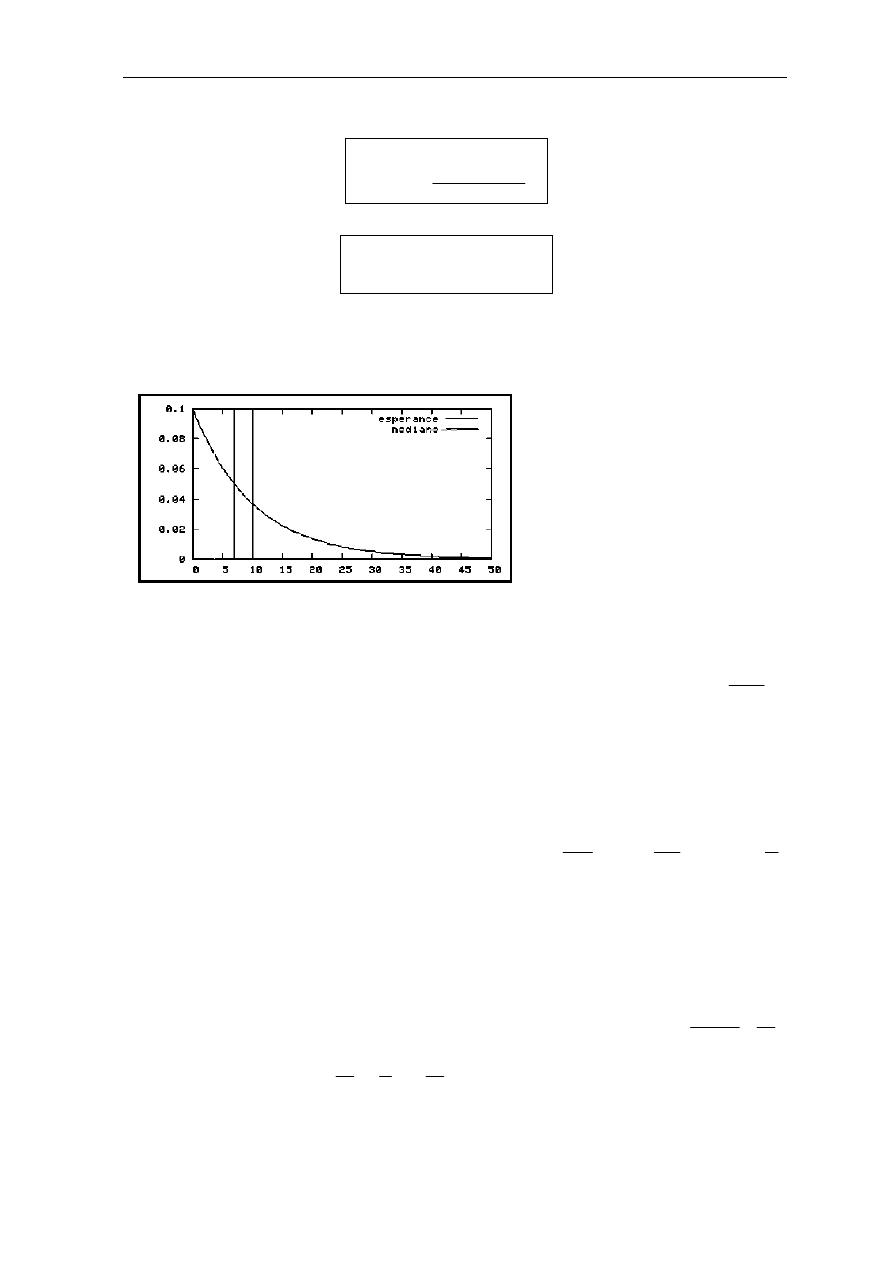
k3 l1Am P ?hCAh ST "
–
lo
1
.
20
9
:
P ;3* > NA :Q $T
: ' pE
:
( )
!
)
(
x
x
p
e
x
λτ
τ
λτ
−
=
:ME
T
Z - VWA V
:
≤
>
=
−
0
,
0
0
,
)
(
τ
τ
λ
τ
λτ
e
f
H A
λ
ea A
.
@( 6C
:
: j9R e qI 6CP
.
4
-
2
-
2
-
2
t
t
M
Med
x
−
=
<
=
=
=
λ
λ
µ
µ
λ
σ
λ
µ
)
(
,
)
2
ln(
,
²
/
1
²
,
/
1
(+=
k3 9 6
CQ - P
:
[ ]
(
)
[
]
.
1
)
(
1
0
0
)
(
.
)
(
,
.
)
(
.
)
(
0
)
(
)
(
0
0
0
0
0
0
0
0
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
=
⇒
−
−
=
−
+
=
−
−
−
=
−
=
−
=
⇒
=
=
⇒
=
=
+
=
=
∫
∫
∫
∫
∫
∫
∞
+
∞
−
−
∞
−
∞
+
∞
−
−
∞
+
∞
+
−
+∞
−
+∞
∞
−
X
E
e
dx
e
e
x
vdu
uv
X
E
e
v
dx
e
dv
dx
du
x
u
udv
dx
e
x
dx
e
x
dx
x
xf
X
E
x
x
x
x
x
x
x
[ ]
(
)
[
]
.
²
1
1
²
2
)²
(
²)
(
)
(
.
²
2
)
(
2
2
0
)
2
(
²
²)
(
.
)
(
,
2
²
.
)
²(
)
²(
0
)
(
²
²)
(
)²
(
²)
(
)
(
2
0
0
0
0
0
0
0
0
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
=
−
=
−
=
=
=
+
=
−
−
−
=
−
=
−
=
⇒
=
=
⇒
=
=
+
=
=
−
=
∫
∫
∫
∫
∫
∫
∫
∞
+
−
∞
+
−
∞
−
∞
+
∞
−
−
∞
+
∞
+
−
∞
+
−
∞
+
∞
−
X
E
X
E
X
V
X
E
dx
xe
dx
x
e
e
x
vdu
uv
X
E
e
v
dx
e
dv
xdx
du
x
u
udv
dx
e
x
dx
e
x
dx
x
f
x
X
E
X
E
X
E
X
V
x
x
x
x
x
x
x
4
5
!
"# $ %&'( ) *+ , -.
.

IV
.
21
!"#$
:
≤
>
−
=
=
=
≤
−
=
+
−
=
−
=
+
=
=
>
−
∞
−
−
−
−
−
∞
−
∞
−
∫
∫
∫
∫
0
,
0
0
,
1
)
(
0
0
)
(
:
0
1
1
0
)
(
)
(
:
0
0
0
0
x
x
e
x
F
du
x
F
x
e
e
e
du
e
du
du
u
f
x
F
x
x
x
x
x
x
u
x
u
x
λ
λ
λ
λ
λ
λ
λ
λ
4
-
2
-
3
&' () $)* +, - . ! ) / 012 3) ( ,
45 &6 , ,
-7 8(
.
3 9(1 :; - !<" =' $
F
>
t
?) >
2
.
"@ A3 ( , B 5
C D)E FG 'H6) H ,
1
.
4
-
2
-
3
-
1
J 6 F$ .K ( , L, M; NO &PQ ! RS$
9
:
≤
>
=
−
−
0
,
0
0
,
)
(
/
1
x
x
e
cx
x
f
x
β
α
T
( )
0
,
0
,
)
(
,
1
0
1
>
>
=
Γ
Γ
=
∫
∞
−
−
β
α
α
α
β
α
α
dx
e
x
c
x
U
0
,
0
,
0
,
0
0
,
)
(
)
(
/
1
>
>
≤
>
Γ
=
−
−
β
α
α
β
α
β
α
x
x
e
x
x
f
x
4V$)
Γ(α, β)
X ~
1
@$;
:
>0)HW ) 0W
1983
>
X
158
.
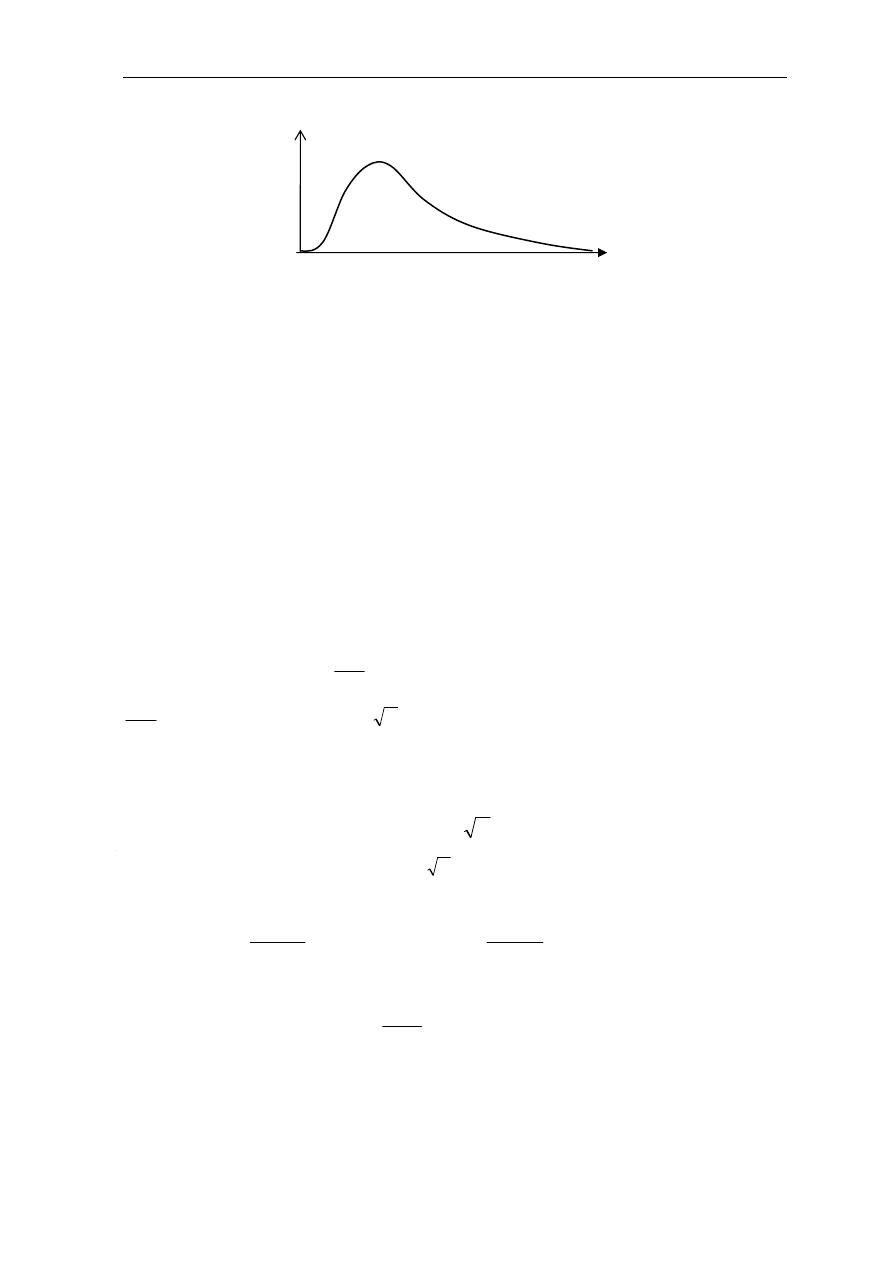
Y Z[ ) \K H
–
Z+^
1
.
22
4
-
2
-
3
-
2
µ = α β , σ² = α β², M(t) = (1 – βt)
–α
_; !
α >1
:
Γ(α) = (α – 1)Γ(α – 1)
` )
α
∈
N
:
Γ(α) = (α – 1)! , Γ(1/2) = √π
!; ( , ! aH " PH <9J > 3 (1 (
α = 1
? , 0; >
2
b "
7 ( , ! aH
α = ν/2
!;
ν
) c 4_ Ld 6
β = 2
.
, .
.
45;
:
( )
( )
( )
.
5
.
2
,
5
.
4
,
7
,
,
,
0
2
/
1
0
6
0
4
Γ
Γ
Γ
∫
∫
∫
∞
−
∞
−
∞
−
dx
x
e
dx
e
x
dt
e
t
x
x
t
( )
=
=
Γ
=
=
=
Γ
=
∫
∫
∞
−
∞
−
,
720
!
6
7
,
24
!
4
)
5
(
0
6
0
4
dx
e
x
dt
e
t
x
t
( )
π
=
Γ
=
=
∫
∫
∞
−
−
∞
−
2
/
1
,
720
0
2
/
1
0
2
/
1
dx
e
x
dx
x
e
x
x
( )
(
)
( )
( )
( )
5
.
1
)
5
.
0
(
5
.
1
)
5
.
2
(
,
720
!
6
7
5
.
2
)
5
.
2
(
5
.
3
5
.
3
5
.
3
1
5
.
3
5
.
4
=
Γ
=
Γ
=
=
Γ
Γ
=
Γ
=
+
Γ
=
Γ
)
( )
π
π
)
5
.
0
)(
5
.
1
)(
5
.
2
(
5
.
3
5
.
0
)
5
.
0
)(
5
.
1
)(
5
.
2
(
5
.
3
5
.
2
=
Γ
=
( )
π
5
.
1
)
5
.
0
(
5
.
1
)
5
.
2
(
,
720
!
6
7
=
Γ
=
Γ
=
=
Γ
2
.
X
Y
Z
! "#
:
( )
≤
>
=
≤
>
Γ
=
−
−
,
0
,
0
0
,
)
6
(
4
)
(
,
0
,
0
0
,
5
2
)
(
4
4
/
3
5
2
/
4
f
y
y
e
y
y
f
x
x
e
x
x
f
y
x
≤
>
=
−
0
,
0
0
,
6
)
(
,
0
0
2
z
z
e
z
z
f
z
,
20
²)
2
(
5
²
²
,
10
)
2
(
5
=
=
=
=
=
=
x
x
αβ
σ
αβ
µ
4
6
f(x)
0 x
%&'
IV
.
() #!* + ,
23
3
²
,
3
)
1
(
3
,
64
²)
4
(
4
²
,
16
)
4
(
4
,
20
=
=
=
=
=
=
=
z
z
y
y
σ
µ
σ
µ
4
-
2
-
4
)
(
"#$ %&'# ()
t²
*
F
+,-. *+,-. *
/0 1#
1
3 4 567 8 9. %&'# *
:
0
1
;< *5 7 = > #-? > # 9. *
.
4
-
2
-
4
-
1
+ ? AB.? >C D? E< F >,GH 6 IH J
:
(
)
(
)
)
0
,
(
0
1
0
,
1
)
(
1
1
>
<
<
−
=
−
−
β
α
β
α
β
β
α
ailleurs
x
x
x
x
f
()
B(α, β)
>& +/
:
0
,
,
)
1
(
)
,
(
1
0
1
1
>
−
=
∫
−
−
β
α
β
α
β
α
du
u
u
B
1
B(α, β)
X ~
4
7
α
β
.
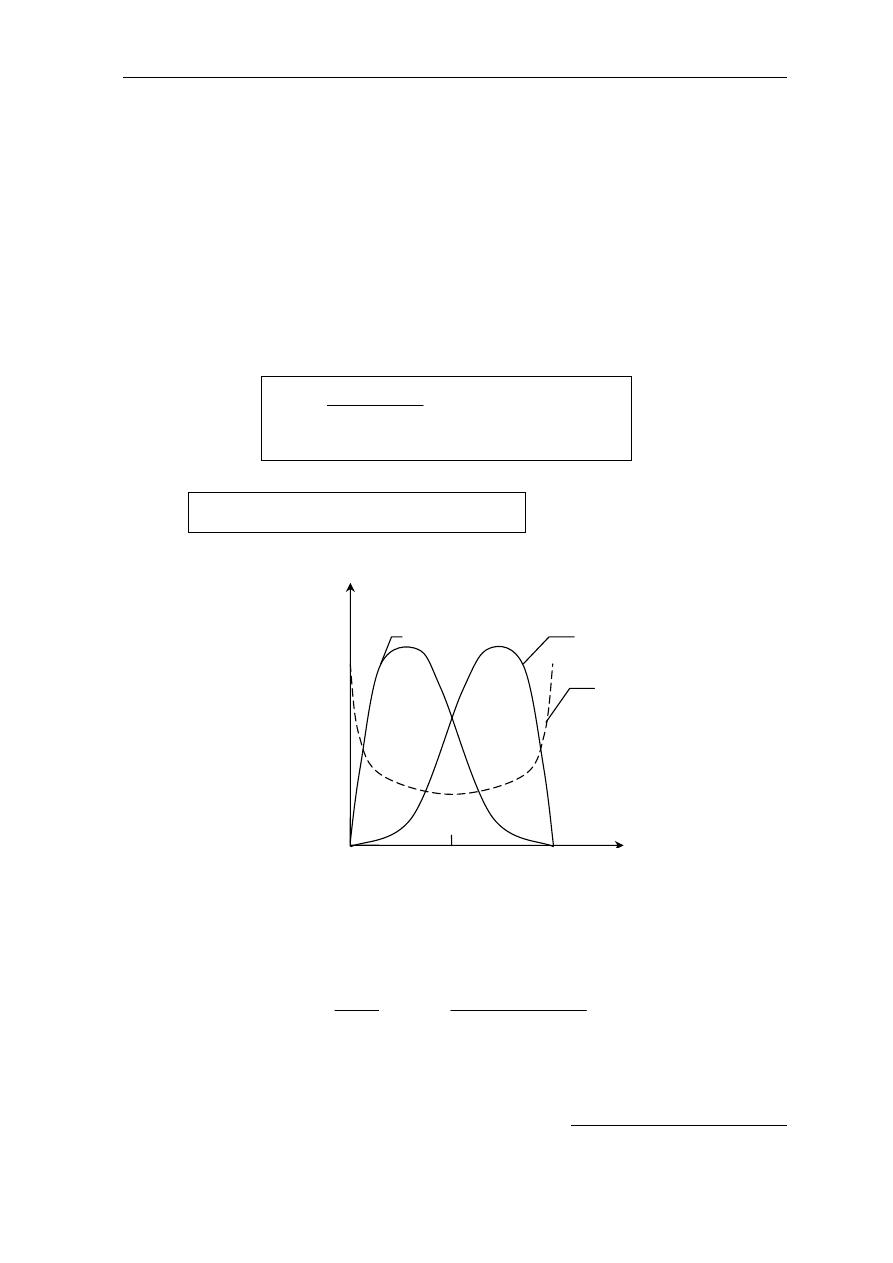
!" #$ % & '(&" )*+
x = 0.5
4
-
2
-
4
-
2
(
) (
)
1
²
²
,
+
+
+
=
+
=
β
α
β
α
αβ
σ
β
α
α
α
,"-" , ."
:
1
L# M7
.
0 0,5 1 X
f(x)
1
α
= 2,
β
= 4
α
= 4,
β
= 2
α
= 1/2,
β
= 1/2

+N OP)Q 5R)R S< 9T&
–
OV
1
.
24
)
(
)
(
)
(
)
,
(
β
α
β
α
β
α
+
Γ
Γ
Γ
=
B
J.
.
+ 1#)
:
)
(
)
1
,
(
),
,
1
(
),
2
,
(
),
2
/
1
,
2
/
1
(
),
4
,
3
(
N
n
n
B
n
B
n
B
B
B
∈
( )( )
B
B
,
)
2
/
1
(
)
2
/
1
(
)
2
/
1
,
2
/
1
(
,
60
1
120
2
)!
1
7
(
)!
1
4
(
)!
1
3
(
)
4
,
3
(
=
+
=
=
=
−
−
−
=
π
π
π
n
n
n
n
B
,
)!
1
(
1
)!
1
2
(
!
1
)!
1
(
)
2
,
(
+
=
+
−
=
n
n
n
n
B
n
n
n
n
n
n
n
B
1
!
1
)!
1
(
)
1
,
(
,
1
)!
1
(
)!
1
(
!
)!
1
(
1
)
,
1
(
=
−
=
=
−
−
=
−
=
J.
2
.
+ 1#)
:
∫
∫
−
−
1
0
1
0
3
4
)
1
(
,
)
1
(
dx
x
x
dx
x
x
,
)
2
,
3
(
B
12
/
1
)]
4
(
3
/[
1
)]
1
(
/[
1
)
2
,
3
(
=
=
+
=
n
n
B
( )
,
280
1
!
8
!
3
!
4
)
4
5
(
)
4
(
5
)
4
,
5
(
)
1
(
1
0
3
4
=
=
+
Γ
Γ
Γ
=
=
−
∫
B
dx
x
x
6
/
1
!
3
!
1
!
1
)
2
,
2
(
)
1
(
1
0
=
=
=
−
∫
B
dx
x
x
>WX J
)
(
)
(
)
(
)
,
(
β
α
β
α
β
α
+
Γ
Γ
Γ
=
B
&Y
1 >B. >C Z
[
:
(
)
(
)
<
<
−
Γ
Γ
+
Γ
=
−
−
ailleurs
x
x
x
x
f
,
0
1
0
,
1
)
(
)
(
)
(
1
1
β
α
β
α
β
α
&-H W I >\T >) / +]
α = 1 , β = 1/λ
.
^
2
&-H W I >\T >) /
α = υ/2 , β = 2
()
υ
_ 1M + ` C&H
.
J.
3
.
= aQ > # D? E< *I = ab >W7 > #- 1#)
c
:
<
<
−
=
sinon
,
0
1
0
,
)
1
(
6
)
(
5
x
x
x
f
-& L# J.7 I
:
).
6
,
1
(
/
1
6
/
1
)
,
1
(
B
n
n
B
=
⇒
=
N
α
β
Z#
1
6
Z &Y *c dH
B(1, 6)
X ~
-
:
(
)
.
20
/
1
)
5
(
16
4
)
1
²(
²
,
2
/
1
=
=
+
+
+
=
=
+
=
β
α
β
α
αβ
σ
β
α
α
µ
J.
4
.
c >#e f g 7 aQ > #
.
>W7 > #- 1#)
Z J)
&
> #-
IH
35
%
.
%
60
5
/
3
2
3
3
)
2
,
3
(
~
)
2
,
3
(
/
1
12
4
*
3
12
sinon
,
0
1
0
),
1
²(
12
)
(
=
=
+
=
+
=
⇒
⇒
=
⇒
=
<
<
−
=
B
X
B
x
x
x
x
f
β
α
α
µ
.
)
1
²(
12
)
35
.
0
(
1
35
,
0
−
=
>
∫
dx
x
x
X
P
9Ph
IV
.
&' .?] >)R 5
25
I
1
²
:
−
=
=
x
u
et
dx
x
v
soit
3125
.
0
²
3
)
1
(
12
)
35
.
0
(
1
1
35
,
0
1
35
,
0
3
=
+
−
=
>
⇒
∫
dx
x
x
x
X
P
x
4
-
2
-
5
!" #
.
2
! "
#
$ %
&'(
)*$+
,-*
X~N(0, 1)
Med = Mod = µ = 0, σ² = 1
P(Z ≤ -z) = P(Z ≥ z)
P(-1 ≤ Z ≤ 1) = 0.6826,
P(-2 ≤ Z ≤ 2) = 0.9544,
P(-3 ≤ Z ≤ 3) = 0.9973.
)
≤
>
=
−
0
,
0
0
,
)
(
x
x
e
x
f
x
λ
λ
µ
= 1/λ, σ² = 1/ λ²
F(x) = 1– e
–λx
Med < µ, P(X ≤
µ
) = 0.63
.
%
X~ Γ(α,β)
0
,
0
0
,
)
(
)
(
/
1
≤
>
Γ
=
−
−
α
β
α
β
α
x
x
e
x
x
f
x
α > 0, β > 0
µ = α β, σ² = α β²
0
,
)
(
0
1
>
=
Γ
∫
∞
−
−
α
α
α
dt
e
t
t
*/ .
B(α, β)
X ~
>
<
<
−
=
−
−
;<=>?
x
B
x
x
x
f
,
0
0
,
,
1
0
,
)
,
(
)
1
(
)
(
1
1
β
α
β
α
β
α
µ
(
) (
)
1
²
²
,
+
+
+
=
+
=
β
α
β
α
αβ
σ
β
α
α
α
du
u
u
B
∫
−
−
−
=
1
0
1
1
)
1
(
)
,
(
β
α
β
α
)
(
)
(
)
(
)
,
(
β
α
β
α
β
α
+
Γ
Γ
Γ
=
B
α > 0, β > 0
B(1, n) = B(n, 1) = 1/n
(n>0, n
∈
)
∞
<
<
∞
−
=
−
z
z
f
e
z
2
/
²
2
1
)
(
π
%& '!( )* +"
–
'-
1
.
26
4
-
2
-
6
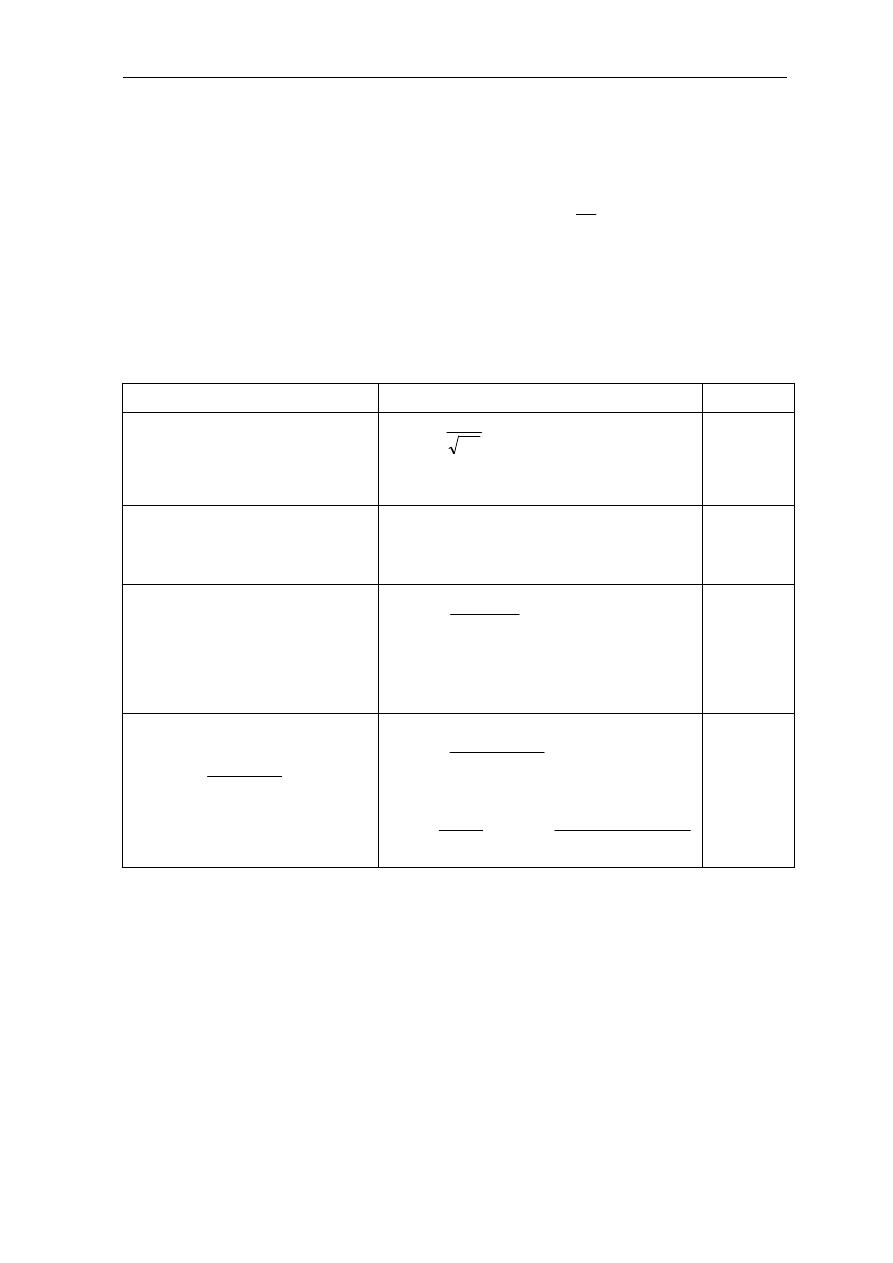
./ + % 0 1 2 23
)
5678 5 "
(...
: ;*
<
=
>?@
1/λ
1A3# 0BC
(vieillissement)
:D ED
6
7F ? .7
T
t
∆
=3G 0HI
t
∆
7J# 0HI
T
K
LD MN
I
+HO P .7 QA R ? @S
.
:
GU A VW +XD P
T
F P Y#ZW8 [ ZHI \]
.
PU
P(t)
7J# ^ )* _W D Z3
t
` a bcOI 1 2 . 5
(t, t
1
)
d
t
1
= t + ∆t
.
'W?
G 23 e#2
:
P(B/A) = P(AB)/P(A)
f
:
P(t
1
/t) = P(t
1
)/P(t)
g -W h"D QX P
Q(t, t
1
)
56i ` j" +Z2 kO
Q(t, t
1
) = 1 – P(t, t
1
) = 1 – P(t
1
)/P(t) = [P(t) – P(t
1
)]/P(t)
= [P(t) – P(t + ∆t)]/P(t) = [P(t) – P(t + ∆t)]∆t/P(t)∆t
:D l#8
:
P'(t) = lim
∆t
0
[P(t + ∆t) – P(t)]/∆t
bW
Q(t, t
1
) = [-P'(t)/P(t)] ∆t + ο(∆t)
0&?
-P'(t)/P(t) = λ(t)
a f
∆t
0
Q(t, t
1
) ≈ λ(t) ∆t
λ(t)
c j" mOI n ZO :D .
(0, t)
op Z2 b#2 Y#Z #H3 7J# a mOI
(taux
de défaillance instantané)
.
qU8
:
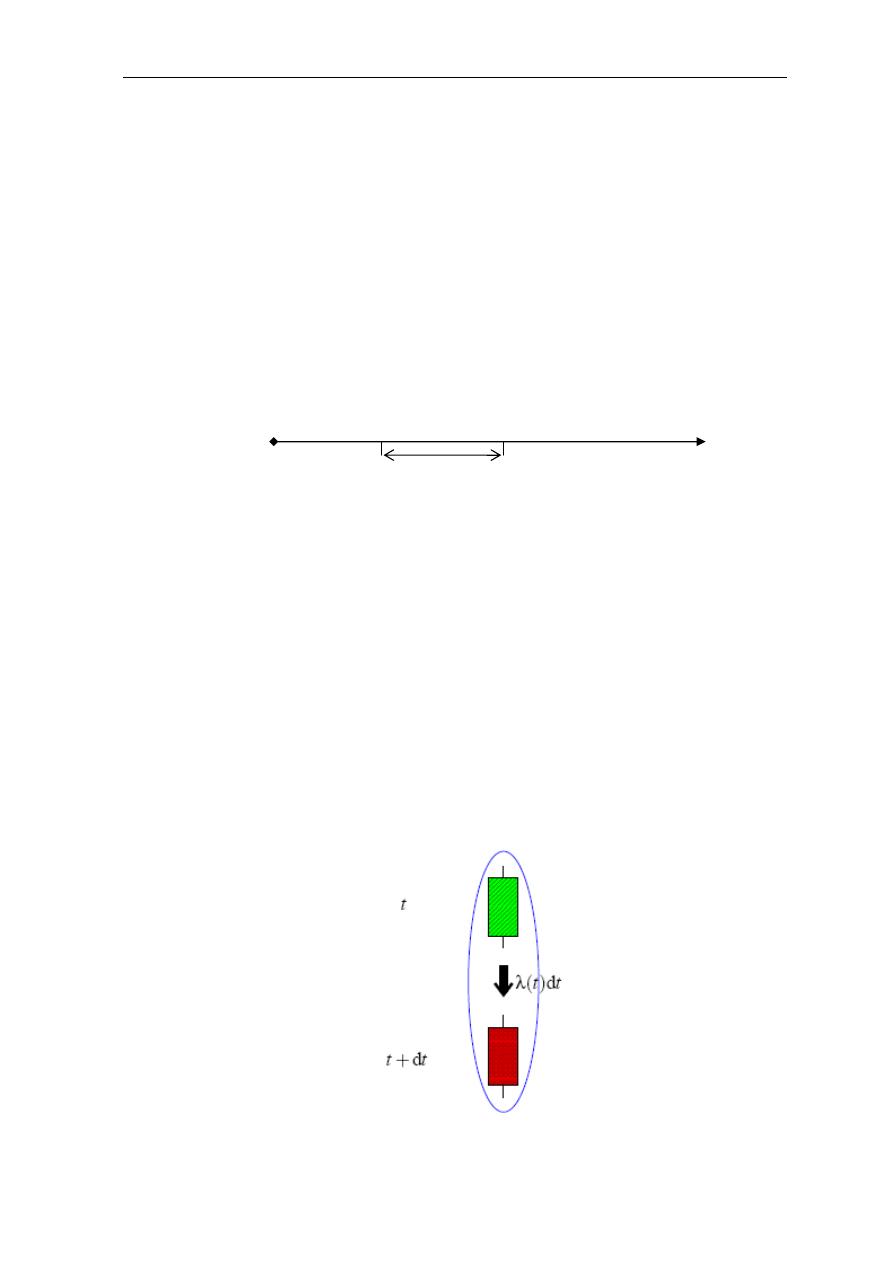
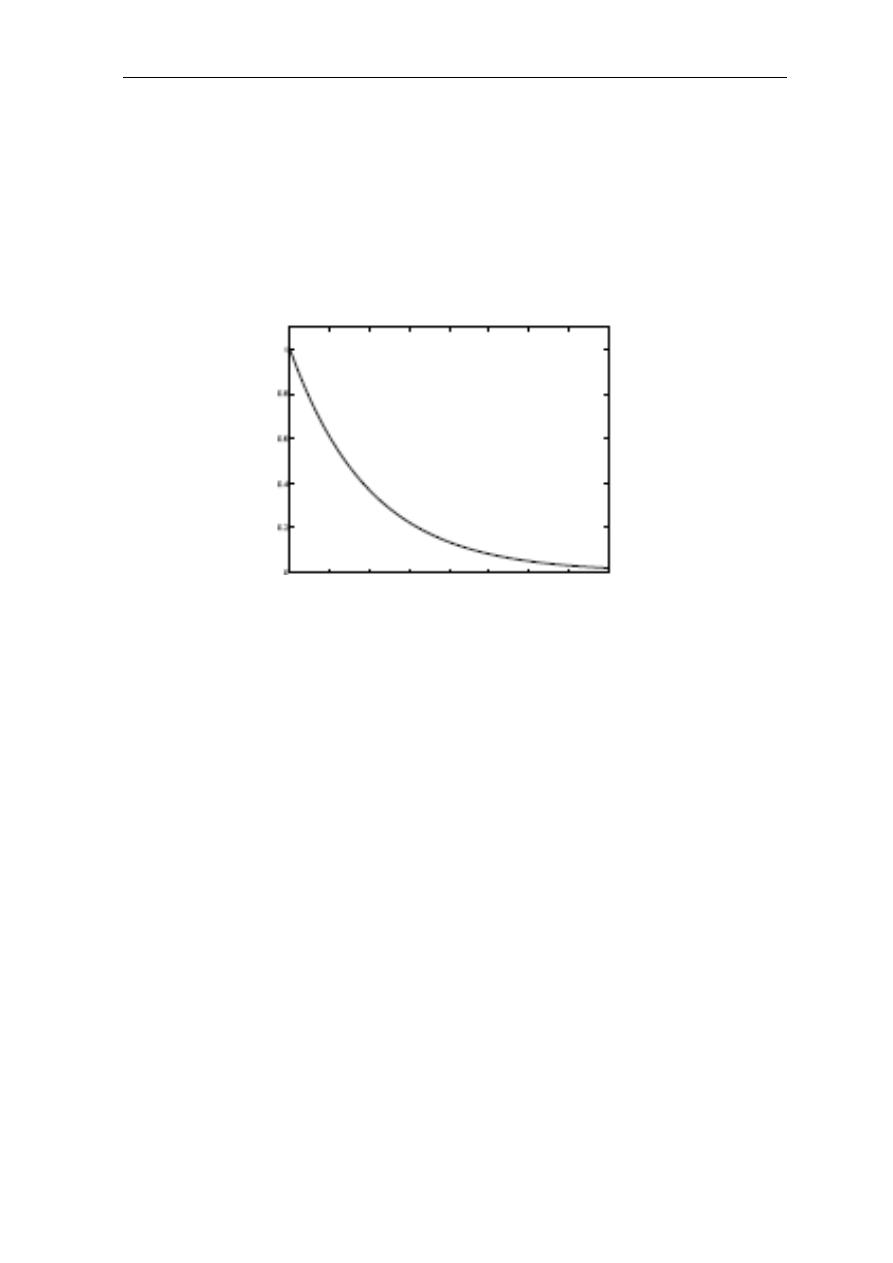
λ(t)dt = P(T
BF
< t + dt | T
BF
> t)
PD
T
BF
7J# iW +Z2 :A Z3 +2 +r
(t = 0)
g 6!" < -W 5
T
.
0 t
∆t
t
1
+!c
IV
.
27
7J# +HO +Z2 kO 1 2
t
-
g b
v(t)
Z3# A D F A +s
)
- 1 8D
R(t)
.(
.
P- P2 jZ j3 G a ED Z2 63 a
t
:U
λ(t) = λ
?@
.
7F ^ )* Z3
t
D kO 1 2 bI; .
&c +/ a 5c ti. j" +Z2 E
Z2 A 2 :U P- P2 <j3 Z2 H@ P2 3?
)
g b -W
X
(
c a
t
: ? 0I 0H
g
P(X = 0) = (λt)
0
e
-λt
/0! = e
-λt
= v(t)
"#
4
$
8
% &' (
v(t) = P(T > t) = e
-λt
λ
Z2 D P a Z2 A 2 =
(taux de défaillance)
.
VW PUs - uc8 P
T
a 03I R Z2 A 2 +r X vw 0&? Z3
P-
(0, t)
:
= P(X > 0) = 1 – P(X = 0) = 1 – e
-λt
F(t) = P(T ≤ t)
vw# GU A e#2 +!x 0 A y3\?
T
:
f(t) = F'(t) = λ e
-λt
(t > 0)
% 0 A %.
.
•
%. Z3 F O
λ
λ
λ
λ
λ
/
1
)
(
/
1
)
(
)
(
0
0
0
0
∫
∫
∫
∫
∞
−
∞
∞
−
∞
=
=
=
=
=
=
=
dt
e
dt
t
v
dt
e
t
dt
t
tf
t
E
MTTF
t
t
Z2 g#3 .
.
•
vwz W G a +Z
dt
Z3
. ? +ZI n
λdt
.
)* + ,
(temps de éparation)
.
# GU A VW +#J a {; 3Z 1 8 :D PUs
#Z ZO |jz* #2 QOwI R
T
R
63} a |jz( A )* +!W 3? Z~ uc8 0H8 d 5
|jz(
:
f(t) = µ e
-µt
(t > 0)
%& '!( )* +"
–
'-
1
.
28
d
µ
P a jz( A 2 = ED |jz(
.
•
|jz( =
MTTR = 1/µ
•
-. )* +Z P 38
)
#!I
(
a
dt
E
µdt
.
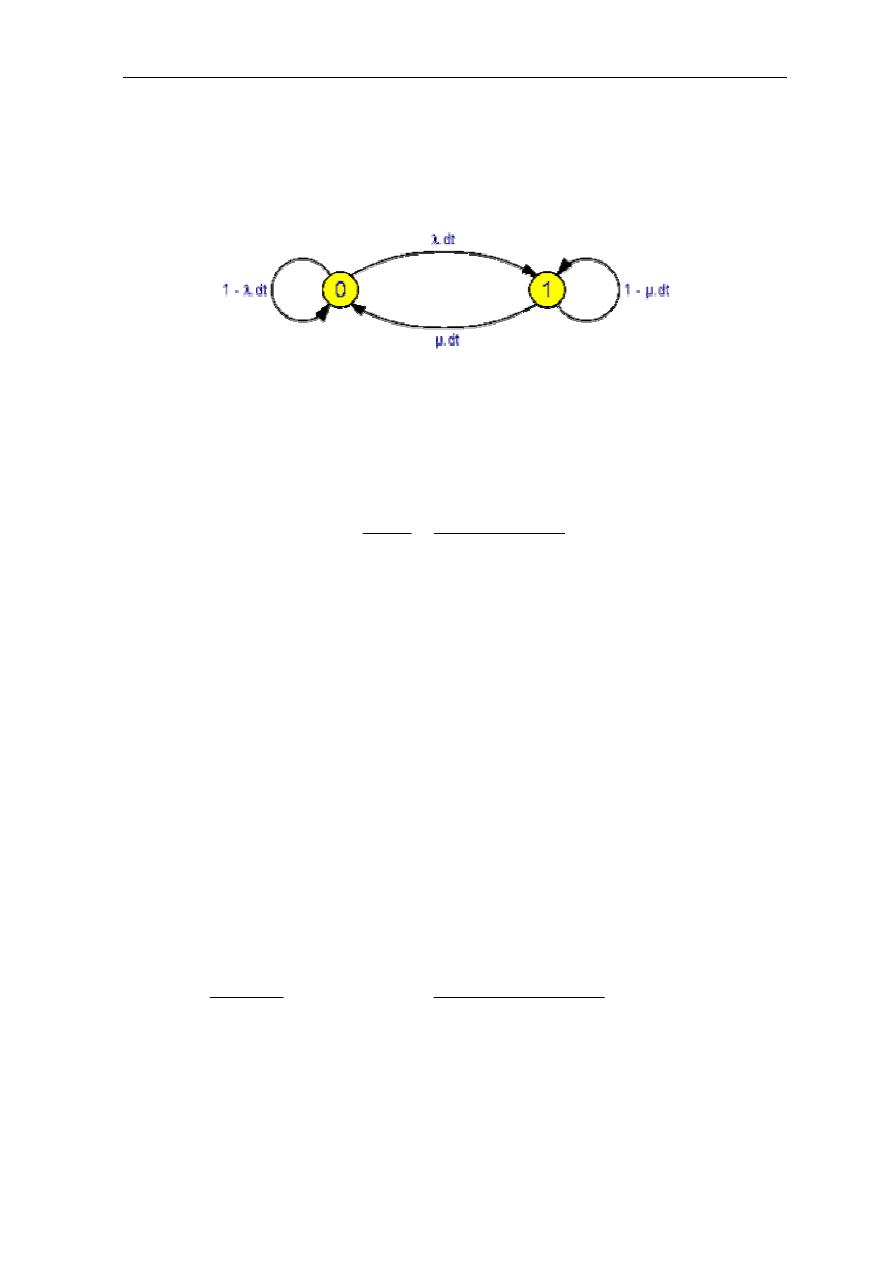
g Q F 8-6 ;*
1
g +Z F
0
38 :UI
+
:
:U 63 a 5G6 ## +s l
:
P'
0
(t) = P'
1
(t) = 0
λP
0
(t) = µP
1
(t)
d
P
0
(t)
-.
P
1
(t)
+Z
.
63 \ +& a
:UI :D ED -. \] . " lQ \] e#2 +!J8 6 78 1 ?
7F a Fz Z3
A(t) = A
t
L )* ]I
:
MTTR
MTTF
MTTR
A
+
=
+
=
µ
λ
µ
.6 3 -.X :G +H e#2
99
%
+I ZO D 17W
24/24
I 1 a 2
7
2
Q a +ZI
W?
15
P2 +3I -.X q#Z 17W uwW Q a +ZI 3OA
%99.965
.
j
78 a % 0 1 8
(théorie de la fiabilité)
>8 ;* Q#ZI +HO +2 +
ucW? +Z# I s 3 p
.
# %. p 2 P W # a A2 i. Y3J
1A3 G yjZ8 G ? Z
.
_W +w ) c a
(période de rodage)
+Z :U
Z3 D p 0W!I #2 a W 38 qH? vH
)
+#" 5 A a +#"
5q a
(...
Z~ i. PU 5
2? 'B
)
MJW 78D
(
%HZ jw G e2 I 8 # S
(période
d'exploitation normale)
3 Z2 :U d
(t) = λ)
λ
(
.
#3 H8 6A8 Z2 :UI d 63 P c ti. ?
2 P2
p
)
P- P2 P
(
1A3 # SI
(période de vieillissement)
- Z2 :U d
= B Q&I qH? 1 qH? p j. Z2 ti. qH :U
)
5?6 56
.(...
0
0I . j + m! Ei
+H
(Weibull)
%#
:
)
(
)
(
1
)
(
,
1
)
(
,
)
/
1
1
²(
)
/
2
1
(
²
,
)
/
1
1
(
0
,
0
0
,
1
)
(
/
2
/
1
t
v
at
e
t
T
P
at
e
t
F
b
abt
t
a
b
b
MTTF
a
b
t
t
at
e
b
abt
t
f
b
b
b
b
b
=
−
=
>
⇒
−
−
=
−
=
+
Γ
−
+
Γ
=
=
+
Γ
=
≤
>
−
=
−
λ
σ
µ
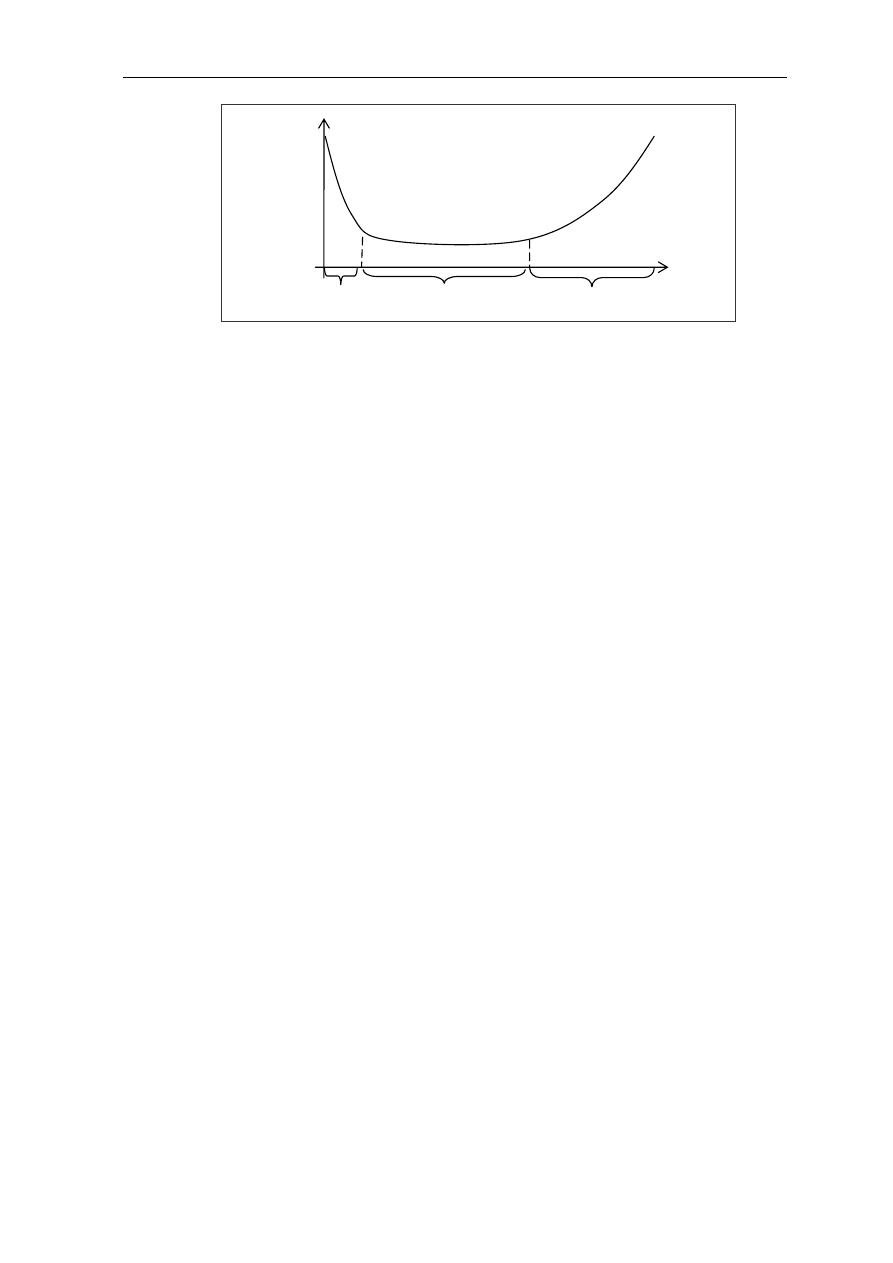
+!c
IV
.
29
bH l _W : ) # qZ I v a 5 c L z" D ; eZ # I
D 3W D 'Z" J!
W :D K0H #2 +HO ED W ] +HO P c W i
XWU 6ZI H _W H l :D +HO 1A3 G )* +!I 6A8 8U(
.
PD +H 0I P z" . % 0
b = 1
8 # a i. Y3J
5?@ Z2 :U PD
g -r ) #
b < 1
g -r v" #
b >1
0O 5
µ
Z2 #U a t6H2 PUs
Z
)
O
(
+Z +HO
(Mean Time To First Failure)
5
λ(t)
=
)
(
a Z2 A 2
P-
v(t)
O@ A
)
BD eI
(
(fonction de la fiabilité)
+ 6 %.
)
AX 1 2
Z2D
(
? )*
t
.
G mz G^s a BD 1 :D PUs +H 0I
(mortalité)
)* G&(? 5c# 62 a
mz b
A 2 ? P vw wz :83 D 5j.j F : 3
n
vw P
0 #@ #3
n
∞
.
"#
4
$
9
.
* &' -.
λ(t)
O@
+Z
0 t
I II III
