
ﻣﺪﺧﻞ ﺇﱃ
ﺍﻻﺣﺘﻤﺎﻻﺕ ﻭ
ﺍﻹﺣﺼﺎﺀ ﺍﻟﺮﻳﺎﺿﻲ
ﺩﺭﻭﺱ
ﻭﲤﺎﺭﻳﻦ
ﺍﳉﺰﺀ ﺍﻟﺜﺎﱐ
:
ﺍﻹﺣﺼﺎﺀ
ﺍﻟﻔﺼﻞ ﺍﻟﺴﺎﺩﺱ
.
ﺍﻟﺪﻭﺍﻝ ﻏﲑ ﺍﳋﻄﻴﺔ ﻭﺍﻟﺘﻘﺎﺭﺏ
ﺑﻮ ﻋﺒﺪ ﺍﷲ ﺻﺎﱀ
ﺃ
ﺳﺘﺎﺫ ﻣﺴﺎﻋﺪ
ﻣﻜﻠﻒ ﺑﺎﻟﺪﺭﻭﺱ
ﺑﻜﻠﻴﺔ ﺍﻟﻌﻠﻮﻡ ﺍﻻﻗﺘﺼﺎﺩﻳﺔ
–
ﺟﺎﻣﻌﺔ ﺍﳌﺴﻴﻠﺔ
.

و تا إ
اء ا
.
ج
2
.
-
2
-
ت س
ا ادس
.
برا و ا لاوا
ﺍﻟﻔﺼﻞ
6
ﺍﻟﺪﻭﺍﻝ ﻏﲑ ﺍﳋﻄﻴﺔ ﻭ ﺍﻟﺘﻘﺎﺭﺏ
................................
......................
3
6-1
ﺍﻟﺴﻠﻮﻙ ﺍﻟﺘﻘﺎﺭﰊ ﻟﺒﻌﺾ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﺍﻻﺣﺘﻤﺎﻟﻴﺔ
................................
........
3
6
-
1
-
1
! ا"ز$او %&' ا"ز$ ا() بر,- .ا$ ن$01
................................
.....
3
6
-
1
-
2
ة4 ة5 إ 6!, ة5 ( ل,0ا
.
................................
..................
5
6
-
1
-
3
ن$9ا$) "ز$:و %&'ا "ز$ا () بر,ا
................................
.......................
5
6
-
1
-
4
! ا"ز$او ن$9ا$) "ز$: () بر,ا
................................
.....................
5
6
-
1
-
5
ا6<& ان$01
6=آ
................................
................................
.................
6
6
-
2
ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﻙ
2
ﺳﺘﻴﻮﺩﻧﺖ ﻭﻓﻴﺸﺮ،
................................
................
7
6
-
2
-
1
ك"ز$:
2
................................
................................
................................
7
6
-
2
-
2
A0د$9 "ز$:
................................
................................
.........................
9
6
-
2
-
3
D. "ز$:
................................
................................
............................
11
6
-
2
-
4
6EF
................................
................................
................................
.
12

Gا
VI
.
رب,ا و 6!Hا I لاوا
3
ا
6
بر ا و ا لاوا
$%اا
ك
2
'%د(و ) ،
-
ك,او برا
-.ار
-
ن%0
1آ 3ا 4ا
ﻋﺮﻓﻨﺎ ﰲ ﻓﺼﻞ ﺍﳌﺘﻐﲑﺓ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ ﺃﻥ ﺃﻱ ﺩﺍﻟﺔ ﰲ ﻣﺘﻐﲑﺓ ﻋﺸﻮﺍﺋﻴﺔ
ﺃﻭ ﺃﻛﺜﺮ
ﺃﺣﺴﻦ ﻣﺜﺎﻝ ﻋﻠﻰ؛ﺔﻴﺋﺍﻮﺸﻋ ﺓﲑﻐﺘﻣ ﺎﻫﺭﻭﺪﺑ ﻲﻫ
ﺫﻟﻚ ﻫﻮ ﺍﳌﺘﻐﲑﺓ ﺍﳌﻌﻴﺎﺭﻳﺔ ﺍﳌﺮﻛﺰﻳﺔ
X* = [(X –
µ
)/σ]
.
ﰲ ﻫﺬﺍ ﺍﻟﻔﺼﻞ ﺳﻮﻑ ﻧﺪ
ﺭﺱ ﻋﺪﺩﺍ ﻣﻦ ﺍﳌﺘﻐﲑﺍﺕ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ
ﺬﻩ ﺍﻟﻄﺮﻳﻘﺔ ﺔﻧﻮﻜﳌﺍ
ﺎﺎﻌﻳﺯﻮﺗ ﻞﺜﲤ ﱵﻟﺍ ﻭ
،
ﻙ
2
ﺩﻭﺍﻝ،ﺖﻧﺩﻮﻴﺘﺳ ﻭ ﺮﺸﻴﻓ ،
ﺫﺍﺕ ﺍﺳﺘ
ﺨﺪﺍﻡ
ﻭﺍﺳﻊ ﰲ
ﺍﻹﺣﺼﺎﺀ
ﺍﻻﺳﺘﺪﻻﱄ
.
ﰲ ﺍﳌﺒﺤﺚ ﺍﻟﺜﺎﱐ ﺳﻨﺘﻄﺮﻕ ﻟﻠﺘﻘﺎﺭﺏ ﺑﲔ
ﻋﺪﺩ ﻣﻦ
ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﺍﻻﺣﺘﻤﺎﻟﻴﺔ ﺍﳌﺨﺘﻠﻔﺔ ﻭﻛﻴﻔﻴﺔ ﺍﺳﺘﺨﺪﺍﻡ
ﺃﺣﺪﻫﺎ
ﳊﺴﺎﺏ
ﺍﺣﺘﻤﺎﻝ ﻣﺎ ﻣﺘﻌﻠﻖ
ﲟﺘﻐﲑﺓ ﺫﺍﺕ ﺗﻮﺯﻳﻊ ﺁﺧﺮ
.
ﰲ ﺍﻷﺧﲑ ﺳﻨﺘﻄﺮﻕ ﻟﻨﻈﺮﻳﺔ ﺍﻟﻨﻬﺎﻳﺔ ﺍﳌﺮﻛﺰﻳﺔ ﺫﺍﺕ ﺍﻻﺳﺘﺨﺪﺍﻡ ﺍﻟﻮﺍﺳﻊ ﰲ
ﺍﻹﺣﺼﺎﺀ ﺍﻟﺮﻳﺎﺿﻲ
ﻭ
ﺍﻟﱵ ﺗﻌﺘﱪ ﺃﺣﺪ ﺃﻫﻢ ﺧﺼﺎﺋﺺ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
.
6
-
1
ا ت زا !ر ا ك#$ا
! ا"ز$او %&' ا"ز$ ا() بر,ا
, ة5 ( ل,0ا
ة4 ة5 إ 6!
ن$9ا$) "ز$:و %&'ا "ز$ا () بر,ا
ن$01
6= اآ6<&ا
ﻬﲑﺓـﺸﻟﺍ ﺔـﻴﻟﺎﻤﺘﺣﻻﺍ ﺕﺎﻌﻳﺯﻮﺘﻟﺍ ﻦﻣ ﺩﺪﻋ ﲔﺑ ﻞﺼﳛ ﻱﺬﻟﺍ ﺏﺭﺎﻘﺘﻟﺍ ﺕﻻﺎﺣ ﺾﻌﺑ ﺚﺤﺒﳌﺍ ﺍﺬﻫ ﰲ ﻝﻭﺎﻨﺘﻧ
.
ﺪـﺼﻘﻧﻭ
ﺑﺎﻟﺘﻘﺎﺭﺏ ﺑﲔ ﺗﻮﺯﻳﻌﲔ
)
ﺍﻟﺜﻨﺎﺋﻲ ﻭﺑﻮﺍﺳﻮﻥ ﻣﺜﻼ
(
ﺃﻥ ﻳﻌﻄﻲ ﺍﻟﺘﻮﺯﻳﻌﺎﻥ ﻧﺘﺎﺋﺞ ﻣﺘﻘﺎ
ﲏـﻌﻳ ﺎـﳑ ،ﲔﻌﻣ ﻝﺎﻤﺘﺣﺍ ﺹﻮﺼﲞ ﺔﺑﺭ
ﺇﻣﻜﺎﻧﻴﺔ ﺍﺳﺘﺨﺪﺍﻡ ﺗﻮﺯﻳﻌﲔ ﺍﺣﺘﻤﺎﻟﻴﲔ
)
ﻭﺃﺣﻴﺎﻧﺎ ﺃﻛﺜﺮ
(
ﳊﺴﺎﺏ ﺍﺣﺘﻤﺎﻝ ﻣﻌﲔ
.
ﻋﻠﻤﺎ ﺃﻧﻨﺎ ﻗﺪ ﺗﻄﺮﻗﻨﺎ ﻣﻦ ﻗﺒﻞ ﺑﺈﳚﺎﺯ ﺇﱃ ﻫﺬﺍ
ﺍﳌﻔﻬﻮﻡ ﻋﻨﺪ ﺩﺭﺍﺳﺘﻨﺎ ﳍﺬﻩ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ
.
6
-
1
-
1
.ا$ ن$01
-
! ا"ز$او %&' ا"ز$ ا() بر,
ﻟﻨﺪﺭﺱ ﺍﻟﺴﻠﻮﻙ ﺍﻟﺘﻘﺎﺭﰊ
ﳌﺘﻐﲑﺓ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ
X ~ B(n, p)
ﻋﻨﺪﻣﺎ ﺗﺆﻭﻝ
n
ﺇﱃ
ﺃﻋﺪﺍﺩ ﻛﺒﲑﺓ ﺟﺪﺍ
.
ﻟﻴﻜﻦ
X
ﳝﺜﻞ ﻋﺪﺩ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺻﻮﺭﺓ ﻋﻨﺪ ﺭﻣﻲ ﻗﻄﻌﺔ ﻧﻘﺪﻳﺔ
:
4
، ﻣﺮﺍﺕ
8
، ﻣﺮﺍﺕ
16
ﻣﺮﺍﺕ
.
Xi
0
1
2
3
4
5
6
7
8
…..
16
P
i
0,0000
0,0002
0,0018
0,0085
0,0278
0,0667
0,1222
0,1746
0,1964
…..
0,0000
4
3
2
1
0
Xi
1/16
4/16
6/4
4/16
1/16
P
i
8
7
6
5
4
3
2
1
0
Xi
0,004
0,031
0,109
0,219
0,273
0,219
0,109
0,031
0,004
P
i

و تا إ
اء ا
.
ج
2
.
4
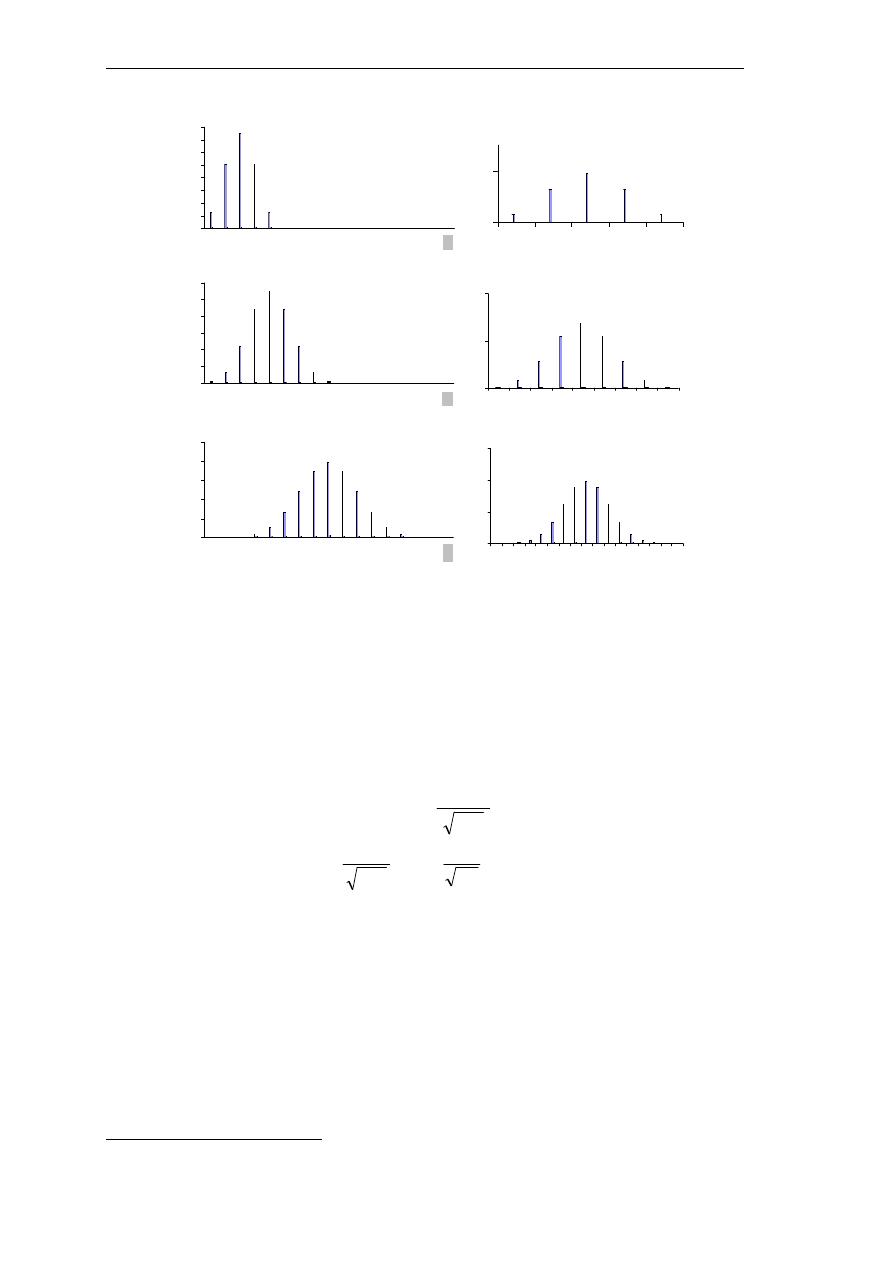
ﺑﺮﺳﻢ ﻣﻨﺤﻨﻴﺎﺕ
P
i
ﻟﻠﺤﺎﻻﺕ
n = 4
،
n = 8
،
n =16
ﻳﻈﻬﺮ
ﺍﻟﺴﻠﻮﻙ ﺍﻟﺘﻘﺎﺭﰊ ﻟﻠﻤﺘﻐﲑﺓ
X
.
Gا
VI
.
رب,ا و 6!Hا I لاوا
5
5(ر
6
-
1
3 -647 ا8ز, -.ر اك, ا
p = 0.5
ري;3ا -;<ا 8زا 5= $و -;<ا 8زا >إ
.
ﻳﻈﻬﺮ ﻣﻦ ﻣﻘﺎﺭﻧﺔ ﺍﳌﻨﺤﻨﻴﺎﺕ ﺍﻷﺭﺑﻌﺔ ﺃﻥ ﺯﻳﺎﺩﺓ ﻗﻴﻤﺔ
n
ﺗﺆﺩﻱ ﺇﱃ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﻣﻨﺤﲎ ﺫﺍ ﺷﻜﻞ ﺟﺮﺳ
ﻲ ﻭﻣﺘﻤﺎﺛﻞ ﺣﻮﻝ
ﺍﻟﺘﻮﻗﻊ
µ
.
ﻫﺬﻩ ﺍﳌﻼﺣﻈﺔ ﺗﺼﺪﻕ ﺃﻳﻀﺎ ﰲ ﺣﺎﻟﺔ
p ≠ 0.5
ﻟﻜﻦ ﺍﻟﺘﺤﻮﻝ ﻳﻜﻮﻥ ﺃﻛﺜﺮ ﺑﻄﺄ
.
ﻣﻦ ﺃﺟﻞ ﺍﻟﺘﻌﻤﻴﻢ ﻧﻌﺘﱪ ﺍﳌﺘﻐﲑﺓ ﺍﳌﻌﻴﺎﺭﻳﺔ
z = (x – µ)/σ
ﺍﳌﻠﺤﻘﺔ ﺑﺬﺍﺕ ﺍﳌﺘﻐﲑﺓ ﺫﺍﺕ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ
X
.
ﺇﻥ ﺍﻟﺴﻠﻮﻙ
ﺍﻟﺘﻘﺎﺭﰊ ﻝ
Z
ﺍﳌﻼ
ﺣ
ﻆ ﰲ ﺍﻟﺸﻜﻞ ﺃﺳﻔﻠﻪ ﻫﻮ ﻣﺎ
ﻳ
ﺜﺒﺘﻪ
ﻗﺎﻧﻮﻥ
ﻣﻮﺍ
ﻓﺮ
:
∫
−
∞
→
∞
→
=
≤
−
≤
→
−
=
b
a
z
n
n
dz
e
b
npq
np
x
a
P
N
npq
np
X
Z
p
n
B
X
2
/
²
2
1
)
(
lim
),
1
.
0
(
:
)
,
(
~
π
ﻗﺎﻋﺪﺓ
:
ﰲ ﺣﺎﻟﺔ
n
ﻛﺒﲑﺓ ﻭ
p
ﻏﲑ ﻗﺮﻳﺐ ﻣﻦ
0
ﳝﻜﻦ ﺍﻋﺘﺒﺎﺭ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ ﻛﺘﻘﺮﻳﺐ ﺟﻴﺪ ﻟﻠﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
.
ﻭﻳﻌﻄﻲ ﺍﻟﺘﻮﺯﻳﻌﺎﻥ
ﻧﺘﺎﺋﺞ ﺃﻛﺜﺮ ﺗﻘﺎﺭﺑﺎ ﻛﻠﻤﺎ ﻛﺎﻧﺖ
n
ﻛﺒﲑﺓ ﺃﻛﺜﺮ
.
ﻭﻧﻜﺘﺐ
Z ≈ N(0, 1)
.
ﻭ ﳑﺎ ﻳﺴﺮﻉ ﺗﻘﺎﺭﺏ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ ﻣﻦ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌ
ﻲ ﻛﻮﻥ
p
ﻗﺮﻳﺐ ﻣﻦ
0.5
.
ﺍﻟ
ﻘﺎﻋﺪﺓ
ﺍﳌﺘﺒﻌﺔ ﻋﻤﻠﻴﺎ ﻫﻲ
:
ﻳ
ﻌﺘﱪ ﺃﻥ ﺍﻟﺘﻘﺮﻳﺐ ﻣﻼﺋﻢ ﻋﻨﺪﻣﺎ
np
ﻭ
nq
ﻛﻼﳘﺎ ﺃﻛﱪ ﻣﻦ
5
.
ﺗﻮﺟﺪ ﻗﻮﺍﻋﺪ ﺃﺧﺮﻯ ﻣﺘﺒﻌﺔ ﻟﻠﺘﻘﺮﻳﺐ
1
ﻣﻨﻬﺎ
:
1
ص،Q)4ا "Rا
262
.
n=4
0
0,4
-2
-1
0
1
2
z
f(
z
)
n=8
0
0,2
0,4
- 3
- 2
- 1
- 1
0
1
1
2
3
z
n=16
0
0,1
0,2
0,3
z
X ~ B(4, 0.5)
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0
1 2
3
4 5
6
7 8
9 10 11 12 13 14 15 16
X
f(x)
X ~ B(8, 0.5)
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0
1 2
3
4 5
6
7
8 9 10 11 12 13 14 15 16
X
f(x)
X ~ B(16, 0.5)
0,00
0,05
0,10
0,15
0,20
0,25
0
1 2
3
4 5
6
7 8
9 10 11 12 13 14 15 16
X
f(x)

و تا إ
اء ا
.
ج
2
.
6
o
npq ≥ 9
o
n ≥ 20 , np ≥ 10, nq ≥ 10
ﰲ ﺣﺎﻟﺔ
p = 0.5
ﺍﻟﺸﺮﻁ،
)
1
(
ﻳﺘﺤﻘﻖ ﻋﻨﺪ
n = 36
ﻭﺍﻟﺜﺎﱐ ﻋﻨﺪ
n = 20
.
ﰲ ﺣﺎﻟﺔ
p = 0.10
ﺍﻟﺸﺮﻃﲔ ﻳﺘﺤﻘﻘﺎﻥ ﻋﻨﺪ،
n = 100
.
6
-
1
-
2
ة5 إ 6!, ة5 ( ل,0ا
ة4
.
ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺑﺪ
ﻻ ﻣﻦ
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ
ﻳﻌﲏ ﺣﺴﺎﺏ ﺍﻻﺣﺘﻤﺎﻝ ﻋﻦ ﻃﺮﻳﻖ ﺗﻮﺯﻳﻊ ﻣﺴﺘﻤﺮ ﺑﻴﻨﻤﺎ ﺍﳌﺘﻐﲑﺓ ﻣﺘﻘﻄﻌﺔ
.
ﻣﻦ ﺃﺟﻞ ﺫﻟﻚ
ﻳﺘﻢ ﺍﻋﺘﺒﺎﺭ ﻛﻞ ﻗﻴﻤﺔ ﰲ ﺍﳌﺘﻐﲑﺓ ﺍﻷﺻﻠﻴﺔ ﳎﺎﻻ
.
ﻣﺜﻼ
ﺍ
ﺣﺘﻤﺎﻝ
4
ﳒﺎﺣﺎﺕ ﺧﻼﻝ
n
ﲡﺮﺑﺔ ﻳﺼﺎﻍ ﻛﻤﺎ ﻳﻠﻲ
:
P(3.5 ≤ X ≤ 4.5)
.
ﻣﺜﺎﻝ
2
:
ﻧﻠﻘﻲ ﻗﻄﻌﺔ ﻧﻘﺪﻳﺔ
20
ﻣﺮﺓ
.
ﻟﻴﻜﻦ
X
ﻋﺪﺩ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺻﻮﺭﺓ
.
ﺃﺣﺴﺐ
P(X = 8)
ﰒ ﺃﺩﺭﺱ ﺇﻣﻜﺎﻧﻴﺔ
ﺍﺳﺘﺨﺪﺍﻡ
ﻗﺎﻧﻮﻥ
ﻣﻮﺍﻓﺮ
-
ﻻﺑﻼﺱ ﳊﺴﺎﺏ ﻧﻔﺲ ﺍﻻﺣﺘﻤﺎﻝ
.
,
X ~ B(20, 0.5) => P(X = 8) = C
8
20
(0.5)
8
(0.5)
12
= 0.1201
ﻟﺪﻳﻨﺎ
np = 10 > 5
ﻭﻛﺬﻟﻚ
nq = 10 > 5
ﻭﺇﺫﺍ ﺷﺌﻨﺎ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﻘﺎﻋﺪﺓ ﺍﻟﺜﺎﻧﻴﺔ ﻓﺈﻧﻨﺎ ﳒﺪ ﺃﻳﻀﺎ ﺃﻥ،
:
n =10
،
np = 10
،
nq = 10
ﳝﻜﻦ ﺇﺫﺍ ﺍﻋﺘﺒﺎﺭ،
X* = (X – 10)/√(20 . 0.5 . 0.5) ≈ N(0 ,1)
.
ﻧﺴﺘﺨﺪﻡ
ﺍﳌﺘﻐﲑﺓ ﺍﳌﺴﺘﻤﺮﺓ
X*
ﺑﺪﻻ ﻣﻦ
X
ﺎﻝ ﺍﳌﻌﱪﺍ ﻝﺎﻤﺘﺣﺍ ﺏﺎﺴﳊ
ﻋﻦ ﺍﻟﻘﻴﻤﺔ
8
ﻭﻫﻮ
[7.5, 8.5]
12
.
0
)
67
.
6
12
.
1
(
24
.
2
10
5
.
8
24
.
2
10
5
.
7
)
5
.
8
*
5
.
7
(
=
−
≤
≤
−
=
−
≤
≤
−
=
≤
≤
Z
P
Z
P
X
P
6
-
1
-
3
ن$9ا$) "ز$:و %&'ا "ز$ا () بر,ا
ﻳﻌﻄﻲ ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ ﻧﺘﺎﺋﺞ ﻗﺮﻳﺒﺔ ﻣﻦ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ ﳌﺎ
n ≥ 30
ﻭ
np < 5
ﺃﻭ
nq < 5
ﻭ ﻳﺴﺘﺨﺪﻡ ﺑﻌﺾ ﺍﻹﺣﺼﺎﺋﻴﲔ ﻛﺸﺮﻁ ﻻﺳﺘﻌﻤﺎﻝ ﻗﺎﻧﻮﻥ ﺑﻮﺍﺳﻮﻥ ﺑﺪﻻ ﻣﻦ ﺍﻟﻘﺎﻧﻮﻥ ﺍﻟﺜﻨﺎﺋﻲ ﺍﻟﻘﺎﻋﺪﺓ ﺍﻟﺘﺎﻟﻴﺔ
1
:
n ≥ 25
ﻭ
p ≤ 0,1
ﻣﺜﺎﻝ
:
10
%
ﻧﺄﺧﺬ،ﺎﻔﻟﺎﺗ ﺪﻌﻳ ﺎﻣ ﺔﻟﺁ ﺝﺎﺘﻧﺇ ﻦﻣ
30
ﻭﺣﺪ
ﺓ
ﻣﻦ ﺍﻧﺘﺎﺝ ﻫﺬﻩ ﺍﻵﻟﺔ ﻋﺸﻮﺍﺋﻴﺎ
.
ﺃﺣﺴﺐ ﺍﺣﺘﻤﺎﻝ ﺃﻥ ﻳﻜﻮﻥ ﻫﻨﺎﻙ ﻭﺣﺪﺗﺎﻥ ﺗﺎﻟﻔﺘﺎﻥ
.
P(X = 2) = C
2
30
(0,1²) (0.9
28
) = 0.22
ﻟﺪﻳﻨﺎ
n ≥ 25
،
p ≤ 0.1
:
ﻻﺳﺘﻌﻤﺎﻝ ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ ﳓﺴﺐ ﺃﻭﻻ ﻗﻴﻤﺔ ﺍﳌﻌ
ﻠﻤﺔ
)
ﻣﻌﻠﻤﺔ ﻗﺎﻧﻮﻥ ﺑﻮﺍﺳﻮﻥ
(
λ = µ = np = 30(0,1) = 3
P(2) = λ
x
e
–
λ
/x! = 3
2
(e
–3
) / 2! = 0.22
6
-
1
-
4
ن$9ا$) "ز$: () بر,ا
! ا"ز$او
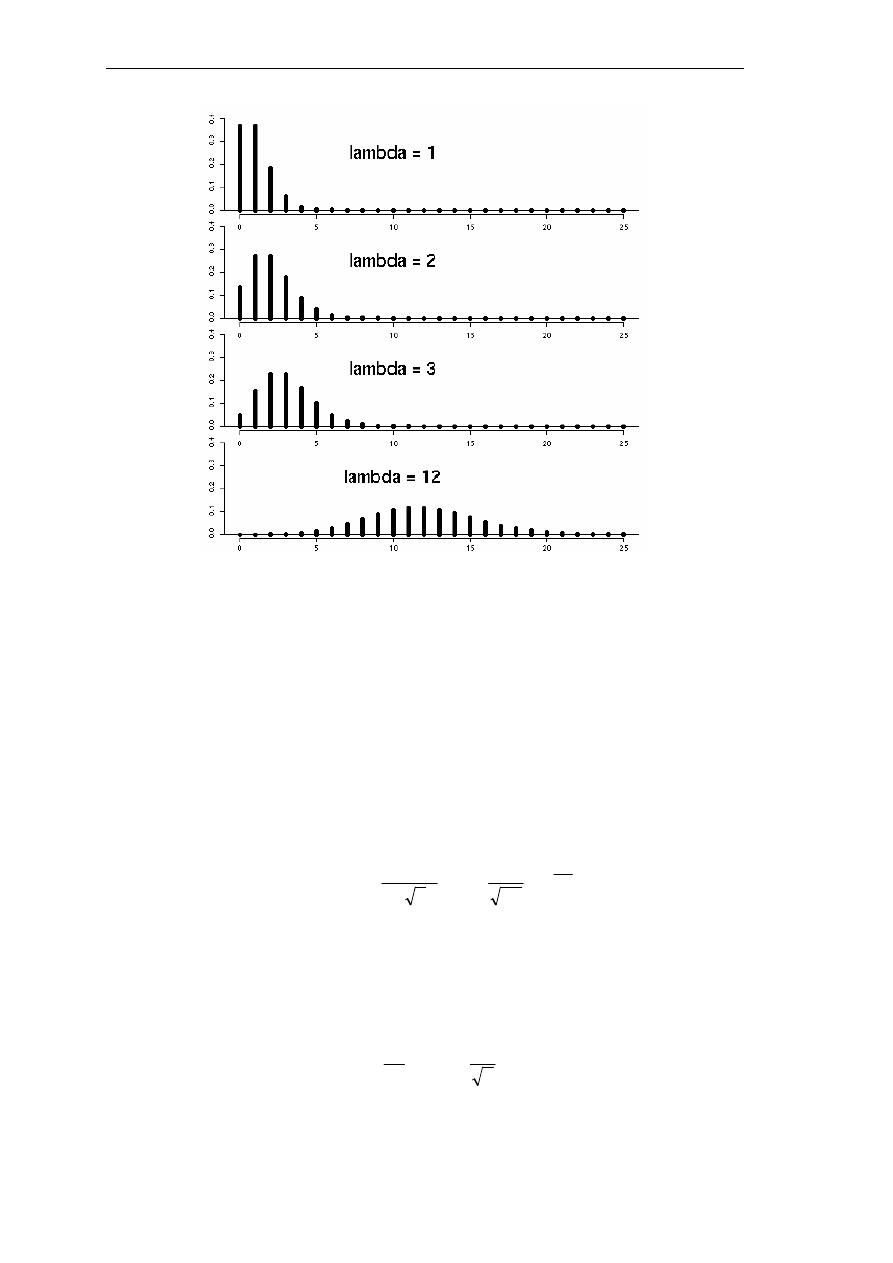
ﻳﺮﺳﻢ ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ،ﻲﺋﺎﻨﺜﻟﺍ ﻊﻳﺯﻮﺘﻟﺍ ﻞﺜﻣ
ﻣﻦ ﺧﻼﻝ ﻣﺪﺭﺝ ﺃﻋﻤﺪﺓ
(Diagramme en bâtons)
ﺎـﻌﻳﺯﻮﺗ ﻪـﻧﻮﻜﻟ
ﻣﺘﻘﻄﻌﺎ
ﻟﻜﻦ ﻟﺘﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ،
ﺳﻠﻮﻛﺎ ﺗﻘﺎﺭﺑﻴﺎ ﳓﻮ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﻋﻨﺪ ﺯﻳﺎﺩﺓ ﻗﻴﻤﺔ ﺍﳌﻌﻠﻤﺔ
λ
ﻭﳝﻜﻦ ﻣﻼﺣﻈﺔ ﺫﻟﻚ،
ﻣﻦ
ﺧﻼﻝ ﻣﻘﺎﺭﻧﺔ ﻋﺪﺩ ﻣﻦ ﺍﻟﺮﺳﻮﻡ ﺍﻟﺒﻴﺎﻧﻴﺔ ﻟﺘﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ ﻣﻦ ﺃﺟﻞ ﻗﻴﻢ ﻣﺘﺰﺍﻳﺪﺓ ﻝ
λ
.
ﺍﻟﺮﺳﻮﻡ ﺍﻟﺒﻴﺎﻧﻴﺔ
ﺍﻟﺘﺎﻟﻴﺔ ﺗﺒﲔ ﺫﻟﻚ
.
1
W4G0 "R ا
.
Gا
VI
.
رب,ا و 6!Hا I لاوا
7
5(ر
6
-
2
ا
ك,
-. ار
A .ا(ن8ز
3,;3 زدة ا4
λλλλ
ﻋﻤﻠﻴﺎ ﳝﻜﻦ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺑﺪﻻ ﻣﻦ ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ ﻋﻨﺪﻣﺎ ﺗﻜﻮﻥ
λ = 15
) .
ﻓﻴﻤﺎ ﻳﺴﺘﺨﺪﻡ ﺑﻌﺾ ﺍﻹﺣﺼﺎﺋﻴ
ﲔ
ﻛﺸﺮﻁ
ﻟ
ﻠﺘﻘﺮﻳﺐ ﻣﻦ ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ ﺇﱃ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
λ = 10
(
6
-
1
-
5
6= اآ6<&ا ن$01
ﻟﺘﻜﻦ ﺍﳌﺘﻐﲑﺍﺕ
X
1
،
X
2
،
. . . .
ﻣﺘﻐﲑﺍﺕ ﻋﺸﻮﺍﺋﻴﺔ ﻣﺴﺘﻘ
ﻠﺔ ﳍﺎ ﻧﻔﺲ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﺑﺘﺒﺎﻳﻦ ﻭﻣﺘﻮﺳﻂ ﳏﺪﺩﻳﻦ
:
ﺇﺫﺍ ﻛﺎﻧﺖ
S
n
= X
1
+ X
2
+ . . . + X
n
(n = 1, 2, . . .),
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻋﻨﺪﻣﺎ
n →∞
ﻓﺈﻥ
:
σ√n)
S
n
~ N(nµ,
ﻛﻨﺘﻴﺠﺔ ﻣﺒﺎﺷﺮﺓ ﻟﻠﻘﺎﻧﻮﻥ ﻓﺈﻥ ﺍﳌﺘﻐﲑﺓ ﺍﳌﻌﻴﺎﺭﻳﺔ ﻝ
S
n
ﺗﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺍﳌﻌﻴﺎﺭﻱ ﻭ ﻧﻜﺘﺐ
:
∫
−
∞
→
=
≤
−
≤
b
a
z
n
n
dz
e
b
n
n
S
a
P
2
²
2
1
lim
π
σ
µ
ﺘﻤﻊ ﺍﻷﺻﻠﻲ ﻃﺒﻴﻌﻴﺎ ﺑﺎﻋﺘﺒﺎﺭﺍ ﻥﻮﻜﻳ ﻻ ﺎﻣﺪﻨﻋ ﺔﻳﺮﻈﻨﻟﺍ ﺢﻤﺴﺗ ﺚﻴﺣ ،ﺔﻨﻳﺎﻌﳌﺍ ﺔﻳﺮﻈﻧ ﰲ ﺔﻳﺰﻛﺮﳌﺍ ﺔﻳﺎﻬﻨﻟﺍ ﺔﻳﺮﻈﻧ ﻡﺪﺨﺘﺴﺗ
ﻣﺘﻮﺳﻂ ﻋﻴﻨﺔ ﻣﺴﺤﻮﺑﺔ ﻋﺸﻮﺍﺋﻴﺎ
ﻳﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺇﺫﺍ ﻛﺎﻥ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
n
ﻛﺒﲑ ﲟﺎ ﻓﻴﻪ ﺍﻟﻜﻔﺎﻳﺔ
.
ﻓﺈﺫﺍ ﺭﻣﺰﻧﺎ ﳌ
ﻔﺮﺩﺍﺕ
ﺍﻟﻌﻴﻨﺔ ﲟﺠﻤﻮﻋﺔ ﻣﻦ ﺍﳌﺘﻐﲑﺍﺕ
x
i
ﺍﻟﺘﻮﻗﻊ ﻭ ﺍﻟﺘﺒﺎﻳﻦ ﻓﺈﻥ ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ،ﻊﻳﺯﻮﺘﻟﺍ ﺲﻔﻨﺑ ﺔﻠﻘﺘﺴﳌﺍ
(M)
ﻳﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
ﻭﻧﻜﺘﺐ
:
ﻋﻨﺪﻣﺎ
(n ≥ 30)
≈
=
n
N
n
S
M
n
σ
µ
,
ﻣﻼﺣﻈﺔ
.
ﰲ ﺍﳊﻘﻴﻘﺔ
ﻳﺘﺤﻘﻖ ﺍﻟﻘﺎﻧﻮﻥ،
ﻋﻨﺪﻣﺎ ﺗﻜﻮﻥ ﺍﳌﺘﻐﲑﺍﺕ ﺍﳌﺴﺘﻘﻠﺔ
Xi
ﳍﺎ ﻧﻔﺲ ﺍﳌﺘﻮﺳﻂ ﻭﺍﻟﺘ
ﺒﺎﻳﻦ ﺣﱴ ﻟﻮ ﱂ ﻳﻜﻦ ﳍﺎ
ﻣﻊ ﺍﻟﻌﻠﻢ ﺃﻧﻪ ﺗﻮﺟﺪ ﺻﻴﻎ ﺃﺧﺮﻯ ﳍﺬﻩ ﺍﻟﻘﺎﻧﻮﻥ ﺣﻴﺚ ﻻ ﻳﺸﺘﺮﻁ ﺃﻥ ﻳﻜﻮﻥ ﻟﻠﻤﺘﻐﲑﺍﺕ ﻧﻔﺲ،ﻊﻳﺯﻮﺘﻟﺍ ﺲﻔﻧ ﺓﺭﻭﺮﻀﻟﺎﺑ

و تا إ
اء ا
.
ج
2
.
8
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﻭﻻ ﺣﱴ ﺃﻥ ﺗﻜﻮﻥ
ﻣﺴﺘﻘﻠﺔ
.
ﲡﺪﺭ ﺍﻹﺷﺎﺭﺓ ﺇﱃ ﺃﻥ ﻗﺎﻧﻮﻥ ﻣﻮﺍﻓﺮ
-
ﻻﺑﻼﺱ ﺍﻟ
ﺬﻱ
ﺗﻄﺮﻗﻨﺎ ﺇﻟﻴﻪ ﺳﺎﺑﻘﺎ ﻫ
ﻮ
ﺣﺎﻟﺔ ﺧﺎﺻﺔ ﻣﻦ
ﻗﺎﻧﻮﻥ
ﺍﻟﻨﻬﺎﻳﺔ ﺍ
ﺫﻟﻚ ﺃﻥ ﻣﺘﻐﲑﺓ ﺗﺘﺒﻊ ﺍﻟﻘﺎﻧﻮﻥ،ﺔﻳﺰﻛﺮﳌ
B(n, p)
ﳝﻜﻦ ﺍﻋﺘﺒﺎﺭﻫﺎ ﳎﻤﻮﻋﺎ ﻟﻌﺪﺩ ﻣﻦ ﺍﳌﺘﻐﲑﺍﺕ
ﺍﳌﺴﺘﻘﻠﺔ ﺫﺍﺕ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﱪﻧﻮﱄ
B(1, p)
.
6
-
2
ت زا
ك
2
&' )د،
و
+,
ك"ز$:
2
A0د$9 "ز$:
D. "ز$:
6
-
2
-
1
ك"ز$:
2
1
ﺗﻌﺮﻳﻒ ﻣﺘﻐﲑﺓ ﺗﻮﺯﻳﻊ ﻙ
2
.
ﺗﻮﺯﻳﻊ ﻙ
2
(Loi en Khi-carré ou Khi-deux)
ﻫﻮ ﻣﻦ ﺃﻛﺜﺮ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﺍﺳﺘﺨﺪﺍﻣﺎ ﰲ ﳎﺎﻝ ﺍﺧﺘﺒﺎﺭ ﺍﻟﻔﺮﻭﺽ
ﻭﳝﻜﻦ ﺗﻌﺮﻳﻔﻪ ﻛﻤﺎ ﻳﻠﻲ،ﺎﻬﻋﺍﻮﻧﺄﺑ
:
ﻟﺘﻜﻦ
X
1
, X
2
, . . . X
ν
ﻣﺘﻐﲑﺍﺕ ﻋﺸﻮﺍﺋﻴﺔ ﻣﺴﺘﻘﻠﺔ ﻛﻞ ﻣﻨﻬﺎ ﺗﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺍﳌﻌﻴﺎﺭﻱ،
)
µ = 0, σ =1
.(
ﺍﳌﺘﻐﲑﺓ
X = X
1
²
+ X
2
²
+ . . . + X
ν
²
ﳍﺎ ﺩﺍﻟﺔ ﺍﻟﻜﺜﺎﻓﺔ ﺍﻟﺘﺎﻟﻴﺔ
:
(
)
( )
≤
>
Γ
=
−
−
0
0
0
2
/
2
)
(
2
/
2
/
1
2
/
x
x
e
x
x
f
x
ν
ν
ν
ﺣﻴﺚ
Γ(α)
ﻫﻲ
ﺍﻟﺪﺍﻟﺔ
ﻗﺎﻣﺎ
:
( )
0
0
1
>
=
Γ
∫
∞
−
−
α
α
α
dt
e
t
t
ﻭ ﻧﻘﻮﻝ ﺃﻥ
X
ﺗﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﻙ
2
ﺏ
ν
ﺩﺭﺟﺔ ﺣﺮﻳﺔ ﻭﻧﻜﺘﺐ
X ~ χ²
ν
.
ﺧﺼﺎﺋﺺ ﺍﻟﺘﻮﺯﻳﻊ
:
<
≥
Γ
=
≤
Χ
∫
−
−
0
0
0
)
2
/
(
2
1
)
²
(
0
2
/
1
)
2
/
(
2
/
x
x
du
e
u
x
P
x
u
ν
ν
ν
E(X) = ν, V(X) = 2ν, M(t) = (1 – 2t)
– ν/2
ﻣﺜﺎﻝ
.
ﻟﺘﻜﻦ
X
ﻡ ﻉ ﺣﻴﺚ
X ~ N(0, 1)
ﺑﲔ ﺃﻥ،
~ χ²
ν=1
X²
.
ﻧﺒﺤﺚ ﻋﻦ ﺩﺍﻟﺔ ﺍﻟﺘﻮﺯﻳﻊ
ﻝ
X² = Y
ﺍﻧﻄﻼﻗﺎ ﻣﻦ ﺩﺍﻟﺔ ﺍﻟﺘﻮﺯﻳﻊ ﻝ
X
ﺍﻟﱵ ﻫﻲ ﺩﺍﻟﺔ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
:
1
ت-ه ف إ "ز$ا ا`ه فDآا . aGا "R
(F. Helmert, 1876)
ن$9) لرآ و
(Karl Pearson, 1900)
.

Gا
VI
.
رب,ا و 6!Hا I لاوا
9
∫
∫
=
=
−
−
−
=
=
≤
≤
−
=
≤
=
≤
y
x
x
x
y
y
x
dx
e
dx
e
y
X
y
P
y
Y
P
y
X
P
0
2
/
²
2
/
²
2
2
2
1
)
(
)
(
)
²
(
π
π
ﻭ ﺫﻟﻚ ﻷﻥ
f(x)
ﻣﺘﻤﺎﺛﻠﺔ ﺣﻮﻝ ﺍﻟﺼﻔﺮ
.
ﻧﺴﺘﺨﺪﻡ
t = x²
ﻛﻤﺘﻐﲑ ﻟﻠﺘﻜﺎﻣﻞ
،
ﻣﻦ ﺃﺟﻞ ﺫﻟﻚ ﻧ
ﺴﺘﺒﺪﻝ
x =√y
ﰲ ﺣﺪ ﺍﻟﺘﻜﺎﻣﻞ
ﺑ
ﺎﻟ
ﻌﺒﺎﺭﺓ
t = y
ﻭ
dx
ﺏ
:
dt
t
t
d
dx
1
,
)
2
/
1
(
)
(
2
/
1
=
=
−
( )
( )
cqfd
dt
t
e
y
P
dt
t
e
y
P
Y
pour
dt
t
e
dt
t
e
y
X
P
y
t
y
t
y
t
y
t
)
1
(
)
2
(
)
2
/
1
(
)
2
(
2
/
1
2
1
)
²
(
1
2
/
2
1
)
²
(
:
)
²(
~
)
1
(
2
1
)
2
/
1
(
2
2
)
²
(
0
2
/
1
2
/
0
1
)
2
/
(
2
/
2
/
0
2
/
1
2
/
0
2
/
1
2
/
=
=>
=
Γ
Γ
=
≤
=>
=
Γ
=
≤
=
=
≤
∫
∫
∫
∫
−
−
−
−
−
−
−
−
π
χ
ν
ν
χ
ν
χ
π
π
ν
ν
ﻣﺜﺎﻝ
2
.
ﻟﺘﻜﻦ
X
1
ﻭ
X
2
ﻡ ﻉ ﻣﺴﺘﻘﻠﺔ ﺗﺘﺒﻊ ﻛﻞ ﻣﻨﻬﻤﺎ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺍﳌﻌﻴﺎﺭﻱ ﺑﲔ ﺃﻥ
:
+ X
2
² ~ χ²
ν = 2
Z = X
1
²
ﻧﻌﻠﻢ ﺃﻧﻪ ﺇﺫﺍ ﻛﺎﻧﺖ ﳌﺘﻐﲑﺗﲔ ﻧﻔﺲ ﺍﻟﺪﺍﻟﺔ ﺍﳌﻮﻟﺪﺓ ﻟﻠﻌﺰﻭﻡ ﻓﺈﻥ ﺗﻮﺯﻳﻌﻬﻤﺎ ﻭﺍﺣﺪ
1
ﻳﻜﻔﻲ ﺇﺫﻥ ﺃﻥ ﻧﺜﺒﺖ ﺃﻥ،
Z
ﻭ
χ²
ν = 2
ﳍﻤﺎ
ﻧﻔﺲ ﺩﺍﻟﺔ
ﺍﻟﻌﺰ
ﻭ
ﻡ
.
ﲟﺎ ﺃﻥ
X
1
ﻭ
X
2
ﻣﺴﺘﻘﻠﺘﺎﻥ ﻓﺈﻥ
:
(t)
M
(t)
M
(t)
M
2
2
2
1
X
X
z
⋅
=
ﻣﻦ ﺟﻬﺔ ﺃﺧﺮﻯ ﻧﻌﻠﻢ ﻣﻦ ﺍﳌﺜﺎﻝ ﺍﻟﺴﺎﺑﻖ ﺃﻥ
X
2
² ~ χ²
ν = 1
ﻭ
X
1
² ~ χ²
ν = 1
ﺇﺫﺍ ﺍﻟﺪﺍﻟﺔ ﺍﳌﻮﻟﺪﺓ ﻟﻠﻌﺰﻭﻡ ﻟﻜﻞ ﻣﻦ،
ﺍﳌﺘﻐﲑﺗﲔ ﻫﻲ
M(t) = (1 – 2t)
– ν/2
= (1 – 2t)
-1/2
-1
2
/
1
2
/
1
-
z
2t)
-
(1
]
2t)
-
[(1
]
2t)
-
[(1
(t)
M
=
=
−
M χ²
ν = 2
(t) = (1 – 2t)
-2/2
= (1 – 2t)
-1
= M
z
(t)
ﻭ ﻫﻮ
ﺍﳌﻄﻠﻮﺏ
.
ﻣﻨﺤﲎ ﺗﻮﺯﻳﻊ ﻙ
2
.
•
ﻻﺣﻆ
ﺃﻥ
ﺍﻟﺘﻮﺯﻳﻊ ﻙ
2
ﻫ
ﻮ
ﺣﺎﻟﺔ ﺧﺎﺻﺔ ﻣﻦ ﺗﻮﺯﻳﻊ ﻗﺎﻣﺎ ﺑﻮﺿﻊ
α = ν/2, β = 2
.
•
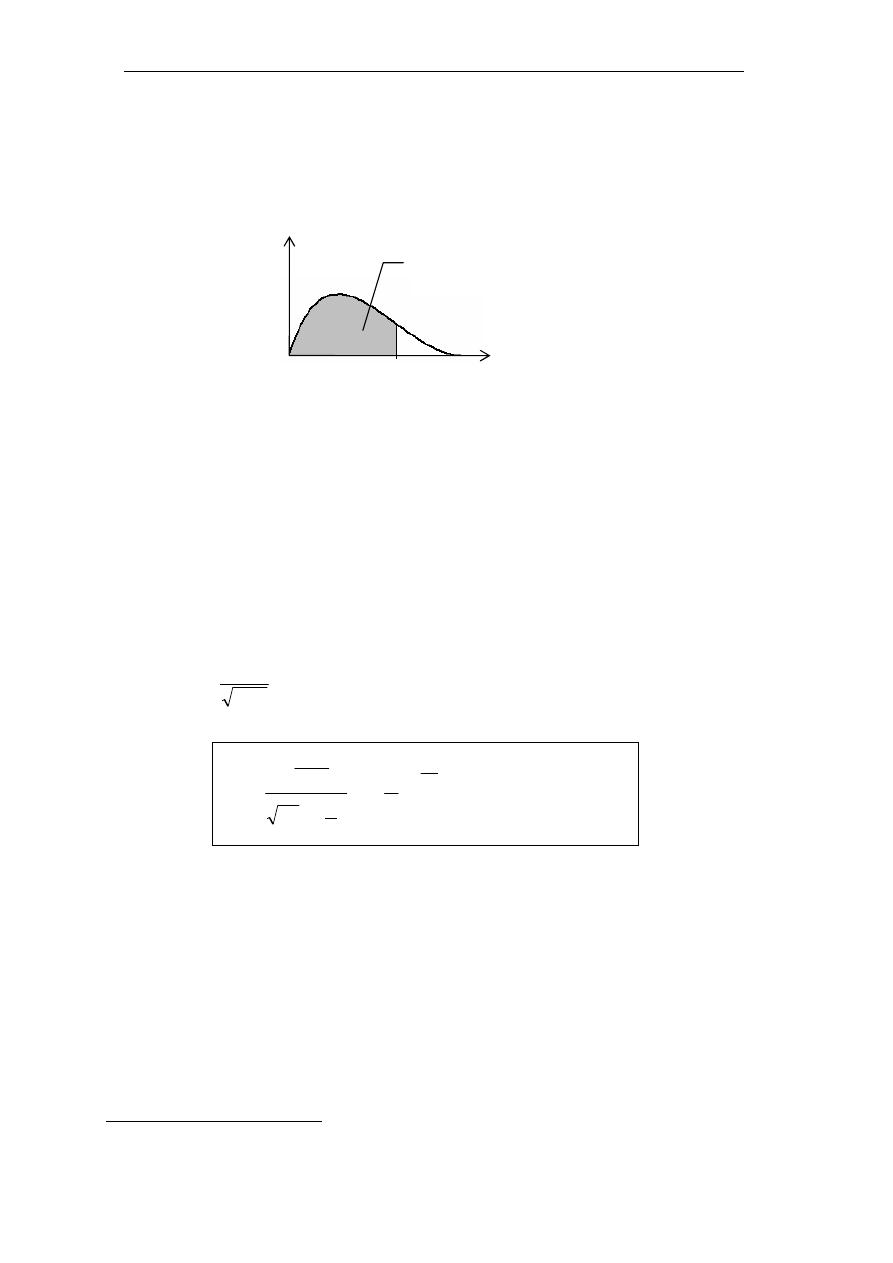
ﻳﺄﺧﺬ ﻣﻨﺤﲎ
f(x)
ﺷﻜﻠﻪ ﺣﺴﺐ ﻗﻴﻤﺔ ﺍﻟﺜﺎﺑﺖ
ν
ﻮﺭـﶈﺍ ﻦﻋ ﺎﺌﻴﺸﻓ ﺎﺌﻴﺷ ﺪﻌﺘﺒﻳ ﲎﺤﻨﳌﺍ ﻥﺃ ﻢﺳﺮﻟﺍ ﻦﻣ ﻆﺣﻼﻧﻭ
ﺍﻟﻌﻤﻮﺩﻱ ﻭﻳﺄﺧﺬ ﺷﻜﻼ ﺟﺮﺳﻴﺎ ﻛﻠﻤﺎ ﺯﺍﺩﺕ ﻗﻴﻤﺔ
ν
.
•
ﳝﻜﻦ ﺃﻥ ﻳﺆﻭﻝ ﻣﻨﺤﲎ ﺗﻮﺯﺑ
ﻊ ﻙ
2
ﺇﱃ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
N(υ,√(2υ))
ﻋﻨﺪﻣﺎ ﻳﻜﻮﻥ
n
ﻛﺒﲑﺍ
.
ﻳﻌﺘﱪ ﺍﻟﺘﻘﺮﻳﺐ
ﺟﻴﺪﺍ ﻋﻨﺪﻣﺎ ﻳﻜﻮﻥ
υ ≥ 30
.
ﻭﻧﱪﻫﻦ ﺃﻧﻪ ﻋﻨﺪ
ν
ﻛﺒﲑ
(ν ≥ 30)
ﻓﺈﻥ
) ~ N(0, 1)
1
2
²
2
−
−
ν
χ
(
.
1
ولcا ء=dا ( e'ا Gا . مو=- ة$ا 6اا ل$ تg&ا g0أ
.
و تا إ
اء ا
.
ج
2
.
10
ﰲ ﺍﳉﺪﺍﻭﻝ ﺍﻻﺣﺼﺎﺋﻴﺔ
،
ﺗﻌﲔ ﻧﻘﻄﺔ
)
ﻗﻴﻤﺔ ﺍﳌﺘﻐﲑﺓ
(
ﻙ
2
ﻋﻠﻰ ﺍﶈﻮﺭ ﺍﻷﻓﻘﻲ
)
ﺃﻧﻈﺮ ﺍﻟﺮﺳﻢ ﺍﳌ
ﻮﺍﱄ
(
ﻣﻦ ﺧﻼﻝ
ν
ﺑﺎﻹﺿﺎﻓﺔ ﺇ
ﱃ
ﺍﳌﺴﺎﺣﺔ
p
ﻋﻠﻰ ﻳﺴﺎﺭ ﻙ
2
ﲢﺖ ﺍﳌﻨﺤﲎ
ﺣﻴﺚ
(p = P(X ≤ χ²
ν;p
))
.
ﻭﺃﺣﻴﺎﻧﺎ ﲢﺪﺩ ﺍﻟﻨﻘﻄﺔ ﻙ
2
ﺑﺪﻻﻟﺔ
ﺍﳌﺴﺎﺣﺔ ﻋﻠﻰ ﳝﻴﻨﻬﺎ
)
α = 1– p
(
ﻟﺬﻟﻚ
ﳒﺪ ﰲ ﻛﺘﺐ ﺍﻹ
ﺣﺼﺎﺀ ﻛﻞ ﻣﻦ ﺍﻟﻜﺘﺎﺑﺘﲔ
:
χ²
p,ν
ﻭ
χ²
α,ν
ﻧﻈﺮﻳﺔ
:
ﻟﺘﻜﻦ
ﻣ
ﺘﻐﲑﺍﺕ ﻋﺸﻮﺍﺋﻴﺔ ﻣ
ﺴﺘﻘﻠﺔ ﻋﺪﺩﻫﺎ
n
ﺣﻴ
ﺚ
X
1
~ χ²
ν
1
, . . . , X
n
~ χ²
ν
n
ﺃﻱ ﻛﻞ ﻣﻨﻬﺎ ﺗﺘﺒﻊ
ﺍﻟﺘﻮﺯﻳﻊ ﻙ
2
، ﺑﺪﺭﺟﺔ ﺣﺮﻳﺔ ﻣﺎ
ﻭ
ﻟﺘﻜﻦ
∑
=
=
n
i
i
T
X
X
1
ﺃﻱ
ﳎﻤﻮﻉ ﻫﺬﻩ ﺍﳌﺘﻐﲑﺍﺕ
ﻭ،
ν
T
= ∑ν
i
ﺃﻱ ﳎﻤﻮﻉ
ﻓ،ﺔﻳﺮﳊﺍ ﺕﺎﺟﺭﺩ
ﺄﻥ
:
~ χ²
ν
T
∑
=
=
n
i
i
T
X
X
1
6
-
2
-
2
A0د$9 "ز$:
ﻟﺘﻜﻦ ﺍﳌﺘﻐﲑﺗﺎﻥ ﺍﻟﻌﺸﻮﺍﺋﻴﺘﺎﻥ ﺍﳌﺴﺘﻘﻠﺘﺎﻥ
Y
ﻭ
Z
ﺣﻴﺚ
Y~N(0, 1)
ﻭ
χ
ν
²
Z ~
؛
ﺍﳌﺘﻐﲑﺓ
ν
/
Z
Y
T
=
ﳍﺎ ﺩﺍ
ﻟﺔ ﺍﻟﻜﺜﺎﻓﺔ
ﺍﻟﺘﺎﻟﻴﺔ
:
∞
<
<
∞
−
+
Γ
+
Γ
=
+
−
t
t
t
f
2
1
²
1
2
2
1
)
(
ν
ν
ν
νπ
ν
( )
0
0
1
>
=
Γ
∫
∞
−
−
α
α
α
dt
e
t
t
ﻭ ﻧﻘﻮﻝ ﺃﻥ ﺍﳌﺘﻐﲑﺓ
X
ﺗﺘﺒﻊ ﺗﻮﺯﻳﻊ
ﺳﺘﻴﻮﺩﻧﺖ
1
)
(Loi Student
ﺏ
ν
ﺩﺭﺟﺔ ﺣﺮﻳﺔ ﻭﻧﻜﺘﺐ
:
T ~ t
ν
ﺧﺼﺎﺋﺺ ﺍﻟﺘﻮﺯﻳﻊ
:
E(T) = Mod = Med = 0,
α
3
= 0, V(T) = ν/(ν –2) (ν > 2)
1
W-9ر ا4 k9ا $ه A0د$9
"
9$1 -9 م-و
(William Sealy Gosset: 1876-1937)
.
مm ن$0,ا ا`ه ل$ W:,
1908
ان$&)
«The probable error of a mean »
g0 أ
:
o)دراوز
1997
ص،
262
.
5(ر
6
-
3
ﺗﻌﻴﲔ ﻧﻘﻄﺔ ﻙ
2
ﻋﻠﻰ ﺍﶈﻮﺭ ﻣﻦ ﺧﻼﻝ ﻗﻴﻤﺔ
p
ﺃﻭ
α
0 χ²
p,ν
X
f(x)
p
α
p = P(T ≤ t)
Gا
VI
.
رب,ا و 6!Hا I لاوا
11
5(ر
6
-
4
ا Gرد HI '%د( >44 جرK
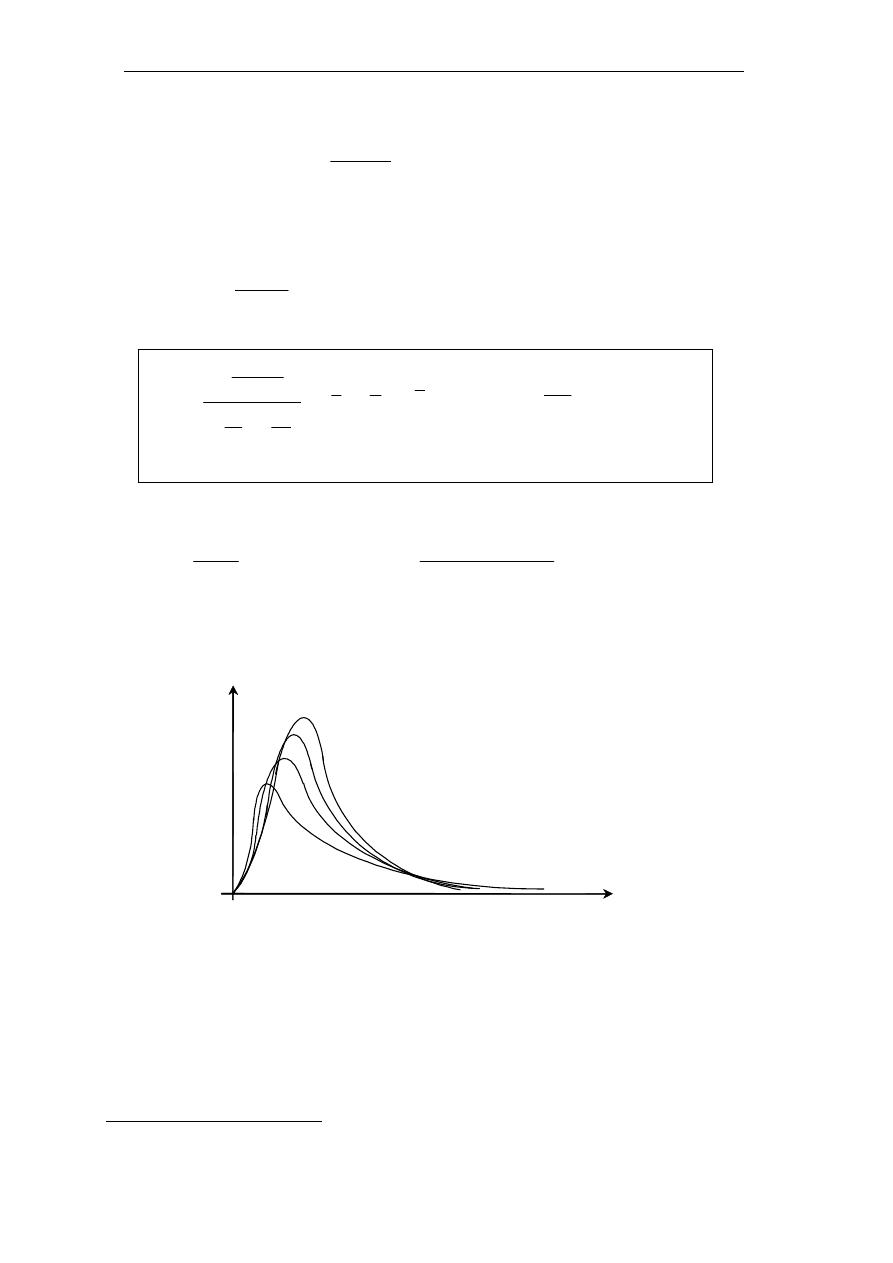
ﻣﻼﺣﻈﺎﺕ
:
•
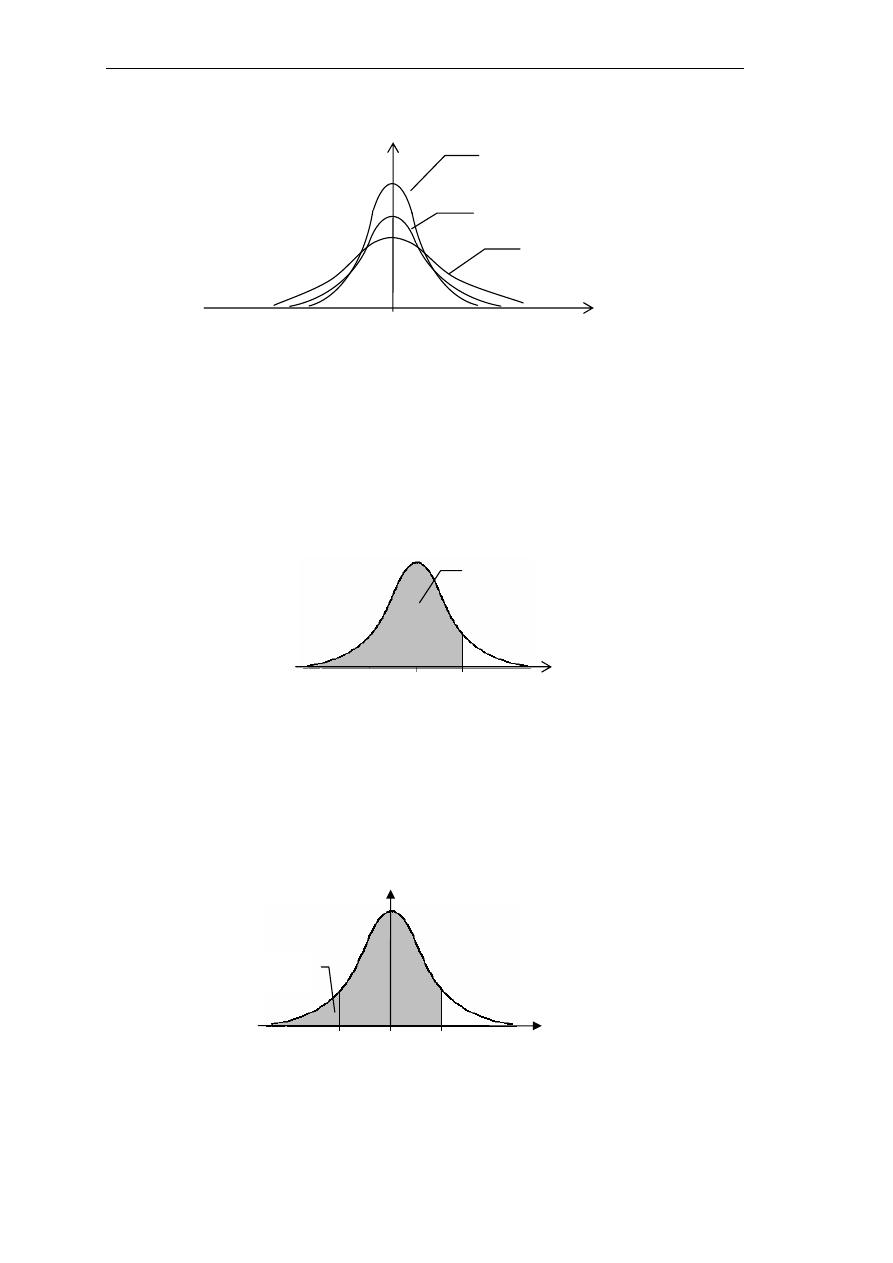
ﻣﻨﺤﲎ
f(t)
ﻳﻘﺘﺮﺏ ﻣﻦ ﺍﳌﻨﺤﲎ ﺍﻟﻄﺒﻴﻌﻲ ﺍﳌﻌﻴﺎﺭﻱ ﻛﻠﻤﺎ ﺯﺍﺩﺕ ﻗﻴﻤﺔ
ν
.
ﻳﻌﺘﱪ ﺍﻹﺣﺼﺎﺋﻴﻮﻥ ﺃﻥ ﺍﳌﻨﺤﻨﻴﺎﻥ
ﻳﺘﻄﺎﺑﻘﺎﻥ ﺗﻘﺮﻳﺒﺎ ﻋﻨﺪ
ν ≥ 30
.
•
ﺗﻌﲔ ﻗﻴﻤﺔ ﺍﳌﺘﻐﲑﺓ
t
ﰲ ﺍﳉﺪﺍﻭﻝ ﺍﻹ
ﺣﺼﺎﺋﻴﺔ
ﺑﺪﻻﻟﺔ
ν
ﻭﺍﳌﺴﺎﺣﺔ
p
ﻋﻠﻰ ﻳﺴﺎﺭ
t
ﲢﺖ ﺍﳌﻨﺤﲎ
)
(p = P(T ≤ t
ν;p
)
.
ﻭﺃﺣﻴﺎﻧﺎ ﲢﺪﺩ
t
ﺑﺪﻻﻟﺔ ﺍﳌﺴﺎﺣﺔ ﻋﻠﻰ ﳝﻴﻨﻬﺎ
)
α = 1 – p
(
ﻓ
ﻨﻜﺘﺐ
:
t
p,ν
ﺃﻭ
t
α,ν
.
•
ﻧﻼﺣﻆ
ﺃﻳﻀﺎ
ﺃﻥ ﻣﻨﺤﲎ
t
ﻣﺘﻤﺎﺛﻞ ﺣﻮﻝ ﺍﳌﺘﻮﺳﻂ
0
،
ﻣﺎ ﻳﻌﲏ ﺃﻥ ﻟﻜﻞ ﻧﻘﻄﺔ ﻣﻮﺟﺒﺔ
t
p
،
ﻧﻘﻄﺔ ﻣﻨﺎﻇﺮﺓ ﳍﺎ
ﺳﺎﻟﺒﺔ
–
t
p
ﺣﻴﺚ ﺍﳌﺴﺎﺣﺔ ﲢﺖ ﺍﳌﻨﺤﲎ ﻋﻠﻰ ﳝﲔ
t
p
ﺗﺴﺎﻭﻱ ﺍﳌﺴﺎﺣﺔ ﲢﺖ
ﺍﳌﻨﺤﲎ ﻋﻠﻲ ﻳﺴﺎﺭ
(–t
p
)
،
ﻭﻧﻜﺘﺐ
t
1 – p
= – t
p
.
اريq "ز$ا
υ≥30
ν = 6
ν = 4
0.4
f(t)
-4 -3
-2 -1 0 1 2 3 4
t
-t
p
= t
1– p
0 t
p
T
1– p
5(ر
6
-
6
'%د( >44 L4K لMN(ا
50
t
<G3 ا5 الMO $ < ا
0 t
p,
ν
ν
ν
ν
T
p = P(T ≤ t
p
)
P
α
5(ر
6
-
5
30 K
t
P Q $A نR
p
و
ν
ν
ν
ν
و تا إ
اء ا
.
ج
2
.
12
•
ﰲ ﺣﺎﻟﺔ
υ = 1
ﺗﺼﺒﺢ
t
ﻋﺒﺎﺭﺓ ﻋﻦ ﻧﺴﺒﺔ ﺑﲔ ﻣﺘﻐﲑ
ﺗﲔ ﻃﺒﻴﻌﻴﺘﲔ ﻣﻌﻴﺎﺭﻳﺘﲔ ﻣﺴﺘﻘﻠﺘﲔ
.
ﺩﺍﻟﺔ ﺍﻟﻜﺜﺎﻓﺔ ﻟﻠﻤﺘﻐﲑﺓ
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﺗﺼﺒﺢ
ﺑﺎﻟﺘﻌﻮﻳﺾ ﰲ
f(t)
ﻛﻤﺎ ﻳﻠﻲ
:
²)
1
(
1
)
(
t
t
f
+
=
π
ﻭ
ﻫﻲ
ﺩﺍﻟﺔ ﺍﻟﻜﺜﺎﻓﺔ ﻟﻘﺎﻧﻮﻥ ﻛﻮﺷﻲ
(Loi de Cauchy)
ﺍﻟﺬﻱ ﻟﻴﺲ ﻟﻪ ﺗﻮﻗﻊ ﺃﻭ ﺗﺒﺎﻳﻦ ﳏﺪﻭﺩ
.
6
-
2
-
3
:
D. "ز$
ﺘﻟ
ﻜﻦ ﺍﳌﺘﻐﲑﺗﺎﻥ ﺍﻟﻌﺸﻮﺍﺋﻴﺘﺎﻥ ﺍﳌﺴﺘﻘﻠﺘﺎﻥ
X
1
~ χ
ν
1
²
ﻭ
χ
ν
2
²
X
2
~
.
ﺍﳌﺘﻐﲑﺓ
:
2
2
1
1
/
/
ν
ν
X
X
X
=
ﳍﺎ ﺩﺍﻟﺔ ﺍﻟﻜﺜﺎﻓﺔ
ﺍﻟﺘﺎﻟﻴﺔ
:
(
)
≤
>
+
Γ
Γ
+
Γ
=
+
−
−
0
0
0
2
2
2
)
(
2
1
2
1
)
2
(
2
2
2
1
2
1
2
1
2
1
1
2
1
x
x
x
x
x
f
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ﻭ ﻧﻘﻮﻝ ﺃﻥ ﺍﳌﺘﻐﲑﺓ
X
ﺗﺘﺒﻊ ﺗﻮﺯﻳﻊ ﻓﻴﺸﺮ
1
(Loi F de Fisher-Snédecor)
ﺏ
1
ν
ﻭ
2
ν
ﺩﺭﺟﺔ ﺣﺮﻳﺔ ﻭﻧﻜﺘﺐ
:
X ~ F
ν1, ν2
(
)(
)
)
4
(
2
4
)
2
(
2
²
,
)
2
(
2
2
2
2
2
1
2
1
2
2
2
2
2
>
−
−
−
+
=
>
−
=
ν
ν
ν
ν
ν
ν
ν
σ
ν
ν
ν
µ
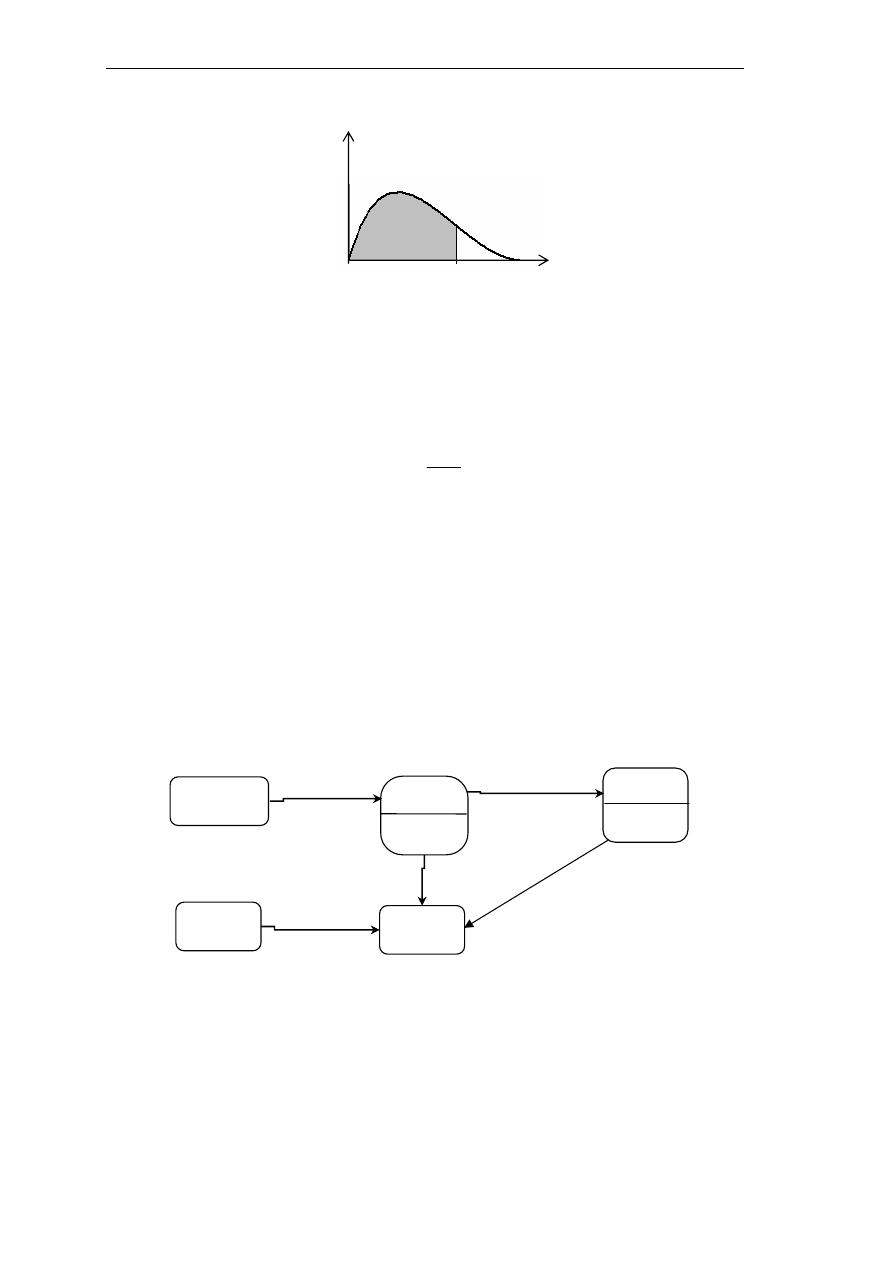
ﻭﻳﻈﻬﺮ ﻣﻦ ﺍﳌﻌﺎﺩﻟﺔ ﺗﺒﻌﻴﺔ ﻣﻨﺤﲎ
f(x)
ﺑﺎﻹﺿﺎﻓﺔ ﻝ
x
ﺇﱃ ﻛﻞ ﻣﻦ
ν
1
ﻭ
ν
2
ﻭﻟﺬﻟﻚ ﲢﺪﺩ ﺃﻱ ﻧﻘﻄﺔ
F
ﻣﻦ ﺧﻼﻝ ﺛﻼﺛﺔ
ﻣﻌﺎﱂ
:
ν
1
ﻭ
ν
2
ﻭ
p
)
ﺍﳌﺴﺎﺣﺔ ﲢﺖ ﺍﳌﻨﺤﲎ ﻋﻠﻰ ﻳﺴﺎﺭ ﺍﻟﻨﻘﻄﺔ
F
(
ﻭﻧﻜﺘﺐ،
F
p, ν1 , ν2
x
(10, 50)
(10, ? )
(10, 10)
1.0
(10, 4)
f(x)
0,5
0
1
2
3
4
5(ر
6
-
7
ا Gرد HI ) >44 جرK
م3ا I Gرد و T<ا
1
D. -s 0رو
(Ronald Aylmer Fisher) (1890-1962)
)
ا-d0إ
(
ر$u&9 لداو جر$R و ,ا 6g0 v9w
(George Waddel Snédecor) (1881-1974)
)
uأ
(
ص،Q)4ا "Rا g0أ
258
.
Gا
VI
.
رب,ا و 6!Hا I لاوا
13
5(ر
6
-
8
30 $;K
F
لMO $ 5 لوUا - 5
ν
1
, ,ν
2
و
P
أو
α
αα
α
.
ﰲ ﺍﻟﻐﺎﻟﺐ ﺗﻌﻄﻲ ﺍﳉﺪﺍﻭﻝ ﺍﻹﺣﺼﺎﺋﻴﺔ ﻗﻴﻢ
F
ﻋﻨﺪ
p = 0.95
ﻭ
p = 0.99
.
ﻧﻈﺮﻳﺔ
1
.
1
2
2
1
,
,
,
,
1
/
1
ν
ν
ν
ν
p
p
F
F
=
−
ﻧﻈﺮﻳﺔ
2
.
2
),
2
/
(
1
,
1
,
1
ν
ν
p
p
t
F
−
−
=
ﻧﻈﺮﻳﺔ
3
.
ν
χ
ν
ν
2
,
,
,
p
p
F
=
∞
6
-
2
-
4
6EF
ﰲ ﺍﳌﺒﺤﺚ ﺍﻷﻭﻝ ﺩﺭﺳﻨﺎ ﺍﻟﻌﻼﻗﺔ ﺑﲔ ﺑﻌﺾ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﺍﻻﺣﺘﻤﺎﻟﻴﺔ ﺃﻱ ﻣﱴ ﳝﻜﻦ ﻟﺘﻮﺯﻳﻊ ﻣﺎ ﺃﻥ ﻳﻌﻄﻲ ﻧﺘﺎﺋﺞ ﻗﺮﻳﺒﺔ ﻣﻦ ﺗﻮﺯﻳﻊ
ﺁﺧﺮ
.
ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺑﺪ
ﻻ ﻣﻦ
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ
ﻳﻌﲏ ﺣﺴﺎﺏ ﺍﻻﺣﺘﻤﺎﻝ ﻋﻦ ﻃﺮﻳ
ﻖ ﺗﻮﺯﻳﻊ ﻣﺴﺘﻤﺮ ﺑﻴﻨﻤﺎ ﺍﳌﺘﻐﲑﺓ
ﻣﺘﻘﻄﻌﺔ
.
ﻣﻦ ﺃﺟﻞ ﺫﻟﻚ
ﻳﺘﻢ ﺍﻋﺘﺒﺎﺭ ﻛﻞ ﻗﻴﻤﺔ ﰲ ﺍﳌﺘﻐﲑﺓ ﺍﻷﺻﻠﻴﺔ ﳎﺎﻻ
.
ﻗﺎﻧﻮﻥ ﺍﻟﻨﻬﺎﻳﺔ ﺍﳌﺮﻛﺰﻳﺔ ﻳﻨﺺ ﻋﻠﻰ ﺃﻥ
S
n
)
ﳎﻤﻮﻉ
ﻣﺘﻐﲑﺍﺕ ﻋﺸﻮﺍﺋﻴﺔ ﻣﺴﺘﻘﻠﺔ ﳍﺎ ﻧﻔﺲ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﺑﺘﺒﺎﻳﻦ ﻭﻣﺘﻮﺳﻂ
ﳏﺪﺩﻳﻦ
(
ﺗﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﻋﻨﺪﻣﺎ
n →∞
ﲟﺘﻮﺳﻂ
E(S
n
) = nµ
ﻭ
σ
Sn
= σ√n
.
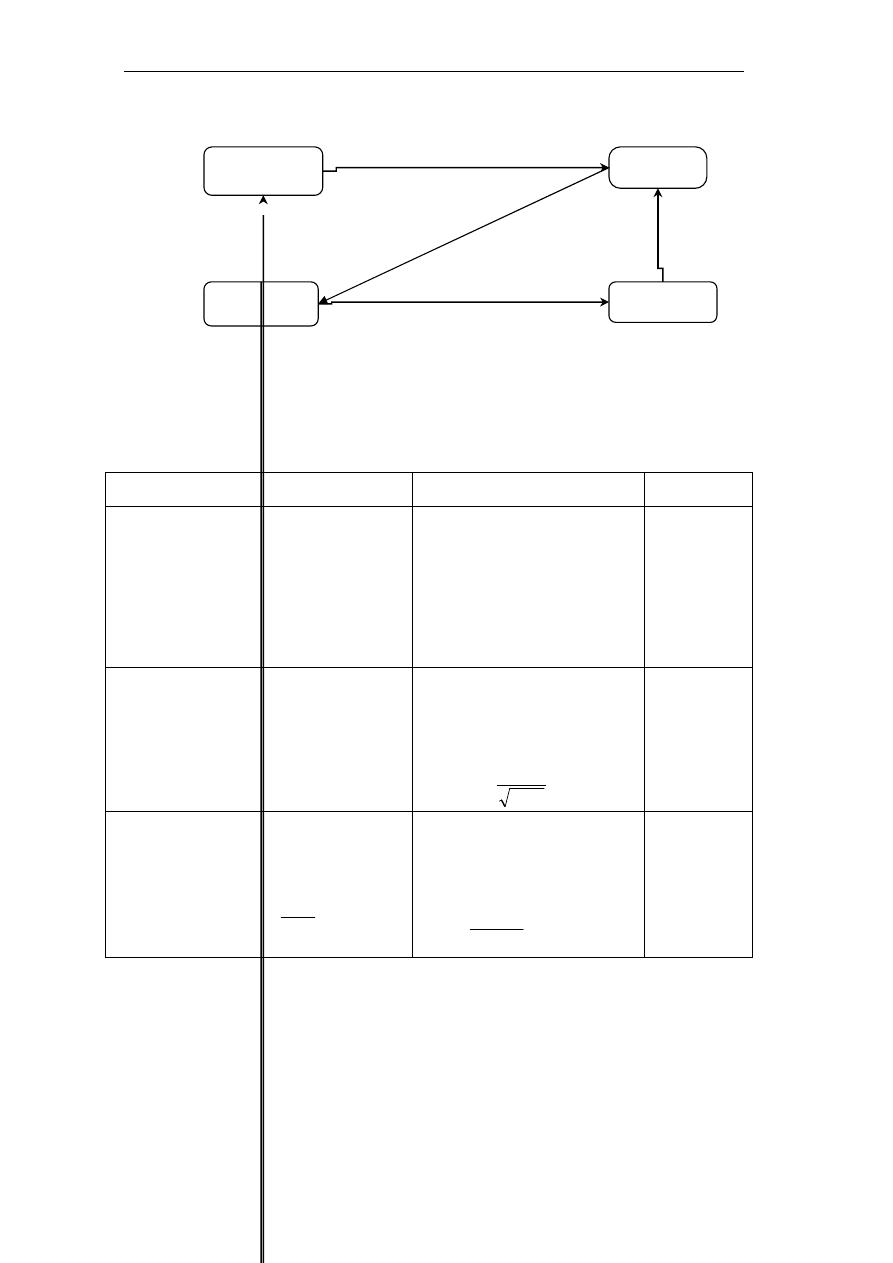
ﺍﻟﺮﺳﻢ ﺍﻟﺒﻴﺎﱐ ﺍﻟﺘﺎﱄ ﻳﺒﲔ ﺍﻟ
ﻘﻮﺍﻋﺪ ﺍﳌﺴﺘﺨﺪﻣﺔ ﻛﺸﺮﻭﻁ ﻟﻠﺘﻘﺮﻳﺐ ﺑﲔ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﺍﻻﺣﺘﻤﺎﻟﻴﺔ
ﺍﳌﺬﻛﻮﺭﺓ ﺁﻧﻔﺎ ﰲ ﺍﳌﺒﺤﺚ
ﺑﺎﻹﺿﺎﻓﺔ ﺇﱃ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ ﺍﻷﺧﺮﻯ ﺍﻟﱵ ﺩﺭﺳﺖ ﰲ ﺍﻟﻔﺼﻮﻝ ﺍﻟﺴﺎﺑﻘﺔ
)
ﺍﻟﺮﻣﺰ
cr
ﻳﻌﲏ ﻣﺘﻐﲑﺓ ﻣﻌﻴﺎﺭﻳﺔ
.(
5(ر
6
-
9
3IXا $%اا $. H ا Aا0
(1)
B (n, p)
B
cr
(n, p)
H(N, n, p)
P (λ)
P
cr
(λ)
N(0, 1)
t
ν
n < N/10
n ≥ 25 ; p ≤ 0,10
np = λ
npq ≥9
λ≥15
ν→ ∞
F
p,ν1, ,ν2
x
f(x)
p
α
و تا إ
اء ا
.
ج
2
.
14
5(ر
6
-
10
3IXا $%اا $. H ا
(2)
ﺗﻌﺮﻓﻨﺎ ﰲ
ﺍﳌﺒﺤﺚ
ﺍﻟﺜﺎﱐ
ﺣﻴﺚ ﺑﻴﻨﺎ ﺑﺎﻟﻨﺴﺒﺔ ﳍﺬﻩ ﺍﻟﺘﻮﺯﻳﻌﺎﺕ،ﺀﺎﺼﺣﻹﺍ ﰲ ﻡﺍﺪﺨﺘﺳﻻﺍ ﺓﲑﺜﻛ ﺓﺮﻤﺘﺴﻣ ﺕﺎﻌﻳﺯﻮﺗ ﺔﺛﻼﺛ ﻰﻠﻋ
ﺗﻌﺮ
ﺷﻜﻞ ﻣﻨﺤﲎ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﻭﺧﺼﺎﺋﺼﻪ،ﺓﲑﻐﺘﳌﺍ ﻒﻳ
.
ﰲ ﺍﳉﺪﻭﻝ ﺍﻟﺘﺎﱄ ﻣﻠﺨﺺ ﳌﻀﻤﻮﻥ ﻫﺬﺍ ﺍﳌﺒﺤﺚ
.
ولG
6
-
1
-
ك 8زK Z6Oو [ ;K $A Z,
2
)و '%د( ،
ﺍﻟﺘﻮﺯﻳﻊ
ﺍﳌﺘﻐﲑﺓ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ
ﺃﻫﻢ ﻣﺎ ﳚﺐ ﻣﻌﺮﻓﺘﻪ ﻋﻦ ﺩﺍﻟﺔ ﺍﻟﻜﺜﺎﻓﺔ
ﺗﻮﺯﻳﻊ ﻙ
2
X ~ χ²
ν
ﺇﺫﺍ
ﻛﺎﻧﺖ
X
i
ﻣﺘﻐﲑﺍﺕ ﻋﺸﻮﺍﺋﻴﺔ ﻣﺴﺘﻘﻠﺔ
،ﻱﺭﺎﻴﻌﳌﺍ ﻲﻌﻴﺒﻄﻟﺍ ﻊﻳﺯﻮﺘﻟﺍ ﻊﺒﺘﺗ ﺎﻬﻨﻣ ﻞﻛ
ﻭ
X = X
1
²
+ X
2
²
+ . . . + X
ν
²
إذن
:
X ~ χ²
ν
E(X) = ν, V(X) = 2ν
ﳌﺎ
ν ≥ 30
ﻓﺈﻥ
:
χ²
ν
≈
N(ν , √(2 ν ))
ﺳﺘﻴﻮﺩﻧﺖ
T ~ t
ν
ﻟﺘﻜﻦ ﺍﳌﺘﻐﲑﺗﺎﻥ ﺍﻟﻌﺸﻮﺍﺋﻴﺘﺎﻥ ﺍﳌﺴﺘﻘﻠﺘﺎﻥ
Y
ﻭ
Z
ﺣﻴﺚ
Y~ N(0, 1)
ﻭ
χ
ν
²
Z ~
؛
ﺇﺫﻥ
:
~ t
ν
ν
/
Z
Y
T
=
E(T) = 0,
ﳌﺎ
V(T) = ν/(ν – 2) : (ν > 2)
ﳌﺎ
υ ≥ 30
ﻓﺈﻥ
≈
N(0, 1)
T
ﺗﻮﺯﻳﻊ ﻓﻴﺸﺮ
X ~ F
ν1, ν2
ﺘﻘﻠﺘﺎﻥـﺴﻣ ﻉ ﻥﺎﺗﲑﻐﺘﻣ ﺎﻨﻳﺪﻟ ﺖﻧﺎﻛ ﺍﺫﺇ
ﺣﻴﺚ
:
X
1
~ χ
ν
1
²
ﻭ
χ
ν
2
²
X
2
~
،
ﻓﺈﻥ
~ F
ν1, ν2
2
2
1
1
/
/
ν
ν
X
X
X
=
1
2
2
1
,
,
,
,
1
/
1
ν
ν
ν
ν
p
p
F
F
=
−
2
),
2
/
(
1
,
1
,
1
ν
ν
p
p
t
F
−
−
=
ν
χ
ν
ν
2
,
,
,
p
p
F
=
∞
ﺳﺆﺍﻝ
:
ﺃﻛﺘﺐ
5
ﺃﻋﺪﺍﺩ
ﻣﺎ
.
ﺃﻛﺘﺐ
5
ﺃﻋﺪﺍ
ﺩ ﻋﻠﻰ ﺃﻥ ﻳﻜﻮﻥ ﳎﻤﻮﻋﻬﺎ
100
.
ﻛﻢ ﻋﺪﺩﺍ ﳝﻜﻦ ﻛﺘﺎﺑﺘﻪ ﲝﺮﻳﺔ ﰲ ﺍﳊﺎﻟﺔ
؟ﺍﻟﺜﺎﻧﻴﺔ
ﺍﳉﻮﺍﺏ
:
ﰲ ﺍﳌﺮﺓ ﺍﻷﻭﱃ ﳝﻜﻦ ﺍﺧﺘﻴﺎﺭ
5
ﰲ ﺍﳌﺮﺓ ﺍﻟﺜﺎﻧﻴﺔ ﳝﻜﻦ ﻛﺘﺎﺑﺔ،ﺔﻳﺮﲝ ﺩﺍﺪﻋﺃ
4
ﺃﻋﺪﺍﺩ ﻓﻘﻂ ﲝﺮﻳﺔ ﻷﻥ ﺍﻟﻌﺪﺩ ﺍﳋﺎﻣﺲ
ﻤﻮﻉﺍ ﻁﺮﺸﻟﺍ ﱯﻠﻳ ﺚﻴﲝ ﺩﺪﳛ ﻥﺃ ﺐﳚ
)
ﻤﻮﻉ ﻳﺴﺎﻭﻱﺍ
100
.(
ﻋﺪﺩ ﺩﺭﺟﺎﺕ ﺍﳊ
،ﺮﻳﺔ ﰲ ﺍﳌﺮﺓ ﺍﻷﻭﱃ
ν = n
ﰲ ﺍﳌﺮﺓ،
ﺍﻟﺜﺎﻧﻴﺔ
ν = n – 1
.
ﻳﻨﻘﺺ ﻋﺪﺩ ﺩﺭﺟﺎﺕ ﺍﳊﺮﻳﺔ ﺃﻛﺜﺮ ﺑﺰﻳﺎﺩﺓ ﻋﺪﺩ ﺍﻟﺸﺮﻭﻁ
.
[N(0, 1)]²
t
ν
²
Χ
ν
2
/ ν
F
ν1, ν2
ν→ ∞
ν = 1
ν
1
= 1
ν
2
= ν
ν
1
= 1
ν
2
→ ∞
ν
1
= ν
ν
2
→ ∞
