
Fundamentals of digital system
First Class
2015-2016
1
Dr. AMMAR ABDUL-HAMED KHADER
Reference
Text book1: M. Mano " Digital Design"
Text book2: Floyd " Digital fundamentals"
Dr. AMMAR ABDUL-HAMED KHADER
2

INTRODUCTION
The binary number system and digital codes, are
fundamental to computers and to digital electronics. Here
the binary number system and its relationship to other
number systems such as Decimal, Hexadecimal and Octal is
presented. Arithmetic operations with binary numbers are
covered to provide a basis for understanding how computers
and many other types of digital system works.
3
Dr. AMMAR ABDUL-HAMED KHADER
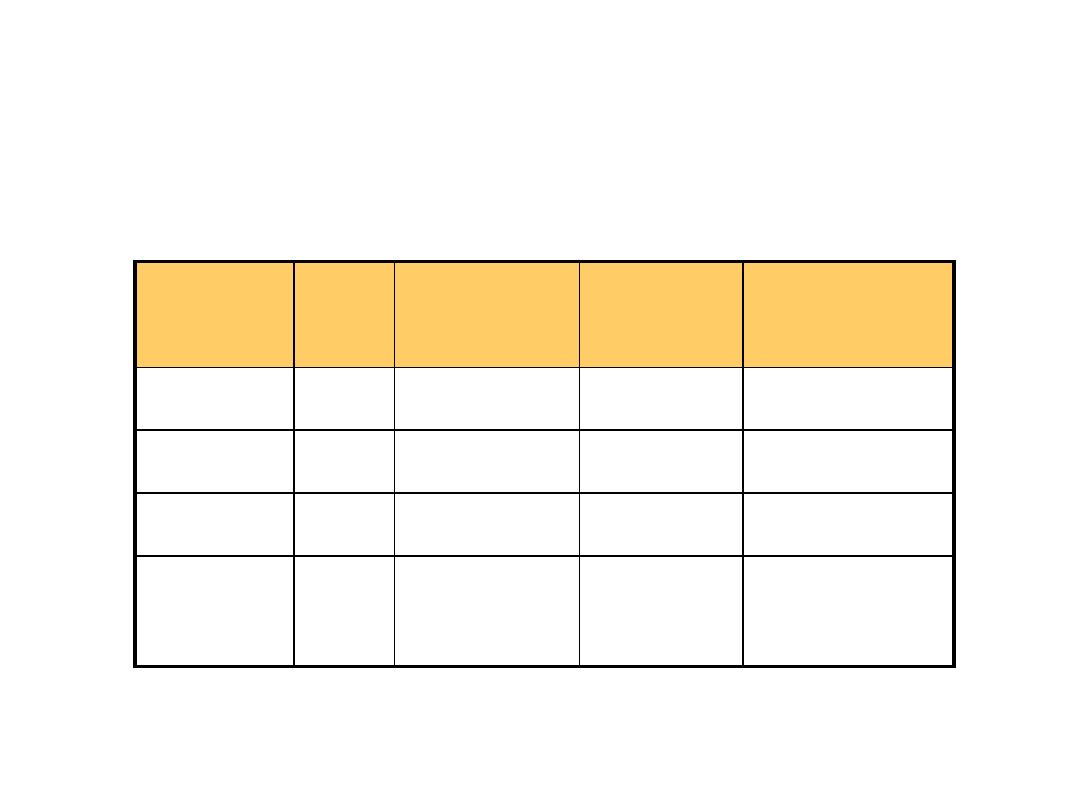
Common Number Systems
System
Base
Symbols
Used by
humans?
Used in
computers?
Decimal
10
0, 1, … 9
Yes
No
Binary
2
0, 1
No
Yes
Octal
8
0, 1, … 7
No
No
Hexa-
decimal
16
0, 1, … 9,
A, B, … F
No
No
4
Dr. AMMAR ABDUL-HAMED KHADER
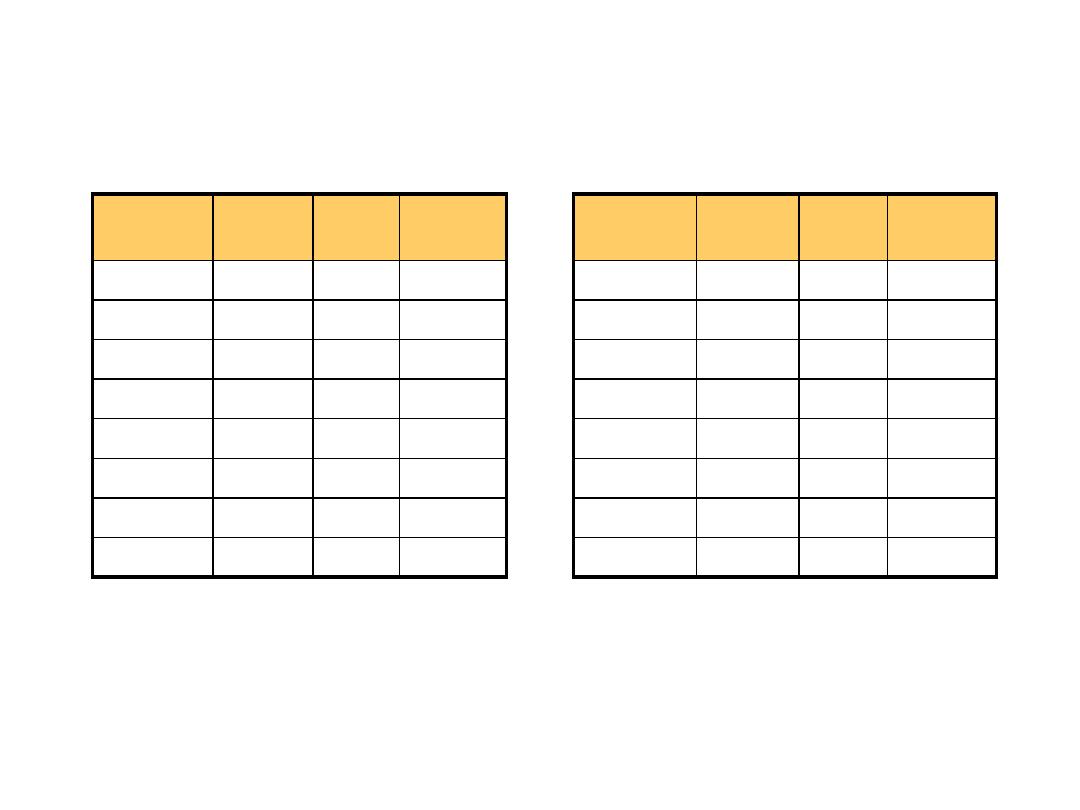
Quantities/Counting
Decimal
Binary
Octal
Hexa-
decimal
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
Decimal
Binary
Octal
Hexa-
decimal
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
Example: 25
10
= 11001
2
= 31
8
= 19
16
5
Dr. AMMAR ABDUL-HAMED KHADER
Decimal Numbers
• For fractional numbers, the weights are negative powers of ten
that decrease from left to right beginning with 10
-1
• ……. 10
3
10
2
10
1
10
0
. 10
-1
10
-2
10
-3
10
-4
…….
• Example: Express the decimal number (68. 34 ) as a sum of
the values of each digit.
• 68. 34 = (6* 10
1
) + ( 8* 10
0
) + ( 3* 10
-1
) + ( 4* 10
-2
)
• = 6* 10 + 8* 1 + 3* 0.1
+ 4* 0.01
• = 60 + 8 + 0.3 + 0.04
146
10
=>
6 x 10
0
= 6
4 x 10
1
= 40
1 x 10
2
= 100
146
Weight
Base
6
Dr. AMMAR ABDUL-HAMED KHADER

Binary Numbers
• To learn to count in
binary system, first
look at how count in
the decimal system.
It is 0 to 9 then start
another digit position.
Decimal
No,
Binary No.
2
3
2
2
2
1
2
0
0
0
0
0
0
1
0
0
0
1
2
0
0
1
0
3
0
0
1
1
4
0
1
0
0
5
0
1
0
1
6
0
1
1
0
7
0
1
1
1
8
1
0
0
0
9
1
0
0
1
10
1
0
1
0
11
1
0
1
1
12
1
1
0
0
13
1
1
0
1
14
1
1
1
0
15
1
1
1
1
7
Dr. AMMAR ABDUL-HAMED KHADER
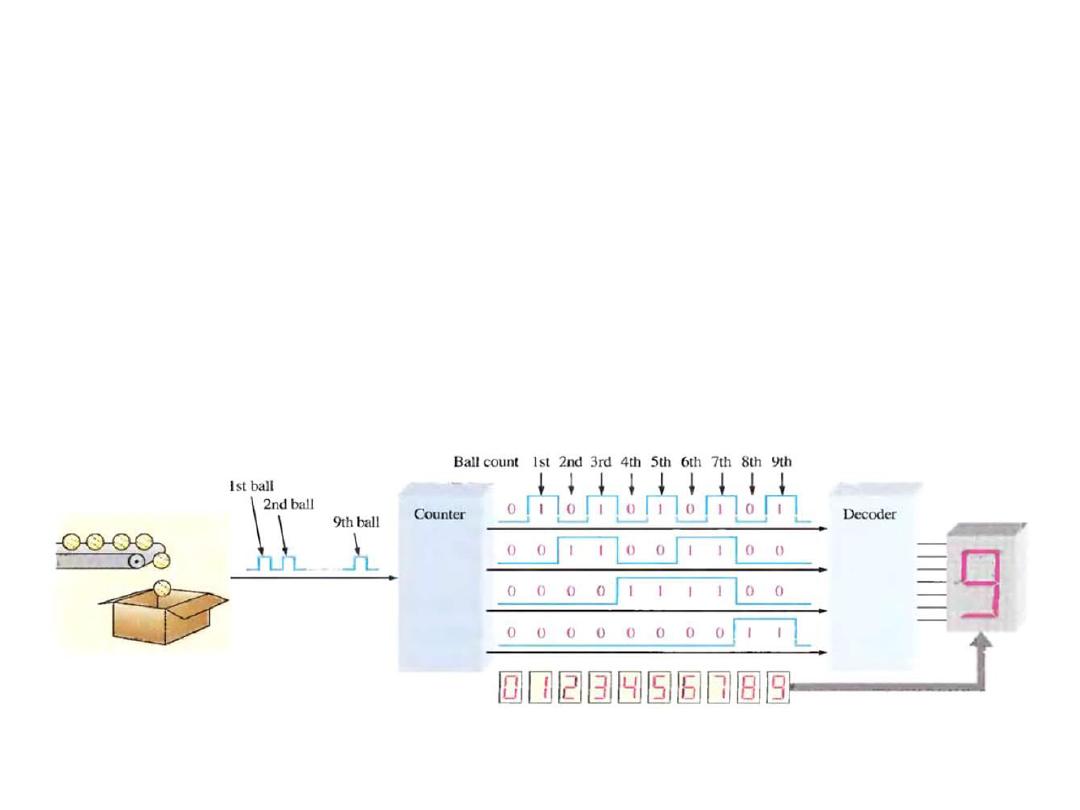
An Application
• Learn to count in binary will help you to basically understand
how digital circuit can be used to count events. In the Fig.
below the counter counts the pulses from a sensor that detects
the passing of a ball and produce a sequence of logic levels
(digital waveform) on each of its four parallel outputs.
8
Dr. AMMAR ABDUL-HAMED KHADER
The Weighting Structure of Binary Bits
• The binary number is weighted number. The right-most it is the
LSB
(Least Significant Bit) and has a weight of 2
0
=1. The left-
most bit is the MSB (Most Significant Bit), like: 2
2
2
1
2
0 .
• Fractional number can also be represented in binary by placing
bits to the right of the binary point. The left-most bit is the MSB
in this case and has a weight of 2
-1
= o.5 .
• …. 2
2
2
1
2
0
. 2
-1
2
-2
2
-3
…….
• …. 4 2 1 0.5 0.25 0.125 ……
• Example: Convert the fractional binary number 0.1011 to decimal
• Weight: 2
-1
2
-2
2
-3
2
-4
• Binary number : 0. 1 0 1 1
• 0.1011 0.5 + 0 + 0.125 + 0.0625 = 0.6875
Binary Point
9
Dr. AMMAR ABDUL-HAMED KHADER
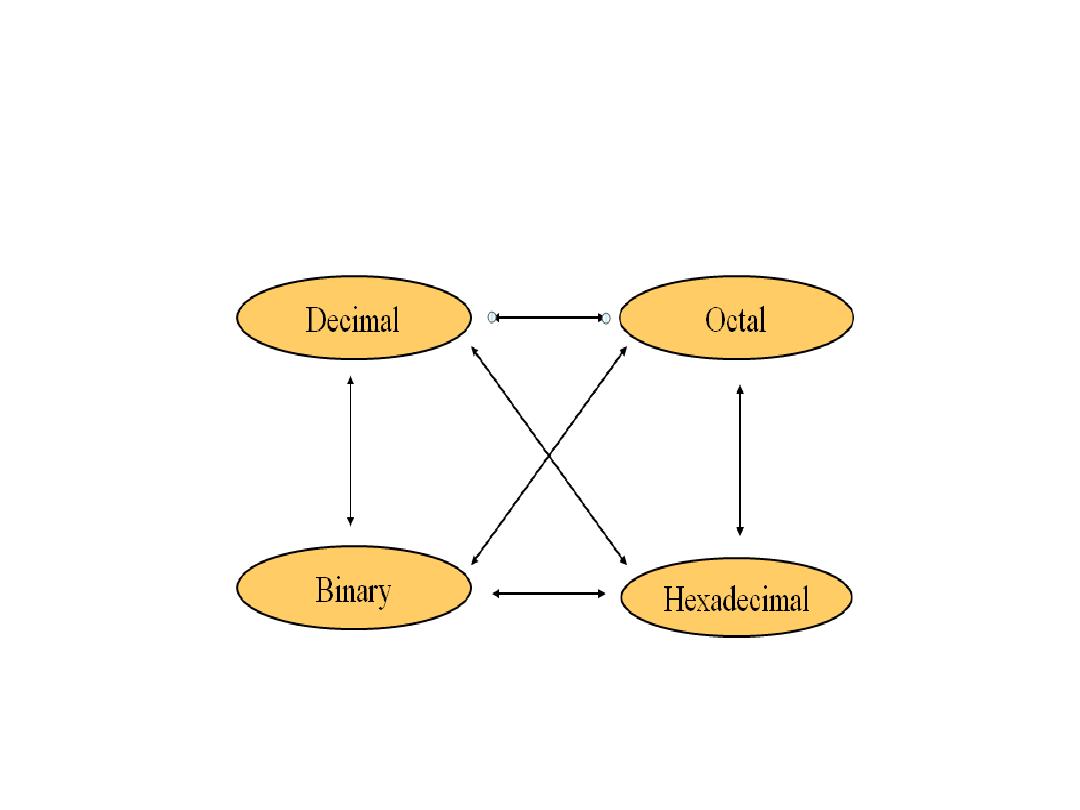
The possibility of Conversion among
basis
10
Dr. AMMAR ABDUL-HAMED KHADER
Binary to Decimal Conversion
• Technique
– Multiply each bit by 2
n
, where n
is the “weight” of the bit
– The weight is the position of the bit, starting from 0 on the
right
– Add the results
•
101011
2
=> 2
5
2
4
2
3
2
2
2
1
2
0
1 x 2
0
= 1
1 x 2
1
=
2
0 x 2
2
= 0
1 x 2
3
= 8
0 x 2
4
=
0
1 x 2
5
= 32
43
10
Bit 0
11
Dr. AMMAR ABDUL-HAMED KHADER

Octal to Decimal
• Technique
– Multiply each bit by 8
n
, where n is the “weight” of the bit
– The weight is the position of the bit, starting from 0 on the
right
– Add the results
– Example:
736
8
=>
6 x 8
0
=
6
3 x 8
1
=
24
7 x 8
2
=
448
478
10
12
Dr. AMMAR ABDUL-HAMED KHADER

Hexadecimal to Decimal
• Technique
– Multiply each bit by 16
n
, where n is the “weight” of the bit
– The weight is the position of the bit, starting from 0 on the
right
– Add the results
• Example:
ABC
16
=>
C x 16
0
= 12 x 1 = 12
B x 16
1
= 11 x 16 = 176
A x 16
2
= 10 x 256 = 2560
2748
10
13
Dr. AMMAR ABDUL-HAMED KHADER
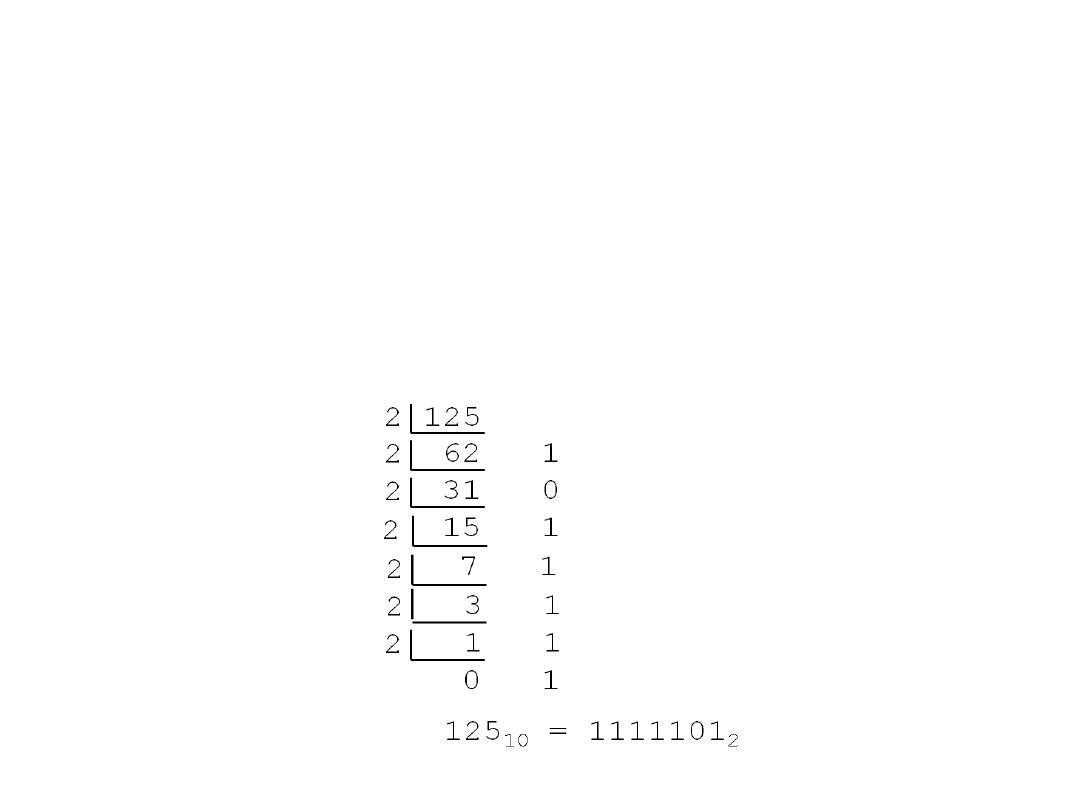
Decimal to Binary
• Technique
– Divide by two, keep track of the remainder
– First remainder is bit 0 (LSB, least-significant bit)
– Second remainder is bit 1 and so on
Example:
125
10
= ?
2
14
Dr. AMMAR ABDUL-HAMED KHADER

Fractional Decimal Number to Binary
• It can be converted by repeated multiplication by 2
• Example: convert 0.3125 to binary number
• 0.3125 * 2 = 0.625 Carry 0
• 0.625 * 2 = 1.25 Carry 1
• 0.25 * 2 = 0.5 Carry 0
• 0.5 * 2 = 1.00 Carry 1
.0101
15
MSB
Dr. AMMAR ABDUL-HAMED KHADER

Octal to Binary
• Technique
– Convert each octal digit to a 3-bit equivalent binary
representation
– Example:
705
8
= ?
2
7 0 5
111 000 101
705
8
= 111000101
2
16
Dr. AMMAR ABDUL-HAMED KHADER

Hexadecimal to Binary
• Technique
– Convert each hexadecimal digit to a 4-bit equivalent binary
representation
• Example
10AF
16
= ?
2
1 0 A F
0001 0000 1010 1111
10AF
16
= 0001000010101111
2
17
Dr. AMMAR ABDUL-HAMED KHADER
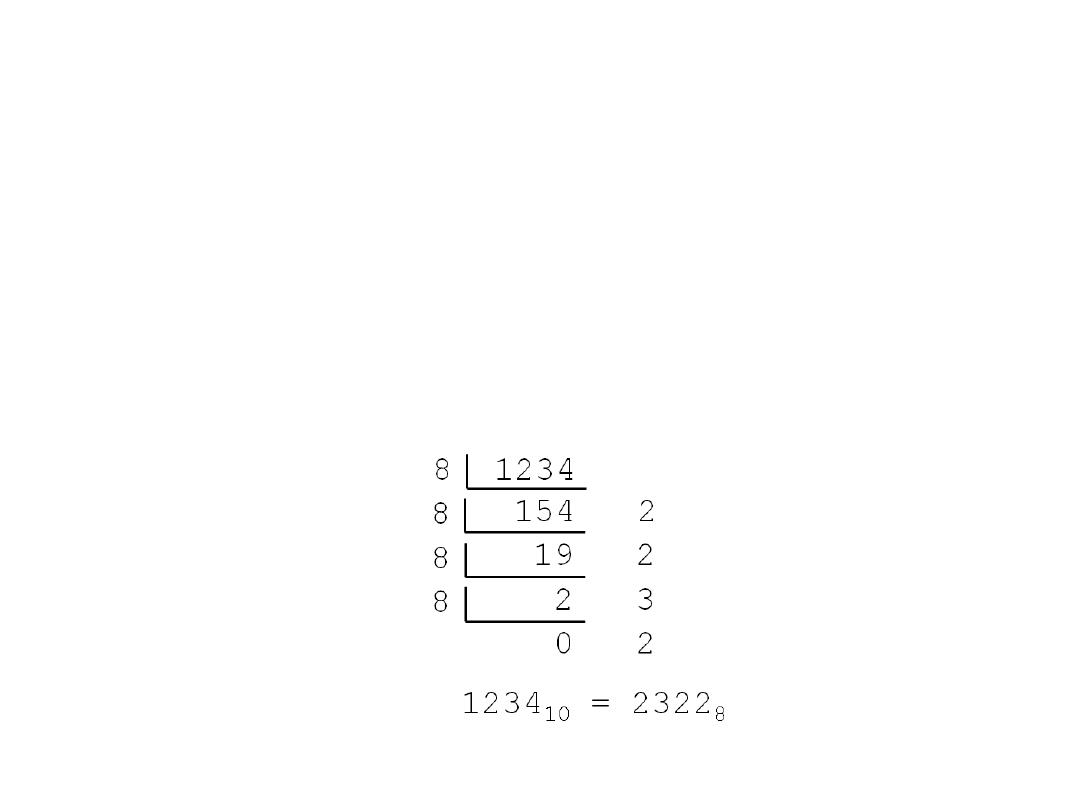
Decimal to Octal
• Technique
– Divide by 8
– Keep track of the remainde
• Example
1234
10
= ?
8
18
Dr. AMMAR ABDUL-HAMED KHADER
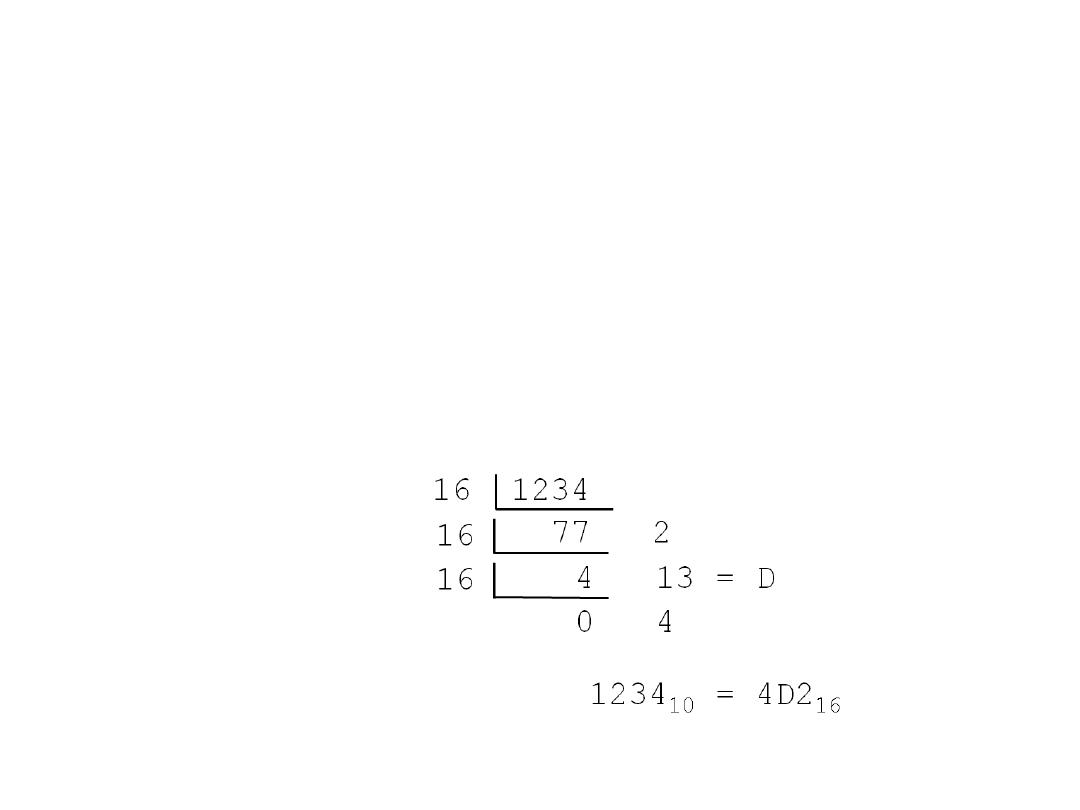
Decimal to Hexadecimal
• Technique
– Divide by 16
– Keep track of the remainder
• Example
1234
10
= ?
16
19
Dr. AMMAR ABDUL-HAMED KHADER

Binary to Octal
• Technique
– Group bits in threes, starting on right
– Convert to octal digits
• Example
1011010111
2
= ?
8
1 011 010 111
1 3 2 7
1011010111
2
= 1327
8
20
Dr. AMMAR ABDUL-HAMED KHADER

Binary to Hexadecimal
• Technique
– Group bits in fours, starting on right
– Convert to hexadecimal digits
• Example:
1010111011
2
= ?
16
10 1011 1011
2
B B
1010111011
2
= 2BB
16
21
Dr. AMMAR ABDUL-HAMED KHADER
Octal to Hexadecimal
• Technique
– Use binary as an intermediary
• Example:
1076
8
= ?
16
1 0 7 6
0 0 1 0 0 0 1 1 1 1 1 0
2 3 E
1076
8
= 23E
16
22
Dr. AMMAR ABDUL-HAMED KHADER
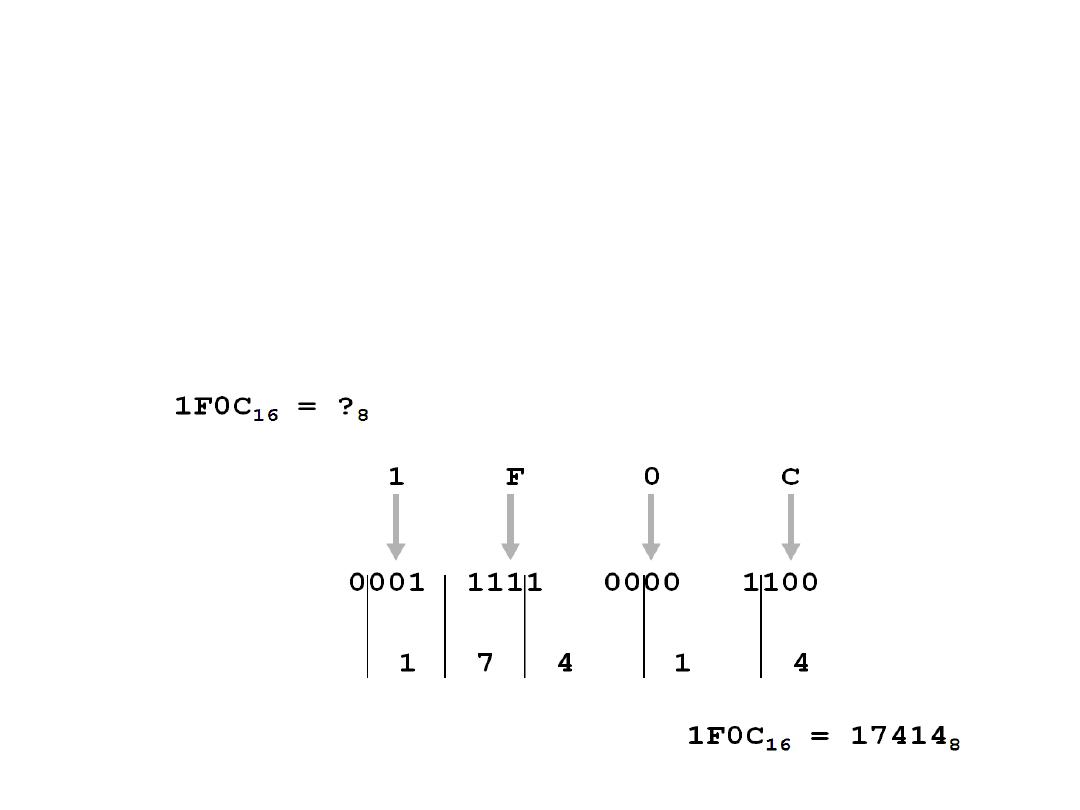
Hexadecimal to Octal
• Technique
– Use binary as an intermediary
• Example:
23
Dr. AMMAR ABDUL-HAMED KHADER
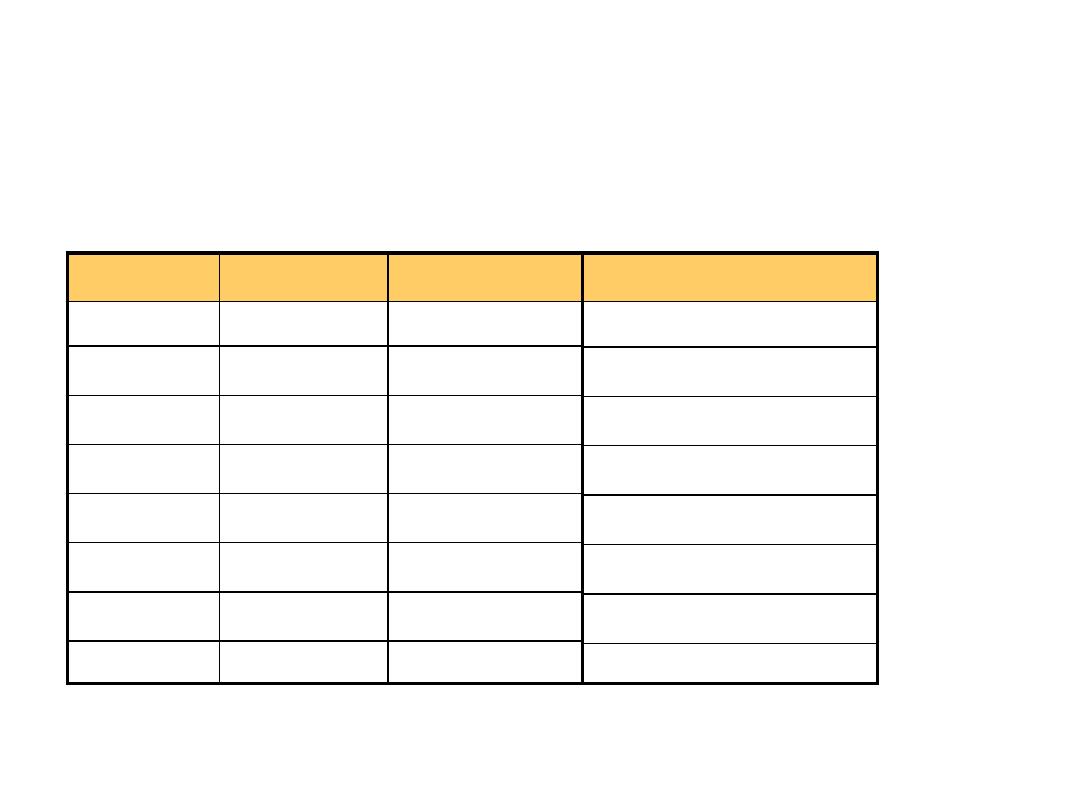
Common Powers
• Base 10
Power
Preface
Symbol
10
-12
pico
p
10
-9
nano
n
10
-6
micro
10
-3
milli
m
10
3
kilo
k
10
6
mega
M
10
9
giga
G
10
12
tera
T
Value
.000000000001
.000000001
.000001
.001
1000
1000000
1000000000
1000000000000
24
Dr. AMMAR ABDUL-HAMED KHADER
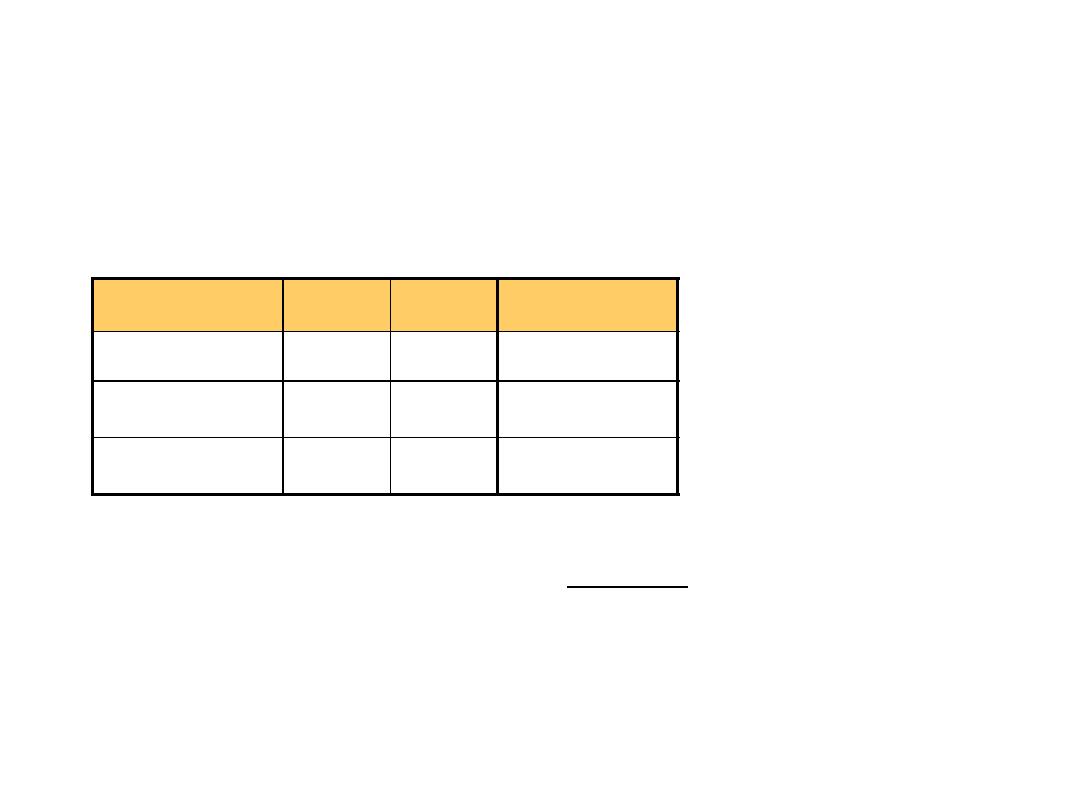
Common Powers
• Base 2
Power
Preface Symbol
2
10
kilo
k
2
20
mega
M
2
30
Giga
G
Value
1024
1048576
1073741824
•
In computing, particularly w.r.t. memory,
the base-2 interpretation generally applies
25
Dr. AMMAR ABDUL-HAMED KHADER
Binary Coded Decimal BCD
• BCD is a way to express each of the decimal digits with a binary
code. There are only ten groups in the BCD system.
• The 8421 Code (2
3
2
2
2
1
2
0
):
is a type of BCD code and it means
that each decimal digit, 0 through 9, is represented by a binary code
of four bits.
• There are six combination codes not used; 1010, 1011, 1100, 1101,
1110, and 1111 WHY?
• Example 1: Convert the decimal number 98 to BCD code.
Solution: 9 8
10011000
• Example 2: Convert the BCD code (001101010001) to decimal.
Solution: It is, 3 5 1
26
Dr. AMMAR ABDUL-HAMED KHADER
Binary Coded Decimal BCD
• Addition
• Example1: Add the BCD codes 0011 and 0100
0011 3
0100 + 4
0 111 7
• Example2:
1001 9
1001 + 9
1 0010 18 Invalid BCD number (> 9), So add (6):
0110 +
0001 1000 18
27
Dr. AMMAR ABDUL-HAMED KHADER

Binary Coded Decimal BCD
• Homework
• Convert these decimal number to BCD code and add them
A) 23+ 15
B) 450 + 417
C) 67 + 53
28
Dr. AMMAR ABDUL-HAMED KHADER
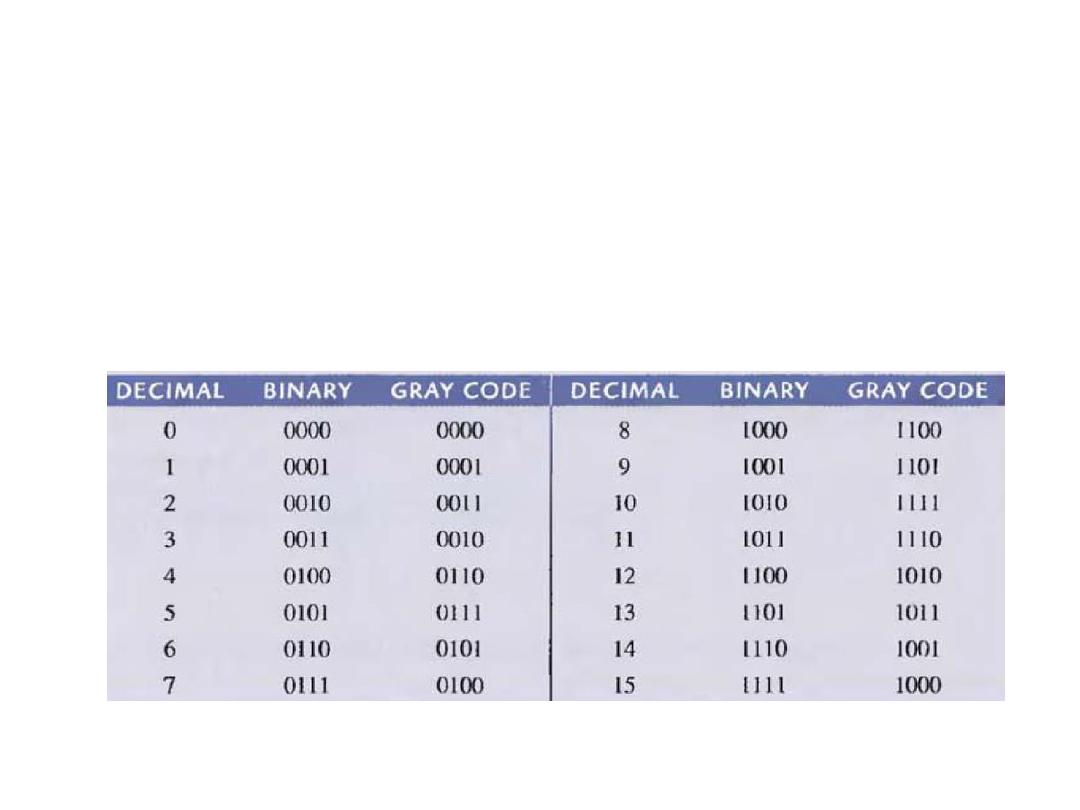
Digital Codes
• The Gray Code: it is unweighted and not an arithmetic code.
The important feature of this code is that it exhibits only a
single bit change from one code to the next in sequence.
29
Dr. AMMAR ABDUL-HAMED KHADER
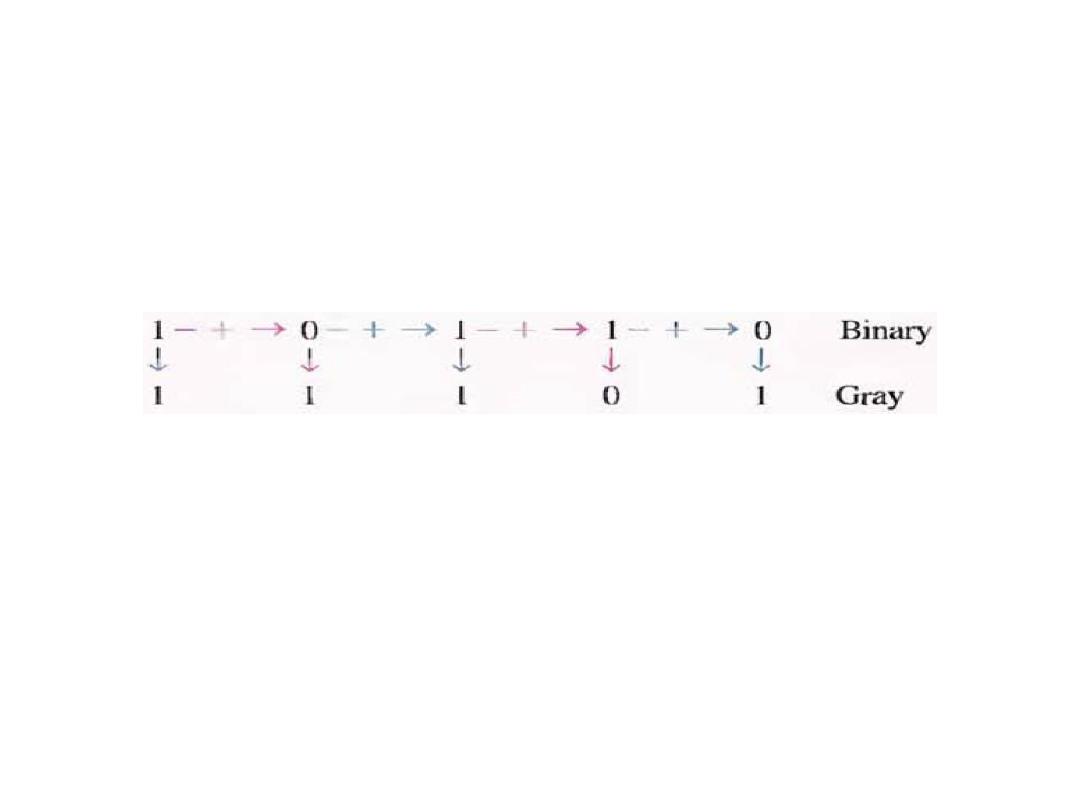
The Gray Code Conversion
• Binary to Gray code conversion:
• Example: Convert the binary number 10110 to Gray code.
Gray to Binary code conversion:
Example:
Convert the Gray code 11011 to binary number.
30
Dr. AMMAR ABDUL-HAMED KHADER

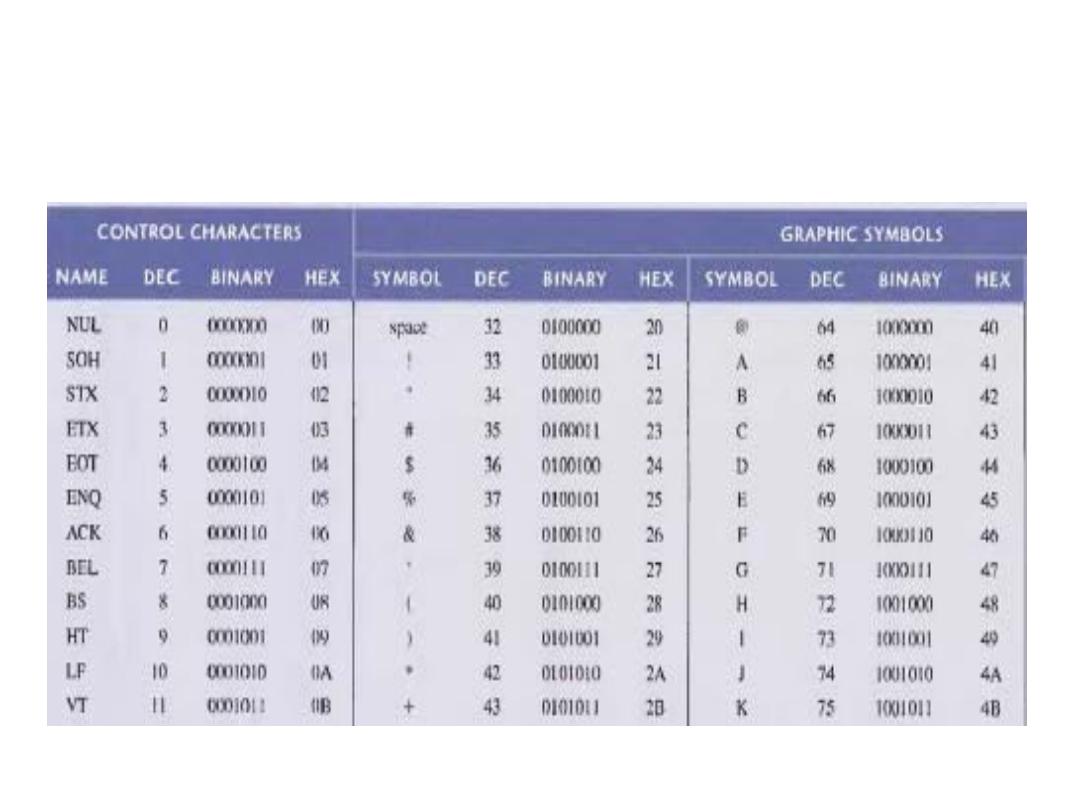
Alphanumeric Code - ASCII Code
• ASCII is the abbreviation for American Standard Code for
I
nformation Interchange. It a universal accepted alphanumeric
code used in must computers and other electronics equipment.
Must computer keyboards are standard ASCII. It has 128
characters and symbols represented by a 7-bit binary code. It
considered an 8-bit code with the MSB always 0.
31
Dr. AMMAR ABDUL-HAMED KHADER
Alphanumeric Code - ASCII Code
32
Dr. AMMAR ABDUL-HAMED KHADER

The Complement
• The One’s Complement
• Example: Find the one’s Complement for 0010.
1111
0010
–
1101
33
The ones' complement of a
value obtained by inverting all the bits in the binary
representation of the number (swapping 0s for 1s and vice
versa). The ones' complement of the number then behaves like
the negative of the original number in some arithmetic
operations.
Dr. AMMAR ABDUL-HAMED KHADER

The Complement
• The Two’s Complement
• Example: Find the two’s Complement for 0010.
1111
0010
–
1101
0001+
1110
34
Dr. AMMAR ABDUL-HAMED KHADER
The Co ple e t’s Applicatio s
Addition of a positive and a negative binary number
Case I:
When the positive number has greater magnitude.
•
Example:
Find the sum of the following binary numbers:
+ 1110 and - 1101
• Solution:
+
1 1 1 0
⇒
0
1 1 1 0
-
1 1 0 1
⇒
1
0 0 1 0
(taking 1’s complement)
0
0 0 0 0
1 carry
0
0 0 0 1
Hence the required sum is
+
0001.
35
Dr. AMMAR ABDUL-HAMED KHADER

The Co ple e t’s Applicatio s
• Case II: When the negative number has greater magnitude.
• Example: Find the sum of the following binary numbers:
+ 1010 and - 1100
• Solution:
+
1 0 1 0
⇒
0
1 0 1 0
-
1 1 0 0
⇒
1
0 0 1 1
(1’s complement)
1
1 1 0 1
Because the number is negative (
1
),
we should take the 1’s
complement of the magnitude bits.
• Hence the required sum is – 0010.
36
Dr. AMMAR ABDUL-HAMED KHADER

The Co ple e t’s Applicatio s
•
Case III:
When the two numbers are negative
• Example: Find the sum of the following negative numbers :
-1010 and -0101
• Solution:
• - 1 0 1 0 ⇒ 1 0 1 0 1 (1’s complement)
- 0 1 0 1
⇒ 1 1 0 1 0 (1’s complement)
0 1 1 1 1
1 carry
1 0 0 0 0
The 1’s complement of the magnitude bits of sum, is 1111 and the sign bit is 1.
Hence the required sum is
-1111.
37
Dr. AMMAR ABDUL-HAMED KHADER
