
Basic Relationships Between
Pixels
• Neighborhood
• Adjacency
• Connectivity
• Paths
• Regions and boundaries

Neighbors of a Pixel
• Any pixel p(x, y) has two vertical and two
horizontal neighbors, given by
(x+1, y), (x-1, y), (x, y+1), (x, y-1)
• This set of pixels are called the 4-neighbors of
P, and is denoted by N
4
(P).
• Each of them are at a unit distance from P.

• The four diagonal neighbors of p(x,y) are
given by,
(x+1, y+1), (x+1, y-1), (x-1, y+1), (x-1 ,y-1)
• This set is denoted by N
D
(P).
• Each of them are at Euclidean distance of
1.414 from P.
Neighbors of a Pixel (Contd..)

• The points N
D
(P) and N
4
(P) are
together known as 8-neighbors of the
point P, denoted by N
8
(P).
• Some of the points in the N
4
, N
D
and
N
8
may fall outside image when P lies
on the border of image.
Neighbors of a Pixel (Contd..)
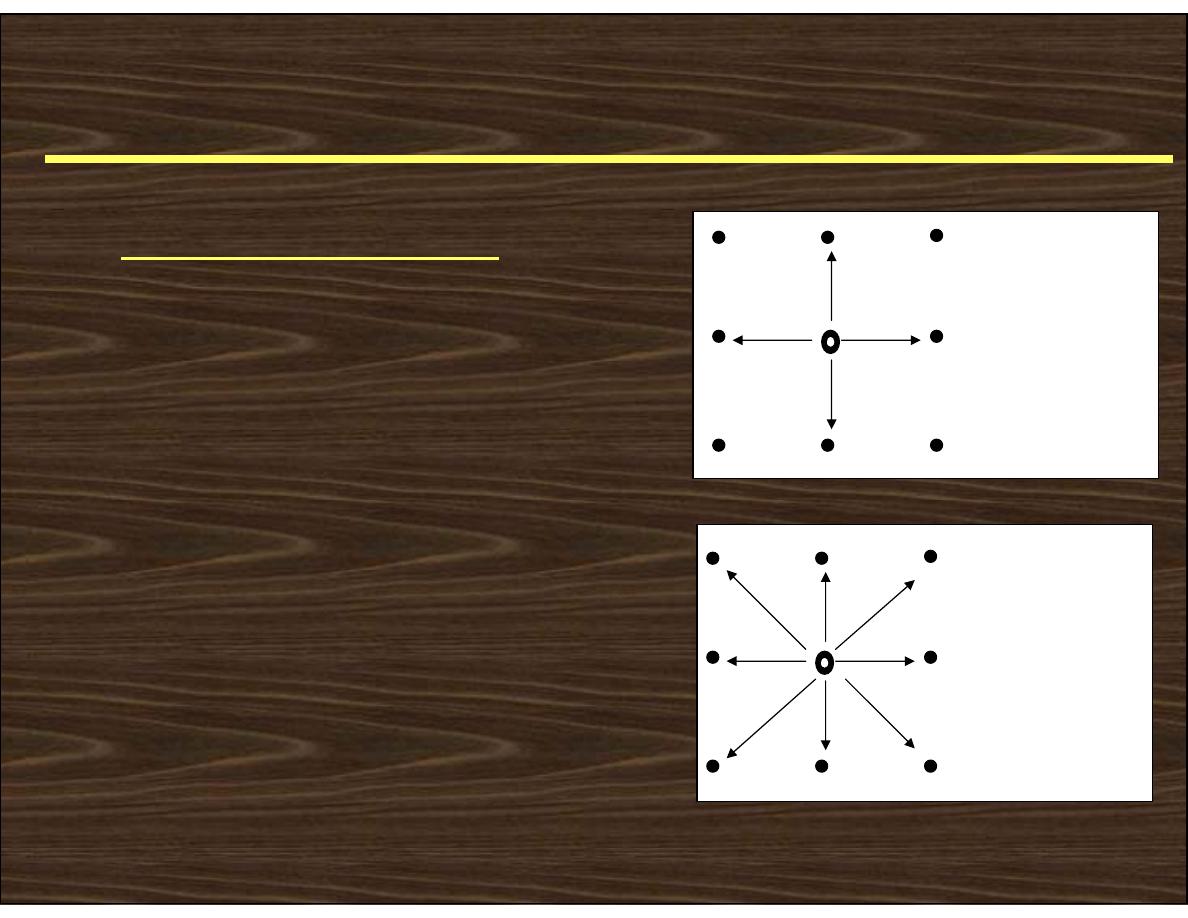
Neighbors of a pixel
a. 4-neighbors of a pixel p
are its vertical and
horizontal neighbors
denoted by N
4
(p)
b. 8-neighbors of a pixel p
are its vertical
horizontal and 4
diagonal neighbors
denoted by N
8
(p)
p
N
4
(p)
p
N
8
(p)
Neighbors of a Pixel (Contd..)
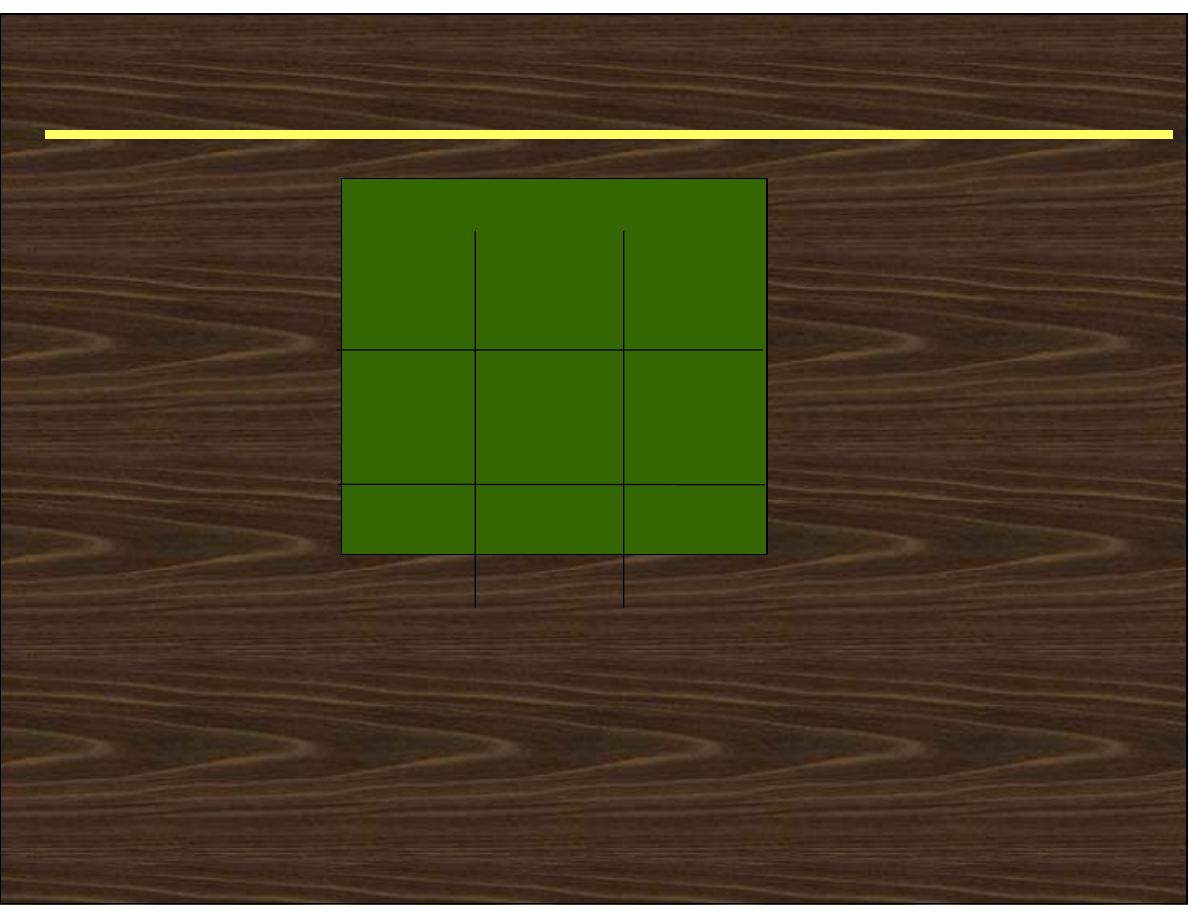
Neighbors of a Pixel (Contd..)
N
D
N
4
N
D
N
4
P N
4
N
D
N
4
N
D
•N
4
- 4-neighbors
•N
D
- diagonal neighbors
•N
8
- 8-neighbors (N
4
U N
D
)

Adjacency
• Two pixels are connected if they are
neighbors and their gray levels satisfy
some specified criterion of similarity.
• For example, in a binary image two pixels
are connected if they are 4-neighbors and
have same value (0/1).

Adjacency (contd.)
• Let V be set of gray levels values used to define adjacency.
• 4-adjacency: Two pixels p and q with values from V are 4-
adjacent
if
q is in the set N
4
(p).
• 8-adjacency: Two pixels p and q with values from V are 8-
adjacent if q is in the set N
8
(p).
• m-adjacency: Two pixels p and q with values from V are m-
adjacent if,
– q is in N
4
(P).
– q is in N
D
(p) and the set [ ] is empty
(has no pixels whose values are from V).
)
(
)
(
4
4
q
N
p
N
I
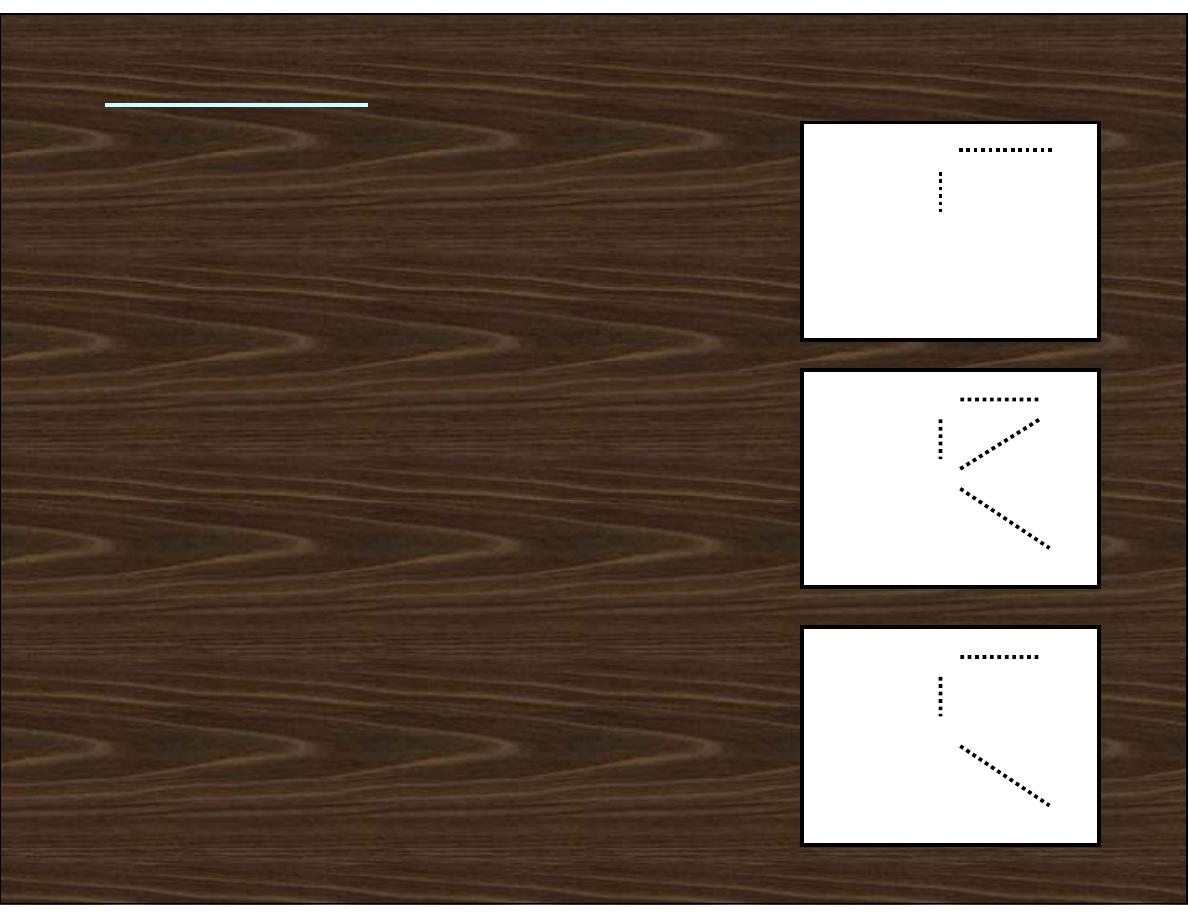
Connectivity :
To determine whether the pixels
are adjacent in some sense.
Let V be the set of gray-level
values used to define connectivity;
then Two pixels p, q that have values
from the set V are:
a. 4-connected, if q is in the set N
4
(p)
b. 8-connected, if q is in the set N
8
(p)
c. m-connected, iff
i.
q is in N
4
(p) or
ii. q is in N
D
(p) and the set
is empty
0
1
1
0
2
0
0
0
1
0
1
1
0
2
0
0
0
1
a.
b.
c.
V = {1, 2}
)
(
)
(
4
4
q
N
p
N
I
0
1
1
0
2
0
0
0
1
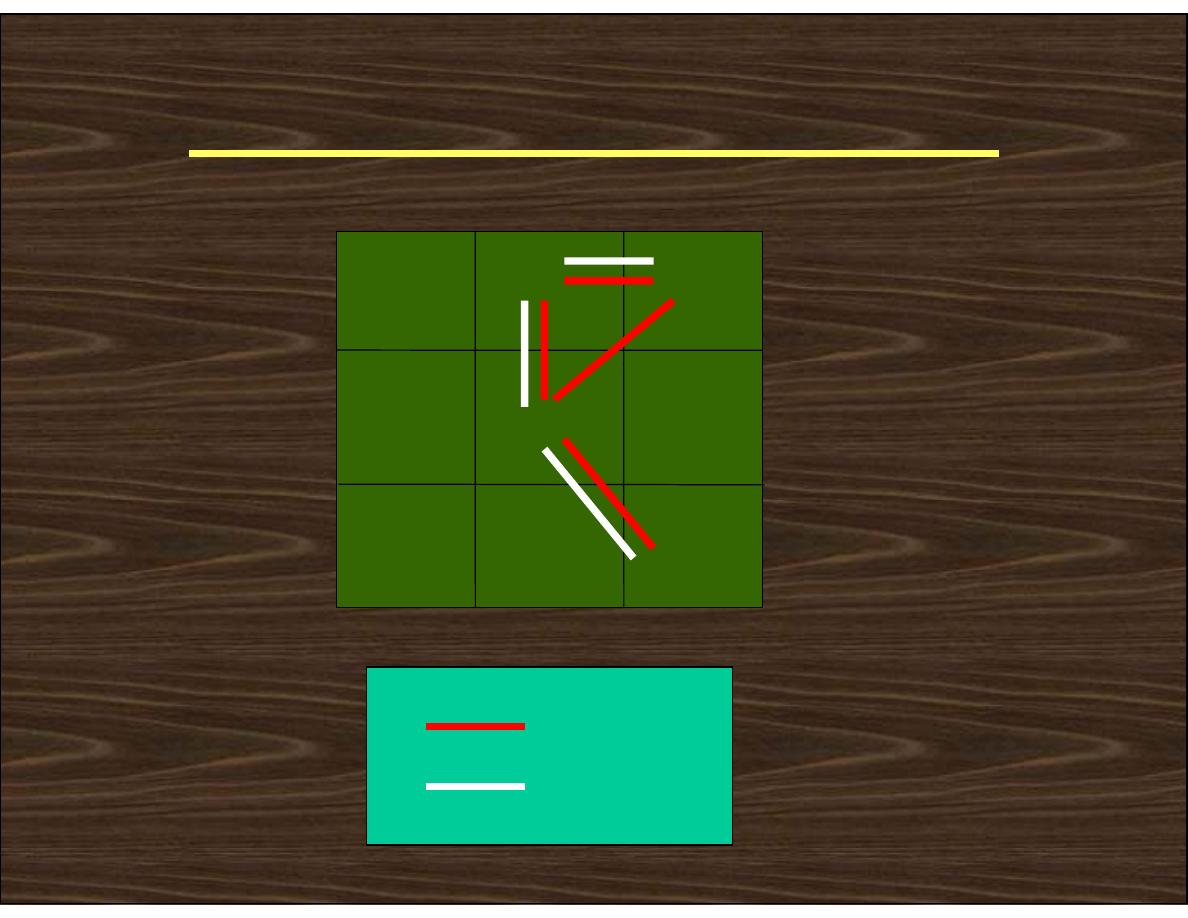
Adjacency/Connectivity
0 1 1
0 1 0
0 0 1
8-adjacent
m-adjacent

• Pixel p is adjacent to pixel q if they are connected.
• Two image subsets S
1
and S
2
are adjacent if some
pixel in S
1
is adjacent to some pixel in S
2
Adjacency/Connectivity
S
1
S
2

Paths & Path lengths
• A path from pixel p with coordinates
(x, y) to pixel q with coordinates (s, t)
is a sequence of distinct pixels with
coordinates:
(x
0
, y
0
), (x
1
, y
1
), (x
2
, y
2
) … (x
n
, y
n
),
where (x
0
, y
0
)=(x, y) and (x
n
, y
n
)=(s, t);
(x
i
, y
i
) is
adjacent
to (x
i-1
, y
i-1
)
• Here
n
is the
length
of the path.
• We can define 4-, 8-, and m-paths based
on type of adjacency used.
n
i
≤
≤
1

Connected Components
• If p and q are pixels of an image subset S
then p is
connected
to q in S if there is a
path from p to q consisting entirely of
pixels in S.
• For every pixel p in S, the set of pixels in
S that are connected to p is called a
connected component
of S.
• If S has only one connected component
then S is called
Connected Set.

Regions and Boundaries
• A subset R of pixels in an image is
called a
Region
of the image if R is a
connected set.
• The
boundary
of the region R is the
set of pixels in the region that have
one or more neighbors that are not
in R.
• If R happens to be entire Image?

Distance measures
Given pixels p, q and z with coordinates
(x, y), (s, t), (u, v) respectively, the distance
function D has following properties:
a. D(p, q) 0 [D(p, q) = 0, iff p = q]
b. D(p, q) = D(q, p)
c. D(p, z) D(p, q) + D(q, z)
≥
≤

The following are the different
Distance measures:
• Euclidean Distance :
D
e
(p, q) = [(x-s)
2
+ (y-t)
2
]
b. City Block Distance:
Æ
D
4
(p, q) = |x-s| + |y-t|
c. Chess Board Distance:
Æ
D
8
(p, q) = max(|x-s|, |y-t|)
2
2
2
2
2
2
1
1
1
2
2
1
0
1
2
2
1
1
1
2
2
2
2
2
2
2
2
1
2
2
1
0
1
2
2
1
2
2

Relationship between pixels (Contd..)
Arithmetic/Logic Operations:
-
Addition :
p + q
– Subtraction:
p – q
– Multiplication:
p*q
– Division:
p/q
– AND:
p AND q
– OR :
p OR q
– Complement:
NOT(q)
Neighborhood based arithmetic/Logic :
Value assigned to a pixel at position ‘e’ is a
function of its neighbors and a set of window
functions.
w
9
w
8
w
7
w
6
w
5
w
4
w
3
w
2
w
1
∑
=
+
+
+
+
+
+
+
+
=
i
i
f
w
w
w
w
w
w
w
w
w
p
i)
h
g
f
e
d
c
b
a
(w
9
8
7
6
5
4
3
2
1
:
i
h
g
..
f
e
d
…
c
b
a
:

Arithmetic/Logic Operations
• Tasks done using neighborhood
processing:
– Smoothing / averaging
– Noise removal / filtering
– Edge detection
– Contrast enhancement

•Issues
– Choice of w
i
‘s (N
2
values)
– Choice of N, window size
– Computation at boundaries
• Do not compute at boundaries
• Pad with zeros and extend image
boundary
• Pad assuming periodicity of image
• Extrapolation of image

END of Neighborhood
and Connectivity

