(Chi square distribution (X2 test pdf - Biostatistics

Lecture 11 - The Chi-Square distribution (X2-test)



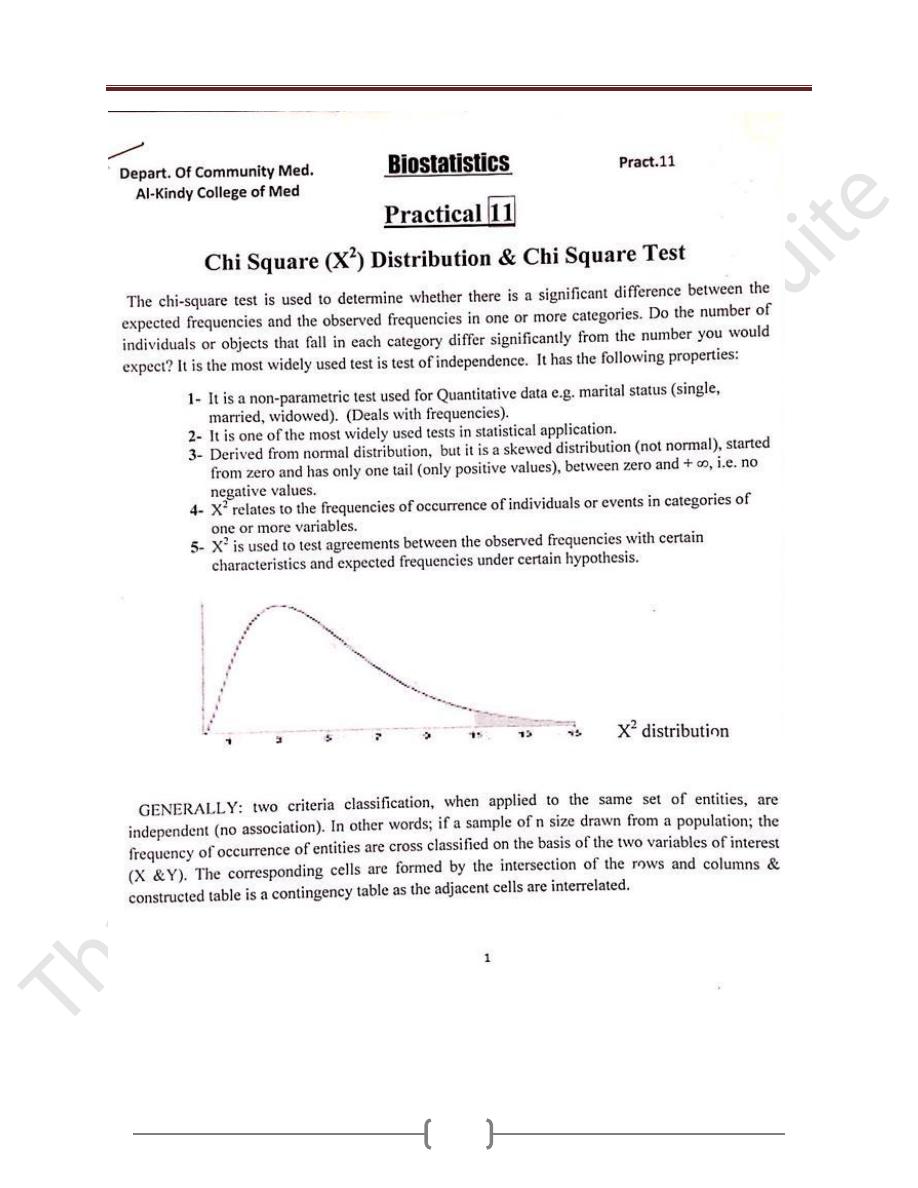
Is the most frequently employed statistical technique for

analysis of count or frequency data to find the
association between two variables or more.



-test statistic is most appropriate for use with

qualitative (categorical) variables e.g. marital status
(single, married, widowed), or with discrete numerical

variable ➨ Used for the frequencies associated with these

variables (most accurate when the variable is
dichotomous e.g. life or death, disease or not, male or
female….etc.).



-test is used to whether there is an association between

the raw variable and the column variable.



Chi-Square distribution may be derived from the normal

distribution, but it is a skewed distribution (not normal),
started from zero and has only one tail (only positive
values). It depends on:

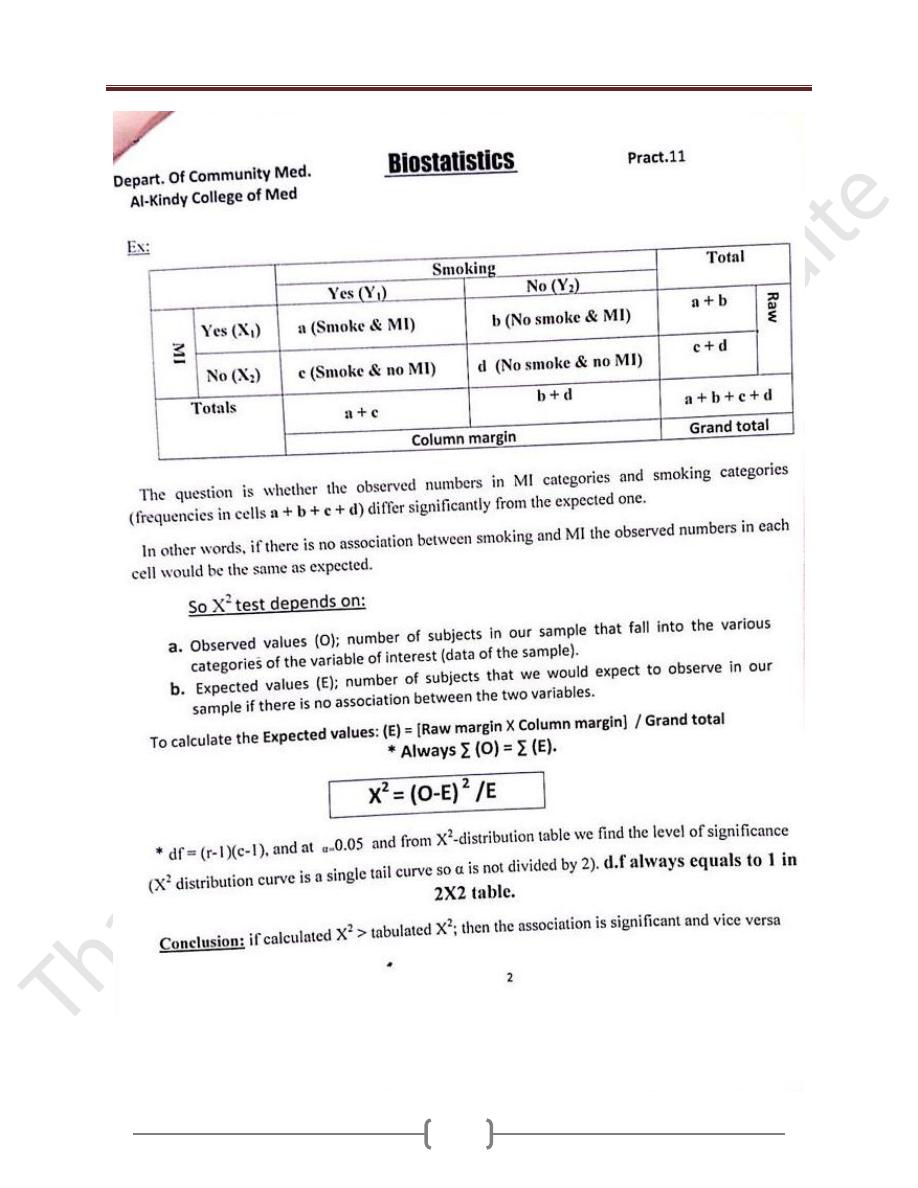
1) Observed values (O); number of subjects in our sample

that fall into the various categories of the variable of
interest (data of the sample).

2) Expected values (E); number of subjects that we would

expect to observe in our sample if the null hypothesis is
true. To calculate the expected values: (E)= [Raw margin
X Column margin] / Grand total

* Always ∑ (O) = ∑ (E).

= (O-E)

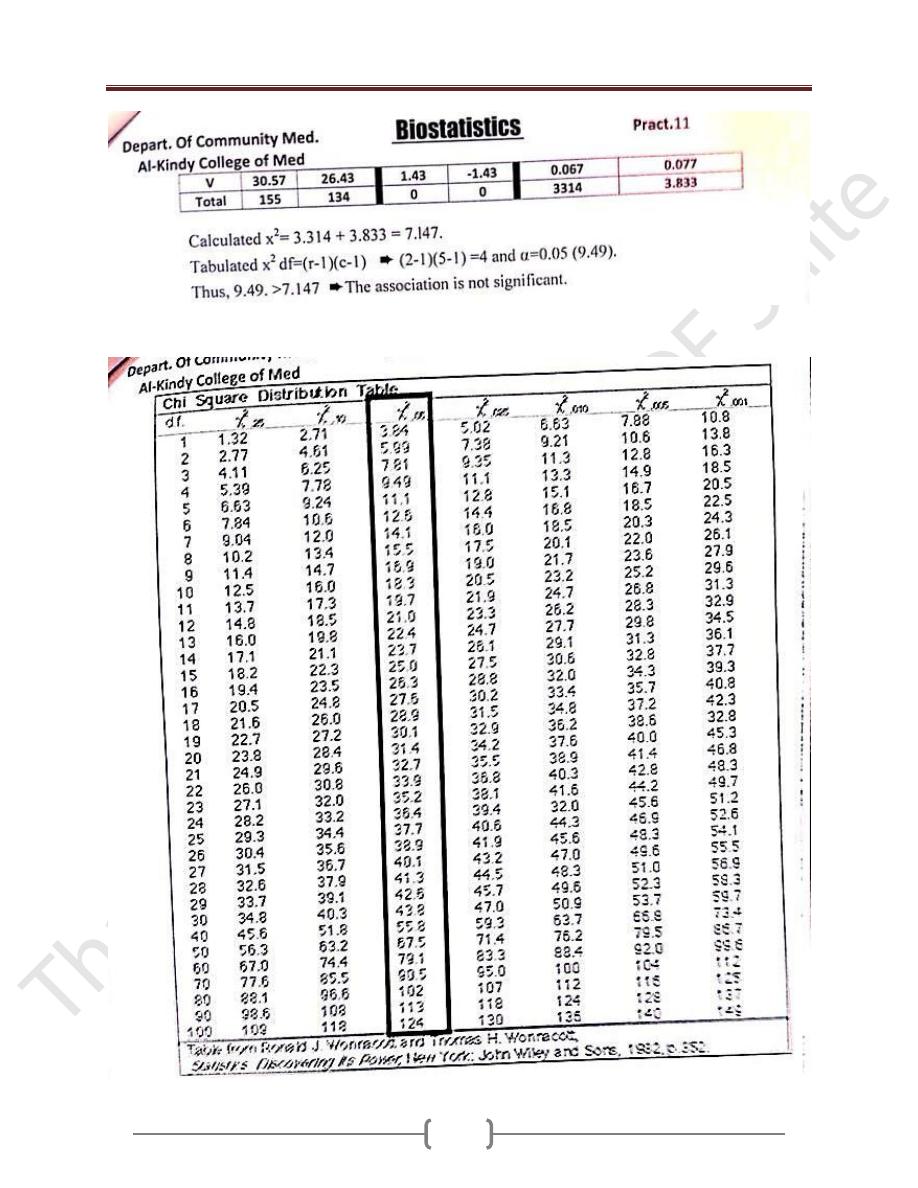
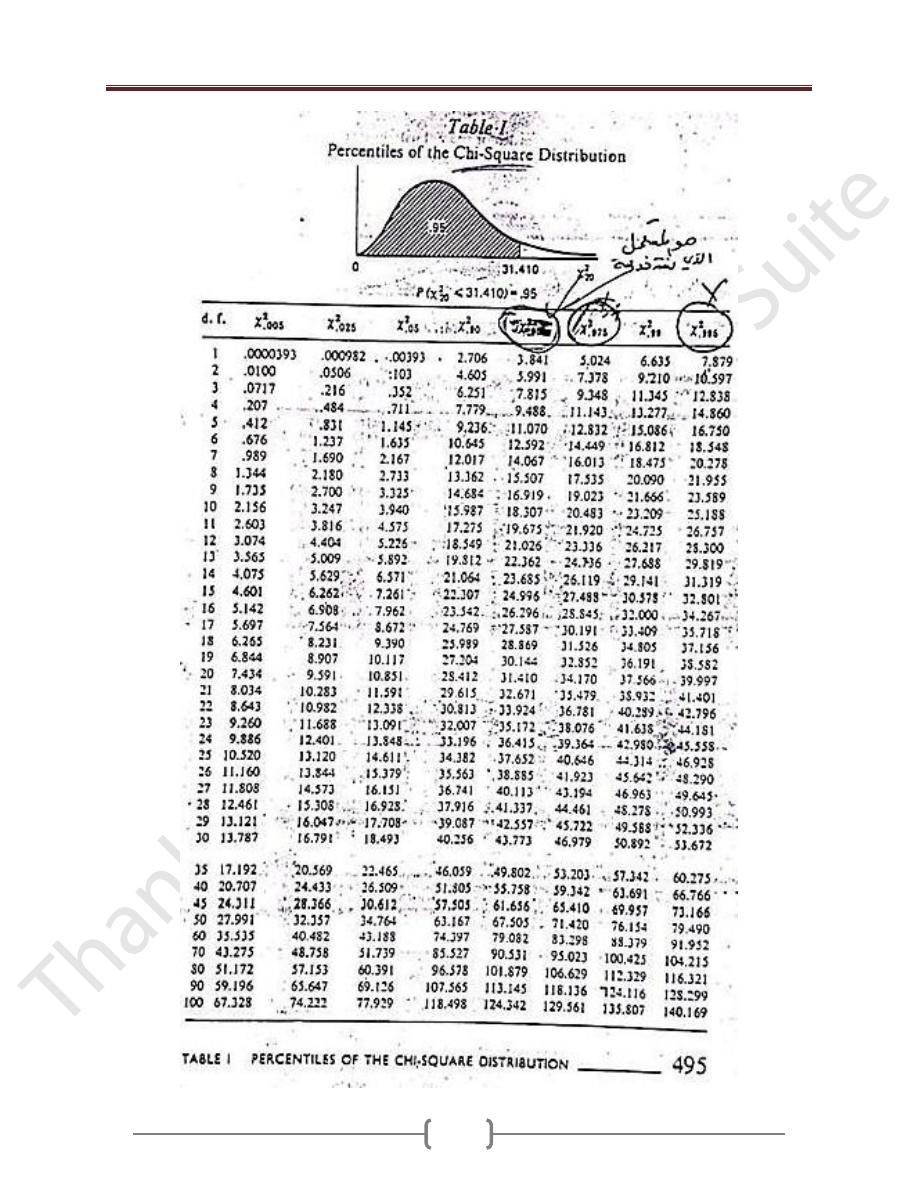
* df=(r-1)(c-1)

⍺

0.05 and from X

-distribution table

we find p-value.

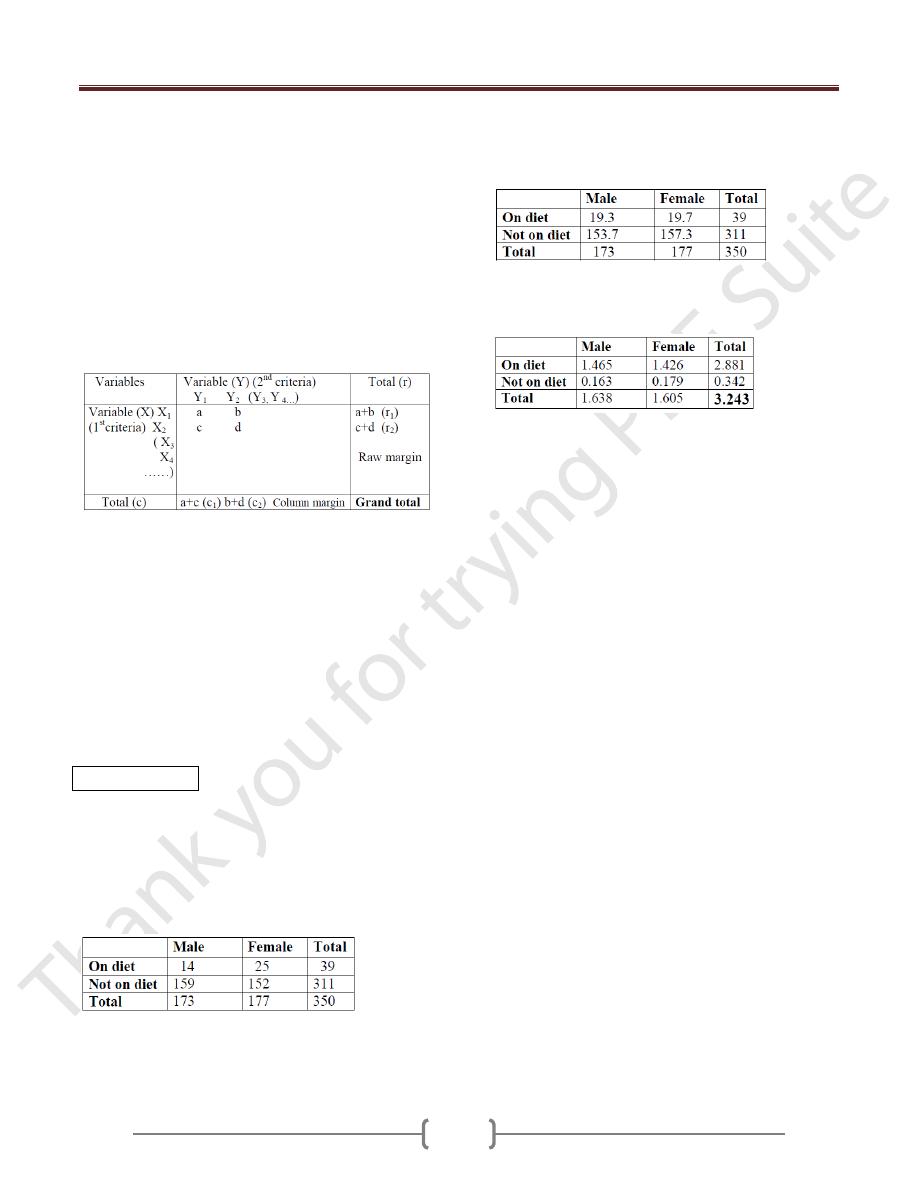
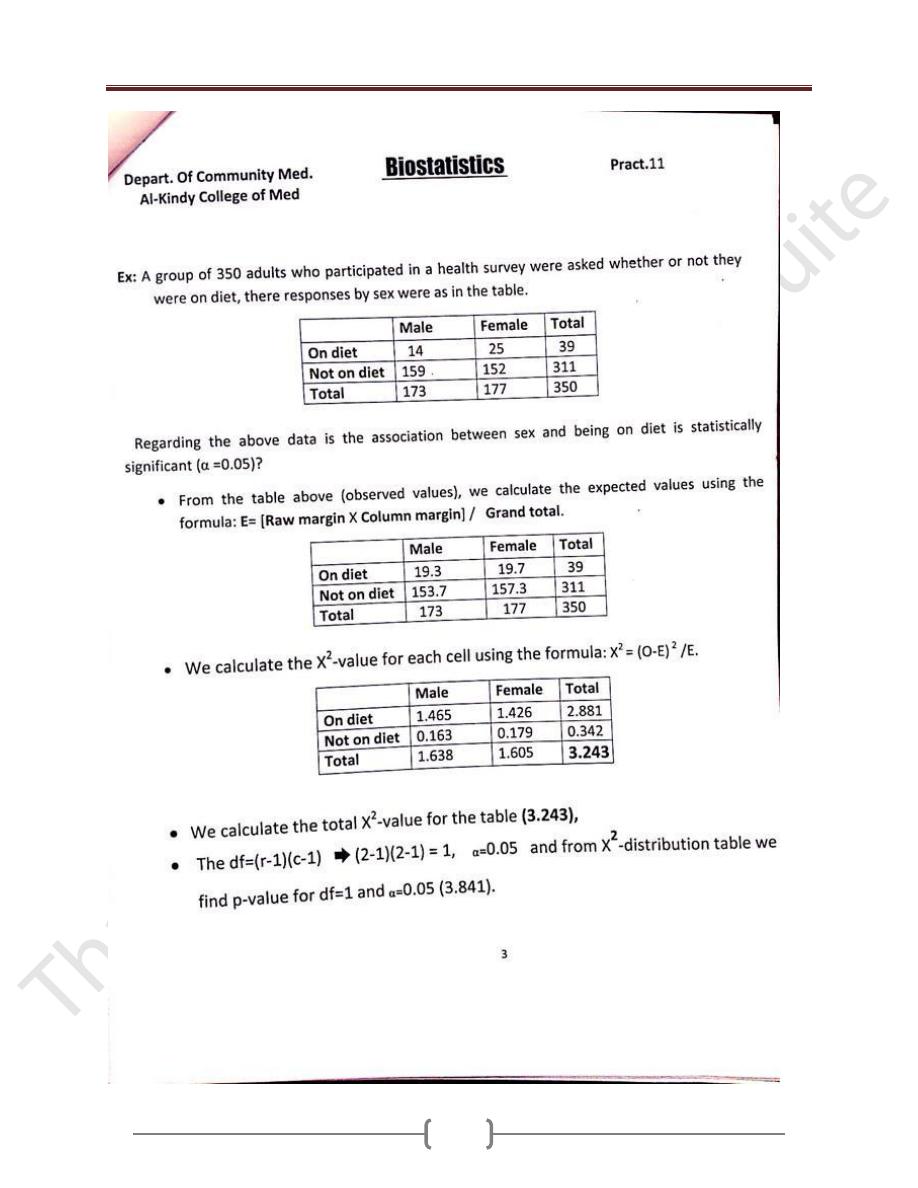
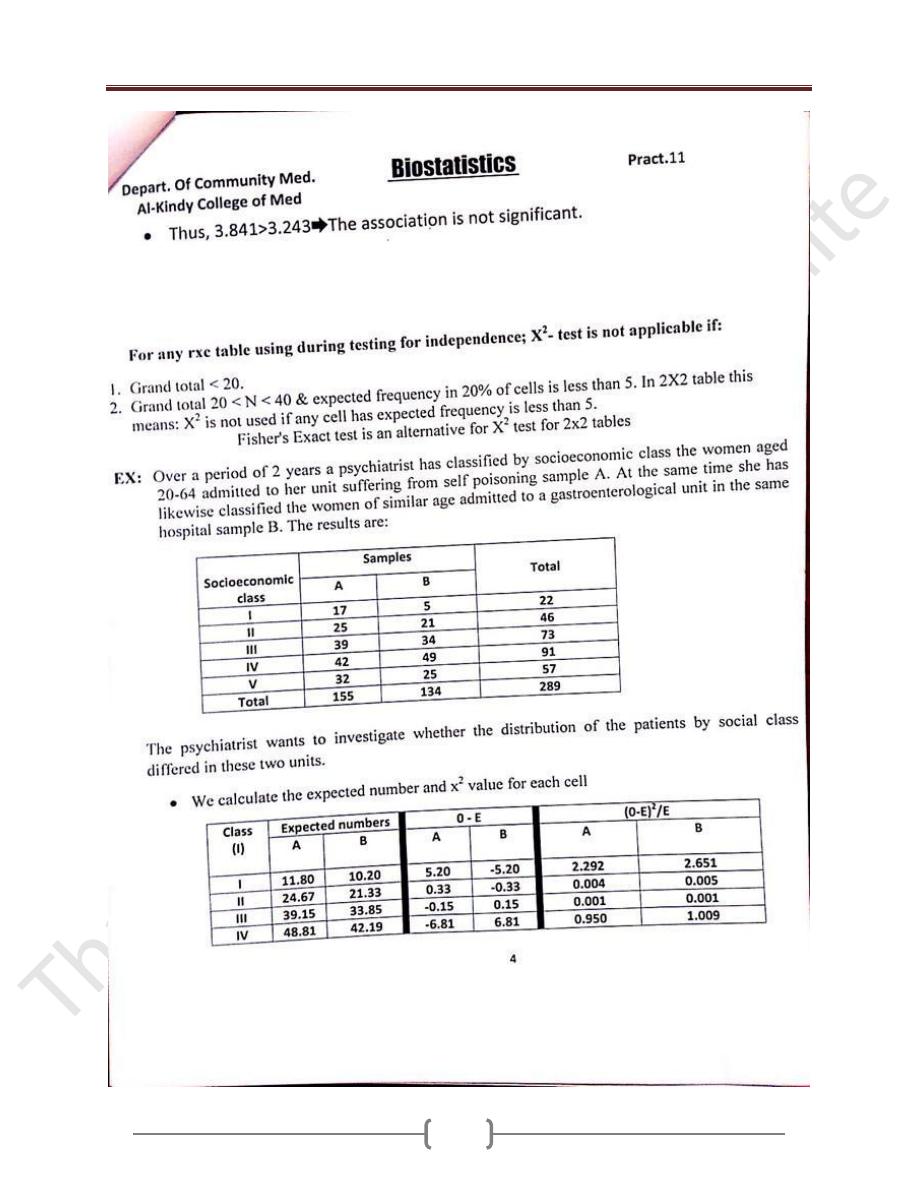
Ex: A group of 350 adults who participated in a health
survey were asked whether or not they were on diet, there
responses by sex were as in the table.



Regarding the above data is the association between sex

and being on diet is statistically significant (

⍺=

0.05)?

-From the table above (observed values), we calculate the
expected values using the formula: E= [Raw margin X
Column margin] / Grand total.

-we calculate the X

-value for each cell using the formula:

= (O-E)

/E.

- We calculate the total X

-value for the table (3.243),

- The df=(r-1)(c-1) ➨ (2-1)(2-1) = 1,

⍺=

0.05 and from

-distribution table we find p-value for df=1 and

⍺=

0.05