Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
2
D
D
i
i
s
s
c
c
r
r
e
e
t
t
e
e
F
F
o
o
u
u
r
r
i
i
e
e
r
r
T
T
r
r
a
a
n
n
s
s
f
f
o
o
r
r
m
m
The Discrete Fourier Transform (DFT) is the equivalent of the continuous Fourier
Transform for signals known only at N instants separated by sample times T (i.e.
a finite sequence of data). The transformation of discrete data between the time and
frequency domain is quite useful in extracting information from the signal.
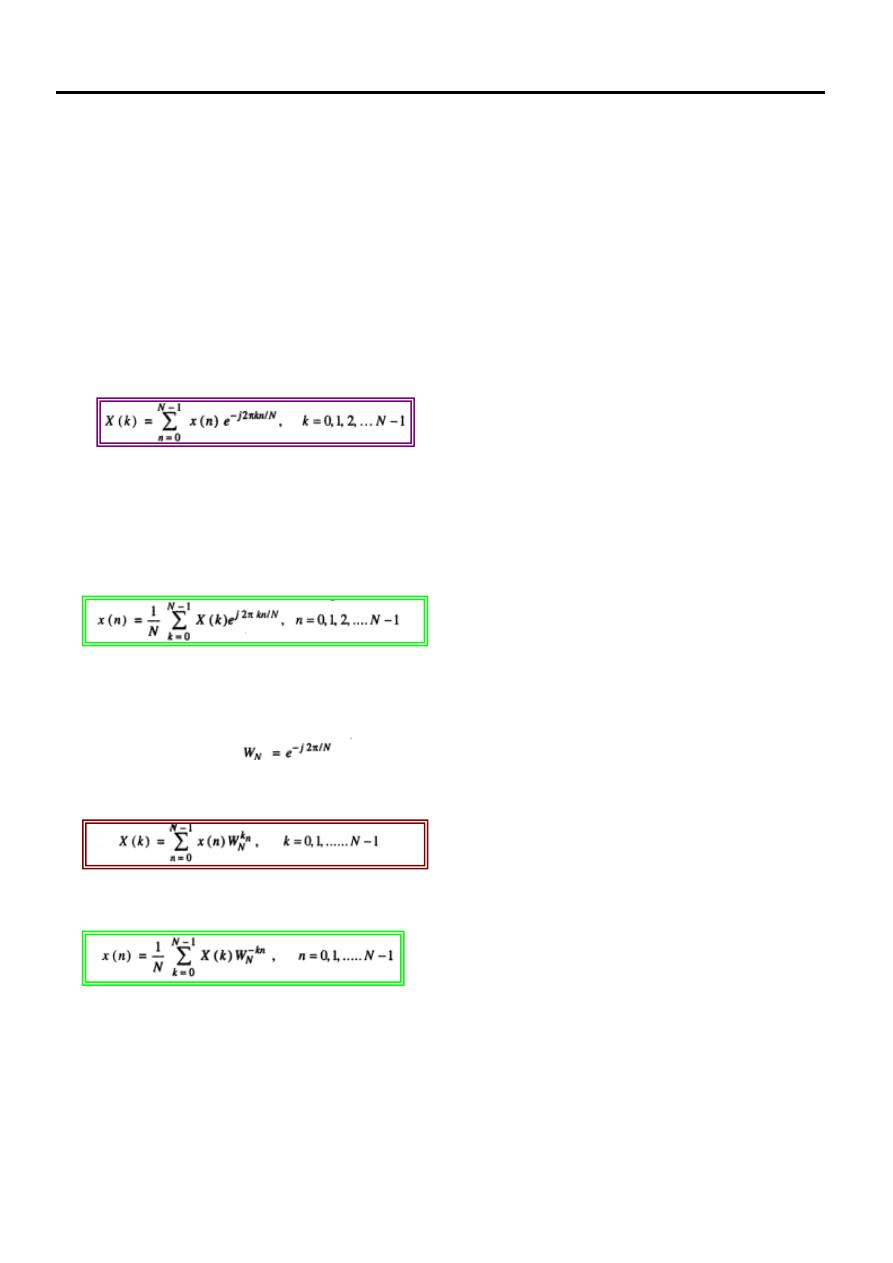
The DFT is denoted by X(k) and given as,
…………………… (1)
Here X(k) is the DFT and it is computed at k=0,1,2,…. N-1. "N" discrete points. Thus
DFT X(k) is the sequence of N samples. The sequence x(n) can be obtained back
from X(k) by taking Inverse Discrete Fourier Transform, i.e. IDFT is given as,
………………….
(2)
Here x(n) is sequence of N samples . thus X(k) and x(n) both contains N number of
samples.
Let us define,
This is called twiddle factor. Hence DFT and IDFT equation can be written as,
………………… (3)
And
…………………… (4)

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
3
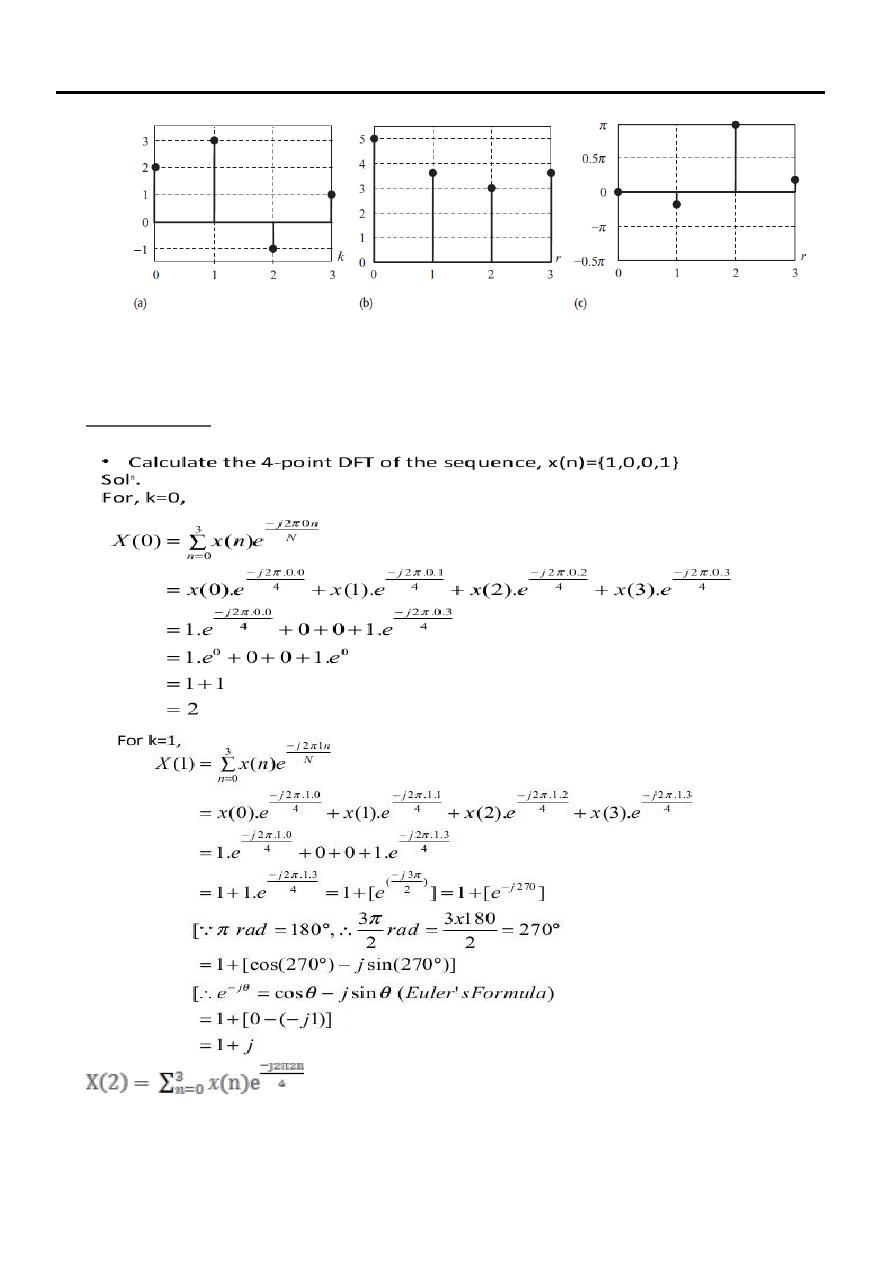
Example One
Calculate the four-point DFT of the aperiodic sequence x[k] of length N = 4,
which is defined as follows:
Solution
Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
4
Fig. 1. (a) DT sequence x[k];(b) magnitude spectrum and
(c) phase spectrum for example one
Example Two

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
5
ث

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
6
Example Three
Calculate the IDFT of
Solution
Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
7
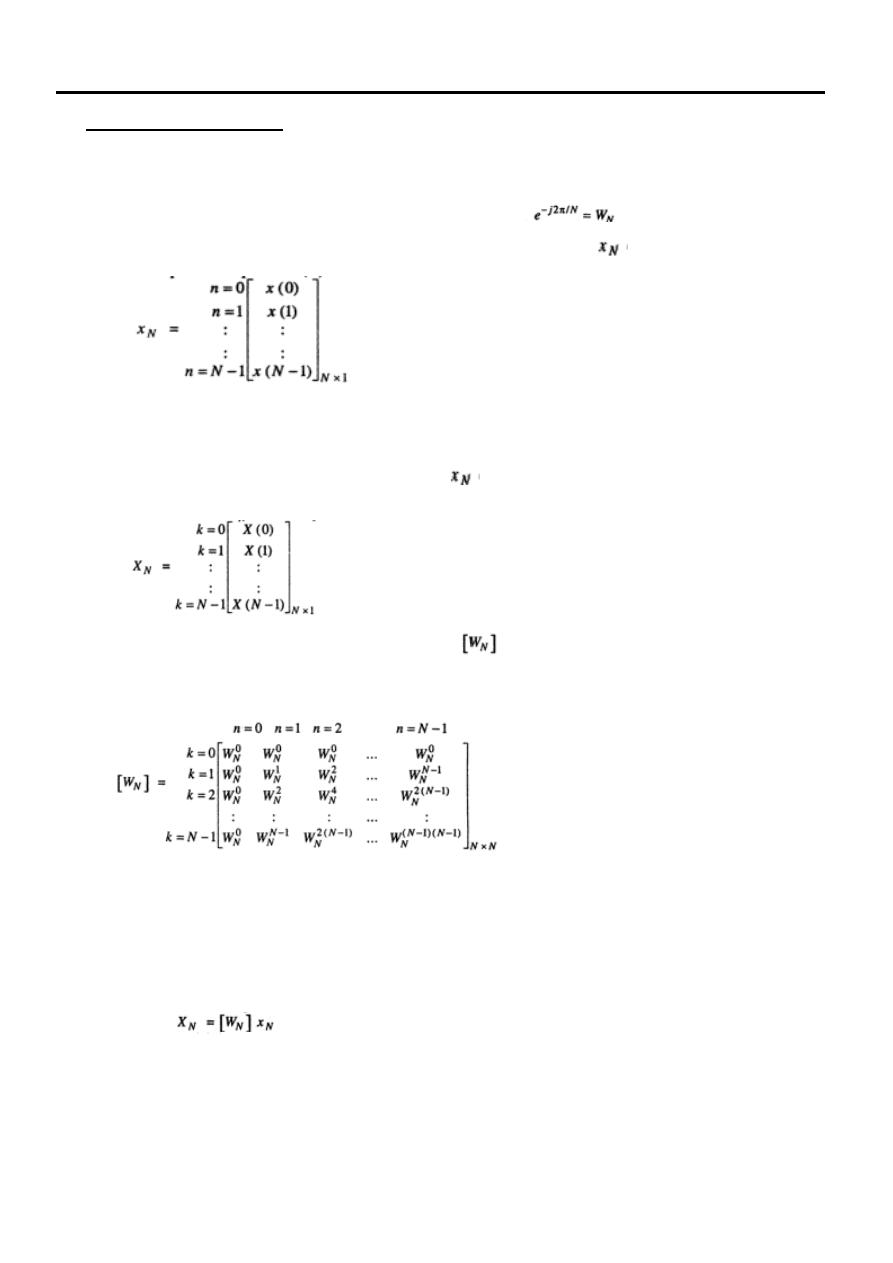
Matrix Multiplication
An alternative representation for computing the DFT is matrix multiplication.
The above DFT and IDFT are obtained by putting
in equation (1)
and equation (2). Let us represents sequence x(n) as
vector of N samples
And X(k) can be represented as a vector
of
N samples
The values of can be represented as a matrix of size N
× N as follows:
…………………. (5)
Here the individual elements are written as with "k" rows and "n" columns. Then N
–
point DFT of equation (3) can be represented as
…………………. (6)
Similarly IDFT of equation (4) can be expressed in matrix form as,
Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
8
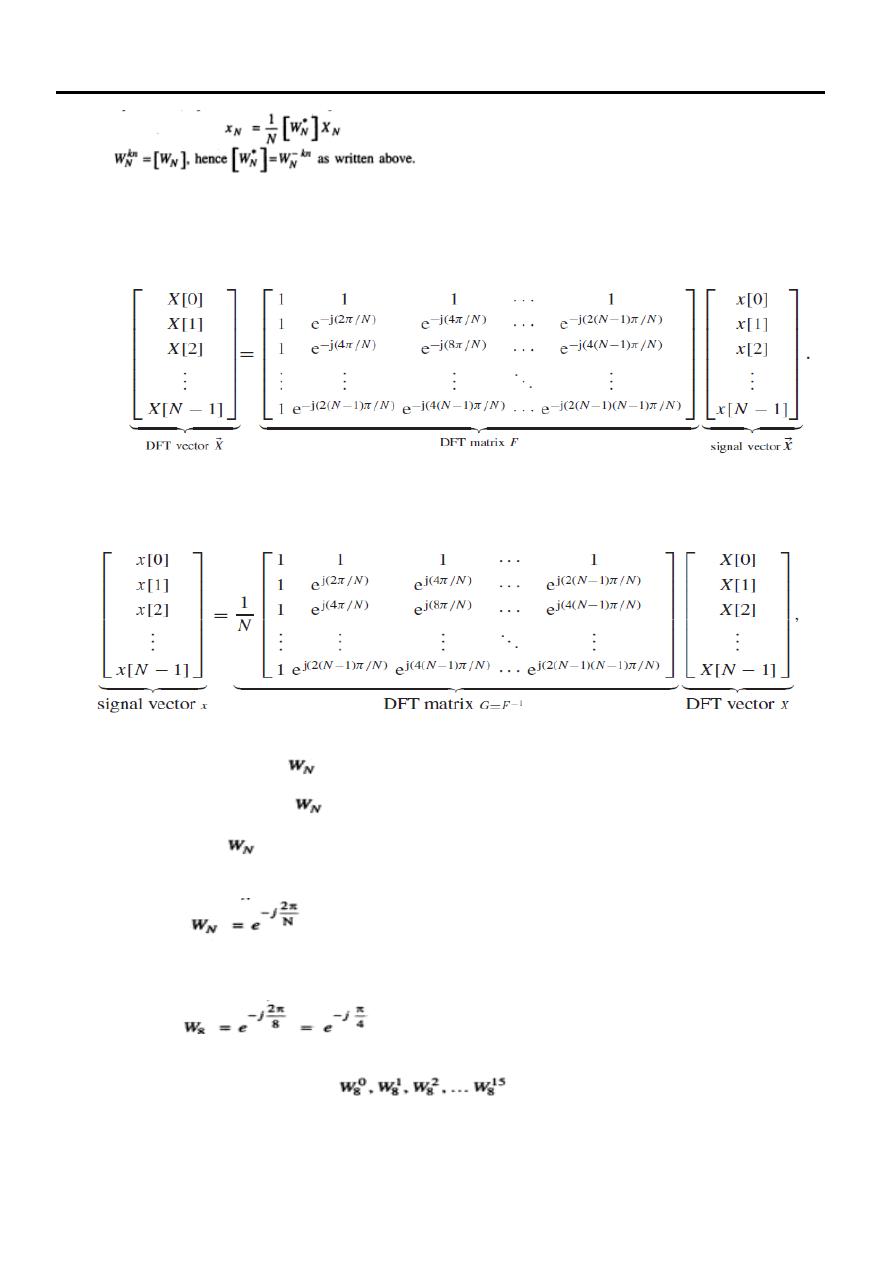
Or in other expression matrix vector format are given by:
Similary, the
expression for IDFT given by:
Periodicity property of
Let us see the values of
for N=8.
We know that
is given as,
With N=8 above equation becomes
Table below shows values of

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
9

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
01
The values of these phasors are observe that,
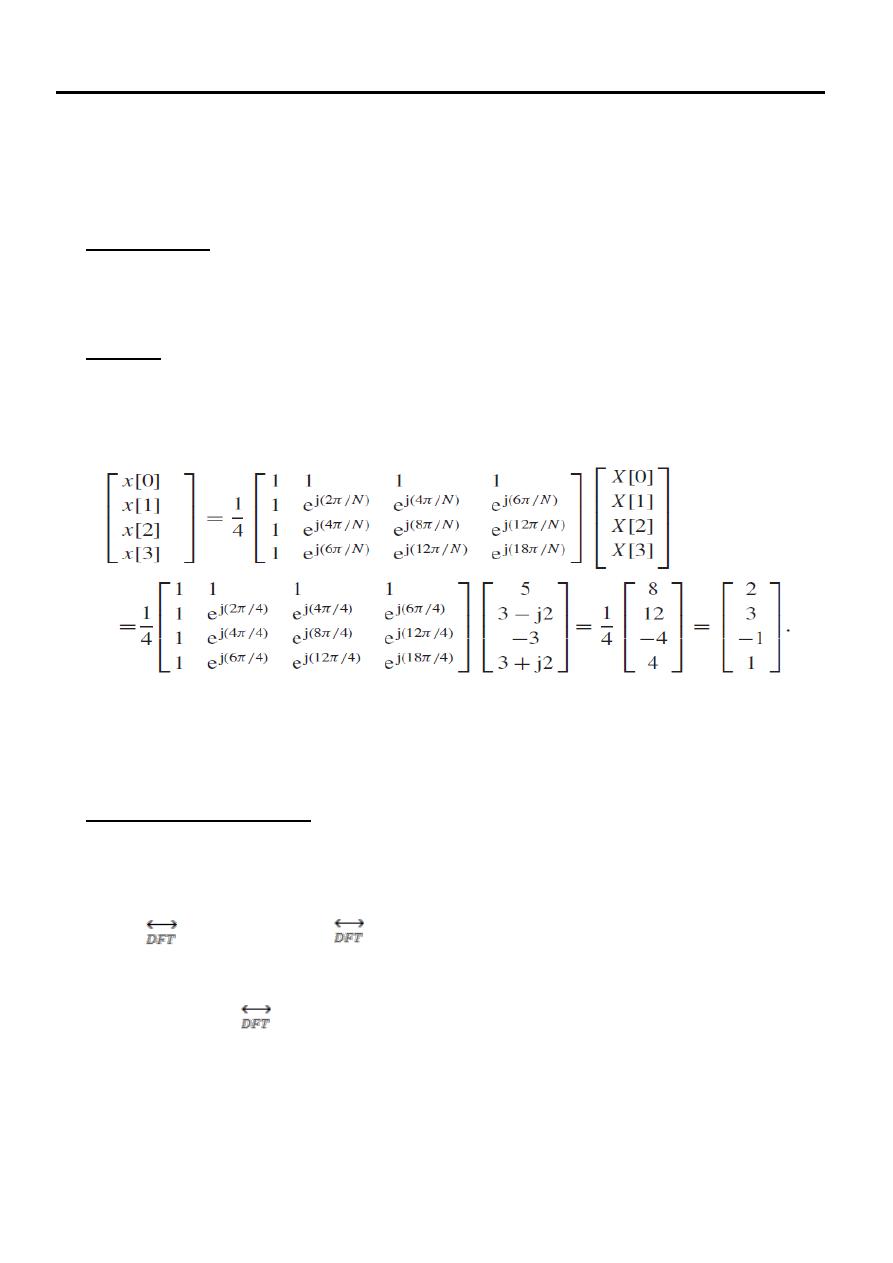
Example Four
Calculate the four-point DFT of the aperiodic signal x[k] considered in Example one.
Solution
Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
00
Example Five
Calculate the inverse DFT of X[r] considered in Example two.
Solution
Arranging the values of the DFT coefficients in the DFT vector X, we obtain
X = [5 3 − j2 −3 3+ j2].
The above values for the DT sequence x[k] are the same as the ones obtained
in Example two.
Properties of the DFT
Linearity
If x1[k] and x2[k] are two DT sequences with the following M-point DFT pairs:
X1[r ] and x2[k]
X2[r ],
x1[k]
then the linearity property states that
a1x1[k] + a2x2[k]
a1X1[r ] + a2X2[r .
for any arbitrary constants a1 and a2.
Time shifting

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
02
If x[k]
X[r ], then
X[r]
x[k−k0]
for an M-point DFT and any arbitrary integer k0.
Circular convolution
If x1[k] and x2[k] are two DT sequences with the following M-point DFT pairs:
x1[k]
X1[r ] and x2[k]
X2[r ],
then
the circular convolution property states that
x1[k] x2[k]
X1[r ]X2[r ] (12.27)
and
x1[k]x2[k]
[X1[r]
X2[r ]],
where
denotes the circular convolution operation. Note that the two sequences
must have the same length in order to compute the circular convolution.
Find the circular convolution between
x[n]=[1,2,3,4]
x[n]=[4,3,2,1]

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
03

Signals & Systems Lecture Eight
Lecturer: Dr.Manal Khadhim.
04
5
