Signals and Systems pdf - م.د منال كاظم عودة

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

Fourier Transform

The Fourier transform is a linear operator that maps a functional space to another

functions space and decomposes a function into another function of its frequency

components.

Like periodic signals, aperiodic signals also can be represented in the frequency

domain. However, unlike the discrete spectrum of the periodic case, we have a

continuous spectrum for the aperiodic case; that is, the frequency components

constituting a given signal x (t ) lie in a continuous range (or ranges), and quite often

this range could be (−∞, ∞) .

The Fourier transform (FT) is a mathematical function that transforms a signal

from the time domain x(t), to the frequency domain, X(f). The time to frequency

domain transformation is given by:

Equivalently, the Inverse Fourier Transform may be used to convert a signal from

the frequency domain to the time domain as follows:

When the Fourier transform is to be expressed in terms of the angular frequency

(rad/sec) rather than the frequency (Hz) the conversion is achieved by letting

dw=2

df ,Therefore Eqs. (1) and (2) when written in terms of ω take the form

…

(

)

…

(

)

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

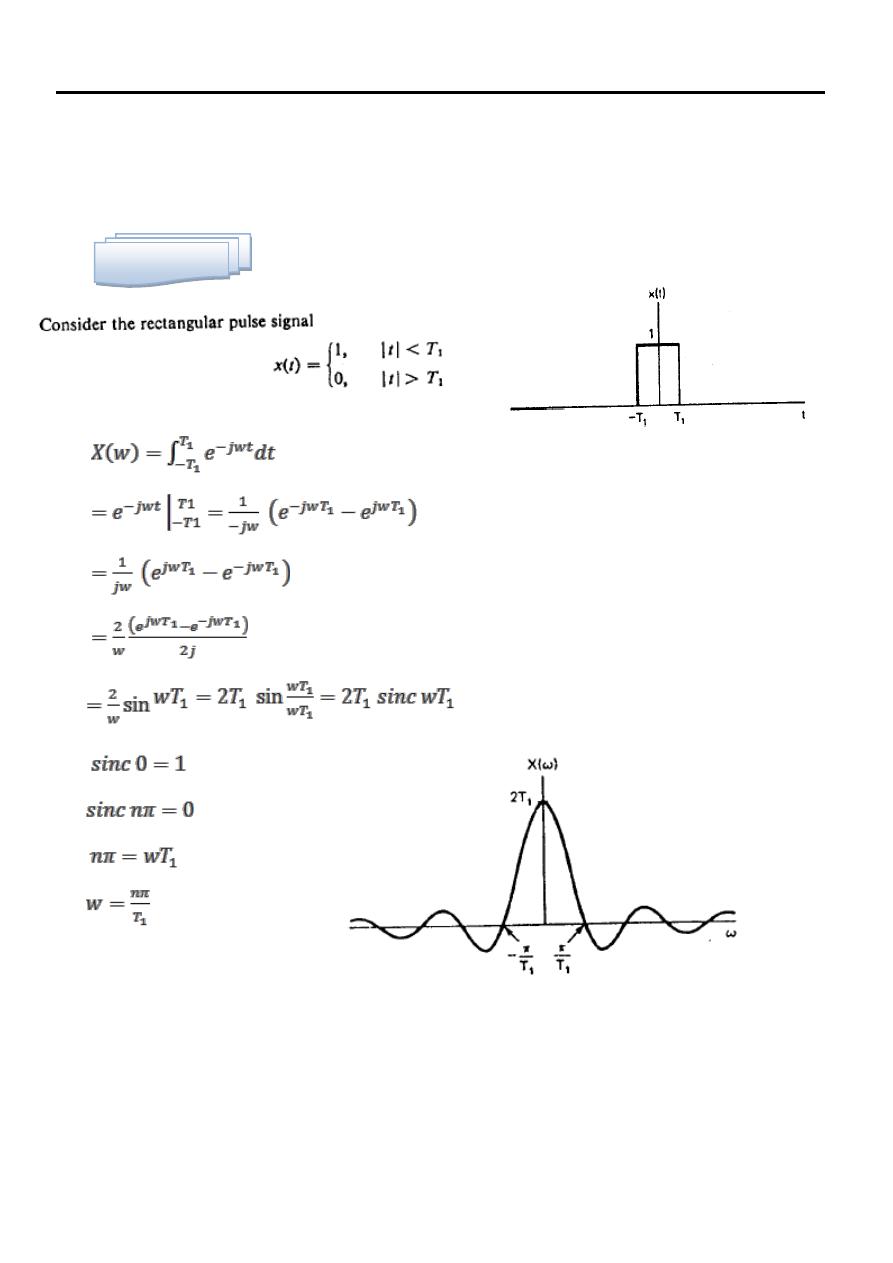
The functions x(t) and X(f) are said to Fourier transform pair, where X(f) is the

Fourier transform of a time function x(t), and x(t) is the Inverse Fourier transform

(IFT) of a frequency-domain function X(f).

Fourier transform for the signal

Example One

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

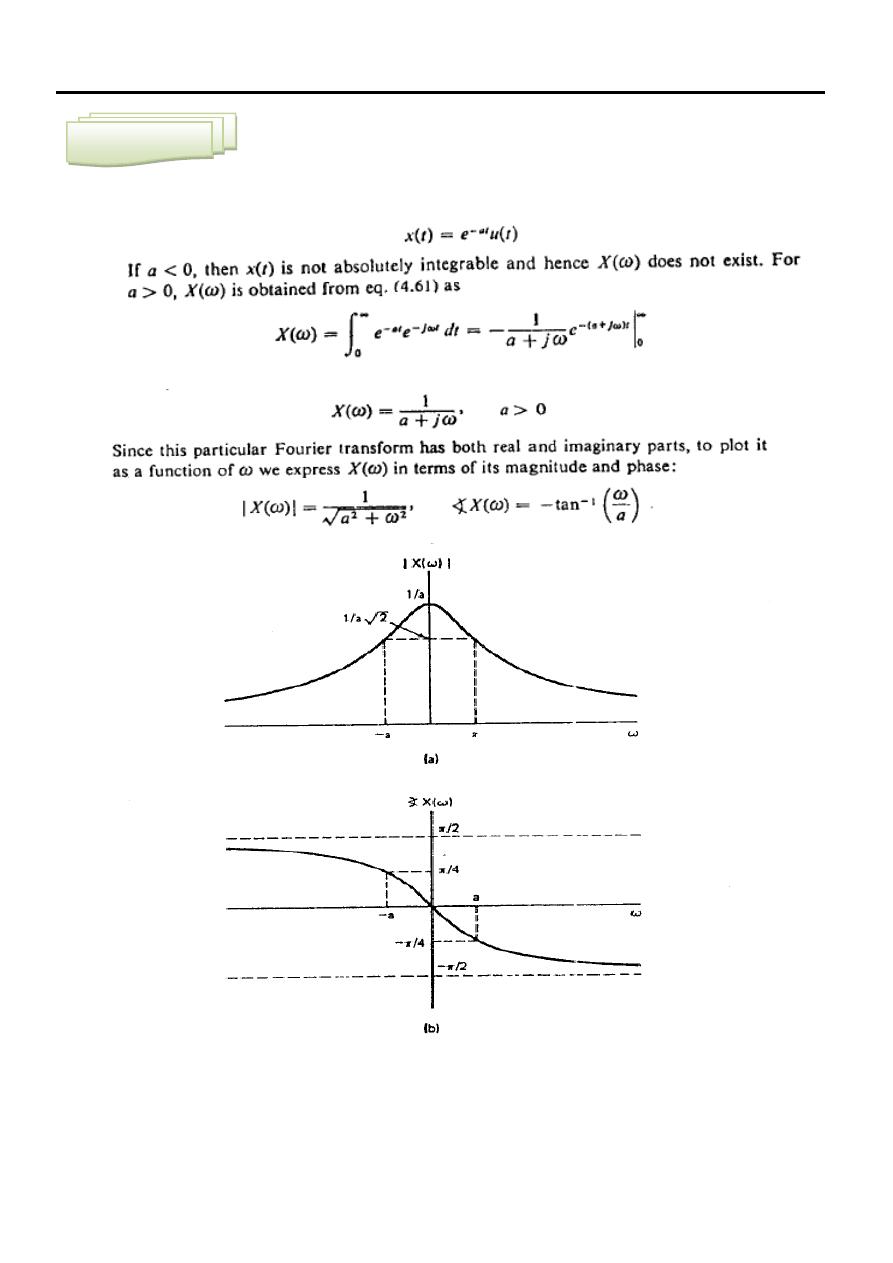
Consider the signal:

Example Two

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

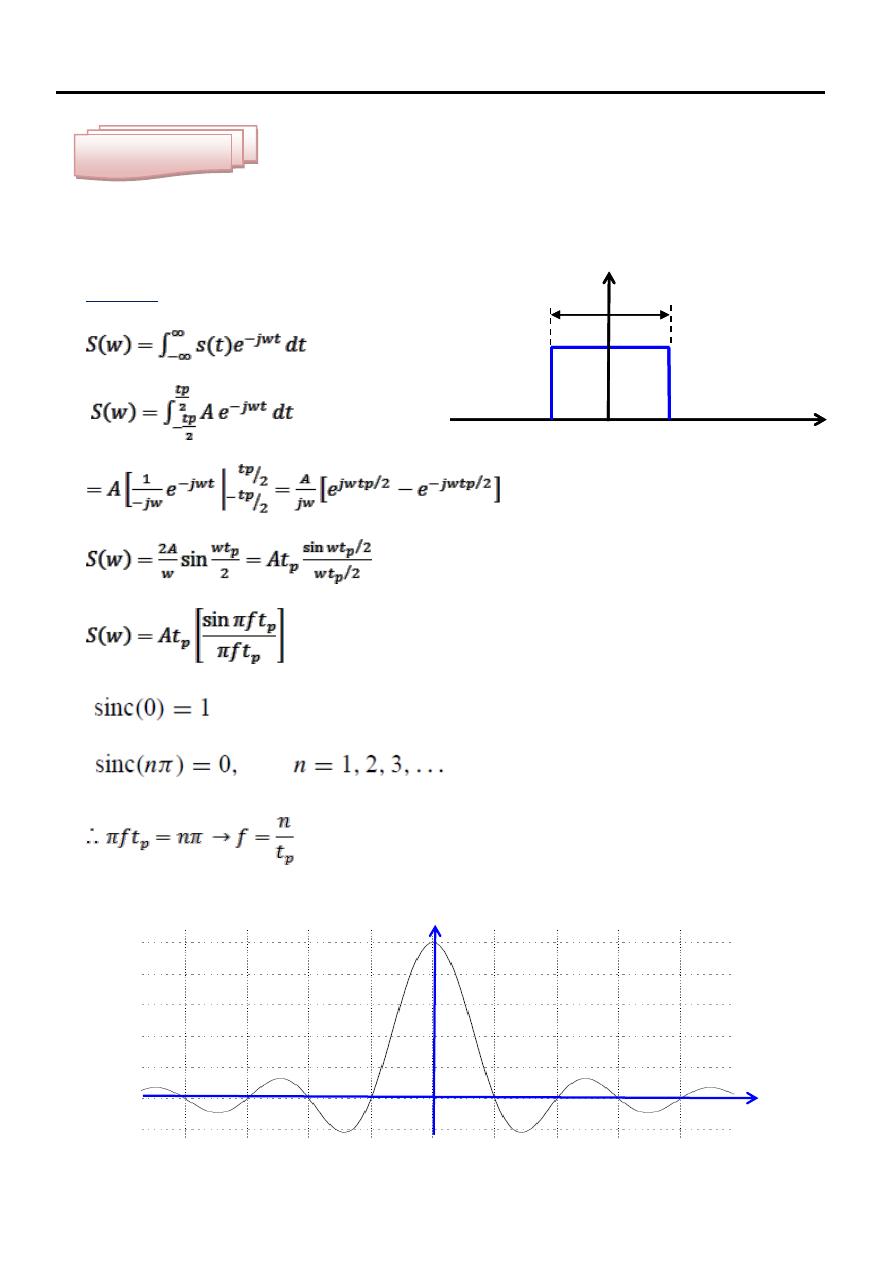
Find the Fourier Transform of S(f) for the signal shown in Figure.

Solution

( this means that Fourier Transform S(f) equal zero at frequencies f= n/tp)

Example Three

(

)

S(t)

(

)

S(t)

(
f
)

S (f)

1/tp

2/tp

-1/tp

A tp

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

Properties of the Continuous Time Fourier Transform

1. Linearity

The F.T. is linear:

2. Scaling Property

Then

3. Time-Shift Property

Then

In other words, a shift in time corresponds to a change in phase in the F.T.

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

4. Frequency-shift Property

This property forms a basis for every radio and TV transmitter in the world. It

simply states that if

Then

But we can

multiply by . Using linearity we get

What we get out is two images in the frequency domain, at positive and

negative frequencies. This is called (amplitude modulation).

5. Convolution Property

Then

(where is convolution) and

6. Time Differentiation

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

7. Time Integration

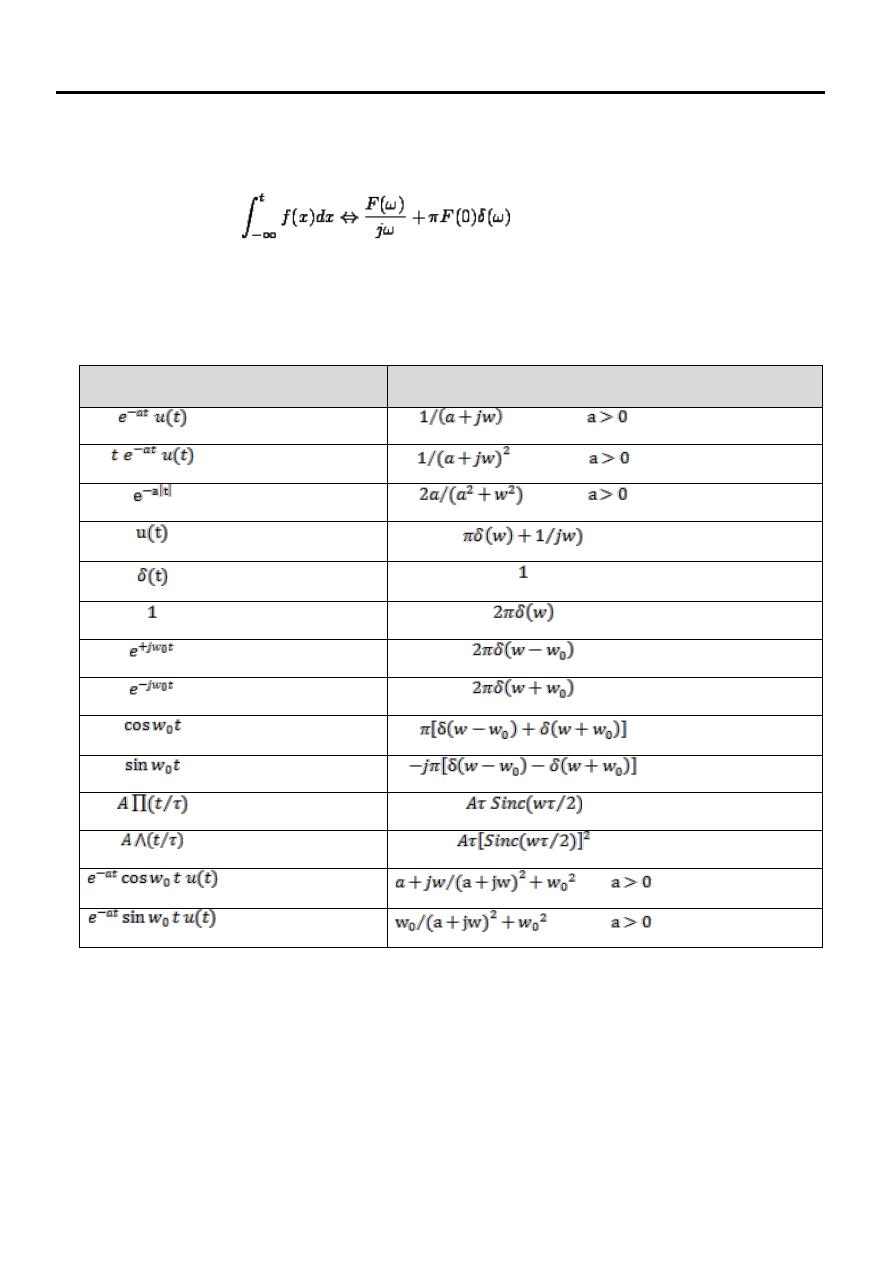
Table (1): some basic Fourier Transform Pairs

F(w)

f(t)

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

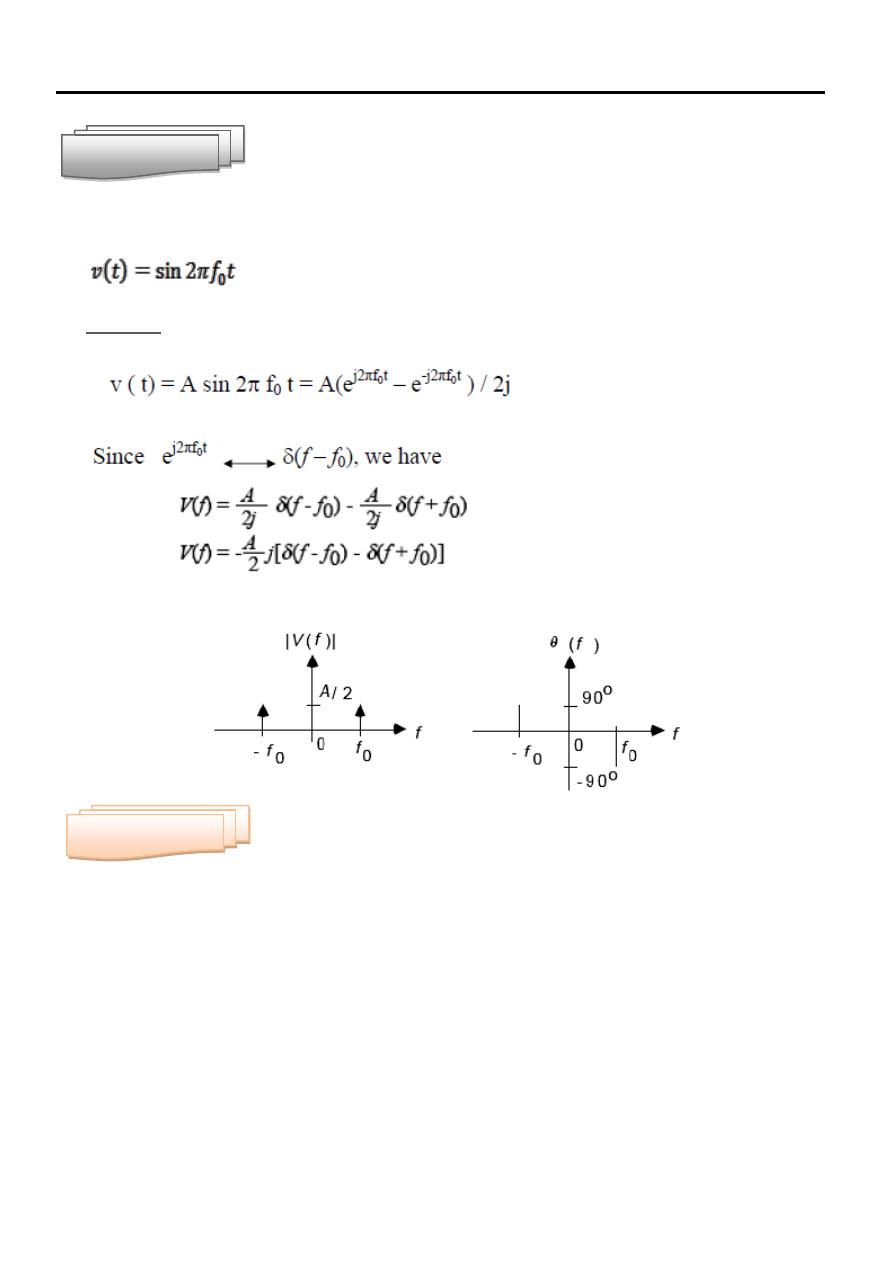
Find the spectrum of sinusoid

Solution

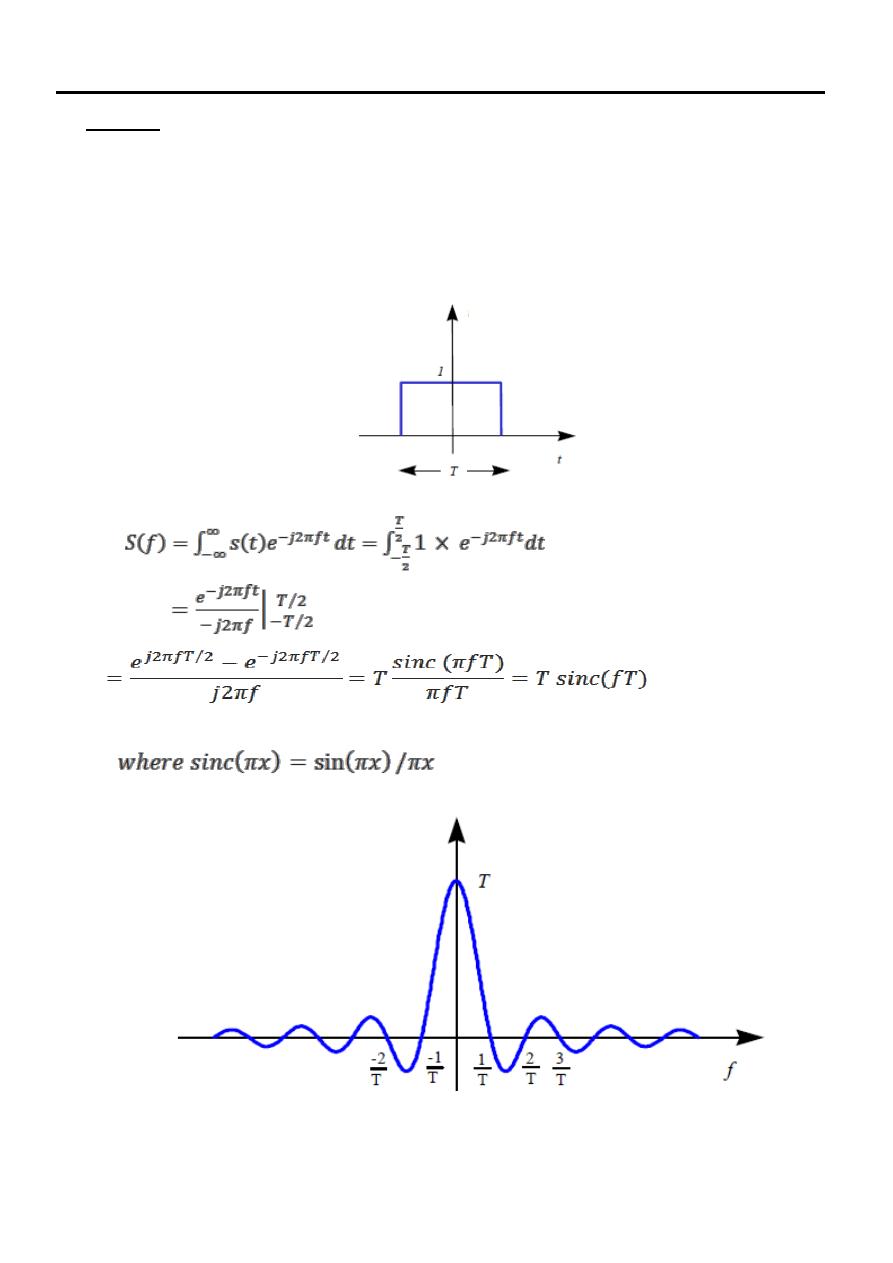
Prove that the Spectrum of a Rectangular Pulse is Sinc Function

Example Four

Example Five

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

Solution

The Fourier transform of a rectangular pulse as shown in Fig. of duration T second

can be obtained as

S(t)

S(f)

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

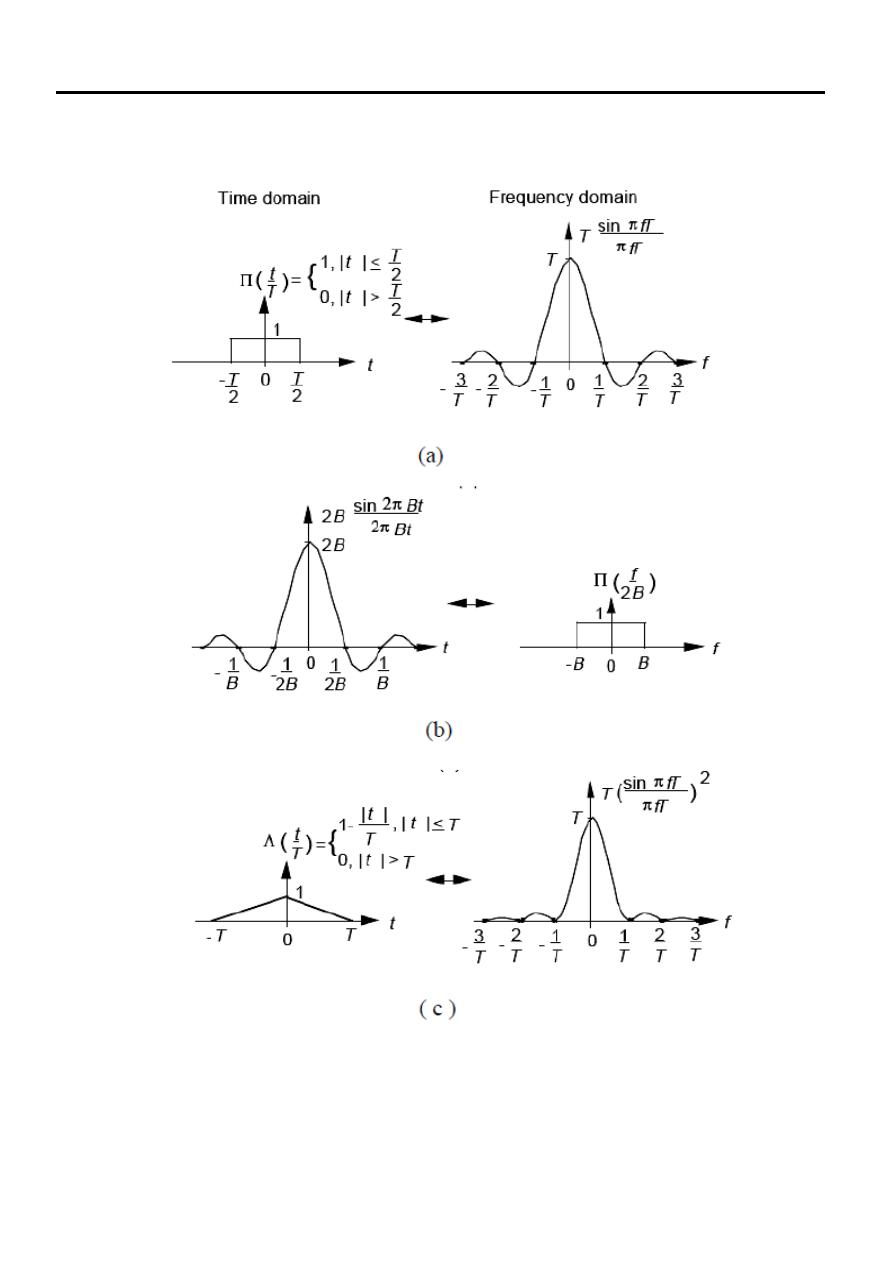
Figures bellow illustrate some basic signals and it´s Fourier Transform:

Figure: (a)Rectangular , (b)sin x/x and (c)Triangular signals

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

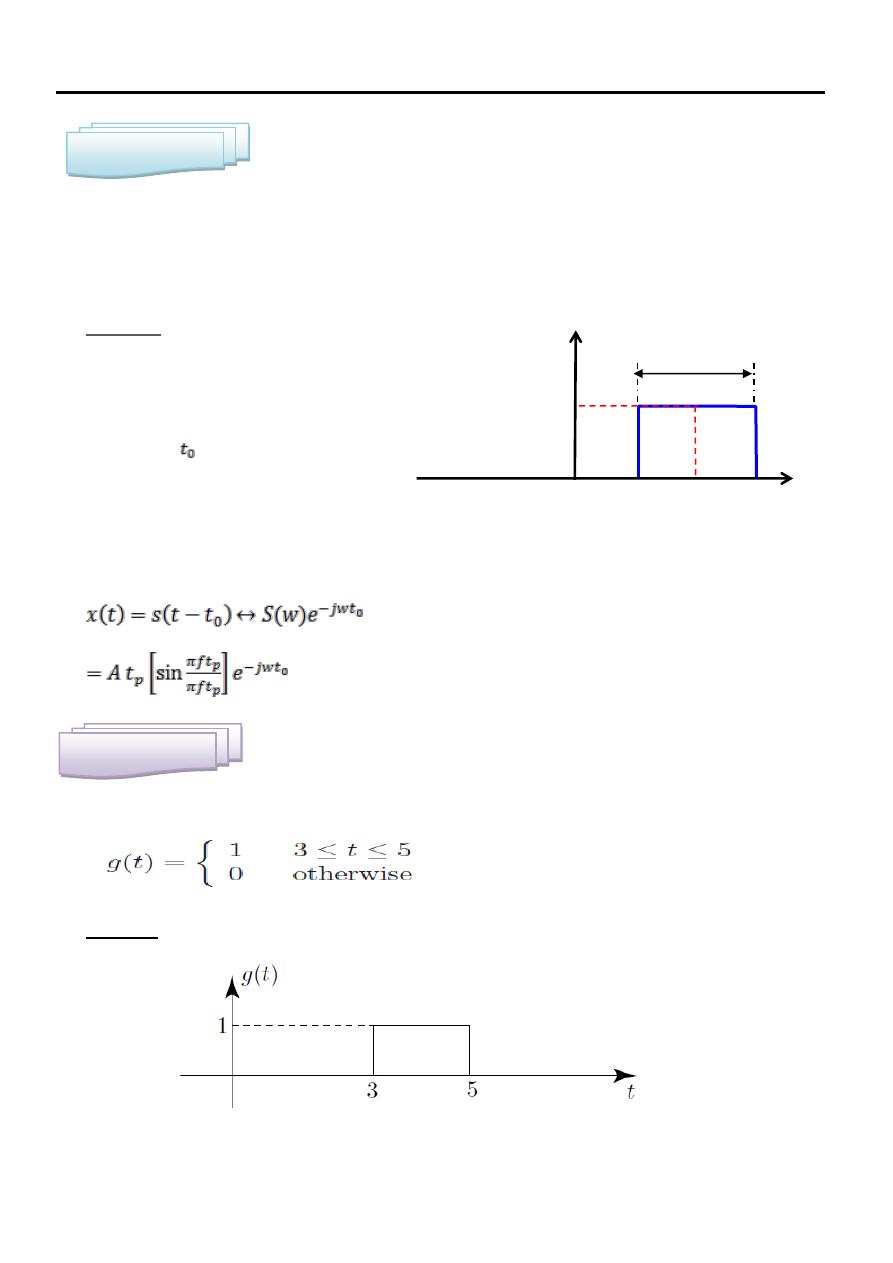
Find the Fourier transform for the signal shown in Fig.

Solution

This signal is the signal of example (3)

shifted by

Using delay property

Use the time-shifting property to find the Fourier Transform of the function

solution

Example Six

X(t)

(

)

X(t)

Example Seven

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

g(t) is a pulse of width 2 and can be obtained by shifting the symmetrical rectangular

pulse by 4 units to the right.

This signal become similar the signal in Example one where Fourier transform equal

By substituting 1 instead of T1 to satisfy the Eq. of

become

Fourier transform

Then t

After this using time-shift property

Hence by putting t0=4 in the time shift theorem

shift property

time

without using

Solution

Signals & Systems Lecture Three

Lecturer: Dr.Manal Khadhim.

Parseval's Relation

If x(t) and X(w) are a Fourier transform pair, then

……………………….……………… (3)

This expression, referred to as Parseval's Relation , follows from direct application of

Fourier transform . specifically ,

Reversing the order of integration gives

But the bracketed term is simply the Fourier transform of x(t); thus,

The quantity on the left side of eq.(3) is the total energy in the signal x(t). Parseval's

Relation, eq.(3), says that this total energy may be determined either by computing

nd integrating over all time, or by computing the

the energy by unit time

. For

integrating over all frequencies

and

energy by unit frequency

density spectrum of the signal.

is often referred to as the energy

this reason