ﻭ
ﺯﺍﺭﺓ ﺍﻟﺘﻌﻠﻴﻡ ﺍﻟﻌﺎﻟﻲ ﻭﺍﻟﺒﺤﺙ ﺍﻟﻌﻠﻤﻲ
ﺍ
ﻟﺠﺎﻤﻌﺔ ﺍﻟﺘﻜﻨﻭﻟﻭﺠﻴﺔ
ﻗ
ﺴﻡ ﻫﻨﺩﺴﺔ ﺍﻟﻤﻜﺎﺌﻥ ﻭﺍﻟﻤﻌﺩﺍﺕ
ﺃ
ﺴﺎﺴﻴﺎﺕ ﺩﺍﻴﻨﻤﻙ ﺍﻟﺤﺭﺍﺭﺓ
ﺒ
ﻭﺤﺩﺍﺕ
(SI)
ﻤ
ﺒﺎﺩﺉ
–
ﺘﻁﺒﻴﻘﺎﺕ
–
ﻤﺴﺎﺌل
(307
)
ﻤﺴﺄﻟﺔ ﻤﺤﻠﻭﻟﺔ ﻭﺃﺠﻭﺒﺔ
(151)
ﻤﺴﺄﻟﺔ
.
ﺘ
ﺄﻟﻴﻑ
ﺍ
ﻟﺪﻛﺘﻮﺭ ﺭﺣﻴﻢ ﺟﻮﻱ ﻣﺤﻲ
ﺃ
ﺴﺘﺎﺫ ﻤﺴﺎﻋﺩ
ﺭ
ﺋﻴﺲ ﻓﺮﻉ ﻫﻨﺪﺳﺔ ﺍﻟﺴﻴﺎ
ﺭ
ﺍﺕ
ﺍ
ﻟﻁﺒﻌﺔ ﺍﻷﻭﻟﻰ
2003

I
ﺑﺴﻢ ﺍﷲ ﺍﻟﺮﺣﻤﻦ ﺍﻟﺮﺣﻴﻢ
)
ﻮﺍﺗﻭﹸﺃ ﻦﻳِﺬﱠﻟﺍﻭ ﻢﹸﻜﻨِﻣ ﻮﺍﻨﻣﺁ ﻦﻳِﺬﱠﻟﺍ ﻪﱠﻠﻟﺍ ِﻊﹶﻓﺮﻳ
ﻴﺮِﺒﺧ ﹶﻥﻮﹸﻠﻤﻌﺗ ﺎﻤِﺑ ﻪﱠﻠﻟﺍﻭ ٍﺕﺎﺟﺭﺩ ﻢﹾﻠِﻌﹾﻟﺍ
(
ﺻﺪﻕ ﺍﷲ ﺍﻟﻌﻈﻴﻢ
)
ﺳﻮﺭﺓ
ﺍﻟﻤﺠﺎﺩﻟﺔ ﺍﻵﻳﺔ
:
11
(

II
ﺒﺴﻡ ﺍﷲ ﺍﻟﺭﺤﻤﻥ ﺍﻟﺭﺤﻴﻡ
ﺍﻟﺤﻤﺩ ﷲ ﺭﺏ ﺍ
ﺩـﻤﺤﻟﺍ،ﻪﻠﻜ ﺭﻤﻻﺍﻭ ﻕﻠﺨﻟﺍ ﻪﻟﻭ،ﻪﻠﻜ لﻀﻔﻟﺍ ﻪﻟﻭ،ﻪﻠﻜ ﺩﻤﺤﻟﺍ ﻪﻟ ﻱﺫﻟﺍ ﷲ ﺩﻤﺤﻟﺍ،ﻥﻴﻤﻟﺎﻌﻟ
ﻡﻟﺎـﻤ ﻥﺎﺴﻨﻻﺍ ﻡﻠﻋ،ﻡﻠﻘﻟﺎﺒ ﻡﻠﻋ ﻱﺫﻟﺍ ﷲ ﺩﻤﺤﻟﺍ، ﻥﻴﻨﻤﺅﻤﻠﻟ ﹰﺍﺭﻭﻨﻭ ﻥﻴﻤﻟﺎﻌﻠﻟ ﺔﻴﺍﺩﻫ،ﻥﻴﺒﻤﻟﺍ ﻪﺒﺎﺘﻜ لﺯﻨﺃ ﻱﺫﻟﺍ ﷲ
ﻭﺼﻼﺓ ﺍﷲ ﻭﺴﻼﻤﻪ ﻋﻠﻰ ﻤﻥ ﻻﺭﺴﻭل ﻤﻥ ﺒﻌﺩﻩ ﻤﺤﻤﺩ ﺒﻥ ﻋﺒﺩ ﺍﷲ،ﻡﻠﻌﻴ
)
ﺹ
(
ﺍﻟﺭﺴﻭل ﺍﻻﻤ
ﻪـﺜﻌﺒ ﻱﺫﻟﺍ ﻥﻴ
ﺍﷲ ﺒﺎﻟﺤﻕ ﻭﻋﻠﻰ ﺁﻟﻪ ﻭﺼﺤﺒﻪ ﻭﻤﻥ ﺴﺎﺭ ﻋﻠﻰ ﻨﻬﺠﻪ
.
ﻓﻘﺩ ﻭﻓﻘﻨﺎ ﻓﻲ ﺇﻨﺠﺎﺯ ﻫﺫﺍ ﺍﻟﻜﺘﺎﺏ ﺍﻟﻤﻭﺴﻭﻡ، ﺩﻌﺒﻭ
"
ﺃﺴﺎﺴﻴﺎﺕ ﺩﺍﻴﻨﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
"
ﺔـﺒﻠﻁ ﺕﺎﺠﺎﺤ ﺔﻴﺒﻠﺘﻟ
ﺔﺴﺩﻨﻬﻟﺍ ﺹﺨﻷﺎﺒﻭ ﺔﻴﺴﺩﻨﻬﻟﺍ ﺔﺴﺍﺭﺩﻟﺍ ﺕﺎﺒﻠﻁﺘﻤﻟ ﺓﺭﺭﻘﻤﻟﺍ ﺞﻬﻨﻤﻟﺍ ﺕﺍﺩﺭﻔﻤ ﻊﻤ ﻰﺸﺎﻤﺘﻴ ﻪﻨﻻ ﺔﺴﺩﻨﻬﻟﺍ ﺕﺎﻴﻠﻜ
ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ
.
ﺇﻥ
ﺍﻟﻤﺼﺎﺩﺭ ﺒﺎﻟﻠﻐﺔ ﺍﻻﻨﻜﻠﻴﺯﻴﺔ ﺍﻟﺘﻲ ﺘﻌﺩ ﻟﻁﻠﺒﺘﻨﺎ ﻟﻐﺔ ﻴﺼﻌﺏ ﺍﺘﻘﺎﻨﻬﺎ ﻤﻥ ﺩﻭﻥ ﻤﻤﺎﺭﺴﺔ ﻭﻟﻔﺘﺭﺓ ﻁﻭﻴﻠﺔ
ﺒﻌ،
ﺽ
، ﻫﺫﻩ ﺍﻟﻤﺼﺎﺩﺭ ﻟﻴﺴﺕ ﻤﺅﻟﻔﺔ ﻟﺘﻨﺎﺴﺏ ﻤﻔﺭﺩﺍﺕ ﺍﻟﻤﻨﺎﻫﺞ ﺍﻟﻤﻘﺭﺭﺓ ﺤﺘﻰ ﻟﻭ ﺘﺭﺠﻤﺕ ﺇﻟﻰ ﺍﻟﻠﻐﺔ ﺍﻟﻌﺭﺒﻴﺔ
ﻟﺫﻟﻙ ﻨﺭﻯ ﻤﻥ ﺍﻟﻀﺭﻭﺭﻱ ﺘﺄﻟﻴﻑ ﻜﺘﺏ ﻤﻨﻬﺠﻴﺔ ﺘﺘﻨﺎﺴﺏ ﻤﻊ ﺍﻟﻤﻔﺭﺩﺍﺕ ﻟﺯﻴﺎﺩﺓ ﻗﺎﺒﻠﻴﺔ ﺍﺴﺘﻴﻌﺎﺏ
ﺍﻟﻁﻠﺒﺔ ﻟﻠﻤﺎﺩﺓ
ﻤﻊ ﺒﻘﺎﺀ ﺍﻟﻜﺘﺏ ﺍﻻﺠﻨﺒﻴﺔ ﻤﺼﺎﺩﺭ ﻤﺴﺎﻋﺩﺓ، ﻙﻟﺫﻟ ﺏﻭﻠﻁﻤﻟﺍ ﺩﻬﺠﻟﺍﻭ ﺕﻗﻭﻟﺍ ﺭﺎﺼﺘﺨﺍﻭ ﺔﻴﻤﻠﻌﻟﺍ
.
ﺎـﻨﺘﺒﻠﻁﻟ ﺀﻲـﻬﻴﻟﻭ ﺔـﺒﻴﺒﺤﻟﺍ ﺎﻨﺘﻐﻠﺒ ﺔﻴﺴﺩﻨﻬﻟﺍ ﻡﻭﻠﻌﻟﺍ لﻘﻨ ﺔﻜﺭﺤ ﻲﻓ ﻡﻬﺴﻴﻟ ﺏﺎﺘﻜﻟﺍ ﺍﺫﻫ ﺀﺎﺠ ﺎﻨﻫ ﻥﻤ
ﺍﻻﻋﺯﺍﺀ ﻤﺎﺩﺓ ﻏﺯﻴﺭﺓ ﺴﻬﻠﺔ ﺍﻟﻘﺭﺍﺀﺓ ﻭﺍﻟﻔﻬﻡ ﻋﻥ ﺃﺴﺎﺴﻴﺎﺕ ﻋﻠﻡ ﺩﺍﻴﻨﻤ
ـﻲ ﻋـﻓ ﺓﺭﺍﺭـﺤﻟﺍ ﻙﻴ
ﺴﻁـﺒﻤ ٍِﺽﺭ
ﻭﻭﺍﻀﺢ
.
ﻴﺘﻀﻤﻥ ﺍﻟﻜﺘﺎﺏ
)
10
(
ﻓﺼﻭل ﺒﺤﺴﺏ ﺍﻟﻤﻨﻬﺞ ﺍﻟﻤﻘﺭﺭ
ﻭﺘﺸﻤل ﺍﻟﻤﻭﺍﻀﻴﻊ ﺍﻟﺘﺎﻟﻴﺔ
:
ﺎﻨﻭﻥـﻘﻟﺍ ، ﺕﺍﺯﺎـﻐﻟﺍ ﺹﺍﻭﺨ ، ﺔﻗﺎﻁﻟﺍ ،ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ ﻁﻐﻀﻟﺍ، ﺔﻴﺴﺎﺴﻷﺍ ﻑﻴﺭﺎﻌﺘﻟﺍﻭ ﺕﺍﺩﺤﻭﻟﺍ
ﺍﻻﻭل
ﻟﺩﺍﻴﻨﻤﻴﻙ
ﺩﺭـﻘﻟﺍ ﺕﺍﺭﻭﺩ ، ﺓﺭﺍﺭـﺤﻟﺍ ﻙﻴﻤﻨﻴﺍﺩـﻟ ﻲﻨﺎـﺜﻟﺍ ﻥﻭﻨﺎﻘﻟﺍ ، ﺔﺤﻭﺘﻔﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ، ﺓﺭﺍﺭﺤﻟﺍ
ﺓ
ﺍﻻﻨﺘﺭﻭﺒﻲ ﻭﺍﻟﺨ،
ﻼ
ﺌﻁ ﺍﻟﻐﺎﺯﻴﺔ
ﺇﻥ ﻫﺫﻩ ﺍﻟﻔﺼﻭل ﺩﻋﻤﺕ،
ـﺒ
)
307
(
ﺩﺍﺕـﺤﻭﺒﻭ ﺔـﻟﻭﻠﺤﻤ ﺔﻟﺄﺴـﻤ
(S1)
،
ﻟﺘﻭﻀﻴﺢ ﺍﻟﻤﻭﺍﻀﻴﻊ ﺍﻟﻨﻅﺭﻴﺔ ﻭﻜﻴﻔﻴﺔ ﺍﺴﺘﻌﻤﺎل
)
257
(
ﻰـﻠﻋ ﹰﺎﻴﻨﻫﺫ ﺏﻟﺎﻁﻟﺍ ﺱﺭﻤﺘﻴ ﻲﻜﻟ ، ﺔﻴﻀﺎﻴﺭ ﺔﻟﺩﺎﻌﻤ
ﻜﻤﺎ ﻴﺤﺘﻭﻱ ﻋﻠﻰ ﺍﺠﻭﺒﺔ،لﺌﺎﺴﻤﻟﺍ ﻩﺫﻫ لﺤ ﺔﻴﻔﻴﻜ
)
151
(
ﻤﺴﺄﻟﺔ ﻭﺭﺩﺕ ﻓﻲ ﺍﻤﺘﺤﺎﻨﺎﺕ ﺍﻟﺴﻨﻭﺍﺕ ﺍﻟﻤ
ﻴﺔـﻀﺎ
ﻥﻭـﻜﺘ ﻲﻜ ﻪﺴﻔﻨﺒ ﺏﻟﺎﻁﻟﺍ ﺎﻬﻠﺤﻴ ﻥﺍ ﻥﺴﺤﺘﺴﻴ ﺓﺭﺭﻘﻤﻟﺍ ﻴﺔﺠﻬﻨﻤﻟﺍ ﻊﻴﻀﺍﻭﻤﻟﺎﺒ ﺔﻘﻠﻌﺘﻤﻟﺍ ﺔﻓﺎﻜ ﺏﻨﺍﻭﺠﻟﺍ ﻲﻁﻐﺘﻟ
ﻋﻭﻨﺎﹰ ﻟﻪ ﻓﻲ ﺘﻌﺭﻑ ﻁﺒﻴﻌﺔ ﻫﺫﻩ ﺍﻟﻤﻭﺍﻀﻴﻊ ﻭﻓﻬﻤﻬﺎ ﻤﻥ ﺨﻼل ﺍﻟﻤﻤﺎﺭﺴﺔ ﻭﺍﻟﺘﺩﺭﻴﺏ
.
ﻭﺃﻭﺩ ﻫﻨﺎ ﺍﻥ ﺍﺘﻘﺩﻡ ﺒﺠﺯﻴل ﺸﻜﺭﻱ ﻭﺘﻘﺩﻴﺭﻱ ﻭﺍ
ﻤﺘ
ﻨﺎﻨﻲ ﻟﻜل ﻤﻥ
ﺃﺒﺩﻯ ﻤﻼﺤﻅﺎﺘﻪ ﻋﻠﻰ
ﺎﺏـﺘﻜﻟﺍ ﺍﺫـﻫ
ﻭﺃﺨﺹ ﺒﺎ
ﻟﺫﻜﺭ ﺍﻻﺴﺎﺘﺫﺓ ﺍﻻﺠﻼﺀ
:
1
. ﺃ
.ﺩ
.
ﺔـﺴﺩﻨﻬﻟﺍ ﺔـﻴﻠﻜ،ﺔﻴﻜﻴﻨﺎﻜﻴﻤﻟﺍ ﺔـﺴﺩﻨﻬﻟﺍ ﻡﺴﻗ ﺱﻴﺌﺭ ، ﻲﺒﻭﺭﺩﻟﺍ ﻲﻠﻋ لﻴﻋﺎﻤﺴﺍ ﺭﺫﻨﻤ ﺱﺩﻨﻬﻤ
–
ﺠﺎﻤﻌﺔ ﺒﻐﺩﺍﺩ
–
ﻤﻘﻴﻡ ﻋﻠﻤﻲ
.
2
. ﺍ
ﻟ
ﻌﻤﻴﺩ ﺃ
.ﻡ
.ﺩ
.
ﻴﻡـﻘﻤ ،ﺔﻴﺭﻜﺴـﻌﻟﺍ ﺔﺴﺩﻨﻬﻟﺍ ﺔﻴﻠﻜ ﺩﻴﻤﻋ ﻥﻭﺎﻌﻤ ،ﻲﻟﺎﺸﺨﻟﺍ ﻱﺩﻬﻤ لﻴﻤﺠ ﺔﺒﻴﺘﻗ ﺱﺩﻨﻬﻤ
ﻋﻠﻤﻲ
.

III
3
.
.ﺃ
.ﻡ
.ﺩ
ﺭ، ﻱﺩﻴﺒﻌﻟﺍ ﻡﻴﻫﺍﺭﺒﺍ ﻲﻫﺎﻨ
ﺌﻴﺱ ﻗﺴﻡ ﺍﻟﻠﻐﺔ ﺍﻟﻌﺭﺒﻴﺔ ﻓﻲ ﻜﻠﻴﺔ ﺍﻟﺘﺭﺒﻴﺔ
-
ﺔـﻌﻤﺎﺠ، ﺩﺸﺭ ﻥﺒﺍ
ﺒﻐﺩﺍﺩ
–
ﻤﻘﻴﻡ ﻟﻐﻭﻱ
.
ﻜﺎﻨﺕ
ﻟﻤﻼﺤﻅﺎﺕ
ﺎﺏـﺘﻜﻟﺍ ﺀﺎﻨﻏﺇ ﻲﻓ ﹰﺍﺭﻴﺒﻜ ﹰﺍﺭﺜﺃ لﻀﺎﻓﻷﺍ ﺓﺫﺘﺎﺴﻻﺍ
ﻭ
ﺭـﺨﻔﺒﻭ ﺕـﺒﺜﺍ ﻥﺃ ﺎـﻨﻫ ﺩﻭﺃ
ﻭﺍﻋﺘﺯﺍﺯ ﻜﺒﻴﺭ ﺒﻌﺽ ﻤﻼﺤﻅﺎﺘﻬﻡ ﺤﻭل ﺍﻟﻜﺘﺎﺏ
:
1
.
ﺘﻡ ﺍﻟﻌﺭﺽ ﺒﺄﺴﻠﻭﺏ ﺠﻴﺩ
.
2
.
ﺍﻟﻤﺼﺎﺩﺭ ﺍﻟﻌﻠﻤﻴﺔ ﻜﺎﻓﻴﺔ
.
3
.
ﺍﻟﻜﺘﺎﺏ ﺠﻴ
ﺨﺎﺼﺔ ﻭﺍﻨﻪ ﻤﻜﺘﻭﺏ ﺒﻠﻐ، ﺱﻴﺭﺩﺘﻠﻟ ﺢﻠﺼﻴ ، ﺩ
ﺔـﻠﺜﻤﺍ ﻱﻭـﺤﻴﻭ ، ﺔـﻤﻭﻬﻔﻤ ﺔﺴﻠﺴ ﺔ
ﻋﺩﻴ
ﺩ
ﺓ ﺠﺩﺍﹰ
ﻤ
ﻤﺎ ﻴﺠﻌﻠﻪ ﺫﺍ ﻓﺎﺌﺩﺓ ﻜﺒﻴﺭﺓ
.
4
.
ﺍﻥ ﺍﻟﻜﺘﺎﺏ ﻴﺼﻠﺢ ﻜﻜﺘﺎﺏ ﻤﻨﻬﺠﻲ ﺸﺭﻁ ﺍﺠﺭﺍﺀ ﺍﻟﺘﺼﺤﻴﺤﺎﺕ ﺍﻟﻤﻘﺘﺭﺤﺔ
∗
ﺫﻫﺎـﺨﺄﻴ ﻥﺃ ﺩﻭﺃ ﻲﺘﻟﺍ
ﻭﻟﻭ ﺘﻡ ﺫﻟﻙ ﻓﺈﻥ ﺍﻟﻜﺘﺎﺏ ﻴﺼﺒﺢ ﻜﺘﺎﺒﺎﹰ ﻗﻴﻤﺎﹰ ﻓﻌﻼﹰ ﺼﺎﻟﺤﺎﹰ، ﺭﺎﺒﺘﻋﻻﺍ ﺭﻅﻨﺒ ﻑﻟﺅﻤﻟﺍ
ﻜﻜﺘﺎﺏ ﻤﻘﺭﺭ
.
5
.
ﺠﺯﺍ ﺍﷲ ﺍﻟﻤﺅﻟﻑ ﻜل ﺨﻴﺭ ﻭﺴﺩﺩ ﺨﻁﺎﻩ ﻟﺨﺩﻤﺔ ﺍﻟﻌﻠﻡ ﻭﻤﺭﻴﺩﻴﻪ
.
ﺔـﻨﺭﺘﻘﻤﻟﺍ ﺕﺍﺩـﻌﻤﻟﺍﻭ ﻥﺌﺎـﻜﻤﻟﺍ ﺔﻴﺴﺩﻨﻫ ﻡﺴﻗ ﺱﻠﺠﻤ ﺔﻴﺼﻭﺘ ﻰﻠﻋ ﺀﺎﻨﺒ ﺏﺎﺘﻜﻟﺍ ﺍﺫﻫ ﻑﻴﻟﺄﺘ ﺀﺎﺠ ﺩﻘﻟ
ﺒﻤﺼﺎﺩﻗﺔ ﺍﻟﺴﻴﺩ ﺭﺌﻴﺱ ﺍﻟﺠﺎﻤﻌﺔ ﺒﻜﺘﺎﺒﻪ ﺍﻟﻤﺭﻗﻡ
18
ﻤﻙـﻫ
/
3
/
239
ﻓﻲ
20
/
4
/
1999
.
ﺎﺯﻩـﺠﻨﺇ ﺩﻌﺒﻭ
ﻭﺘﻘﻴﻴﻤﻪ ﺍﻹﻴﺠﺎﺒﻲ
ﺤﺼﻠﺕ ﻤﻭﺍﻓﻘﺔ ﻭﺯﺍﺭﺓ ﺍﻟﺜﻘﺎﻓﺔ ﻭﺍﻻﻋﻼﻡ،
/
ﺍﻟﺭﻗﺎﺒﺔ
/
ﺭﻗﻡـﺒ ﻪـﻌﺒﻁ ﻰـﻠﻋ ، ﺕﺍﺩﻭﺴﻤﻟﺍ
ﺍﻹﺠﺎﺯﺓ
847
ﺍﻟﻨﺎﻓﺫﺓ ﺒﺘﺎﺭﻴﺦ
11
/
10
/
2000
.
ﺔـﺒﻠﻁﻟﺍ ﻰﻠﻋ ﻉﺯﻭﺘﺴ ﻲﺘﻟﺍ ﺔﻴﺠﻬﻨﻤﻟﺍ ﺏﺘﻜﻟﺍ ﻥﻤﻀ ﺭﺒﺘﻋﺍﻭ
ﺤﺴﺏ ﻤﺫﻜﺭﺓ
ﺭﺌﻴﺱ
ﻗﺴﻡ ﻫﻨﺩﺴﺔ ﺍﻟﻤﻜﺎﺌﻥ ﻭﺍﻟﻤﻌﺩﺍﺕ ﺍﻟﻤﻭﺠﻬﺔ ﺇﻟﻰ ﺍﻟﻠﺠﻨﺔ ﺍﻟﺠﺎﻤﻌﻴﺔ ﻟﻠﺸﺅﻭﻥ ﺍﻟﻌﻠﻤﻴﺔ ﺒﺘﺎﺭﻴﺦ
16
/
10
/
2000
.
ﻭﺘﻘﺭﺭ ﺍﻋﺘﻤﺎﺩﻩ ﻜﺘﺎﺒﺎﹰ
"
ﻤﻨﻬﺠﻴﺎﹰ
"
ﺔـﻨﺠﻠﻟﺍ ﺔﻴﺼﻭﺘ ﻰﻠﻋ ﺀﺎﻨﺒ ﺓﺭﺍﺭﺤﻟﺍ ﻙﻴﻤﺎﻨﻴﺩ ﻉﻭﻀﻭﻤﻟ
ﺍﻟﺠﺎﻤﻌﻴﺔ ﻟﻠﺸﺅﻭﻥ ﺍﻟﻌﻠﻤﻴﺔ ﻭﺍﻻﻤﺭ ﺍﻟﺠﺎﻤﻌﻲ ﺍﻟﻤﺭﻗﻡ ﺕ ﻡ
/
609
ﻓﻲ
30
/
10
/
2000
.
ﻭﻨﺭﺤﺏ ﺒﺄﻱ ﻨﻘﺩ ﺒﻨﺎﺀ ﺃﻭ ﻤﻘﺘﺭﺡ ﺍﻭ ﻤﻼﺤﻅﺔ ﺘﺴﻬﻡ ﻓﻲ ﺇﻏﻨﺎﺀ ﻫﺫﺍ، ﺓﻭﻔﻫ لﻜ ﻥﻋ ﺭﺫﺘﻌﻨ ﻡﺎﺘﺨﻟﺍ ﻲﻓﻭ
ﺍﻟﻜﺘﺎﺏ ﺍﻟ
ﺫﻱ ﺃﻤل ﺍﻥ ﻴﻌﻭﺩ ﺒﻔﺎﺌﺩﺓ ﻜﺒﻴﺭﺓ ﻋﻠﻰ ﺍﻟﻁﺎﻟﺏ ﻋﻨﺩ ﺩﺭﺍﺴﺘﻪ ﻟﻠﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻬﻨﺩﺴﻴﺔ
.
ﻭﺍﷲ ﻭﻟﻲ ﺍﻟﺘﻭﻓﻴﻕ، ﻥﻴﻤﻟﺎﻌﻟﺍ ﺏﺭ ﷲ ﺩﻤﺤﻟﺍ ﻥﺃ ﺎﻨﺍﻭﻋﺩ ﺭﺨﺁﻭ
.
.ﺃ
.ﻡ
ﺩ
.
ﺭﺤﻴﻡ ﺠﻭﻱ ﻤﺤﻲ
ﺭﺌﻴﺱ ﻓﺭﻉ ﻫﻨﺩﺴﺔ ﺍﻟﺴﻴﺎﺭﺍﺕ
ﻗﺴﻡ ﻫﻨﺩﺴﺔ ﺍﻟﻤﻜﺎﺌﻥ ﻭﺍﻟﻤﻌﺩﺍﺕ
ﺍﻟﺠﺎﻤﻌ
ﺔ ﺍﻟﺘﻜﻨﻭﻟﻭﺠﻴﺔ
ﺃﻴﻠﻭل
-
2003
∗
ﻭﺒﻌﺩ ﺍﺠﺭﺍﺀ ﺍﻟﺘﺼﺤﻴﺤﺎﺕ ﺍﻟﻤﻘﺘﺭﺤﺔ ﺃﻀﻴﻔ
ﺕ
ﺍﻟﻤﻼﺤﻅﺔ ﺍﻟﺘﺎﻟﻴ
ﺔ
:
ﻭﻻﻤﺎﻨﻊ ﻤﻥ ﺍﻋﺘﻤﺎﺩﻩ، ﺓﺭﺍﺭﺤﻟﺍ ﻙﻴﻤﺎﻨﻴﺩ ﺞﻬﻨﻤ ﺕﺎﺒﻠﻁﺘﻤﻟ ﻲﻓﺍﻭ ﺏﺎﺘﻜﻟﺍ ﺭﺒﺘﻌﻴ
.

IV
ﺍﻟﻤﺤﺘﻭﻴﺎﺕ
ﺍﻟﻤﻭﻀﻭﻉ
ﺍﻟﺼﻔﺤﺔ
ﺍﻟﻤﻘﺩﻤﺔ
................................
................................
.............................
II
ﻤﻘﺩﻤﺔ ﺍﻟﻰ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
................................
................................
.........
X
ﺍﻟﺭﻤﻭﺯ ﻭﺍﻟﻭﺤﺩﺍﺕ ﺍﻟﻤﺴﺘﺨﺩﻤﺔ
................................
................................
.......
XI
1
.
ﺍﻟﻔﺼل ﺍﻷﻭل
ﺍﻟﻭﺤﺩﺍﺕ ﻭﺍﻟﺘﻌﺎﺭﻴﻑ
)
1
-
25
(
1.1
-
ﺍﻻﺒﻌﺎﺩ ﻭﺍﻟﻭﺤﺩﺍﺕ ﻭﺍﻟﺭﻤﻭﺯ
................................
................................
...
1
1.2
-
ﺍﻟﻨﻅﺎﻡ ﺍﻟﻌﺎﻟﻤﻲ ﻟﻠﻭﺤﺩﺍﺕ
................................
................................
......
1
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
9
1.3
-
ﺘﻌﺎﺭﻴﻑ ﻭﻤﻔﺎﻫﻴﻡ ﺃﺴﺎﺴﻴﺔ
................................
................................
.....
10
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
18
1.4
-
ﺍﻟﺘﺤﻠﻴل ﺍﻟﺒﺼﺭﻱ ﻭﺍﻟﺘﺤﻠﻴل ﺍﻟﻤﺠﻬﺭﻱ
................................
..........................
20
1.5
-
ﺍﻟﺨﻭﺍﺹ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ
................................
................................
.....
21
1.5.1
-
ﺍﻟﺨﻭﺍﺹ ﺍﻟﻤﺴﺘﻘﻠﺔ ﻭﻏﻴﺭ ﺍﻟﻤﺴﺘﻘﻠﺔ
................................
..........................
21
1.5.2
-
ﺍﻟﺨﻭﺍﺹ ﺍﻟﻤﺭﻜﺯﺓ ﻭﺍﻟﺸﺎﻤﻠﺔ
................................
................................
21
1.6
-
ﻤﺨﻁﻁ ﺍﻟﺤﺎﻟﺔ
................................
................................
................
22
1.7
-
ﺩﺍﻟﺔ ﺍﻟﺤﺎﻟﺔ ﻭﺩﺍﻟﺔ ﺍﻟﻤﺴﺎﺭ
................................
................................
.....
23
1.8
-
ﺍﻟﺘﻭﺍﺯﻥ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ
................................
................................
......
23
1.9
-
ﺍﻟﻌﻤﻠﻴﺔ ﻭﺍﻻﺠﺭﺍﺀ
................................
................................
.............
25
2
.
ﺍﻟﻔﺼل ﺍﻟﺜﺎﻨﻲ
ﺍﻟﻀﻐﻁ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
)
26
-
44
(
2.1
-
ﺍﻟﻤﻔﻬﻭﻡ ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﻟﻠﻀﻐﻁ
................................
................................
...
26
2.2
-
ﺍﻟﻀﻐﻁ ﺍﻟﺫﻱ ﻴﺴﺒﺒﻪ ﻋﻤﻕ ﺍﻟﻤﺎﺌﻊ
................................
..............................
27
2.3
-
ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
................................
................................
..............
27
2.4
-
ﻤﻘﻴﺎﺱ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ ﻭﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ
................................
...........................
28
2.5
-
ﺍﻟﻤﺎﻨﻭ
ﻤﻴﺘﺭ
................................
................................
...................
30
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
32
2.6
-
ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ ﺍﻟﻤﺎﺌل
................................
................................
.............
33
2.7
-
ﻤﻘﻴﺎﺱ ﺒﻭﺭﺩﻥ
................................
................................
...............
33
2.8
-
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
................................
................................
...............
34

V
2.8.1
-
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺘﻭﺍﺯﻥ ﺍﻟﺤﺭﺍﺭﻱ
................................
...............
35
2.8.2
-
ﻤﻘﺎﻴﻴﺱ ﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ
................................
................................
...
35
ﺍﻤﺜﻠﺔ ﻭﻤﺴﺎﺌل ﻤﺤﻠﻭﻟﺔ
................................
................................
...............
39
ﺍﻟﻔﺼل ﺍﻟﺜﺎﻟﺙ
ﺍﻟﻁﺎﻗﺔ
)
45
-
71
(
3.1
-
ﺍﻟﻁﺎﻗﺔ
................................
................................
.......................
45
3.2
-
ﻤﺼﺎﺩﺭ ﻭﺍﺸﻜﺎل ﺍﻟﻁﺎﻗﺔ
................................
................................
......
45
3.2.1
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﺨﺯﻭﻨﺔ
................................
................................
...........
46
3.2.2
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﻨ
ﺘ
ﻘﻠﺔ
ﺍ
ﻭﺍﻟﻌﺎﺒﺭﺓ
................................
................................
...
49
3.3
-
ﺤﻔﻅ ﺍﻟﻁﺎﻗﺔ
................................
................................
..................
49
3.4
-
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ
................................
................................
.............
52
3.4.1
–
ﺨﻠﻔﻴﺔ ﺘﺄﺭﻴﺨﻴﺔ
................................
................................
............
52
3.4.2
-
ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل
................................
...............................
53
3.4.3
-
ﺍﺸﺎﺭﺓ ﻭﻭﺤﺩﺍﺕ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل
................................
...........................
54
3.5
-
ﺍ
ﺸﻜﺎل ﺍﻟﺸﻐل
................................
................................
................
57
3.5.1
-
ﺍﻟﺸﻐل ﺍﻟﺩﻴﻨﺎﻤﻴﻜﻲ
................................
................................
..........
57
3.5.2
-
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
................................
................................
............
58
3.5.3
-
ﺍﻟﺸﻐل ﺍﻟﺼﺎﻓﻲ
................................
................................
............
59
3.5.4
-
ﺍﻟﻘﺩﺭﺓ ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ
................................
................................
..........
61
3.5.5
-
ﺍﺸﻜﺎل ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ
................................
................................
...
61
3.6
-
ﺍﻟﻤﻔﻬﻭﻡ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ ﻟﻠﺤﺭﺍﺭﺓ
................................
..............................
63
3.7
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ
................................
................................
.............
64
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ ﻭﻤﺴﺎﺌل
................................
................................
...............
67
4
.
ﺍﻟﻔﺼل ﺍﻟﺭﺍﺒﻊ
ﺎﺯﺍﺕــــﻐﻟﺍ ﺹﺍﻭﺨ
)
72
-
84
(
4.1
-
ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﺤﻘﻴﻘﻴﺔ ﻭﺍﻟﻤﺜﺎﻟﻴﺔ
................................
................................
....
72
4.2
-
ﻗﺎﻨﻭﻥ ﺒﻭﻴل
................................
................................
..................
74
4.3
-
ﻗﺎﻨﻭﻥ ﺸﺎﺭل ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ
................................
.........................
75
4.4
-
ﺍﻟﻤﺤﺭﺍﺭ ﺍﻭ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻐﺎﺯﻱ ﺫﻭ ﺍﻟﻀﻐﻁ ﺍﻭ ﺍﻟﺤﺠﻡ ﺍﻟﺜﺎﺒﺕ
................................
......
77
4.5
-
ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ
................................
................................
.
78
4.6
-
ﺍﻻﻨﺜﺎﻟ
ﺒ
ﻲ
................................
................................
.....................
80

VI
4.7
-
ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺍﻟﺤﺭﺍﺭﺘﻴﻥ ﺍﻟﻨﻭﻋﻴﺘﻴﻥ
................................
.............................
81
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
82
5
.
ﺍﻟﻔﺼل ﺍﻟﺨﺎﻤﺱ
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻟﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
)
85
-
159
(
5.1
-
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻟﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
................................
..............................
85
5.2
-
ﺘﺠﺭﺒﺔ ﺠﻭل
................................
................................
.................
85
5.3
-
ﺼﻴﻎ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
................................
................................
..........
86
5.4
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ
................................
................................
................
88
5.5
-
ﺍﻟﻌﻤﻠﻴﺎﺕ ﺸﺒﻪ
ﺍﻟﺴﺎﻜﻨﺔ
................................
................................
........
89
5.6
-
ﻨﺘﺎﺌﺞ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
................................
................................
..........
90
5.7
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺍﻭ ﻗﺎﻨﻭﻥ ﺠﻭل
................................
................................
91
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
92
5.8
-
ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﻼﺠﺭ
ﻨﺎﻴ
ﻴﺔ
)
ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ
(
................................
.....................
98
5.9
-
ﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻋﻠﻰ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ
................................
..................
99
5.9.1
-
ﻋﻤﻠﻴﺔ ﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
................................
................................
.......
99
5.9.2
-
ﻋﻤﻠﻴﺔ ﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
................................
................................
.......
100
5.9.3
-
ﻋﻤﻠﻴﺔ ﺜﺒﻭﺕ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
................................
................................
101
5.9.4
-
ﺍﻟﻌﻤﻠﻴﺔ ﺍﻻﺩﻴﺎﺒﺎﺘﻴﺔ
................................
................................
..........
101
5.9.5
-
ﺍﻟﻌﻤﻠﻴﺔ ﺍﻟﺒﻭﻟﺘﺭﻭ
ﺒ
ﻴﺔ
................................
................................
.........
106
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
111
6
.
ﺍﻟﻔﺼل ﺍﻟﺴﺎﺩﺱ
ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
)
160
-
216
(
6.1
-
ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
................................
................................
............
160
6.2
-
ﺍﻟﺸﻐل ﺍﻟﺼﺎﻓﻲ
................................
................................
...............
160
6.2.1
-
ﺸﻐل ﻋﻤﻭﺩ ﺍﻻﺩﺍﺭﺓ
................................
................................
........
161
6.2.2
-
ﺸﻐل ﺃﻭ ﻁﺎﻗﺔ ﺍﻟﺠﺭﻴﺎﻥ
................................
................................
.....
161
6.3
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
................................
..........................
163
6.4
-
ﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻋﻠﻰ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
................................
................
165
6.4.1
-
ﺍﻟﻤﺭﺠل ﻭﺍﻟﻤﻜﺜﻔﺎﺕ ﺍﻟﺒﺨﺎﺭﻴﺔ
................................
...............................
165
6.4.2
-
ﺍﻟﻀﺎﻏﻁ ﻭﺍﻟﺘﻭﺭﺒﻴﻥ
................................
................................
........
167
6.4.3
-
ﺘﺴﻠﺴل ﺍﻟﻌﻤﻠﻴﺎﺕ ﻓﻲ ﺍﻟﻀﺎﻏﻁ ﻭﺍﻟﺘﻭﺭﺒﻴﻥ
................................
....................
168

VII
6.4.4
-
ﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ ﺍﻟﻐﺎﺯﻴﺔ
................................
................................
........
172
6.4.5
-
ﺍﻟﻤﻨﻔﺙ
)
ﺍﻟﺒﻭﻕ
(
ﻭﺍﻟﻨﺎﺸﺭ
)
ﺍﻟﻤﺒ
ﺩﺩ
(
................................
...........................
173
6.4.6
-
ﻤﺤﺭﻙ ﺍﻟﻁﺎﺌﺭﺓ ﺍﻟﺩﻓﻌﻲ
)
ﺍﻟﻨﻔﺎﺙ
(
................................
............................
175
6.4.7
-
ﻤﻌﺎﺩﻟﺔ ﺍﻻﺴﺘﻤﺭﺍﺭﻴﺔ
................................
................................
........
179
6.4.8
-
ﺍﻨﻭﺍﻉ ﺍﺨﺭﻯ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
................................
.........................
179
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
185
7
.
ﺍﻟﻔﺼل ﺍﻟﺴﺎﺒﻊ
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺜﺎﻨﻲ ﻟﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
)
217
-
239
(
7.1
-
ﺍﻻﺤﺘﻜﺎﻙ
................................
................................
....................
217
2.7
-
ﺍﻻﻨﻌﻜﺎﺴﻴﺔ ﺍﻭ ﺍﻻﺠﺭﺍﺀ ﺍﻻﻨﻌﻜﺎﺴﻲ
................................
..............................
218
7.3
-
ﺍﻻﺠﺭﺍﺀ ﺍﻻ
ﻨﻌﻜﺎﺴﻲ
................................
................................
..........
219
7.4
-
ﺍﻨﻭﺍﻉ ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﻼﺍﻨﻌﻜﺎﺴﻴﺔ
................................
................................
221
7.5
-
ﺍﻟﻤﺤﺭﻙ ﺍﻟﺤﺭﺍﺭ
ﻱ
................................
................................
...........
222
7.6
-
ﻜﻔﺎﺀﺓ ﻨﻅﺎﻡ ﺘﺤﻭﻴل ﺍﻟﻁﺎﻗﺔ ﺍﻭ ﻜﻔﺎﺀﺓ ﺍﻟﻤﺤﺭﻙ ﺍﻟﺤﺭﺍﺭﻴﺔ
................................
.........
224
7.7
-
ﺍﻟﻤﺤﺭﻙ ﺍﻟﺤﺭﺍﺭﻱ ﺍﻟﻤﻌﻜﻭﺱ
)
ﺍﻟﻤﻀﺨﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ
(
................................
.............
225
7.8
-
ﻤﻌﺎﻤل ﺍﻷﺩﺍﺀ
................................
................................
................
226
7.9
-
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺜﺎﻨﻲ ﻟﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
................................
..............................
227
7.10
-
ﺼﻴﻎ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺜﺎﻨﻲ
................................
................................
........
229
7.11
-
ﺘﻜﺎﻓﺅ
)
ﺘﻤﺎﺜل
(
ﻨﺼﻲ ﻜﻠﻔﻥ ﺒﻼﻨﻙ ﻭﻜﻠ
ﻭ
ﺯﻴﻭﺱ
................................
................
230
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ ﻭﻤﺴﺎﺌل
................................
................................
...............
232
8
.
ﺍﻟﻔﺼل ﺍﻟﺜﺎﻤﻥ
ﺩﻭﺭﺍﺕ ﺍﻟﻘﺩﺭﺓ
)
240
-
276
(
8.1
-
ﺩﻭﺭﺓ ﺍﻟﻐﺎﺯ
ﺍﻟﻤﺜﺎﻟﻲ
................................
................................
...........
240
8.2
-
ﻤﺒﺎﺩﺉ ﻜﺎﺭﻨﻭ
................................
................................
................
240
8.3
-
ﺩﻭﺭﺓ ﻜﺎﺭﻨﻭ
................................
................................
.................
242
8.4
-
ﺍﻟﻜﻔﺎﺀﺓ ﺍﻟﺤﺭﺍﺭﻴﺔ
................................
................................
.............
243
8.5
-
ﺩﻭﺭﺓ ﻜﺎﺭﻨﻭ ﺍﻟﻤﻌﻜﻭﺴﺔ
................................
................................
.......
245
8.6
-
ﺩﻭﺭﺓ ﻜﺎﺭﻨﻭ ﻭﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﻁﻠﻕ ﻟﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
................................
................
246
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
247

VIII
9
.
ﺍﻟﻔﺼل ﺍﻟﺘﺎﺴﻊ
ﺍﻻﻨﺘﺭﻭﺒﻲ
)
277
-
324
(
9.1
-
ﺍﻻﻨﺘﺭﻭﺒﻲ
................................
................................
...................
277
9.2
-
ﻤﺨﻁﻁ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
–
ﺍﻻﻨﺘﺭﻭﺒﻲ
(T-S)
................................
..................
277
9.3
-
ﺍﻻﻨﺘﺭﻭﺒﻲ ﺩﺍﻟﺔ ﺍﻟﺤﺎﻟﺔ
................................
................................
........
280
9.4
-
ﻤﺘﺒﺎﻴﻨﺔ ﻜﻠﻭﺯﻴﻭﺱ
................................
................................
.............
281
9.5
-
ﺘﻐﻴﺭ ﺍﻻﻨﺘﺭﻭﺒﻲ ﻓﻲ ﺍﻟﻌﻤﻠﻴﺔ ﺍﻻﺩﻴﺎﺒﺎﺘﻴﺔ ﻭﺍﻻﻨﺜﺭﻭﻤﻠﻴﺔ ﺍﻻﻨﻌﻜﺎﺴﻴﺔ
ﻭﺍﻟﻼﺍﻨﻌﻜﺎﺴﻴﺔ
...................
283
9.6
-
ﺍﻟﻜﻔﺎﺀﺓ ﺍﻻﻴﺯﻨﺘﺭﻭﺒﻴ
ﺔ
................................
................................
..........
284
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
287
9.7
-
ﺘﻐﻴﺭ ﺍ
ﻻﻨﺘﺭﻭ
ﺒﻲ ﻓﻲ ﺍﻟﻌﻤﻠﻴﺎﺕ ﺍﻻﻨﻌﻜﺎﺴﻴﺔ
................................
......................
294
9.8
-
ﺩﻭﺭﺓ ﻜﺎﺭﻨﻭ ﻋﻠﻰ ﻤﺨﻁﻁ
(T-S)
................................
.............................
299
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ ﻭﻤﺴﺎﺌل
................................
................................
...............
300
10
.
ﺍﻟﻔﺼل ﺍﻟﻌﺎﺸﺭ
ﺔــــﻴﺯﺎﻐﻟﺍ ﻁــﺌﻼﺨﻟﺍ
)
325
-
370
(
10.1
-
ﺍﻟﻌﻨﺎﺼﺭ ﻭﺍﻟﻤﺭﻜﺒﺎﺕ ﻭﺍﻟﺨﻼﺌﻁ
................................
..............................
325
10.2
-
ﺍﻟﺫﺭﺓ ﻭﺍﻟﻜﺘﻠﺔ ﺍﻟﺫﺭﻴﺔ ﺍﻟﻨﺴﺒﻴﺔ
)
ﺍﻟﻭﺯﻥ ﺍﻟﺫﺭﻱ
(
................................
.................
325
10.3
ﺍﻟﻜﺘﻠﺔ ﺍﻟﺠ
ﺯﻴﺌﻴﺔ ﻭﺍﻟﻜﺘﻠﺔ ﺍﻟﺠﺯﻴﺌﻴﺔ ﺍﻟﻨﺴﺒﻴﺔ
)
ﺍﻟﻭﺯﻥ ﺍﻟﺠﺯﻴﺌﻲ
(
................................
....
325
10.4
-
ﺍﻟﺠﺯﻱﺀ ﺍﻟﻐﺭﺍﻤﻲ ﺍﻭ ﺍﻟﻤﻭل
................................
................................
.
326
10.5
-
ﻓﺭﻀﻴﺔ ﻭﻋﺩﺩ ﺍﻓﻭﻜﺎﺩﺭﻭ
................................
................................
....
327
10.6
-
ﺍﻟﺨﻼﺌﻁ ﺍﻟﻐﺎﺯﻴﺔ
................................
................................
............
327
10.7
-
ﺨﻭﺍﺹ ﺍﻟﺨﻼﺌﻁ ﺍﻟﻐﺎﺯﻴ
ﺔ
................................
................................
....
328
10.8
-
ﻀﻐﻁ ﺍﻟﺨﻠﻴﻁ ﻭﺍﻟﻀﻐﻭﻁ ﺍﻟﺠﺯﻴﺌﻴﺔ
................................
...........................
328
10.9
-
ﺍﻟﺠﺯﻱﺀ ﺍﻟﻐﺭﺍﻤﻲ ﺍﻭ
)
ﺍﻟﻤﻭﻟﻲ
(
ﻟﻠﺨﻠﻴﻁ
................................
.......................
329
10.10
-
ﺍﻟﺤﺠﻡ ﺍﻟﻤﻭﻟﻲ ﻭﺜﺎﺒﺕ ﺍﻟﻐﺎﺯ ﺍﻟﻌﺎﻡ
................................
...........................
330
10.11
-
ﺍﻟﻨﺴﺒﺔ ﺍﻟﺠﺯﻴﺌﻴﺔ ﺍﻟﻐﺭﺍﻤﻴﺔ
)
ﺍﻟﻨﺴﺒﺔ ﺍﻟﻤﻭﻟﻴﺔ
(
................................
..................
331
10.12
-
ﻤﻌﺩل ﺍﻟﻜﺘﻠﺔ ﺍﻟﺠﺯﻴﺌﻴﺔ ﺍﻟﻨﺴﺒﻴﺔ
)
ﺍﻟﻜﺘﻠﺔ ﺍﻟﻤﻭﻟﻴﺔ
(
ﻟﻠﺨﻠﻴﻁ
................................
........
333
10.13
-
ﺍﻟﺘﺤﻠﻴل ﺍﻟﺤﺠﻤﻲ ﻭﺍﻟﻭﺯﻨﻲ
................................
................................
.
333
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
................................
................................
.......................
334
10.14
-
، ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﻭﺍﻻﻨﺘﺭﻭﺒﻲ ﻟﻠﺨﻠﻴﻁ،ﻲﻟﺎﺜﻨﻻﺍ
...............................
335
10.15
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺍﻟﺠﺯﻴﺌﻴﺔ ﺍﻟﻐﺭﺍﻤﻴﺔ
)
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺍﻟﻤﻭﻟﻴﺔ
(
..............................
336

IX
10.16
-
ﻤﻌﺩل ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺍﻟﺠﺯﻴﺌﻴﺔ ﺍﻟﻐﺭﺍﻤﻴﺔ ﻟﻠﺨﻠﻴﻁ ﺍﻟﻐﺎﺯﻱ
................................
...
337
10.17
-
ﺘﻐﻴﺭ ﺍﻻﻨﺘﺭﻭﺒﻲ ﻨﺘﻴﺠﺔ ﺨﻠﻁ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﻤﺜﺎﻟﻴﺔ
................................
...............
338
10.18
-
ﺨﻼﺌﻁ
ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﻤﺜﺎﻟﻴﺔ ﺫﺍﺕ ﺩﺭﺠﺎﺕ ﺤﺭﺍﺭﺓ ﻭﻀﻐﻭﻁ ﻤﺨﺘﻠﻔﺔ
..............................
339
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ ﻭﻤﺴﺎﺌل
................................
................................
...............
340
ﺍﻟﻤﺭﺍﺠﻊ
................................
................................
............................
371

X
ﻤﻘﺩﻤﺔ ﺇﻟﻰ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
Introduction to Thermodynamics
ﻤﻊ ﺒﺩﺍﻴﺎﺕ ﺍﻟﻘﺭﻥ ﺍﻟﺘﺎﺴﻊ ﻋﺸﺭ ﻅﻬﺭ
ﻋﻠﻡ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺨﺭﺍﺭﺓ
)
ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻜﺱ
(
ﺭـﺜﻟﺍ
ﺸﻤلـﻴ ﻱﺫـﻟﺍ
ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
ﺍﻟﻌﺎﻡ
، ﺍﻭ ﺍﻟﻔﻴﺯﻴﺎﺌﻲ
ﺍﻟﻜﻴﻤﻴﺎﺌﻲ
،
ﺜﻡ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻬﻨﺩﺴﻲ ﺍﻟﺫﻱ ﻴﻬﻤﻨﺎ ﻓﻲ، ﻲﺌﺎﺼﺤﻻﺍ
ﺘﻡــــــــــﻬﻴ ﻪــــــــــﻨﻻ ﺔــــــــــﻴﺭﺍﺭﺤﻟﺍ ﺔــــــــــﺴﺩﻨﻬﻟﺍ
ﺒﻤﺎ ﻴﺄﺘﻲ
:
1
.
ﺩﺭﺍﺴﺔ ﺍﻟﻁﺎﻗﺔ
)
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل
(
ﺃﻱ ﺍﻟﺘﺤﻭل ﺍﻟﻤﺘﺒﺎﺩل ﺒﻴﻥ ﺍﻟﻁﺎﻗﺔ،ﺭﺨﻵ لﻜﺸ ﻥﻤ ﺎﻤﻬﺘﻻﻭﺤﺘﻭ
ﺍﻟﺤﺭﺍﺭﻴﺔ ﻭﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ ﺍﻟﺫﻱ ﻴﺤﺩﺙ ﻤﺜﻼﹰ ﻓﻲ ﺍﻟﻤﺤﺭﻜﺎﺕ ﺍﻟﺤﺭﺍ
ﺔ ﺍﻭـﻴﺯﺎﻐﻟﺍ ﺕﺎﻨﻴﺒﺭﻭﺘﻟﺍ ، ﺔﻴﺭ
ﺍﻟﺒﺨﺎﺭﻴﺔ
…
.
ﻭﻜﺫﻟﻙ ﺍﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﺒﻭﺴ، ﺦﻟﺍ
ﺯﺓ ﺍﻟـﻬﺠﺃ ﺔﻁﺎ
ﺘﻜ
ﻴ
ﺔـﻗﺎﻁﻟﺍ لﺎﻤﻌﺘـﺴﺄﺒ ﻑـﻴ
ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ
.
2
.
ﺩﺭﺍﺴﺔ ﺍﻟﺘﻐﻴﺭﺍﺕ ﻓﻲ ﺨﻭﺍﺹ ﺍﻭ ﺴﻠﻭﻙ ﺍﻟﻤﺎﺌﻊ
(Fluid)
ﻴﺴﺨﻥ ﺃﻭ، ﺩﺩﻤﺘﻴ ﻭﺃ ﻁﻐﻀﻨﻴ ﺎﻤﺩﻨﻋ
ﻴﺒﺭﺩ
.
ﻭﻗﺩ ﻴﻜﻭﻥ ﺍﻟﻤﺎﺌﻊ ﻏﺎﺯﺍﹰ
)
ﻤﺜل ﺍﻟﻬﻭﺍﺀ
(
ﺃﻭ ﺒﺨﺎﺭﺍﹰ
)
ﺎﺭـﺨﺒ لﺜﻤ
ﺎﺀـﻤﻟﺍ
(
ﺎﺌﻼﹰ ﺃﻭـﺴ ﻭﺃ ،
ﺨﻠﻴﻁﺎﹰ ﻤﻥ ﻫﺫﻩ ﺍﻟﻤﻭﺍﺩ ﺸﺭﻴﻁﺔ ﺃﻥ ﻻﺘﺘﻔﺎﻋل ﻤﻊ ﺒﻌﻀﻬﺎ ﻜﻴﻤﻴﺎﺌﻴﺎﹰ
.
3
.
ﺩﺭﺍﺴﺔ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺘﻐﻴﺭ ﺨﻭﺍﺹ ﺍﻟﻤﺎﺌﻊ ﻭﻜﻤﻴﺎﺕ ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﺴﺒﺒﺔ ﻟﻬﺫﺍ ﺍﻟﺘﻐﻴﺭ
.
ﻴﺴﺘﻨﺩ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﺍﻟﻰ ﺃﺭﺒﻌﺔ ﻤﺒﺎﺩﺉ ﺃﻭ ﻗﻭﺍﻨﻴﻥ ﺃﺴﺎﺴﻴﺔ
ﻭﺠﺩﺕ
، ﺒﺎﻟﺘﺠﺭﺒﺔ ﻭﻟﻴﺱ ﺒﺎﻻﺸﺘﻘﺎﻕ ﺍﻟﺭﻴﺎﻀﻲ
ﻫﺫﻩ ﺍ
ﻟﻘﻭﺍﻨﻴﻥ ﻫﻲ
:
1
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺼﻔﺭﻱ
:
، ﺭﺍﺭﺓـﺤﻟﺍ ﺔﺠﺭﺩ ﻑﻴﺭﻌﺘ ﻡﺘﻴ ﻪﺒﺠﻭﻤﺒ ﻱﺫﻟﺍ ﻱﺭﺍﺭﺤﻟﺍ ﻥﺯﺍﻭﺘﻟﺍ ﻥﻭﻨﺎﻗ ﻭﻫﻭ
ﺴﻤﻲ ﺒﺎﻟﺼﻔﺭﻱ ﻻﻥ ﺼﻴﺎﻏﺘﻪ ﺠﺎﺀﺕ ﺒﻌﺩ ﺼﻴﺎﻏﺔ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
.
2
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
:
ﻭﻫﻭ ﺼﻴﻐﺔ ﺨﺎﺼﺔ ﻤﻥ ﺼﻴﻎ ﻗﺎﻨﻭﻥ ﺤﻔﻅ ﺍﻟﻁﺎﻗﺔ
.
3
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺜﺎﻨﻲ
:
ﺃﻱ ﺍﺘﺠﺎ، ﺕﺎﻴﻠﻤﻌﻟﺍ ﺭﻴﺴ ﻩﺎﺠﺘﺍ ﺩﺩﺤﻴ
ﺔـﻗﺎﻁﻟﺍ لـﻴﻭﺤﺘ ﺔﺒﺴﻨﻭ ﺔﻗﺎﻁﻟﺍ لﺎﻘﺘﻨﺍ ﻩ
ﺍﻟﻤﺘﻨﻘﻠﺔ
.
4
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺜﺎﻟﺙ
:
ﻴﺤﺩﺩ ﺍﻻﻨﺘﺭﻭﺒﻲ ﻭﻴﺒﻴﻥ ﺍﺴﺘﺤﺎﻟﺔ ﺍﻟﻭﺼﻭل ﻟﺩﺭﺠﺔ ﺍﻟﺼﻔﺭ ﺍﻟﻤﻁﻠﻕ
.
ﺔـﻗﺎﻁﻟﺍ ﺩـﻴﻟﻭﺘ ﺕﺎﻁﺤﻤﻜ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺕﺎﻜﺭﺤﻤﻟﺍ ﻡﻴﻤﺼﺘﺒ ﻡﻠﻌﻟﺍ ﺍﺫﻫ ﻙﻴﻨﺎﻜﻴﻤﻟﺍ ﻭﺴﺩﻨﻬﻤ لﻤﻌﺘﺴﻴ ﻙﻟﺫﻟ
ﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ،ﺦﻴﺭﺍﻭﺼﻟﺍﻭ ﺔﺜﺎﻔﻨﻟﺍﻭ ﺔﻴﺩﺩﺭﺘﻟﺍ ﺕﺎﻜﺭﺤﻤﻟﺍ،
، ﻤﺭﺍﺠل ﺍﻟﺒﺨﺎﺭ،ﺔﻴﺭﺎﺨﺒﻟﺍﻭ ﺔﻴﺯﺎﻐﻟﺍ
ﺍﻟﻀﻭﺍﻏﻁ
،
ﺍﺠﻬﺯﺓ ﺍﻟﺘﻜﻴﻴﻑ ﻭﻏﻴﺭﻫﺎ
.
ﻫﻨﺎ ﺍﺼﺒﺢ ﻤﻥ ﺍﻟﻀﺭﻭﺭﻱ ﻟﻠﻤﻬﻨﺩﺱ ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﺃﻥ ﻴﻠﻡ ﺒﻘﻭﺍﻨﻴﻥ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﻭﻴﺘﻔﻬﻡ
ﺃﺴﺴﻪ
.
ﻟﻘﺩ ﻜﺎﻥ ﺘﺤﻭﻴل ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﺇﻟﻰ ﺤﺭﺍﺭﺓ ﻤﻌﺭﻭﻓﺎﹰ ﻤﻨﺫ ﺍﻟﻘﺭﻥ ﺍﻟﺜﺎﻤﻥ ﻋﺸﺭ
.
ﻲ ﻤﻨـﻓﻭ
ـﺘ
ﺼﻑ
ﺍﻟﻘﺭﻥ ﺍﻟﺘﺎﺴﻊ ﻋﺸﺭ ﺍﻭﺠﺩ ﺍﻟﻌﺎﻟﻡ
ﺠﻭل
(Joule)
ﺩـﻗﻭ، ﺔـﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍﻭ ﻲﻜﻴﻨﺎﻜﻴﻤﻟﺍ لﻐﺸﻟﺍ ﻥﻴﺒ ﺔﻗﻼﻌﻟﺍ
ﺃﺴﻬﻡ ﺍﻟﻜﺜﻴﺭ ﻤﻥ ﺍﻟﻌﻠﻤ
ﺎﺀ ﻓﻲ ﺘﻁﻭﻴﺭ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﺃﻤﺜﺎل ﻜﺎﺭ
ﻨ
ﻜ،ﻭ
ﻠﻴ
ﻜﻠﻭﺯﻴﻭ،ﻥﻔ
ﺱ
ﺭﻥـﻘﻟﺍ ﺫـﻨﻤﻭ ، ﻡﻫﺭـﻴﻏﻭ
ﺍﻟﻤﺎﻀﻲ ﺘﻭﺴﻊ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﺒﺤﻴﺙ ﺸﻤل ﺠﻤﻴﻊ ﺍﻟﻤﻜﺎﺌﻥ ﺍﻟﺤﺭﺍﺭﻴﺔ ﻭﺃﺠﻬﺯﺓ ﺍﻟﺘﻜﻴﻴﻑ
.
XI
ﺍﻟﺭﻤﻭﺯ ﻭﺍﻟﻭﺤﺩﺍﺕ ﺍﻟﻤﺴﺘﺨﺩﻤﺔ
ﺍﻟﻭﺤﺩﺓ
∗
ﺍﻟﺭﻤ
ﺯ
ﺍﻟﻜﻤﻴﺔ
SI
BU
A Area
ﺍﻟﻤﺴﺎﺤﺔ
m
2
ft
2
a Acceleration
ﺍﻟﺘﻌﺠﻴل
m
/s
2
ft/sec.
2
C Velocity
ﺍﻟﺴﺭﻋﺔ
m/s ft/sec.
C Specific
heat
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ
J/kg.k Btu/lbm.
D Diameter
ﺍﻟﻘﻁﺭ
m ft
E Energy
ﺍﻟﻁﺎﻗﺔ
J=N.m Ft.lb,Btu
F Force
ﺍﻟﻘﻭﺓ
N=kg.m/s
2
Lb
f=
slug.ft/sec
2
g Local
acceleration
of
grafity
ﺍﻟﺘﻌﺠﻴل ﺍﻻﺭﻀﻲ
m/s
2
ft/sec
2
H Enthalby
ﺍﻻﻨﺜﺎﻟﺒﻲ
kJ Btu
h
Specific enthalby
ﺍﻻﻨﺜﺎﻟﺒﻲ ﺍﻟﻨﻭﻋﻲ
kJ/kg Btu/lbm
J
Mechanical equivalent of
heat
ﺍﻟﻤﻜﺎﻓىﺎﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﻟﻠﺤﺭﺍﺭﺓ
kcal=427kg.m 778,2ft.lbf/Btu
M Molecular
weight
ﺍﻟﻜﺘﻠﺔ ﺍﻟﺠﺯﻴﺌﻴﺔ
kg/kg.mol Lbm/lbm.mole
m Mass
ﺍﻟﻜﺘﻠﺔ
kg Slug,lbm
•
m
Mass flow rate
ﻤﻌﺩل ﺍﻟﺘﺩﻓﻕ
ﺍﻟﻜﺘﻠﻲ
kg/s Slug/sec,lbm/s
ec.
N Mole
ﺍﻟﺠﺯﺌﻲ
n Polytropic
index
ﺍﻻﺱ ﺍﻟﺒﻭﻟﺘﺭﻭﺒﻲ
P Pressure
ﺍﻟﻀﻐﻁ
Pa = N/m
2
Lb
f
/in
2
=psi
P Power
ﺍﻟﻘﺩﺭﺓ
W = J/s
Ft.lb/s,h.p
Q Heat
ﺍﻟﺤﺭﺍﺭﺓ
kJ Btu
•
Q
Heat rate
ﻤﻌﺩل ﺍﻟﺤﺭﺍﺭﺓ
kJ/s = kW
Btu/sec.
q
Heat per unit
ﺍﻟﺤﺭﺍﺭﺓ ﻟﻜل ﻭﺤﺩﺓ ﻜﺘﻠﺔ
kJ/kg Btu/Lbm
∗
ﻴﺭﻤﺯ ﻟﻠﻨﻅﺎﻡ ﺍﻟﻌﺎﻟﻤﻲ ﻟﻠﻭﺤﺩﺍﺕ ﺏ
(SI)
(System International)
ﺍﻤﺎ ﺍﻟﻨﻅﺎﻡ ﺍﻟﺒﺭﻴﻁﺎﻨﻲ ﻟﻠﻭﺤﺩﺍﺕ ﻓﺭﻤﺯﻩ
(British units ) (Bu)
ﺍﻭ
(English)
ﻜﻤﺎ ﺴﻴﺭﺩ ﺘﻔﺎﺼﻴﻠﻪ ﻻﺤﻘﺎ
.
XII
R Gas
Constant
ﺜﺎﺒﺕ ﺍﻟﻐﺎﺯ
kJ/.kg.K
Btu/ Lb. F
R
Universal Gas Constant
ﺍﻟﺜﺎﺒﺕ ﺍﻟﻌﺎﻡ ﻟﻠﻐﺎﺯﺍﺕ
8.314kJ/kmol.K 1545
ft.lbf/mole.R
S Entropy
ﺍﻻﻨﺘﺭﻭﺒﻲ
kJ / K
Btu /F
s
Specific Entropy
ﺍﻻﻨﺘﺭﻭﺒﻲ ﺍﻟﻨﻭﻋﻲ
kJ / kg . k
Btu/Lbm.ft
T
Absolute Temperature
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ
K F
T Torque
ﺍﻟﻌﺯﻡ
N.m
Lbf . Ft
U Internal
Energy
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
kJ Btu
u
Specific Internal E .
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺍﻟﻨﻭﻋﻴﺔ
kJ / kg
Btu / Lbm
V Volume
ﺍﻟﺤﺠﻡ
m
3
,
Liter
Ft
3
W Work
ﺍﻟﺸﻐل
J= N.m
Ft . Lb
•
W Work Rate
ﻤﻌﺩل ﺍﻟﺸﻐل
kJ/s =kW
Lbf . Ft/s
w
Work per Unit mass
ﺍﻟﺸﻐل ﻟﻜل ﻭﺤﺩﺓ ﻜﺘﻠﺔ
kJ/kg
Btu / Lbm
X Displacement.
ﺯﺍ
ﺍﺤﺔ ﻋﺎﻤﺔ
m Ft
Z Hight
ﺍﻻﺭﺘﻔﺎﻉ
m Ft
XIII
ﺒﻌﺽ ﺍﻟﺭﻤﻭﺯ ﺍﻟﻴﻭﻨﺎﻨﻴﺔ
:
ﺍﻟﺭﻤﺯ
ﺍﻟﺭﻤﺯ
α
Alpha
ø
Function , ph
β
Beta
π
ﺍﻟﻨﺴﺒﺔ ﺍﻟﺜﺎﺒﺘﺔ
)
ﺒﺎﻱ
(
γ
Gamma, Ratio of Specific heat d
Differential,(derivative)
ﺘﻔﺎﻀل
)
ﻤﺸﺘﻕ
(
∆
Delta
ﻤﺤﺩﺩ ﻕﺭﻓ
θ
Theta
η
Efficiency , Etta
ﺍﻟﻜﻔﺎﺀﺓ
∫
Integration
ﺘﻜﺎﻤل
ρ
Density , Rho
ﺍﻟﻜﺜﺎﻓﺔ
∑
Sigma , Summation
ﺠﻤﻊ

X
ﻤﻘﺩﻤﺔ ﺇﻟﻰ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
Introduction to Thermodynamics
ﻤﻊ ﺒﺩﺍﻴﺎﺕ ﺍﻟﻘﺭﻥ ﺍﻟﺘﺎﺴﻊ ﻋﺸﺭ ﻅﻬﺭ
ﻋﻠﻡ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺨﺭﺍﺭﺓ
)
ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻜﺱ
(
ﺭـﺜﻟﺍ
ﺸﻤلـﻴ ﻱﺫـﻟﺍ
ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
ﺍﻟﻌﺎﻡ
، ﺍﻭ ﺍﻟﻔﻴﺯﻴﺎﺌﻲ
ﺍﻟﻜﻴﻤﻴﺎﺌﻲ
،
ﺜﻡ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻬﻨﺩﺴﻲ ﺍﻟﺫﻱ ﻴﻬﻤﻨﺎ ﻓﻲ، ﻲﺌﺎﺼﺤﻻﺍ
ﺘﻡــــــــــﻬﻴ ﻪــــــــــﻨﻻ ﺔــــــــــﻴﺭﺍﺭﺤﻟﺍ ﺔــــــــــﺴﺩﻨﻬﻟﺍ
ﺒﻤﺎ ﻴﺄﺘﻲ
:
1
.
ﺩﺭﺍﺴﺔ ﺍﻟﻁﺎﻗﺔ
)
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل
(
ﺃﻱ ﺍﻟﺘﺤﻭل ﺍﻟﻤﺘﺒﺎﺩل ﺒﻴﻥ ﺍﻟﻁﺎﻗﺔ،ﺭﺨﻵ لﻜﺸ ﻥﻤ ﺎﻤﻬﺘﻻﻭﺤﺘﻭ
ﺍﻟﺤﺭﺍﺭﻴﺔ ﻭﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ ﺍﻟﺫﻱ ﻴﺤﺩﺙ ﻤﺜﻼﹰ ﻓﻲ ﺍﻟﻤﺤﺭﻜﺎﺕ ﺍﻟﺤﺭﺍ
ﺔ ﺍﻭـﻴﺯﺎﻐﻟﺍ ﺕﺎﻨﻴﺒﺭﻭﺘﻟﺍ ، ﺔﻴﺭ
ﺍﻟﺒﺨﺎﺭﻴﺔ
…
.
ﻭﻜﺫﻟﻙ ﺍﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﺒﻭﺴ، ﺦﻟﺍ
ﺯﺓ ﺍﻟـﻬﺠﺃ ﺔﻁﺎ
ﺘﻜ
ﻴ
ﺔـﻗﺎﻁﻟﺍ لﺎﻤﻌﺘـﺴﺄﺒ ﻑـﻴ
ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ
.
2
.
ﺩﺭﺍﺴﺔ ﺍﻟﺘﻐﻴﺭﺍﺕ ﻓﻲ ﺨﻭﺍﺹ ﺍﻭ ﺴﻠﻭﻙ ﺍﻟﻤﺎﺌﻊ
(Fluid)
ﻴﺴﺨﻥ ﺃﻭ، ﺩﺩﻤﺘﻴ ﻭﺃ ﻁﻐﻀﻨﻴ ﺎﻤﺩﻨﻋ
ﻴﺒﺭﺩ
.
ﻭﻗﺩ ﻴﻜﻭﻥ ﺍﻟﻤﺎﺌﻊ ﻏﺎﺯﺍﹰ
)
ﻤﺜل ﺍﻟﻬﻭﺍﺀ
(
ﺃﻭ ﺒﺨﺎﺭﺍﹰ
)
ﺎﺭـﺨﺒ لﺜﻤ
ﺎﺀـﻤﻟﺍ
(
ﺎﺌﻼﹰ ﺃﻭـﺴ ﻭﺃ ،
ﺨﻠﻴﻁﺎﹰ ﻤﻥ ﻫﺫﻩ ﺍﻟﻤﻭﺍﺩ ﺸﺭﻴﻁﺔ ﺃﻥ ﻻﺘﺘﻔﺎﻋل ﻤﻊ ﺒﻌﻀﻬﺎ ﻜﻴﻤﻴﺎﺌﻴﺎﹰ
.
3
.
ﺩﺭﺍﺴﺔ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺘﻐﻴﺭ ﺨﻭﺍﺹ ﺍﻟﻤﺎﺌﻊ ﻭﻜﻤﻴﺎﺕ ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﺴﺒﺒﺔ ﻟﻬﺫﺍ ﺍﻟﺘﻐﻴﺭ
.
ﻴﺴﺘﻨﺩ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﺍﻟﻰ ﺃﺭﺒﻌﺔ ﻤﺒﺎﺩﺉ ﺃﻭ ﻗﻭﺍﻨﻴﻥ ﺃﺴﺎﺴﻴﺔ
ﻭﺠﺩﺕ
، ﺒﺎﻟﺘﺠﺭﺒﺔ ﻭﻟﻴﺱ ﺒﺎﻻﺸﺘﻘﺎﻕ ﺍﻟﺭﻴﺎﻀﻲ
ﻫﺫﻩ ﺍ
ﻟﻘﻭﺍﻨﻴﻥ ﻫﻲ
:
1
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺼﻔﺭﻱ
:
، ﺭﺍﺭﺓـﺤﻟﺍ ﺔﺠﺭﺩ ﻑﻴﺭﻌﺘ ﻡﺘﻴ ﻪﺒﺠﻭﻤﺒ ﻱﺫﻟﺍ ﻱﺭﺍﺭﺤﻟﺍ ﻥﺯﺍﻭﺘﻟﺍ ﻥﻭﻨﺎﻗ ﻭﻫﻭ
ﺴﻤﻲ ﺒﺎﻟﺼﻔﺭﻱ ﻻﻥ ﺼﻴﺎﻏﺘﻪ ﺠﺎﺀﺕ ﺒﻌﺩ ﺼﻴﺎﻏﺔ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
.
2
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
:
ﻭﻫﻭ ﺼﻴﻐﺔ ﺨﺎﺼﺔ ﻤﻥ ﺼﻴﻎ ﻗﺎﻨﻭﻥ ﺤﻔﻅ ﺍﻟﻁﺎﻗﺔ
.
3
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺜﺎﻨﻲ
:
ﺃﻱ ﺍﺘﺠﺎ، ﺕﺎﻴﻠﻤﻌﻟﺍ ﺭﻴﺴ ﻩﺎﺠﺘﺍ ﺩﺩﺤﻴ
ﺔـﻗﺎﻁﻟﺍ لـﻴﻭﺤﺘ ﺔﺒﺴﻨﻭ ﺔﻗﺎﻁﻟﺍ لﺎﻘﺘﻨﺍ ﻩ
ﺍﻟﻤﺘﻨﻘﻠﺔ
.
4
.
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺜﺎﻟﺙ
:
ﻴﺤﺩﺩ ﺍﻻﻨﺘﺭﻭﺒﻲ ﻭﻴﺒﻴﻥ ﺍﺴﺘﺤﺎﻟﺔ ﺍﻟﻭﺼﻭل ﻟﺩﺭﺠﺔ ﺍﻟﺼﻔﺭ ﺍﻟﻤﻁﻠﻕ
.
ﺔـﻗﺎﻁﻟﺍ ﺩـﻴﻟﻭﺘ ﺕﺎﻁﺤﻤﻜ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺕﺎﻜﺭﺤﻤﻟﺍ ﻡﻴﻤﺼﺘﺒ ﻡﻠﻌﻟﺍ ﺍﺫﻫ ﻙﻴﻨﺎﻜﻴﻤﻟﺍ ﻭﺴﺩﻨﻬﻤ لﻤﻌﺘﺴﻴ ﻙﻟﺫﻟ
ﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ،ﺦﻴﺭﺍﻭﺼﻟﺍﻭ ﺔﺜﺎﻔﻨﻟﺍﻭ ﺔﻴﺩﺩﺭﺘﻟﺍ ﺕﺎﻜﺭﺤﻤﻟﺍ،
، ﻤﺭﺍﺠل ﺍﻟﺒﺨﺎﺭ،ﺔﻴﺭﺎﺨﺒﻟﺍﻭ ﺔﻴﺯﺎﻐﻟﺍ
ﺍﻟﻀﻭﺍﻏﻁ
،
ﺍﺠﻬﺯﺓ ﺍﻟﺘﻜﻴﻴﻑ ﻭﻏﻴﺭﻫﺎ
.
ﻫﻨﺎ ﺍﺼﺒﺢ ﻤﻥ ﺍﻟﻀﺭﻭﺭﻱ ﻟﻠﻤﻬﻨﺩﺱ ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﺃﻥ ﻴﻠﻡ ﺒﻘﻭﺍﻨﻴﻥ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﻭﻴﺘﻔﻬﻡ
ﺃﺴﺴﻪ
.
ﻟﻘﺩ ﻜﺎﻥ ﺘﺤﻭﻴل ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﺇﻟﻰ ﺤﺭﺍﺭﺓ ﻤﻌﺭﻭﻓﺎﹰ ﻤﻨﺫ ﺍﻟﻘﺭﻥ ﺍﻟﺜﺎﻤﻥ ﻋﺸﺭ
.
ﻲ ﻤﻨـﻓﻭ
ـﺘ
ﺼﻑ
ﺍﻟﻘﺭﻥ ﺍﻟﺘﺎﺴﻊ ﻋﺸﺭ ﺍﻭﺠﺩ ﺍﻟﻌﺎﻟﻡ
ﺠﻭل
(Joule)
ﺩـﻗﻭ، ﺔـﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍﻭ ﻲﻜﻴﻨﺎﻜﻴﻤﻟﺍ لﻐﺸﻟﺍ ﻥﻴﺒ ﺔﻗﻼﻌﻟﺍ
ﺃﺴﻬﻡ ﺍﻟﻜﺜﻴﺭ ﻤﻥ ﺍﻟﻌﻠﻤ
ﺎﺀ ﻓﻲ ﺘﻁﻭﻴﺭ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﺃﻤﺜﺎل ﻜﺎﺭ
ﻨ
ﻜ،ﻭ
ﻠﻴ
ﻜﻠﻭﺯﻴﻭ،ﻥﻔ
ﺱ
ﺭﻥـﻘﻟﺍ ﺫـﻨﻤﻭ ، ﻡﻫﺭـﻴﻏﻭ
ﺍﻟﻤﺎﻀﻲ ﺘﻭﺴﻊ ﻫﺫﺍ ﺍﻟﻌﻠﻡ ﺒﺤﻴﺙ ﺸﻤل ﺠﻤﻴﻊ ﺍﻟﻤﻜﺎﺌﻥ ﺍﻟﺤﺭﺍﺭﻴﺔ ﻭﺃﺠﻬﺯﺓ ﺍﻟﺘﻜﻴﻴﻑ
.

)
1
(
ﺍﻟﻔﺼﻞ ﺍﻷﻭﻝ
–
ﺍﻟﻮﺣﺪﺍﺕ ﻭﺍﻟﺘﻌﺎﺭﺑﻒ
)
1.1
(
-
ﺍﻻﺒﻌﺎﺩ ﻭﺍﻟﻭﺤﺩﺍﺕ ﻭﺍﻟﺭﻤﻭﺯ
Dimensions, Units & Symbols
ﻟﻜل ﻋﻠﻡ ﻤﺼﻁﻠﺤﺎﺕ ﺘﻌﺒﺭ ﻋﻥ ﺍﻟﻤﻌﺎﻨﻲ ﺍﻟﺩﻗﻴﻘﺔ ﺍﻟﻤﺨﺘﻠﻔﺔ ﺍﻟﺘﻲ ﺘﺨﺘﺹ ﺒﻪ
.
ﺎـﻤ ﹰﺍﺭﻴﺜﻜ ﻅﺎﻔﻟﻻﺍ ﻩﺫﻫﻭ
ﻭﻤﻥ ﻫﻨﺎ ﺴﻤﻴﺕ ﺒﺎﻟﻤﺼﻁﻠﺤﺎﺕ،ﻡﺎﻌﻟﺍ ﻱﻭﻐﻠﻟﺍ ﺎﻫﺎﻨﻌﻤ ﻥﻋ ﻲﺤﻼﻁﺼﻻﺍ ﺎﻫﺎﻨﻌﻤ ﻑﻠﺘﺨﻴ
.
ﺍﻤﺎ ﺍ
ﺄﻥـﻓ ﺯﻭﻤﺭﻟ
ﻭﺍﺹـﺨ ﻭﺍ ﺕﺍﺭﻴﻐﺘﻤ ﻭﺍ ﺕﺎﻴﻤﻜ ﻰﻠﻋ ﺔﻟﻻﺩﻠﻟ لﻤﻌﺘﺴﺘ ﺯﻭﻤﺭﻟﺍ ﻥﻤ ﺔﻋﻭﻤﺠﻤ ﻡﻠﻋ لﻜﻟ
(Properties)
ﺍﻭ
ﻭﺤﺩﺍﺕ
(Units)
ﻤﺨﺘﻠﻔﺔ
.
ﻭﻗﺩ ﺒﺎﺕ ﻜﺜﻴﺭ ﻤﻥ ﻫﺫﻩ ﺍﻟﺭﻤﻭﺯ ﺍﻟﻌﻠﻤﻴﺔ ﺸﺎﺌﻌﺎﹰ ﻭﻤﺸﺘﺭﻜﺎﹰ ﺒﻴﻥ ﻤﺨﺘﻠﻑ ﺍﻟﻠﻐﺎﺕ ﻓﻲ
ﺒﺤﻴﺙ ﺍﺘﺨﺫ ﺼﻔﺔ ﻋﺎﻟﻤﻴﺔ ﺘﺴﺘﻠﺯﻡ ﺍﻷﺒﻘﺎﺀ ﻋﻠﻴﻪ ﻭﻋﺩﻡ ﺘﺭﺠﻤﺘﻪ،ﺔﻤﺩﻘﺘﻤﻟﺍ لﻭﺩﻟﺍ
.
ﻴﻤﻜﻥ ﻤﻼﺤﻅﺔ ﺍﻻﺒﻌﺎﺩ ﺍﻭ ﺍﻟﻜﻤﻴﺎﺕ ﺍﻟﻁﺒﻴﻌﻴﺔ ﺍﻭ ﺍﻟﻤﻘﺎﺩﻴﺭ ﺍﻟﻔﻴﺯﻴﺎﻭﻴﺔ
.
ﺔـﻤﻴﻘﻟﺍ ﺩﺩﺤﺘ ﺎﻬﻨﺄﻓ ﺓﺩﺤﻭﻟﺍ ﺎﻤﺍ
ﺍﻟﻌﺩﺩﻴﺔ ﻟﻬﺫﺍ ﺍﻟﺒﻌﺩ
.
ﺩﺓـﺤﻭﻟﺍ ﻲﻬﻓ ﺔﻋﺎﺴﻟﺍ ﻭﺍ ﺔﻘﻴﻗﺩﻟﺍ ﻭﺍ ﺔﻴﻨﺎﺜﻟﺍ ﺎﻤﺍ ﺩﻌﺒﻟﺍ ﻭﻫ ﻥﻤﺯﻟﺍ ﹰﻼﺜﻤﻓ
.
ﻡـﻗﺭ لﻭﺩـﺠﻭ
)
1.1
(
ﻴﻭﻀﺢ ﻫﺫﻩ ﺍﻻﺒﻌﺎﺩ ﻭﻭﺤﺩﺍﺘﻬﺎ ﻓﻲ ﺍﻟﻨﻅﺎﻡ ﺍﻟﻌﺎﻟﻤﻲ ﻟﻠﻭﺤﺩﺍﺕ
.
ﺠﺩﻭل
)
1.1
(
ﺍﻻﺒﻌﺎﺩ ﻭﺍﻟﻭﺤﺩﺍﺕ ﻭﺍﻟﺭﻤﻭﺯ
ﺍﻻﺒﻌﺎﺩ
)
ﺍﻟﻜﻤﻴﺎﺕ ﺍﻟﻔﻴﺯﻴﺎﻭﻴﺔ
(
ﺍﻟﻭﺤﺩﺓ
ﺍﻻﺴﻡ
ﺍﻟﺤﺭﻑ ﺍﻟﺭﻤﺯﻱ
ﺍﻻﺴﻡ
ﺍﻟﺤﺭﻑ ﺍﻟﺭﻤﺯﻱ
ﺍﻟﺘﻌﺒﻴﺭ ﻓﻲ
SI
ﺍﻟﺯﻤﻥ
t
ﺍﻟﺜﺎﻨﻴﺔ
s
s
ﺍﻟﺤﺠﻡ
V
ﺍﻟﻠﺘﺭ
L
10
-3
m
3
ﺍﻟﻜﺘﻠﺔ
m
ﺍﻟﻜﻴﻠﻭﻏﺭﺍﻡ
kg
kg
ﺍﻟﻘﻭﺓ
F
ﺍﻟﻨﻴﻭﺘﻥ
N
kg.m/s
2
ﺍﻟﻀﻐﻁ
P
ﺍﻟﺒﺎﺴﻜﺎل
Pa
N/m
2
ﺍﻟﻁﺎﻗﺔ
E
ﺍﻟﺠﻭل
J
N.m
ﺍﻟﻘﺩﺭﺓ
P
ﺍﻟﻭﺍﺕ
W
J/s
ﺍﻟﺸﻐل
W
ﺍﻟﺠﻭل
J
N.m
ﺍﻟﺤﺭﺍﺭﺓ
Q
ﺍﻟﺠﻭل
J
N.m
)
1.2
(
-
ﺍﻟﻨﻅﺎﻡ ﺍﻟﻌﺎﻟﻤﻲ ﻟﻠﻭﺤﺩﺍﺕ
International System of Units
ﻓﻲ ﻋﺎﻡ
)
1960
(
ﺃﻗﺭ ﺍﻟﻤﺅﺘﻤﺭ ﺍﻟﻌﺎﻡ ﺍﻟﺤﺎﺩﻱ ﻋﺸﺭ ﻟﻠﻤﻌﺎﻴﻴﺭ ﻭﺍﻻﻭﺯﺍﻥ ﺍﺴﺘﻌﻤﺎل ﻫﺫﺍ ﺍﻟﻨﻅﺎﻡ
.
ٍﺒﻌﺩﺌﺫ
ﻨﺎل ﺘﺒﺎﻋﺎﹰ ﺇﻋﺘﺭﺍﻑ ﺠﻤﻴﻊ ﺍﻟﻬ
ﻴﺌﺎﺕ ﺍﻟﺩﻭﻟﻴﺔ ﻭﺍﻜﺜﺭﻴﺔ ﺩﻭل ﺍﻟﻌﺎﻟﻡ
.
ﺍﻥ ﺍﻟﺤﺎﺠﺔ ﺍﻟﻰ ﻟﻐﺔ ﻋﺎﻟﻤﻴﺔ ﻟﻠﻭﺤﺩﺍﺕ ﺠﻌﻠﺕ
ـﺍﻟﻤﻨﻅﻤﺔ ﺍﻟﻌﺎﻟﻤﻴﺔ ﻟﻠﻘﻴﺎﺴﺎﺕ ﺘﻭﺼﻲ ﺒﺄﺴﺘﻌﻤﺎل ﻫﺫﺍ ﺍﻟﻨﻅﺎﻡ ﺍﻟﺫﻱ ﻴﺭﻤﺯ ﻟﻪ ﺒ
(SI)
.
ﺎﻡـﻅﻨ ﻪـﻨﻭﻜﺒ ﻑﺼﺘﻴ

)
2
(
ﻭﺤﺩﺍﺕ ﻤﻨﺴﺠﻤﺎﹰ
.
لـﺜﻤﻴ ﻪﻴﻓ ﻥﻴﺘﻴﻤﻜ ﻱﺃ ﺕﺍﺩﺤﻭ ﺔﻤﺴﻗ ﻭﺍ ﺏﺭﻀ لﺼﺎﺤ ﻥﻭﻜﻴ ﻱﺫﻟﺍ ﻭﻫ ﻡﺠﺴﻨﻤﻟﺍ ﻡﺎﻅﻨﻟﺍ
ﻭﺤﺩﺓ ﺍﻟﻜﻤﻴﺔ
ﺍﻟﻨﺎﺘﺠﺔ
.
ﻓﻤﺜﻼﹰ ﺍﻟﻤﺘﺭ ﻭﺤﺩﺓ ﺍﻟﻁﻭل ﻭﺍﻟﻤﺘﺭ ﺍﻟﻤﺭﺒﻊ ﻭﺤﺩﺓ ﺍﻟﻤﺴﺎﺤﺔ
…
.
ﺍﻟﺦ
.
ﻫﺫﺍ ﺍﻟﻨﻅﺎﻡ ﻴﺴﻤﻰ
ﺍﻴﻀﺎﹰ ﺒﺎﻟﻨﻅﺎﻡ ﺍﻟﻤﺘﺭﻱ ﺍﻟﻬﻨﺩﺴﻲ
.
ﺠﺩﻭل
)
1.2
(
ﺍﻟﻭﺤﺩﺍﺕ ﺍﻻﺴﺎﺴﻴﺔ ﻭﺍﻟﻤﺴﺎﻋﺩﺓ
Units
Quantity
ﺍﻟﻜﻤﻴﺔ
ﺍﻟﺭﻤﺯ
SI English
A
ﺍﻟﻭﺤﺩﺍﺕ ﺍﻻﺴﺎﺴﻴﺔ
1.
Length
ﺍﻟﻁﻭل
L meter m
foot
ft
2.
Mass
ﺍﻟﻜﺘﻠﺔ
m Kilogram kg
Slug
or
pound
Lbm
3.
Time
ﺍﻟﺯﻤﻥ
t second S second sec.
4.
Electric current
ﺍﻟﺘﻴﺎﺭ ﺍﻟﻜﻬﺭﺒﺎﺌﻲ
I ampere A Ampere A
5.
Absolute Temperature
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ
T Kelvin K RanKine
°R
6. Amount
of
substance
ﻜﻤﻴﺔ ﺍﻟﻤﺎﺩﺓ
kg-mole
Pound-mole
Lbm-
mole
7.
Luminous intensity
ﺎﺀﺓــــﻀﻻﺍ ﺓﺩــــﺸ
)
ﺍﻭ ﺍﻟﻭﻤﻴﺽ
(
candela Cd Candela Cd
B
ﺍﻟﻭﺤﺩﺍﺕ ﺍﻟﻤﺴﺎﻋﺩﺓ
1.
Plane angle
ﺍﻟﺯﺍﻭﻴﺔ ﺍﻟﻤﺴﺘﻭﻴﺔ
radian Rad Radian Rad
2.
Solid angle
ﺍﻟﺯﺍﻭﻴﺔ ﺍﻟﻤﺠﺴﻤﺔ
steradian Sr Steradian
Sr
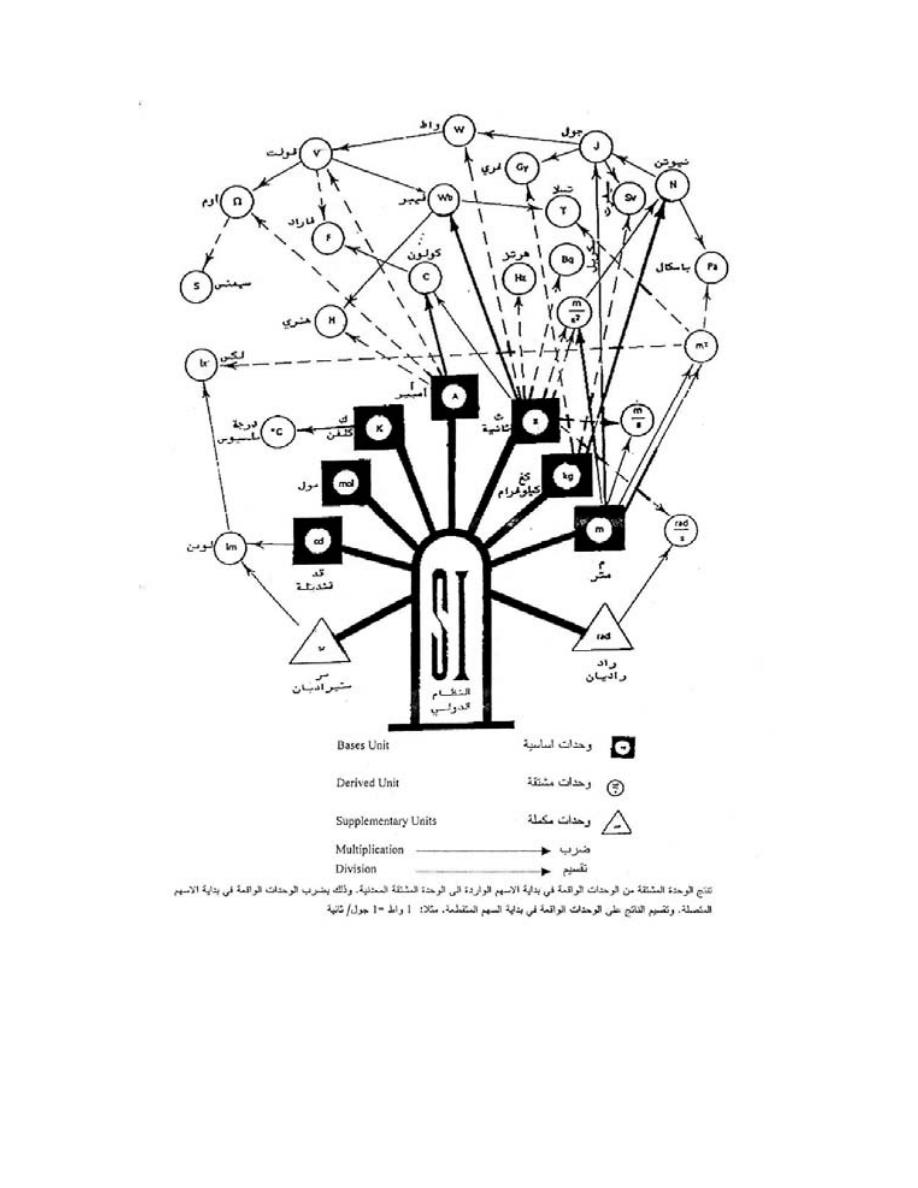
)
3
(
ﺸﻜل
)
1.1
(
-
ﺸﺠﺭﺓ ﺍﻟﻭﺤﺩ
ﺍﺕ

)
4
(
ﻴﺘﻜﻭﻥ ﺍﻟﻨﻅﺎﻡ ﻤﻥ
)
7
(
ﻡـﻗﺭ لﻭﺩﺠ ﻲﻓ ﺔﺤﻀﻭﻤﻟﺍﻭ ﺓﺩﻋﺎﺴﻤ ﻭﺍ ﺔﻠﻤﻜﻤ ﻥﻴﺘﺩﺤﻭﻭ ﺔﻴﺴﺎﺴﺍ ﺕﺍﺩﺤﻭ
)
1.2
.(
،ﻭﻤﻥ ﻤﻤﻴﺯﺍﺕ ﻫﺫﺍ ﺍﻟﻨﻅﺎﻡ ﺍﻨﻪ ﻴﻤﻜﻥ ﺍﺸﺘﻘﺎﻕ ﻭﺤﺩﺍﺕ ﺃﺨﺭﻯ ﺘﺴﻤﻰ ﺒﺎﻟﻭﺤﺩﺍﺕ ﺍﻟﻤﺸﺘﻘﺔ ﺍﻭ ﺍﻟﻤﺭﻜﺒﺔ
ﻭﺫﻟﻙ ﻤﻥ ﺨﻼل ﻋﻤﻠﻴﺎﺕ ﻀﺭﺏ ﺍﻭ ﻗ،ﺔﻴﺴﺩﻨﻬﻟﺍ ﻡﻭﻠﻌﻟﺍ ﻲﻓ ﺎﻬﻴﻟﺍ ﺝﺎﺘﺤﻨ ﺔﻴﺴﺎﺴﻻﺍ ﺕﺍﺩﺤﻭﻟﺍ ﻥﻤ ﻕﺘﺸﺘ
ﺴﻤﺔ
ﺸﻜل ﺭﻗﻡ،ﺕﺍﺩﺤﻭﻟﺍ ﺓﺭﺠﺸ ﻲﻓ ﺢﻀﻭﻤ ﺎﻤﻜﻭ ،ﺔﻴﺴﺎﺴﻻﺍ ﺕﺍﺩﺤﻭﻠﻟ
)
1.1
(
ﺍﻭ ﺠﺩﻭل ﺭﻗﻡ،
)
1.3
.(
ﻓﻤﺜﻼﹰ ﻭﺤﺩﺓ ﺍﻟﻘﻭﺓ ﻫﻲ ﺍﻟﻨﻴﻭﺘﻥ
(N)
ﺩـﺤﺍﻭ ﻡﺍﺭـﻏ ﻭﻠﻴﻜ ﺔﻠﺘﻜ لﺠﻌﺘ ﻲﺘﻟﺍ ﺓﻭﻘﻟﺍ ﻪﻨﺄﺒ ﻑﺭﻌﻴ ﻱﺫﻟﺍ
(kg)
ﻤﺘﺭﺍﹰ ﻭﺍﺤﺩﺍﹰ ﻟﻜل ﻤﺭﺒﻊ ﺜﺎﻨﻴﺔ
(m/s
2
)
.
ﻭﺓـﻘﻟﺍ ﺓﺩﺤﻭ ﺢﺒﺼﺘﻓ
(N = kg.m/s
2
)
ﺸﻐلـﻟﺍ ﺓﺩـﺤﻭﻭ ،
(N.m)
…
ﺍﻟﺦ
.
ﻭلـﺠﻟﺍ لﻐﺸـﻟﺍ ﺓﺩـﺤﻭ ﹰﻼﺜـﻤﻓ ،ﻁﻴﺴـﺒ ﺢﻠﻁﺼـﻤﺒ ﺔﻘﺘﺸﻤﻟﺍ ﺕﺍﺩﺤﻭﻟﺍ ﺭﺼﺘﺨﺘ ﺩﻗﻭ
(J = N.m)
ﻭﻭﺤﺩﺓ ﺍﻟﻘﺩﺭﺓ ﺍﻟﻭﺍﺕ،
(W = J/s)
ﻭﻭﺤﺩﺓ ﺍﻟﻀﻐﻁ ﺍﻟﺒﺎﺴﻜﺎل
(Pa = N/m
2
)
…
.
ﺍﻟﺦ
.
ﺎﻨﻲـﻁﻴﺭﺒﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻭﻫ لﺎﻤﻌﺘﺴﻻﺍ لﻴﻠﻗ ﺕﺍﺩﺤﻭﻠﻟ ﺭﺨﺁ ﻡﺎﻅﻨ ﻙﺎﻨﻫﻭ
(British Units)
.
ﺜﻼﹰـﻤﻓ
ﻭﺤﺩﺓ ﺍﻟﻜﺘﻠﺔ ﻓﻲ ﻫﺫﺍ ﺍﻟ
ﻨﻅﺎﻡ
(Pound – mass)
ﻭﺭﻤﺯﻫﺎ
(Lbm)
ﻴﻘﺎﺒﻠﻪ ﻓﻲ ﻨﻅﺎﻡ
(SI)
ﺭﺍﻡـﻏ ﻭـﻠﻴﻜﻟﺍ
ﺍﻟﻜﺘﻠﻲ
(Kilogram – mass)
ﻭﺭﻤﺯﻩ،
(kg.m)
.
ﺩـﻨﻭﺎﺒﻟﺍ ﻭـﻫ ﻲﻨﺎﻁﻴﺭﺒﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻲﻓ ﺓﻭﻘﻟﺍ ﺓﺩﺤﻭ ﺎﻤﺍ
ﺍﻟﺜﻘﻠﻲ
(Pound – Force)
ﻭﺭﻤﺯﻩ
(Lbf)
.
ﻴﻘﺎﺒﻠﻪ ﻓﻲ ﻨﻅﺎﻡ
(SI)
ﺍﻟﻨﻴﻭﺘﻥ
(N)
ﺎـﻤﻜ ،ﻯﺭﺨﺍ ﺕﺍﺩﺤﻭﻭ
ﻓﻲ ﺠﺩﻭل
)
1.3
.(
ﺍﻥ ﻭﺤ
ﺩﺓ ﺍﻟﻜﻤﻴﺎﺕ ﻓﻲ ﻨﻅﺎﻡ
(SI)
ﻜﻤﺎ ﺘﻭﻀﺢ ﺠﺩﺍﻭل،ﻲﻨﺎﻁﻴﺭﺒﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻲﻓ ﺕﺎﻴﻤﻜ ﺓﺩﺤﻭ ﺎﻬﻠﺒﺎﻘﻴ
)
1.2
(
،
)
1.3
(
ﺍﻟﺫﻱ ﻴﺒﻴﻥ ﻭﺤﺩﺍﺕ ﺒﻌﺽ ﺍﻟﻜﻤﻴﺎﺕ ﻓﻲ ﺍﻟﻨﻅﺎﻤﻴﻥ
.
ﻭﺠﺩﻭل
)
1.4
(
ﺩﺍﺕـﺤﻭﻟﺍ ﺽـﻌﺒ ﻥﻴﺒﻴ
ﺍﻟﺒﺭﻴﻁﺎﻨﻴﺔ
.
ﺩﻭلـﺠ ﻲـﻓ ﺔﻨﻴﺒﻤﻟﺍ لﻴﻭﺤﺘﻟﺍ لﻤﺎﻌﻤ ﺏﺠﻭﻤﺒ ﺭﺨﻵ ﻡﺎﻅﻨ ﻥﻤ ﺕﺍﺩﺤﻭﻟﺍ ﻩﺫﻫ لﻴﻭﺤﺘ ﻥﻜﻤﻴ ﺎﻤﻜ
)
1.5
(،
ﺃﻭ ﺒﻤﻭﺠﺏ ﺍﻟﺤﺴﺎﺒﺎﺕ ﻟﻸﻤﺜﻠﺔ ﺍﻟﺘﻲ ﺴﺘﺭﺩ ﻻﺤﻘﺎﹰ
.

)
5
(
ﺠﺩﻭل ﺭﻗﻡ
)
1.3
(
ﺍﻟﻭﺤﺩﺍﺕ ﺍﻟﻤﺸﺘﻘﺔ
Quantity
ﺍﻟﻜﻤﻴﺔ
ﺍﻟﺭﻤﺯ
Dimensions
Units
SI
English
Area
ﺍﻟﻤﺴﺎﺤﺔ
A L
2
m
2
ft
2
Volume
ﺍﻟﺤﺠﻡ
V L
3
m
3
ft
3
Velocity
ﺍﻟﺴﺭﻋﺔ
C L/t
m/s
ft/sec.
Acceleration
ﺍﻟﺘﻌﺠﻴل
a L/t
2
m/s
2
ft/sec
2
Angular Velocity
ﺍﻟﺴﺭﻋﺔ ﺍﻟﺯﺍﻭﻴﺔ
ω
t
-1
s
-1
sec
-1
Force
ﺍﻟﻘﻭﺓ
F m.L/t
2
kg.m/s
2
= N (newton)
slug.ft/sec
2
= Lb (pound)
Density
ﺍﻟﻜﺜﺎﻓﺔ
ρ m/L
3
kg/m
3
Slug/ft
3
Specific weight
ﺍﻟﻭﺯﻥ ﺍﻟﻨﻭﻋﻲ
m/L
2
t
2
N/m
3
Lb/ft
3
Frequency
ﺍﻟﺘﺭﺩﺩ
ƒ t
-1
s
-1
Sec
-1
Pressure
ﺍﻟﻀﻐﻁ
P m/Lt
2
N/m
2
= Pa (pascal)
Lb/ft
2
Energy, Work, Torque
ﺍﻟﻌﺯﻡ،لﻐﺸﻟﺍ ،ﺔﻗﺎﻁﻟﺍ
E
W
T
mL
2
/t
2
N.m = J
(Joule)
Ft.Lb
Heat rate, Power
ﺍﻟﻘﺩﺭﺓ،ﺓﺭﺍﺭﺤﻟﺍ لﺩﻌﻤ
•
Q
mL
2
/t
3
J/s
= W (watt)
Btu/sec.
Mass Flux
ﺘﺩﻓﻕ ﻜﺘﻠﻲ
•
m
m/t kg/s
Slug/sec.
Flow rate
ﻤﻌﺩل ﺍﻟﺘﺩﻓﻕ
•
V
L
3
/t m
3
/s Ft
3
/sec.
Specific heat
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ
C L
2
/t
2
.T J/kg.K Btu/slug.
°R

)
6
(
ﺠﺩﻭل
)
1.4
(
ﺒﻌﺽ ﺍﻟﻭﺤﺩﺍﺕ ﺍﻟﺒﺭﻴﻁﺎﻨﻴﺔ
ﺍﻟﻭﺤﺩﺓ
ﺍﻟﺭﻤﺯ
ﺍﻟﻭﺤﺩﺓ
ﺍﻟﺭﻤﺯ
ﻗﺩﺭﺓ ﺤﺼﺎﻨﻴﺔ
Horse-Power
h.p
British-Thermal Unit
ﻭﺤﺩﺓ ﺤﺭﺍﺭﻴﺔ ﺒﺭﻴﻁﺎﻨﻴﺔ
Btu
ﺍﻻﻨﺞ
-
ﻋﻘﺩﺓ
Inch
in
ﺴﻌﺭﺓ
Calorie
Cal
ﻤﻴل ﺍﺭﻀﻲ
Mile Statute
mi
ﺍﻟﻘﺩﻡ
Foot
Ft
ﻤﻴل ﺒﺤﺭﻱ
-
ﻋﻘﺩﺓ
Mile Nautical
nmi
Foot-Pound
Ft.P
ﺍﻭﻨﺱ
Ounce
oz
ﻗﺎﻤﺔ
Fatham
Fath
ﻭﺤﺩﺍﺕ ﺍﺨﺭﻯ
:
Barel
ﺒﺭﻤﻴل ﻨﻔﻁ ﺍﻤﺭﻴﻜﻲ ﻴﻌﺎﺩل
(159 L)
.
Bushel
ﻤﻜﻴﺎل ﺴﻌﺘﻪ
(35 L)
.
Carat
ﻗﻴﺭﺍﻁ
.
Chaldron
ﻤﻜﻴﺎل ﺍﻨﻜﻠﻴﺯﻱ ﻴﻌﺎﺩل
(36.4 L)
.
Cord
ﻤﻘﻴﺎﺱ ﺤﺠﻤﻲ ﻟﻠﺨﺸﺏ ﻴﻌﺎﺩل
(128 ft
3
)
.
Grain
ﺤﺒﺔ
)
ﻗﻤﺢ
.(
PecK
ﻤﻜﻴﺎل ﺴﻌﺘﻪ
(9.092 L)
.
PoundaL (PdL) = Lb.ft/s
2
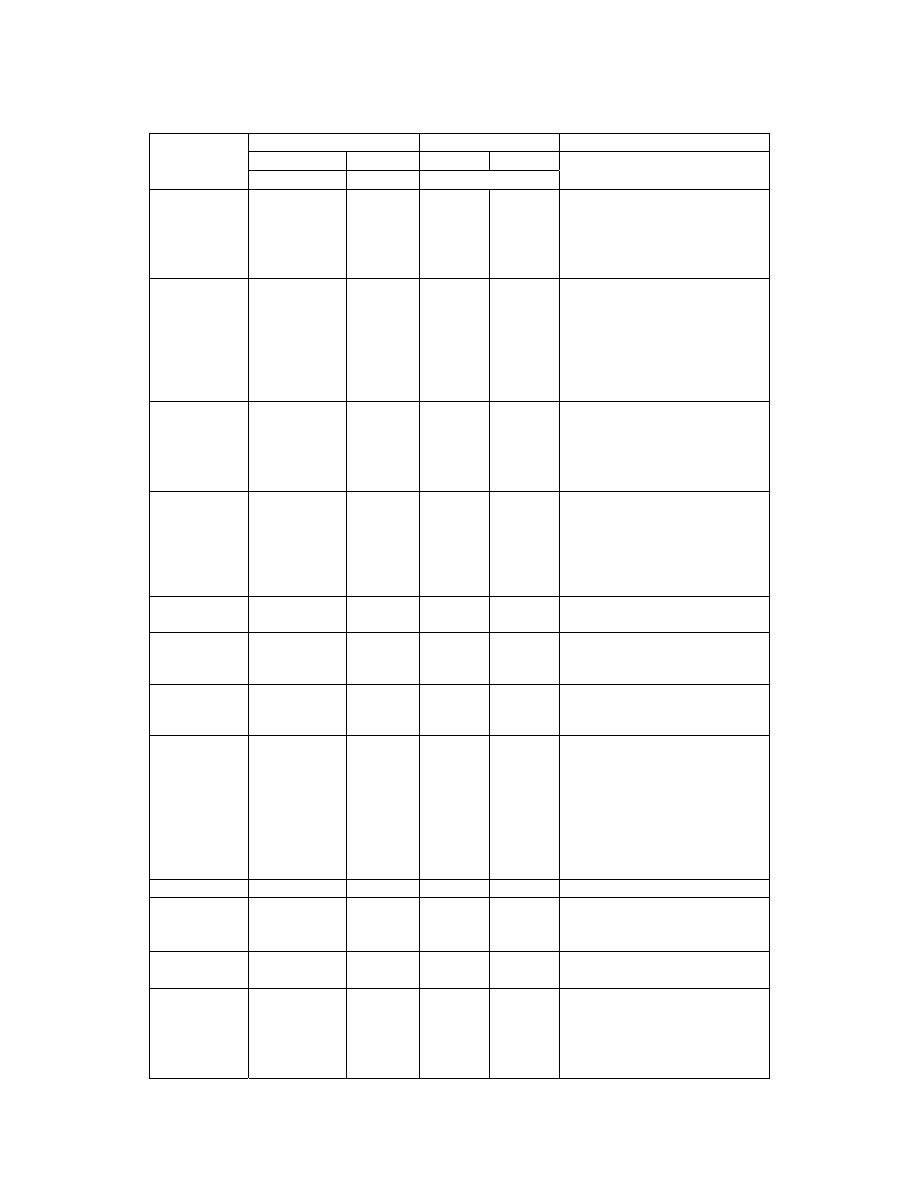
)
7
(
ﺠﺩﻭل
)
1.5
(
ﻤﻌﺎﻤل ﺍﻟﺘﺤﻭﻴل
Units
to Convert from
Conversion
English (E.)
SI
E. to SI
SI to E
Quantity
multiply
by
Area in
2
ft
2
acre
cm
2
m
2
ha
6,452
0,093
0,405
0,1550
10,76
2,471
m
2
=1550 in
2
= 10.76 ft
2
=
1.2
yd
2
=
2.471.10
-4
acres
=
10
-4
ha
Length In
Ft
Mile
cm
m
km
2,54
0,305
1,609
0,394
3,281
0,622
m
=1.05.10
-6
ﺴﻨﺔ ﻀﻭﺌﻴﺔ
=
5.4.10
-4
nmi
=
1.1
yd
=
0.55
fath
yd
= 3 ft
nmi
= 1.85 km
Volume in
3
ft
3
US gallon
=
cm
3
m
3
m
3
L
16.387
0.028
0.004
3.785
0.061
35.32
264.2
0,264
m
3
= 10
3
L=10
6
cm
3
=
1.31
yd
3
= 4 barely
L
=10
3
cm
3
=dcm
3
Br.gal. = 4.546 L
Mass Lbm
Slug
kg
kg
0.454
14.59
2,205
0,069
kg
= 35.274 Ounce
=
10
-3
ﻁﻥ ﻤﺘﺭﻱ
Lbm
= 16 Ounce
Carat = 1/24 kg
Grain = 0.065 g
Force Lbf
Kip(10
3
Lb)
N
N
4,448
4448
0,225 N
=
10
5
Dyn
=
3.6
Ounce
Density
ﺍﻟﻜﺘﻠﻴﺔ
slug/ft
3
kg/m
3
515,4
1,94.10
-3
kg/m
3
=0.001 g/cm
3
Density
ﺍﻟﺜﻘﻴﻠﺔ
Lbf/ft
3
N/m
3
0.064
=
0.063
Lbm/ft
3
= 0.008 Lbm/US gal.
WorK,
Energy,
Heat
ft.Lb
f
BTU
BTU
therm
J
kJ
kWh
kWh
1.356
1.054
0.0003
29.3
0.738
0.948
3413
0.034
J
= 0.239 Cal.
=
10
7
dyn.cm
=
10
7
Eng.
= 0.102 kg.m
therm = 10 Btu
= 105.5 MJ
Btu
= 0.252kcaL
Lb
f
.ft = 0.138 kg.m
Power
h.p
kw
0.746
1.341
W
= 0.239 cal/s
Heat Rate
ft. Lbf/sec.
BTU/hour
W
W
1.356
0.293
0.738
3.414
= 0,057 BTU/min.
metric h.p. = 0,736 kw
1Tref = 3kW=12000 BTU
Flow Rate
ft
3
/sec
=
m
3
/s
L/s
0.028
28.32
35.32
0.035
Pressure Lb
f
/in
2
Lb
f
/ft
2
Foot of H
2
O
Inches of Hg
kPa
kPa
kPa
kPa
6.895
0.048
2.983
3.374
0.145
20.89
0.335
0.296
kPa
= 10.2 cm H
2
O
= 4.015 in H
2
O
=
0.75
cm
Hg
=
0.01
atm.
=
10
-2
bar
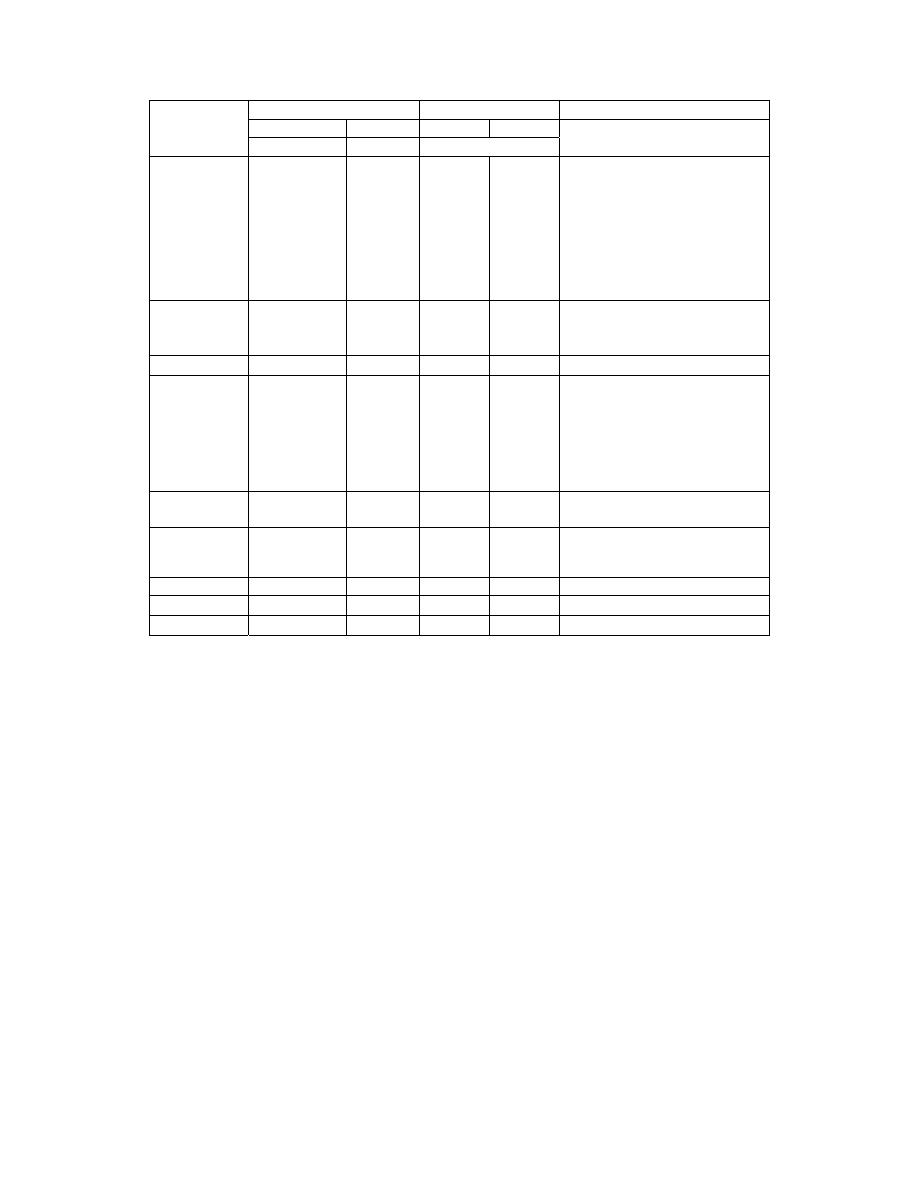
)
8
(
Units
to Convert from
Conversion
English (E.)
SI
E. to SI
SI to E
Quantity
multiply
by
=
7.5
torr
Pa
= 10 dyn/cm
2
atm.
= 76 cm Hg
=
1034
cm
H
2
O
torr
= mm Hg
=
1/760
atm.
kg/cm
2
= 98100 Pa
≅ 0.1 MN/m
2
Velocity ft/sec.
Mile/hr
=
m/s
m/s
km/hr
0.305
0.447
1.609
3.281
2.237
0.622
m/s
= 3.6 km/h
=
6.2.10
-4
mi/s
= 1.944 nmi
Acceleration ft/sec
2
.
m/s
2
0.305 3.281
Temperature
F
ْ
F
ْ
ْ
C
K
0.55
(
ْ
F-
32
)
0.55
(
ْ
F-460
)
1.8
o
C-32
1.8K-460
Torque Lb
f
.ft
Lb
f
.in
N.m
N.m
1.356
0.113
0.738
8.85
Viscosity,
Kinematic,
Viscosity
Lb
f
.sec/ft
2
Ft
2
/sec.
N.s/m
2
m
2
/s
47.88
0.093
0.021
10.76
C Btu/Lbm.R
kJ/kg.K
Btu/Lbm.R=4.2
kJ/kg.K
µ
Btu/Lbm kJ/kg
Btu/Lbm=2.326
kJ/kg
υ
m
3
/kg Ft3/slug
m
3
/kg=515.384 ft
3
/slug
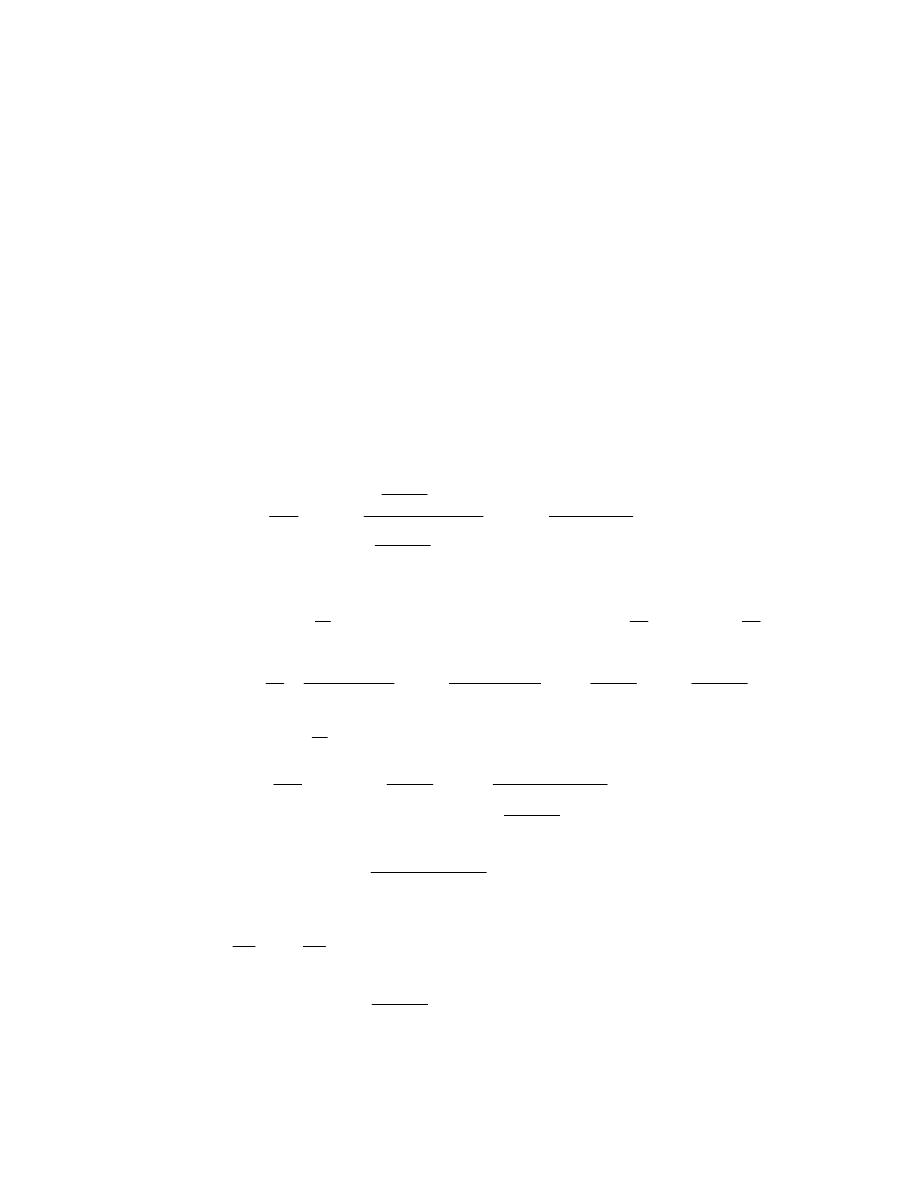
)
9
(
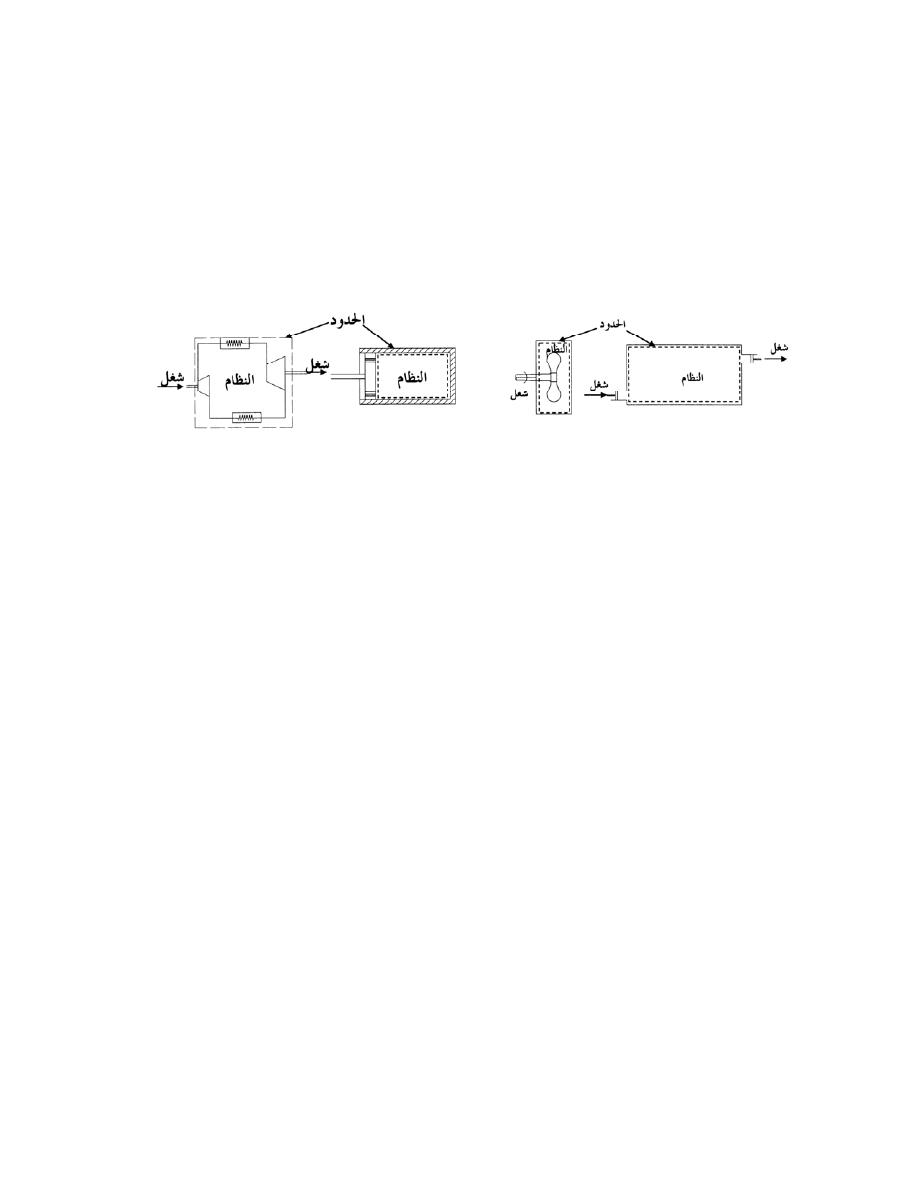
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
)
1.1
(
ﺍﺫﺍ ﻋﻠﻤﺕ ﺍﻥ
:
-
1Lb
f
= 4.448N = 4.448×10
-3
kN, 1 in
)
ﺇﻨﺞ
( = 2.54 cm = 0.0254m
h.p = 550 Lb
f
.ft/s, 1 Lbm = 0.454 kg, 1 bar = 10
5
N/m
2
1kW =kJ / s = kN.m/s, ,1 ft
)
ﻗﺩﻡ
( = 12 in
ﺤﻭل
:
-
1-
bar
→ PSI = Lb
f
/ in
2
2-
h.p
→ kW = kN . m/s
3-
KW
→ h.p
4-
ρHg → Lb
m
/ in
3
5-
kW h
→ kJ
6-
kW h
→ kcal
3
m
3
m
3
3
m
3
Hg
/in
Lb
0.49
in
61023.744
1
Lb
2.2
13600
in
0.0254
1
1
Lb
0.454
1
13600
m
kg
13600
4
=
×
×
=
⎟
⎠
⎞
⎜
⎝
⎛
×
×
=
=
ρ
−
2
f
2
f
5
2
2
f
5
2
5
/in
Lb
14.5
in
1550
Lb
0.225
10
in
0.0254
1
Lb
4.448
1
10
m
N
10
bar
1
1
=
×
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
=
−
s
m
.
kN
0.74
s
m
0.0254
12
kN
10
4.448
550
s
ft
Lb
550
h.p
2
3
-
f
=
×
×
×
×
=
×
×
=
−
s
ft
Lb
737.5
ft
0.3048
1
Lb
4.448
1000
ft/s
0.0254
12
1
Lb
10
.
4.448
1
s
m
.
kN
W
k
3
f
f
f
3
-
×
=
×
=
×
×
=
=
−
kJ
3600
3600S
s
kJ
h
s
kJ
kWh
5
=
×
=
×
=
−
kcal
859.845
4.1868
1
3600
kJ
3600
kWh
6
=
×
=
=
−
)
10
(
)
1.3
(
-
ﺘﻌﺎﺭﻴﻑ ﻭﻤﻔﺎﻫﻴﻡ ﺍﺴﺎﺴﻴﺔ
Fundamental Concepts & Definitions
)
1.3.1
(
-
ﺍﻟﻨﻅﺎﻡ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ
Thermodynamic System
ﻫﻭ ﻜﻤﻴﺔ ﻤﺤﺩﻭ
ﻼﻑـﻐﺒ ﺔـﻁﺎﺤﻤ ﺩﻭﺩﺤﻤ ﺯﻴﺤ لﺨﺍﺩ ﺓﺩﺎﻤﻟﺍ ﻥﻤ ﺔﺘﺒﺎﺜﻭ ﺓﺩ
(envelope)
ﺭﺍﺩـﻴ ،
ﺩﺭﺍﺴﺔ ﺴﻠﻭﻜﻬﺎ
.
ﻗﺩ ﻴﻜﻭﻥ ﺍﻟﻨﻅﺎﻡ ﺤﻘﻴﻘﻲ ﺍﻭ ﻤﺜﺎﻟﻲ
.
ﺒﺱـﻜﻤﺒ ﺭﻭﺼـﺤﻤ ﺯﺎﻐﻜ ﺓﺩﺎﻤﻟﺍ ﻥﻤ ﺔﻴﻤﻜ ﻭﻫ ﻲﻘﻴﻘﺤﻟﺍ
ﺩﺍﺨل ﺍﺴﻁﻭﺍﻨﺔ
.
ﻲـﻓ ﺩﻭـﺠﻭﻤ ﺭـﻴﻏ ﻭﻫﻭ ،ﺔﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜﻟﺍ لﺌﺎﺴﻤﻟﺍ لﻴﻬﺴﺘﻟ ﻱﺭﻅﻨ ﻡﺎﻅﻨ ﻭﻬﻓ ﻲﻨﺎﺜﻟﺍ ﺎﻤﺍ
ﺃﻱ ﻨﻅﺎﻡ،ﺔﻌﻴﺒﻁﻟﺍ
ﺍﻓﺘﺭﺍﻀﻲ
.
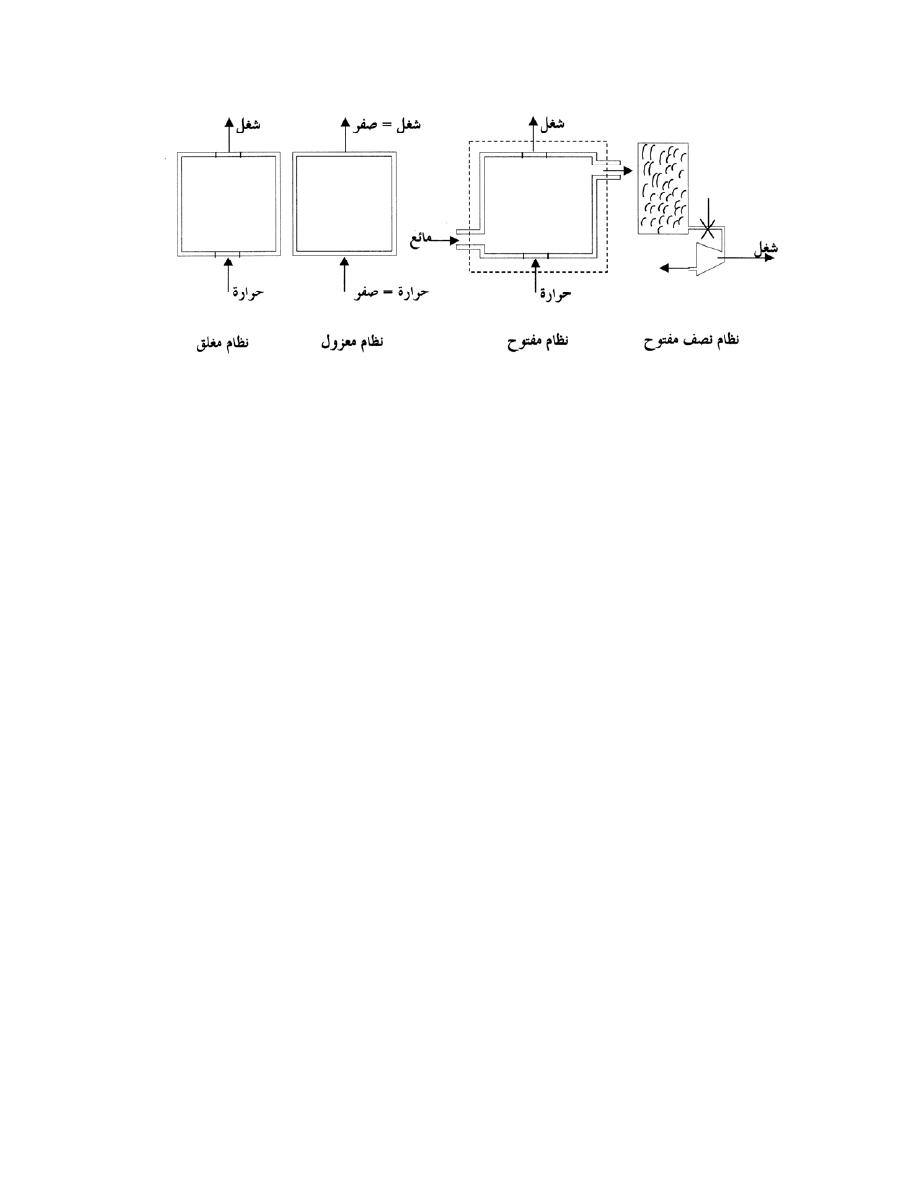
ﺸﻜل
)
1.3
(
-
ﺍﻟﻨﻅﺎﻡ
ﻴﺤﺎﻁ ﺍﻟﻨﻅﺎﻡ ﺒﺤﺩﻭﺩ
(Boundary)
ﺎـﻤﻜ ،ﺱﺒﻜﻤﻟﺍﻭ ﺔﻨﺍﻭﻁﺴﻻﺍ ﻥﺍﺭﺩﺠﻜ ﺔﺘﺒﺎﺜ ﺔﻴﻘﻴﻘﺤ ﻥﻭﻜﺘ ﺩﻗ ،
ﻓﻲ ﺍﻟﺸﻜل
)
1.3
.(
ﺩﺩـﻤﺘ ﻭﺍ ﻁﺎﻐﻀﻨﺍ ﻭﺍ ،ﻭﺠﻟﺍ ﻲﻓ ﻙﺭﺤﺘﻤﻟﺍ ﻥﺎﺨﺩﻟﺎﻜ ﺓﺭﻴﻐﺘﻤ ﺔﻴﻤﻫﻭ ﺩﻭﺩﺤﻟﺍ ﻥﻭﻜﺘ ﺩﻗ ﻭﺍ
ﺤﻴﺙ ﻴﻨﺘﻘل ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﻋﺒﺭ ﺍﻟﺤﺩﻭﺩ،ﺯﺎﻐﻟﺍ ﻥﻤ ﺔﻴﻤﻜ
.
ﻭﻜل ﻤ
ﺎ ﻴﻘﻊ ﺨﺎﺭﺝ ﺤﺩﻭﺩ ﺍﻟﻨﻅﺎﻡ ﻫﻭ ﺍﻟﻤﺤﻴﻁ
(Surroundings)
ﻠﻭﻙـﺴ ﻲـﻓ ﺭـﺸﺎﺒﻤ ﺭﻴﺜﺄﺘ ﻪﻟ
ﻭﺒﺎﻟﺘﺎﻟﻲ ﻗﺩ ﻴﺘﺄﺜﺭ ﺒﺎﻟﺘﻐﻴﺭﺍﺕ ﺍﻟﺤﺎﺼﻠﺔ ﺩﺍﺨل ﺍﻟﻨﻅﺎﻡ،ﻪﻌﻤ ﺔﻗﺎﻁﻟﺍ لﺩﺎﺒﺘﻴ ﻪﻨﻻ ،ﻡﺎﻅﻨﻟﺍ
.
ﻴﻁـﺤﻤﻟﺍ لﻜﺸﻴ ﺎﻤﺒﺭ
ﻨﻔﺴﻪ ﻨﻅﺎﻤﺎﹰ ﺁﺨﺭ
.
ﻟﺤﺩﻭﺩ ﺍﻟﻨﻅﺎﻡ ﺨﻭﺍﺹ ﻤﻌﻴﻨﺔ ﺘﺴﻤﺢ ﺍﻭ ﻻ ﺘﺴﻤﺢ ﺒﺘﺒﺎﺩل ﺍﻟﻁﺎﻗﺔ ﺍﻭ ﺍﻟﻤﺎﺩﺓ ﻤﻊ ﺍﻟﻤ
ﻁـﺴﻭﻟﺍ ﻭﺍ ﻁﻴـﺤ
ﺍﻟﻤﺤﻴﻁ
(Surroundings)
ﺎﻡـﻅﻨﻟﺍ لﺨﺍﺩ ﻡﺘﺘ ﻲﺘﻟﺍ ﺕﺍﺭﻴﻐﺘﻟﺎﺒ ﺭﺜﺄﺘﻴ ﻱﺫﻟﺍﻭ ﺎﻡﻅﻨﻟﺎﺒ ﻁﻴﺤﻤﻟﺍ ﺯﻴﺤﻟﺍ ﻭﻫﻭ
.
ﻟﺫﻟﻙ ﻭﻜﻤﺎ ﻤﺒﻴﻥ ﻓﻲ ﺍﻟﺸﻜل
)
1.4
(
ﺘﺼﻨﻑ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻰ ﺍﻻﻨﻭﺍﻉ ﺍﻵﺘﻴﺔ
:
ﺃ
-
ﺍﻟﻨﻅﺎﻡ ﺍﻟﻤﻐﻠﻕ
)
ﻏﻴﺭ ﻤﻌﺯﻭل
(
Closed System
ﻫﻭ ﺍﻟﻨﻅﺎﻡ ﺍﻟﺫﻱ ﻻ ﺘﺴﻤﺢ ﺤﺩﻭﺩﻩ ﺒﺄﻨﺘﻘﺎل ﺍﻟﻤﺎﺩﺓ ﺩﺍﺨل
ﺴﻤﻰـﻴ ﻙﻟﺫﻟ ،ﺔﺘﺒﺎﺜ ﺔﻠﺘﻜﻟﺍ ﻰﻘﺒﺘ ﻱﺃ ،ﻡﺎﻅﻨﻟﺍ
ﺒﻨﻅﺎﻡ ﺍﻟﻜﺘﻠﺔ ﺍﻟﻤﺤﺩﺩﺓ
.
ﻭﻟﻜﻥ ﻴﺘﻡ ﺍﻨﺘﻘﺎل ﺍﻟﻁﺎﻗﺔ
)
ﺸﻐل ﺍﻭ ﺤﺭﺍﺭﺓ
(
ﻜﻐﺎﺯ ﻤﺤﺼﻭﺭ ﺒﻤﻜﺒﺱ،ﻁﻘﻓ ﺩﻭﺩﺤﻟﺍ ﺭﺒﻋ
ﺩﺍﺨل ﺍﺴﻁﻭﺍﻨﺔ
.
ﺍﻭ ﻜﺎﻟﻤﺭﺠل ﺍﻟﺒﺨﺎﺭﻱ ﻓﻲ ﺍﺜﻨﺎﺀ ﻓﺘﺭﺓ ﺒﺩﺍﻴﺔ ﺍﻟﺘﺸﻐﻴل ﻟﻠﺤﺼﻭل ﻋﻠﻰ ﻀﻐﻁ ﻤﻌﻴﻥ ﻟﻠﺒﺨﺎﺭ
.
)
11
(
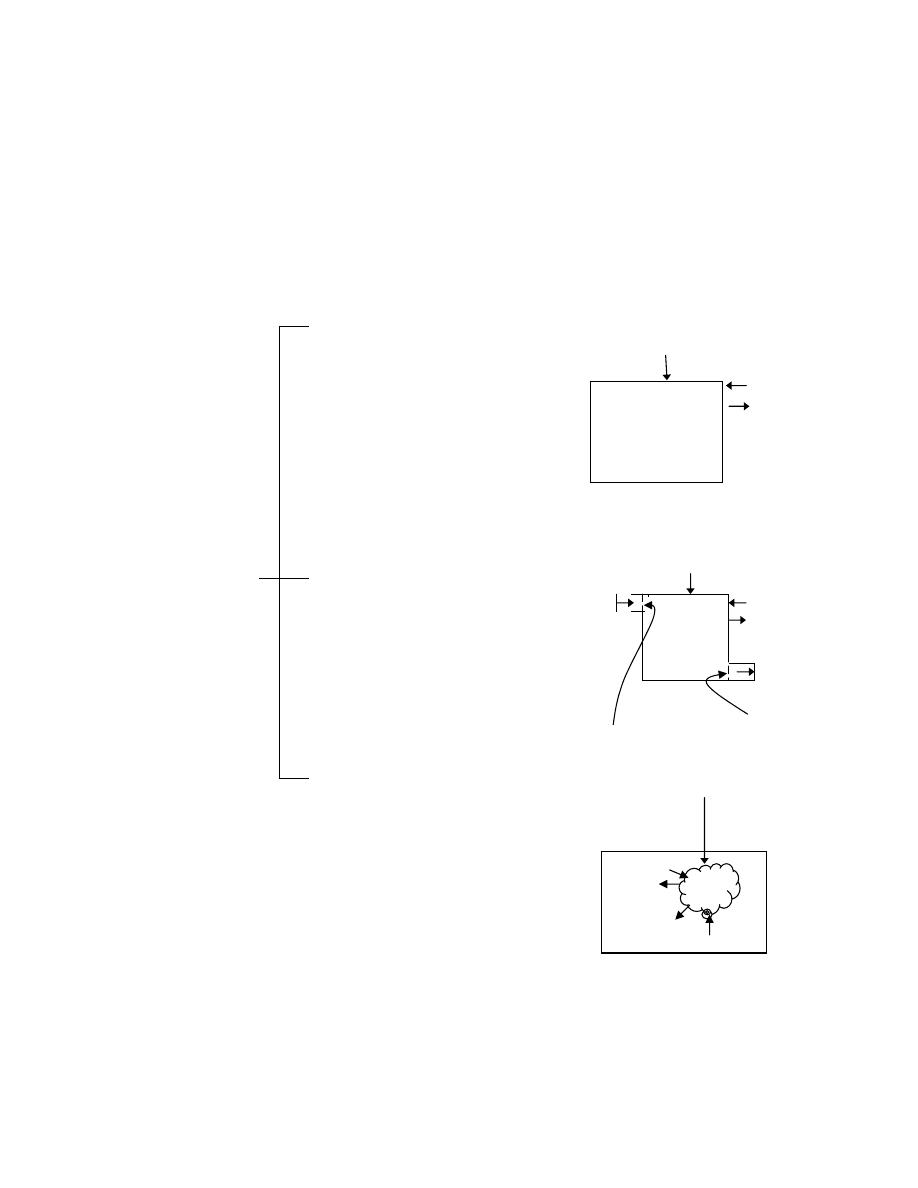
ﺸﻜل
)
1.4
(
-
ﺍﻨﻭﺍﻉ ﺍﻻﻨﻅﻤﺔ
ﺏ
-
ﺍﻟﻨﻅﺎﻡ
ﺍﻟﻤﻌﺯﻭل
Isolated System
ﺄﺜﺭـﺘﻴ ﻻ ﻪـﻨﻭﻜﻟ ،ﹰﺎـﺘﺒﺎﺜ ﻪﻴﻓ ﺔﻗﺎﻁﻟﺍ ﻉﻭﻤﺠﻤ ﻰﻘﺒﻴ ﻱﺃ ،ﺔﻗﺎﻁﻟﺍ ﻭﺍ ﺓﺩﺎﻤﻟﺍ لﺎﻘﺘﻨﺄﺒ ﻩﺩﻭﺩﺤ ﺢﻤﺴﺘ ﻻ
ﺒﺎﻟﻭﺴﻁ ﺍﻟﻤﺤﻴﻁ
.
ﻤﺜﺎل ﺍﻟﺘﺭﻤﺱ ﺍﻟﻤﻭﻀﻭﻉ ﺒﺩﺍﺨﻠﻪ ﻤﺎﺀ ﺒﺎﺭﺩ ﺍﻭ ﺴﺎﺨﻥ
.
ـﺠ
-
ﺍﻟﻨﻅﺎﻡ ﺍﻟﻤﻔﺘﻭﺡ
Open System
ﻫﻭ ﺍﻟﻨﻅﺎﻡ ﺍﻟﺫﻱ ﺘﺴﻤﺢ ﺤﺩﻭﺩﻩ ﺒﺄﻨﺘﻘﺎل ﺍﻟﻤﺎﺩﺓ ﻭﺍﻟﻁﺎﻗﺔ
)
ﺸ
ﻐل ﺍﻭ ﺤﺭﺍﺭﺓ
(
ﺒﻌﻤﻠﻴﺔ ﺠﺭﻴﺎﻨﻴﺔ
.
ﺴﻤﻰـﻴ
ﻜﺎﻟﻤﺎﺀ ﻓﻲ ﺍﻟﻤﺭﺠل ﺤﻴﺙ ﻴﻤﺘﺹ ﺤﺭﺍﺭﺓ ﻭﻴﻔﻘﺩ ﺠﺯﺀ ﻤﻥ ﻜﺘﻠﺘﻪ ﺨﻼل ﺍﻟﺘﺒﺨﺭ،ﺩﺩﺤﻤﻟﺍ ﻡﺠﺤﻟﺍ ﻡﺎﻅﻨﺒ
.
ﺨﻠﻴﻁ
ﺍﻟﻐﺎﺯﺍﺕ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﻤﺤﺭﻙ ﺍﺤﺘﺭﺍﻕ ﺩﺍﺨﻠﻲ ﻴﺘﺨﻠﺹ ﻤﻥ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﻐﺎﺯﺍﺕ ﻤﻥ ﺨﻼل ﺍﻟﻌﺎﺩﻡ
.
ﺍﻥ ﺍﻟﻤﺎﺩﺓ
ﺍﻤﺎ ﺍﻟﻁﺎ،ﺕﺎﺤﺘﻓ لﻼﺨ ﻥﻤ ﺝﺭﺨﺘ ﻭﺍ لﺨﺩﺘ ﻥﺍ ﻥﻜﻤﻴ
ﻗﺔ ﻓﺘﻨﺘﻘل ﻋﺒﺭ ﺍﻟﺤﺩﻭﺩ
.
ﺍﺫﺍ ﻜﺎﻨﺕ ﺍﻟﻜﺘﻠﺔ ﺒﻭﺤﺩﺓ ﺍﻟﺯﻤﻥ ﺍﻟﺩﺍﺨﻠﺔ ﻭﺍﻟﺨﺎﺭﺠﺔ ﻤﺘﺴﺎﻭﻴﺔ ﻓﺈﻨﻬﺎ ﺘﺒﻘﻰ ﺜﺎﺒﺘﺔ ﻭﺘﺴﻤﻰ ﺒﻌﻤﻠﻴﺔ ﺍﻟﺠﺭﻴﺎﻥ
ﺍﻟﻤﺴﺘﻘﺭ ﻜﻤﺎ ﻓﻲ ﺍﻟﺘﻭﺭﺒﻴﻥ ﺍﻭ ﻀﺎﻏﻁ ﺍﻟﻬﻭﺍﺀ
.
ﺩ
-
ﺍﻨﻅﻤﺔ ﺍﺨﺭﻯ
ﺔـﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺍﺩﻋ ﺎﻤ ﺔﻗﺎﻁﻟﺍﻭ ﺔﻠﺘﻜﻟﺍ ﻪﻴﻓ لﻘﺘﻨﺘ ﻱﺫﻟﺍ ﻲﺘﺎﺒﻴﺩﻻﺍ ﻡﺎﻅﻨﻟﺎﻜ ﻯﺭﺨﺍ ﺔﻤﻅﻨﺍ ﻙﺎﻨﻫﻭ
ﺘﻜﻭﻥ ﻗﻴﻤﺘﻬﺎ ﺼﻔﺭ ﻤﺜل ﺍﻟﺘﻭﺭﺒﻴﻥ ﺍﻟﺒﺨﺎﺭﻱ ﺍﻟﻤﻌﺯﻭل ﺍﻟﺘﺎﻡ
.
ﻭﻫﻨﺎﻙ ﺍﻨﻅﻤﺔ ﻨﺼﻑ ﻤﻔﺘﻭﺤﺔ ﺘﺴﻤﺢ ﺒﺩﺨﻭل ﺍﻭ
ﺨﺭﻭﺝ ﺍﻟﻜﺘﻠﺔ ﻓﻘﻁ ﻤﺜل ﻗﻨﻴﻨﺔ ﺍﻟﻐﺎﺯ
.
ﻓﻲ ﺒﻌﺽ ﺍﻻﺤﻴﺎﻥ ﺘﻜﻭﻥ ﺍﻟﻤﻨﻅﻭﻤﺔ ﻤﻐﻠﻘﺔ ﻓﻲ ﻟﺤﻅﺔ ﻤﻌﻴﻨﺔ ﻭﻤﻔﺘﻭﺤﺔ ﻓﻲ ﻟﺤﻅﺔ ﺍﺨﺭﻯ
.
ﻤﺜﺎل ﺫﻟﻙ
ﺍﺴﻁﻭﺍﻨﺔ ﻤﺤﺭﻙ ﺍﺤﺘﺭﺍﻕ ﺩﺍﺨﻠﻲ
.
ﺘﻜﻭﻥ ﺍﻟﻤﻨﻅﻭﻤﺔ ﺍﻟﻜﻠﻴﺔ
(Total System)
ﺩـﻗﻭ ،ﺓﺩـﻘﻌﻤﻭ ﺓﺭﻴﺒﻜ ﹰﺓﺩﺎﻋ
ﻴﻤﻜﻥ ﺘﺠﺯﺌﺘﻬﺎ ﻭﻤﻥ ﺜﻡ ﺠﻤﻊ ﺃﺠﺯﺍﺀ ﺍﻟﻤﻨﻅﻭﻤﺔ ﺍﻟﻤﺠﺯﺃﺓ
.
ﻲـﺘﻟﺍ ﺔﻘﻠﻐﻤﻟﺍ ﺔﻴﺌﺎﺒﺭﻬﻜﻟﺍ ﺓﺭﺩﻘﻟﺍ ﺔﻁﺤﻤ ﻙﻟﺫ لﺎﺜﻤ
)
12
(
ﻏﻼﻑ ﻓﻴﺯﻴﺎﻭﻱ
)
ﺍﻟﻤﻨﻴﻭﻡ
(
ﻁﺎﻗﺔ
ﺨﺯﺍﻥ ﻤﺎﺀ
)
ﻨﻅﺎﻡ ﻤﻐﻠﻕ
(
ﻏﻼﻑ ﺨﻴ
ﺎﻟﻲ
ﻜﺘﻠﺔ
ﻤﻨﺘﻘﻠﺔ
ﻁﺎﻗﺔ ﻤﻨﺘﻘﻠﺔ
ﺨﺯﺍﻥ ﻤﺎﺀ
)
ﻨﻅﺎﻡ ﻤﻔﺘﻭﺡ
(
ﻴﻤﻜﻥ ﺩﺭﺍﺴﺔ ﺍﺠﺯﺍﺌﻬﺎ
)
ﺍﻟﻤﻀﺨﺎﺕ،ﻥﻴﺒﺭﻭﺘﻟﺍ ،ﻱﺭﺍﺭﺤﻟﺍ لﺩﺎﺒﻤﻟﺍ ،لﺠﺭﻤﻟﺍ
…
ﺍﻟﺦ
(
،ﺔـﺤﻭﺘﻔﻤ ﺕﺎﻤﻭﻅﻨﻤﻜ
ﺃﻱ ﺍﻥ ﺍﻟﻤﺎﺌﻊ ﻴﺩﺨل ﻭﻴﺨﺭﺝ ﻤﻥ ﻜل ﻭﺍﺤﺩﺓ ﻤﻥ ﻫﺫ
ﻩ ﺍﻟﻤﻨﻅﻭﻤﺎﺕ ﺍﻟﻤﺼﻐﺭﺓ ﺍﻟﻤﻔﺘﻭﺤﺔ
.
ـﻫ
-
ﻏﻼﻑ ﺍﻟﻨﻅﺎﻡ
ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ
.
ﻴﻤﻜﻥ ﻓﻬﻡ ﺍﻟﻐﻼﻑ ﺍﻟﻤﺤﻴﻁ ﺒﺎﻟﻨﻅﺎﻡ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ ﻤﻥ ﺨﻼ ل ﺍﻟﻤﺨﻁﻁ ﺍﻟﺘﺎﻟﻲ
:
(1). Physical
ﺍﻟﻔﺯﻴﺎﻭﻱ
.*
ﻻﻴﺴﻤﺢ ﺒﺄﻨﺘﻘﺎل ﺍﻟﻜﺘﻠﺔ
.
ﺎﻥـﻜ ﺍﺫﺄـﻓ
لـﺜﻤﻴ ﻕﺍﺭـﺘﺤﻻﺍ ﺔﻓﺭﻏ ﻲﻓ ﻁﻴﻠﺨﻟﺍ
ﻨﻅﺎﻡ ﻓﺄﻥ ﺠﺩ
\
ﺭﺍﻥ ﺍﻻﺴﻁﻭﺍﻨﺔ ﻭﺴﻁﺢ
ﺭﻙــﺤﻤﻟﺍ ﺀﺎــﻁﻏﻭ ﺱﺒــﻜﻤﻟﺍ
لـﺜﻤﺘ ﺔـﻘﻠﻐﻤ ﻲـﻫﻭ ﺕﺎﻤﺎﻤﺼﻟﺍﻭ
ﺠﻤﻴﻌﻬﺎ ﺍﻟﻐﻼﻑ ﺍﻟﻔﻴﺯﻴﺎﻭﻱ
.
(2) Party Physical and Party
Immaginary.
ﻓﻴﺯﻴﺎﻭﻱ ﺠﺯﺌﻴﺎﹰ ﻭﺨﻴﺎﻟﻲ ﺠﺯﺌﻴﺎﹰ
.*
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺼﻤﺎﻡ ﺍﻭ ﺍﻜﺜﺭ ﻤﻔﺘﻭﺤﺎ
ﺀﺯـﺠﻟﺍ لﺜﻤﻴ ﺡﻭﺘﻔﻤﻟﺍ ﻡﺎﻤﺼﻟﺍ ﻥﺄﻓ
ﺍﻟﺨﻴﺎﻟﻲ
.
Boundary
ﺍﻟﻐﻼﻑ
(3) Immaginary
ﺍﻟﺨﻴﺎﻟﻲ
.*
لـﺨﺍﺩ ﺀﺍﻭـﻬﻟﺍ ﻥﻤ ﺓﺭﻴﻐﺼ ﺔﻴﻤﻜ
ﻓﻨﺘﺨﻴل ﺍﻥ ﻟﻬﺫﻩ ﺍﻟﻜﻤﻴﺔ ﻏﻼﻓﺎﹰ،ﺔﻓﺭﻏ
ﺕﺍﺭـﻴﻐﺘ ﺔـﺴﺍﺭﺩ ﻥﻤ ﻥﻜﻤﺘﻨ ﻲﻜﻟ
ﺔﻗﺎﻁﻟﺍ لﺎﻘﺘﻨﺍ ﺏﺒﺴﺒ ﺀﺍﻭﻬﻟﺍ ﺹﺍﻭﺨ
ﻭﺍﻟﻜﺘﻠﺔ ﺍﻟﻰ ﺍﻟﻬﻭﺍﺀ
.
ﻫﻭﺍﺀ
ﺍﻟﺠﺯﺀ ﺍﻟﻔﻴﺯﻴﺎﻭﻱ ﻤﻥ ﺍﻟﻐﻼﻑ
ﻁﺎﻗﺔ
ﻤﺎﺌﻊ
ﻤﺎﺌﻊ
ﺍﻟﺠﺯﺀ ﺍﻟﺨﻴﺎﻟﻲ ﻤﻥ ﺍﻟﻐﻼﻑ

)
13
(
)
1.3.2
(
-
ﺍﻟﻤﺴﺎﺤﺔ
Area
ﻭﺘﺤﺴﺏ ﺒﺤﺎﺼل،ﺎﻬﻨﻤ ﻑﻭﺸﻜﻤﻟﺍ ﺀﺯﺠﻟﺍ ﻲﻫ ﻡﺴﺠﻟﺍ ﺔﺤﺎﺴﻤ ﻥﺃ
ﻀﺭﺏ ﺍﻟﻁﻭل ﻓﻲ ﺍﻟﻌﺭﺽ
.
ﻭﺤﺩﺓ
ﺍﻟﻤﺴﺎﺤﺔ
)
m
2
(
ﻭﻥـﻜﻴ ﺎﻤﺩﻨﻋﻭ ، ﺱﺒﻜﻤﻟﺍ ﺢﻁﺴ ﺔﺤﺎﺴﻤﻜ ﺔﻴﺭﺌﺍﺩﻟﺍ ﺡﻭﻁﺴﻟﺍ ﺔﻟﺎﺤ ﻲﻓﻭ
)
D
(
ﺭـﻁﻗ لـﺜﻤﺘ
ﺍﻟﺩﺍﺌﺭﺓ ﻓﺎﻥ ﺍﻟﻤﺴﺎﺤﺔ
)
A
(
ﺘﺴﺎﻭﻱ
:
)
1
.
1
(
4
D
A
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
×
π
=
)
1.3.3
(
-
ﺍﻟﺤﺠﻡ
)
Volume
(
ﺤﺠﻡ ﺍﻟﺠﺴﻡ
)
ﺍﻭ ﺍﻟﻤﺎﺩﺓ
(
ﺴﺎﺤﺘﻪـﻤ ﺏﺭـﻀ لـﺼﺎﺤ ﻱﻭﺎﺴﻴﻭ ﺯﻴﺤ ﻥﻤ ﻪﻠﻐﺸﻴﺎﻤ ﺭﺍﺩﻘﻤ ﻭﻫ
ﻲـﻓ
ﺍﺭﺘﻔﺎﻋﻪ
.
ﻭﺤﺩﺓ ﺍﻟﺤﺠﻡ ﻫﻲ
)
m
3
(
ﺍﻭ ﺍﻟﻠﺘﺭ
)
1 Liter = 1dm
3
=10
-3
m
3
.(
ﺩـﻨﻋ ﹰﻼﺜﻤ ﻪﺘﻴﻤﻫﺃ ﺭﻬﻅﺘﻭ
ﺀﺎﻨﺜﺃ ﺱﺒﻜﻤﻟﺍ ﻪﻠﻐﺸﻴ ﻱﺫﻟﺍ ﺯﻴﺤﻟﺍ ﺱﺎﻴﻗ ﺩﻨﻋ ﺭﺨﺍ ﻰﻨﻌﻤﺒ ﻭﺃ ،ﻙﺭﺤﻤﻟﺍ ﺔﻨﺍﻭﻁﺴﺍ لﺨﺍﺩ ﺱﺒﻜﻤﻟﺍ ﺔﺤﺍﺯﺇ ﺱﺎﻴﻗ
ﺘﺤﺭﻜﻪ ﺨﻼل ﺍﺤﺩ ﺍﻻﺸﻭﺍﻁ ﺩﺍﺨل ﺍﻻﺴﻁﻭﺍﻨﺔ
.
ﻓﺄﺫﺍ ﻜﺎﻥ
)
L
(
ﺘﻤﺜل ﻁﻭل ﺍﻟﺸﻭﻁ ﻭﺃﻥ
(ِ
A
(
ﻓﺄﻥ،ﺔﺤﺎﺴﻤﻟﺍ
ﺍﻟﺤﺠﻡ
)
V
(
ﻴﺴﺎﻭﻱ
:
3
2
m
m
m
)
2
.
1
(
L
A
V
=
×
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
×
=
ﺎـﻬﻤﺠﺤ لـﻘﻴ ﻁﻐﻀـﻨﺘ ﺎﻤﺩـﻨﻋﻭ ،ﺎـﻬﻤﺠﺤ ﺩﺍﺩﺯـﻴ ﺓﺩﺎـﻤﻟﺍ ﺩﺩـﻤﺘﺘ ﺎﻤﺩﻨﻋ
.
ﻭﻋﻲـﻨﻟﺍ ﻡـﺠﺤﻟﺍ ﺎـﻤﺍ
)
Specific Volume
(
ﻓﻬﻭ ﺤﺠﻡ ﻭﺤﺩﺓ ﺍﻟﻜﺘﻠﺔ
)
m
(
ﺭﻤﺯﻩ
)
υ
(
ﻭﻴﺴﺎﻭﻱ
:
)
3
.
1
(
m
V
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
υ
ﺍﻤﺎ ﺍﻟﺜﻘل ﺍﻭ ﺍﻟﻭﺯﻥ ﺍﻟﻨﻭﻋﻲ
)
Specific Gravity
(
ﻓﻬﻭ ﺍﻟﻨﺴﺒﺔ ﺒﻴﻥ ﻜﺜﺎﻓﺔ ﺍﻟﻤﺎﺩﺓ ﺍﻟﻰ ﻜﺜﺎﻓﺔ ﺍﻟﻤﺎﺀ
.
)
1.3.4
(
-
ﺍﻟﻜﺜﺎﻓﺔ ﺍﻟﻜﺘﻠﻴﺔ
Mass Density
.
ﻫﻲ ﻜﺘﻠﺔ ﻭﺤﺩﺓ ﺍﻟﺤﺠﻭﻡ
.
ﻀﻐﻁـﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺕﻭﺒﺜ ﺝﺩﻨﻋ ﺔﺘﺒﺎﺜ ﻰﻘﺒﺘ
.
ﺼﺎﺭﺍﹰـﺘﺨﺃ ﻰﻤﺴـﺘ
ﻴﺭﻤﺯ ﻟﻬﺎ ﺒﺎﻟﺤﺭﻑ ﺍﻟﻴﻭﻨﺎﻨﻲ ﺭﻭ،ﺔﻓﺎﺜﻜﻟﺎﺒ
)
ρ
(
ﻭﺤﺩﺘﻬﺎ
)
kg/m
3
.(
ﻭ،ﻲﻋﻭﻨﻟﺍ ﻡﺠﺤﻟﺍ ﺏﻭﻠﻘﻤ ﻲﻫ
ﺘﺴﺎﻭﻱ
:
)
4
.
1
(
1
V
m
⋅
⋅
⋅
⋅
⋅⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅⋅
⋅
⋅
⋅
υ
=
=
ρ
ﺄﻥـﻓ ﺍﺫـﻟ ،ﻯﺭﺨﻻﺍ ﺏﻭﻠﻘﻤ ﺓﺩﺤﺍﻭﻟﺍ ﻥﻻ ﺎﻤﻬﻀﻌﺒ ﻥﻋ ﻥﻴﺘﻠﻘﺘﺴﻤ ﺭﻴﻏ ﺔﻓﺎﺜﻜﻟﺍﻭ ﻲﻋﻭﻨﻟﺍ ﻡﺠﺤﻟﺍ ﻥﺃﻭ
ﻴﺔــﺼﺎﺨﺒ ﺕﺴــﻴﻟ ﺔــﻓﺎﺜﻜﻟﺍ
.
ﺎﺀــﻤﻟﺍ ﺔــﻓﺎﺜﻜ ﻥﺍ
)
1000kg/m
3
(
ﻕــﺒﺌﺯﻟﺍﻭ
)
13600kg/m
3
.(
ﻲــﻓﻭ
ﺍﻟﺜﺭﻤﻭﺩﺍﻴﻨﻤﻜﺱ ﻴﺴﺘﻌﻤل ﺍﻟﺤﺠﻡ ﺒﺩﻻ ﻤﻥ ﺍﻟﻜﺜﺎﻓﺔ
.

)
14
(
)
1.3.5
(
-
ﺍﻟﺴﺭﻋﺔ
Velocity
ﻭﻫﻲ ﻨﻭﻋﺎﻥ،ﻡﻴﻘﺘﺴﻤ ﻁﺨ ﻲﻓ ﻡﺴﺠ ﺔﻜﺭﺤ لﺩﻌﻤ ﻲﻫ
:
1
.
ﺍﻟﺴﺭﻋﺔ
ﺍﻟﻤﻨﺘﻅﻤﺔ
:
ﻭﻫﻲ ﻤﻌﺩل ﺤﺭﻜﺔ ﺍﻟﺠﺴﻡ ﻓﻲ ﺨﻁ ﻤﺴﺘﻘﻴﻡ ﺒﺤﻴﺙ ﻴﺜﺒﺕ ﻤﻘﺩﺍﺭﻫﺎ ﻓﻲ ﻜل ﻭﺤﺩﺓ
ﺯﻤﻨﻴﺔ
.
ﺩﺓـﺤﻭ ﻲـﻓ ﻡﻴﻘﺘﺴﻤ ﻁﺨ ﻲﻓ ﺔﻤﻅﺘﻨﻤ ﺔﻜﺭﺤﺒ ﻡﺴﺠﻟﺍ ﺎﻬﻌﻁﻘﻴ ﻲﺘﻟﺍ ﺔﻓﺎﺴﻤﻟﺎﺒ ﺎﻫﺭﻴﺩﻘﺘ ﻥﻜﻤﻴﻭ
ﺯﻤﻥ
.
ﻓﺄﺫﺍ ﻜﺎﻥ
)
L
(
ﻴﻤﺜل ﺍﻟﻁﻭل ﺒﻭﺤﺩﺍﺕ ﺍﻟﻤﺘﺭ
)
m
(
ﻭ
)t
(
ﺔـﻴﻨﺎﺜﻟﺍ ﺕﺍﺩـﺤﻭﺒ ﻥﻤﺯـﻟﺍ لﺜﻤﺘ
)s
(
ﻓﺴﺘﻜﻭﻥ ﺍﻟﺴﺭﻋﺔ
)
C
(
ﺘﺴﺎﻭﻱ
:
)
5
.
1
(
s
m
t
L
C
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
2
.
ﺍﻟﺴﺭﻋﺔ ﺍﻟﻤﺘﻐﻴﺭﺓ
:
ﺃﻱ ﺍﻥ،ﻯﺭـﺨﺃ ﻰـﻟﺍ ﺔـﻅﺤﻟ ﻥﻤ ﺓﺭﻴﻐﺘﻤ ﻡﺴﺠﻟﺍ ﺔﻟﺎﺤ ﻥﻭﻜﺘ ﺎﻤﺩﻨﻋ ﺄﺸﻨﺘ ﻲﻫﻭ
ﻱﺃ ﻲﻓ ﻡﺴﺠﻟﺍ ﺎﻬﻌﻁﻘﻴ ﻲﺘﻟﺍ ﺔﻓﺎﺴﻤﻟﺍ ﺱﻔﻨ ﻱﻭﺎﺴﺘﻻ ﺔﻴﻨﻤﺯ ﺓﺩﺤﻭ ﻱﺃ ﻲﻓ ﻡﺴﺠﻟﺍ ﺎﻬﻌﻁﻘﻴ ﻲﺘﻟﺍ ﺔﻓﺎﺴﻤﻟﺍ
ﻭ
ﺤ
ﺩﺓ ﺯﻤﻨﻴﺔ ﺍﺨﺭﻯ
.
ﻟﻬﺫﺍ ﻴﺤﺴﺏ ﻏﺎﻟﺒﺎﹰ ﻤﺘﻭﺴﻁ ﺴﺭﻋﺔ ﺍﻟﺠﺴﻡ
.
)
1.3.6
(
-
ﺍﻟﺘﻌﺠﻴل
Acceleration
ﻭﻫﻭ ﻤﻌﺩل ﺘﻐﻴﺭ ﺍﻟﺴﺭﻋﺔ
)
C
(
ﻓﻲ ﻭﺤﺩﺓ ﺍﻟﺯﻤﻥ
.
ﺭﻤﺯﻩ
)
a
(
ﻭﻭﺤﺩﺘﻪ
)
m/s
2
(
ﻭﻴﺴﺎﻭﻱ
:
)
6
.
1
(
t
L
t
t
C
a
2
t
L
⋅
⋅
⋅
⋅
⋅
⋅
⋅⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅⋅
⋅
⋅
=
=
=
)
7
.
1
(
t
C
C
a
or
2
1
2
2
aver
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
−
=
ﻭﺘﻌﺠﻴل ﺍﻟﺠﺴﻡ ﺍﻤﺎ ﻤﻨﺘﻅﻤﺎﹰ ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺴﺭﻋﺔ ﺍﻟﺠﺴﻡ
ﻭﺍﻤﺎ ﻤﺘﻐﻴﺭﺍﹰ ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ،ﹰﺎﻤﻅﺘﻨﻤ
ﺏـﺠﻭﻤ ﺎـﻤﺃ ﻙﻟﺫﻜ ﻭﻫﻭ ،ﻪﺘﻤﻴﻗ ﻁﺴﻭﺘﻤ ﺱﺎﻘﻴ ﺓﺭﻴﺨﻻﺍ ﺔﻟﺎﺤﻟﺍ ﻲﻓﻭ ﻡﻅﺘﻨﻤ ﺭﻴﻏ ﻡﺴﺠﻟﺍ ﺔﻋﺭﺴ ﻲﻓ ﺭﻴﻐﺘﻟﺍ
ﺍﻟﻘﻴﻤﺔ ﻓﻴﺯﻴﺩ ﺴﺭﻋﺔ ﺍﻟﺠﺴﻡ ﺍﻟﻤﺘﺤﺭﻙ
)
ﺘﺴﺎﺭﻉ
(
ﻨﻘﺹـﺘﻓ ﺔـﻤﻴﻘﻟﺍ ﺏﻟﺎـﺴ ﺎﻤﺍﻭ ،ﺏﺠﻭﻤﻟﺍ لﻴﺠﻌﺘﻟﺎﺒ ﻰﻤﺴﻴﻭ
ﺴﺭﻋﺘﻪ ﻭﻴﺴﻤﻰ ﺍﻟﺘﺒﺎﻁﺅ
.
)
1.3.7
(
-
ﺍﻟﻘﻭﺓ
Force
ﺍﻥ ﺍﻟﻌ
ﺤﻕـﺴﺍ لـﺒﻗ ﻥﻤ ﺕﻌﻀﻭ ﻲﺘﻟﺍ ﺙﻼﺜﻟﺍ ﺔﻜﺭﺤﻟﺍ ﻥﻴﻨﺍﻭﻗ ﻰﻠﻋ ﺔﻴﻨﺒﻤ ﺔﻜﺭﺤﻟﺍﻭ ﺓﻭﻘﻟﺍ ﻥﻴﺒ ﺔﻗﻼ
ﻨﻴﻭﺘﻥ
.
ﻴﻨﺹ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻋﻠﻰ ﻤﺎﻴﻠﻲ
))
ﻁـﺨ ﻰﻠﻋ ﺔﻤﻅﺘﻨﻤﻟﺍ ﺔﻜﺭﺤﻟﺍ ﻭﺍ ﻥﻭﻜﺴﻟﺍ ﺔﻟﺎﺤ ﻲﻓ ﻡﺴﺠﻟﺍ ﺭﺘﻤﺴﻴ
ﻤﺴﺘﻘﻴﻡ ﺍﻻ ﺍﺫﺍ ﺍﺠﺒﺭ ﻋﻠﻰ ﺘﻐﻴﻴﺭ ﺘﻠﻙ ﺍﻟﺤﺎﻟﺔ ﺒﻔﻌل ﻗﻭﺓ ﺨﺎﺭﺠﻴﺔ
((
.
ﺍﻥ ﺴﻴﺎﺭﺓ ﻭﺍﻗﻔﺔ ﻋﻠﻰ ﻁﺭﻴ،ﻼﺜﻤﻓ
ﻕ ﺍﻓﻘﻲ ﺴﻭﻑ ﺘﺴﺘﻤﺭ ﺒﺎﻗﻴﺔ ﻓﻲ ﺤﺎﻟﺔ ﺍﻟﻭﻗﻭﻑ ﻤﺎﻟﻡ ﺘﺅﺜﺭ ﻋﻠﻴﻬﺎ ﻗﻭﺓ
ﺨﺎﺭﺠﻴﺔ
.
ﻭﻟﻭ ﺃﻥ ﺍﻟﺴﻴﺎﺭﺓ ﻜﺎﻨﺕ ﺘﺘﺤﺭﻙ ﻓﺒﺄﺴﺘﺨﺩﺍﻡ ﺍﻟﻤﻜﺎﺒﺢ ﺴﺘﺘﺒﺎﻁﺄ ﺍﻟﺴﻴﺎﺭﺓ ﻭﺘﺘﻭﻗﻑ
.
ﻭﺘﻥـﻴﻨ ﻥﻭﻨﺎﻗ ﻥﻤﻓ
ﺍﻻﻭل ﻴﻤﻜﻥ ﺘﻌﺭﻴﻑ ﺍﻟﻘﻭﺓ ﻜﺎﺘﺎﻟﻲ
:

)
15
(
))
لـﺠﻌﻴ ﻭﺍ ،ﺔﻜﺭﺤﻟﺍ ﻥﻋ ﺎﻤﺴﺠ ﻑﻗﻭﻴ ﻭﺍ ،ﻥﻭﻜﺴﻟﺍ ﻥﻤ ﻡﺴﺠ ﻙﻴﺭﺤﺘ ﺏﺒﺴﻴ ﺊﺸ ﻱﺃ ﻲﻫ ﺓﻭﻘﻟﺍ
ﺍﻭ
ﻴﺒﻁﺄ ﺍﻭ ﻴﺤﺭﻑ ﺍﻟﺠﺴﻡ ﻋﻥ ﺍﻟﻤﺴﺎﺭ ﺍﻟﻤﺴﺘﻘﻴﻡ ﻭﻴﺠﻌﻠﻪ ﻴﺘﺤﺭﻙ ﺒﻤﺴﺎﺭ ﻤﻨﺤﻨﻲ
((
.
ﻭﻤﻥ ﺍﻨﻭﺍﻋﻬﺎ ﻫﻲ
:
)
1
.(
ﻗﻭﻯ ﺍﻟ
ﺸ
ﺩ ﻤﺜل ﺍﻟﻘﻭﻯ ﺍﻟﺘﻲ ﺘﺠﺫﺏ ﻁﺭﻓﻲ ﻗﻀﻴﺏ ﻤﻥ ﺍﻟﺤﺩﻴﺩ
.
)
2
.(
ﻗﻭﻯ ﺍﻟﻀﻐﻁ ﻤﺜل ﺍﻟﺘﻲ ﺘﺘﻭﻟﺩ ﻋﻠﻰ ﺍﻟﻤﻜﺒﺱ ﻋﻨﺩ ﺍﺤﺘﺭﺍﻕ ﺍﻟﻭﻗﻭﺩ
.
)
3
.(
ﻗﻭﻯ ﺍﻟﺠﺎﺫﺒﻴﺔ ﺍﻟﻨﺎﺘﺠﺔ ﻤﻥ ﺠﺫﺏ ﺍﻻﺭﺽ ﻟﻠﺠﺴﻡ
.
)
4
.(
ﻗﻭﺓ
ﻭﻫﻲ ﺍﻟﻘﻭﺓ ﺍﻟﺘﻲ ﺘﻘﺎﻭﻡ ﺍﻟﺤﺭﻜﺔ ﺒﻴﻥ ﺠﺴﻤﻴﻥ ﻤﺘﻼﺼﻘﻴﻥ،ﻙﺎﻜﺘﺤﻻﺍ
.
ﺭﻤﺯ ﺍﻟﻘﻭﺓ
)
F
.(
)
1.3.8
(
-
ﺍﻟﻜﻠﺘﻠﺔ
Mass
ﻫﻲ ﻤﻘﺩﺍﺭ ﻤﺎ ﻴﺤﺘﻭﻴﻪ ﺍﻟﺠﺴﻡ ﻤﻥ ﻤﺎﺩﺓ ﺍﻭ ﻋﺩﺩ ﺍﻟﺠﺯﻴﺌﺎﺕ
.
ﺭﻤﺯﻫﺎ
)
m
(
ﻭ ﻭﺤﺩﺘﻬﺎ
)
kg
.(
ﻗﻴﻤﺘﻬﺎ ﻻ
ﺘﺘﻐﻴﺭ ﺒﺘﻐﻴﺭ ﺍﻟﻤﻜﺎﻥ
.
ﻓﻜﺘﻠﺔ ﺠﺴﻡ ﺍﻻﻨﺴﺎﻥ ﺜﺎﺒﺘﺔ ﻋﻨﺩ ﻤﺴﺘﻭﻯ ﺴﻁﺢ ﺍﻟﺒﺤﺭ ﺍﻭ ﻓﻲ ﺍﻻﻋ
ﻤﺎﻕ ﺍﻭ ﻋﻠﻰ ﻗﻤﺔ ﺠﺒل
ﺍﻭ ﻓﻲ ﺍﻟﻔﻀﺎﺀ
.
ﻓﺎﺫﺍ ﺃﺜﺭﺕ،ﺔﻜﺭﺤﻟﺍ ﺭﺤ ﻥﻭﻜﻴ ﻥﻴﺤ ﻪﻴﻓ ﺎﻤ ﺓﻭﻗ ﺭﻴﺜﺄﺘ ﻯﺩﻤﺒ ﻥﻴﻌﻤ ﻡﺴﺠﻟ ﺓﺩﺎﻋ ﺱﺎﻘﺘ ﻲﻫﻭ
ﻗﻭﺓ
)
F
(
ﻋﻠﻰ ﺠﺴﻡ ﻤﺎ ﺒﺤﻴﺙ ﻴﺒﺩﺃ ﻤﻥ ﺍﻟﺴﻜﻭﻥ ﻟﻴﺘﺤﺭﻙ ﺒﺘﻌﺠﻴل ﻤﻨﺘﻅﻡ
)
a
(
ﺴﻡـﺠﻟﺍ ﺍﺫـﻫ ﺔﻠﺘﻜ ﻥﺈﻓ
)
m
(
ﺘﺴﺎﻭﻱ
:
)
8
.
1
(
kg
s
/
m
s
/
m
.
kg
s
/
m
N
a
F
m
2
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
=
⇒
=
ﺃﻥ ﻤﺤ
ﺎ
ﻭﻟ
ﺫﺍﺘﻲـﻟﺍ ﺭﻭﺼـﻘﻟﺍ ﻰﻋﺩـﺘ ﺔـﻤﻅﺘﻨﻤﻟﺍ ﺔﻜﺭﺤﻟﺍ ﻭﺃ ﻥﻭﻜﺴﻟﺍ ﺔﻟﺎﺤ ﻰﻠﻋ ﺔﻅﻓﺎﺤﻤﻠﻟ ﻡﺴﺠ ﺔ
)
Inertia
.(
ﻭﻗﺩ ﻭﺠﺩ ﺒﺄﻥ ﻫﺫﻩ ﺍﻟﺨﺎﺼﻴﺔ ﺘﻌﺘﻤﺩ ﻋﻠﻰ ﻜﺘﻠﺔ ﺍﻟﺠﺴﻡ
.
ﺍﻟﻭﺤﺩﺓ ﺍﻟﺩﻭﻟﻴﺔ
)
SI
(
ﻭـﻠﻴﻜﻟﺍ ﻲﻫ ﺔﻠﺘﻜﻠﻟ
ﻏﺭﺍﻡ
)
kg
(
ﺩﻴﻭﻡـﻴﺭﻴﻻﺍﻭ ﻥﻴﺘﻼﺒﻟﺍ ﻥﻤ ﺔﻋﻭﻨﺼﻤ ﺔﻴﻨﺍﻭﻁﺴﺍ ﺔﻠﺘﻜ ﺎﻬﻨﺄﺒ ﺔﻓﺭﻌﻤ ،
)
Platinum
–
aridum
(
ﻤﺤﻔﻭﻅﺔ
ﻓﻲ
)
Severs
(
ﻓﻲ ﻓﺭﻨﺴﺎ
.
ﻭﺍﻟﻭﺤﺩﺓ ﺍﻟﻜﺒﺭﻯ ﻟﻠﻜﺘﻠﺔ ﻫﻲ ﺍﻟﻤﻴﻜﺎﻜﺭﺍﻡ
)
Megagramme
) (
Mg
(
ﺎﻟﻁﻥـﺒ لﻭﺩﻟﺍ ﺽﻌﺒ ﻪﻴﻤﺴﺘﻭ
ﺍﻟﻤﺘﺭﻱ ﻭﺍﻟﻁﻥ
)
tonne
) (
t
(
ﻭﻴﺴﺎﻭﻱ
:
1Mg=1t=10
3
kg=10
6
g
)
1.3.9
(
-
ﺍﻟﺘﻌﺠﻴل ﺍﻻﺭﻀﻲ
Acceleration du to gravity
ﺭﻤﺯﻩ،ﺕﺒﺎﺜﻟﺍ لﻴﺠﻌﺘﻠﻟ ﺕﺒﺎﺜﻟﺍ لﺎﺜﻤﻟﺍ ﻭﻫ
)
g
.(
ﻴﻌﺒﺭ ﻋﻥ ﻗﻭ
ﺓ ﺘﺠﺎﺫﺏ ﺒﻴﻥ ﺍﻻﺭﺽ ﻭﺍﻟﺠﺴﻡ
.
ﻪـﺘﻤﻴﻗ
ﺜﺎﺒﺘﺔ ﻋﻨﺩ ﻤﺴﺘﻭﻯ ﺴﻁﺢ ﺍﻟﺒﺤﺭ ﻭﺘﺒﻠﻎ
)
9.88m/s
2
.(
ﻭﻴﻜﻭﻥ ﺍﻟﻔﺭﻕ ﻋﻨﺩ ﺍﻻﻨﺘﻘﺎل ﻤﻥ ﻤﻨﻁﻘﺔ ﺨﻁ ﺍﻻﺴﺘﻭﺍﺀ
ﺍﻟﻰ ﺍﻟﻘﻁﺏ
)
5
(%
ﺃﻱ
)
9.78m/s
2
(
ﻋﻨﺩ ﺨﻁ ﺍﻻﺴﺘﻭﺍﺀ ﻭ
)
9.832m/s
2
.(
ﻴﻥـﺒﻁﻘﻟﺍ ﺩﻨﻋ
.
ﻪـﺘﻤﻴﻗ ﻥـﻜﻟ
ﺘﻨﺨﻔﺽ ﻜﺜﻴﺭﺍﹰ ﻜﻠﻤﺎ ﺍﺒﺘﻌﺩﻨﺎ ﻋﻥ ﻤﺭﻜﺯ ﺍﻻﺭﺽ ﺤﺘﻰ ﺘﻨﻌﺩﻡ ﺘﻤﺎ
ﻤﺎ ﻓﻲ ﺍﻟﻔﻀﺎﺀ
.
ﺔـﻴﺒﺫﺎﺠﻟﺍ ﺓﻭـﻘﺒ ﺽﺭﻻﺍ ﺯـﻜﺭﻤ ﻭـﺤﻨ ﺏﺫـﺠﻴ ،ﻥﻴـﻌﻤ ﻉﺎـﻔﺘﺭﺍ ﻥـﻤ ﻡﺴـﺠ ﻁﻘﺴـﻴ ﺎﻤﺩﻨﻋ
)
Force Gravity
.(
ﺴﺎﻭﻱـﻴ ﻡﻅﺘﻨﻤ لﻴﺠﻌﺘﺒ ﺩﻴﺍﺯﺘﺘ ﻡﺜ ﻥﻭﻜﺴﻟﺍ ﻥﻤ ﻪﺘﻋﺭﺴ ﺃﺩﺒﺘﻭ
)
9.81m/s
2
.(
ﺴﻤﻰـﻴ

)
16
(
ﺒﺎﻟﺘﻌﺠﻴل ﺍﻻﺭﻀﻲ
.
ﻭﺍﺀـﻬﻟﺍ ﻙﺎـﻜﺘﺤﺃ ﺓﻭﻗ ﺭﻴﺜﺄﺘ لﺎﻤﻫﺍ ﻁﺭﺸ ﻡﺴﺠﻟﺍ ﻡﺠﺤ ﻭﺍ ﺔﻠﺘﻜ ﻰﻠﻋ ﻑﻗﻭﺘﺘ ﻻ ﻪﺘﻤﻴﻗ
ﺒﺎﻟﺠ
ﺴﻡ ﺃﺜﻨﺎﺀ ﺴﻘﻭﻁﻪ
.
ﻟﻘﺩ ﺍﺜﺒﺕ ﺍﺴﺤﻕ ﻨﻴﻭﺘﻥ ﻓﻲ ﻗﺎﻨ
ﻭﻨﻪ
ﺍﻟﺜﺎﻟﺙ ﺒﺄﻥ ﻗﻭﺓ ﺍﻟﺠﺎﺫﺒﻴﺔ ﻟﻠﺠﺴﻡ ﺃﻱ ﻭﺯﻨﻪ
)
W
(
ﺘﺘﻨﺎﺴﺏ ﻤﻊ ﻜﺘﻠﺘﺔ
ﺍﻟﺠﺴﻡ
)
m
(
ﻭﻋﻠﻴﻪ ﻴﻜﻭﻥ،
:
)
9
.
1
(
g
m
W
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
×
=
)
1.3.10
(
-
ﺍﻟﻭﺯﻥ
Weight
ﺍﺫﺍ ﻭﻀﻊ ﺠﺴﻡ ﻤﺎ ﻋﻠﻰ ﺴﻁﺢ ﻤﻌﻴﻥ ﻓﺄﻥ ﺍﻟﻀﻐﻁ ﺍﻟﺫﻱ ﻴﺴﻠﻁ
ﻪ
ﻫﻭ ﺩﺍﻟﺔ ﺍﻟﻭﺯﻥ
.
ﻭﺇﺫﺍ ﺴﻘﻁ ﺠﺴﻡ ﻓﺄﻥ
ﻗﻭﺓ ﺠﺫﺏ ﻨﺤﻭ ﺍﻻﺭﺽ ﺩﺍﻟﺔ ﻟﻭﺯﻨﻪ
.
لـﻤﻌﺘ ﺓﻭﻘﻟﺍ ﻩﺫﻫ ،ﻡﺴﺠﻠﻟ ﺽﺭﻻﺍ ﺏﺫﺠ ﺓﻭﻗ ﻥﻋ ﺭﻴﺒﻌﺘﻟﺍ ﻭﻫ ﻥﺯﻭﻟﺎﻓ
ﻲـﻀﺭﻟﺍ لﻴﺠﻌﺘﻟﺍ ﻭﺍ ﺏﺫﺠﻟﺍ ﺓﻭﻗ ﻥﺍ ﺎﻤﺒﻭ ﺽﺭﻻﺍ ﺯﻜﺭﻤ ﻩﺎﺠﺘﺎﺒ لﻔﺴﻻﺍ ﻰﻟﺍ ﹰﺎﻴﻟﻭﻗﺎﺸ
)
g
(
ﺎـﻤﻠﻜ ﺭـﻴﻐﺘﺘ
،ﺍﺒﺘﻌﺩﻨﺎ ﻋﻥ ﻤﺭﻜﺯ ﺍﻻﺭﺽ ﻟﺫﺍ ﻓﺄﻥ ﻭﺯﻥ ﺠﺴﻡ ﺍﻻﻨﺴﺎﻥ ﻴﻨﻌﺩﻡ ﻓﻲ ﺍﻟﻔﻀﺎﺀ ﻻﻨﻌﺩﺍﻡ ﺍﻟﺠﺎﺫﺒﻴﺔ
ﻭﺓـﻗ ﻥﺄﻓ ﻪﻴﻠﻋ
ﺠﺫﺏ ﺍﻻﺭﺽ ﻟﻠﺠﺴﻡ
)
F
(
ﺍﻭ ﻭﺯﻥ ﺍﻟﺠﺴﻡ
)
W
(
ﻴﺴﺎﻭﻱ
:
)
10
.
1
(
N
s
/
m
kg
g
m
W
F
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
×
⇒
×
=
=
ﻻﻴﻤﻜﻥ ﻋﺩ ﺍﻟﻭﺯﻥ ﻭﺤﺩﺓ ﺍﺴﺎﺴﻴﺔ ﻟﻌﺩﻡ ﻭﺠﻭﺩ ﻗﻴﻤﺔ ﺜﺎﺒﺘﺔ ﻟﻪ
.
ﻰـﻠﻋ ﻪﺘﻠﺘﻜ ،ﺀﺎﻀﻔﻟﺍ لﺠﺭ ﹰﻼﺜﻤ ﺫﺨﺄﻨﻟ
ﺍﻻﺭﺽ
)
80kg
(
ﻭﻭﺯﻨﻪ ﻴﺴﺎﻭﻱ
)
784.8N
=
9.81
×
80
.(
ﻭﻜﺘﻠﺘﻪ ﻓﻲ ﺍﻟﻔﻀﺎﺀ
)
80kg
(
ﻟﻜﻨﻪ ﺴﻴﻜﻭﻥ ﻓﻲ
ﺤﺎﻟﺔ ﻓ
ﻘﺩﺍﻥ ﺍﻟﻭﺯﻥ ﻻﻨﻌﺩﺍﻡ ﺍﻟﺠﺎﺫﺒﻴﺔ ﺍﻻﺭﻀﻴﺔ
.
)
1.3.11
(
-
ﺍﻟﺯﺨﻡ
Momentum
ﻲـﻫ ﺎـﻤﻤ ﺭﺒﻜﺍ لﻤﺎﻜﻟﺎﺒ ﺔﻠﻤﺤﻤ ﻥﻭﻜﺘ ﺎﻤﺩﻨﻋ ﺔﻜﺭﺤﻟﺍ ﺃﺩﺒﺘﻟ ﻊﻓﺩ ﺓﻭﻗ ﻰﻟﺍ ﺝﺎﺘﺤﺘ ﺔﻠﻴﻘﺜ ﺔﻴﺭﺎﺠﺘ ﺓﺭﺎﻴﺴ
ﻓﺎﺭﻏﺔ
.
ﺴﺭﻋﺔـﻟﺍ ﺱﻔﻨﺒ ﺭﻴﺴﺘ ﺓﺭﻴﻐﺼ ﺓﺭﺎﻴﺴ ﻥﻤ ﺭﺒﻜﺍ ﺢﺒﻜ ﺓﻭﻗ ﺏﻠﻁﺘﻴ ﺔﻴﺭﺎﺠﺘﻟﺍ لﻤﺤﻟﺍ ﺓﺭﺎﻴﺴ ﻑﺎﻘﻴﻻﻭ
.
ﻴﻘﺎل ﻟﻠﺴﻴﺎﺭﺓ
)
ﺍﻻﺜ
ﻘل
(
ﺒﺄﻨﻬﺎ ﺫﺍﺕ ﻜﻤﻴﺔ ﺤﺭﻜﺔ ﺍﻭ ﺯﺨﻡ
ﺍﻜﺒﺭ
ﻤﻥ ﺘﻠﻙ ﺍﻻﺨﻑ
.
ﻴﻌﺘﻤﺩ ﺍﻟﺯﺨﻡ ﻋﻠﻰ ﺍﻟﻜﺘﻠﺔ ﻭﺍﻟﺴﺭﻋﺔ
.
ﺴﺭﻋﺘﻴﻥـﺒ ﻥﺎـﻜﺭﺤﺘﻴ ﺎـﻤﻬﻨﻜﻟﻭ ﺔﻠﺘﻜﻟﺍ ﺱﻔﻨ ﺎﻤﻬﻟ ﻥﻴﻤﺴﺠ ﻥﺈﻓ ﻙﻟﺫﻟ
ﻤﺨﺘﻠﻔﺘﻴﻥ ﺴﻴﻅﻬﺭﺍﻥ ﺯﺨﻤﻴﻥ ﻤﺨﺘﻠﻔﻴﻥ
.
ﻴﻘﺎﺱ ﺯﺨﻡ ﺍﻟﺠﺴﻡ ﺒﺤﺎﺼل ﻀﺭﺏ ﻜ
ﺘ
ﺃﻱ،ﻪﺘﻋﺭﺴ ﻲﻓ ﻪﺘﻠ
:
)
11
.
1
(
C
m
Mometum
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
×
=
)
1.3.12
(
-
ﺘﻐﻴﺭ ﺍﻟﺯ
ﺨﻡ
-
ﻗﺎﻨﻭﻥ ﻨﻴﻭﺘﻥ ﺍﻟﺜﺎﻨﻲ ﻟ
ﻠ
ﺤﺭﻜﺔ
ﻴ
ﻨﺹ ﻗﺎﻨﻭﻥ ﻨﻴﻭﺘﻥ ﺍﻟﺜﺎﻨﻲ ﻋﻠﻰ ﺍﻥ
))
ﻴﺘﻨﺎﺴﺏ ﺯﺨﻡ ﺍﻟﺠﺴﻡ ﻁﺭﺩﻴﺎﹰ ﻤﻊ ﺍﻟﻘﻭﺓ ﺍﻟﻤﺅﺜﺭﺓ
((
.
ﻓﺎﺫﺍ ﺃﺜﺭﺕ ﻗﻭﺓ
)
F
(
ﻋﻠﻰ ﺠﺴﻡ ﻜﺘﻠﺘﻪ
)
m
(
ﻟﻤﺩﺓ
)t
(
ﻭﻏﻴﺭﺕ ﺴﺭﻋﺘﻬﺎ ﻤﻥ
)
C
1
(
ﺍﻟﻰ
)
C
2
(
ﻓﺎﻥ ﺘﻐﻴﺭ ﺍﻟﺯﺨﻡ ﻴﺴﺎﻭﻱ
:
)
12
.
1
(
)
C
C
(
m
Momentum
1
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
−
=
∆
ﻭﻤﻌﺩل ﺘﻐﻴﺭ ﺍﻟﺯﺨﻡ ﻴﺴﺎﻭﻱ
:

)
17
(
)
13
.
1
(
t
)
C
C
(
m
Momentum
1
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
−
=
∆
ﻭﺤﺴﺎﺏ ﻗﺎﻨﻭﻥ ﻨﻭﻴﺘﻥ ﺍﻟﺜﺎﻨﻲ ﻓﺈﻥ
:
)
14
.
1
(
t
)
C
C
(
m
F
1
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
−
∝
Q
Acceleration
t
C
C
)
a
(
1
2
−
=
)
15
.
1
(
ma
F
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
∝
∴
ـﻴﻤﻜﻥ ﺘﻌﺭﻴﻑ ﻭﺤﺩﺓ ﺍﻟ
)
F
(
لـﻴﺠﻌﺘﻟﺍ ﺓﺩـﺤﻭ ﺔﻠﺘﻜﻟﺍ ﺓﺩﺤﻭ ﺀﺎﻁﻋﻻ ﺔﺒﻭﻠﻁﻤﻟﺍ ﺓﻭﻘﻟﺍ ﺎﻬﻨﺎﺒ
.
ﺩﻋﻰـﺘ
ﺍﻟﻭﺤﺩﺓ ﺍﻟﺩﻭﻟﻴﺔ
)
SI
(
ﻟﻠﻘﻭﺓ ﻨﻴﻭﺘﻥ
)
N
.(
ﺩﺍﺭﻫﺎـﻘﻤ ﺔـﻠﺘﻜ ﺀﺎـﻁﻋﻻ ﺔﺒﻭﻠﻁﻤﻟﺍ ﺓﻭﻘﻟﺍ ﺎﻬﻨﺄﺒ ﻑﺭﻌﺘﻭ
)
1kg
(
ﺘﻌﺠﻴﻼﹰ ﻤﻘﺩﺍﺭﻩ
)
1m/s
2
(
ﻟﺫﻟﻙ
:
1N=1kg
× 1m/s
2
ﻓﺄﺫﺍ ﻜﺎﻨﺕ
)
F
(
ﺍﻟﻤﻁﻠﻭﺒﺔ ﻻﻋﻁﺎﺀ ﺠﺴﻡ ﻜﺘﻠﺘﻪ،ﻥﺘﻭﻴﻨﻟﺎﺒ ،ﺓﻭﻘﻟﺍ ﻲﻫ
)
m
(
ﻴﻼﹰـﺠﻌﺘ ،ﻡﺍﺭﻏﻭﻠﻴﻜﻟﺎﺒ ،
)
a
(
ـﺒﺎﻟ
)
m/s
2
(
ﻓﺄﻥ
:
)
16
.
1
(
N
s
m
kg
a
m
F
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
×
×
=

)
18
(
ﺃﻤﺜﻠﺔ ﻤﺤ
ﻠﻭﻟﺔ
)
1.1
(
ﺃﻭﺠﺩ ﻤﺴﺎﺤﺔ ﺴﻁﺢ ﺍﻋﻠﻰ ﺍﻟﻤﻜﺒﺱ ﺍﻟﻲ ﻗﻁﺭﻩ
)
0.67mm
(
2
2
2
cm
2
.
35
4
)
7
.
6
(
14
.
3
4
D
A
=
×
=
×
π
=
)
1.2
(
ﻤﻜﺒﺱ ﻗﻁﺭﻩ
)
67mm
(
ﻭﻁﻭل ﺸﻭﻁﻪ
)
90mm
(
ﺍﻭﺠﺩ ﺍﻟﺤﺠﻡ ﺍﻟﺫﻱ ﻴﺯﻴﺤﻪ ﺍﺜﻨﺎﺀ ﺍﻟﺸﻭﻁ
.
2
2
2
cm
2
.
35
4
)
7
.
6
(
14
.
3
4
D
A
=
×
=
×
π
=
3
cm
8
.
316
9
2
.
35
L
A
V
=
×
=
×
=
)
1.3
(
ﺃﻭﺠﺩ ﻤﺘﻭﺴﻁ ﺴﺭﻋﺔ ﺍﻟﻤﻜﺒﺱ
)
Sp
(
ﺍﺫﺍ ﻜﺎﻥ ﻁﻭل،
ﺍﻟﺸﻭﻁ
)
200mm
(
ﻭﻴﺅﺩﻱ
)
30
(
ﺸﻭﻁﺎ ﻓﻲ ﺍﻟﺜﺎﻨﻴﺔ
.
s
/
m
6
1
30
2
.
0
t
L
Sp
=
×
=
=
)
1.4
(
ﺃﺜﺭﺕ ﻗﻭﺓ ﻤﺎ ﻋﻠﻰ ﺠﺴﻡ ﻓﻲ ﺤﺎﻟﺔ ﺴﻜﻭﻥ ﻓﺄﺼﺒﺤﺕ ﺴﺭﻋﺘﻪ
)
3000m/min
(
ﺒﻌﺩ
)
5
(
ﺩﺀـﺒ ﻥـﻤ ﻲﻨﺍﻭﺜ
ﺍﻟﺤﺭﻜﺔ
.
ﺃﺤﺴﺏ ﻤﺘﻭﺴﻁ ﺍﻟﺘﻌﺠﻴل
.
2
s
/
m
10
5
60
/
3000
t
C
a
=
=
=
)
1.5
(
ﺃﺤﺴﺏ ﺍﻟﻘﻭﺓ ﺒﺎﻟﻨﻴﻭﺘﻥ ﺍﻟﻼﺯﻤﺔ ﻹﻨﺘﺎﺝ ﺘﻌﺠﻴل
)
0.2 m/s
2
(
ﻟﻜﺘﻠﺔ
)
0.04kg
.(
N
008
.
0
2
.
0
04
.
0
a
m
F
=
×
=
×
=
)
1.6
(
ﺃﺤﺴﺏ ﻜﺘﻠﺔ ﺠﺴﻡ ﻭﺯﻨﻪ
)
180N
(
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﺘﻌﺠﻴل ﺍﻻﺭﻀﻲ
)
9.81 m/s
2
(
kg
35
.
18
81
.
9
180
g
W
m
=
=
=
)
1.7
(
ﻭﺠﺩ ﻋﻤﻠﻴﺎﹰ
ﺍ
ﻥ ﻤﻘﺩﺍﺭ ﺍﻟﺠﺎﺫﺒﻴﺔ ﻋﻠﻰ ﺴﻁﺢ ﺍﻟﻘﻤﺭ ﻴﺴﺎﻭﻱ
)
6
1
(
ﻗﻴﻤﺘﻪ ﻋﻠﻰ ﺴﻁﺢ
.
ﺨﺹـﺸ ﻥﺯﻭ ﻭـﻫ ﺎﻤ
ﻜﺘﻠﺘﻪ
)
60kg
(
ﻋﻠﻰ ﺴﻁﺢ ﺍﻟﻘﻤﺭ
.
N
98
6
81
.
9
60
g
m
W
moon
=
×
=
×
=
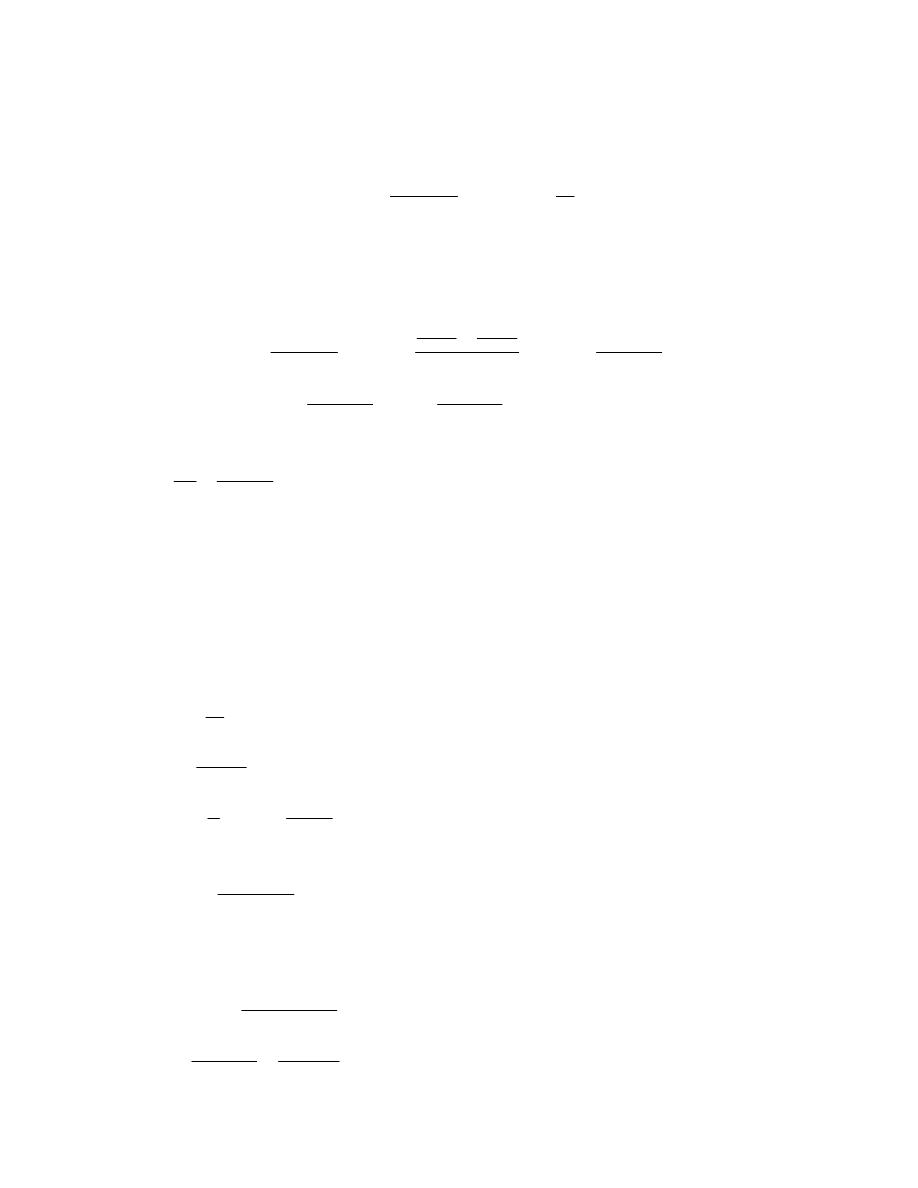
)
19
(
)
1.8
(
ﺴﻴﺎﺭﺓ ﻜﺘﻠﺘﻬﺎ
)
2t
(
ﺘﺴﻴﺭ ﺒﺴﺭﻋﺔ
)
72km/h
.(
ﺃﺤﺴﺏ ﺯﺨﻡ ﺍﻟﺴﻴﺎﺭﺓ
.
s
m
.
kg
40000
3600
10
72
10
2
C
m
Mometum
3
3
=
×
×
×
=
×
=
)
1.9
(
ﻋﺭﺒﺔ ﻜﺘﻠﺘﻬﺎ
)
2
(
ﻁﻥ
.
ﺘﺘﻌﺠل ﺒﺎﻨﺘﻅﺎﻡ ﻤﻥ
)
27km/h
(
ﺍﻟﻰ
)
72km/h
(
ﻲـﻓ
)
20s
.(
ﻭﺓـﻘﻟﺍ ﺏﺴـﺤﺍ
ﺍﻟﻤﻁﻠﻭﺒﺔ
)
ﻗﻭﺓ ﺍﻟﺠﺫﺏ
.(
ﻭﺍﻟﺸﻐل ﺍﻟﻜﻠﻲ ﺍﻟﻤﻨﺠﺯ
.
ﻭﻤﻌﺩل ﺍﻟﻘﺩﺭﺓ ﺍﻟﻤﺘﻭﻟﺩﺓ ﻓﻲ ﺍﻨﺘﺎﺝ ﻫﺫﺍ ﺍﻟﺘﻌﺠﻴل
.
kN
250
.
1
20
5
.
7
20
2000
20
2000
t
C
C
m
a
m
F
3600
10
27
3600
10
72
1
2
3
3
=
−
×
=
−
×
=
−
×
=
×
=
×
×
ﺍﻟﻤﺴﺎﻓﺔ ﺍﻟﻤﻘﻁﻭﻋﺔ
m
275
20
2
20
5
.
7
t
2
C
C
)
L
(
2
1
=
×
⎟
⎠
⎞
⎜
⎝
⎛
+
=
×
⎟
⎠
⎞
⎜
⎝
⎛
+
=
kJ
75
.
343
275
25
.
1
L
F
W
=
×
=
×
=
kW
187
.
17
20
75
.
343
t
W
P
=
=
=
)
1.10
(
ﻋﺭﺒﺔ ﻜﺘﻠﺘﻬﺎ
)
1500kg
(
ﺘﺴﻴﺭ ﺒﺴﺭﻋﺔ
)
90km/h
.(
ﺍﺭﻴﺩ ﺨﺘﺒﺎﺭ ﺍﻟﻤﻜﺎﺒﺢ
.
ﺎﺝـﺘﻨﻻ ﺢﺒﺍﻭـﻜﻟﺍ ﺕﻁﻠﺴ ﺩﻗﻭ
ﺍﻗﺼﻰ ﻜ
ﺒﺢ
.
ﻤﻌﺎﻤل ﺍﻻﺤﺘﻜﺎﻙ ﺒﻴﻥ ﺍﻻﻁﺎﺭﺍﺕ ﻭﺍﻟﻁﺭﻴﻕ ﻫﻭ
)
0.8
.(
ﺃﺤﺴﺏ
:
)
1
(
ﻗﻭﺓ ﺍﻟﻜﺒﺢ ﺍﻟﻤﺴﻠﻁﺔ
)
2
(
ﺍﻟﺘﺒﺎﻁﺅ ﺍﻟﻤﻨﺘﺞ
)
3
(
ﻜﻔﺎﺀﺓ ﺍﻟﻜﺒﺢ
)
4
(
ﺍﻟﺯﻤﻥ ﺍﻟﻤﺴﺘﻐﺭﻕ ﻟﻠﺘﻭﻗﻑ
.
kN
772
.
11
81
.
9
1500
8
.
0
g
m
W
F
)
1
(
=
×
×
=
×
×
µ
=
µ
=
)
ma
F
(
m
F
a
)
2
(
=
=
ﻷﻥ
2
s
/
m
848
.
7
1500
11772 =
=
%
80
100
81
.
9
848
.
7
100
g
a
)
3
(
=
×
=
×
=
η
s
/
m
25
3600
1000
90
C
)
4
(
1
=
×
=
0
C
2
=
ﻷﻥ ﺍﻟﺴﻴﺎﺭﺓ ﺘﻭﻗﻔﺕ
2
s
/
m
484
.
7
a
−
=
ﺍﻟﺘﻌﺠﻴل
t
)
C
C
(
m
a
.
m
F
1
2
−
/
=
/
=
s
185
.
3
848
.
7
25
0
a
C
C
t
1
2
=
−
−
=
−
=
∴

)
20
(
)
1.4
(
-
ﺍﻟﺘﺤﻠﻴل ﺍﻟﺒﺼﺭﻱ ﻭﺍﻟﺘﺤﻠﻴل ﺍﻟﻤﺠﻬﺭﻱ
Macroscopic & Microscopic Analysis
ﺍﻟﺘﺤﻠﻴل ﺍﻟﺒﺼﺭﻱ
)
ﺍﻟﻤﺎﻜﺭﻭﺴﻜﻭﺒﻲ
(
ﻫﻭ ﺘﺤﻠﻴل ﺨﻭﺍﺹ ﺍﻟﻨﻅﺎﻡ
ﺭﺍﺭﺓـﺤﻟﺍ ﺔﺠﺭﺩﻭ ﻡﺠﺤﻟﺍﻭ ﻁﻐﻀﻟﺎﻜ
ﻭﺍﻟﺘﻲ ﻫﻲ ﺨﻭﺍﺹ ﻴﻤﻜﻥ ﻗﻴﺎﺴﻬﺎ ﻟﺘﻌﻁﻲ ﻭﺼﻔﺎﹰ ﺒﺼﺭﻴﺎﹰ
.
ﺭﺍﻕـﺘﺤﺍ ﻙﺭـﺤﻤ ﺔﻨﺍﻭﻁﺴﺍ ﺕﺎﻴﻭﺘﺤﻤ ﹰﻼﺜﻤ ﺫﺨﺄﻨﻟ
ﻓﺎﻨﻬﺎ ﺘﺘﺤﺩﺩ ﺒﺄﺭﺒﻌﺔ ﻤﻘﺎﺩﻴﺭ ﺍﻭ ﺍﺤﺩﺍﺜﻴﺎﺕ ﺍﻭ ﺨﻭﺍﺹ ﻫﻲ،ﻡﺎﻅﻨﻜ ﻲﻠﺨﺍﺩ
:
1
-
ﺍﻟﺘﺭﻜﻴﺏ
:
ﺍﻟﺘﺤﻠﻴل ﺍﻟﻜﻴﻤﻴﺎﻭﻱ ﻴﺒﻴﻥ ﺍﻥ ﺍﻟﺨﻠﻴﻁ ﻗﺒل ﺍﻻﺤﺘﺭﺍﻕ ﻫﻭ ﻋﺒﺎﺭﺓ ﻋﻥ ﻫﻭﺍﺀ ﻭﻭﻗﻭﺩ ﺒ
ﻨﺴﺏ ﻤﻌﻴﻨﺔ
.
ﻭﺒﻌﺩ ﺍﻻﺤﺘﺭﺍﻕ ﺴﻴﺘﺤﻭل ﺍﻟﻰ ﻏﺎﺯ ﺍﻟﻌﺎﺩﻡ
.
ﻑـﺼﻭﺘ ﺔـﻴﻭﺎﻴﻤﻴﻜ ﺕﺎﺒﻜﺭﻤ ﻲﻫ ﻡﺩﺎﻌﻟﺍ ﺯﺎﻏﻭ ﻁﻴﻠﺨﻟﺍ ﻥﺇ
ﻤﻜﻭﻨﺎﺕ ﺍﻟﻨﻅﺎﻡ
.
2
-
ﺍﻟﻀﻐﻁ
:
ﺎﺩﻡـﻌﻟﺍ ﻁﻭـﺸ ﺔﻴﺎﻬﻨ ﻲﻓ ﺽﻔﺨﻨﻴ ﻡﺜ ﹰﺍﺩﺠ ﺭﻴﺒﻜ ﻕﺍﺭﺘﺤﻻﺍ ﺩﻌﺒ ﺯﺎﻐﻟﺍ ﻁﻐﻀ
.
ﺎﺱـﻴﻗ ﻥـﻜﻤﻴ
ﺍﻟﺘﻐﻴﺭﺍﺕ ﻓﻲ ﺍﻟﻀﻐﻁ ﺒﻭﺴﺎﻁﺔ ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭﺍﺕ ﻓﻲ ﺍﻟﻤﺨﺘﺒﺭ
.
3
-
ﺍﻟﺤﺠﻡ
:
ﻴﺘﻐﻴﺭ ﺤﺠﻡ
ﺍﻟﻐﺎﺯ ﺘﺒﻌﺎﹰ ﻟﺘﻐﻴﺭ ﻤﻭﻀﻊ ﺍﻟﻤﻜﺒﺱ ﺩﺍﺨل ﺍﻻﺴﻁﻭﺍﻨﺔ
.
ﻲـﻤﺠﺤﻟﺍ ﺭﻴﻐﺘﻟﺍ ﺱﺎﻴﻗ ﻥﻜﻤﻴ
ﺒﻭﺴﺎﻁﺔ ﺠﻬﺎﺯ ﻴﺭﺒﻁ ﻤﻊ ﺍﻟﻤﻜﺒﺱ
.
4
-
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
:
ﻴﻤﻜﻥ ﻗﻴﺎﺴﻬﺎ ﺒﺴﻬﻭﻟﺔ ﻜﺒﻘﻴﺔ،ﻙﺭﺤﻤﻟﺍ لﻤﻋ ﻥﻋ ﺔﺤﻀﺍﻭ ﺓﺭﻜﻓ ﻥﻴﻭﻜﺘ ﺎﻬﻨﻭﺩﺒ ﻥﻜﻤﻴ ﻻ
ﺍﻟﺨﻭﺍﺹ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ
.
ـﻴﺘﻀﺢ ﺍﻥ ﻫﺫﺍ ﺍﻟﺘﺤﻠﻴل ﻴﺘﻤﻴﺯ ﺒ
:
ﺃ
-
ﻻ ﻴﺘﻀﻤﻥ ﻓﺭﻀﻴﺎﺕ ﺨﺎﺼ
ﺔ ﺒﺘﺭﻜﻴﺏ ﺍﻟﻤﺎﺩﺓ
.
ﺏ
-
ﻴﺤﺘﺎﺝ ﺍﻟﻰ ﺒﻀﻊ ﺨﻭﺍﺹ ﻴﻤﻜﻥ ﺘﻘﺩﻴﺭﻫﺎ ﺒﺎﻟﺤﻭﺍﺱ ﺍﻭ ﻗﻴﺎﺴﻬﺎ ﻤﺒﺎﺸﺭﺓﹰ
.
ﻴﺴﺘﻌﻤل ﺍﻟﺘﺤﻠﻴل ﺍﻟﺒﺼﺭﻱ ﻤﻥ ﻗﺒل ﺍﻟﻤﻬﻨﺩﺱ ﻟﺩﺭﺍﺴﺔ ﺍﻟﻤﻜﺎﺌﻥ ﺍﻟﺤﺭﺍﺭﻴﺔ ﻭﺍﻟﺜﺭﻤﻭﺩﺍﻴﻨﻤﻴﻙ ﺍﻟﻬﻨﺩﺴﻲ
.
ﺎـﻤﺍ
ﺍﺫـﻟ ،ﻡﻭـﻴﻨﺍﺭﻭﻴﻠﻟ ﻱﺭﺫﻟﺍ ﺭﺎﻁﺸﻨﻻﺍ لﻴﻠﺤﺘﻜ ﺓﺩﺎﻤﻟﺍ ﺕﺎﺌﻴﺯﺠﻭ ﺕﺍﺭﺫ ﻙﻭﻠﺴ لﻴﻠﺤﺘ ﻭﻬﻓ ﻱﺭﻬﺠﻤﻟﺍ لﻴﻠﺤﺘﻟﺍ
ﻴﺴ
ﺘﻌﻤل ﻓﻲ ﺒﻌﺽ ﺩﺭﺍﺴﺎﺕ ﺍﻟﻔﻴﺯﻴﺎﺀ ﺍﻟﻨﻭﻭﻴﺔ
.
ﺒﺤﺴﺏ ﻤﻔﻬﻭﻡ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻙ ﺍﻻﺤﺼﺎﺌﻲ ﻓﺎﻥ ﺍﻟﻨﻅﺎﻡ ﻴﺘﻜﻭﻥ
ﻤﻥ ﻋﺩﺩ ﻻ ﻴﺤﺼﻰ ﻤﻥ ﺍﻟﺠﺯﻴﺌﺎﺕ ﻭﻓﻲ ﺤﺎﻟﺔ ﺘﻔﺎﻋل ﻭﺘﺼﺎﺩﻡ ﻭﺘﺠﺎﺫﺏ ﻭﺘﻨﺎﻓﺭ
.
ﺯـﻴﻤﺘﻴ لﻴﻠﺤﺘﻟﺍ ﺍﺫﻫ ﻥﺄﻓ ﺍﺫﻟ
ـﺒ
:
ﺃ
-
ﺍﻓﺘﺭﺍﺽ ﻭﺠﻭﺩ ﺍﻟﺠﺯﻴﺌﺎﺕ،ﺓﺩﺎﻤﻟﺍ ﺏﻴﻜﺭﺘﺒ ﺔﺼﺎﺨ ﺕﺎﻴﻀﺭﻓ ﻊﻀﻭ
.
ﺏ
-
ﻭﺼﻑ ﻜﻤﻴﺎﺕ ﻜﺜﻴﺭﺓ ﻤﻥ ﺍﻟ
ﺠﺯﻴﺌﺎﺕ ﻻ ﻴﻤﻜﻥ ﺘﻘﺩﻴﺭﻫﺎ ﺒﺎﻟﺤﻭﺍﺱ ﺍﻭ ﻗﻴﺎﺴﻬﺎ ﻤﺒﺎﺸﺭﺓﹰ
.

)
21
(
)
1.5
(
-
ﺍﻟﺨﻭﺍﺹ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ
Thermodynamic Properties
ﺘﺘﻌﻴﻥ ﺤﺎﻟﺔ ﺍﻟﻨﻅﺎﻡ ﻤﻥ ﺨﻼل ﺨﻭﺍﺼﻪ ﺍﻟﺘﻲ ﺘﺘﻤﻴﺯ ﺒﻤﺎ ﻴﺄﺘﻲ
:
-
1
-
،ﺔـﻨﻴﻌﻤ ﺔـﻟﺎﺤ ﻲـﻓ ﻊﺌﺎـﻤﻟﺍ ﻥﻭﻜﻴ ﺎﻤﺩﻨﻋ ﺔﻴﺩﺩﻋ ﺔﻤﻴﻗ ﺎﻬﻟ ﻥﻭﻜﺘ ﻥﺍ ﺏﺠﻴ ﻱﺃ ،ﺎﻬﻀﻌﺒ ﺱﺎﻴﻗ ﻥﻜﻤﻴ
ﻜﺎﻟﻀﻐﻁ
(P)
ﻭﺍﻟ
ﺤﺠﻡ
(V)
ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
(T)
.
ﻭﻴﻤﻜﻥ ﺤﺴﺎﺏ ﺍﻟﺒﻌﺽ ﺍﻵﺨﺭ ﺭﻴﺎﻀﻴﺎﹰ
)
1
(
.
2
-
ﺃﻱ ﺘﻌﺘﻤﺩ ﻋﻠﻰ ﺍﻟﺤﺎﻟﺔ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ ﻭﺍﻟﻨﻬﺎﺌﻴﺔ،ﺔﻟﺎﺤﻟﺍ ﻰﻟﺍ لﻭﺼﻭﻠﻟ ﺀﺍﺭﺠﻻﺍ ﻥﻋ ﺔﻠﻘﺘﺴﻤ ﺔﻴﺼﺎﺨﻟﺍ ﺔﻤﻴﻗ
.
ﺩﺍﺜﻴﺎﺕـﺤﻻﺎﺒ ﻰﻤﺴـﺘ ﻥﻴﺘﻴـﺼﺎﺨ ﻥـﻋ لـﻘﻴ ﻻ ﺎـﻤ ﺔـﻓﺭﻌﻤ ﺏﻠﻁﺘﻴ ﺓﺩﻴﺩﺠﻟﺍ ﺔﻟﺎﺤﻟﺍ ﺩﻴﺩﺤﺘ ﻥﺇ
ﻴﻌﺒﺭ ﻋﻨﻬﺎ ﺒ،ﺔﻴﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜﻟﺍ
ﻘﺎﻋﺩﺓ ﺍﻟﺨﺎﺼﻴﺘﻴﻥ
(Two Property Rule)
.
ﺔ ﺃﻱـﻤﻴﻗ ﺩﺎـﺠﻴﺍ ﻥﻜﻤﻴ ﺍﺫﻟ
ﺍﺤﺩﺍﺜﻲ
)
ﺨﺎﺼﻴﺔ
(
ﻓﻤﺜﻼﹰ ﺍﻥ ﺍﻟﻌﻼﻗﺔ،ﻥﻴﺭﺨﻵﺍ ﻥﻴﻴﺜﺍﺩﺤﻻﺍ ﺔﻟﻻﺩﺒ
[V =
∅ (P, T)]
ﺘﻌﻨﻲ ﺍﻥ ﻗﻴﻤﺔ ﺍﻟﺤﺠﻡ
ﺘﻌﺘﻤﺩ ﻋﻠﻰ ﻗﻴﻤﺔ ﺍﻟﻤﺘﻐﻴﺭﻴﻥ ﺍﻟﻤﺴﺘﻘﻠﻴﻥ
)
P
،
T
(
ـ ﻓﺈﺫﺍ ﺘﻐﻴﺭ ﺍﻟ،ﺩﺤﺍﻭ ﻥﺁ ﻲﻓ
(P)
ـ ﻭﺒﻘﻴﺕ ﺍﻟ
(T)
ﺔـﺘﺒﺎﺜ
ﺴﻴﺘٍﺫﺌﺩﻨﻋ
ﻐﻴﺭ ﺍﻟﺤﺠﻡ
.
ﻭﻟﻜﻥ ﻗﻴﻤﺔ
(P)
ﻻ ﻴﺸﺘﺭﻁ ﺍﻥ ﺘﻌﺘﻤﺩ ﻋﻠﻰ ﻗﻴﻤﺔ
(T)
.
ﻓﺈﺫﺍ ﻜﺎﻥ
)
2
(
(dP)
ﺘﻤﺜل ﺘﻐﻴﺭ
ﻓﺈﻥ ﺍﻟﺘﻐﻴﺭ ﺍﻟﻜﻠﻲ ﺒﻴﻥ ﺍﻟﺤﺎﻟﺘﻴﻥ،ﻁﻐﻀﻟﺍ ﻲﻓ ﺭﻐﺼﻟﺍ ﻲﻫﺎﻨﺘﻤ
)
1
(
ﻭ
)
2
(
ﻫﻭ
:
ﻴﺔـﺼﺎﺨﻟﺍ ﻙﺎـﻨﻫ ﺔـﺤﻭﺘﻔﻤﻟﺍ ﺔـﻤﻅﻨﻻﺍ ﻲﻓﻭ ﻴﺔﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜﻟﺍ ﻴﺔﺼﺎﺨﻟﺍ ﻙﺎﻨﻫ ﺔﻘﻠﻐﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﻲﻓ
ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﻓﻀ
ﻼﹰ ﻋﻥ ﺍﻟﺨﺎﺼﻴﺔ ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ
.
1.5.1
ﺍﻟﺨﻭﺍﺹ ﺍﻟﻤﺴﺘﻘﻠﺔ ﻭﻏﻴﺭ ﺍﻟﻤﺴﺘﻘﻠﺔ
Independent & dependent Properties
ﺭـﻴﻐﺘﻟ ﺎـﻌﺒﺘ ﻁﻐﻀـﻟﺍ ﺭﻴﻐﺘﻴﺴﻓ ،ﻪﻗﻭﻓ ﺔﻜﺭﺤﻟﺍ ﺭﺤ ﺱﺒﻜﻤﺒ ﺔﻘﻠﻐﻤ ﺯﺎﻏ ﻱﻭﺘﺤﺘ ﺔﻨﺍﻭﻁﺴﺍ ﺕﻨﺎﻜ ﺍﺫﺃ
ﺯـﺨ ﻲﻓ ﺩﻭﺠﻭﻤ ﺯﺎﻏ ﻰﻟﺍ ﺓﺭﺍﺭﺤ ﺕﻔﻴﻀﺃ ﺍﺫﺍﻭ ،ﺔﻠﻘﺘﺴﻤ ﺔﻴﺼﺎﺨ ﺩﻌﻴ ﻁﻐﻀﻟﺎﻓ ﻙﻟﺫﻟ ،لﺎﻘﺜﻻﺍ
ﺴﺘﺯﺩﺍﺩـﻓ ﻥﺍ
ﻟﺫﻟﻙ ﺘﻜﻭﻥ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺨﺎﺼﻴﺔ ﻤﺴﺘﻘﻠﺔ،ﻪﺘﺭﺍﺭﺤ ﺔﺠﺭﺩ
)
Independent
(
ﺴﺘﻘﻠﺔـﻤﻟﺍ ﺹﺍﻭـﺨﻟﺍ ﺍﺫﺃ
ـﻴﻤﻜﻥ ﻗﻴﺎﺴﻬﺎ ﻜﺎﻟ
)
T,P
(
ـ ﺍﻤﺎ ﺍﻟﺨﻭﺍﺹ ﺍﻟﺘﺎﺒﻌﺔ ﻓﻴﻤﻜﻥ ﺤﺴﺎﺒﻬﺎ ﺒﺩﻻﻟﺔ ﺍﻟ،
)
T,P
.(
)
1
(
ﺎﻟﺒﻲـﺜﻨﻻﺎﻜ ﹰﺎﻘﺤﻻ ﺎﻫﺭﻜﺫ ﺩﺭﻴﺴ ﻯﺭﺨﺍ ﺔﻴﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜ ﺹﺍﻭﺨ ﻙﺎﻨﻫ
(H)
ﺔـﻴﻠﺨﺍﺩﻟﺍ ﺔـﻗﺎﻁﻟﺍﻭ
(U)
ﻭﺍﻻﻨﺘﺭﻭﺒﻲ
(S)
ﻨﺎﺘﺠﺔ ﻋﻥ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻭ،
ﺍﻟﺜﺎﻨﻲ
.
، ﻏﻴﺭ ﻤﺭﻜﺯﺓ،ﺔﻠﻘﺘﺴﻤ ﺭﻴﻏ ،ﺔﻌﺒﺎﺘ ﺹﺍﻭﺨﻟﺍ ﻩﺫﻫ
ﻲﻋﻭـﻨﻟﺍ ﻡﺠﺤﻟﺍﻭ ﻁﻐﻀﻟﺎﻜ ﺱﺍﻭﺤﻟﺎﺒ ﹰﺓﺭﺸﺎﺒﻤ ﺎﻬﺘﺒﻗﺍﺭﻤ ﻥﻜﻤﻴ ﻻ ﻪﻨ ﻻ ،ﹰﺎﻴﻀﺎﻴﺭ ﺏﺴﺤﺘ ،ﺔﻠﻤﺎﺸ ﺭﻴﻏ
ﻭﻤﻊ ﺫﻟﻙ ﻓﺈﻨﻬﺎ ﺨﻭﺍﺹ ﺍﺴﺎﺴﻴﺔ ﻟﻬﻴﻜل ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﺱ،ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ
.
)
2
(
ﻤﻥ ﺍﻟﻨﺎﺤﻴﺔ ﺍﻟﺭﻴﺎﻀﻴﺔ ﻓﺈﻥ
(dP)
ﻫﻭ ﻤﺸﺘﻕ ﺘﺎﻡ
)
ﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﺨﺎﺼ
ﻴﺔ
(
لـﻤﺎﻜ ﻭﺍ ﺢﻴﺤـﺼ ﻕﺘﺸـﻤ ﻭﺍ
(Exact or Perfect Differential)
.
(1.17)
.......
P
-
P
dP
2
1
1
2
∫
=
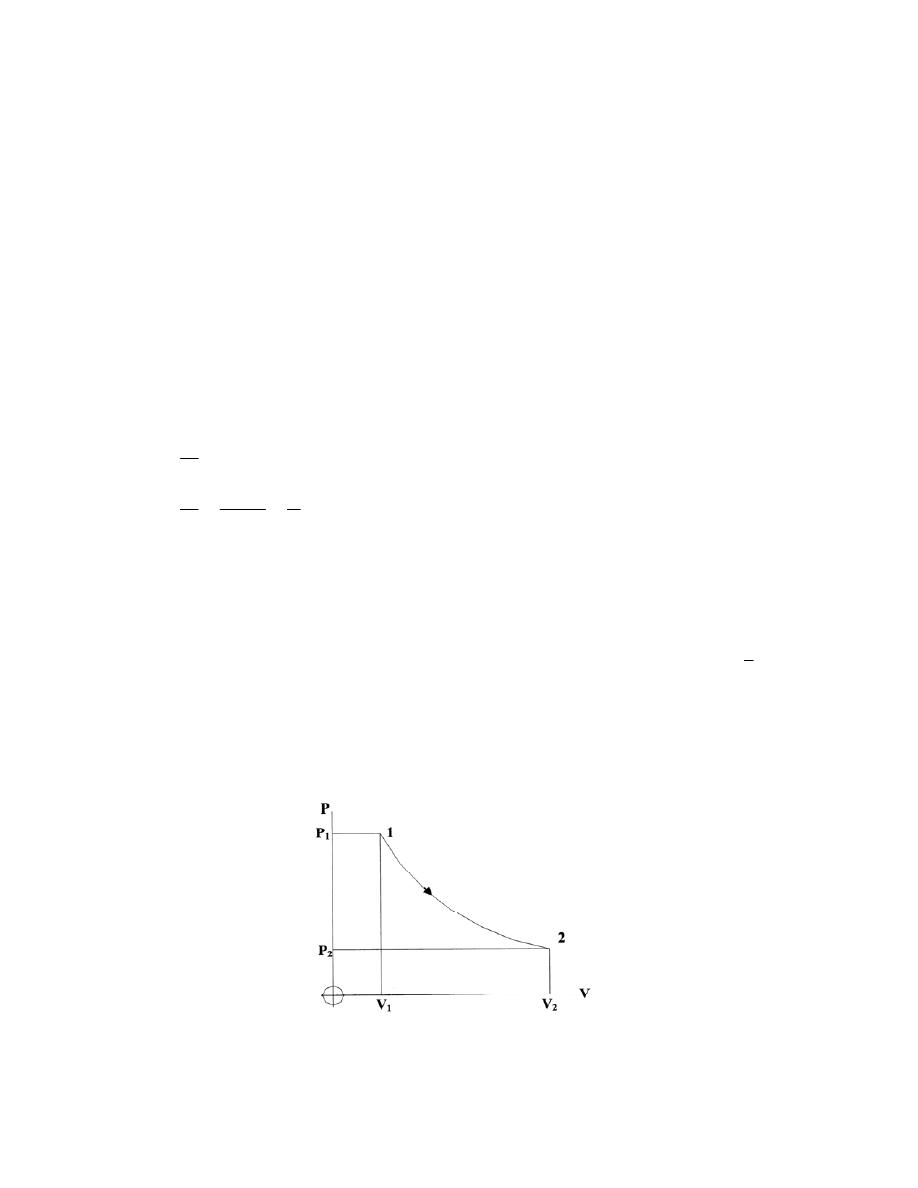
)
22
(
1.5.2
ﺍﻟﺨﻭﺍﺹ ﺍﻟﻤﺭﻜﺯﺓ ﻭﺍﻟﺸﺎﻤﻠﺔ
Intensive & Extensive Properties
ﺇﺫﺍ ﺍﺨﺫﻨﺎ ﻨﻅﺎﻤﺎﹰ ﻓﻲ ﺤﺎﻟﺔ ﺘ
ﻰـﻘﺒﺘ ﺕﺎﻔﺼﻟﺍ ﺽﻌﺒ ﻥﺈﻓ ،ﺔﻠﺘﻜﻟﺍ ﻲﻓ ﻥﻴﻴﻭﺎﺴﺘﻤ ﻥﻴﻤﺴﻗ ﻰﻠﻋ ﻩﺎﻨﻤﺴﻗﻭ ﻥﺯﺍﻭ
ﻭﺍ ﺔﻴﻨﻤﻀـﻟﺎﺒ ﻰﻋﺩـﺘ ﺹﺍﻭـﺨﻟﺍ ﻩﺫـﻫ ﺔﻓﺎﺜﻜﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ ﻁﻐﻀﻟﺎﻜ ﻡﺎﻅﻨﻟﺍ ﺍﺫﻫ ﻥﻤ ﻑﺼﻨ لﻜﻟ ﺔﺘﺒﺎﺜ
ﺍﻟﻤﺭﻜﺯﺓ ﺍﻭ ﺍﻟﻤﺅﻜﺩﺓ
(Intensive)
ﻭﻫﻲ ﻻ ﺘﻌﺘﻤﺩ ﻋﻠﻰ ﻜﺘﻠﺔ ﺍﻟﻨﻅﺎﻡ
.
ﺍﻤﺎ ﺍﻟﺨﻭﺍﺹ ﺍﻟﺘﻲ ﺘﺘﻨﺼﻑ ﻜﺎﻟﺤﺠﻡ ﻭﺍﻟﻁﻭل ﻭﺍﻟﻤﺴﺎﺤﺔ ﻭ
ﺩﻋﻰـﺘ ﺎـﻬﻨﺈﻓ ،ﺔـﻴﻠﺨﺍﺩﻟﺍ ﺔـﻗﺎﻁﻟﺍﻭ ﻥﺯﻭﻟﺍ
ﺒﺎﻟﺨﻭﺍﺹ ﻏﻴﺭ ﺍﻟﻀﻤﻨﻴﺔ ﺍﻭ ﻏ
ﻴ
ﺍﻭ ﻏﻴﺭ ﺍﻟﻤﺅﻜﺩﺓ ﺍﻭ ﺍﻟﺸﺎﻤﻠﺔ،ﺓﺯﻜﺭﻤﻟﺍ ﺭ
(Extensive)
ﻭﻫﻲ ﺘﻌﺘﻤﺩ ﻋﻠﻰ ﻜﺘﻠﺔ
ﺍﻟﻨﻅﺎﻡ
.
ﻙـﻠﺘﻟ ﺔـﻴﻋﻭﻨﻟﺍ ﺔﻤﻴﻘﻟﺎﺒ ﻰﻤﺴﺘﻓ ،ﻡﺎﻅﻨﻟﺍ ﺕﻻﻭﻤ ﺩﺩﻋ ﻰﻠﻋ ﻭﺍ ﺔﻠﺘﻜﻟﺍ ﻰﻠﻋ ﺔﻠﻤﺎﺸﻟﺍ ﺹﺍﻭﺨﻟﺍ ﺕﻤﺴﻗ ﺍﺫﺇﻭ
ﺍﻟﺨﺎﺼﻴﺔ
.
ﻭﺴﻴﺭﻤﺯ ﻟﻠﺨﻭﺍﺹ ﺍﻟﺸﺎﻤﻠﺔ ﺒ
ﻭﻟﻠﻘﻴﻡ ﺍﻟﻨﻭﻋﻴﺔ ﺍﻟﻤﻨﺎﻅﺭﺓ ﻟﻬﺎ ﺒﺤﺭﻭﻑ ﺼﻐﻴﺭﺓ،ﺓﺭﻴﺒﻜﻟﺍ ﻑﻭﺭﺤﻟﺎ
.
ﺈﺫﺍـﻓ
ﺭﻤﺯ ﻟﻠﺤﺠﻡ ﺍﻟﻜﻠﻲ ﻟﻠﻨﻅﺎﻡ ﺒﺎﻟﺤﺭﻑ
(V)
ﻓﺎﻥ ﺍﻟﺤﺠﻡ ﺍﻟﻨﻭﻋﻲ ﻴﺭﻤﺯ ﻟﻪ ﺒﺎﻟﺤﺭﻑ
(
ν)
ﺎﻡـﻅﻨﻟﺍ ﺔﻠﺘﻜ ﺕﻨﺎﻜ ﻭﻟﻭ ،
ﻫﻲ
(m)
ﻓﺈﻥ
:
ﺃﻱ،ﺔﻓﺎﺜﻜﻟﺍ ﺏﻭﻠﻘﻤ ﻭﻫ ﻲﻋﻭﻨﻟﺍ ﻡﺠﺤﻟﺍﻭ
:
ﻭﻟﻤﺎ ﻜﺎﻨﺕ ﻜﺜﺎﻓﺔ ﻤﺎﺩﺓ ﻓﻲ ﺤﺎﻟﺔ ﻤﻌﻴﻨﺔ ﻻ ﺘﻌﺘﻤﺩ ﻋﻠﻰ
ﺔـﻓﺎﺜﻜﻟﺍ ﻥﺎﻓ ﻥﺎﺒﺴﺤﻟﺎﺒ ﺓﺫﻭﺨﺄﻤﻟﺍ ﺔﻠﺘﻜﻟﺍ ﺭﺍﺩﻘﻤ
ﻭﻟﺫﻟﻙ ﻓﺎﻟﺤﺠﻡ ﺍﻟﻨﻭﻋﻲ ﻤﻘﺩﺍﺭ ﻤﺭﻜﺯ ﺍﻴﻀﺎﹰ،ﺯﻜﺭﻤ ﺭﺍﺩﻘﻤ
.
ﻭﻋﻨﺩ ﻗﺴﻤﺔ ﺍﻟﺨﺎﺼﻴﺔ ﺍﻟﺸﺎﻤﻠﺔ ﻜﺎﻟﻭﺯﻥ
(F)
ﻋﻠﻰ ﺸﺎﻤﻠﺔ ﺍﺨﺭﻯ ﻜﺎﻟﻤﺴﺎﺤﺔ
(A)
ﻀﻐﻁـﻟﺍ ﺞﺘﻨﻴﺴـﻓ ،
ﺍﻟﺫﻱ ﻫﻭ ﺨﺎﺼﻴﺔ ﻤﺭﻜﺯﺓ
.
)
1.6
(
-
ﻤﺨﻁﻁ ﺍﻟﺤﺎﻟﺔ
State Diagram
ﻤﺨﻁﻁ ﺍﻟﺤﺎﻟﺔ ﻴ
ﻓﻤﺜﻼﹰ ﻤﺨﻁﻁ ﺤﺎﻟﺔ ﺍﻟﻀﻐﻁ،ﻪﺼﺍﻭﺨ ﺽﻌﺒ ﺭﻴﻐﺘ ﺩﻨﻋ ﻡﺎﻅﻨﻠﻟ ﺔﻠﻤﺎﺸﻟﺍ ﺔﻟﺎﺤﻟﺍ ﻥﻴﺒ
–
ﺍﻟﺤﺠﻡ ﺍﻟﻤﻭﻀﺢ ﻓﻲ ﺸﻜل ﺭﻗﻡ
)
1.5
.(
ﺸﻜل
)
5
.
1
(
-
ﻤﺨﻁﻁ
ﺍﻟﻀﻐﻁ
-
ﺍﻟﺤﺠﻡ
(1.18)
......
m
V
=
ν
(1.19)
.......
1
m
/
V
1
V
m
υ
=
=
=
ρ
⎟
⎠
⎞
⎜
⎝
⎛ =
A
F
P

)
23
(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∫
2
1
V
V
dV
ﺤﻴﺙ ﻴﻤﺜل ﺍﻟﻀﻐﻁ ﺍﻟﻤﺤﻭﺭ ﺍﻟﺼﺎﺩﻱ ﻭﺍﻟﺤﺠﻡ ﺍﻟﻤﺤﻭﺭ ﺍﻟﺴﻴﻨﻲ
.
ﺎﺘﻴﻥـﻬﻟ ﺔـﻠﺒﺎﻘﻤﻟﺍ ﻡﻴﻘﻟﺍ ﻡﺴﺭ ﻥﻜﻤﻴﻭ
ﺍﻟﺨﺎﺼﻴﺘﻴﻥ ﻋﻠﻰ ﺍﻟﻤﺨﻁﻁ
.
ﺃﻏﻠﺏ ﺍﻟﻤﺨﻁﻁﺎﺕ ﺘﺘﻜﻭﻥ
ﻴﺘﻴﻥـﺼﺎﺨﻟﺍ ﺓﺩـﻋﺎﻗ ﻕﻴﺒﻁﺘﺒﻭ ﺎﻨﻫ ﻥﻤﻭ ﻥﻴﺩﻌﺒ ﻥﻤ
.
ﻭﻗﻭﺍﻨﻴﻥ ﻭﺠﺩﺍﻭل ﺍﻟﺨﻭﺍﺹ ﺍﻟﺘﻲ ﺴﻨﺩﺭﺴﻬﺎ ﻻﺤﻘﺎﹰ ﻴﻤﻜﻥ ﺤﺴﺎﺏ ﻗﻴﻡ ﺍﻟﺨﻭﺍﺹ ﺍﻻﺨﺭﻯ
.
)
1.7
(
-
ﺩﺍﻟﺔ ﺍﻟﺤﺎﻟﺔ ﻭﺩﺍﻟﺔ ﺍﻟﻤﺴﺎﺭ
State, Path Function
ـﺨﻭﺍﺹ ﺍﻟﻨﻅﺎﻡ ﻜﺎﻟ
)
P
،
V
،
T
(
ﻟﺫﻟﻙ ﺘﺴﻤﻰ ﺒﺩﺍﻟﺔ ﺍﻟﺤﺎﻟ،ﺔﻴﺌﺎﻬﻨﻟﺍﻭ ﺔﻴﺌﺍﺩﺘﺒﻻﺍ ﺔﻟﺎﺤﻟﺍ ﻰﻠﻋ ﺩﻤﺘﻌﺘ
ﺔ
.
ﻥـﻤ ﻑﺎـﻜ ﺩﺩـﻋ ﻰـﻠﻋ ﻱﻭـﺘﺤﻴ ﻱﺃ ،ﺱﻭﺴﺤﻤ ﻪﻨﻜﻟ ،ﹰﺍﺩﺠ ﹰﺍﺭﻴﻐﺼ ﺹﺍﻭﺨﻟﺍ ﻩﺫﻫ ﻲﻓ ﺭﻴﻐﺘﻟﺍ ﻥﺎﻜ ﻭﻟﻭ
ﺔــﻴﻘﻴﻘﺤ ﺔــﻟﺍﺩ ﺩــﻌﻴ ﻙﻟﺫــﻟ ،ﺕﺎــﺌﻴﺯﺠﻟﺍ
.
ﻀﺒﻭﻁــﻤ ﻭﺍ ﻡﺎــﺘ لــﻀﺎﻔﺘﺒ ﹰﺎﻴــﻀﺎﻴﺭ لــﺜﻤﺘ
(Exact Differential)
ﺃﻱ
)
dP
،
dV
،
dT
(
ﻴﻌﺒﺭ ﻋﻨﻬﺎ ﻋﻠﻰ ﻤﺨﻁﻁ ﺍﻟﺤﺎﻟﺔ ﺒﺩﻭﺍل ﻨﻘﻁﻴﺔ،
.
ﻓﺈﺫﺍ ﺘﻐﻴﺭ ﺍﻟﺤﺠﻡ
(V)
ﺘﻐﻴﺭﺍﹰ ﻤﺘﻨ
ﺎﻫﻴﺎﹰ ﻓﻲ ﺍﻟﺼﻐﺭ ﻓﻴﻌﺒﺭ ﻋﻨﻪ ﺒﺘﻔﺎﻀل ﺘﺎﻡ ﻟﺩﺍﻟﺔ ﺍﻟﺤﺎﻟﺔ
(V)
ﻭﻴﻜﺘﺏ
(dV)
.
ﺔـﻟﺎﺤﻟﺍ ﺔـﻟﺍﺩﻟ ﻡﺎـﺘ لﻀﺎﻔﺘ لﻤﺎﻜﺘ ﻥﺍﻭ
ﺃﻱ،ﺔﻴﺼﺎﺨﻟﺍ ﻩﺫﻫ ﻲﺘﻤﻴﻗ ﻥﻴﺒ ﻕﺭﻔﻟﺍ ﻲﻁﻌﻴ
:
ﺍﻤﺎ ﺍﻨﺘﻘﺎل ﺍﻟﺸﻐل
(W)
ﺍﻭ ﺍﻟﺤﺭﺍﺭﺓ
(Q)
ﻥـﻤ ﺱﻴـﻟ ﺎﻤﻬﻓ ،ﺭﻐﺼﻟﺍ ﺔﻴﻫﺎﻨﺘﻤ ﺕﺎﻴﻤﻜ ﻥﺎﻜ ﻭﻟ ﻰﺘﺤ ،
ﻟﺫﻟﻙ ﻴﻌﺘﻤﺩﺍ،ﻡﺎﻅﻨﻟﺍ ﺹﺍﻭﺨ
ﺎﻗﺹـﻨ ﻭﺍ ﻁﻭﺒﻀﻤ ﺭﻴﻏ ﻭﺍ ،ﻡﺎﺘ ﺭﻴﻏ لﻀﺎﻔﺘﺒ ﹰﺎﻴﻀﺎﻴﺭ لﺜﻤﻴ ،ﺭﺎﺴﻤﻟﺍ ﻰﻠﻋ ﻥ
(Inexact Differential)
ﺃﻱ،
)
dQ
،
dW
(
ﺭﺍﺀـﺠﺍ ﻭﺍ ﻲﺠﺭﺎـﺨ ﻁﺎﺸﻨ ﺎﻤﻫ ﺓﺭﺍﺭﺤﻟﺍ ﻭﺍ لﻐﺸﻟﺍ ﻥﻷ ،
ﻴﺅﺩﻱ ﺍﻟﻰ ﺘﻐﻴﻴﺭ ﻁﺎﻗﺔ ﺍﻟﺠﺴﻡ
.
ﻟﺫﺍ ﻓﺎﻥ
(dQ)
ﺍﻭ
(dW)
ﻲـﻁﻌﻴ ﻻ لﻤﺎﻜﺘﻟﺍ ﻥﺍﻭ لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻠﻟ ﺭﻐﺼﻟﺍ ﻲﻓ ﺔﻴﻫﺎﻨﺘﻤ ﺔﻴﻤﻜ لﺜﻤﺘ
ﺃﻱ،ﺓﺩﻭﺩﺤﻤ ﺔﻴﻤﻜ ﻲﻁﻌﻴ ﻥﻜﻟﻭ ﻥﻴﺘﻤﻴﻗ ﻥﻴﺒ ﻕﺭﻔﻟﺍ
:
.(1.20)
..........
V
V
V
dV
1
2
V
V
2
1
−
=
∆
=
∫
∫
∫
=
=
2
1
2
1
12
12
(1.21)
.......
W
OR
W
dW
،
Q
OR
Q
dQ
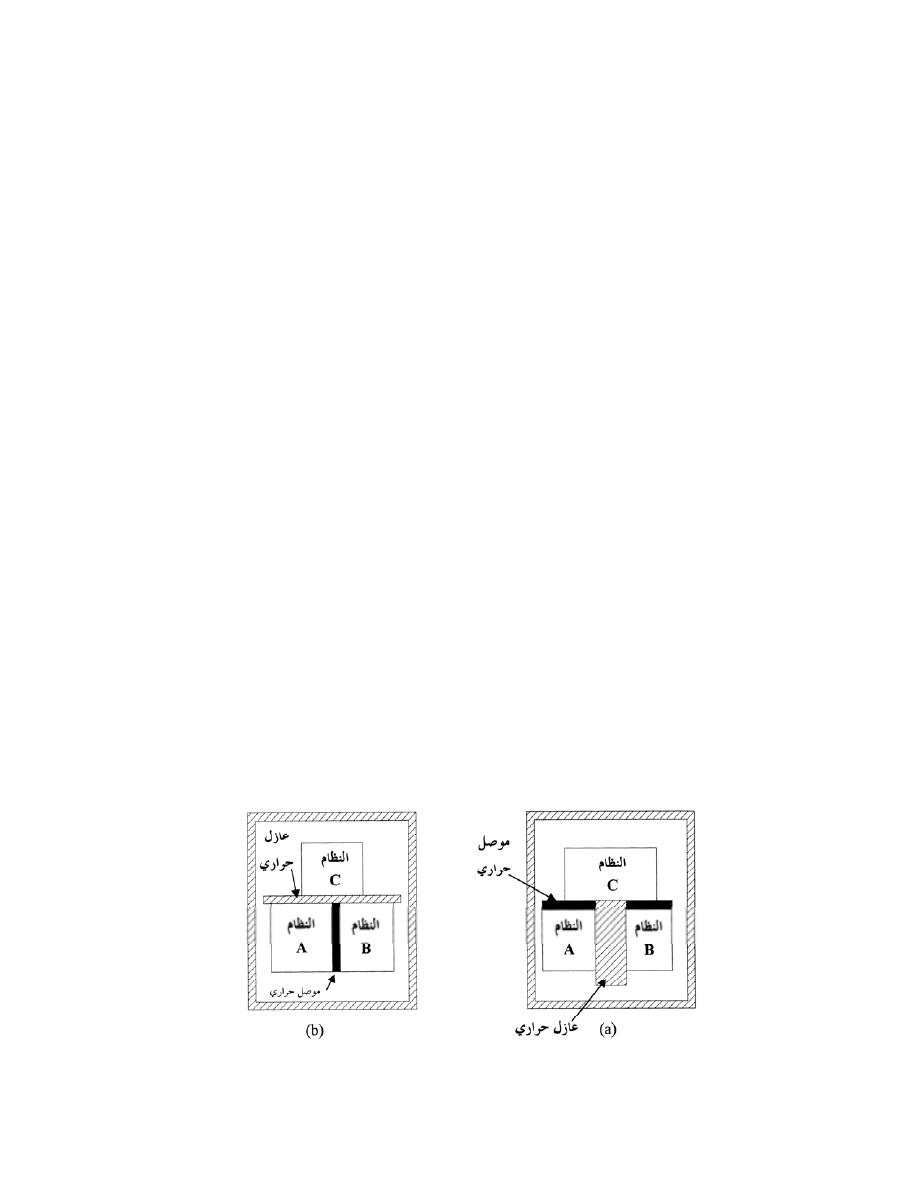
)
24
(
)
1.8
(
-
ﺍﻟﺘﻭﺍﺯﻥ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ
Thermodynamic Equilibrium
ﺯﻤﻥـﻟﺍ ﻊﻤ ﺭﻴﻐﺘﺘﺴ ﺎﻬﻨﺎﻓ ﺔﻓﺎﺜﻜﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ ﻁﻐﻀﻟﺎﻜ ﺔﻔﻠﺘﺨﻤ لﺯﻌﻤ ﻡﺎﻅﻨ ﺹﺍﻭﺨ ﺕﻨﺎﻜ ﺍﺫﺍ
ﻭﺨﻼل ﻫﺫﻩ ﺍﻟﻔﺘﺭﺓ ﺴﻨﻼﺤﻅ ﺍﻵﺘﻲ
:
-
ﺃ
-
ﻋﻨﺩ ﺇﺨﺘﻼﻑ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﺴﺘﻨﺘﻘل ﺍﻟﺤﺭﺍ
ﺴﺎﻭﻯـﺘﺘ ﻰﺘﺤ ﻰﻨﺩﻻﺍ ﻰﻟﺍ ﻰﻠﻋﻻﺍ ﻊﻗﻭﻤﻟﺍ ﻥﻤ ﹰﺎﻴﺌﺎﻘﻠﺘ ﺓﺭ
ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺍﻟﻨﻅﺎﻡ ﺃﻱ ﻴﺘﺯﻥ ﺤﺭﺍﺭﻴﺎﹰ
.
ﺏ
-
، ﺘﺘﻭﻟﺩ ﺤﺭﻜﺔ ﻭﺘﻴﺎﺭﺍﺕ ﺘﻨﻘل ﺍﻟﻤﺎﺩﺓ ﻤﻥ ﺍﻟﺠﺯﺀ ﺍﻻﻜﺜﻑ ﺍﻟﻰ ﺍﻟﺠﺯﺀ ﺍﻻﻗل ﻜﺜﺎﻓﺔ،ﻁﻐﻀﻟﺍ ﻑﻼﺘﺨﺇ ﺩﻨﻋ
ﺤﺘﻰ ﺘﺼﺒﺢ ﺍﻟﻜﺜﺎﻓﺔ ﻤﻨﺘﻅﻤﺔ ﻭﺒﺎﻟﺘﺎﻟﻲ ﻴﺘﺯﻥ ﺍﻟﻨﻅﺎﻡ ﻤﻴﻜﺎﻨﻴﻜﻴﺎﹰ
.
ﺇﺫﻥ ﺤﺎﻟﺔ ﺍﻟﺘﻭﺍﺯﻥ ﺘﺘﺤﻘﻕ ﻋﻨ
ﺩﻤﺎ ﻴﻜﻭﻥ
:
1
-
ﻋﺯل ﺍﻟﻨﻅﺎﻡ ﻋﻥ ﺍﻟﻤﺤﻴﻁ ﺒﺤﻴﺙ ﻻ ﺘﻨﺘﻘل ﺤﺭﺍﺭﺓ ﺍﻭ ﺸﻐل ﻋﺒﺭ ﺤﺩﻭﺩﻩ
.
2
-
ﺘﺴﺎﻭﻱ ﺍﻟﻀﻐﻁ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ ﻜﺎﻓﺔ ﺍﺠﺯﺍﺀ ﺍﻟﻨﻅﺎﻡ
.
ﺫﺍـﻬﺒﻭ ،ﺀﺍﺭـﺠﻻﺍ ﺔـﻴﺎﻬﻨﻭ ﺔﻴﺍﺩﺒ ﺩﻨﻋ ﻥﺯﺍﻭﺘ ﺔﻟﺎﺤ ﻲﻓ ﻡﺎﻅﻨﻟﺍ ﻥﺄﺒ ﺏﺎﺘﻜﻟﺍ ﺫﺍﻫ ﻲﻓ ﺽﺭﺘﻔﻨ ﻑﻭﺴ
ﻨﺴﺘﻁﻴﻊ ﺘﺤﺩﻴﺩ ﺍﻟﺤﺎﻟﺔ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ ﻭﺍﻟﻨﻬﺎﺌﻴﺔ ﻟﻠﺨﺎﺼﻴﺘﻴﻥ
.
ﻭﻤﺠﻤل
ﺯﺍﻥـﺘﺍ ﺔـﻟﺎﺤ ﻲﻓ ﻥﻭﻜﻴ ﻡﺎﻅﻨﻟﺍ ﻥﺈﻓ لﻭﻘﻟﺍ
ﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ ﻋﻨﺩﻤﺎ ﺘﻜﻭﻥ ﺨﻭﺍﺼﻪ ﺜﺎﺒﺘﺔ
.
ﻨﻔﺘﺭﺽ ﻭﺠﻭﺩ ﺜﻼﺜﺔ ﺍﻨﻅﻤﺔ
(A)
ﻭ
(B)
ﻭ
(C)
ﻤﺤﺎﻁﺔ ﺒﺠﺩﺍﺭ ﻋﺎﺯل
)
ﺍﺩﻴ
ﺎ
ﺒﺎﺘﻲ
(
ﺸﻜلـﻟﺍ ﻲﻓ ﺎﻤﻜ
)
1.6
.(
ﺇﻥ ﺍﻟﺸﻜل
(1.6-a)
ﻴﺒﻴﻥ ﺍﻨﻪ ﺍﺫﺍ ﻜﺎﻥ
(A)
ﻭ
(B)
ﻓﺄﻥ،ﻥﺍﺯﺘﺍ ﺔﻟﺎﺤ ﻲﻓ
(C)
ﺔـﻟﺎﺤ ﻲﻓ ﻥﻭﻜﻴﺴ
ﺍﺘﺯﺍﻥ ﻤﻊ
(A)
ﻭ
(B)
ﻟﻭﺠﻭﺩ ﺠﺩﺍﺭ ﻤﻭﺼل ﻟﻠﺤﺭﺍﺭﺓ
.
ﺍﻤﺎ ﺍﻟﺸﻜل
(1.6-b)
ﺎﻥـﻜ ﺍﺫﺍ ﻪـﻨﺍ ﻥﻴﺒﻴﻓ
(A)
ﻭ
(B)
ﻓﻲ ﺤﺎﻟﺔ ﺇﺘﺯﺍﻥ ﻤﻊ
(C)
ﻓﺴﻴﻜﻭﻥ،ﻲﺘﺎﺒﻴﺩﺍ ﺭﺍﺩﺠ ﺩﻭﺠﻭﻟ
(A)
ﻭ
(B)
ﻀﻬﻤﺎـﻌﺒ ﻊﻤ ﻥﺍﺯﺘﺇ ﺔﻟﺎﺤ ﻲﻓ
ﻟﻭﺠﻭﺩ ﺠﺩﺍﺭ ﻤﻭﺼل ﻟﻠﺤﺭﺍﺭﺓ
.
ﻫﺫﻩ ﺍﻟﺤﻘﻴﻘﺔ ﺍﻜﺩﻫﺎ
)
ﺭ
.
ـﻫ
.
ﻓﻭﻟﺭ
(
ﺼﻔﺭﻱـﻟﺍ ﻥﻭﻨﺎﻘﻟﺎﺒ ﺎﻫﺎﻤﺴﻭ
(The Zeroth Law)
ـ ﻟﻠ
ﺩﻴﻨﺎﻤﻴﻜﺎ
ﺍﻟﺤﺭﺍﺭﻴﺔ ﺍﻟﺫﻱ ﻴﻨﺹ ﻋﻠﻰ ﺍﻨﻪ
" :
ﻲـﻓ ﻥﻴﻤﺎﻅﻨﻟﺍ ﻥﻭﻜﻴﺴﻓ ،ﺙﻟﺎﺜ ﻡﺎﻅﻨ ﻊﻤ ﻥﺍﺯﺘﺇ ﺔﻟﺎﺤ ﻲﻓ ﻥﺎﻤﺎﻅﻨ ﻥﺎﻜ ﺍﺫﺇ
ﺤﺎﻟﺔ ﺇﺘﺯﺍﻥ ﻤﻊ ﺒﻌﻀﻬﻤﺎ
."
ﺸﻜل
)
1.6
(
-
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺼﻔﺭﻱ

)
25
(
)
1.9
(
-
ﺍﻟﻌﻤﻠﻴﺔ ﻭﺍﻻﺠﺭﺍﺀ
Process
ﻴﺘﺤﻭل ﺍﻟﻨﻅﺎﻡ ﻤﻥ ﺤﺎﻟﺔ ﺘﻭﺍﺯﻥ ﺍﻟﻰ ﺤﺎﻟﺔ ﺘﻭﺍﺯﻥ ﺍﺨﺭﻯ ﻋﻨﺩﻤﺎ ﺘﺘﻐﻴﺭ ﺨﻭﺍﺼﻪ ﻓﻲ ﺍﺠﺭﺍﺀ ﻤﻌ
ﻴﻥ
.
ﻓﻠﻭ
ﻓﺴﻴﺘﻐﻴﺭ ﺍﻟﺤﺠﻡ ﻭﺍﻟﻜﺜﺎﻓﺔ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ،ﺯﺎﻏ ﻰﻠﻋ ﻁﻠﺴﻤﻟﺍ ﻁﻐﻀﻟﺍ ﺩﺍﺩﺯﺇ
…
.
ﺍﻟﺦ
.
ﻤﻥ ﺍﻟﻤﻤﻜﻥ ﺍﻥ ﺘﺘﻐﻴﺭ ﺨﻭﺍﺹ ﺍﻟﻨﻅﺎﻡ ﻤﻊ ﺒﻘﺎﺀ ﺨﺎﺼﻴﺔ ﺍﻭ ﺍﻜﺜﺭ ﺜﺎﺒﺘﺔ
.
ﺔـﺠﺭﺩ ﺕﻭـﺒﺜ ﺩـﻨﻋ ﹰﻼﺜﻤﻓ
ﺕﻭـﺒﺜ ﺩـﻨﻋﻭ ،ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺄﺒ ﺎﻫﺩﻭﺩﺤ ﺢﻤﺴﺘ ﻲﺘﻟﺍ ﺔﻨﺍﻭﻁﺴﻻﺎﻜ ،ﻲﻠﻤﺭﺜﻭﺯﻴﻻﺍ ﺀﺍﺭﺠﻻﺍ ﻰﻤﺴﻴﻓ ﺓﺭﺍﺭﺤﻟﺍ
ﻜﻤﻴﺔ
ﻤﺜل ﺍﻨﻔﺠﺎﺭ ﻤﻔﺎﺠﺊ ﻟﻌﺠﻠﺔ ﺍﻟﺩﺭﺍﺠﺔ ﺍﻟﻬﻭﺍﺌﻴﺔ ﺍﻭ ﺍﺜﻨﺎﺀ ﺸﻭﻁ ﺍﻟﻘﺩﺭﺓ،ﻲﺘﺎﺒﻴﺩﺍ ﺀﺍﺭﺠﻻﺍ ﻰﻤﺴﻴﻓ ﺓﺭﺍﺭﺤﻟﺍ
ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﻤﺤﺭﻙ ﺍﺤﺘﺭﺍﻕ ﺩﺍﺨﻠﻲ
.
ﺭﺍﺀﺍﺕـﺠﻻﺍ ﺔـﻴﺎﻬﻨﻭ ﺔـﻴﺍﺩﺒ ﻲـﻓ ﻪﺼﺍﻭﺨ ﻊﻴﻤﺠ ﻥﺍ ﻱﺃ ،ﺔﻴﻠﺼﻻﺍ ﻪﺘﻟﺎﺤ ﻰﻟﺍ ﻡﺎﻅﻨﻟﺍ ﺓﺩﻭﻋ ﺩﻨﻋﻭ
، ﻓﺎﻨﻪ ﻴﻜﻭﻥ ﻗﺩ ﻤﺭ ﺒﺩﻭﺭﺓ ﺍﻟﺘﻲ ﻫﻲ ﻤﺠﻤﻭﻋﺔ ﺍﺠﺭﺍﺀﺍﺕ،ﺔﻴﻭﺎﺴﺘﻤ
ﺎـﻤﻴﻓ ﺎـﻫﺭﻜﺫ ﺩﺭﻴﺴ ﻲﺘﻟﺍ ﻭﻨﺭﺎﻜ ﺓﺭﻭﺩﻜ
ﺩﻭﺭﺓ ﻤﺤﺭﻜﺎﺕ ﺍﻻﺤﺘﺭﺍﻕ ﺍﻟﺩﺍﺨﻠﻲ ﺍﻭ ﺍﻟﻤﺤﺭﻜﺎﺕ ﺍﻟﺒﺨﺎﺭﻴﺔ،ﺩﻌﺒ
.
ﺘﺘﻐﻴﺭ ﺤﺎﻟﺔ ﺍﻟﻨﻅﺎﻡ ﻓﻲ ﺍﻟﻌﻤﻠﻴﺎﺕ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﺍﻟﺘﻲ ﻴﻤﻜﻥ ﺘﺼﻨﻴﻔﻬﺎ ﻜﻤﺎ ﻴﺄﺘﻲ
:
-
1
-
ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﻼﺠﺭﻴﺎﻨﻴﺔ
(Non Flow)
ﺭـﻴﻐﺘﺘ ﻻ ﻲﺘﻟﺍﻭ ﺔﻘﻠﻐﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﻲﻓ ﻥﻭﻜﺘ ﻲﺘﻟﺍ ﺔﻨﻜﺎﺴﻟﺍ ﻭﺍ
ﻓﻴﻬﺎ
ﺍﻟﻜﺘﻠﺔ ﺍﻭ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ ﻭﺍﻟﻜﺎﻤﻨﺔ
.
2
-
ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﺠﺭﻴﺎﻨﻴﺔ
(Flow)
ﺍﻭ ﺍﻟﺘﺩﻓﻘﻴﺔ ﺍﻟﺘﻲ ﺘﻜﻭﻥ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ ﻭﺍﻟﺘﻲ ﺘﺘﻐﻴﺭ ﻓﻴﻬﺎ ﺍﻟﻁﺎﻗﺔ
ﺍﻟﺤﺭﻜﻴﺔ ﻭﺍﻟﻜﺎﻤﻨﺔ ﻭﺘﻘﺴﻡ ﺍﻟﻰ
:
ﺃ
-
ﺍﻟﺘﺩﻓﻕ ﺍﻟﻤﺴﺘﻘﺭ
(Steady Flow)
ﻻ ﺘﺘﻐﻴﺭ ﻓﻴﻪ ﻤﻌﺩل ﺠﺭﻴﺎﻥ ﺍﻟﻜﺘﻠﺔ،
.
ﺏ
-
ﺍﻟﺘﺩﻓﻕ ﻏﻴﺭ ﺍﻟﻤﺴﺘﻘﺭ
(Non Steady Flow)
،
ﺔـﻠﺘﻜﻟﺍ ﻥﺎﻴﺭﺠ لﺩﻌﻤ ﻪﻴﻓ ﺭﻴﻐﺘﺘ
.
ﺢـﻀﻭﻴ ﺎـﻤﻭﻤﻋ
ﺍﻟﻤﺨﻁﻁ ﺍﻟﺘﺎﻟﻲ ﺘﺼﻨﻴﻑ ﺍﻟﻌﻤﻠﻴﺎﺕ
:
Non-Flow
Process Steady
SFEE
Flow
Non-Steady
NFEE
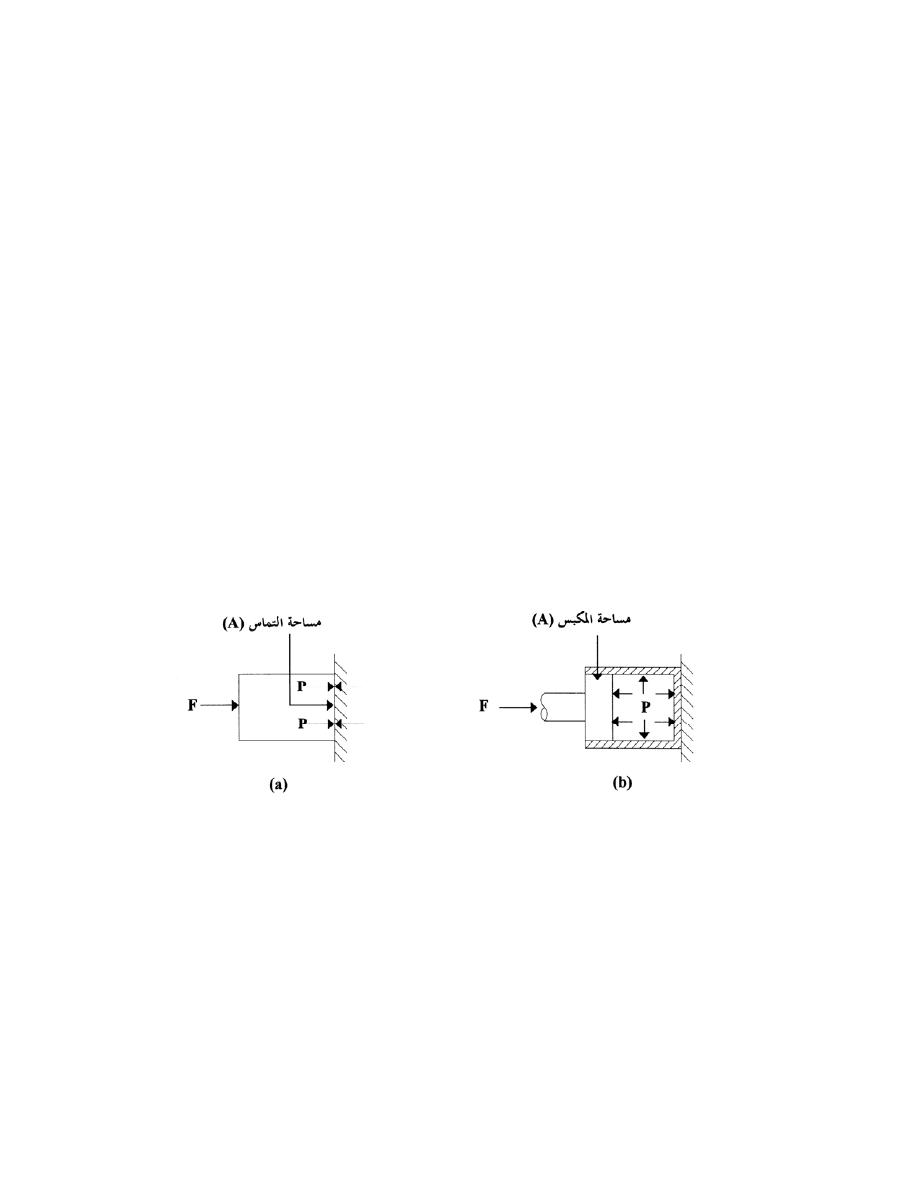
)
26
(
ﺍﻟﻔﺼﻞ ﺍﻟﺜﺎ
ﻧﻲ
–
ﺍﻟﻀﻐﻂ ﻭﺩﺭﺟﺔ ﺍﻟﺤﺮﺍﺭﺓ
)
2.1
(
-
ﺍﻟﻤﻔﻬﻭﻡ ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﻟﻠﻀﻐﻁ
Mechanical Concept of Pressure
ﺎﺯﺍﺕـﻐﻟﺎﺒ لﻭﻐﺸـﻤﻟﺍ ﻡﺠﺤﻟﺍﻭ ،لﺌﺍﻭﺴﻠﻟ ﻥﺎﻴﻠﻐﻟﺍ ﺔﻁﻘﻨﻭ ،ﺔﺒﻠﺼﻟﺍ ﺩﺍﻭﻤﻠﻟ ﺭﺎﻬﺼﻨﻻﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩ ﻥﺇ
ﻭﻤﻌﻅﻡ ﺨﻭﺍﺹ ﺍﻟﻤﻭﺍﺩ ﺘﻌﺘﻤﺩ ﻋﻠﻰ ﺍﻟﻀﻐﻁ ﺍﻟﻤﺴﻠﻁ ﻋﻠﻴﻬﺎ،ﺓﺭﺨﺒﻻﺍﻭ
.
ﻭﻋﻨﺩﻤﺎ ﻴﻤﻸ ﺍ
ﻓﻴﻭﻟﺩ ﺍﻟﻬﻭﺍﺀ ﺍﻟﻤﻀﻐﻭﻁ ﺩﻓﻌﺎﹰ ﺍﻭ ﻗﻭﺓ ﻋﻠﻰ ﺍﻟﺴﻁﺢ ﺍﻟﺩﺍﺨﻠﻲ ﻟﻸﻁﺎﺭ،ﺀﺍﻭﻬﻟﺎﺒ ﺓﺭﺎﻴﺴ ﺭﺎﻁ
ﺒﺴﺒﺏ ﺍﺼﻁﺩﺍﻡ ﺠﺯﻴﺌﺎﺕ ﺍﻟﻬﻭﺍﺀ ﻋﻠﻰ ﺍﻟﺴﻁﺢ
.
ﻟﺫﻟﻙ ﻴﻌﺭﻑ ﺍﻟﻀﻐﻁ ﺒﺄﻨﻪ ﺍﻟﻘﻭﺓ ﺍﻟﻤﺴﻠﻁﺔ ﻋﻤﻭﺩﻴﺎﹰ ﻋﻠ
ﻰ
ﻭﺤﺩﺓ
ﺭﻤﺯﻩ،ﺡﻭﻁﺴﻟﺍ
(P)
.
ﻋﻨﺩ ﺘﺴﻠﻴﻁ ﻗﻭﺓ ﻤﻘﺩﺍﺭﻫﺎ
(F)
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﺏﻠﺼ ﻡﺴﺠ ﻰﻠﻋ
(2.1-a)
ﻤﻭﻀﻭﻉ ﻋﻠﻰ ﺠﺩ
ﺍﺭ ﻤﺴﺎﺤﺔ
ﺘﻤﺎﺴﻪ
(A)
ﻋﻨﺩﺌﺫ ﺴﻴﻜﻭﻥ ﻫﻨﺎﻟﻙ ﻀﻐﻁ ﻤﺴﻠﻁ ﻋﻤﻭﺩﻴﺎﹰ ﻋﻠﻰ ﺴﻁﺢ ﺍﻟﺘﻤﺎﺱ ﻤﻘﺩﺍﺭﻩ،
(P = F/A)
ﻭﺴﻴﻨﺘﻘل
ﺒﺄﺘﺠﺎﻩ ﺍﻟﻘﻭﺓ ﺍﻟﻤﺴﻠﻁﺔ
.
ﻭﺍﺫﺍ ﺴﻠﻁﺕ ﻗﻭﺓ
(F)
ﻋﻠﻰ ﻤﻜﺒﺱ ﻤﺴﺎﺤﺔ ﻤﻘﻁﻌﻪ
(A)
ﻜﻤﺎ ﻓﻲ ﺸﻜل،
(2.1-b)
ﻴﻜﻭﻥـﺴ ﺫﺌﺩﻨﻋ
ﻫﻨﺎﻟﻙ ﻀﻐﻁ ﻤﺴﻠﻁ ﻋﻠﻰ ﺍﻟﻤﺎﺌﻊ ﻤﻘﺩﺍﺭﻩ
(P = F/A)
ﻭﺴﻴﻨﺘﻘل ﺍﻟﻰ ﺠﻤﻴﻊ ﺍﻻ
،ﺘﺠﺎﻫﺎﺕ ﻓﻲ ﺍﻻﺴﻁﻭﺍﻨﺔ
ﺸﻜل
)
2.1
(
-
ﺍﻟﻀﻐﻁ ﺍﻟﻌﻤﻭﺩﻱ ﻋﻠﻰ ﻭﺤﺩﺓ ﺍﻟﺴﻁﻭﺡ
ﻜﻌﻤﻠﻴﺔ ﻨﻔﺦ ﻜﺭﺓ ﻤﻁﺎﻁﻴﺔ ﺤﻴﺙ ﺘﻨﺘﻔﺦ ﻓﻲ ﺠﻤﻴﻊ ﺍﻻﺘﺠﺎﻫﺎﺕ
.
ﻭﺍﺫﺍ ﻜﺎﻨﺕ ﺍﻟﻘﻭﺓ
(F)
ﺒﺎﻟﻨﻴﻭﺘﻥ
(N)
ﻭﺍﻟﻤﺴﺎﺤﺔ
(A)
ﺔـﻌﺒﺭﻤﻟﺍ ﺭﺎﺘﻤﻷﺎﺒ
(m
2
)
ﻴﻜﻭﻥـﺴ ٍﺫـﺌﺩﻨﻋ ،
ﺍﻟﻀﻐﻁ
(P)
ـ ﺒﺎﻟ
(N/m
2
)
ﻭﻫﻲ ﻭﺤﺩﺓ ﺍﺴﺎﺴﻴﺔ ﻟﻠﻀﻐﻁ ﻓﻲ ﻨﻅﺎﻡ
(SI)
ﻭ
ﺘﺴﻤﻰ ﺒﺎﻟﺒﺎﺴﻜﺎل
(Pa)
ﺎﻥـﻜﻭ
ﺒﺎﺴﻜﺎل
(Pascal)
ﺍﻭل ﻤﻥ ﺍﻫﺘﻡ ﺒﻘﻭﺍﻨﻴﻥ ﺍﻟﻀﻐﻁ
.
ﻥـﻤ ﺭـﺒﻜﺍ ﺔﻔﻋﺎﻀـﻤ ﺕﺍﺩﺤﻭ ﺔﻴﻠﻤﻌﻟﺍ ﺓﺎﻴﺤﻟﺍ ﻲﻓ لﻤﻌﺘﺴﺘﻓ ،ﹰﺍﺩﺠ ﺓﺭﻴﻐﺼ لﺎﻜﺴﺎﺒﻟﺍ ﺓﺩﺤﻭ ﻥﻭﻜﻟﻭ
ﻜﺎﻟﻜﻴﻠﻭ ﺒﺎﺴﻜﺎل،لﺎﻜﺴﺎﺒﻟﺍ
(kPa)
ﻭﺍﻟﻤﻴﻜﺎ ﺒﺎﺴﻜﺎل
(MPa)
ﻭﺍﻟﻌﻼﻗﺔ ﺒﻴﻨﻬﻡ ﻫﻲ،
:
-
MPa (MN/m
2
) = 10
3
kPa (kN/m
2
)
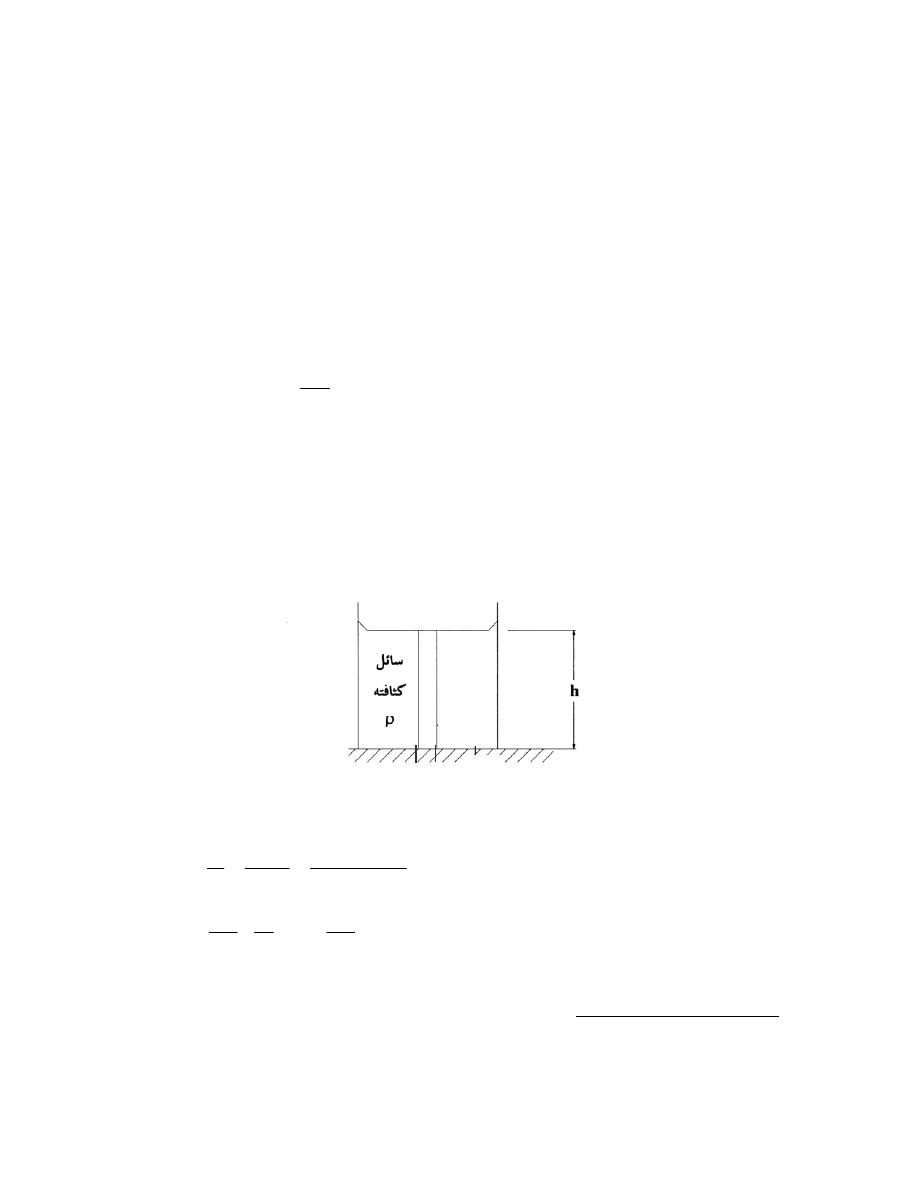
)
27
(
= 10
6
Pa (N/m
2
)
= 1N/mm
2
ﻭﻜﺫﻟﻙ ﺘﺴﺘﻌﻤل ﻭﺤﺩﺍﺕ ﺍﻟﺒﺎﺭ
(bar)
ﻭﺍﻟﻬﻴﻜﺘﻭﺒﺎﺭ
:
hectobar = 10
2
bar
= 10
4
kPa
= 10
7
Pa
ﺍﻥ
)
ﺍﻟﺒﺎﺭ
(
∗
ﻪـﻋﺎﻔﺘﺭﺍ ﻕﺒﺌﺯﻟﺍ ﻥﻤ ﺩﻭﻤﻋ ﻪﺒﺒﺴﻴ ﻱﺫﻟﺍ ﻁﻐﻀﻟﺍ ﻭﻫ
(750mm)
ﺩﺍﺕـﺤﻭﻟﺍ ﻲـﻓﻭ ،
ﺍﻟﺒﺭﻴﻁﺎﻨﻴﺔ ﺘﻜﻭﻥ ﺍﻟﻘﻭﺓ ﺒﺎﻟﺒﺎﻭﻨﺩ
(Lb)
ﻭﺍﻟﻤﺴﺎﺤﺔ ﺒﺎﻻﻨﺞ ﺍﻟﻤﺭﺒﻊ
(in
2
)
ﻭـﻜﺘ ﻪـﻴﻠﻋ ،
ﻀﻐﻁـﻟﺍ ﺓﺩـﺤﻭ ﻥ
(Lb/in
2
)
ﻭﻴﺴﻤﻰ
(PSI)
ـ ﻋﻼﻗﺘﻪ ﻤﻊ ﺍﻟ،
(atm.)
ﻫﻲ
:
)
2.2
(
-
ﺍﻟﻀﻐﻁ ﺍﻟﺫﻱ ﻴﺴﺒﺒﻪ ﻋﻤﻕ ﺍﻟﻤﺎﺌﻊ
Pressure due to a head of fluid
ﺎﺌﻊـﻤ ﻰﻠﻋ ﻱﻭﺘﺤﻴ ،ﻪﻴﻠﻋ ﺭﺜﺅﻴ ﻻ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﻥﺍ ﻱﺃ ،ﺀﺍﻭﻬﻟﺎﺒ ﻁﺎﺤﻤ ﺭﻴﻏ ﻥﺍﺯﺨ ﺩﻭﺠﻭ ﺽﺭﺘﻔﻨ
ﻜﺜﺎﻓﺘﻪ
(
ρ)
ﺜﺎﺒﺘﺔ ﻓﻠﻭ ﺍﺨﺫﻨﺎ ﻤﻘﻁﻌﺎﹰ ﻁﻭﻟﻴﺎﹰ
ﻟﻬﺫﺍ ﺍﻟﻤﺎﺌﻊ ﺍﺭﺘﻔﺎﻋﻪ
(h)
ﻭﻤﺴﺎﺤﺔ ﻤﻘﻁﻌﻪ
(A)
ﻜلـﺸ ﻲﻓ ﺎﻤﻜ ،
(2.2)
ﻓﺴﺘﻜﻭﻥ ﻜﺘﻠﺔ ﻫﺫﺍ ﺍﻟﻤﻘﻁﻊ،
(m=
ρV)
ﻭﺤﺠﻤﻪ،
(V=A ×h)
ﻋﻨﺩﺌﺫ ﺴﻴﻜﻭﻥ ﺍﻟﻀﻐﻁ،
:
)
2.3
(
-
ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
Atmospheric Pressure
∗
ﺍﻥ ﺍﻟﺒﺎﺭ
(bar)
ﻻ ﻴﻨﺘﻤﻲ ﺍﻟﻰ ﺍﺴﺭﺓ ﺍﻟﻭﺤﺩﺍﺕ
(SI)
ﻭﻤﻊ ﺫﻟﻙ ﻴﺴﺘﻌﻤل ﻜﺜﻴﺭﺍﹰ ﻓﻲ ﺍﻟﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﺼﻨﺎﻋﻴﺔ،
ﻭﻓﻲ ﺍﻟﺤﺴﺎﺒﺎﺕ ﺍﻟﻤﺨﺘﻠﻔﺔ ﺸﺭﻁ ﺘﺤﻭﻴﻠﻪ ﺍﻟﻰ ﺍﻟﻭﺤﺩﺍﺕ ﺍﻟﻤﻨﺎﺴﺒﺔ
.
⎟
⎠
⎞
⎜
⎝
⎛
=
2
in
Lb
PSI
7
.
14
.
atm
1
(2.1)
...
..........
h
g
A
g
h
A
A
g
m
A
F
P
×
×
ρ
=
×
×
×
ρ
=
×
=
=
Pa
m
N
m
s
m
m
kg
2
2
3
=
=
×
×
=
A
ﺸﻜل
)
2.2
(
-
ﻀﻐﻁ ﺍﻟﻤﻭﺍﺌﻊ
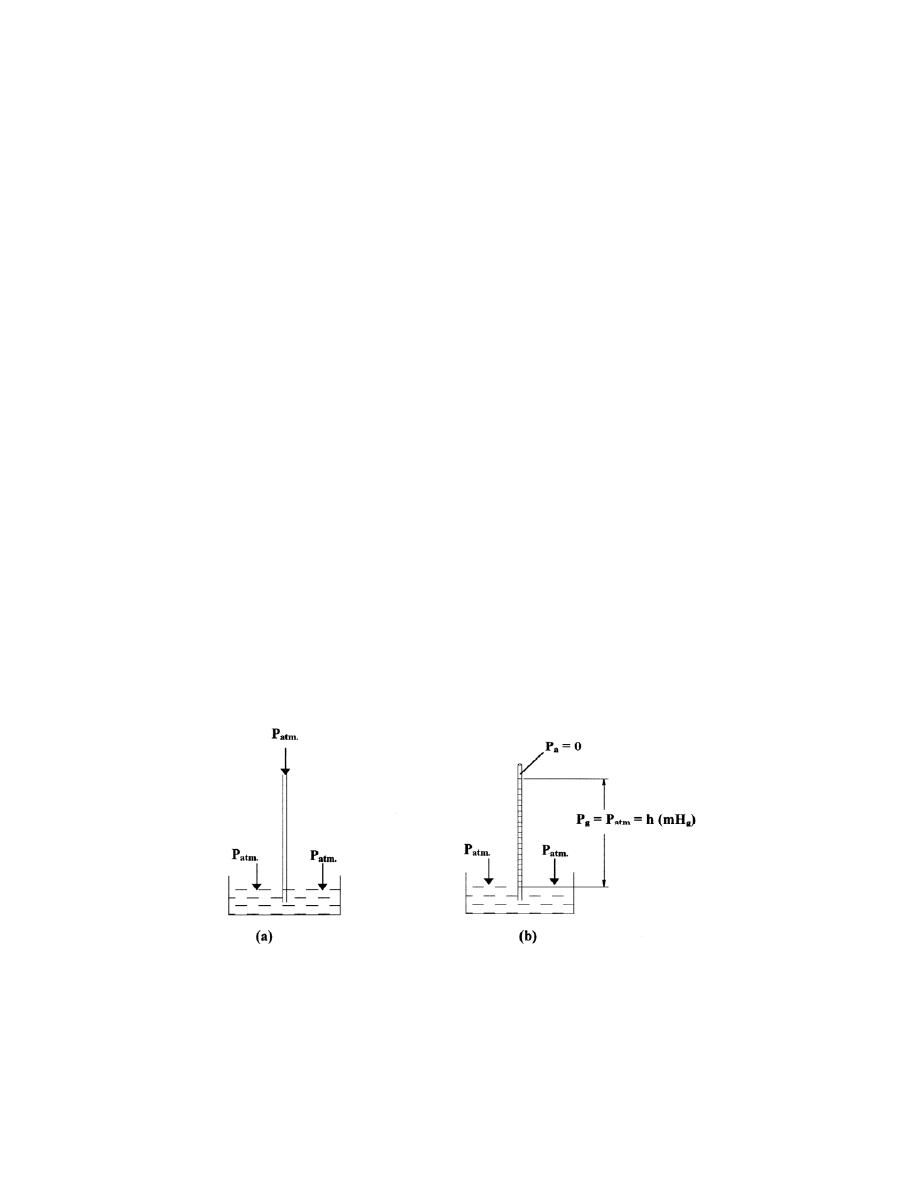
)
28
(
ﺍﻟﻜﺭﺓ ﺍﻻﺭﻀﻴﺔ ﻤﺤﺎﻁﺔ ﺒﺎﻟﻬﻭﺍﺀ ﺍﻟﺠﻭﻱ ﻴﻤﺘﺩ ﺍﻟﻰ ﻋﺩﺓ ﻜﻴﻠﻭﻤﺘﺭﺍﺕ ﻓﻭﻕ ﺴﻁﺤﻬﺎ
.
ﻫﺫﺍ ﺍﻟﻬﻭﺍﺀ ﻴ
ﻭﻟﺩ
ﺯﻩـﻤﺭﻭ ﻱﻭـﺠﻟﺍ ﻁﻐﻀﻟﺎﺒ ﻰﻤﺴﻴ ﺢﻁﺴﻟﺍ ﺍﺫﻫ ﻕﻭﻓ ﻪﻨﺯﻭﻟ ﺔﺠﻴﺘﻨ ﺽﺭﻻﺍ ﺢﻁﺴ ﻰﻠﻋ ﹰﺎﻁﻐﻀ
(Patm.)
.
ﻁﺢـﺴ ﻥﻤ ﺩﺤﺍﻭ ﻊﺒﺭﻤ ﺭﺘﻤ ﻰﻠﻋ ﻁﻐﻀﻟﺍ ﻥﻭﻜﻴﺴﻓ ،ﺔﺤﺎﺴﻤﻟﺍ ﺓﺩﺤﻭ ﻰﻠﻋ ﺓﻭﻘﻟﺍ ﻱﻭﺎﺴﻴ ﻁﻐﻀﻟﺍ ﻥﺎﻜ ﺎﻤﻟﻭ
ﺩﺤﺍﻭ ﻊﺒﺭﻤ ﺭﺘﻤ ﻪﻌﻁﻘﻤ ﺏﻭﺒﻨﺍ ﻲﻓ ﹰﻼﺜﻤ ﻩﺀﺍﻭﺘﺤﺍ ﻙﻟﺫﺒ ﹰﺎﻀﺭﺘﻔﻤ ﺎﻬﻗﻭﻓ ﺀﺍﻭﻬﻟﺍ ﺩﻭﻤﻋ ﻥﺯﻭ ﻱﻭﺎﺴﻴ ﺽﺭﻻﺍ
ﻭﻁﻭﻟﻪ ﻴﺴﺎﻭﻱ ﺍﺭﺘﻔﺎﻉ ﺍﻟﻐﻼﻑ ﺍﻟﺠﻭﻱ ﻓﻭﻕ ﺍﻻﺭﺽ
.
ﻼﻑـﻐﻟﺍ ﻉﺎـﻔﺘﺭﻷ ٍﻭﺎﺴـﻤ ﻪﻟﻭﻁ ﺀﺍﻭﻬﻟﺍ ﻥﻤ ﺩﻭﻤﻋ ﻩﺩﻟﻭﻴ ﻱﺫﻟﺍ ﻁﻐﻀﻟﺍ ﻭﻫ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﻥﺫﺍ
ﺍﻟﺠﻭﻱ ﻓﻭﻕ ﺍﻻﺭﺽ
.
ﻗﻴﻤﺘﻪ ﻋﻨﺩ ﻤﺴﺘﻭﻯ ﺴﻁﺢ ﺍﻟﺒﺤﺭ
(101.325 kN/m
2
)
ﻭﻤﻊ ﺫﻟﻙ ﻻ ﻴﺸﻌﺭ ﺍﻻﻨﺴﺎﻥ،
ﺒﻪ ﻟﺘﺴﺎﻭﻱ ﻀﻐﻁﻪ ﻤﻊ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
.
ﻫﺫﻩ ﺍﻟﻘﻴﻤﺔ ﺘﻨﺨﻔﺽ ﻜﻠﻤﺎ
ﺜﻼﹰـﻤﻓ ﻱﻭﺠﻟﺍ ﻑﻼﻐﻟﺍ ﻉﺎﻔﺘﺭﺍ ﺽﻔﺨﻨﺍ
ﺘﻜﻭﻥ،ﻡﻟﺎﻌﻟﺍ ﻲﻓ ﺔﻴﻠﺒﺠ ﺔﻤﻗ ﻰﻠﻋﺍ ﻲﻫﻭ ،ﺕﺴﺭﻔﻴﺍ لﺒﺠ ﺔﻤﻗ ﺩﻨﻋ ﻪﺘﻤﻴﻗ
(40 KN/m
2
)
ﻲـﻓ ﻪﺘﻤﻴﻗ ﻡﺩﻌﻨﺘﻭ
ﺍﻟﻔﺭﺍﻍ ﺍﻟﻤﺤﻴﻁ ﺒﺎﻟﻜﺭﺓ ﺍﻻﺭﻀﻴﺔ
.
ﻴﻜﻭﻥ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ ﺍﻟﻘﻴﺎﺴﻲ
(standard)
:
Patm. = 760 mmHg
= 14.7 Lb/in
2
= 1.013 bar
= 1.01325 kg/cm
2
)
2.4
(
-
ﻤﻘﻴﺎﺱ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ ﺍﻭ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ
The Barometer
ﺭـﻴﻤﺍ ﺭﺼﻗ ﻲﻓ ﻥﺎﻜ ﺙﻴﺤ ،ﺎﻴﻟﺎﻁﻴﺍ ﺕﺎﻌﻁﺎﻘﻤ ﻯﺩﺤﺍ ﻲﻓ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﻑﺎﺸﺘﻜﺍ ﺓﺭﻜﻓ ﺕﺃﺩﺒ ﺩﻘﻟ
ﺍﻟﻤﻘﺎﻁﻌﺔ ﺒﺌﺭ ﻋﻠﻴﻪ ﻤﻀﺨﺔ ﻤﺎﺼﺔ ﺘﺴﻘﻲ ﺤﺩﻴﻘﺔ ﺍﻟﻘﺼﺭ
.
ﻊـﻓﺭ ﺔﺨﻀﻤﻟﺍ ﻊﻁﺘﺴﺘ ﻡﻟ ﻑﻴﺼﻟﺍ ﻡﺎﻴﺍ ﺩﺤﺍ ﻲﻓﻭ
ﻓﺄﺴﺘﺩﻋﻲ ﻟﺫﻟﻙ ﺍﻟﻌﺎﻟﻡ ﺍﻻﻴﻁ،ﺭﺌﺒﻟﺍ ﻥﻤ ﺀﺎﻤﻟﺍ
ﺎﻟﻲ ﻏﺎﻟﻴﻠﻭ
(1638)
)
ﻭﻫﻭ ﺍﺴﺘﺎﺫ ﺍﻟﻌﺎﻟﻡ ﺘﻭﺭﺸﻴﻠﻲ ﻭﻤﻥ ﻋﻠﻤﺎﺀ
ﺍﻟﻔﻠﻙ ﻭﺍﻟﻔﻴﺯﻴﺎﺀ ﺍﻟﻤﺸﻬﻭﺭﻴﻥ
(
ﻭﻋﻨﺩﻤﺎ ﻗﺎﻡ ﻏﺎﻟﻴﻠﻭ ﺒﻔﺤﺹ ﺍﻟﻤﻀﺨﺔ ﻭﺠﺩﻫﺎ ﺒﺤ،ﺏﺒﺴﻟﺍ ﻥﻋ ﻱﺭﺤﺘﻠﻟ ،
ـ
ﺎﻟﺔ
ﺸﻜل
)
2.3
(
-
ﻤﺒﺩﺃ ﺘﻭﺭﺸﻴﻠﻲ ﻓﻲ ﺘﺼﻤﻴﻡ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ

)
29
(
ﻟﺫﺍ ﻋﺯﻯ ﺴﺒﺏ ﻋﺩﻡ ﺍﺭﺘﻔﺎﻉ ﺍﻟﻤﺎﺀ ﺍﻟﻰ ﺍﻨﺨﻔﺎﺽ ﻤﺴﺘﻭﺍﻩ ﻓﻲ ﺍﻟﺒﺌﺭ ﻟﺩﺭﺠﺔ،ﺓﺩﻴﺠ
ﻟﻡ ﻴﺴﺘﻁﻊ ﻤﻌﻬﺎ ﺍﻟﻀﻐﻁ
ﺍﻟﺠﻭﻱ ﻋﻠﻰ ﺭﻓﻊ ﺍﻟﻤﺎﺀ ﺍﻟﻰ ﻤﺴﺘﻭﻯ ﺍﻟﺤﺩﻴﻘﺔ
.
ﻴﻠﻲـﺸﺭﻭﺘ ﻡﻟﺎـﻌﻟﺍ ﺕـﻌﻓﺩ ﺔﺜﺩﺎﺤﻟﺍ ﻩﺫﻫ
)
1644
–
1608
(
ﺒﺎﺨﺘﺭﺍﻉ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ ﺍﻟﺫﻱ ﻴﻌﺘﻤﺩ ﺍﻟﻤﺒﺩﺃ ﺍﻟﺘﺎﻟﻲ
:
-
ﺍﻟﺸﻜل
)
2.3
(
ﻤﻐﻤﻭﺭ ﻓﻴﻪ ﺍﻨﺒﻭﺏ ﺫﻭ ﻤﻘﻁﻊ ﻻ ﻴﺴﻤﺢ ﺒﻭﺠﻭﺩ ﺘﺄﺜﻴﺭ،لﺌﺎﺴ ﻰﻠﻋ ﻱﻭﺘﺤﻴ ﹰﺎﻨﺍﺯﺨ ﻥﻴﺒﻴ
ﺸﻌﺭﻱ ﻨﺎﺘﺞ ﻋﻥ ﺘﻭﺘﺭ ﺍﻟ
ﺴﻁﺢ
.
ﺴﺎﻭﻴﺎﹰـﺘﻤ ﺏﻭـﺒﻨﻻﺍﻭ ﻥﺍﺯـﺨﻟﺍ ﻲﻓ لﺌﺎﺴﻟﺍ ﺢﻁﺴ ﻥﻭﻜﻴﺴﻓ ﻰﻠﻋﻻﺍ ﻥﻤ ﹰﺎﺤﻭﺘﻔﻤ ﺏﻭﺒﻨﻻﺍ ﻥﺎﻜ ﺍﺫﺎﻓ
ﻟﺘﺴﺎﻭﻱ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
(Patm.)
ﻜﻤﺎ ﻓﻲ ﺸﻜل
(2.3-a)
.
ﺍﻤﺎ ﺍﺫﺍ ﻜﺎﻥ ﺍﻻﻨﺒﻭﺏ ﻤﻐﻠﻕ ﻭﻤﻔﺭﻍ ﻤﻥ ﺍﻟﻬﻭﺍﺀ
ﻤﻥ ﺍﻻﻋﻠﻰ ﻓﺴﻭﻑ ﻴﺭﺘﻔﻊ ﺍﻟﺴﺎﺌل ﺩﺍﺨل ﺍﻻﻨﺒﻭﺏ ﺒﻤﻘﺩﺍﺭ
(h)
ﻀﻐﻁ ﺍـﻟﺍ ﺔـﻤﻴﻘﻟ ﺔﻴﻭﺎﺴـﻤ ﺎﻬﺘﻤﻴﻗ
ﻭﻱـﺠﻟ
(Patm.)
ﻜﻤﺎ ﻓﻲ ﺸﻜل،
(2.3-b)
ﺍﻤﺎ ﺍﻟﻔﺭﺍﻍ ﺍﻟﺫﻱ ﻴﺤﺼل ﻓﻲ ﺍﻻﻨﺒﻭﺏ ﻓﻭﻕ ﺴﻁﺢ ﺍﻟﺴﺎﺌل ﻓﻴﺴﻤﻰ ﺒﻔﺭﺍﻍ
ﺘﻭﺭﺸﻴﻠﻲ
.
ﺇﻥ ﻗﻴﻤﺔ
(h)
ﻓﺈﺫﺍ ﻜﺎﻥ ﺯﺌﺒﻘﺎﹰ،لﺌﺎﺴﻟﺍ ﺔﻴﻋﻭﻨ ﻰﻠﻋ ﺩﻤﺘﻌﺘ
)
ﻜﺜﺎﻓﺘﻪ
(
ﻓﻴﻜﻭﻥ
:
ﺎﻭﻱـﺴﺘ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻠﻟ ﺔﺘﺒﺎﺜﻟﺍ ﺔﻤﻴﻘﻟﺍ
(
101.3kN/m
2
)
.
ﺎﺀـﻤ ﻥﺎـﻜ ﺍﺫﺇﻭ
)ﻜ
ﺜﺎﻓﺘﻪ
(
ﻓﺈﻥ
:
ﺇﻥ ﻋﻤﻭﺩﺍ ﻤﻥ ﺍﻟﻤﺎﺀ ﺍﺭﺘﻔﺎﻋﻪ
(10.326m)
ﻴﻜﻭﻥ ﻁﻭﻴﻼﹰ ﺠﺩﺍﹰ ﻟﻸﻏﺭﺍﺽ ﺍﻟﻘﻴﺎﺴﻴﺔ ﻭﻋﺭﻀﺔ ﻟﻠﻜﺴﺭ
ـ ﻟﺫﺍ ﻓﻜﺭ ﺘﻭﺭﺸﻴﻠﻲ ﺒﺎﺴﺘﻌﻤﺎل ﺍﻟﺯﺌﺒﻕ ﻻﻨﻪ ﺍﻜﺜﻑ ﻤﻥ ﺍﻟﻤﺎﺀ ﺒ،ﻪﻟﺎﻤﻌﺘﺴﺍ ﻭﺍ ﻪﻠﻤﺤ ﺀﺎﻨﺜﺍ
(13.6)
ﻤﺭﺓ ﻭﻤﻨﻪ
ﻓﺎﻥ ﻋﻤﻭﺩ ﺍﻟﺯﺌﺒﻕ ﺴﻴﻜﻭﻥ ﻤﺭﺓ ﺒﺎﺭﺘﻔﺎﻉ ﻋﻤﻭﺩ
ﺃﻱ،ﺀﺎﻤﻟﺍ
:
ﻭﺒﻤﺎ ﺍﻨﻪ،ﹰﻻﻭﻘﻌﻤ ﻉﺎﻔﺘﺭﻻﺍ ﺍﺫﻫ
(Hg)
ﺎﻉـﻔﺘﺭﺍ ﻥﻭﻜﻴـﺴ ٍﺫـﺌﺩﻨﻋ ،ﻕﺒﺌﺯﻠﻟ ﻱﻭﺎﻴﻤﻴﻜﻟﺍ ﺯﻤﺭﻟﺍ ﻭﻫ
ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ ﺍﻟﺯﺌﺒﻘﻲ
(760 mmHg)
.
ﺩﺍﺕـﺤﻭﺒ ﻁﻐﻀـﻟﺍ ﻥﻭﻜﻴ ﺔﻴﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜﻟﺍ ﺕﺎﺒﺎﺴﺤﻟﺍ ﻲﻓﻭ
(Pa)
ﻭﻤﻀﺎﻋﻔﺎﺘﻪ
.
ﻓﺈﺫﺍ ﻜﺎﻥ ﺍﻻﺭﺘﻔﺎﻉ ﺍﻟﺒﺎﺭﻭﻤﺘﺭﻱ
(h=mm)
ﺴﻴﻜﻭﻥ ﺍﻟﻀﻐﻁٍﺫﺌﺩﻨﻋ
:
-
3
m
/
kg
13600
mHg
76
.
0
9.81
13600
10
3
.
101
g
.
Patm
h
3
=
×
×
=
ρ
=
( )
6
.
13
1
m
76
.
0
6
.
13
326
.
10
h
=
=
)
bar
(
h
10
4
.
133
)
(MN/m
h
10
133.4
)
(kN/m
h
10
4
.
133
)
(N/m
h
4
.
133
10
h
9.81
13600
gh
P
5
-
2
6
-
2
3
-
2
3
×
=
×
=
×
=
=
×
×
=
ρ
=
3
3
m
/
Kg
10
O
H
m
326
.
10
9.81
10
10
3
.
101
g
P
h
2
3
3
=
×
×
=
ρ
=
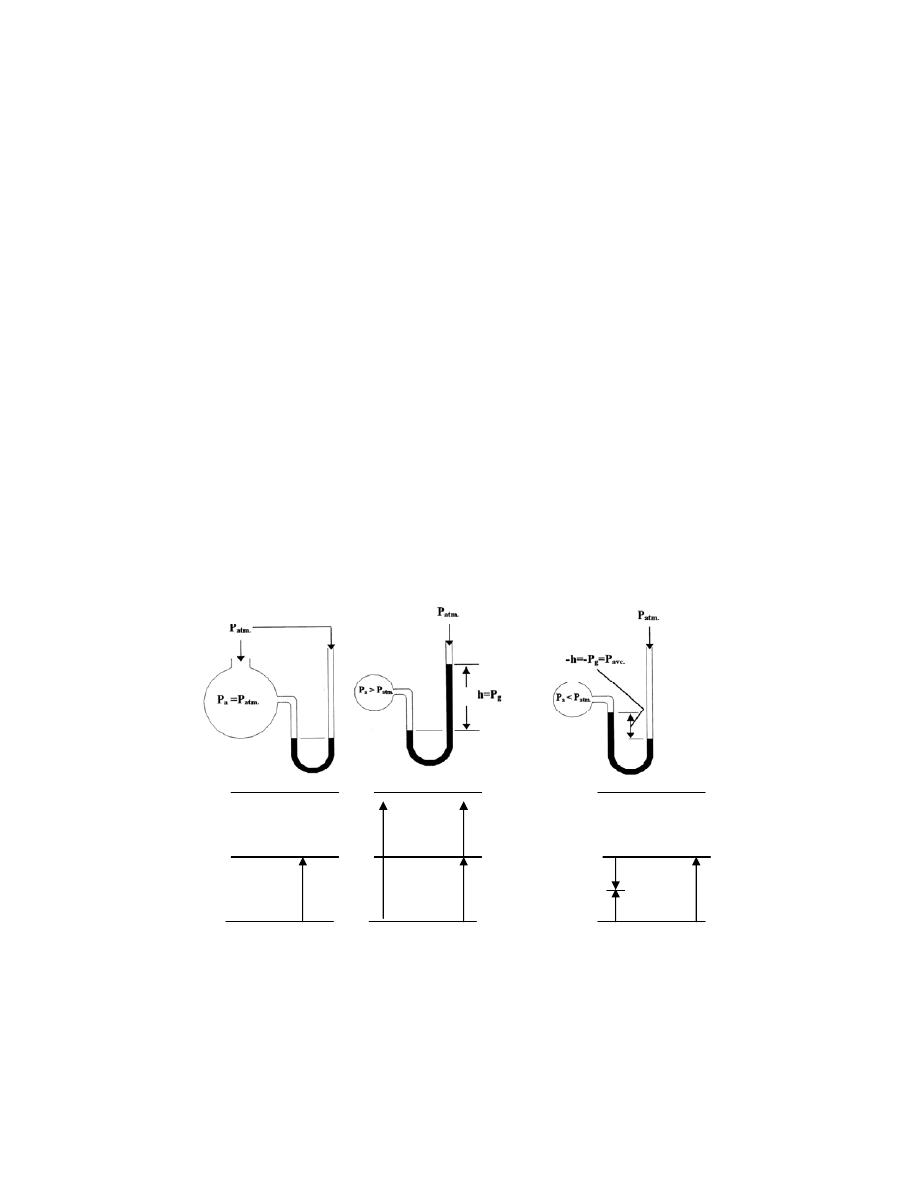
)
30
(
ﻭﻋﻤﻠﻴﺎﹰ
ﺴﻴﺯﺩﺍﺩ ﺍﻻﺭﺘﻔﺎﻉ ﺍﻟﺒﺎﺭﻭﻤﺘﺭﻱ ﺒﺯﻴﺎﺩﺓ ﺍﻟﻀﻐﻁ ﻭﺍﻟﻌﻜﺱ ﺒﺎﻟﻌﻜﺱ
.
ﻴﺘﻐﻴﺭ ﻤﻘﺩﺍﺭ ﺍﻟﻀﻐﻁ ﻤﻥ
ﺩـﺤﺍﻭﻟﺍ ﻥﺎـﻜﻤﻟﺍ ﻲﻓ ﻁﻐﻀﻟﺍ ﺭﻴﻐﺘﻴ ﺎﻤﻜ ،ﺭﺤﺒﻟﺍ ﺢﻁﺴ ﻯﻭﺘﺴﻤ ﻥﻋ ﻥﺎﻜﻤﻟﺍ ﻉﺎﻔﺘﺭﺇ ﺏﺴﺤ ﺭﺨﺁ ﻰﻟﺍ ﻥﺎﻜﻤ
ﻭـﺠﻟﺍ ﻲﻓ ﺔﺒﻭﻁﺭﻟﺍ ﺭﺍﺩﻘﻤﻭ ،ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ ،ﺢﻴﺭﻟﺍ ﺔﻋﺭﺴﺒ ﻩﺭﺜﺄﺘ ﺔﺠﻴﺘﻨ ﺭﺨﻵ ﺕﻗﻭ ﻥﻤ ﹰﺎﻀﻴﺍ
.
ﺫﻟﻙـﻟ
ﺼﻨﻌﺕ ﺍﻟﺒ
ﻭﻓﻭﺭﺘﻥ،لﺠﺴﻤﻟﺍ ﻲﻨﺩﻌﻤﻟﺍﻭ ،ﻲﻨﺩﻌﻤﻟﺍﻭ ،ﻲﻘﺒﺌﺯﻟﺍ ﺎﻬﻨﻤ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﺱﺎﻴﻘﻟ ﺕﺍﺭﺘﻴﻤﻭﺭﺎ
.
)
2.5
(
-
ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ
The Manometer
ﻋﺒﺎﺭﺓ ﻋﻥ ﺍﻨﺒﻭﺏ ﻋﻠﻰ ﺸﻜل ﺤﺭﻑ
(U)
ﺼلـﺘﻴﻭ ،ﻪﺒﻨﺍﻭﺠ ﺩﺤﺍ ﺩﻨﻋ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﻰﻟﺍ ﺡﻭﺘﻔﻤ
ﻕــﻠﻁﻤﻟﺍ ﻁﻐﻀــﻟﺍ ﻭﺍ ﻲــﻘﻴﻘﺤﻟﺍ ﻪﻁﻐــﻀ ﺱﺎــﻴﻗ ﺏﻭــﻠﻁﻤﻟﺍ ﺀﺎــﻋﻭﻟﺎﺒ ﺭــﺨﻵﺍ ﻑﺭــﻁﻟﺍ ﺩــﻨﻋ
(Absolute Press.. Pa)
.
ﻟﻜﻭﻥ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ ﻏﺎﻟﺒﺎﹰ ﻤﺎ ﻴﻘﺎﺱ ﺒﺄﺭﺘﻔﺎﻉ ﻋﻤﻭﺩ ﻤﻥ،ﺏﻭﺒﻨﻻﺍ ﻲﻓ ﻕﺒﺌﺯﻟﺍ لﺎﻤﻌﺘﺴﺍ ﻊﺌﺎﺸﻟﺍ ﻥﻤ
ﺍﻟﺯﺌﺒﻕ
.
ﻭﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ ﻗﻠﻴﻼﹰ
)
ﻟﺤﺩ
50mm
(
ﻲـﻁﻌﻴ ﻪﻨﻷﻭ ﺔﺌﻁﺍﻭﻟﺍ ﻪﺘﻓﺎﺜﻜﻟ ﺀﺎﻤﻟﺍ لﻤﻌﺘﺴﻴﻓ
ﺩﻗﺔ ﻓﻲ ﺍﻟﻘﻴﺎﺴﺎﺕ ﻜﺎﻟﻤﺎﻨﻭﻤﻴﺘﺭ ﺍﻟﻤﺎﺌل
(Inclined Manometer)
.
ﻋﻨﺩﻤ
ﺈﻥـﻓ ﻪـﻴﻠﻋﻭ ،ﻕـﻠﻁﻤ ﺔﻤﻠﻜ ﺭﻜﺫﻟ ﻲﻋﺍﺩ ﻻ ،ﺔﻘﻠﻁﻤ ﻁﻭﻐﻀﻟﺍ ﻥﻭﻜﺘ ﺎ
(250kPa)
ﻲـﻨﻌﺘ
(250 kPa. Pa)
.
ﺍﻥ ﻨﻘﻁﺔ ﺍﻟﺼﻔﺭ ﻓﻲ ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭﺍﺕ ﻫﻲ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
(Patm.)
ﻀﻐﻁـﻟﺍ ﻥﻭﻜﻴ ﻥﺍ ﻥﻜﻤﻴ ﻪﻴﻠﻋ ،
ﻭﻜﻤﺎ ﻤﻭﻀﺢ ﻓﻲ ﺍﺩﻨﺎﻩ،ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﻥﻤ ﺭﻐﺼﺍ ﻭﺍ ﺭﺒﻜﺍ ﻭﺍ ﻱﻭﺎﺴﻴ ﺀﺎﻋﻭﻠﻟ ﻕﻠﻁﻤﻟﺍ
.
ﺸﻜل
)
2.4
(
-
ﻤﺒﺎﺩﺉ
ﻋﻤل ﺍﻟﺒﺎﺭﻭﻤﺘﺭ
a
b
c
Patm
Pg
Pa
Pg=0
Pa
Patm
Pg
Pg=Pa-Patm>0
Pg=Patm-Pa<0
Pg
(
)
Pa
Patm
Patm

)
31
(
1
-
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ
(Pa = Patm.)
ﻜﻤﺎ ﻓﻲ ﺸﻜل
(2.4-a)
ﻭﺏـﺒﻨﻻﺍ ﻲﻓﺭﻁ ﻲﻓ لﺌﺎﺴﻟﺍ ﻯﻭﺘﺴﻤ ﻯﻭﺎﺴﺘﻴﻓ
ﺎﺱـﻘﻤﻟﺍ ﻁﻐﻀـﻟﺍ ﻥﻭﻜﻴﺴﻭ ﻥﻴﻓﺭﻁﻟﺍ ﻰﻠﻋ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﺭﻴﺜﺄﺘ ﺏﺒﺴﺒ
(Gauge Pressure. Pg)
ﺃﻱ ﺍﻥ،ﹰﺍﺭﻔﺼ ﻱﻭﺎﺴﻴ
:
Pg = 0
…… (2.2)
2
-
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ
(Pa > Patm.)
ﻜﻤﺎ ﻓﻲ ﺸﻜل
(2.4-b)
ﻓﺴﻴﺭﺘ
ﻥـﻤﻴﻻﺍ ﻑﺭﻁﻟﺍ ﻲﻓ لﺌﺎﺴﻟﺍ ﻯﻭﺘﺴﻤ ﻊﻔ
ﻟﻸﻨﺒﻭﺏ ﺒﻤﻘﺩﺍﺭ
(+h)
ﺍﻭ
(Pg)
ﺍﻟﺫﻱ ﻴﻤﺜل ﻤﻘﻴﺎﺱ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻭﺠﺏ
.
لـﺠﺍﺭﻤﻟﺍ ﻲـﻓ لﺎﺤﻟﺍ ﻲﻫ ﺎﻤﻜ
ﺍﻟﺒﺨﺎﺭﻴﺔ ﻭﺴﻴﻜﻭﻥ
:
Pg = Pa – Patm. > 0
…….. (2.3)
3
-
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ
(Pa < Patm.)
ﻜﻤﺎ ﻓﻲ ﺸﻜل
(2.4-c)
ﺴﺘﻭﻯـﻤ ﺽﻔﺨﻨﻴﺴـﻓ ،ﻲـﻠﺨﻠﺨﺘ ﻁﻐﻀ ﻱﺃ ،
ﺍﻟﺴﺎﺌل ﻓﻲ ﺍﻟﻁﺭﻑ ﺍﻻ
ﻴﻤﻥ ﻟﻸﻨﺒﻭﺏ ﺒﻤﻘﺩﺍﺭ
(-h)
ﺍﻭ
(-Pg)
ﺍﻭ
(Pvac.)
ﻀﻐﻁـﻟﺍ ﺱﺎﻴﻘﻤ لﺜﻤﻴ ﻱﺫﻟﺍ
ﺍﻟﺴﺎﻟﺏ ﺍﻭ ﻤﻘﻴﺎﺱ ﺍﻟﺘﻔﺭﻴﻎ ﺍﻭ ﺍﻟﺘﺨﻠﺨل
(Gauge Vacuum)
ﺔـﻴﺭﺎﺨﺒﻟﺍ ﺕﺎﻔﺜﻜﻤﻟﺍ ﻲﻓ لﺎﺤﻟﺍ ﻭﻫ ﺎﻤﻜ
ﻭﺴﻴﻜﻭﻥ
:
Pg = Patm. – Pa < 0
…….. (2.4)
ﻭﻋﻨﺩ ﺤﺴﺎﺏ ﻗﻴﻤﺔ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ
(Pa)
ﻴﺠﺏ ﺍﻥ ﺘﻜﻭﻥ ﻭﺤﺩﺍﺕ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻘﺎﺱ
(Pg)
ﻭﺍﻟﻀﻐﻁ
ﺍﻟﺠﻭﻱ
(Patm.)
ﻭﻫﺫﺍ ﻤﺎ ﺴﻨﻭﻀﺤﻪ ﻓﻲ ﺍﻻﻤﺜﻠﺔ ﺍﻵﺘﻴﺔ،ﺓﺩﺤﻭﻤ
:

)
32
(
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
:
1
-
ﺍﺫﺍ ﻜﺎﻥ ﻀﻐﻁ ﺍﻟﻤﻘﻴﺎﺱ
(127kPa)
ﺴﺎﻭﻱـﺘﻭ ﻱﻭـﺠﻟﺍ ﻁﻐﻀـﻟﺍ ﺔـﻤﻴﻗ ﺱﻴـﻘﻴ ﺭﺘﻴﻤﻭﺭﺎﺒﻟﺍ ﻥﺎﻜﻭ
(740 mmHg)
ﻓﻴﻜﻭﻥ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ
:
Pa
= Patm. + Pg
= (13600
× 9.81 × 0.74) × 10
-3
+ 127 = 225.728 kPa
2
-
ﻋﻨﺩ ﻗﻴﺎﺱ ﻀﻐﻁ ﻏﺎﺯ ﺒﻤﺎﻨﻭﻤﻴﺘﺭ ﺯﺌﺒﻘﻲ
.
ﺩﺍﺭﻩـﻘﻤ ﻲـﻠﺨﻠﺨﺘ ﺱﺎـﻴﻗ ﻥﻴـﺒﻴ ﻕـﺒﺌﺯﻟﺍ ﺩﻭـﻤﻋ ﻥﺎـﻜ
(660 mmHg)
ﺎﺭﻭﻤﻴﺘﺭـﺒﻟﺍ ﺎﻬﺴﻴﻘﻴ ﻲﺘﻟﺍ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﺔﻤﻴﻗ ﺕﻨﺎﻜﻭ
(740 mmHg)
ﻭﻥـﻜﻴﻓ
ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ
:
Pa
= Patm. – Pg
= (13600
× 9.81 × 0.74 – 13600 × 9.81 × 0.66) × 10
-3
= 10.673 kpa
3
-
ﻋﻨﺩ ﻗﻴ
ﺩﺍﺭﻩـﻘﻤ ﻁﻐﻀـﻟﺍ ﺱﺎـﻴﻘﻤ ﻥﻴـﺒﻴ ﺀﺎـﻤﻟﺍ ﺩﻭـﻤﻋ ﻥﺎـﻜ ﻲﺌﺎـﻤ ﺭﺘﻴﻤﻭﻨﺎﻤﺒ ﺯﺎﻏ ﻁﻐﻀ ﺱﺎ
(150mm H
2
O)
ﻭﻜﺎﻨﺕ ﻗﻴﻤﺔ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ ﺍﻟﺘﻲ ﻴﻘﻴﺴﻬﺎ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ،
(740mm Hg)
ﻭﻥـﻜﻴﻓ ،
ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ
:
Pa = Patm + Pg
=(13600
× 9.81 × 0.74 + 1000 × 9.81 × 0.15) × 10
-3
= 100.2 kPa
4
-
ﻋﻨﺩ ﻗﻴﺎﺱ ﻀﻐﻁ
ﻏﺎﺯ ﻓﻲ ﺨﺯﺍﻥ ﺒﻤﺎﻨﻭﻤﻴﺘﺭ ﻴﺤﺘﻭﻱ ﻋﻠﻰ ﻤﺎﺌﻊ ﻭﺯﻨﻪ ﺍﻟﻨﻭﻋﻲ
(0.85)
.
ﺎﻉـﻔﺘﺭﺍ ﻥﺎﻜ
ﻋﻤﻭﺩ ﺍﻟﻤﺎﺌﻊ
(55cm)
ﻭﻜﺎﻨﺕ ﻗﻴﻤﺔ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ،
(96kPa)
ﻓﻴﻜﻭﻥ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ
:
Pa = Patm + Pg
kPa
6
.
100
Pa
10
1kPa
m
0.55
s
m
9.81
m
kg
10
0.85
kPa
96
3
2
3
3
=
×
×
×
×
+
=
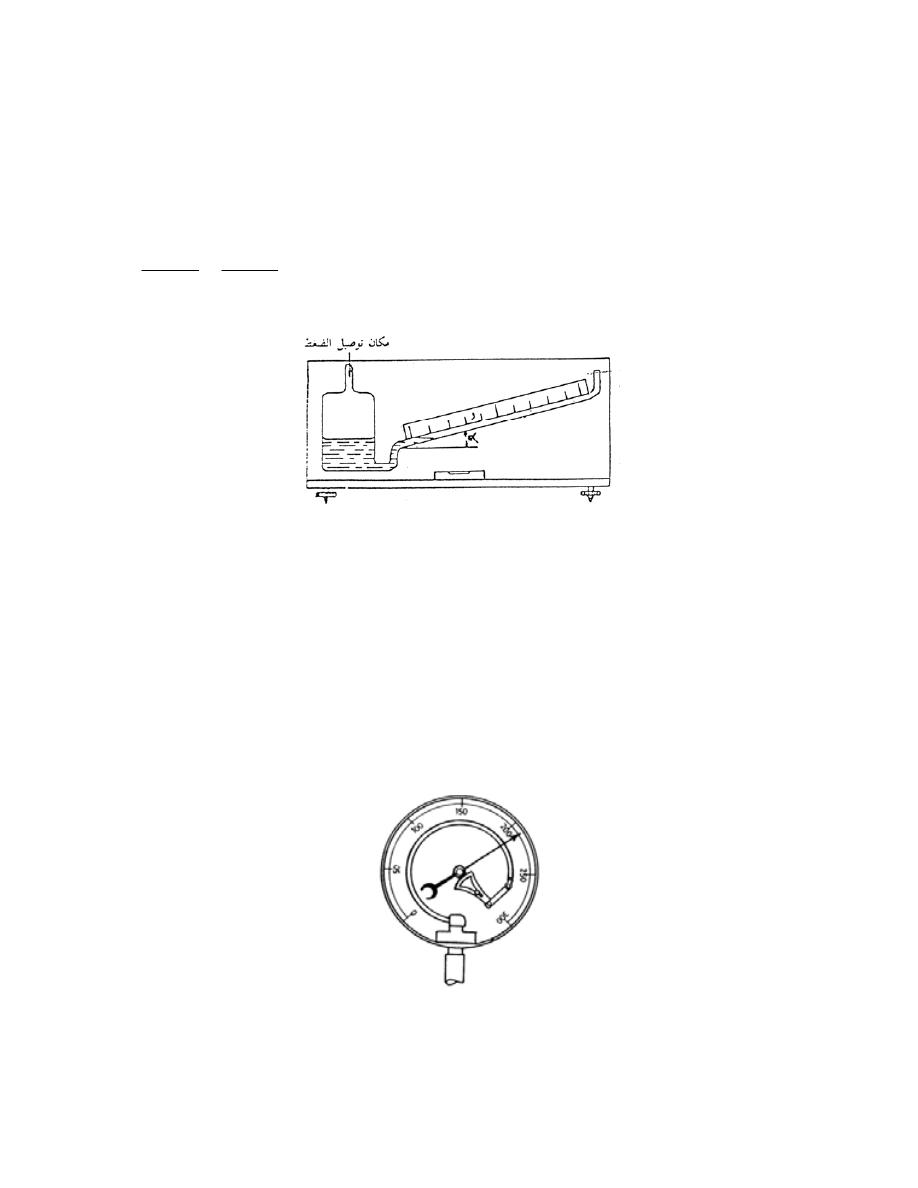
)
33
(
)
2.6
(
-
ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ ﺍﻟﻤﺎﺌل
The Inclined Manometer
ﻴﺴﺘﻌﻤل ﻟﻘﻴﺎﺱ ﻓﺭﻭﻕ ﺍﻟﻀﻐﻁ ﺍﻟﺼﻐﻴﺭﺓ ﺠﺩﺍﹰ ﻤﺜﻼﹰ ﺍﻟﻰ ﺤ
ﺩ
(50mm H
2
O)
ﻜلـﺸ ﻲـﻓ ﻥﻴﺒﻤﻟﺍﻭ
)
2.5
.(
ﺇﻥ ﺯﺍﻭﻴﺔ ﻤﻴل ﺍﻨﺒﻭﺏ ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ ﺍﻟﻤﺎﺌل ﻋﻥ ﺍﻟﻤﺴﺘﻭﻯ ﺍﻻﻓﻘﻲ
(
α)
ﻤﺴﺎﻭﻴﺔ ﻟﻘﻴﻤﺔ ﻤﻌﻴﻨﺔ
.
ﻓﺈﺫﺍ ﻜﺎﻥ
(30mm)
ﻭﻜﺎﻥ،
(
α=10°)
ﻓﺎﻥ ﻁﻭل ﺍﻟﻤﻘﻴﺎﺱ ﻋﻠﻰ ﻁﻭل ﺍﻻﻨﺒﻭﺏ ﺍﻟﻤﺎﺌل
:
ﺸﻜل
)
2.5
(
-
ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ ﺍﻟﻤﺎﺌل
ﻴﺴﺘﻌﻤل ﺍﻟﻤﺎﺀ ﺍﻭ ﺯﻴﺕ ﺍﻟﺒﺎﺭﺍﻓﻴﻥ ﺍﻟﺫﻱ ﻟﻪ
ﻭﺯﻥ ﻨﻭﻋﻲ
(0.8)
ﺘﻘﺭﻴﺒﺎﹰ
.
ﻰـﻠﻋ لﺼـﺤﻨ ﺎﻨﻨﺎﻓ ﻪﻨﻤﻭ
ﻓﻀﻼﹰ ﻋﻥ ﺍﻥ ﻤﻌﺩل ﺘﺒﺨﺭﻩ ﺍﻗل ﻤﻥ ﺍﻟﻤﺎﺀ،ﺀﺎﻤﻟﺍ ﺎﻨﻠﻤﻌﺘﺴﺍ ﻭﻟ ﺎﻤﻤ ﻯﻭﺘﺴﻤﻟﺍ ﻲﻓ ﺭﺒﻜﺍ ﺭﻴﻐﺘ
.
)
2.7
(
-
ﻤﻘﻴﺎﺱ ﺒﻭﺭﺩﻥ
The Bourdon Gauge
ﺇﻥ ﺍﺠﻬﺯﺓ ﻗﻴﺎﺱ ﺍﻟﻀﻐﻁ ﻫﻲ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭﺍﺕ ﻭﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭﺍﺕ ﻜﻤﺎ ﺴﺒﻕ ﺫﻜﺭﻫﺎ
.
ﺎﺱـﻴﻘﻤ ﻙﻟﺫـﻜﻭ
ﺒﻭﺭﺩﻥ ﺍﻟﻤﻭﻀﺢ ﻓ
ﻲ ﺸﻜل
)
2.6
(
ﺸﻜل
)
2.6
(
-
ﻤﻘﻴﺎﺱ ﺒﻭﺭﺩﻥ
mm
173
1737
.
0
30
10
sin
30
=
=
o

)
34
(
ﻲـﺘﻟﺍ ﻁﻭﻐﻀـﻟﺍﻭ ﺔﻴﺭﺎﺨﺒﻟﺍ لﺠﺍﺭﻤﻟﺍﻭ ﺕﺍﺭﺎﻴﺴﻟﺍ ﺕﺍﺭﺎﻁﺍ ﻁﻐﻀﻜ ﺓﺭﻴﺒﻜﻟﺍ ﻁﻭﻐﻀﻟﺍ ﺱﻴﻘﻴ ﻱﺫﻟﺍ
ﺘﺯﻴﺩ ﻋﻠﻰ
(0.12 MPa)
ﻭﻴﻘﻴﺱ ﻀﻐﻁ ﺍﻟﻤﻘﻴﺎﺱ،
(Pg)
ﻭﻱـﺠﻟﺍ ﻁﻐﻀـﻟﺍ ﺓﺩﺎﻴﺯ ﺏﺠﺘ ﻙﻟﺫﻟ
(Patm.)
ﻷﻴﺠﺎﺩ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ
(Pa)
.
ﺇﻥ ﺠﻤﻴﻊ ﺍﻻﺠﻬﺯﺓ ﺍﻟﺘﻲ ﻤﺭﺕ ﻫﻲ ﻤﻘﺎﻴﻴﺱ
ﻲـﻓ ﺭﺎـﺨﺒﻟﺍ ﻁﻭﻐﻀ لﺜﻤ ﺓﺭﻘﺘﺴﻤﻟﺍ ﻁﻭﻐﻀﻟﺍ ﺱﺎﻴﻘﻟ
ﺍﻟﻤﺤﺭﻜﺎﺕ ﻭﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ ﺍﻭ ﻓﻲ ﺍﻻﺴﻁﻭﺍﻨﺎﺕ ﺍﻟﺘﻲ ﺘﺤﺘﻭﻱ ﻋﻠﻰ ﻫﻭﺍﺀ ﻤﻀﻐﻭﻁ
.
ﻀﻐﻭﻁـﻟﺍ ﺕﺍﺭـﻴﻐﺘ ﺎﻤﺍ
ﻲﻨﺎﻴﺒ ﻁﻁﺨﻤ ﻰﻠﻋ ﻁﻐﻀﻟﺍ لﻴﺠﺴﺘﻟ ﻲﻜﻴﻨﺎﻜﻴﻤﻟﺍ ﻉﻭﻨﻟﺍ لﺎﻤﻌﺘﺴﺍ ﻥﻜﻤﻴﻓ ﻙﺭﺤﻤ ﺔﻨﺍﻭﻁﺴﺍ ﻲﻓ ﺎﻤﻜ ،ﺔﻌﻴﺭﺴﻟﺍ
ﺒﺴﺭﻋﺔ ﺜﺎﺒﺘﺔ ﻴﺴﻤﻰ ﺒﺠﻬﺎﺯ ﺍﻟﺘﺄﺸﻴﺭ
(Indicator)
،
ﺎﻁﺔـﺴﻭﺒ ﻡﺘـﻴﻓ ﻁﻐﻀﻟﺍ ﺱﺎﻴﻘﻤ ﺎﻤﺍ ،ﺭﺸﺅﻤ ﻭﻫ ﻱﺫﻟﺍ
ﻤﻘﻴﺎﺱ ﺒﻭﺭﺩﻥ
.
)
2.8
(
-
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
Temperature
ﻭﻡـﻬﻔﻤ ﻥﺍ ﻱﺃ ،ﻥﺎﺴﻨﻻﺍ ﺱﺍﻭﺤﺒ ﺔﻁﺒﺘﺭﻤﻟﺍ ﺔﻴﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜﻟﺍ ﺹﺍﻭﺨﻟﺍ ﻡﻫﺍ ﻥﻤ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺩﻌﺘ
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻭ ﺍﻟﺒﺭﻭﺩﺓ ﻴﻨﺸﺄ ﻤﻥ ﺍﻻﺤﺴﺎﺱ ﺍﻟﺫﻱ ﻨﺸﻌﺭ ﺒﻪ ﻋﻨﺩ ﺘﻼﻤﺱ ﻤﺨﺘﻠﻑ ﺍﻻﺸﻴﺎﺀ
.
ﻟﺫﻟﻙ ﻴﻤﻜﻥ
ﺍﺴﺘﻌﻤﺎل
ﺍﻟﻴﺩ ﻟﺘﺤﺩﻴﺩ ﺴﺨﻭﻨﺔ ﺍﻭ ﺒﺭﻭﺩﺓ ﺍﻻﺠﺴﺎﻡ
.
ﻓﻤﺜﻼﹰ ﺤﻴﻥ ﻨﻠﻤﺱ ﻗﻁﻌﺔ ﻤﻌﺩﻨﻴﺔ ﺴﺎﺨﻨﺔ ﻓﺈﻥ ﻨﻬﺎﻴﺎﺕ ﺍﻻﻋﺼﺎﺏ ﻋﻨﺩ
ﺱﻭـﻤﻠﻤﻟﺍ ﻡﺴـﺠﻟﺍ ﻙـﻟﺫ ﻥﺍ ﺭﺴﻔﻴ ﻱﺫﻟﺍ لﻘﻌﻟﺍ ﻰﻟﺍ ﺱﺎﺴﺤﻻﺍ ﻙﻟﺫ لﻘﺘﻨﻴﻭ ﺔﻨﻭﺨﺴﻟﺎﺒ ﺱﺤﺘﺴ ﺱﻤﻠﻟﺍ ﻥﺎﻜﻤ
ﺴﺎﺨﻥ
.
ﺍﻤﺎ ﺍﺫﺍ ﺘﻡ ﻟﻤﺱ ﻗﻁﻌﺔ ﻤﻥ ﺍﻟﺠﻠﻴﺩ ﻓﻴﻤﻜﻥ ﺍﻻﺴﺘﻨﺘﺎﺝ ﺩﻭﻥ ﻋﻨﺎﺀ ﺍﻨﻪ ﺒﺎﺭ
ﻭﺍﻟﺴﺒﺏ ﻓﻲ ﻫﺫﺍ ﺍﻻﺴﺘﻨﺘﺎﺝ،ﺩ
ﺩـﻴﻟﺍ ﻥﻤ ﺓﺭﺍﺭﺤﻟﺍ ﺹﺘﻤﺘ ﺩﻴﻠﺠﻟﺍ ﺔﻌﻁﻗ ﺎﻤﻨﻴﺒ ﺱﻤﻠﻟﺍ ﺩﻨﻋ ﺩﻴﻠﻟ ﺓﺭﺍﺭﺤ ﻲﻁﻌﻴ ﻥﺨﺎﺴﻟﺍ ﻡﺴﺠﻟﺍ ﻥﺍ ﻰﻟﺍ ﺩﻭﻌﻴ
.
ﻓﺈﺫﺍ ﻭﻀﻌﺕ ﻴﺩﻙ ﻋﻠﻰ،ﺓﺭﻴﻐﺼ ﻡﺎﻬﺴ ﻰﻠﻋ ﻱﻭﺘﺤﻴ ﺩﻴﻠﺠﻟﺍ ﻥﺍ ﺓﺩﻭﺭﺒﻟﺍ ﺓﺭﻫﺎﻅ ﺭﻴﻐﺘ ﻉﻭﻀﻭﻤ ﻲﻓ لﻴﻗ ﺩﻘﻟ
ﻓﺈﻨﻙ ﻟﻥ ﺘﺸﻌﺭ ﺒﺎﻟﺒﺭﻭﺩﺓ ﻓﺤﺴﺏ ﻭﻟﻜ،ﹰﻼﺜﻤ ﺩﻴﻠﺠﻟﺍ ﻥﻤ ﺔﻌﻁﻗ
ﻥ ﺒﺒﻌﺽ ﺍﻻﻟﻡ ﺍﻴﻀﺎﹰ
.
ﻭﻗﺩ ﻓﺴﺭ ﺫﻟﻙ ﻋﻠﻰ ﺍﻥ
ﺼﺤﺏـﻴﻭ ﺓﺩﺭﺎﺒ ﺩﻴﻟﺍ ﺢﺒﺼﺘ ﻙﻟﺫﺒﻭ ﺩﻴﻟﺍ ﻰﻟﺍ ﺩﻴﻠﺠﻟﺍ ﻥﻤ لﻘﺘﻨﺘ ﻡﺎﻬﺴﻟﺎﺒ ﺔﻬﻴﺒﺸﻟﺍ ﺓﺭﻴﻐﺼﻟﺍ ﻡﺎﺴﺠﻻﺍ
ﺫﻟﻙ ﺸﻌﻭﺭ ﺒﺎﻻﻟﻡ
.
ﺎﺭﺩﺓـﺒ ﻭﺍ ﺓﺭﺎﺤ ﻥﻜﺎﻤﻻﺍ ﺽﻌﺒ ﻥﺍ ﺭﺭﻘﻨ ﻲﻜﻟ ﻲﻘﻴﻘﺤﻟﺍ ﺱﻤﻠﻟ ﻥﺎﻴﺤﻻﺍ ﺽﻌﺒ ﻲﻓ ﺔﺠﺎﺤ ﺩﺠﻭﺘ ﻻﻭ
.
ﻓﻌﻨﺩ ﺨﺭﻭﺠﻨﺎ ﻤﻥ ﻏﺭﻓﺔ ﻭﺩﺨﻭﻟﻨﺎ ﺍﻟﻰ
ﺭﺝـﺨﻨ ﺎﻤﺩﻨﻋ ﻭﺍ ،ﺔﻓﺭﻐﻟﺍ ﺔﻨﻭﺨﺴ ﻭﺍ ﺓﺩﻭﺭﺒﺒ ﺭﻌﺸﻨ ﻥﺍ ﻥﻜﻤﻴ ﻯﺭﺨﺍ
ﻤﻥ ﻤﺒﻨﻰ ﺍﻟﻰ ﺍﻟﻬﻭﺍﺀ ﺍﻟﻁﻠﻕ
.
ﺭﺍﺭﺓـﺤ ﻥـﻤ ﺹﻠﺨﺘـﻨﻟ لﻼﻀﻟﺍ ﻥﻋ ﺙﺤﺒﻨ ﻙﻟﺫﻟ ﻑﻴﺼﻟﺍ ﺭﺍﺭﺓﺤﺒ ﻙﻟﺫﻜﻭ
ﺍﻟﺸﻤﺱ ﺍﻟﻤﺒﺎﺸﺭﺓ
.
ﻲـﺘﻟﺍ ﺔﻴﺼﺎﺨﻟﺎﻓ ،ﹰﺓﺭﺸﺎﺒﻤ ﻪﺒ ﺱﺎﺴﺤﻻﺍ ﻥﻜﻤﻴ ﺊﺸ ﻥﻋ ﺓﺭﺎﺒﻋ ﻲﻫ ﺓﺩﻭﺭﺒﻟﺍ ﻭﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺈﻓ ﻙﻟﺫﻟ
ﺘﺠﻌﻠﻨﺎ ﻨﺸﻌﺭ ﺒﺤﺭﺍﺭﺓ ﺍﻟ
ﺠﺴﻡ ﺍﻭ ﺒﺭﻭﺩﺘﻪ ﺘﺴﻤﻰ
)
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
.(
ﺴﺒﺔـﻨﻟﺎﺒ ﻡﺎـﻅﻨﻟﺍ ﺔﻨﻭﺨـﺴ ﻭﺍ ﺓﺩﻭﺭﺒ ﻑﺼﺘ ﻡﺎﻅﻨﻟﺍ ﺹﺍﻭﺨ ﻥﻤ ﺔﻴﺼﺎﺨ ﻲﻫ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻥﺫﺍ
ﻟﻠﻤﺤﻴﻁ
.

)
35
(
)
2.8.1
(
-
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺘﻭﺍﺯﻥ ﺍﻟﺤﺭﺍﺭﻱ
ﻭﺍﺯﻥـﺘ ﺔـﻟﺎﺤ ﻲـﻓ ﻥﺎﻨﻭﻜﻴ ﺎﻤﻬﻨﺄﻓ ﺎﻤﻬﻨﻴﺒ ﻱﺭﺍﺭﺤ لﺩﺎﺒﺘ ﺙﺩﺤﻴ ﻻﻭ ﺭﺜﻜﺍ ﻭﺍ ﻥﺎﻤﺴﺠ ﺱﻤﻼﺘ ﺍﺫﺇ
ﺤﺭﺍﺭﻱ ﻭﺘ
ﻜﻭﻥ ﻟﻬﻤﺎ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﻭﺍﺤﺩﺓ
.
ﻭﺇﺫﺍ ﺘﻼﻤﺱ ﺠﺴﻤﺎﻥ ﺘﺨﺘﻠﻑ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻬﻤﺎ ﻓﺒﻌﺩ ﻓﺘﺭﺓ ﺯﻤﻨﻴﺔ
ﻥﺇ ،ﺎـﻤﻬﻨﻴﺒ ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺇ ﻑﻗﻭﺘﻴ ﺎﻤﺩﻨﻋ ﻱﺭﺍﺭﺤﻟﺍ ﻥﺯﺍﻭﺘﻟﺍ ﺔﻟﺎﺤ ﻰﻟﺍ لﺼﺘﺴ ﻡﺎﺴﺠﻻﺍ ﻩﺫﻫ ﻥﺈﻓ ،ﺔﺒﺴﺎﻨﻤ
ﺘﻭﻗﻑ ﺍﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﻴﻌﻨﻲ ﻅﻬﻭﺭ ﺨﺎﺼﻴﺔ ﻤﺸﺘﺭﻜﺔ ﻫﻲ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
.
ﺎـﻨﺯﺍﻭﺘﻤ ﻡﺎـﻅﻨﻟﺍ ﻥﺎـﻜ ﺍﺫﺍ ﺎﻤﻴﻓ ﻥﻴﻌﺘ ﻲﺘﻟﺍ ﺔﻴﺼﺎﺨﻟﺍ ﻙﻠﺘ ﺎﻬﻨﺄﺒ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻑﻴﺭﻌﺘ ﻥﻜﻤﻴ ﺍﺫﻟ
ﺤﺭﺍﺭﻴﺎﹰ ﻤﻊ ﻨﻅﺎﻡ ﺍﻭ ﺍﻜﺜﺭ ﻤﺠﺎﻭﺭ ﻟﻪ
.
ﻀﻬﺎـﻌﺒ ﻊـﻤ ﺔﻁﺒﺘﺭﻤ ﻡﻴﻫﺎﻔﻤ ﻱﺭﺍﺭﺤﻟﺍ ﻥﺯﺍﻭﺘﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺍ ﺢﻀﺘﻴ ﻙﻟﺫ ﻥﻤ
ﺇﺭﺘﺒﺎﻁﺎﹰ ﻭﺜﻴﻘﺎﹰ
.
ﻓﺎﻟﺤﺭﺍﺭﺓ ﺸﻜل ﻤﻥ ﺍﺸﻜﺎل ﺍﻟﻁﺎﻗﺔ ﺘﻨﺘﻘل ﻤﻥ ﺠﺴﻡ ﻵ
ﺭﺍﺭﺓـﺤ ﺔـﺠﺭﺩ ﻥﻴﺒ ﻕﺭﻔﻟﺍ ﺏﺒﺴﺒ ﺭﺨ
ﺍﻟﺠﺴﻤﻴﻥ
.
ﺴﺎﻭﻱـﺘ ﺔـﻠﻘﺘﻨﻤﻟﺍ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻥﺍ ﻲﻨﻌﻴ ﻙﻟﺫ ﻥﺈﻓ ﻥﻴﻤﺴﺠﻟﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩ ﺕﻭﺎﺴﺘ ﺍﺫﺇ ﺎﻤﺍ
ﺍ ﻭﺃﻥ ﺍﻟﺠﺴﻤﻴﻥ ﻓﻲ ﺤﺎﻟﺔ ﺘﻭﺍﺯﻥ ﺤﺭﺍﺭﻱﺭﻔﺼ
.
)
2.8.2
(
-
ﻤﻘﺎﻴﻴﺱ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
Scales of Temperature
ﺇﻥ ﺤﺎﺴﺔ ﺍﻟﻠﻤﺱ ﻋﺎﺠﺯﺓ ﻋﻥ ﺘﻘﺩﻴﺭ ﺩﺭﺠﺔ ﺒﺭﻭﺩﺓ ﺍﻭ ﺴﺨ
ﻙـﻟﺫ ﺏﻨﺎﺠ ﻰﻟﺍ ﹰﺎﻴﻤﻗﺭ ﹰﺍﺭﻴﺩﻘﺘ ﻡﺴﺠﻟﺍ ﺔﻨﻭ
ﻓﺈﻥ ﺤﺎﺴﺔ ﺍﻟﻠﻤﺱ ﺘﺘﺤﺴﺱ ﻓﻘﻁ ﻀﻤﻥ ﻤﺩﻯ ﻤﺤﺩﺩ ﺠﺩﺍﹰ ﻤﻥ ﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ
.
ﺱـﻤﻟ ﻥﺎﺴـﻨﻻﺍ لﻤﺤﺘﻴ ﻼﻓ
ﺭـﻴﻏ ﹰﺎـﻋﺎﺒﻁﻨﺍ ﻲﻁﻌﺘ ﺎﻤ ﹰﺍﺭﻴﺜﻜ ﺱﻤﻠﻟﺍ ﺔﺴﺎﺤ ﻥﺈﻓ ﻙﻟﺫ ﻥﻋ ﹰﻼﻀﻓ ،ﹰﺍﺩﺠ ﺓﺩﺭﺎﺒﻟﺍ ﻭﺍ ﹰﺍﺩﺠ ﺔﻨﺨﺎﺴﻟﺍ ﻡﺎﺴﺠﻻﺍ
ﺼﺤﻴﺢ ﻋﻥ ﺩﺭﺠﺔ ﺴﺨﻭﻨﺔ ﺍﻻﺠﺴﺎﻡ
.
ﻓﻤﺜﻼﹰ ﻋﻨﺩ ﻟﻤ
ﺴﻡ ﺍﻻﻭلـﺠﻟﺍ ﻥﺈـﻓ ﻲﺒﺸـﺨ ﺭﺨﻵﺍﻭ ﻲﻨﺩﻌﻤ ﺎﻤﻫﺩﺤﺍ ﺀﺎﺘﺸﻟﺍ لﺼﻓ ﻲﻓ ﻥﻴﻤﺴﺠ ﺱ
ﻥﻭـﻜ ﻰﻟﺍ ﺩﻭﻌﻴ ﺏﺒﺴﻟﺍﻭ ﺎﻤﻬﺘﺭﺍﺭﺤ ﺔﺠﺭﺩ ﻱﻭﺎﺴﺘ ﻥﻤ ﻡﻏﺭﻟﺍ ﻰﻠﻋ ﻲﻨﺎﺜﻟﺍ ﻡﺴﺠﻟﺍ ﻥﻤ ﺩﺭﺒﺍ ﺱﻤﻠﻟﺍ ﺩﻨﻋﻭﺩﺒﻴ
لﺎـﻘﺘﻨﺎﺒ ﺢﻤﺴﻴ ﻻ لﺯﺎﻋ ﻲﻨﺎﺜﻟﺍ ﻡﺴﺠﻟﺍ ﺎﻤﻨﻴﺒ ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺄﺒ ﺢﻤﺴﻴ ﺓﺭﺍﺭﺤﻠﻟ ﺩﻴﺠ لﺼﻭﻤ ﻲﻨﺩﻌﻤﻟﺍ ﻡﺴﺠﻟﺍ
ﺍﻟﺤﺭﺍﺭﺓ
.
ﻤﺜﺎل
ﻋﻨﺩ ﻭﻀﻊ ﺍﺤﺩﻯ ﺍﻟﻴﺩﻴﻥ ﻓﻲ ﺴﺎﺌل ﺴﺎﺨﻥ ﻭﺍﻻﺨﺭﻯ ﻓﻲ ﺴﺎﺌل ﺒﺎﺭﺩ ﺜﻡ ﺭﻓﻊ ﺍﻟﻴﺩﻴﻥ ﻤﻌﺎﹰ،ﺭﺨﺁ
ﻪﺴﻔﻨ ﺀﺎﻤﻟﺍ ﻥﺍ ﺭﻌﺸﺘﺴ ﺔﻴﻨﺎﺜﻟﺍ ﺩﻴﻟﺍ ﺎﻤﻨﻴﺒ ،ﺩﺭﺎﺒ ﺀﺎﻤﻟﺍ ﻥﺍ ﺭﻌﺸﺘﺴ ﻰﻟﻭﻻﺍ ﺩﻴﻟﺍ ﻥﺎﻓ ﺊﻓﺍﺩ لﺌﺎﺴ ﻲﻓ ﺎﻤﻬﺴﻤﻏﻭ
ﺴﺎﺨﻥ
.
ﻋﻠﻴﻪ ﻜﺎﻥ ﻤﻥ ﺍﻟﻀﺭﻭﺭﻱ ﺍﻻﺴﺘﻐﻨﺎﺀ ﻋﻥ ﺍﻟﻁﺭﻴﻘﺔ ﺍﻟﺒﺩﺍﺌﻴﺔ ﻓﻲ ﺘﻘﺩﻴﺭ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﻠﺠﻭﺀ
ﺍﻟﻰ ﻁﺭﻴﻘﺔ
ﻋﻠﻤﻴﺔ ﻭﺩﻗﻴﻘﺔ ﻓﻲ ﻗﻴﺎﺱ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
.
ﺎﺭﻴﺭـﺤﻤﻟﺎﺒ ﻰﻤﺴـﺘ ﺓﺭﺍﺭـﺤﻟﺍ ﺔـﺠﺭﺩﻟ ﺱﻴﻴﺎﻘﻤ ﺕﻤﻤﺼ ﻙﻟﺫﻟ
(Thermometers)
ﺭﻭﺩﺓـﺒﻟﺍ ﻭﺍ ﺓﺭﺍﺭـﺤﻟﺍ ﻲﻓ ﺭﻴﻐﺘﻠﻟ ﹰﺎﻌﺒﺘ ﺹﻠﻘﺘﺘ ﻭﺍ ﺩﺩﻤﺘﺘ ﺩﺍﻭﻤ ﻰﻠﻋ ﻱﻭﺘﺤﺘ ،
.
ﺫﻩـﻫ
ﻭﻱـﺠﻟﺍ ﻁﻐﻀـﻟﺍ ﺩـﻨﻋ ﻪـﻨﺎﻴﻠﻏﻭ ﹰﺎـﻴﻭﺎﻴﻤﻴﻜ ﻲﻘﻨﻟﺍ ﺀﺎﻤﻟﺍ ﺩﺎﻤﺠﻨﺇ ﻲﺘﻁﻘﻨ ﻰﻠﻋ ﺩﻤﺘﻌﺘ ﺱﻴﻴﺎﻘﻤﻟﺍ
ﻲـﺴﺎﻴﻘﻟﺍ
(760 mmHg)
ﺩـﻨﻋ ﹰﻼﻴـﻠﻓ ﺽﻔﺨﻨـﺘﻭ ﻥﺎﻴﻠﻐﻟﺍ ﺩﻨﻋ ﺩﺍﺩﺯﺘ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻥﺈﻓ ﻁﻐﻀﻟﺍ ﺓﺩﺎﻴﺯﺒ ﻪﻨﺍ ﺫﺇ ،
ﺍﻻﻨﺠﻤﺎﺩ
.
ﻭﺘﻘﺴﻡ ﺍﻟﻤﺴﺎﻓﺔ ﺒﻴﻥ ﺍﻟﻨﻘﻁﺘﻴﻥ ﺍﻟﺜﺎﺒﺘﺘﻴﻥ ﻋﻠﻰ ﻋﺩﺩ ﻤﻌﻴﻥ ﻤﻥ ﺍﻻﻗﺴﺎﻡ ﻭﻴﺴﻤﻰ ﻜل ﻗﺴﻡ ﺩﺭﺠﺔ
.

)
36
(
ﺘﻘﺴﻡ ﻤﻘﺎﻴﻴﺱ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻋﻠﻰ ﺍﻻﻨﻭﺍﻉ ﺍﻵﺘﻴﺔ
:
1
-
ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻨﺴﺒﻲ
(Relative Temperature Scale)
.
ﻭﻴﺸﻤل
ﺃ
-
ﻤﻘﻴﺎﺱ ﺴﻠﺯﻴﻭﺱ
(Celsius Scale)
ﻫﻭ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﺌﻭﻱ ﻨﻔﺴﻪ
(Centigrade Scale)
(
°C)
ﺴﻤﻲ ﺒﺴﻠﺯﻴﻭﺱ ﻋﺎﻡ،
)
1742
(
ﺴﺒﺔﹰـﻨ
ﺍﻟﻰ ﻤﺨﺘﺭﻋﻪ ﺍﻟﻌﺎﻟﻡ ﺍﻟﺴﻭﻴﺩﻱ ﺍﻨﺩﺭﻴﻪ ﺴﻠﺯﻴﻭﺱ
)
1701
–
1744
.(
ﻸﻭﺯﺍﻥـﻟ ﻊـﺴﺎﺘﻟﺍ ﺭﻤﺘﺅـﻤﻟﺍ ﺭﺭـﻗ
ﻭﺍﻟﻘﻴﺎﺴﺎﺕ ﺍﻟﻤﻨﻌﻘﺩ ﻋﺎﻡ
)
1948
(
ﺍﺴﺘﻌﻤﺎل ﻜﻠﻤﺔ ﺴ
ﺘﻜﻭﻥ ﻓﻴﻪ ﺩﺭﺠﺔ ﺍﻨﺠﻤﺎﺩ ﺍﻟﻤﺎﺀً ﺎﻴﻤﻟﺎﻋ ﻱﻭﺌﻤ لﺩﺒ ﺱﻭﻴﺯﻠﻴ
ﺍﻟﻨﻘﻲ
(0
°C)
ﻭﺍﻟﻐﻠﻴﺎﻥ
(100
°C)
.
ﺩﺍﺕـﺤﻭﻠﻟ ﻲﻤﻟﺎﻌﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻊﻤ لﻤﻌﺘﺴﻴ ﺱﺎﻴﻘﻤﻟﺍ ﺍﺫﻫ
.
ﺔـﺠﺭﺩ ﺯـﻤﺭ
ﺍﻟﺤﺭﺍﺭﺓ ﻋﻠﻰ ﻫﺫﺍ ﺍﻟﻤﻘﻴﺎﺱ
(t
°C)
ﺍﻭ
(t)
.
ﻭﻭﺤﺩﺘﻬﺎ
(
°C)
.
ﺏ
-
ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻔﻬﺭﻨﻬﺎﻴﺘﻲ
(Fahrenheit Scale)
ﺴﻤﻲ ﺒﺎﺴﻡ ﻤﺨﺘﺭﻋﻪ ﺩﺍﻨﻴل ﺠﺎﺒﺭﻴﻴ
ل ﻓﻬﺭﻨﻬﺎﻴﺕ
)
1686
–
1736
(
ﺔـﻘﻁﺎﻨﻟﺍ ﻥﺍﺩـﻠﺒﻟﺍ ﻲﻓ لﻤﻌﺘﺴﻴ
ﺒﺎﻻﻨﻜﻠﻴﺯﻴﺔ
.
ﺘﻜﻭﻥ ﻓﻴﻪ ﺩﺭﺠﺔ ﺍﻨﺠﻤﺎﺩ ﺍﻟﻤﺎﺀ ﺍ
ﻟ
ﻨﻘﻲ
(32
°F)
ﻭﺍﻟﻐﻠﻴﺎﻥ
(212
°F)
.
ﺭﺍﺭﺓـﺤﻟﺍ ﺔـﺠﺭﺩ ﺯﻤﺭ
(t
°F)
ﻭﺤﺩﺘﻪ
(
°F)
.
ﻴﻘﺴﻡ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﺌﻭﻱ ﻋﻠﻰ
)
100
(
ﺩﺭﺠﺔ ﻭﺍﻟﻔﻬﺭﻨﻬﺎﻴﺘﻲ ﺍﻟﻰ
)
180
(
ﺒﺫﻟﻙ ﺘﺼﺒﺢ ﺍﻟﺩﺭﺠﺔ،ﺔﺠﺭﺩ
ﻋﻠﻰ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟ
ﻤﺌﻭﻱ ﻤﻥ ﺍﻟﺩﺭﺠﺔ ﻋﻠﻰ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻔﻬﺭﻨﻬﺎﻴﺘﻲ
.
ﺍﻤﺎ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺍﻟﺩﺭﺠﺔ ﺍﻟﻤﺌﻭﻴﺔ
(t
°C)
ﻭﺍﻟﻔﻬﺭﻨﻬﺎﻴﺘﻴﺔ
(t
°F)
ﺘﻌﻁﻰ ﺒﺎﻟﻌﻼﻗﺔ ﺍﻵﺘﻴﺔ
:
ﻤﺜﺎل
)
2.5
(
1
-
ﺤﻭل
(50
°C)
ﻤﻥ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﺌﻭﻱ ﺍﻟﻰ ﺍﻟﻔﻬﺭﻨﻬﺎﻴﺘﻲ
:
t
°F = 1.8 t °C + 32 = 1.8
×50 + 32 = 122 °F
2
-
لّﻭﺤ
(176
°F)
ﻤﻥ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟ
ﻔﻬﺭﻨﻬﺎﻴﺘﻲ ﺍﻟﻰ ﺍﻟﻤﺌﻭﻱ
:
ﺍﻥ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻔﻬﺭﻨﻬﺎﻴﺘﻲ ﻟﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻗﺩ ﺯﺍل ﺍﺴﺘﻌﻤﺎﻟﻪ ﻭﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﺌﻭﻱ
)
ﻴﻠﺯﻴﻭﺱـﺴ
(
ﻻﺯﺍل
ﺍﻻ ﺍﻥ ﻤﺎ ﻴﻌﻭل ﻋﻠﻴﻪ ﺍﻵﻥ ﻫﻭ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﻁﻠﻕ،لﺎﻤﻌﺘﺴﻻﺍ ﻊﺴﺍﻭ
)
ﻜﻠﻔﻥ
(
ﻟﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ
.
⎟
⎠
⎞
⎜
⎝
⎛
5
9
(2.5)
.....
)
F
(
32
)
C
(
t
8
.
1
32
C
t
5
9
F
t
o
o
+
=
+
=
o
o
C
80
8
.
1
32
176
8
.
1
32
F
t
C
t
o
o
o
=
−
=
−
=
)
37
(
)
2
(
-
ﻤﻘﻴﺎﺱ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ
Absolute Temperature Scale
ﻓﻲ ﻋﺎﻡ
)
1954
(
ﻲـﺘﻟﺍ ﺔﺠﺭﺩﻟﺍ ﻰﻠﻋ ﺩﻤﺘﻌﻴ ﻱﺫﻟﺍ ﻕﻠﻁﻤﻟﺍ ﺱﺎﻴﻘﻤﻟﺍ لﺎﻤﻌﺘﺴﺍ ﻰﻠﻋ ﹰﺎﻴﻟﻭﺩ ﻕﺎﻔﺘﻻﺍ ﻡﺘ
ﺴﻡـﺠﻟﺍ لﺨﺍﺩ ﺔﻨﻭﺯﺨﻤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺔﻴﻤﻜ ﹰﺎﻤﺎﻤﺘ ﻰﺸﻼﺘﺘ ﺎﻫﺩﻨﻋ
.
ﺴﺎﺒﺎﺕـﺤﻟﺍ ﻲـﻓ ﺱﺎـﻴﻘﻤﻟﺍ ﺍﺫـﻫ لﻤﻌﺘﺴـﻴ
ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﻭﻴﺸﻤل
:
-
ﺃ
-
ﻤﻘﻴﺎﺱ ﻜﻠﻔﻥ
Kelvin Scale
ﺴﻤﻲ ﺒﻜﻠﻔﻥ ﻋﺎﻡ
)
1851
(
ﻨﺴﺒﺔﹰ ﺍﻟﻰ ﻤﺨﺘﺭﻋ
ﻥـﻔﻠﻜ ﺩﺭﻭﻟ ﻲﻨﺎﻁﻴﺭﺒﻟﺍ ﻡﻟﺎﻌﻟﺍ ﻪ
)
1824
–
1907
.(
ﺭﻤﺯ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻋﻠﻰ ﻫﺫﺍ ﺍﻟﻤﻘﻴﺎﺱ
(TK)
ﺍﻭ
(T)
ﻭﻭﺤﺩﺘﻪ ﻜﻠﻔﻥ
(K)
ﻴﻨﺎﻅﺭ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﺌﻭﻱ ﻭﺘﻜﻭﻥ
ﺩﺭﺠﺔ ﺍﻟﺼﻔﺭ ﺍﻟﻤﻁﻠﻕ ﺘﺴﺎﻭﻱ
(-273.16
°C)
ﻕـﻠﻁﻤﻟﺍ ﺭﻔﺼـﻟﺍ ﻥﻭـﻜﻴ ٍﺫﺌﺩﻨﻋ ،ﻱﻭﺌﻤﻟﺍ ﺱﺎﻴﻘﻤﻟﺍ ﻰﻠﻋ
ﻟﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻫﻭ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎ
ﻟﻲ ﺍﻟﺘﻲ ﺘﻔﻘﺩ ﺍﻟﺠﺯﻴﺌﺎﺕ ﻋﻨﺩﻫﺎ ﺠﻤﻴﻊ ﻁﺎﻗﺘﻬﺎ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
ﺩﺭﺠﺔ
ﺍﻨﺠﻤﺎﺩ ﺍﻟﻤﺎﺀ
(273.16 K)
ﻭﻴﻤﻜﻥ ﺍﻋﺘﺒﺎﺭﻫﺎ
(273 K)
.
ﻭﻓﻲ ﺍﻟﺤﺴﺎﺒﺎﺕ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﻜﻤﺎ ﺫﻜﺭﻨﺎ ﻓﺈﻥ
ﺃﻱ،ﻥﻔﻠﻜﻟﺎﺒﻭ ﺔﻘﻠﻁﻤ ﻥﻭﻜﺘ ﻥﺍ ﺏﺠﻴ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ
:
T
K
= t
°C + 273 (K) or T = t + 273 [K]
…… (2.6)
ﻭﻴﻼﺤﻅ
،ﺎـﻬﻟ ﺓﺭﻅﺎﻨﻤﻟﺍ ﺔﻴﻭﺌﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺕﺎﺠﺭﺩ ﻕﺭﻓ ﻱﻭﺎﺴﻴ ﺔﻘﻠﻁﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺕﺎﺠﺭﺩ ﻕﺭﻓ ﻥﺍ
ﺃﻱ
(
∆T = ∆t)
ﻜﻤﺎ ﻤﻭﻀﺢ ﻓﻲ ﺍﺩﻨﺎﻩ
:
∆T = T
2
– T
1
= (t
2
+ 273) – (t
1
+ 273) = t
2
– t
1
=
∆t
…. (2.7)
ﺸﻜل
)
2.7
(
-
ﻤﻘﺎﻴﻴﺱ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
373.15
100
ﻨﻘﻁﺔ ﻏﻠﻴﺎﻥ ﺍﻟﻤﺎﺀ ﺍﻟﻨﻘﻲ
ﻋﻨﺩ
)
1atm
(
273.15
0
ﻨﻘﻁﺔ ﺍﻨﺠﻤﺎﺩ ﺍﻟﻤﺎﺀ ﺍﻟﻨﻘﻲ
0
273.15
-
ﺍﻟﺼﻔﺭ ﺍﻟﻤﻁﻠﻕ
o
C K
672
212
492
32
0
460
-
o
F
o
R

)
38
(
ﺏ
-
ﻤﻘﻴﺎﺱ ﺭﻨﻜﻥ
Rankine Scale
ﻴﺴﺘﻌﻤل ﻓﻲ ﺍﻟﺩﻭ
ﺎﺱـﻴﻘﻤﻟﺍ ﺍﺫـﻫ ﻰﻠﻋ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺯﻤﺭ ،ﺔﻴﺯﻴﻠﻜﻨﻻﺍ ﺔﻐﻠﻟﺎﺒ ﺔﻘﻁﺎﻨﻟﺍ ل
(T
°R)
ﻭﻭﺤﺩﺘﻬﺎ
(
°R)
.
ﺴﺎﻭﻱـﺘ ﻕـﻠﻁﻤﻟﺍ ﺭﻔﺼﻟﺍ ﺔﺠﺭﺩ ﻥﻭﻜﺘﻭ ،ﻲﺘﻴﺎﻬﻨﺭﻬﻔﻟﺍ ﺱﺎﻴﻘﻤﻟﺍ ﺭﻅﺎﻨﻴ
(-459.67
°F)
ﻴﻤﻜﻥ ﺇﻋﺘﺒﺎﺭﻫﺎ
(460
°F)
ﻋﻠﻰ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻔﻬﺭﻨﻬﺎﻴﺘﻲ
.
ﺩﺭﺠﺔ ﺇﻨﺠﻤﺎﺩ ﺍﻟﻤﺎﺀ
(492
°R)
.
ﺍﻟﻤﻘﺎﻴﻴﺱ ﺍﻟﻨﺴﺒﻴﺔ
ﻭﺍﻟﻤﻁﻠﻘﺔ ﻤ
ﻭﻀﺤﺔ ﻓﻲ ﺸﻜل
(2.7)
ﻭﺍﻟﺘﻲ ﻴﻤﻜﻥ ﺘﻠﺨﻴﺼﻬﺎ ﺒﺤﺴﺏ ﺍﻟﻤﺨﻁﻁ ﺍﻵﺘﻲ
:
ﻋﻼﻗﺔ ﺍﻟﺭﻨﻜﻥ ﺒﺎﻟﻜﻠﻔﻥ ﻭﺍﻟﻔﻬﺭﻨﻬﺎﻴﺕ ﻤﻭﻀﺤﺔ ﻓﻲ ﺍﻟﻤﻌﺎﺩﻻﺕ ﺍﻟﺘﺎﻟﻴﺔ
:
-
T
°R = 1.8 TK = t °F + 460
……. (2.8)
ﺭﺍﺭﺓـﺤﻟﺍ ﺔـﺠﺭﺩ ﺱﺎﻴﻘﻤ ﺓﺀﺍﺭﻗ ﺏﺘﻜﺘ
)
°C
،
K
،
°F
،
°R
(
ﺴﺘﻌﻤل ﺍﻭـﻤﻟﺍ ﺱﺎـﻴﻘﻤﻟﺍ ﺏﺴـﺤﺒ
)
deg. C
،
K
،
deg. F
،
deg. R
.(
ﻤﺜﺎل
)
2.6
(
لّﻭﺤ
(-1
°C)
ﺭﻨﻜﻥ ﻭﻜﻠﻔﻥ،ﻲﺘﻴﺎﻬﻨﺭﻬﻔﻟﺍ ﻰﻟﺍ ﻱﻭﺌﻤﻟﺍ ﺱﺎﻴﻘﻤﻟﺍ ﻥﻤ
.
t
°F = 1.8 t °C + 32 = 1.8 . (-1) + 32 = 30.2 (°F)
T
°R = t °F + 460 = 30.2 + 460 = 490.2 °R
TK = t
°C + 273 = -1 + 273 = 272 K
Temperature Scale
Relative
Absolute
Celsius (Centigrade)
Fahrenheit
Kelvin
Rankine

)
39
(
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
:
)
2.7
(
ﻗﻭﺓ ﻤﻘﺩﺍﺭﻫﺎ
(7500N)
ﺴﻠﻁﺕ
ﺭﻩـﻁﻗ ﺱﺒﻜﻤ ﻰﻠﻋ ﹰﺎﻴﻭﺎﺴﺘﻤ ﹰﺎﻁﻴﻠﺴﺘ
(100mm)
ﺩﺍﺭـﻘﻤ ﺎـﻤ ،
ﺍﻟﻀﻐﻁ ﻋﻠﻰ ﺍﻟﻤﻜﺒﺱ ﺒﻭﺤﺩﺍﺕ
(kN/m
2
)
؟
)
2.8
(
ﺯﻴﺕ ﻭﺯﻨﻪ ﺍﻟﻨﻭﻋﻲ
(0.8)
ﻤﻭﻀﻭﻉ ﻓﻲ ﺍﻨﺎﺀ ﺍﻟﻰ ﻋﻤﻕ ﻤﻘﺩﺍﺭﻩ
(2m)
ﺎﺱـﻴﻘﻤﻟﺍ ﻁﻐﻀ ﺏﺴﺤﺍ ،
ﺒﻭﺤﺩﺍﺕ
(kN/m
2
)
.
P =
ρgh
= 0.8
× 9.81 × 2
= 15.7 kN/m
2
)
2.9
(
ﻜﺎﻨﺕ ﻗﺭﺍﺀﺓ ﺍﻟﺒﺎﺭﻭﻤﺘﺭ ﻭﺍﻟﺘﻲ
ﺴﺠﻠﺕ
(765mmHg)
.
ﺩﺍﺕـﺤﻭ ﻰـﻟﺍ ﺓﺀﺍﺭـﻘﻟﺍ ﻩﺫـﻫ لﻭـﺤ
(MN/m
2
)
.
P =
ρ g h = 13600
× 9.81 × 0.765
= 102063.24 N/m
2
= 0.102 MN/m
2
)
2.10
(
ﺭﻓﻊ ﺍﻟﻀﻐﻁ ﺩﺍﺨل ﻭﻋﺎﺀ ﺒﻭﺴﺎﻁﺔ ﻤﺎﻨﻭﻤﺘﺭ ﺯﺌﺒﻘﻲ ﻋﻨﺩ ﻀﻐﻁ ﻤﻌﻴﻥ
.
ﺎﻉـﻔﺘﺭﺍ ﻲـﻓ ﻕﺭـﻔﻟﺍ ﻥﺎﻜ
ﻤﺴﺘﻭﻯ ﺍﻟﺯﺌﺒﻕ ﻓﻲ ﺍﻟﻤﺎﻨﻭﻤﺘﺭ
(260 mmHg)
ﻭﻱـﺠﻟﺍ ﻁﻐﻀـﻟﺍ ﻕﻭﻓ
.
ﻭ
ﺎﺭﻭﻤﻴﺘﺭـﺒﻟﺍ ﺓﺀﺍﺭـﻗ ﺕـﻨﺎﻜ
(758 mmHg)
.
ﺍﻭﺠﺩ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ ﻓﻲ ﺍﻟﻭﻋﺎﺀ ﺒﻭﺤﺩﺍﺕ
(MN/m
2
)
،
(bar)
.
Pa =Patm.+Pg=13600
× 9.81 × 0.758+13600 × 9.81 × 0.26
=135817.48 N/m
2
= 0.1358 MN/m
2
= 1.358 bar
2
2
2
kN/m
956
(0.1)
4
7500
4
D
7500
A
F
P
=
×
π
×
=
×
π
=
=

)
40
(
)
2.11
(
ﻤﺎﻨﻭﻤﻴﺘﺭ ﻤﺎﺌﻲ ﻴﺒﻴﻥ ﺍﻥ ﺍﻟﻀﻐﻁ ﻓﻲ ﻭﻋﺎﺀ ﻤﺎ ﻴﺴ
ﺎﻭﻱ
(400mm)
ﺘﺤﺕ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
.
ﺍﺫﺍ ﻜﺎﻥ
ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
(763 mmHg)
.
ﺍﻭﺠﺩ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ ﻓﻲ ﺍﻟﻭﻋﺎﺀ ﺒﻭﺤﺩﺍﺕ
(kN/m
2
)
.
Pa = Patm. – Pg = 13600
× 9.81 × 0.763 – 1000 × 9.81 × 0.4
= 97872.41N/m
2
= 97.87 kN/m
2
)
2.12
(
ﻤﻘﻴﺎﺱ ﺒﻭﺭﺩﻥ ﻟﻠﻀﻐﻁ ﻴﺴﺠل ﻀﻐﻁﺎﹰ ﻤﻘﺩﺍﺭﻩ
(1.75 MN/m
2
)
ﻟﻠﻤﻘﻴﺎﺱ
.
ﺎﻉـﻔﺘﺭﻻﺍ ﻥﺎـﻜ ﺍﺫﺇ
ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭﻱ
(757 mmHg)
.
ﺍﻭﺠﺩ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ
.
Pa. = Patm. + Pg
= 13600
× 9.81 × 0.757 × 10
-6
+ 1.75
= 1.851 MN/m
2
)
2.13
(
ﻜﺎﻥ ﻤﻘﺩﺍﺭ ﺍﻟﻀﻐﻁ ﺍﻟﺘﺨﻠﺨﻠﻲ ﻓﻲ ﻤﺒﺨﺭ
(284 mmHg)
ﻭﻱـﺠﻟﺍ ﻁﻐﻀـﻟﺍ ﻥﺍ ﺕـﻤﻠﻋ ﺍﺫﺈـﻓ ،
(742 mmHg)
.
ﺍﺤﺴﺏ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ ﺒﻭﺤ
ﺩﺍﺕ
(Pa)
.
Pa = Patm. – Pg
= 13600
× 9.81 (0.742 – 0.284)
= 61104.53 Pa
)
2.14
(
ﺍﻭﺠﺩ ﺇﺭﺘﻔﺎﻉ ﻋﻤﻭﺩ ﺍﻟﻤﺎﺀ ﻭﻋﻤﻭﺩ ﺍﻟﺯﺌﺒﻕ ﺍﻟﻤﻜﺎﻓﺊ ﻟﻠﻀﻐﻁ ﺍﻟﺠﻭﻱ ﺍﻟﻌﻴﺎﺭﻱ
(101325N/m
2
)
.
Hg
m
76
.
0
13600
10.329
1000
Hg
h
Hg
h
O
H
m
329
.
10
9.81
1000
101325
g
w
P
h
2
w
1
w
1
2
2
w
1
=
×
=
ρ
×
ρ
=
=
×
=
×
ρ
=

)
41
(
)
2.15
(
ﺍﺤﺴﺏ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻜﺎﻓﺊ ﻟﻌﻤﻭﺩ ﻤﻥ ﺍﻟﺯﺌﺒﻕ ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﺭﺘﻔﺎﻋﻪ
:
760mm
،
750mm
،
1mm
.
P =
ρgh = 13600
× 9.81 × 0.76 = 101.396 kPa
= 13600
× 9.81 × 0.75 = 100 kPa
= 13600
× 9.81 × 0.001 = 0.133 kPa
)
2.16
(
ﺍﺫﺍ ﺍﺭﺩﻨﺎ ﻗﻴﺎﺱ ﻓﺭﻕ ﺍﻟﻀﻐﻁ ﻤﻘﺩﺍﺭﻩ
(200 Pa)
،ﻕـﺒﺌﺯﻟﺍ لﺌﺎﺴـﻜ ﻪـﻴﻓ لﻤﻌﺘﺴﺍ ﺭﺘﻴﻤﻭﻨﺎﻤ ﺔﻁﺎﺴﻭﺒ
ﻭلــﺤﻜﻟﺍ ،ﺀﺎــﻤﻟﺍ
.
ﺴﺎﺌلــﻟﺍ ﺩﻭــﻤﻋ ﻉﺎــﻔﺘﺭﺍ ﺏﺴــﺤﺍ
.
ﺎــﻜ ﺍﺫﺍ
ﻥ
(
ρ
Hg
=13600kg/m
3
)
،
(
ρ
w
= 1000 kg/m
3
)
،
(
ρ
alc.
= 800 kg/m
3
)
.
)
2.17
(
ﻤﻘﻴﺎﺱ ﺒﻭﺭﺩﻥ ﻴﻘﻴﺱ ﻀﻐﻁ ﻤﻘﺩﺍﺭﻩ
(1.75 MPa)
.
ﻓﺈﺫﺍ ﻜﺎﻥ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
(757 mmHg)
،
ﺍﺤﺴﺏ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ ﺒﻭﺤﺩﺍﺕ
(MPa)
،
(mmHg)
.
Pa = Patm. + Pg = 1.75 + 13600
× 9.81 × 0.757
= 1.851 MPa
Alc
mm
5
.
25
9.81
800
200
W
mm
4
.
20
9.81
1000
200
mmHg
5
.
1
9.81
13600
200
g
P
h
=
×
=
=
×
=
=
×
=
×
ρ
=
mmHg
13874
mHg
874
.
13
9.81
13600
10
851
.
1
h
6
=
=
×
×
=
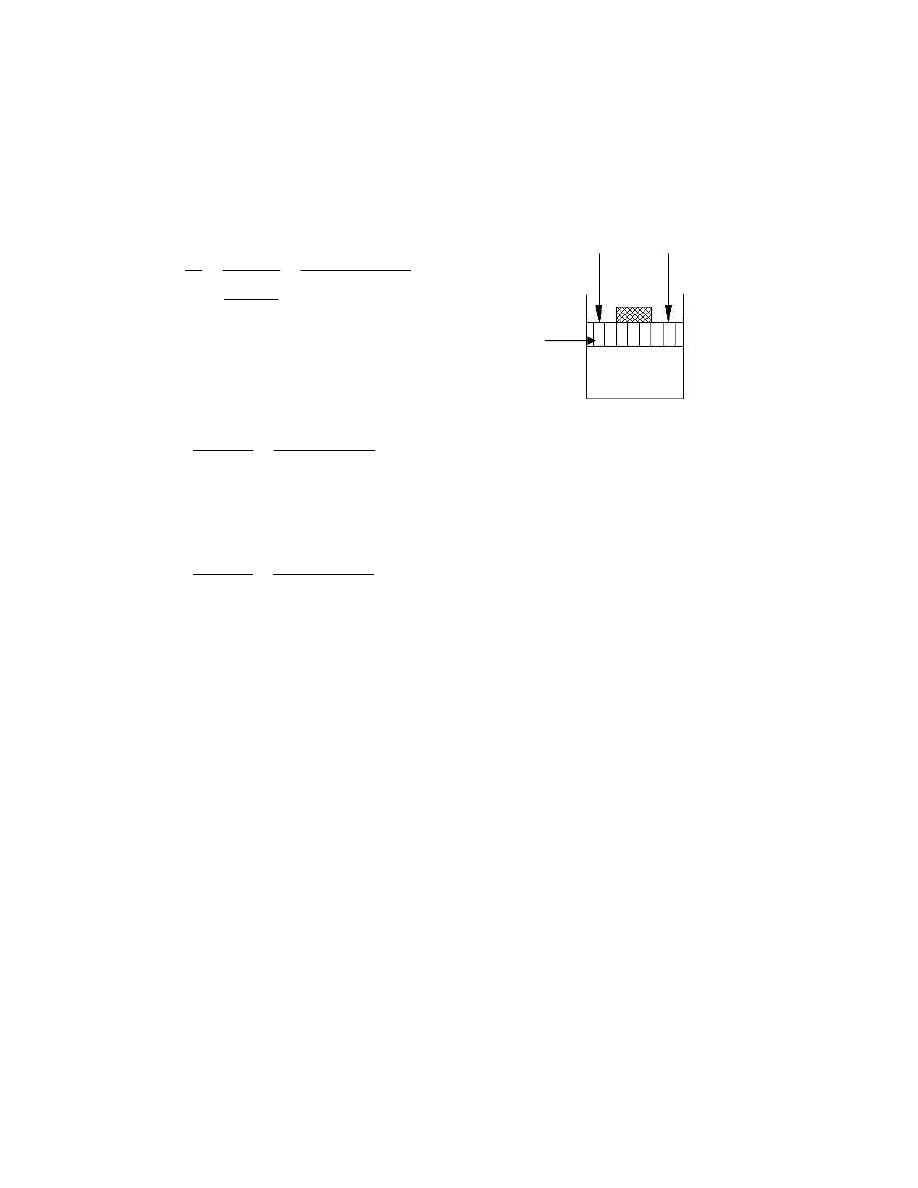
)
42
(
)
2.18
(
ﺍﺴﻁﻭﺍﻨﺔ ﻓﻴﻬﺎ ﻏﺎﺯ ﻤﻐﻠﻘﺔ ﺒﻤﻜﺒﺱ ﻗﻁﺭﻩ
(24cm)
ﻋﻠﻴﻪ ﺜﻘل
)
ﻜﺘﻠﺔ ﺍﻟﻤﻜﺒﺱ
+
ﻜﺘﻠﺔ ﺍﻟﺜﻘل
(
ﺘﺴﺎﻭﻱ
(2kg)
.
ﻕـﺒﺌﺯﻟﺍ ﻉﺎـﻔﺘﺭﺍ ﻥﺎـﻜﻭ ،ﻲﻘﺒﺌﺯ ﺭﺘﻴﻤﻭﺭﺎﺒ ﺔﻁﺎﺴﻭﺒ ﻱﻭﺠﻟﺍ ﻁﻐﻀﻟﺍ ﺱﺎﻴﻗ ﻡﺘ
(750mmHg)
.
ﺍﺤﺴﺏ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻘﺎﺱ ﻭﺍﻟﻤﻁﻠﻕ ﺒﻭﺤﺩﺍﺕ
:
kPa
،
bar
،
PSI
،
mmHg
.
)
2.19
(
ﺍﺴﻁﻭﺍﻨﺔ
ﻓﻴﻬﺎ ﻏﺎﺯ ﺭﺒﻁ ﻋﻠﻴﻬﺎ ﻤﺎﻨﻭﻤﻴﺘﺭ ﺯﺌﺒﻘﻲ ﻓﺈﺫﺍ ﻜﺎﻥ
)ﺃ
(
ﺎﻨﻭﻤﻴﺘﺭـﻤﻟﺍ ﺓﺀﺍﺭﻗ
(15 cm Hg)
،
)
ﺏ
(
ﻗﺭﺍﺓ ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ ﺒﻀﻐﻁ ﺘﺨﻠﺨل ﻤﻘﺩﺍﺭﻩ
(10 cm Hg)
ﻭﻜﺎﻨﺕ ﻗﺭﺍﺀﺓ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ ﻓﻲ ﺍﻟﺤﺎﻟﺘﻴﻥ
(1.01
bar)
.
ﺇﺤﺴﺏ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ ﻟﻠﻐﺎﺯ ﻓﻲ ﺍﻟﺤﺎﻟﺘﻴﻥ ﺒﻭﺤﺩﺍﺕ
)
1
(
kN/m
2
)
2
(
bar
.
1
-
Pa= Patm. + Pg = 1.01
× 10
5
+ 13600
× 0.15 × 9.81
= 121012.4 Pa
= 121.0124 kPa = 1.21 bar
ﺏ
-
Pa = Patm. – Pg = 1.01
× 10
5
– 13600
× 0.1 × 9.81
= 87658.4 Pa
= 87.6524 kPa
= 0.876584 bar
mmHg
7532
.
0
9.81
13600
100496
g
P
h
bar
1.00496
kPa
100.496
Pa
100496
434
0.75
9.81
13600
P
P
P
mmHg
253
.
3
9.81
13600
434
g
P
P
h
PSI
0.063
14.7
10
0.434
bar
10
0.434
kPa
0.434
Pa
434
(0.24)
3.14
4
9.81
2
4
D
g
m
A
F
Pg
Hg
.
abs
Hg
g
.
atm
a
Hg
g
Hg
2
-
2
-
2
2
=
×
=
×
ρ
=
=
=
=
+
×
×
=
+
=
=
×
=
×
=
=
×
×
=
×
=
=
=
×
×
×
=
×
π
×
=
=
ﺎﺯــﻏ
Patm
Patm
ﻤﻜﺒﺱ

)
43
(
)
2.20
(
ﺇﺫﺍ ﻜﺎﻨﺕ ﻗﺭﺍﺀﺓ ﺒﺎﺭﻭﻤﻴﺘﺭ ﺯﺌﺒﻘﻲ
ﻋﻨﺩ ﻗﺎﻋﺩﺓ ﺠﺒل
(740 mmHg)
.
ﻭﻓﻲ ﻗﻤﺔ ﺍﻟﺠﺒل ﺘﻜﻭﻥ ﻗﺭﺍﺀﺓ
ﻨﻔﺱ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ
(590 mmHg)
.
ﺇﺤﺴﺏ ﺇﺭﺘﻔﺎﻉ ﺍﻟﺠﺒل
.
ﻋﻠﻤﺎﹰ ﺒﺄﻥ
:
(
ρa=1.225 kg/m
3
)
.
P =
ρ g ∆ h = 13600
× 9.81 × (0.74 – 0.59) × 10
-3
= 20.013 kPa
)
2.21
(
ﺍﺴﻁﻭﺍﻨﺔ ﻓﻴﻬﺎ ﻏﺎﺯ ﻤﻐﻠﻘﺔ ﺒﻤﻜﺒﺱ ﻤﺴﺎﺤﺔ
ﻤﻘﻁﻌﻪ ﺍﻟﻌﺭﻀﻲ
(0.04m
2
)
ﻭﻜﺘﻠﺘﻪ
(60kg)
.
ﻭﻜﺎﻨﺕ
ﻗﻴﻤﺔ ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
(0.97 bar)
.
ﺍﺤﺴﺏ ﺍﻟﻀﻐﻁ ﺍﻟﻤﻁﻠﻕ ﻟﻠﻐﺎﺯ
.
m
1665
9.81
225
.
1
10
013
.
20
g
p
h
3
a
=
×
×
=
×
ρ
=
bar
117
.
1
Pa
10
bar
1
m/s
.
kg
1
N
1
m
04
.
0
m/s
9.81
kg
60
bar
0.97
A
g
m
.
Patm
A
F
.
Patm
Pg
.
Patm
Pa
5
2
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
×
+
=
×
+
=
+
=
+
=

)
44
(
ﻤﺴﺎﺌل
(2.1)
ﻪـﻴﻠﻋ ﺔﻜﺭﺤﻟﺍ ﺭﺤ ﺱﺒﻜﻤ ﻪﻗﻭﻓ ﺯﺎﻏ ﺩﺠﻭﻴ ،لﻜﺸﻟﺍ ﻲﻓ ﺢﻀﻭﻤﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻲﻓ
ﺜﻘل
.
ﻜﻭﻥـﺴ ﺔـﻟﺎﺤ ﻲـﻓ ﻡﺎـﻅﻨﻟﺍ ﻥﺎﻜ ﺍﺫﺍ ﻥﻴﻌﻤﺘﺠﻤ لﻘﺜﻟﺍﻭ ﺱﺒﻜﻤﻟﺍ ﻥﺯﻭ ﺏﺴﺤﺍ
ﻭﺍﺤﺴ
ﻀﻐﻁـﻟﺍ ﻥﺍ ﺕـﻤﻠﻋ ﺍﺫﺇ ﺯﺎـﻐﻠﻟ ﺱﺎﻘﻤﻟﺍ ﻀﻐﻁﻟﺍﻭ ﻕﻠﻁﻤﻟﺍ ﻀﻐﻁﻟﺍ ﻙﻟﺫﻜ ﺏ
ﻭﻱــــــــﺠﻟﺍ
(1.01bar)
ﻕــــــــﺒﺌﺯﻟﺍ ﺔــــــــﻓﺎﺜﻜﻭ
(13.6 g/cm
3
)
.
ﺍﻥ،ﺯﺎﻐﻟﺍ ﻥﺯﻭ لﻤﻫﺍ
(D=20 cm)
(d=2 cm)
.
ﺝ
) :
3560.87 N
(
(2.2)
ﻭﻀﻊ ﻤﻘﻴﺎﺱ ﻀﻐﻁ ﻤﺘﺨﻠﺨل
)
ﻓﺎﻜﻴﻭﻡ
(
ﻋﻨﺩ ﺩﺨﻭل ﺍﻟﻐﺎﺯ ﺍﻟﻰ ﻀﺎﻏﻁ ﻭﻜﺎﻨﺕ ﻗﺭﺍﺀﺘﻪ
(0.5 bar)
.
ﻭﻜﺎﻨﺕ ﻗﺭﺍﺀﺓ ﻤ
ﻘﻴﺎﺱ ﺍﻟﻀﻐﻁ ﻋﻨﺩ ﺍﻟﺨﺭﻭﺝ ﻤﻥ ﺍﻟﻀﺎﻏﻁ
(0.8 MPa)
.
ﺎﺯـﻐﻠﻟ ﻕـﻠﻁﻤﻟﺍ ﻁﻐﻀﻟﺍ ﺏﺴﺤﺇ
ﻭﻱـﺠﻟﺍ ﻁﻐﻀـﻟﺍ ﻥﺎـﻜ ﺍﺫﺍ ،ﻁﻏﺎﻀـﻟﺍ ﻥﻤ ﺝﻭﺭﺨﻟﺍﻭ لﻭﺨﺩﻟﺍ ﺩﻨﻋ
(760 mmHg)
ﻕـﺒﺌﺯﻟﺍ ﺔـﻓﺎﺜﻜﻭ
(13600 kg/m
3
)
.
ﺇﺫﺍ ﻭﻀﻊ ﻤﺎﻨﻭﻤﻴﺘﺭ ﺯﺌﺒﻘﻲ ﻋﻠﻰ ﺸﻜل
(U)
ﺒﻴﻥ ﺍﻟﺩﺨﻭل ﻭﺍﻟﺨﺭﻭﺝ
.
ﺭﻕـﻓ ﺏﺴـﺤﺍ
ﺇﺭﺘﻔﺎﻉ ﺍﻟﺯﺌﺒﻕ ﺒﻴﻥ ﺴﺎﻗﻲ ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ
.
ﺝ
) :
51.3 kPa
،
901.3 kPa
،
0.64 cm Hg
.(
D
D
d
85cm

)
45
(
ﺍﻟﻔﺼﻞ ﺍﻟﺜﺎﻟﺚ
–
ﺍﻟﻄﺎﻗﺔ
)
3.1
(
-
ﺍﻟﻁﺎﻗﺔ
Energy
ﻴﻬﺘﻡ ﻋﻠﻤﺎﺀ ﺍﻟﺩﻴﻨﺎﻤﻴﻜﺎ ﺍﻟﺤﺭﺍﺭﻴﺔ ﺒﺎﻟﻁﺎﻗﺔ ﻭﺘﺤﻭﻻﺘﻬﺎ ﻤﻥ ﺸﻜل ﻵﺨﺭ
.
ﻫﺫﻩ ﺍﻟﺘﺤﻭﻻﺕ ﺘﻨﻅﻡ ﺒﻀﻭﺍﺒﻁ
ﻤﻌﻴﻨﺔ ﻫﻲ ﻗﻭﺍﻨﻴﻥ ﺍﻟﺩﻴﻨﺎﻤﻴﻜﺎ ﺍﻟﺤﺭﺍﺭﻴﺔ
.
ﻭﻡـﻬﻔﻤ ﻥﻋ ﺭﺒﻌﻴ ﻱﺫﻟﺍ لﻭﻻﺍ ﻥﻭﻨﺎﻘﻟﺍ ﺔﻏﺎﻴﺼ ﻲﻓ ﺩﻋﺎﺴﺘ ﺔﻗﺎﻁﻟﺎﻓ
ﺍﻟﻁﺎﻗﺔ
.
ﻴﻤﻜﻥ ﺘﻌﺭﻴﻑ ﺍﻟﻁﺎﻗﺔ ﺒﺄﻨﻬﺎ ﺍ
ﺭﻤﺯﻫﺎ،لﻐﺸ ﺯﺎﺠﻨﺇ ﻰﻠﻋ ﺓﺭﺩﻘﻟ
(E)
.
ﺔـﻜﺭﺤﻟ ﺔﺠﻴﺘﻨ ﻭﻬﻓ لﻐﺸﻟﺍ ﺎﻤﺍ
لﻭـﺤﺘﺘ ﻙﺭﺤﻤﻟﺍ ﻲﻓ ﻪﻗﺭﺤ ﺩﻨﻌﻓ ،ﺔﻴﻭﺎﻴﻤﻴﻜ ﺔﻐﻴﺼﺒ ﺔﻨﻤﺎﻜ ﺔﻗﺎﻁ ﻰﻠﻋ ﺩﻭﻗﻭﻟﺍ ﻱﻭﺘﺤﻴ ،ﺔﻨﻴﻌﻤ ﺔﻓﺎﺴﻤ ﺎﻤ ﺓﻭﻗ
ﺎـﻬﻜﻴﺭﺤﺘ ﻱﺭـﺠﻴ ﺓﻭﻗ ﻥﻷ لﺼﺤ ﺩﻗ ﹰﻼﻐﺸ ﻥﺄﻓ ﻪﻨﻤﻭ ،ﺓﺭﺎﻴﺴﻟﺍ ﻙﺭﺤﺘ ﺔﻴﻜﻴﻨﺎﻜﻴﻤ ﺔﻗﺎﻁ ﻰﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻩﺫﻫ
ﺒﻤﺴﺎﻓﺔ ﻤﻌﻴﻨﺔ ﻨﺘﻴﺠﺔ ﻟ
ﺤﺭﻕ ﺍﻟﻭﻗﻭﺩ ﺘﺅﺩﻱ ﺍﻟﻰ ﺯﻴﺎﺩﺓ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻠﻤﺎﺌﻊ
ﺇﻥ ﻭﺤﺩﺍﺕ ﺍﻟﻁﺎﻗﺔ ﻫﻲ
)
ﺍﻟﻘﻭﺓ
×
ﺍﻟﻤﺴﺎﻓﺔ
(
ﺃﻱ
(N.m)
ﻭﻫﻭ ﺍﻟﺠﻭل
(J)
ﻐﻴﺭﺓـﺼ ﺓﺩـﺤﻭ ﻪﻨﻷﻭ
ﻓﻴﺴﺘﻌﻤل ﺍﻟﻜﻴﻠﻭ ﺠﻭل
(kJ)
ﺍﻟﺫﻱ ﻴﺴﺎﻭﻱ
(10
3
J)
.
)
3.2
(
-
ﻤﺼﺎﺩﺭ ﻭﺍﺸﻜﺎل ﺍﻟﻁﺎﻗﺔ
Sources & Forms of Energy
1
-
ﻤﺼﺎﺩﺭ ﺫﺍﺕ ﻜﻤﻴﺎﺕ
ﻤﺤﺩﻭﺩﺓ ﻭﺘﺸﻤل ﺍﻟﻭﻗﻭﺩ
)
ﺍﻟﻨﻭﻭﻱ،ﻡﺤﻔﻟﺍ ،ﻱﺩﺎﻌﻟﺍ
.(
2
-
ﻤﺼﺎﺩﺭ ﺫﺍﺕ ﻜﻤﻴﺎﺕ ﻏﻴﺭ ﻤﺤﺩﻭﺩﺓ ﻟﺘﻭﻟﻴﺩ ﺍﻟﻘﺩﺭﺓ ﺍﻟﻜﻬﺭﺒﺎﺌﻴﺔ ﻤﺜﻼﹰ ﻭﺘﺸﻤل
:
.ﺃ
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺸﻤﺴﻴﺔ
ﺏ
-
ﺍﻟﻤﺩ ﻭﺍﻟﺠﺯﺭ
ـﺠ
-
ﺍﻤﻭﺍﺝ ﺍﻟﺒﺤﺭ
ﺩ
-
ﻤﺴﺎﻗﻁ ﺍﻟﻤﻴﺎﻩ
ـﻫ
-
ﻁﺎﻗﺔ ﺍﻟﺭﻴﺎﺡ
ﻭ
–
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﺨﺯﻭﻨﺔ ﺘﺤﺕ ﺍﻻﺭﺽ
.
ﺍﻤﺎ ﺍﺸﻜﺎل ﺍﻟﻁﺎﻗﺔ ﻓﻤﻭﻀﺤﺔ ﻓﻲ ﺍﻟﻤﺨﻁ
ﻁ ﺍﻟﺘﺎﻟﻲ
:
-
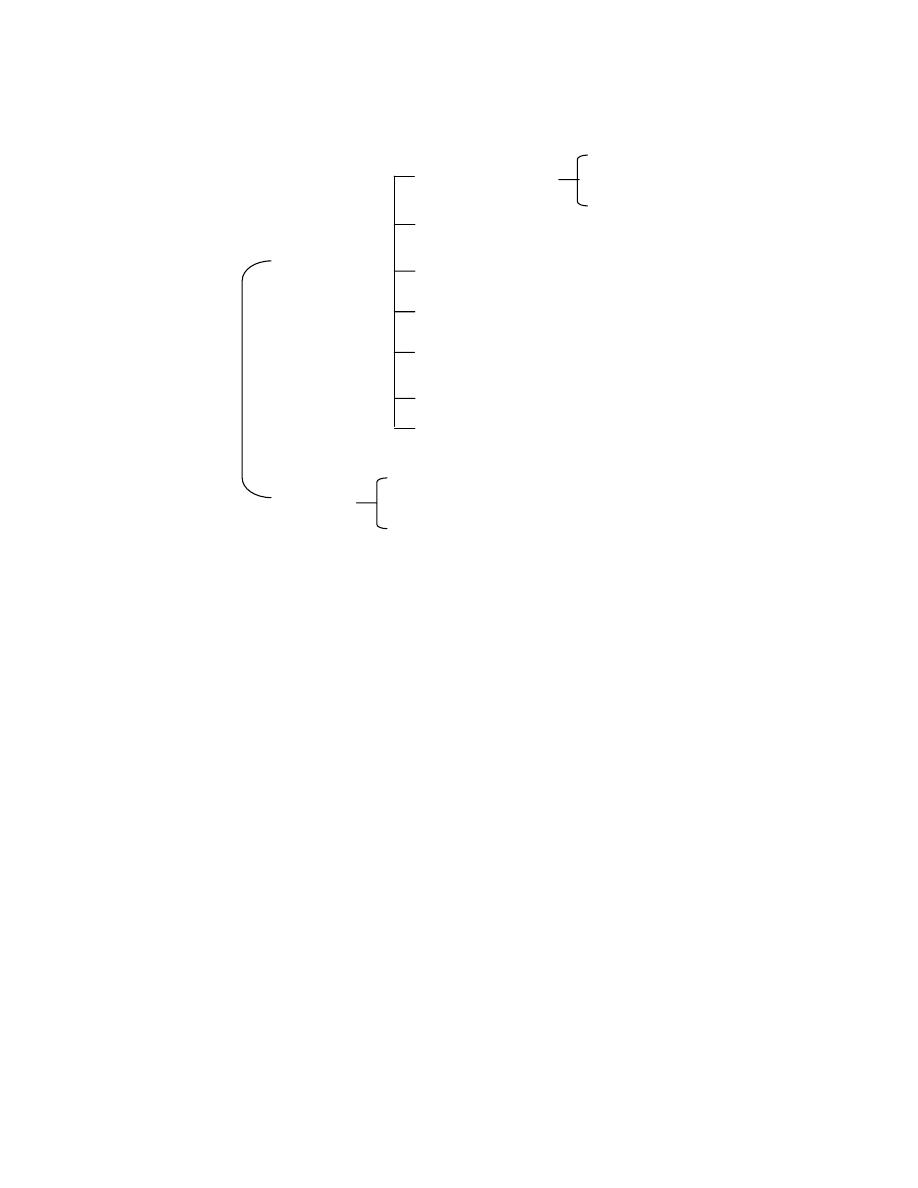
)
46
(
)
3.2.1
(
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﺨﺯﻭﻨﺔ
Stored Energy
ﻭﺘﺸﻤل،ﻪﺴﻔﺘ ﻊﺌﺎﻤﻟﺍ ﻥﻤﻀ ﺓﺩﻭﺠﻭﻤ ﻊﺌﺎﻤﻟﺍ ﺔﻗﺎﻁﻟ ﺔﻔﻠﺘﺨﻤﻟﺍ لﺎﻜﺸﻻﺍ ﻲﻫ
:
ﺃ
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ
Potential Energy
ﺭﻤﺯﻫﺎ،ﻊﻀﻭﻟﺍ ﺔﻗﺎﻁﺒ ﹰﺎﻀﻴﺍ ﻰﻤﺴﺘ
(PE)
ﺘﺘﻭﻗﻑ ﻋﻠﻰ ﻭﺯﻥ ﺍﻟﺠﺴﻡ ﻭﺍﺭﺘﻔﺎﻋﻪ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻤﻨﺴﻭﺏ،
ﺜﺎﺒﺕ ﻜﻁﺎﻗﺔ ﺍﻟﻤ
ﻴﺎﻩ ﺍﻟﻤﺤﺠﻭﺯﺓ ﻋﻠﻰ ﻤﻨﺴﻭﺏ ﻤﻌﻴﻥ ﻭﺭﺍﺀ ﺍﺤﺩ ﺍﻟﺴﺩﻭﺩ ﺃﻱ ﺍﻨﻬﺎ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺘﻲ ﻴﻜﺘﺴﺒﻬﺎ ﺍﻟﺠﺴﻡ
ﺍﻭ ﺍﻟﻤﺎﺌﻊ
)
ﺍﻟﻨﻅﺎﻡ
(
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﻋﻠﻰ ﺍﺭﺘﻔﺎﻉ ﻤﻘﺩﺍﺭﻩ
(Z)
ﺴﻁﺢ ﺍﻻﺭﺽـﻟ ﺔﺒﺴـﻨﻟﺎﺒ
.
ﺫﺏـﺠﻟﺍ ﺓﻭـﻗ ﻥﺇ
ﺍﻻﺭﻀﻲ ﻟﻠﻜﺘﻠﺔ ﻴﺴﺎﻭﻱ
(F= m×g)
ﺤﻴﺙ
(g)
ﻭﺓـﻘﻟﺍ ﻩﺫـﻫ ﺕـﻜﺭﺤﺘ ﺍﺫﺈـﻓ ،ﻲﻀﺭﻻﺍ لﻴﺠﻌﺘﻟﺍ لﺜﻤﺘ
)
ﺍﻭ ﺍﻟﻭﺯﻥ
(
ﺨﻼ
ل ﻤﺴﺎﻓﺔ ﺸﺎﻗﻭﻟﻴﺔ ﻤﻘﺩﺍﺭﻫﺎ
(Z)
ﻓﺈﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ ﺘﺴﺎﻭﻱ،
:
PE = F × Z = m×g× z
…… (3.1)
ﺍﻤﺎ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ
:
∆PE = mg× ∆Z
……..
(3.2)
ﻭﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ ﺍﻟﻨﻭﻋﻴﺔ ﺘﺴﺎﻭﻱ
:
PE = g ×Z
……….. (3.3)
Ener
gy
Stored E.
Transit E.
Mechanical E.
Internal E.
Flow or Displacement E.
Internal E.
Chemical E.
Electrical E.
Potential E.
Kinetic E.
Work
Heat
Nuclear E
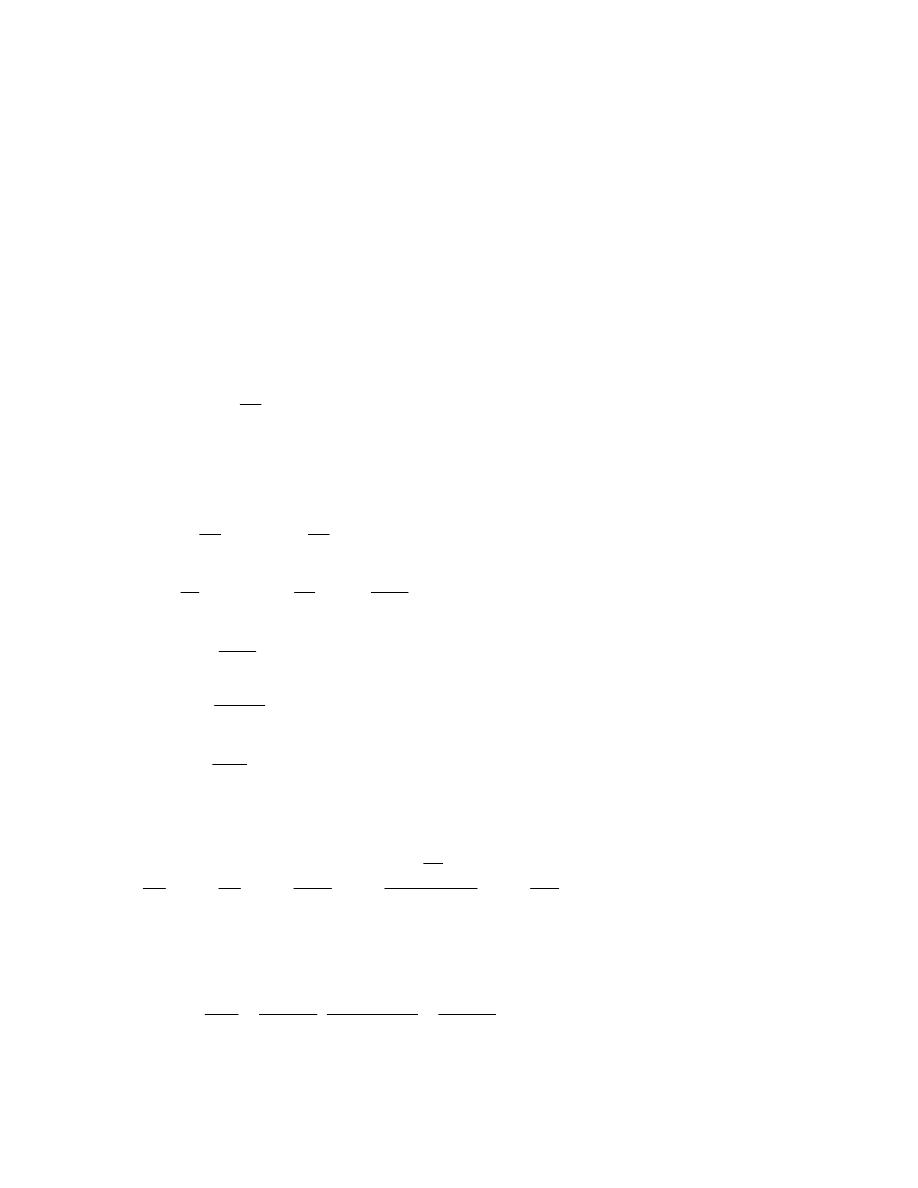
)
47
(
ﺤﻴﺙ ﻴﻜﻭﻥ ﺍﻟﺘﻐﻴﺭ ﺼﻐﻴﺭﺍﹰ،ﺓﺭﻴﺒﻜ ﺔﻴﻤﻫﺍ ﺔﻨﻤﺎﻜﻟﺍ ﺔﻗﺎﻁﻠﻟ ﺱﻴﻟ
ﻡـﻅﻌﻤ ﻲﻓ ﺭﻔﺼﻟﺍ ﻥﻤ ﺏﺭﺘﻘﻴ ﹰﺍﺩﺠ
ﺍﻟﻤﺤﺭﻜﺎﺕ ﺍﻟﺤﺭﺍﺭﻴﺔ
.
ﺏ
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ
Kinetic Energy
ﺭﻤﺯﻫﺎ
(KE)
.
ﺘﺘﻭﻗﻑ ﻋﻠﻰ ﻭﺯﻥ ﺍﻟﺠﺴﻡ ﻭﺴﺭﻋﺘﻪ،ﻡﺎﻅﻨﻟﺍ ﺔﻗﺎﻁ ﻱﺃ ،ﻊﺌﺎﻤﻟﺍ ﻭﺍ ﻡﺴﺠﻟﺍ ﺔﻗﺎﻁ ﻲﻫ
ﺍﺫﺍ ﻜﺎﻥ ﻓﻲ ﺤﺎﻟﺔ ﺤﺭﻜﺔ ﺍﻭ ﻋﻨﺩ ﺘﺒﻁﻴﺌﻪ
.
ﻴﻜﻭﻥ ﺤﺩﻫﺎ ﺍﻻﻗﺼﻰ ﻋﻨﺩﻤﺎ ﻴﺒﻁﺊ ﺍﻟﺠﺴﻡ ﺍﻟﻰ ﺍﻟﺴﻜﻭﻥ
.
ﻴﻤﻜﻥ ﺍﻥ
ﺘﻜﻭﻥ
ﻀﻭﺍﻏﻁـﻟﺍﻭ ﺯﺎﻐﻟﺍﻭ ﺭﺎﺨﺒﻟﺍ ﺕﺎﻨﻴﺒﺭﻭﺘ ،ﺔﺜﺎﻔﻨﻟﺍ ﺕﺎﻜﺭﺤﻤﻟﺍ لﺜﻤ ﺔﻤﻅﻨﻻﺍ ﺽﻌﺒ ﻲﻓ ﺓﺭﻴﺒﻜ ﺔﻴﻤﻫﺍ ﺕﺍﺫ
…
.
ﺍﻟﺦ
.
ﻭﻋﻨﺩﻤﺎ ﺘﻜﻭﻥ
(C)
، ﺍﻟﺴﺭﻋﺔ
(t)
، ﺍﻟﺯﻤﻥ
(m)
، ﺍﻟﻜﺘﻠﺔ
(a)
ﻭﺓـﻘﻟﺍ ﻥﻭﻜﺘﺴـﻓ ،ﺔـﻠﺘﻜﻟﺍ لﻴﺠﻌﺘ
ﺍﻟﺨﺎﺭﺠﻴﺔ ﺍﻟﻜﻠﻴﺔ ﺍﻟﻤﺅﺜﺭﺓ ﻓﻲ ﺍﻟﺠﺴﻡ ﻓﻲ ﺍﻻﺘﺠﺎﻩ ﺍﻟﻤﻭﺍﺯﻱ ﻷﺯﺍﺤﺘﻪ
(dL)
ﻴﺴﺎﻭﻱ
:
ﻭﺴﻴﻜﻭﻥ
ﺍﻟﺸﻐل ﺍﻟﻜﻠﻲ ﺍﻟﻤﺒﺫﻭل ﺍﻭ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻠﻴﺔ ﺒﻭﺴﺎﻁﺔ ﺍﻟﺠﺴﻡ ﻀﺩ ﻫﺫﻩ ﺍﻟﻘﻭﺓ ﻟﺘﻘﻠﻴل ﺍﻟﺴﺭﻋﺔ ﻤﻥ
(C)
ﺍﻟﻰ ﺍﻟﺼﻔﺭ ﻴﺴﺎﻭﻱ
:
ﺍﻤﺎ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ ﻓﻴﺴﺎﻭﻱ
:
ﺍﻤﺎ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ ﺍﻟﻨﻭﻋﻴﺔ ﻓﺘﺴﺎﻭﻱ
:
ﻭﻨﺘﻌﺭﻑ
ﻋﻠﻰ
ﻭﺤﺩﺍﺕ
(KE)
ﻤﻥ ﺨﻼل ﺍﻟﺘﺤﻭﻴل ﺍﻟﺘﺎﻟﻲ ﻟﻠﻭﺤﺩﺍﺕ
:
ﻓﺈﺫﺍ ﺍﺭﻴﺩ ﺍﻥ
ـﺘﻜﻭﻥ ﺍﻟ
(KE)
ﺒﻭﺤﺩﺍﺕ
)
kJ/kg
(
ﻓﺘﺼﺒﺢ ﺍﻟﻤﻌﺎﺩﻟﺔ
(3.8)
ﻜﺎﻟﺘﺎﻟﻲ
:
(3.4)
...
..........
dt
dc
m
.a
m
F
=
=
(3.6)
.
..........
2
mc
KE
2
mc
2
c
m
(c)
d
2
m
mcdc
dc
.
dt
dc
m
dL
.
dt
dc
m
(3.5)
.........
FdL
W
2
2
c
o
2
2
t
=
∴
∆
=
⎥⎦
⎤
⎢⎣
⎡
=
=
=
=
=
=
∫
∫
∫
∫
∫
)
7
.
3
(
..........
2
c
m
KE
2
∆
=
∆
)
8
.
3
(
..........
2
c
KE
2
∆
=
∆
(3.9)
.........
s
m
10
kg
m
s
m
kg
10
kg
m
.
N
10
kg
J
10
kg
kJ
2
2
3
2
3
3
3
=
×
×
=
=
=
)
10
.
3
(
..........
kJ/kg)
(
10
2
c
s
/
m
10
kJ/kg
.
2
s
/
m
2
c
KE
3
2
2
2
3
2
2
2
×
∆
=
=
∆
=
∆
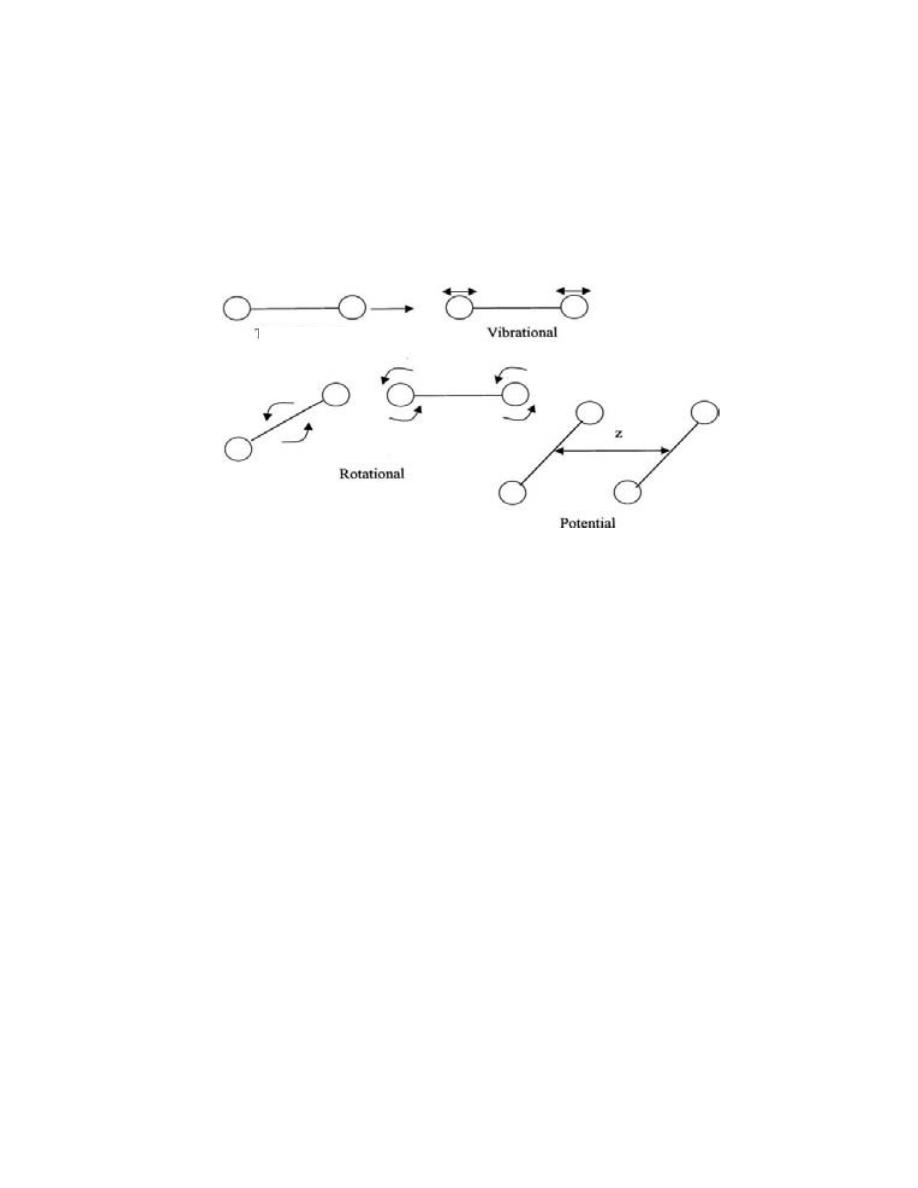
)
48
(
ـﺠ
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
Internal Energy
ﺘﺘﺄﻟﻑ ﺍﻟﻤﺎﺩﺓ ﻤﻥ ﺍﻟﺫﺭﺍﺕ ﻭﺍﻟﺠﺯﻴﺌﺎﺕ
.
ﺴﺒﺏـﺒ ﺔـﻴﻜﺭﺤ ﺔﻗﺎﻁ ﻰﻠﻋ ﺓﺩﺎﻤﻟﺍ لﺼﺤﺘﺴ ﻥﻴﺨﺴﺘﻟﺍ ﺩﻨﻌﻓ
ﺔـﻴﻟﺎﻘﺘﻨﻻﺍ ﺕﺎﺌﻴﺯﺠﻟﺍ ﺔﻜﺭﺤ
(Transition)
ﺔـﻴﺯﺍﺯﺘﻫﻻﺍ ،
(Vibration)
ﺔـﻴﻨﺍﺭﻭﺩﻟﺍﻭ ،
(Rotation)
،
ﻜلـﺸ ﻲـﻓ ﺎﻤﻜ ،ﺕﺎﺌﻴﺯﺠﻟﺍ ﻥﻴﺒ ﺓﺩﻭﺠﻭﻤﻟﺍ ﺏﺫﺎﺠﺘﻟﺍ ﺓﻭﻗ ﺏﺒﺴﺒ ﺔﻨﻤﺎﻜ ﺔﻗﺎﻁ ﻰﻠﻋ ﺓﺩﺎﻤﻟﺍ لﺼﺤﺘﺴ ﻙﻟﺫﻜﻭ
)
3.1
.(
ﺸﻜل
)
3.1
(
-
ﺤﺭﻜﺔ ﺍﻟﺠﺯﺌﻴﺎﺕ ﺩﺍﺨل ﺍﻟﻤﺎﺩﺓ
ﺎـﻬﻟ ﺯـﻤﺭﻴ ،ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺎﺒ ﻰﻤﺴﺘ ﺎﻬﻴﻓ ﺔﻨﻭﺯﺨﻤﻟﺍﻭ ﺓﺩﺎﻤﻟﺍ ﺎﻬﻜﻠﺘﻤﺘ ﻲﺘﻟﺍ ﺕﺎﻗﺎﻁﻟﺍ لﻜ ﻥﺫﺇ
(U)
ﻭﺍﻟﻨﻭﻋﻴﺔ
(
µ)
.
ﻓﻲ ﺍﻟﻐﺎﺯﺍﺕ ﺘﺘﺤﺭﻙ
ﻟﺫﺍ،ﺔﺒﻠﺼﻟﺍ ﺩﺍﻭﻤﻟﺍ ﻲﻓ ﻪﻴﻠﻋ ﻭﻫ ﺎﻤﻤ ﺭﺒﻜﺍ ﺔﻴﺭﺤﺒ ﺕﺍﺭﺫﻟﺍﻭ ﺕﺎﺌﻴﺯﺠﻟﺍ
ﺴﻴﻭﻟﺩ ﺍﺭﺘﻁﺎﻤﻬﺎ ﻭﺤﺭﻜﺘﻬﺎ ﻀﻐﻁﺎﹰ ﻋﻠﻰ ﺍﻟﺠﺩﺍﺭ
.
،ﻟﺫﺍ ﻓﺈﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺩﺍﻟﺔ ﻟﺤﺭﻜﺔ ﺍﻟﺠﺯﻴﺌﺎﺕ ﻭﺍﻟﺫﺭﺍﺕ
ﻭﺒﺎﻟﺘﺎﻟﻲ ﻓﻬﻲ ﺨﺎﺼﻴﺔ ﻤﻥ ﺨﻭﺍﺹ ﺍﻟﻤﺎﺩﺓ ﺘﻌﻴﻥ ﺒﺩﻻﻟﺔ ﺃﻱ ﺨﺎﺼﻴﺘﻴﻥ ﻤﺴﺘﻘﻠﺘﻴﻥ ﻤﺜل
)
P
،
T
.(
ﺇﻥ ﺯﻴﺎﺩﺓ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨ
ﻰـﻟﺍ ﺀﺎـﻤﻟﺍ ﺭﻴﻐﺘ ﺩﻨﻋ ﹰﻼﺜﻤﻓ ،ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺓﺩﺎﻴﺯ ﻰﻟﺍ ﹰﺎﻤﺌﺍﺩ ﻱﺩﺅﻴ ﻻ ﺔﻴﻠ
ﺀﺎـﻤﻟﺍ لﻭﺤﺘﻴﻟ ﺕﺎﺌﻴﺯﺠﻟﺍ لﺼﻔﻨﺘﻭ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺩﺍﺩﺯﺘ ﻥﻴﺤ ﻲﻓ ﺔﺘﺒﺎﺜ ﻰﻘﺒﺘﺴ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻥﺈﻓ ﺭﺎﺨﺒ
ﺍﻟﻰ ﺒﺨﺎﺭ
.
ﺭﺓـﻘﻔﻟﺍ ﻲﻓ ﺢﻀﻭﺘﻴﺴ ﺎﻤﻜ لﺌﺎﺴ ﻰﻟﺍ ﺏﻠﺼﻟﺍ لﻴﻭﺤﺘ ﻰﻠﻋ ﻕﺒﻁﻨﺘ ﺔﻟﺎﺤﻟﺍ ﻩﺫﻫﻭ
)
4.1
(
ﺭـﻅﻨﺍ ،
ﺸﻜل
)
4.2
(.
ﺭ ﺃﻱـﻴﻐﺘﻟﺍ ﺭﺍﺩـﻘﻤﺒ لـﺜﻤﺘ لـﺒ ،ﻕـﻠﻁﻤ ﺱﺎـﺴﺍ ﻰـﻠﻋ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺔﻤﻴﻗ ﺩﻴﺩﺤﺘ ﻥﻜﻤﻴ ﻻ
(
∆U
12
=U
2
-U
1
)
.
ﻓﻌﻨﺩ ﺘﺴﺨﻴﻥ ﺍﻟﻨﻅﺎﻡ ﺘﺭﺘﻔﻊ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﻭﺘﺯﺩﺍﺩ ﺤﺭﻜﺔ ﺍﻟﺠﺯﻴﺌﺎﺕ ﻭﺍﻟﺫﺭﺍﺕ ﻭﺒﺎﻟﺘﺎﻟﻲ
ﺔﻗﺎﻁﻟﺍ ﻥﻭﻜﺘﻓ ﻥﻭﻜﺴ ﺔﻟﺎﺤ ﻲﻓ ﺕﺍﺭﺫﻟﺍﻭ ﺕﺎﺌﻴﺯﺠﻟﺍ ﻥﻭﻜﺘ ﺎﻤﺩﻨﻌﻓ ،ﺢﻴﺤﺼ ﺱﻜﻌﻟﺍﻭ ،ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺩﺍﺩﺯﺘ
ﺍﻟﺩﺍﺨﻠﻴﺔ ﺼﻔﺭﺍﹰ
.
ﺃﻱ ﺍﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺩﺍﻟﺔ ﻟﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻜﻤﺎ ﺴﻴﺘﻭﻀﺢ ﻓﻴﻤﺎ ﺒﻌﺩ
.
Transitional

)
49
(
ﺩ
-
ﺍﻟﻁﺎﻗﺔ ﺍﻻﺯﺍﺤﻴﺔ ﺍﻭ ﺍﻟﺘﺩﻓﻘﻴﺔ
)
ﻁﺎﻗﺔ ﺍﻟﺠﺭﻴﺎﻥ
(
Flow or Displacement Energy
ﻫﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻨﺎﺘﺠﺔ ﺒﺴﺏ ﺃﺯﺍﺤﺔ ﺍﻭ ﺠﺭﻴﺎﻥ
)
ﺘﺩﻓﻕ
(
ﺍﻟ
ﻤﺎﺌﻊ ﺴﻭﺍﺀ ﻜﺎﻥ ﻏﺎﺯﺍﹰ ﺃﻭ ﺴﺎﺌﻼﹰ
.
ﻰـﻠﻋ ﻥﻭﻜﺘ
ﺸﻜل ﻨﻭﻋﻴﻥ
:
.ﺃ
ﻁﺎﻗ
ﺔ ﺍﻭ ﺸﻐل ﺃﺯﺍﺤﻲ
.
ﺏ
.
ﻁﺎﻗﺔ ﺃﻭ ﺸﻐل ﺠﺭﻴﺎﻨﻲ
)
ﺘﺩﻓﻘﻲ
.(
ﺯﺍـﺠﻨﻤ ﺭـﺨﻵ ﻥﺎﻜﻤ ﻥﻤ ﻪﺤﻴﺯﺘ ﺱﺒﻜﻤ ﻰﻠﻋ ﺓﺭﺜﺅﻤ ﺓﻭﻗ ﺔﻁﺴﺍﻭﺒ لﻭﺫﺒﻤﻟﺍ لﻐﺸﻟﺍ ﻭﻫ ﻲﺤﺯﺍﻻﺍ لﻐﺸﻟﺍ ﻥﺃ
ﺒﺫﻟﻙ ﺸﻐﻼ ﺍﺯﺍﺤﻴﺎﹰ
.
ﺍﺒﺴﻁ ﻤﺜﺎل ﻋﻠﻰ ﺫﻟﻙ ﻫﻭ ﻤﺎﻴﺤﺩﺙ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﻤﺤﺭﻙ
.
لـﺨﺍﺩ ﺩﻭﻗﻭﻟﺍ ﻕﺍﺭﺘﺤﺍ ﺩﻌﺒﻓ
ﺍﻻﺴﻁﻭﺍﻨﺔ ﺘﺘﻭﻟﺩ ﻁﺎﻗﺔ
.
ﻓﺘﻤﺩﺩ ﺍﻟﻐﺎﺯﺍﺕ
ﺍﻟﺘﻲ ﺘﺩﻓﻊ
)
ﺍﻭ ﺘﺯﻴﺢ
(
ﺫﻟﻙـﺒ ﺍﺯـﺠﻨﻤ ﻯﺭﺨﻻ ﺔﻁﻘﻨ ﻥﻤ ﺱﺒﻜﻤﻟﺍ
ﺸﻐﻼ ﺨﺎﺭﺠﻴﺎ ﻤﻭﺠﺒﺎ
.
ﺔـﻁﻘﻨ ﻥﻤ ﺎﻀﻴﺍ ﺡﺍﺯﻴﻟ ﺎﺒﻟﺎﺴ ﺎﻴﻠﺨﺍﺩ ﻼﻐﺸ ﺱﺒﻜﻤﻟﺍ ﺝﺎﺘﺤﻴ ﺕﺍﺯﺎﻐﻟﺍ ﻁﺎﻐﻀﻨﺍ ﺩﻨﻋﻭ
ﻻﺨﺭﻯ
.
ﻓﺄﺫﺍ ﻜﺎﻥ
)
P
(
ﺘﻤﺜل ﺍﻟﻀﻐﻁ ﺍﻟﻤﺅﺜﺭ ﺍﻟﺜﺎﺒﺕ
)
ﻭﺯﻥ ﺍﻟﻤﻜﺒﺱ ﻤﺜﻼ
.(
ﻭﺍﻥ
)
V
1
(
ﺩﺍﺌﻲـﺘﺒﻻﺍ ﻡـﺠﺤﻟﺍ
،ﻟﻠﻐﺎﺯ
)
V
2
(
ﺍﻟﺤﺠﻡ ﺍﻟﻨﻬﺎﺌﻲ
.
ﻓﺄﻥ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ ﻤﻥ ﻗﺒل ﺍﻟﻐﺎﺯ
)
W
(
ﺔـﻁﻘﻨ ﻥـﻤ ﺱﺒـﻜﻤﻟﺍ ﺢﻴﺯﻴ ﻱﺫﻟﺍﻭ
)
V
1
(
ﺍﻟﻰ ﻨﻘﻁﺔ
)
V
2
(
ﺴﻴﻜﻭﻥ
:
W
12
= P
∆V
12
= P(V
2
-V
1
)
)
3.2.2
(
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﻨﺘﻘﻠﺔ ﺍﻭ ﺍﻟﻌﺎﺒﺭﺓ
Transit Energy
ﺎﺀـﻤ ﻰـﻟﺍ ﺭﻁﻤﻟﺍ ﺍﺫﻫ لﻭﺤﺘﻴ ﺓﺭﻴﺤﺒ ﻰﻠﻋ ﺭﻁﻤﻟﺍ لﻁﻬﻴ ﺎﻤﺩﻨﻌﻓ ،ﺭﻁﻤﻟﺎﺒ ﺔﻗﺎﻁﻟﺍ ﻩﺫﻫ ﻪﻴﺒﺸﺘ ﻥﻜﻤﻴ
ﺍﻀﺎﻓﻲ ﻀﻤﻥ
ﺎـﻤﻨﻴﺒ ،ﺔـﻨﻭﺯﺨﻤﻟﺍ ﺔـﻗﺎﻁﻟﺍ ﻪﺒﺸﻴ ﺓﺭﻴﺤﺒﻟﺍ ﻥﻤﻀ ﺀﺎﻤﻟﺎﻓ ،ﹰﺍﺭﻁﻤ ٍﺫﺌﺩﻨﻋ ﻰﻤﺴﻴ ﻻﻭ ،ﺓﺭﻴﺤﺒﻟﺍ
ﺍﻟﻤﻁﺭ ﻴﺸﺒﻪ ﺍﻟﺸﻐل ﺍﻭ ﺍﻟﺤﺭﺍﺭﺓ
.
ﺔـﻨﻭﺯﺨﻤ ﺔﻗﺎﻁ ﻰﻟﺍ ﻥﻻﻭﺤﺘﻴ ﻡﺎﻅﻨﻟﺍ ﻰﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻭﺍ لﻐﺸﻟﺍ لﺎﻘﺘﻨﺍ ﺩﻌﺒﻓ
.
ﻭﺇﻨﻤﺎ ﻴﻘﺎل ﺍﻨﻪ ﻴﺤﺘﻭﻱ ﻋﻠﻰ ﻁﺎﻗ،ﺓﺭﺍﺭﺤ ﺔﻴﻤﻜ ﻰﻠﻋ ﻱﻭﺘﺤﻴ ﻡﺎﻅﻨﻟﺍ ﻥﺍ لﺎﻘﻴ ﻥﺍ ﺄﻁﺨﻟﺍ ﻥﻤ ﻙﻟﺫﻟ
،ﺔ ﻤﺨﺯﻭﻨﺔ
ﻴﻨﺘﻬﻲ ﻭﺠﻭﺩﻫﻤﺎ ﻜﺸﻐل ﺍﻭ ﺤﺭﺍﺭﺓ ﻭﻴﺘﺤﻭﻻﻥ ﺍﻟﻰ ﺯﻴﺎﺩﺓ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻭﺍﻟﺤﺭﻜﻴﺔ ﻭﺍﻟﻜﺎﻤﻨﺔ
.
ﺔـﻨﻭﺯﺨﻤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺩﺍﺩﺯﺘﺴﻓ ﺝﺭﺎﺨﻟﺍ لﻐﺸﻟﺍ ﻥﻤ ﺭﺒﻜﺍ ﻡﺎﻅﻨﻟﺍ ﻰﻟﺍ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺔﻴﻤﻜ ﺕﻨﺎﻜ ﺍﺫﺍ
ﻓﻲ ﺍﻟﻨﻅﺎﻡ ﻭﺍﻟﻌﻜﺱ ﺼﺤﻴﺢ
.
ﻴﺘﺒﻴﻥ ﻤﻥ ﺍﻟﻤﻨﺎﻗﺸﺔ ﺍﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﻨﺘﻘﻠﺔ ﺘﺸﻤل ﺍﻟﺸﻐل ﻭﺍ
ﻟﺤﺭﺍﺭﺓ
.
)
3.3
(
-
ﺤﻔﻅ ﺍﻟﻁﺎﻗﺔ
The Conservation of Energy
ﻴﻨﺹ ﻗﺎﻨﻭﻥ ﺤﻔﻅ ﺍﻟﻁﺎﻗﺔ ﻋﻠﻰ ﺍﻥ ﺍﻟﻁﺎﻗﺔ ﻻ ﺘﻔﻨﻰ ﻭﻻ ﺘﺴﺘﺤﺩﺙ ﻭﺇﻨﻤﺎ ﺘﺘﺤﻭل ﻤﻥ ﺸﻜل ﺍﻟﻰ ﺁﺨﺭ
.
ﻰـﻟﺍ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ لﻭﺤﺘ ﻲﺘﻟﺍ ﺔﻴﺌﺎﺒﺭﻬﻜﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺩﻴﻟﻭﺘ ﺕﺎﻁﺤﻤ ﻭﻫ ﻡﻭﻬﻔﻤﻟﺍ ﺍﺫﻫ ﺢﻴﻀﻭﺘﻟ لﺎﺜﻤ ﻁﺴﺒﺍ
ﻁﺎﻗﺔ ﻤﻴﻜﺎﻨﻴﻜﻴﺔ ﺜﻡ ﺍﻟﻰ ﺸﻐل ﻴ
ﺔـﻴﺌﺎﺒﺭﻬﻜﻟﺍ ﺓﺩﻟﻭﻤﻟﺍ ﺭﻴﻭﺩﺘﺒ ﻡﻭﻘ
(Electrical generator)
.
ﺫﺍـﻫ ﻥﺍ ﻱﺃ
ﻭﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺝﺎﺘﻨﻷ ﺔﻔﻠﺘﺨﻤ ﺓﺯﻬﺠﺍ ﻲﻓ ﺎﻬﻟﺎﻤﻌﺘﺴﻷ ﻙﻠﻬﺘﺴﻤﻟﺍ ﻰﻟﺍ لﺴﺭﺘ ﺔﻴﺌﺎﺒﺭﻬﻜ ﺔﻗﺎﻁ ﻰﻟﺍ لﻭﺤﺘ ﺩﻗ لﻐﺸﻟﺍ
ﺍﻟﻀﻭﺀ ﺍﻭ ﺍﻟﻘﻭﺓ
.
ﺔ ﺍﻭـﻗﺎﻁﻟﺍ ﺏﺭﺴـﺘ ﺏﺒﺴﺒ ﺔﻴﺌﺎﺒﺭﻬﻜ ﺔﻗﺎﻁ ﻰﻟﺍ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ لﻜ لﻭﺤﺘﺘ ﻻ ﺩﻴﻜﺄﺘﻟﺎﺒﻭ
ﺍﻟﻤﻔﻘ
ﻭﺍﻻﻤﺜﻠﺔ ﻋﻠﻰ ﻤﺤﻁﺎﺕ ﺘﻭﻟﻴﺩ ﺍﻟ،ﺔﻴﺭﺍﺭﺤﻟﺍ ﺕﺍﺩﻭ
ﻁﺎﻗﺔ ﻫﻲ
:
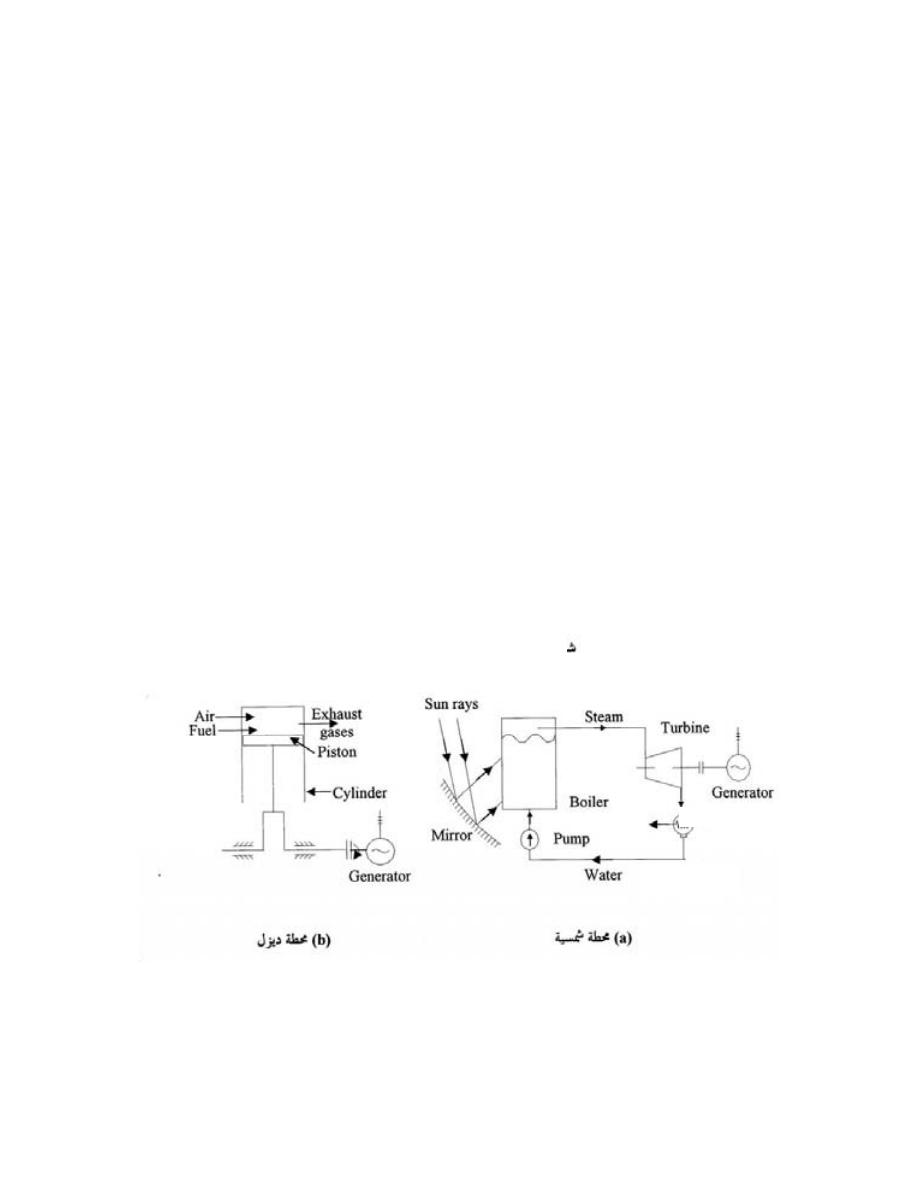
)
50
(
1
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﺸﻤﺴﻴﺔ ﺸﻜل
Solar Power Plant (3.2-a)
2
-
ﻤﺤﻁﺔ ﺩﻴﺯل ﺸﻜل
Diesel Engine Power Plant (3.2-b)
3
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﻐﺎﺯﻴﺔ ﺸﻜل
Gas Turbine Power Plant (3.3-a)
4
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﺒﺨﺎﺭﻴﺔ ﺸﻜل
Steam Power Plant (3.3-b)
5
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﻨﻭﻭﻴﺔ
ﺍﻟﻐﺎﺯﻴﺔ ﺸﻜل
Nuclear Gas Turbine Power Plant (3.4-a)
6
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﻬﻴﺩﺭﻭﻟﻴﻜﻴﺔ ﺸﻜل
Hydraulic Power Plant (3.4-b)
ﻭﻏﻴﺭﻫﺎ ﻤﻥ ﻤﺤﻁﺎﺕ ﺘﺤﻭﻴل ﺍﻟﻁﺎﻗﺔ
.
ﻭﺴﻨﺴﻠﻁ ﺍﻟﻀﻭﺀ ﻋﻠﻰ ﺒﻌﺽ ﻤﻥ ﻫﺫﻩ ﺍﻟﻤﺤﻁﺎﺕ
.
1
-
ﻤﺤﻁﺔ ﺩﻴﺯل
ﺘﺘﺤﻭل ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻴﻤﻴﺎﻭﻴﺔ ﺍﻟﻤﻭﺠﻭﺩﺓ ﻓﻲ ﺍﻟﻭﻗ،لﺯﻴﺩ ﻙﺭﺤﻤ لﺨﺍﺩ ﺩﻭﻗﻭﻟﺍ ﻕﺭﺤ ﺩﻌﺒ
ﺔـﻗﺎﻁ ﻰﻟﺍ ﺩﻭ
ﻨﻭﺍﺘﺞ ﺍﻻﺤﺘﺭﺍﻕ،ﺔﻴﺭﺍﺭﺤ
(Product of Combustion)
ﺔـﻴﺩﺩﺭﺘ ﺔـﻜﺭﺤ ﺱﺒـﻜﻤﻟﺍ ﻙﺭـﺤﺘﻴﻭ ﺩﺩﻤﺘﺘ
(Reciprocating)
ﺜﻡ ﺘﺘﺤﻭل ﺍﻟﻰ ﺤﺭﻜﺔ ﺩﻭﺭﺍﻨﻴﺔ
(Rotary)
ﻴلـﺼﻭﺘﻟﺍ ﻉﺍﺭﺫﻭ ﻕـﻓﺭﻤﻟﺍ ﺔﻴﻟﺁ ﺔﻁﺎﺴﻭﺒ
(Crank Connecting rod mechanism)
ﻴﺴﺘﻐﻠﻬﺎ ﺍﻟﻤﻭﻟﺩ ﻷﻨﺘﺎﺝ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻬﺭﺒﺎﺌﻴﺔ
.
ﺃﻱ ﺍﻥ
:
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻴﻤﻴﺎﺌﻴﺔ
←
ﻤﺤﺭﻙ ﺩﻴﺯل
←
ﻁﺎﻗﺔ ﻤﻴﻜﺎﻨﻴﻜﻴﺔ
←
ﺍﻟﻤﻭﻟﺩ
←
ﻁﺎﻗﺔ ﻜﻬﺭﺒﺎﺌﻴﺔ
ﺸﻜل
)
3.2
(
–
ﻤﺤﻁﺔ ﺘﻭﻟﻴﺩ ﺍﻟﻁﺎﻗﺔ
Condenser
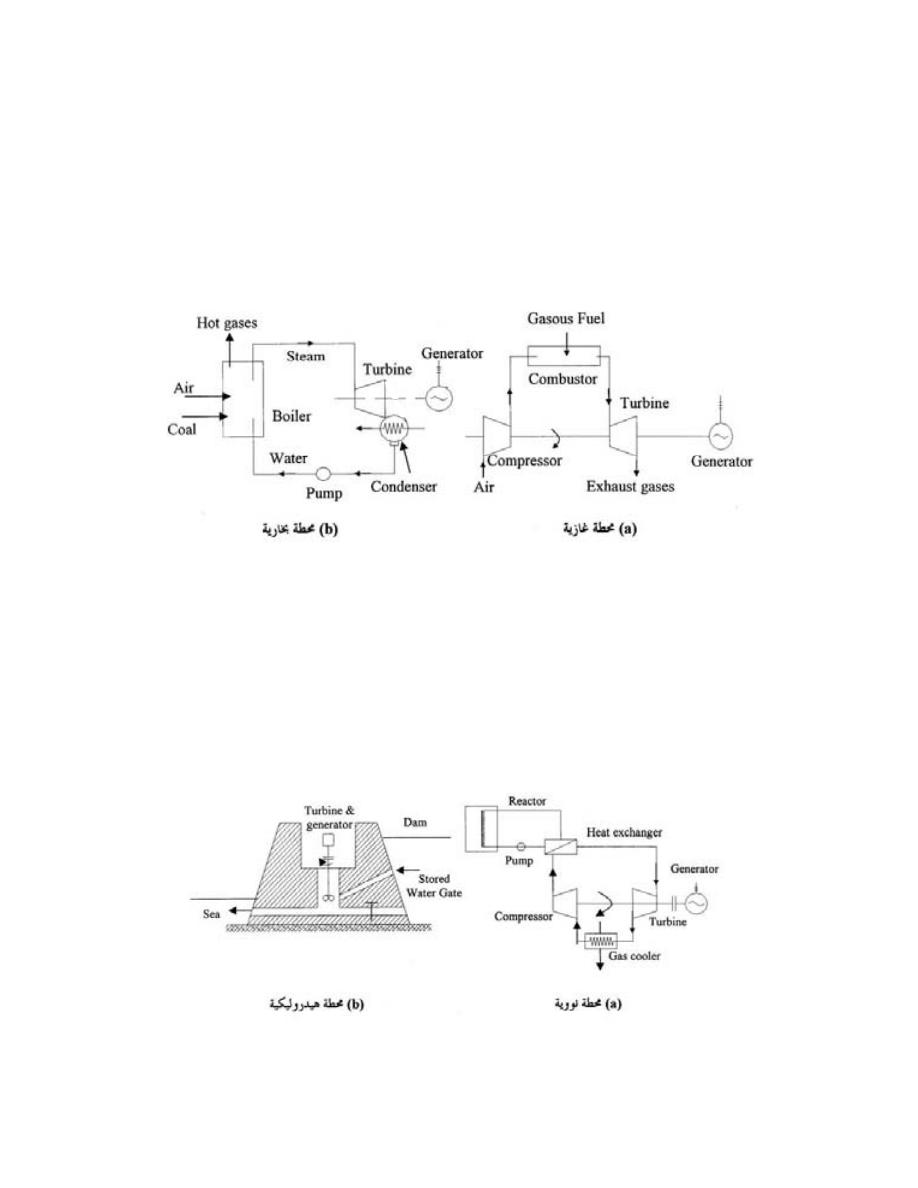
)
51
(
2
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﻐﺎﺯﻴﺔ
ﻴﻀﻐﻁ ﺍﻟﻬﻭﺍﺀ ﺨﻼل ﺍﻟﻀﺎﻏﻁ
(Compressor)
.
ﺭﺍﻕـﺘﺤﻻﺍ ﺔﻓﺭﻏ ﻲﻓ ﺔﺠﺘﺎﻨﻟﺍ ﺭﺍﻕﺘﺤﻻﺍ ﺞﺘﺍﻭﻨ
(Combustor)
ﺘﺘﻤﺩﺩ ﺨﻼل ﺍﻟﺘﻭﺭﺒﻴﻥ
(Turbine)
ﻭﺘﻌﻁﻲ ﺍﻟﺸﻐ
ل ﺍﻟﻼﺯﻡ ﻷﺩﺍﺭﺓ ﺍﻟﻤﻭﻟﺩ ﺍﻟﻜﻬﺭﺒﺎﺌﻲ
.
ﺸﻜل
)
3.3
(
–
ﻤﺤﻁﺔ ﺘﻭﻟﻴﺩ ﺍﻟﻁﺎﻗﺔ
3
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﺒﺨﺎﺭﻴﺔ
ﻋﻨﺩ ﺤﺭﻕ ﺍﻟﻭﻗﻭﺩ
)
ﺴﻭﻻﺭ ﺍﻭ ﻓﺤﻡ
(
ﺘﻌﻤل ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ ﺍﻟﻤﺭﺠل،
(Boiler)
ﺎﺭـﺨﺒﻟﺍ ﺩﻴﻟﻭﺘ ﻰﻠﻋ
.
ﻋﻨﺩﻤﺎ ﻴﺘﻤﺩﺩ ﺍﻟﺒﺨﺎﺭ ﺨﻼل ﺍﻟﺘﻭﺭﺒﻴﻥ ﻓﺎﻥ ﺠﺯﺀ ﻤﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ ﺍﻟﻤﺨﺯﻭﻨﺔ ﻓﻲ ﺍﻟﺒﺨﺎﺭ ﺘﺘﺤﻭل ﺍﻟﻰ ﻁﺎ
ﻗﺔ
ﻴﺴﺘﺨﺩﻤﻬﺎ ﺍﻟﻤﻭﻟﺩ ﻷﻨﺘﺎﺝ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻬﺭﺒﺎﺌﻴﺔ،ﺔﻴﻜﻴﻨﺎﻜﻴﻤ
.
ﺃﻱ ﺍﻥ
:
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻴﻤﻴﺎﺌﻴﺔ
←
ﺍﻟﻤﺭﺠل
←
ﻁﺎﻗﺔ ﺤﺭﺍﺭﻴﺔ
←
ﺍﻟﺘﻭﺭﺒﻴﻥ
←
ﻁﺎﻗﺔ ﻤﻴﻜﺎﻨﻴﻜﻴﺔ
←
ﺍﻟﻤﻭﻟﺩ
←
ﺔـﻗﺎﻁ
ﻜﻬﺭﺒﺎﺌﻴﺔ
.
ﺸﻜل
)
3.4
(
–
ﻤﺤﻁﺔ ﺘﻭﻟﻴﺩ ﺍﻟﻁﺎﻗﺔ
)
52
(
4
-
ﺍﻟﻤﺤﻁﺔ ﺍﻟﻨﻭﻭﻴﺔ ﺍﻟﻐﺎﺯﻴﺔ
ﻴﻀﻐﻁ ﺍﻟﻐﺎﺯ ﺨﻼل ﺍﻟﻀﺎﻏﻁ
(Compressor)
ﻁﺔـﺴﺍﻭﺒ ﻱﺭﺍﺭـﺤﻟﺍ لﺩﺎـﺒﻤﻟﺍ ﻲﻓ ﻥﺨﺴﻴ ﻡﺜ ،
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﺘﻭﻟﺩﺓ ﻓﻲ ﺍﻟﻤﻔﺎﻋل
(Reactor)
ﺎﺩﺓـﻤ ﺔﻁـﺴﺍﻭﺒ ﻱﺭﺍﺭﺤﻟﺍ لﺩﺎﺒﻤﻟﺍ ﻰﻟﺍ لﻋﺎﻔﻤﻟﺍ ﻥﻤ ﺔﻠﻘﺘﻨﻤﻟﺍﻭ ،
ﺕﺍﺯﺎـﻐﻟﺍ ﻲـﻓ ﺔﻨﻭﺯﺨﻤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻥﻤ ﺀﺯﺠ ،ﻥﻴﺒﺭﻭﺘﻟﺍ لﻼﺨ ﺔﻨﺨﺎﺴﻟﺍ ﺕﺍﺯﺎﻐﻟﺍ ﺩﺩﻤﺘﺘ ﺎﻤﺩﻨﻋ ،ﺓﺭﺍﺭﺤﻠﻟ ﺔﻠﻗﺎﻨ
ﺃﻱ ﺍﻥ،ﻲﺌﺎﺒﺭﻬﻜﻟﺍ ﺩﻟﻭﻤﻟﺍ ﺓﺭﺍﺩﺇ ﻰﻠﻋ لﻤﻌﻴ لﻐﺸ ﻰﻟﺍ لﻭﺤﺘﺘ
:
ﺍﻟﻴﻭﺭﺍﻨﻴﻭﻡ
←
ﺍﻟﻤﻔ
ﺎﻋل
←
ﻁﺎﻗﺔ ﺤﺭﺍﺭﻴﺔ
←
ﻤﺒﺎﺩل ﺤﺭﺍﺭﻱ
←
ﻁﺎﻗﺔ ﺤﺭﺍﺭﻴﺔ
ﻁﺎﻗﺔ ﻜﻬﺭﺒﺎﺌﻴﺔ
→
ﺍﻟﻤﻭﻟﺩ
→
ﻁﺎﻗﺔ ﻤﻴﻜﺎﻨﻴﻜﻴﺔ
→
ﺘﻭﺭﺒﻴﻥ
ﻭﺨﻼﺼﺔ ﺍﻟﻘﻭل ﺇﺫﺍ ﻜﺎﻨﺕ ﻤﺤﻁﺎﺕ ﺘﺤﻭﻴل ﺍﻟﻁﺎﻗﺔ ﺍﻨﻅﻤﺔ ﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﻓﺴﻴﻜﻭﻥ ﻤﺠﻤﻭﻉ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﺔ
ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ
(
∑E
in
)
ﺘﺴﺎﻭﻱ ﻤﺠﻤﻭﻉ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺨﺎﺭﺠﺔ
(
∑E
out
)
ﻭﺘﻐﻴﺭ ﺍﻟﻁﺎﻗﺔ ﺩﺍﺨ
ل ﺍﻟﻨﻅﺎﻡ
∆Esystem
ﻜﻤﺎ ﻓﻲ ﺸﻜل
)
3.5
(
ﺃﻱ،
:
ﺸﻜل
)
3.5
(
-
ﻁﺎﻗﺔ ﺍﻟﻨﻅﺎﻡ
∑E
in
=
∑
out
+
∆∑E
system
……. (3.11)
ﻭﻋﻨﺩﻤﺎ ﺘﻜﻭﻥ ﺤﺎﻟﺔ ﺍﻟﻨﻅﺎﻡ ﻤﺴﺘﻘﺭﺓ ﺃﻱ
(
∆∑E
system
= 0)
ﻓﺴﻴﻜﻭﻥ
:
∑E
in
=
∑E
out
=
∑E
constant
ﻭﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﻨﻅﺎﻡ ﻤﻌﺯﻭل
(Isolated)
ﻓﺄﻥ
:
E
system
= Constant
)
3.4
(
-
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ
Work and Heat
)
3.4.1
(
-
ﺨﻠﻔﻴﺔ ﺘﺄﺭﻴﺨﻴﺔ
Historical Background
ﺯﻥـﺨﺘ ﺓﺩﺎـﻤ ﺎـﻬﻨﺍ ﻱﺃ ﻊﺌﺍﻭﻤﻟﺍ ﻉﺍﻭﻨﺍ ﺩﺤﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺩﻌﺘ ﺭﺸﻋ ﻥﻤﺎﺜﻟﺍ ﻥﺭﻘﻟﺍ ﻲﻓ ﺔﻴﺭﻅﻨ ﺕﺭﻬﻅ
ﻭﺘﻨﺴﺎﺏ ﻤﻥ ﺍﻻﺠﺴﺎﻡ ﺍﻟﺤﺎﺭﺓ ﺍﻟﻰ ﺍﻟﺒﺎﺭﺩﺓ
.
ﺭـﻴﻏ ﺭـﻀﺎﺤﻟﺍ ﺕﻗﻭﻟﺍ ﻲﻓ ﺕﺤﺒﺼﺍﻭ ﺕﺩﻨﻓ ﺔﻴﺭﻅﻨﻟﺍ ﻩﺫﻫ ﻥﻜﻟ
ﻤﻘﺒﻭﻟﺔ ﻷﻨﻪ ﺒﺭﻫ
ﻥ ﻭﺃﺜﺒﺕ ﻋﻤﻠﻴﺎﹰ ﻭﻋﻠﻤﻴﺎﹰ ﺍﻥ ﺍﻟﺤﺭﺍﺭﺓ
)
1
(
ﺘﺘﻜﻭﻥ ﺒﺎﻻﺤﺘﻜﺎﻙ ﻭ
)
2
(
ﻥـﻤ ﻰـﺘﺤ ﺏﺎﺴـﻨﺘ
ﺍﻻﺠﺴﺎﻡ ﺍﻟﺒﺎﺭﺩﺓ ﻭ
)
3
(
ﺘﻨﺘﻘل ﻤﻥ ﺍﻻﺠﺴﺎﻡ ﺍﻟﺤﺎﺭﺓ ﺍﻟﻰ ﺍﻟﺒﺎﺭﺩﺓ ﺘﻠﻘﺎﺌﻴﺎﹰ
.
ﺎﻵﺨﺭـﺒ ﺎﻤﻫﺩﺤﺍ ﺢﺴﻤ ﻡﺜ ﺎﻤﻬﻀﻌﺒ ﻥﻤ ﻥﻴﺩﺭﺎﺒ ﻥﻴﻤﺴﺠ ﺏﻴﺭﻘﺘﺒ ﻲﻔﻴﺩ ﻱﺭﻔﻤﻫ ﺭﻴﺴﻟﺍ ﻡﻟﺎﻌﻟﺍ ﻡﺎﻗ ﺩﻘﻟ
ﻓﻭﺠﺩ ﻅﻬﻭﺭ ﺍﻟﺤﺭﺍﺭﺓ ﻨﺘﻴﺠﺔ ﺍﻻﺤﺘﺎﻙ
ﻤﺎ ﺒﻴﻥ ﻫﺫﻴﻥ ﺍﻟﺠﺴﻤﻴﻥ ﺍﻟﺒﺎﺭﺩﻴﻥ
.
ﻭﻗﺎﻡ ﺍﻟﻌﺎﻟﻡ ﻨﻔﺴﻪ ﺒﺄﺨﺫ ﻗﻁﻌﺘﻴﻥ ﻤﻥ
ﻥﻴـﺘﻌﻁﻘﻟﺍ ﺕﺭﻬﺼـﻨﺄﻓ ﺽﻌﺒﻟﺍ ﺎﻤﻬﻀﻌﺒﺒ ﺢﺴﻤﻟﺍ ﺔﻴﻠﻤﻋ ﺃﺩﺒﻭ ﻯﺭﺨﻻﺍ ﻕﻭﻓ ﻥﻴﺘﻌﻁﻘﻟﺍ ﻯﺩﺤﺍ ﻊﻀﻭﻭ ﺞﻠﺜﻟﺍ
∆Esystem
E
out
E
in

)
53
(
ﺎﺕـﺌﻴﺯﺠﻟﺍ ﻩﺫـﻫ ﻥﻷ ﺓﺩﺎﻤﻟﺍ ﺎﺕﺌﻴﺯﺠ ﻥﻴﺒ ﺎﻤ ﻙﺎﻜﺘﺤﻻﺎﺒ ﻥﻭﻜﺘﺘ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺍ ﺕﺒﺜﺍ لﻴﻟﺩﻟﺍ ﺍﺫﻬﺒﻭ ًﺀﺎﻤ ﺎﻨﻭﻜﻭ
ﺘﻜﻭﻥ ﻓﻲ ﺤﺎﻟﺔ ﺤﺭﻜ
ﺔ ﺩﺍﺌﻤﻴﺔ ﻟﺫﻟﻙ ﺘﻨﺴﺎﺏ ﺤﺘﻰ ﻤﻥ ﺍﻻﺠﺴﺎﻡ ﺍﻟﺒﺎﺭﺩﺓ
.
ﺍﻤﺎ ﺍﻟﻌﺎﻟﻡ ﻜﻭﻨﺕ ﺭﻤﻔﻭﺭﺩ ﺍﻟﺫﻱ ﺍﻜﺩ ﻋﺎﻡ
)
1798
(
ﺍﻥ ﺍﻟﺤﺭﺍﺭﺓ ﺘﺘﻭﻟﺩ ﺒﺎﻻﺤﺘﻜﺎﻙ ﻤﻥ ﺨﻼل ﺇﺭﺘﻔﺎﻉ
ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺭﺍﻴﺵ ﺍﻟﻨﺤﺎﺱ ﺍﻻﺼﻔﺭ ﻓﻲ ﻋﻤﻠﻴﺔ ﺘﺠﻭﻴﻑ ﻤﺎﺴﻭﺭﺓ ﻤﺩﻓﻊ
.
ﻼـﺨ ﻥﻤﻭ ﻙﻟﺫﻟ ،ﺓﺭﺍﺭﺤﻟﺍ ﺏﺎﻴﺴﻨﺍ ﻥﻋ لﻭﺅﺴﻤﻟﺍﻭ لﻭﺫﺒﻤﻟﺍ لﻐﺸﻟﺍ ﻙﺎﻜﺘﺤﻻﺎﺒ ﺩﺼﻘﻴ
ﺎﺭﺏـﺠﺘﻟﺍ ل
ﺱﻤﻴﺠ ﺭﻭﺘﻜﺩﻟﺍ ﻩﺩﺠﻭﺍ ﺅﻓﺎﻜﺘﻟﺍ ﺍﺫﻫ ،لﻭﺫﺒﻤﻟﺍ لﻐﺸﻟﺍﻭ ﺔﺠﺘﺎﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻴﺒ ﹰﺎﻨﻴﺘﻤ ًﺅﻓﺎﻜﺘ ﻙﺎﻨﻫ ﻥﺍ ﻥﻴﺒﺘ ﻩﻼﻋﺍ
ﺒﺭﻴﺴﻜﻭ ﺠﻭل
)
1818
–
1889
(
ﺅﺘﻤﺭـﻤ ﻲـﻓ ﻲﺨﻴﺭﺄـﺘﻟﺍ ﻪﺜﺤﺒ لﻼﺨ ﻥﻤ ﻱﺯﻴﻠﻜﻨﺍ ﻱﻭﺎﻴﺯﻴﻓ ﻡﻟﺎﻋ ﻭﻫﻭ
ﺍﻟﺭﺍﺒﻁﺔ ﺍﻟﺒﺭﻴﻁﺎﻨﻴﺔ ﻓﻲ ﻜﻭﺭﻙ ﻋﺎﻡ
)
1843
(
ﺇﺫ ﻗﺎﻡ ﺒﺤﺴﺎﺏ ﺍﻟﻘﻴﻤﺔ ﺍﻟﻌﺩﺩ،
ﺭﺍﺭﺓـﺤﻟﺍ ﻥﻴﺒ ﺔﻗﻼﻌﻠﻟ ﺔﺘﺒﺎﺜﻟﺍ ﺔﻴ
ﻭﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﻭﺍﻟﺘﻲ ﺘﺴﺎﻭﻱ
(J=4.186 kJ/kcal)
ﺃﻱ ﺍﻥ،لﻭـﺠ ﺊﻓﺎـﻜﻤﺒ ﻰﻤﺴـﺘﻭ
(W/Q=J)
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﺸﻐل
(W)
ﺒﻭﺤﺩﺍﺕ ﺍﻟﺠﻭل
(J)
ﻭﺍﻟﺤﺭﺍﺭﺓ
(Q)
ﺒﻭﺤﺩﺍﺕ
(Kcal)
.
ﺩﺍﺕـﺤﻭﻟﺍ ﻡﺎﻅﻨ ﻲﻓﻭ
ﺍﻟﻌﺎﻟﻤﻲ
(SI)
ﻓﺈﻥ ﻭﺤﺩﺍﺕ ﺍﻟﺤﺭﺍﺭﺓ ﻨﻔﺱ ﻭﺤﺩﺍﺕ ﺍﻟﺸﻐل ﻭﻫﻲ ﺍﻟﺠﻭل
(J)
ﻭ
ﻴﺴﺎﻭﻱ
(J=N.m)
ﺈﻥـﻓ ﺍﺫﻟ ،
ﻓﺒﻘﻴﺕ ﻗﻴﻤﺘﻪ ﺍﻟﺘﺄﺭﻴﺨﻴﺔ ﻓﻘﻁ،ﺕﻻﺩﺎﻌﻤﻟﺍ ﻲﻓ ﹰﺎﻴﺭﻭﺭﻀ ﺱﻴﻟ ﺊﻓﺎﻜﻤﻟﺍ ﺔﻤﻴﻗ
.
)
3.4.2
(
-
ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل
Relationship between Heat & Work
ﻋﻨﺩ ﺇﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﺍﻭ ﺍﻟﺸﻐل ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ ﻴﺘﺤﻭﻻﻥ ﺍﻟﻰ ﻁﺎﻗﺔ ﻤﺨﺯﻭﻨﺔ ﺒﻌﺩ ﺩﺨﻭﻟﻬﻤﺎ ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ ﻻ
ﻴﻤﻜﻥ ﺘ
ﻤﻴﻴﺯﻫﻤﺎ ﺍﻭ ﻓﺼﻠﻬﻤﺎ ﻋﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺘﻲ ﻴﻤﺘﻠﻜﻬﺎ ﺍﻟﻨﻅﺎﻡ
.
،ﺭﺓـﻴﺤﺒﻟﺍ ﻲـﻓ ﺭﻁﻤﻟﺎـﺒ ﻙـﻟﺫ ﻪﻴﺒﺸﺘ ﻥﻜﻤﻴ
ﻭﻤﺎﺀ ﺍﻟﻤﻁﺭ ﻓﻲ ﺍﻟﺒﺤﻴﺭﺓ ﻴﺸﺒﻪ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﺨﺯﻭﻨﺔ،لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﻭﻫ ﺭﻁﻤﻟﺎﻓ
.
ﻙ ﺍﻥـﻟﺫ ﻥـﻤ ﺞﺘﻨﺘﺴـﻨ
ﺃﻱ ﺍﻨﻬﺎ ﻅﺎﻫﺭﺓ ﻭﻗﺘﻴﺔ ﺘﻼﺤﻅ ﻋﻨﺩ ﺤﺩﻭﺩ ﺍ،ﻡﺎﻅﻨﻟﺍ ﺩﻭﺩﺤ ﺭﺒﻋ ﺔﻠﻘﺘﻨﻤ ﺔﻗﺎﻁ ﺎﻤﻫ لﻐﺸﻟﺍ ﻭﺍ ﺓﺭﺍﺭﺤﻟﺍ
،ﺎﻡـﻅﻨﻟ
ﻭﺘﺘﻭﻗﻑ ﻋﻨﺩﻤﺎ ﻴﺘﻭﻗﻑ ﺍﻻﻨﺘﻘﺎل
.
ﺔـﻟﺍﺩ ﺎﻤﻬﻓ ﻙﻟﺫﻟ ،ﺔﻴﺼﺎﺨ ﺱﻴﻟﻭ ﺔﻠﻘﺘﻨﻤ ﺔﻴﻤﻜ ،ﺔﻗﺎﻁﻟﺍ لﺎﻜﺸﺍ ﻥﻤ لﻜﺸ ﺎﻤﻫ ﺓﺭﺍﺭﺤﻟﺍﻭ لﻐﺸﻟﺍ ﻥﺫﺇ
ﺃﻱ ﻻ ﻴﻌﺘﻤﺩﺍﻥ ﻓﻘﻁ ﻋﻠﻰ ﺍﻟﺤﺎﻟﺔ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ ﻭﺍﻟﻨﻬﺎﺌﻴﺔ ﺒل ﺍﻴﻀﺎﹰ ﻋﻠﻰ ﺍﻟﺤﺎﻻﺕ ﺍﻟﺒﻴﻨﻴﺔ،ﺭﺎﺴﻤﻠﻟ
)
ﻁﻴﺔـﺴﻭﻟﺍ
(
،
ﺃﻱ ﻋﻠﻰ ﺍﻟﻤﺴﺎﺭ
.
)
54
(
)
3.4.3
(
-
ﺍﺸﺎﺭﺓ ﻭﻭﺤﺩﺍﺕ
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل
Sign. of Heat & Work
ﺭﻤﺯ ﺍﻟﺸﻐل
(W)
ﻭﺍﻟﻨﻭﻋﻲ
(w)
ﺍﻟﺫﻱ ﻴﺴﺎﻭﻱ
(w=W/m)
ﺭﺍﺭﺓـﺤﻟﺍ ﺯﻤﺭﻭ ،
(Q)
ﺭﺍﺭﺓـﺤﻟﺍﻭ
ﻟﻜل
(1Kg)
ﺒﺎﻟﺭﻤﺯ
(q)
ﻭﺍﻟﺘﻲ ﺘﺴﺎﻭﻱ
(q=Q/m)
.
ﻴﻁـﺤﻤﻟﺍ ﻰﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻥﻤ لﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍ ﻥﻋ لﺎﻘﻴﻭ
ﺒﺎﻟﺸﻐل ﺍﻟﺨﺎﺭﺠﻲ
(External Work)
ﻭﺭﻤ
ﺯ
ﻩ
(W
out
)
ﻭﺍﺸﺎﺭﺘﻪ ﻤﻭﺠﺒﺔ
.
ﻭﻋﻥ
ﻥـﻤ لـﻘﺘﻨﻤﻟﺍ لﻐﺸـﻟﺍ
ﺍﻟﻤﺤﻴﻁ ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ ﺒﺎﻟﺸﻐل ﺍﻟﺩﺍﺨﻠﻲ
(Internal Work)
ﻭﺭﻤﺯﻩ
(W
in
)
ﻭﺇﺸﺎﺭﺘﻪ ﺴﺎﻟﺒﺔ
.
ﺭﺍﺭﺓـﺤﻟﺍ ﺎـﻤﺍ
ﻭﻜﻤﺎ ﻤﺒﻴﻥ ﻓﻲ ﺸﻜل،لﻐﺸﻟﺍ ﺓﺭﺎﺸﺇ ﺱﻜﻋ ﺎﻬﺘﺭﺎﺸﺄﻓ ﺔﻠﻘﺘﻨﻤﻟﺍ
)
3.6
.(
ﺸﻜل
)
3.6
(
-
ﺭﻤﺯ ﻭ ﺍﺸﺎﺭﺓ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل
ﻭﻟﻸﺸﺎﺭﺓ ﺍﻟﻰ ﻤﻌﺩل ﺇﻨﺠﺎﺯ ﺍﻟﺸﻐل ﻨﻀﻊ ﻨﻘﻁ
ﺔ ﻓﻭﻕ ﺍﻟﺭﻤﺯ
(W)
ﺩﺓـﺤﻭ لـﻜﻟ ﺯـﺠﻨﻤﻟﺍ لﻐﺸﻟﺍ ﻱﻭﺎﺴﻴﻭ
ﺯـﻤﺭﻟﺍ ﻕﻭﻓ ﺔﻁﻘﻨ ﻊﻀﻨ ،ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺇ لﺩﻌﻤ ﻰﻟﺍ ﺓﺭﺎﺸﻸﻟﻭ ﻱﺃ ،ﺔﻴﻨﻤﺯ
(Q)
ﺃﻱ،ﺔﻴﻨﻤﺯ ﺓﺩﺤﻭ لﻜﻟ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻱﻭﺎﺴﻴﻭ
.
ﻭﻟﻜﻲ ﻨﻤﻴﺯ ﺒﻴﻥ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﻨﻨﻅﺭ ﺍﻟﻰ ﺸﻜل
)
3.7
(
ﺄـﻓ ،
ﻥ
)ﺃ
(
ﺩﺩـﻤﺘﻴ ﻊﺌﺎـﻤﻟﺍ ﻥﺍ ﺢـﻀﻭﻴ
ﺒﻴﻨﻤﺎ ﻴﻅل ﺍﻟﻤﺎﺌﻊ ﻗﺭﻴﺒﺎﹰ ﻤﻥ ﺤﺎﻟﺔ ﺍﻻﺘﺯﺍﻥ،ﹰﻼﻐﺸ ﺯﺠﻨﻴﻭ ﻥﺯﻭﻟﺍ ﺽﻴﻔﺨﺘﺒ ،ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ
.
ﻭﻓﻲ
)
ﺏ
(
ﺘﻨﺘﻘل ﺤﺭﺍﺭﺓ
ﻭﻓﻲ،لﻐﺸ ﻥﻭﺩﺒ
)
ـﺠ
(
ﺘﻨﺘﻘل ﺤﺭﺍﺭﺓ ﻓﻴﺘﻤﺩﺩ ﺍﻟﻤﺎﺌﻊ ﻭﻴﻨﺠﺯ ﺸﻐﻼﹰ
.
⎟
⎠
⎞
⎜
⎝
⎛
=
•
KW"
"
t
/
W
W
⎟
⎠
⎞
⎜
⎝
⎛ =
•
KW"
"
t
/
Q
Q
ﺎﻡـــﻅﻨﻟﺍ
ﺍﻟﻤﺤﻴﻁ
+
−
in
in
Q
,
W
+
−
o
o
W
,
Q
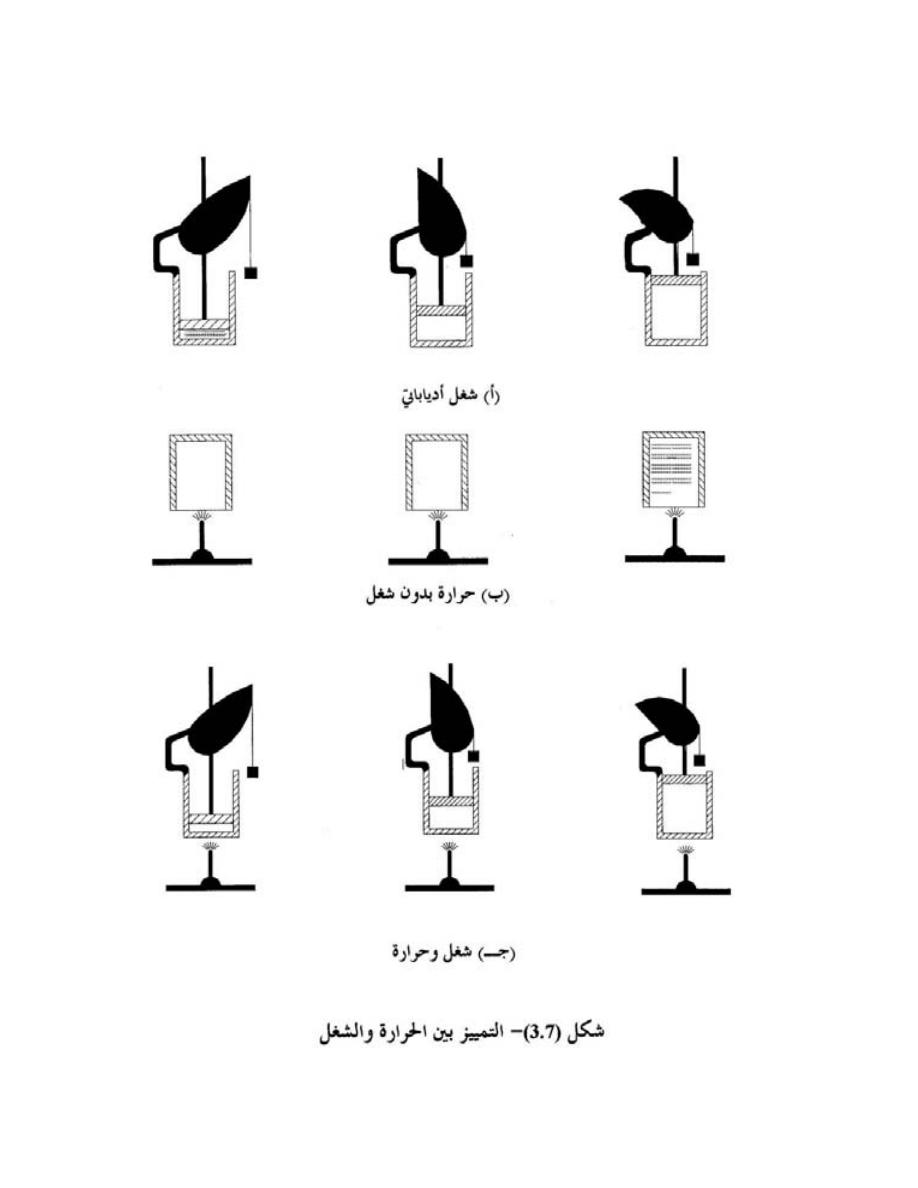
)
55
(
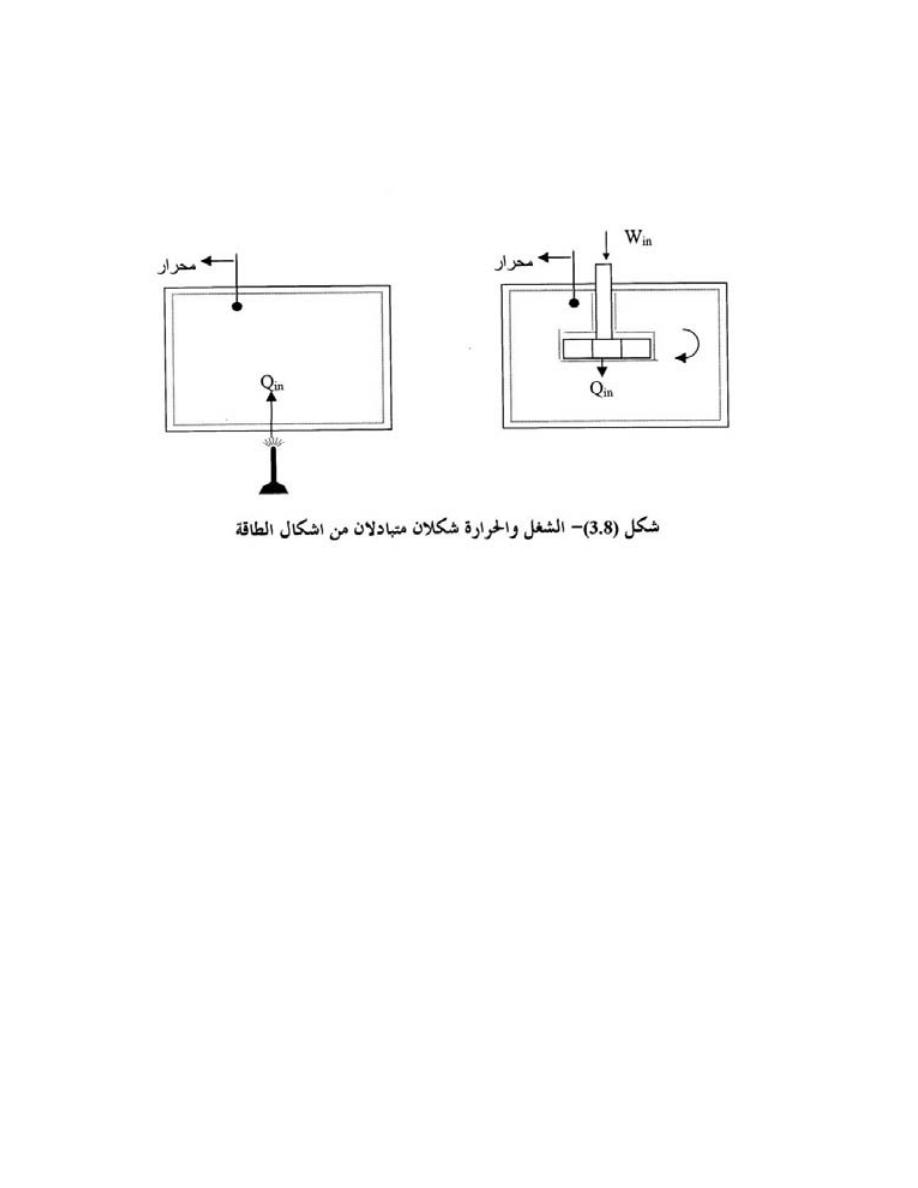
)
56
(
ﻭﻤﻥ ﺍﻟﻤﻤﻜﻥ ﺍﻥ ﻨﻁﺭﺡ ﺍﻟﺴﺅﺍل ﺍﻟﺘﺎﻟﻲ
:
ﻤﺎﺫﺍ ﻴﺤﺩﺙ ﻟﻠﺤﺭﺍﺭﺓ ﺒﻌﺩ ﺍﻨﺘﻘﺎﻟﻬﺎ
؟
ﺩﻭﺩـﺤﻟﺍ ﺭﻭﺒﻌﺒﻓ ،ﺓﺭﺍﺭﺤ لﻜﺸ ﻰﻠﻋ ﺔﻗﺎﻁﻟﺍ ﻥﺯﺨ ﻊﻴﻁﺘﺴﻴ ﻻ ﻡﺎﻅﻨﻟﺍ ﻥﺍ ﺎﻤﺒ ﻭﻫ ﻙﻟﺫ ﻰﻠﻋ ﺏﺍﻭﺠﻟﺍ ﻥﻭﻜﻴﻓ
ﺩﺙـﺤﻴﻭ ،ﻡﺎـﻅﻨﻟﺍ ﻪﺒ ﻅﻔﺘﺤﻴ ﻥﺍ ﻥﻜﻤﻴ ﻱﺫﻟﺍﻭ ﺔﻗﺎﻁﻟﺍ لﺎﻜﺸﺍ ﻥﻤ ﺭﺨﺁ لﻜﺸ ﻰﻟﺍ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ لﻭﺤﺘﺘ
ﻜﻤﺎ ﻓﻲ ﺸﻜل،لﻐﺸﻟﺍ ﺔﻗﺎﻁ لﺎﻘﺘﻨﺇ ﺩﻨﻋ لﺜﺎﻤﻤ لﻴﻭﺤﺘ
)
3.8
(
ﺍﻟﺫﻱ ﻴﻭﻀﺢ ﺒﺎﻥ ﺍﻟﻤﺎﺀ ﺍﻟﻤﻭﺠﻭ
ﺯﺍﻥـﺨ ﻲﻓ ﺩ
ﺘﺭﺘﻔﻊ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺒﻨﻔﺱ ﺍﻟﻤﻘﺩﺍﺭ ﺴﻭﺍﺀ ﻋﻥ ﻁﺭﻴﻕ ﺍﻟﺘﺴﺨﻴﻥ
(a)
ﺍﻭ ﻋﻥ ﻁﺭﻴﻕ ﺍﻻﺤﺘﻜﺎﻙ
(b)
ﺫﻟﻙـﻟ
ﻓﺄﻥ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﻫﻤﺎ ﺸﻜﻼﻥ ﻤﺘﺒﺎﺩﻻﻥ ﻤﻥ ﺍﺸﻜﺎل ﺍﻟﻁﺎﻗﺔ
.
ﻴﻤﻜﻥ ﺍﻟﺘﻌﺒﻴﺭ ﻋﻥ ﺍﻟﺤﺭﺍﺭﺓ ﺒﻭﺤﺩﺍﺕ ﺍﻟﺸﻐل ﺍﻟﺘﻲ ﻫﻲ ﺍﻟﺠﻭل
(J)
ﺸﻐلـﻟﺍ ﺭﺍﺩـﻘﻤ ﻪـﻨﺄﺒ ﻑﺭﻌﻴﻭ
ﺍﻟﻤﻨﺠﺯ ﺒﻭﺴﺎﻁﺔ ﻗﻭﺓ ﻤﻘﺩﺍﺭﻫﺎ ﻨ
ﻴﻭﺘﻥ ﻭﺍﺤﺩ
(N)
ﻋﻨﺩﻤﺎ ﺘﺘﺤﺭﻙ ﻫﺫﻩ ﺍﻟﻘﻭﺓ ﻤﺴﺎﻓﺔ ﻤﺘﺭﺍﹰ ﻭﺍﺤﺩﺍﹰ
(m)
ﺒﺎﻻﺘﺠﺎﻩ
ﺃﻱ ﺍﻥ،ﺓﻭﻘﻟﺍ ﻙﻠﺘ ﻪﻴﻓ لﻤﻌﺘ ﻱﺫﻟﺍ
:
(J=N.m)
.
(a)
(b)
)
57
(
)
3.5
(
-
ﺍﺸﻜﺎل ﺍﻟﺸﻐل
Forms of Work
ﻴﻤﻜﻥ ﺍﻥ ﻴﻜﻭﻥ ﺍﻟﺸﻐل ﺒﺄﺸﻜﺎل ﻤﺨﺘﻠﻔﺔ ﻤﻭﻀﺤﺔ ﻓﻲ ﺍﻟﻤﺨﻁﻁ ﺍﻵﺘﻲ
:
)
3.5.1
(
-
ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ
ﻴﻌﺘﻤﺩ ﻋﻠﻰ ﻤ
ﻟﻡ ﻴﻜﻥ ﺸﻐل،ﺔﻜﺭﺤ ﻥﻜﺘ ﻡﻟ ﺍﺫﺇ ،ﺃﺩﺒ
.
ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﻫﻭ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﺒﺫﻭﻟﺔ ﻟﻠﺘﻐﻠﺏ
ﻋﻠﻰ ﻗﻭﺓ ﻤﺎ ﺍﻭ ﻤﻘﺎﻭﻤﺔ
.
ﺫﺏـﺠﻟﺍ ﻰـﻠﻋ ﺏﻠﻐﺘﻠﻟ ﻲﻠﻀﻌﻟﺍ ﺱﺎﺴﺤﻻﺍ ﻥﺈﻓ ،ﺔﻠﺘﻜ ﻊﻓﺭﻟ ﺔﻗﺎﻁ لﺫﺒ ﺩﻨﻋ ﹰﻼﺜﻤﻓ
ﺍﻻﺭﻀﻲ ﻟﻠﻜﺘﻠﺔ
)
ﺃﻱ ﻭﺯﻨﻬﺎ
(
ﻫﻭ ﺸﻌﻭﺭ ﺒﻭﺠﻭﺩ ﻗﻭﺓ
.
ﻌﻭﺭﺍﹰـﺸ ﺩﻟﻭﻴﺴ ﺩﻴﻟﺎﺒ ﺽﺒﺎﻨ ﻁﻐﻀﻟ ﺔﻗﺎﻁ لﺫﺒ ﺩﻨﻋﻭ
ﺒﻭﺠ
ﻭﺩ ﻤﻘﺎﻭﻤﺔ
.
ﻓﺎﻟﺸﻐل ﻴﻨﺠﺯ ﺤﻴﻥ ﺘﺘﺤﺭﻙ ﻗﻭﺓ ﻋﺒﺭ ﻤﺴﺎﻓﺔ ﻤﻌﻴﻨﺔ
.
ﺸﻜل
)
3.9
(
-
ﻟﻡ ﻴﻜﻥ ﺸﻐﻼﹰ،ﺔﻜﺭﺤ ﻥﻜﺘ ﻡﻟ ﺍﺫﺍ
ﻭﻜﻤﺎ ﻤﻭﻀﺢ ﻓﻲ ﺍﻟﺸﻜل،لﻐﺸﻟﺍ ﻑﻴﺭﻌﺘ ﻥﻜﻤﻴ ﺍﺫﻟ
)
3.9
(
ﻭﺓـﻘﻟﺍ ﺏﺭﻀ لﺼﺎﺤ ﻪﻨﺎﺒ
(F)
ﻲـﻓ
ﺍﻟﻤﺴﺎﻓﺔ
(L)
.
ﺃﻱ
:
ﺍﻟﻤﺴﺎﻓﺔ
L … Distance
F
F
Work, W.
Mechanical W.
(W
mech.
)
Electrical W.
(W
e
)
Displacement W. (W
dis.
)
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
OR Moving Boundary W. (W
b
)
Gravitational W. (W
g
)
ﺸﻐل ﺍﻟﺠﺎﺫﺒﻴﺔ
Accelerational W. (W
a
)
ﺸﻐل ﺍﻟﺘﻌﺠﻴل
Shaft W. (W
sh.
)
ﺸﻐل ﺍﻟﻌﻤﻭﺩ
Spring W. (W
sp.
)
ﺸﻐل ﺍﻟﻨﺎﺒﺽ
∫
=
=
2
1
.
mech
(3.12)
..
..........
FdL
L
.
F
W
)
58
(
)
3.5.2
(
-
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
Displacement Work
ﺍﻥ ﺍﻟﺸﻐل ﺸﻲﺀ ﻴﻅﻬﺭ ﻋﻨﺩ ﺍﻟﺤﺩﻭﺩ ﻋﻨﺩﻤﺎ ﺘﺘﻐﻴﺭ ﺤﺎﻟﺔ ﺍﻟﻨﻅﺎﻡ ﺒﺴﺒﺏ ﺘﺤﺭﻙ ﺠﺯﺀ ﻤﻥ ﺍﻟﺤﺩﻭﺩ ﺘﺤﺕ
ﺍﺫﺈﻓ ،ﺔﻨﻴﻌﻤ ﺔﻓﺎﺴﻤ ﺭﺒﻋ ﺓﻭﻗ ﻙﺭﺤﺘﺘ ﻥﻴﺤ ﺯﺠﻨﻴ لﻐﺸﻟﺍ ﻥﺍ لﻭﻘﻨ ﻙﻴﻨﺎﻜﻴﻤﻟﺍ ﻲﻓ لﺎﺤﻟﺍ ﻭﻫ ﺎﻤﻜﻭ ﺓﻭﻘﻟﺍ ﺭﻴﺜﺄﺘ
ﺘﻌﺭﺽ ﺠﺯﺀ ﻤﻥ ﺍﻟﺤﺩﻭﺩ ﺍﻟﻰ ﺍﻹﺯﺍﺤﺔ ﺘﺤﺕ ﺘﺄﺜﻴﺭ ﺍﻟﻀﻐﻁ ﻓﺎﻥ ﻫﺫﺍ ﻫﻭ ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
.
ﺸﻜل
)
3.10
(
-
ﺍﻟﻤﺴﺎﺤﺔ ﺘﻤﺜل ﺍﻟﺸﻐل
ﺒﺱـﻜﻤ ﻰﻠﻋ ﺓﺭﺜﺅﻤ ﺓﻭﻗ ﺔﻁﺎﺴﻭﺒ لﻭﺫﺒﻤﻟﺍ لﻐﺸﻟﺍ ﻭﻫ ﻕﻓﺩﺘﻟﺍ ﻡﺩﻋ ﺕﺍﺀﺍﺭﺠﺍ ﻲﻓ ﻲﺤﺍﺯﻻﺍ لﻐﺸﻟﺍ
ﻨﺯﻴﺤﻪ ﻤﻥ ﻤﻜﺎﻥ ﻵﺨﺭ ﻟﻨﻔﺘﺭﺽ ﻭﺠﻭﺩ ﻜﻤﻴﺔ ﻤﻥ ﻏﺎﺯ ﺤﺠﻤﻪ
(V)
ﻭﻀﻐﻁﻪ
(P)
ﺔـﻤﻜﺤﻤ ﺔﻨﺍﻭﻁـﺴﺍ ﻲﻓ
ﻴﺘﺤﺭﻙ ﺒﺩﺍﺨﻠﻬﺎ ﻤﻜﺒﺱ ﻤﺴﺎﺤﺔ ﻤﻘﻁﻌﻪ ﺍﻟﻌﺭﻀﻲ
(A)
ﻋﺩﻴﻡ ﺍﻟﺘﺴﺭﺏ ﻭﺍﻻ
ﻭﺓـﻗ ﻪـﻴﻓ ﺭﺜﺅـﺘ ،ﻙﺎﻜﺘﺤ
(F)
ﺘﺯﻴﺤﻪ ﻤﻥ ﺍﻟﺤﺎﻟﺔ
)
1
(
ﺍﻟﻰ ﺍﻟﺤﺎﻟﺔ
)
2
(
ﻜﻤﺎ ﻓﻲ ﺸﻜل
)
3.10
.(
ﻋﻨﺩﻤﺎ ﻨﻔﺘﺭﺽ ﺍﻥ
(P)
ﺎﺀـﻨﺜﺍ ﺔـﺘﺒﺎﺜ ﻰﻘﺒﺘ
ﺘﺤﺭﻙ ﻤﺘﻨﺎﻫﻲ ﺍﻟﺼﻐﺭ ﻟﻠﻤﻜﺒﺱ ﻟﻤﺴﺎﻓﺔ
(dL)
ﻓﺎﻥ
:
dW = F . dL = PA dL = P dV ……….. (3.13)
ﺃﻱ ﺍﻟﻘﻭﺓ
×
ﺍﻟﻤﺴﺎﻓﺔ ﺍﻟﺘﻲ ﺘﻘﻁﻌﻬﺎ ﺍﻟﻘﻭﺓ ﻓﻲ ﻨﻔﺱ ﺇﺘﺠﺎﻫﻬﺎ
.
ﻫﺫﺍ ﺘﻐ
ﺼﻐﺭـﻟﺍ ﻲﻫﺎﻨﺘﻤ ﺭﻴ
.
ﺸﻐلـﻟﺎﻓ
ﺍﻻﺯﺍﺤﻲ ﻨﻭﺠﺩﻩ ﺒﻭﺴﺎﻁﺔ ﺠﻤﻊ ﺍﻟﺘﺯﺍﻴﺩﺍﺕ ﺃﻱ
:
∫ dW = ∫ P dV
……….. (3.14)
W
dis.
= P∆V = area 1234 ………..
(3.15)
P
V
1
4
2
3
P
V
1
4
3
2
P
A
dL
F
| ← L→|
P
A
dL
F
| ← L→|
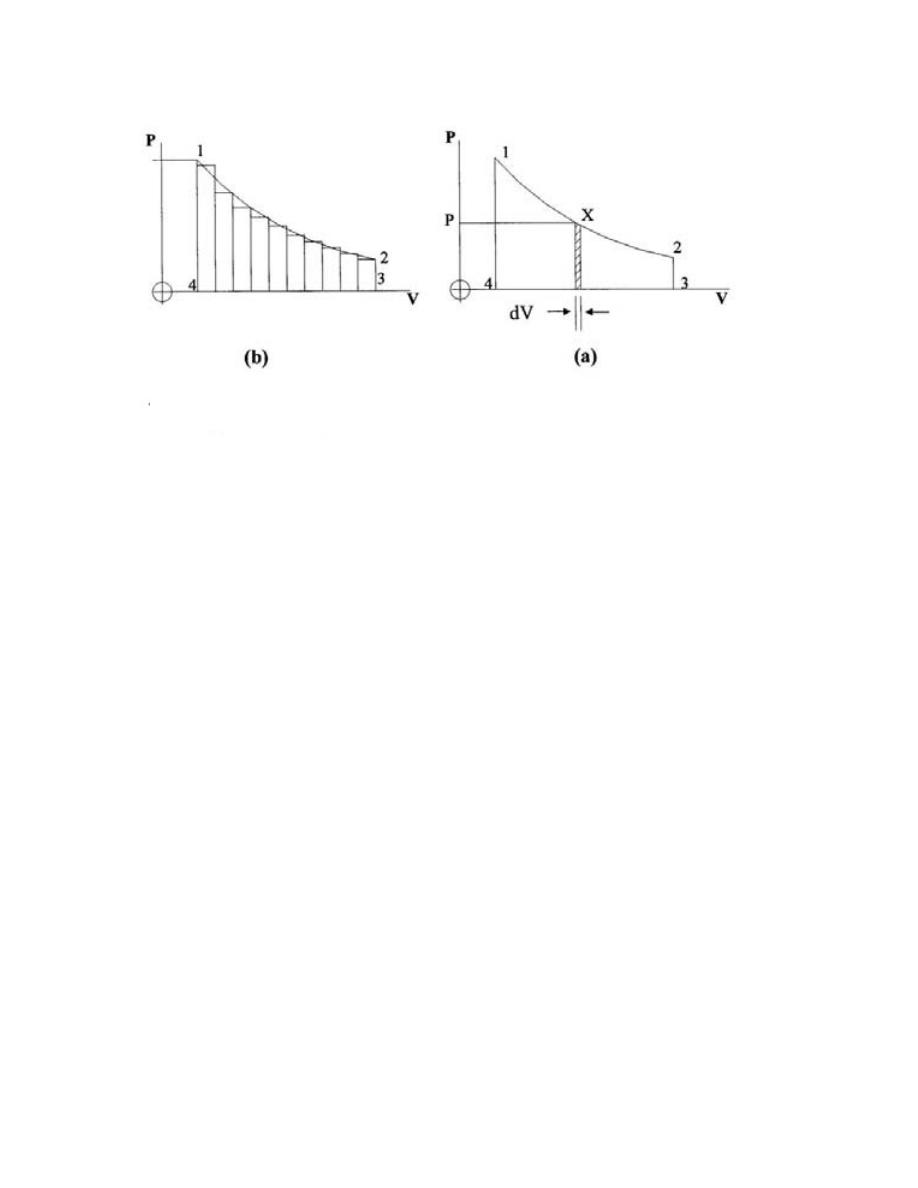
)
59
(
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻷﺠﺭﺍﺀ ﻋﻠﻰ ﺸﻜل ﻤﻨﺤﻨﻲ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
ﻭﻷﻴﺠﺎﺩ ﺍﻟﻤﺴﺎﺤﺔ ﺍﻟﺘﻲ ﺘﻤﺜل ﺍﻟﺸﻐل
ﻨﻘﺴﻡ ﺍﻟﻤﺴﺎﺤﺔ ﺘﺤﺕ ﺍﻟﻤﻨﺤﻨﻲ ﻋﻠﻰ ﻤﺴﺘﻁﻴﻼﺕ ﺼﻐﻴﺭﺓ ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل،لﻘﺘﻨﻤﻟﺍ
(3.11-b)
لـﻜ ﺔﺤﺎﺴﻤ ،
ﻤﺴﺘﻁﻴل ﺘﻤﺜل ﺍﻟﺸﻐل ﺍﻟﺠﺯﺌﻲ ﻭﻤﺠﻤﻭﻉ ﺍﻟﻤﺴﺎﺤﺎﺕ ﺍﻟﺠﺯﺌﻴﺔ ﻴﺴﺎﻭﻱ ﺍﻟﻤﺴﺎﺤﺔ ﺍﻟﻜﻠﻴﺔ ﺍﻟﻤﻜﺎﻓﺌﺔ ﻟﻠﺸﻐل ﺍﻟﻜﻠﻲ
.
ﻓﻠﻭ ﺍﺨﺫﻨﺎ ﻨﻘﻁﺔ
(X)
ﻜﻤﺎ ﻓﻲ ﺍﻟ،ﺩﺩﻤﺘﻟﺍ ﻲﻨﺤﻨﻤ ﻰﻠﻋ
ﺸﻜل
(3.11-a)
ﻲـﺌﺯﺠ ﺭﻴﻐﺘ لﺜﻤﺘ ﺔﻁﻘﻨﻟﺍ ﻩﺫﻫ ﻥﺈﻓ ،
ﻟﺫﻟﻙ ﺴﻴﻜﻭﻥ ﻟﻠﺸﻐل ﺍﻟﺠﺯﺌﻲ،ﹰﺎﺘﺒﺎﺜ ﺩﻌﻴ ﻩﺭﻐﺼﻠﻓ ﻁﻐﻀﻟﺍ ﺎﻤﺍ ،ﻡﺠﺤﻠﻟ ﺭﻴﻐﺼ ﻭﺍ
(dW)
ﺴﺎﺤﺔـﻤﻠﻟ ٍﻭﺎﺴـﻤ
ﺍﻟﺠﺯﺌﻴﺔ ﻟﻠﻤﺴﺘﻁﻴل ﺍﻟﺼﻐﻴﺭ ﺍﻟﺘﻲ ﺘﻤﺜل ﺒﺘﻔﺎﻀل ﻨﺎﻗﺹ
(Inexact Differential)
.
ﺃﻱ ﺍﻥ
:
dW = P dV =
ﺍﻟﻤﺴﺎﺤﺔ ﺍﻟﺠﺯﺌﻴﺔ
ﻭﻤﺠﻤﻭﻉ ﺍﻟﻤﺴﺎﺤﺎﺕ ﺍﻟ
ﺴﺎﺤﺔـﻤﻟﺍ ﺔـﻤﻴﻗ ﻱﺃ ﻲـﻠﻜﻟﺍ لﻐﺸﻠﻟ ﺔﺌﻓﺎﻜﻤﻟﺍ ﺔﻴﻠﻜﻟﺍ ﺴﺎﺤﺔﻤﻟﺍ لﺜﻤﺘ ﺔﻴﺌﺯﺠ
ﺒﺤﺴﺎﺒﺎﺕ ﺍﻟﺘﻜﺎﻤل
.
ﻓﻌﻨﺩ ﺘﻜﺎﻤل ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﻴﺼﺒﺢ
:
∴W = P ∆ V12 = area 1234
……… (3.17)
)
3.5.3
(
-
ﺍﻟﺸﻐل ﺍﻟﺼﺎﻓﻲ
Net Work
ﺇﻥ ﺤﺎﻟﺔ ﺍﻻﻨﻀﻐﺎﻁ ﻫﻲ ﻋﻜﺱ ﺤﺎﻟﺔ ﺍﻟﺘﻤﺩﺩ ﻤﻥ ﺤﻴﺙ ﺍﻻﺘﺠﺎﻩ ﻋﻠﻰ ﻤﺨﻁ
ﻁ
(P-V)
.
ﻭﺍﻥ ﺍﻟﻤﻨﺎﻗﺸﺔ
ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﺘﻨﻁﺒﻕ ﻋﻠﻰ ﺍﻟﺤﺎﻟﺘﻴﻥ ﻤﺎﻋﺩﺍ ﺍﻋﺘﺒﺎﺭ ﻤﺴﺎﺤﺔ ﺍﻟﺘﻤﺩﺩ ﻜﻘﻴﻤﺔ ﻤﻭﺠﺒﺔ
ﺸﻜل
)
3.11
(
-
ﺍﻟﺸﻐل
ﻫﻭ ﻤﺠﻤﻭﻉ ﺍﻟﻤﺴﺎﺤﺎﺕ ﺍﻟﺠﺯﺌﻴﺔ
∫
∫
∑
=
=
)
16
.
3
......(
..........
dV
P
dV
P
dW
2
1
V
V
(3.18)
.....
dL
)
F
A
P
Friction
(
W
W
W
2
1
crank
atm
crank
atm
Friction
∫
+
+
=
+
+
=
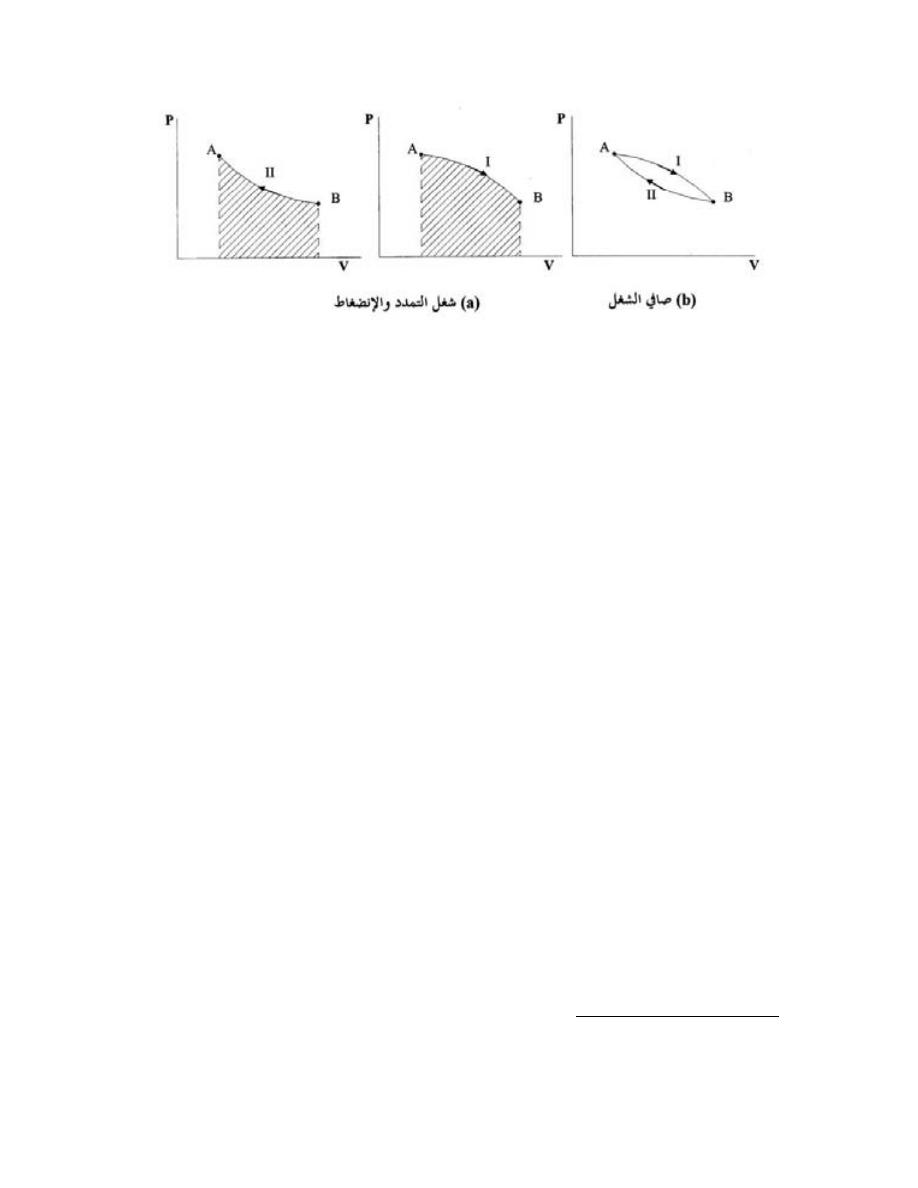
)
60
(
ﻭﻤﺴﺎﺤﺔ ﺍﻻﻨﻀﻐﺎﻁ ﻜﻘﻴﻤﺔ ﺴﺎﻟﺒﺔ
.
ﻓﺎﻟﺸﻜل
(3.12-a)
ﻴﺒﻴﻥ ﺤﺎﻟﺔ ﺍﻟﺘﻤﺩﺩ ﻤﻥ
(A)
ﺍﻟﻰ
(B)
ﺴﺎﺭـﻤﻟﺍ ﺭـﺒﻋ
(I)
.
ﻭﺍﻻﻨﻀﻐﺎﻁ ﻤﻥ
(B)
ﺍﻟﻰ
(A)
ﻋﺒﺭ ﺍﻟﻤﺴﺎﺭ
(II)
.
ﻲـﻓ ﺭﻴﻐﺘﻟﺍ ﻥﺍ ﻡﻏﺭﺒﻓ
ﻭﺍﺹـﺨﻟﺍ
)
P
∆
،
∆V
(
ﻭﻫﺫﺍ ﻤﻭﻀﺢ ﺒﺎﻟﻤﺴﺎﺤﺔ ﺍﻟﻤﻅﻠﻠﺔ،ﻑﻠﺘﺨﻤ لﻐﺸﻟﺍ ﻥﺍ ﻻﺇ ،ﻪﺒﺎﺸﺘﻤ ﻥﻴﺭﺎﺴﻤﻟﺍ لﻼﺨ
.
ﺔـﻘﻠﻐﻤﻟﺍ ﺔﺤﺎﺴـﻤﻟﺍ ﺎﻤﺍ
(A
→I→B→II⎯A)
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل،ﺓﺭﻭﺩﻟﺍ ﻲﻓ ﻲﻓﺎﺼﻟﺍ ﻭﺍ ﺯﺠﻨﻤﻟﺍ لﻐﺸﻟﺍ لﺜﻤﺘﻓ
(3.12-b)
ﺍﻟﺫﻱ،
ﻴﻭﻀﺢ ﺍﻥ ﺍﻟﻨﻅﺎﻡ ﻴﻤﺭ ﺒﺩﻭﺭﻩ
.
ـﻭﻴﺭﻤﺯ ﻟﺘﻜﺎﻤل ﺍﻟﻤﻘﺩﺍﺭ ﺒ
(
∫ )
ﺇﺫ ﺘﻌﻭﺩ ﺨﻭﺍ،
ﺎـﻬﺘﻟﺎﺤ ﻰـﻟﺍ ﻡﺎـﻅﻨﻟﺍ ﺹ
ﺃﻱ،ﺔﻴﻠﺼﻻﺍ
ﺍﻥ
)
dT=0
∫
،
dV=0
∫
،
dP=0
∫
.(
ﻭﻟﻜﻥ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ ﺍﻟﺫﻱ ﻴﻤﺜل ﺍﻟﻤﺴﺎﺤﺔ ﺍﻟﻤﻐﻠﻘﺔ
ﻓﻲ ﺸﻜل
(3.12-b)
ﺃﻱ ﺍﻥ،ﹰﺍﺭﻔﺼ ﻱﻭﺎﺴﻴ ﻻ
(
∫dW≠0)
.
ﻴﻤﻜﻥ ﺍﻟﻘﻭل ﺍﻥ
ﻭل ﺍﻥ ﻷﻥـﻘﻟﺍ ﺄـﻁﺨﻟﺍ ﻥـﻤ ﻥﻜﻟﻭ،
ﺍﻟﺸﻐل ﻻ ﻴﻅﻬ
ﺎﻟﺘﻴﻥـﺤﻟﺍ ﻥﻴـﺒ ﺭـﻬﻅﻴ ﺎﻤﻨﺇﻭ ،ﻡﺎﻅﻨﻟﺍ ﺹﺍﻭﺨ ﻲﻓ ﺎﻤﻜ ،ﺔﻴﺌﺎﻬﻨﻟﺍﻭ ﺔﻴﺌﺍﺩﺘﺒﻻﺍ ﺎﻟﺘﻴﻥﺤﻟﺍ ﺩﻨﻋ ﺭ
ﻟﺫﺍ ﻓﺎﻟﺸﻐل،ﺭﺎﺴﻤﻟﺍ لﻼﺨ ﻱﺃ ،ﺔﻴﺌﺎﻬﻨﻟﺍﻭ ﺔﻴﺌﺍﺩﺘﺒﻻﺍ
)
ﺍﻭ ﺍﻟﺤﺭﺍﺭﺓ
(
ﺎﻡـﺘ ﺭـﻴﻏ لﻀﺎﻔﺘﺒ لﺜﻤﺘ ﺭﺎﺴﻤﻠﻟ ﺔﻟﺍﺩ
•
*
،
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∫
2
1
12
)
orW
(
W
dW
ﺍﻤﺎ ﺨﻭﺍﺹ ﺍﻟﻨﻅﺎﻡ ﻓﻬﻤﺎ ﺩﺍﻟﺔ ﺍ
ﺎﻡـﺘ لﻀﺎﻔﺘﺒ لﺜﻤﺘ ﺔﻟﺎﺤﻟ
ﻤﺜﻼﹰ
)
dP
،
dV
،
dT
،
…
.
ﺍﻟﺦ
.(
ﺔـﻁﻘﻨﻟﺍ ﻥﻤ لﻘﺘﻨﻴ ﺔﺠﺍﺭﺩ ﺏﻜﺍﺭ ﺭﻭﺼﺘﻨ ﺎﻤﺩﻨﻋ ﺎﻬﻤﻬﻔﻨ ﻥﺍ ﻊﻴﻁﺘﺴﻨ ﺔﺸﻗﺎﻨﻤﻟﺍ ﻩﺫﻫ
)
1
(
ﺎﻉـﻔﺘﺭﺎﺒ
(Z
1
,m)
ﻓﻭﻕ ﺴﻁﺢ ﺍﻟﺒﺤﺭ ﺍﻟﻰ ﺍﻟﻨﻘﻁﺔ
)
2
(
ﻋﻠﻰ ﺭﺍﺒﻴﺔ ﺍﺭﺘﻔﺎﻋﻬﺎ
(Z
2,
m)
ﻓﻭﻕ ﺴﻁﺢ ﺍﻟﺒﺤﺭ
.
ﻓﺈﺫﺍ ﺍﻋﺘﺒﺭﻨﺎ
ﻴﻤﻜﻥ ﺇﻋﺘ،ﻡﺎﻅﻨﻟﺍ ﻪﻨﺄﺒ ﺔﺠﺍﺭﺩﻟﺍ ﺏﻜﺍﺭ
ﻲـﻓ ﺭـﻴﻐﺘﻟﺍ ﻥﻷ ﻡﺎـﻅﻨﻠﻟ ﺔﻴﺼﺎﺨ ﺭﺤﺒﻟﺍ ﺢﻁﺴ ﻕﻭﻓ ﻪﻋﺎﻔﺘﺭﺇ ﺭﺎﺒ
ﺍﻻﺭﺘﻔﺎﻉ
(Z
2
-Z
1
)
ﺃﻱ ﺍﻻﺠﺭﺍﺀ ﻤﻥ،ﺔﺠﺍﺭﺩﻟﺍ ﺏﻜﺍﺭ ﻪﻜﻠﺴﻴ ﻱﺫﻟﺍ ﻕﻴﺭﻁﻟﺍ ﻥﻋ لﻘﺘﺴﻤ
)
1
(
ﻰـﻟﺍ
)
2
.(
ﺇﻥ
•
dW,dQ
ﻤﺸﺘﻘﺘﻴﻴﻥ ﻏﻴﺭ ﺼﺤﻴﺤﺘﻴﻥ
)
ﺘﻔﺎﻀل ﻏﻴﺭ ﺘﺎﻡ ﺍﻭ ﻨﺎﻗﺹ
(
⎠
⎞
⎜⎜
⎝
⎛
−
=
∆
=
∫
2
1
1
2
12
V
V
V
dV
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
∆
=
∫
2
1
1
2
12
W
W
W
dW
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
∫
2
1
12
orQ)
(
Q
dQ
ﺸﻜل
)
3.12
(
-
ﺍﻟﺸﻐل ﺍﻟﺼﺎﻓﻲ ﻋﻨﺩ ﻤﺭﻭﺭ ﺍﻟﻨﻅﺎﻡ ﺒﺩﻭﺭﻩ
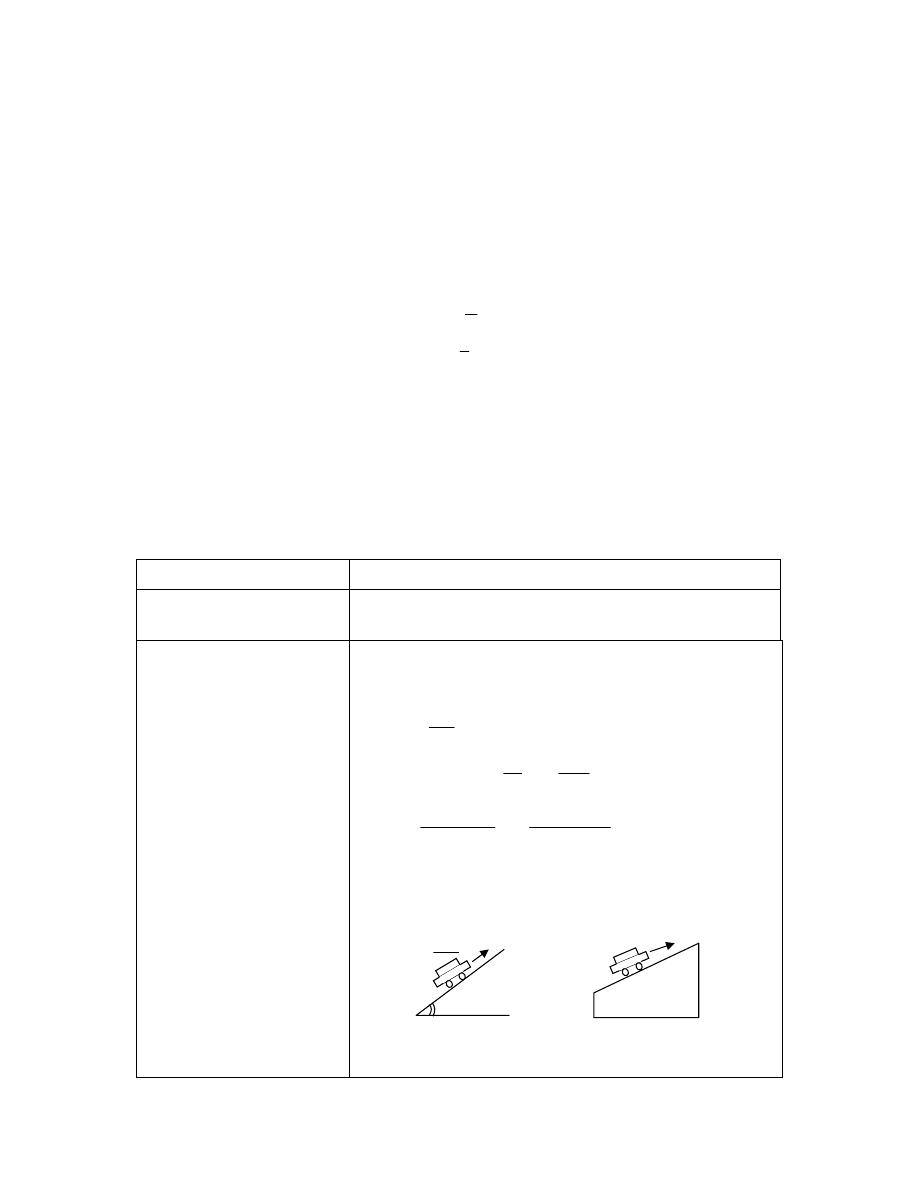
)
61
(
KW
147
s
/
m
10
Kg
/
KJ
h
/
Km
6
.
3
s
/
m
30
sin
h
Km
90
s
m
9.81
1200Kg
C
.
mg
t
Z
mg
W
Z
mg
mgdz
FdZ
W
2
2
3
2
vertical
g
2
1
2
1
g
=
⎟
⎠
⎞
⎜
⎝
⎛
×
⎟
⎠
⎞
⎜
⎝
⎛
×
×
×
×
=
=
∆
∆
=
∆
=
=
=
•
•
∑
∑
ﺍﻟﺸﻐل ﺍﻟﺫﻱ
ﻴ
ﻕـﻴﺭﻁﻟﺍ ﺭﺼـﻗ ﻭﺍ لﻭﻁ ﻰﻠﻋ ﺩﻤﺘﻌﻴ ﻪﻨﻻ ﺀﺍﺭﺠﻻﺍ ﻥﻋ لﻘﺘﺴﻤ ﺭﻴﻏ ﺔﺠﺍﺭﺩﻟﺍ ﺏﻜﺍﺭ ﻪﺒ ﻡﻭﻘ
ﻭﻜﺫﻟﻙ ﻓﻴﻤﺎ ﺇﺫﺍ ﻜﺎﻨﺕ ﺍﻟﺭﻴﺎﺡ ﻤﺭ
ﺍﻓﻘﺔ ﻟﻪ ﺍﻭ ﻤﻌﺎﻜﺴﺔ
.
ﺫﻩـﻫ ﻕﺒﻁﻨﺘﻭ ﺔﻴﺼﺎﺨﺒ ﺱﻴﻟ ﻪﻨﺍ ﻻﺍ ﺱﺎﻴﻘﻠﻟ ﺔﻠﺒﺎﻗ ﺔﻴﻤﻜ لﻭﺫﺒﻤﻟﺍ لﻐﺸﻟﺍ ﻥﺍ ﻥﻤ ﻡﻏﺭﻟﺎﺒ ﻪﻨﺍ ﻯﺭﻨ ﻙﻟﺫ ﻥﻤﻭ
ﺍﻟﺤﺎﻟﺔ ﻋﻠﻰ ﺍﻟﺤﺭﺍﺭﺓ ﺒﻭﺼﻔﻬﺎ ﻁﺎﻗﺔ ﻤﻨﺘﻘﻠﺔ
.
)
3.5.4
(
-
ﺍﻟﻘﺩﺭﺓ ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻴﺔ
Mechanical Power
ﺃﻱ ﺒﻭﺤﺩﺍﺕ ﺍﻟﻭﺍﻁ،لﻐﺸ ﺯﺎﺠﻨﻷ ﻲﻨﻤﺯﻟﺍ لﺩﻌﻤﻟﺍ ﻲﻫ
(W)
ﺍﻭ
(KW)
ﺍﻭ
(MW)
.
ﺍﻟﻭﺍﻁ ﻫﻭ ﺸﻐل
ﻤ
ﻨﺠﺯ
(J)
ﻟﻜل ﺜﺎﻨﻴﺔ
(s)
ﺃﻱ،
.
ﺩﺭﺓـﻘﻟﺎﺒ ﺓﺎﻤﺴﻤﻟﺍ ﺔﻤﻴﺩﻘﻟﺍ ﺓﺩﺤﻭﻠﻟ لﻴﺩﺒ ﻭﻫﻭ
ﺍﻟﺤﺼﺎﻨﻴﺔ
(HP)
.
ﺍﻥ ﺍﻟﺘﺴﻤﻴﺔ ﻭﺍﻁ ﻨﺴﺒﺔ ﺍﻟﻰ ﺠﻴﻤﺱ ﻭﺍﻁ
)
1736
-
1814
(
ﻤﺨﺘﺭﻉ ﺍﻟﻤﺎﻜﻨﺔ ﺍﻟﺒﺨﺎﺭﻴﺔ
.
3.5.5
ﺍﺸﻜﺎل ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﻠﻨﻴﻜﻲ
Mechanical Forms of Work
ﻴﻌﺩ ﺍ
ﻊـﻤﻭ ،ﺔﻴﺭﺍﺭﺤﻟﺍ ﺎﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜﻟﺍ ﺔﺴﺍﺭﺩ ﻲﻓ ﻲﻜﻴﻨﺎﻜﻴﻤﻟﺍ لﻐﺸﻟﺍ ﻉﺍﻭﻨﺍ ﻡﻫﺍ ﻥﻤ ﻲﺤﺍﺯﻻﺍ لﻐﺸﻟ
ﺫﻟﻙ ﻻﺒﺩ ﻤﻥ ﺍﻥ ﻨﺘﻌﺭﻑ
ﻋﻠﻰ
ﺒﻘﻴﺔ ﺍﺸﻜﺎل ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ ﻭﺍﻟﻤﻭﻀﺤﺔ ﻓﻲ ﺠﺩﻭل
)
3.1
.(
ﺠﺩﻭل
)
3.1
(
ﺍﺸﻜﺎل ﺍﻟﺸﻐل ﺍﻟﻤﻴﻜﺎﻨﻴﻜﻲ
Work
ﺍﻟﻤﻌﺎﺩﻻﺕ ﻭﺍﻻﻤﺜﻠﺔ
1- Displacement W.
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
W
dis.
= ∫ FdL = ∫ PadL = ∫ PdV = P∆V
12
2- Gravitational W.
ﺸﻐل ﺍﻟﺠﺎﺫﺒﻴﺔ
(
)
t
w
P
=
(
)
s
J
W
=
Z
2
Z=0
Z
2
Z
1
Reference Level
30
o
Z
1
m=1200Kg
C=90
h
Km
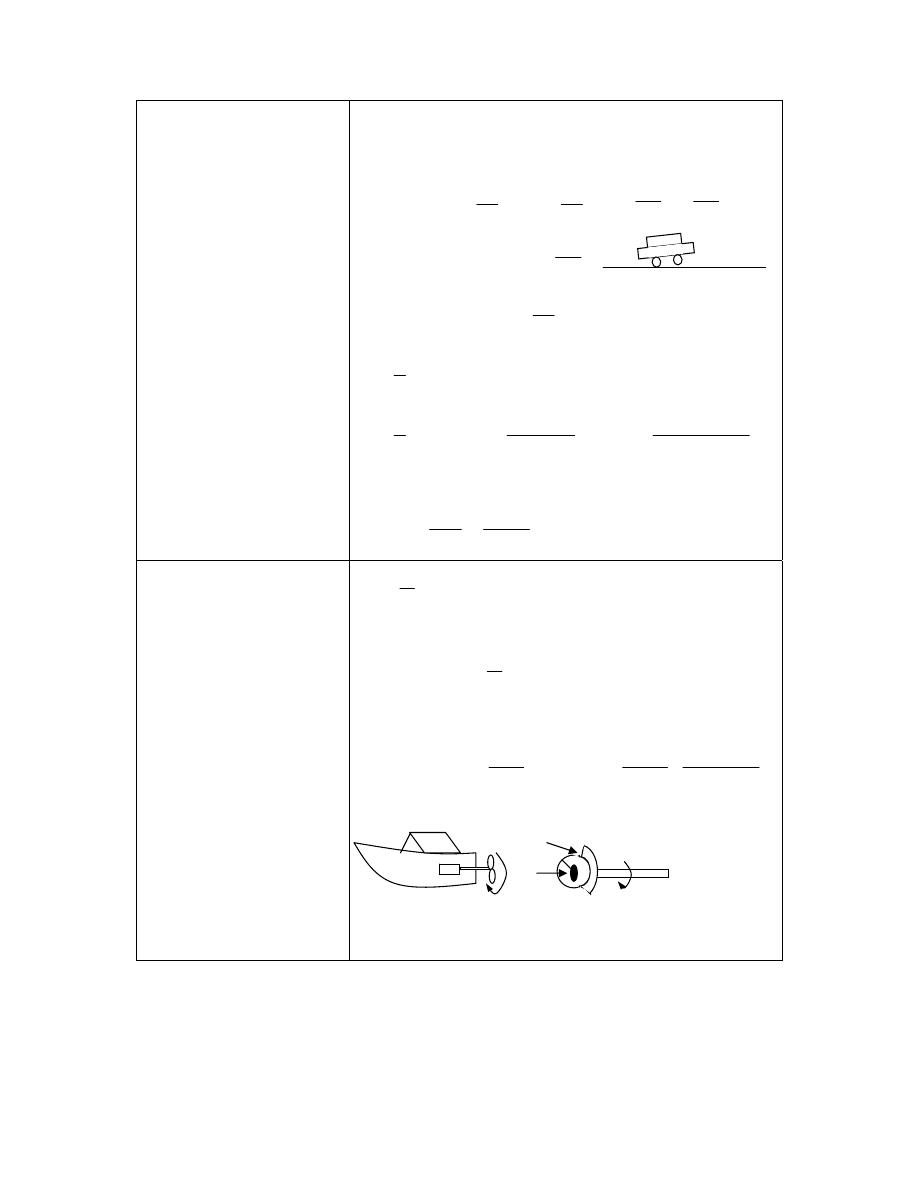
)
62
(
3- Accelerational W.
ﺸﻐل ﺍﻟﺘﻌﺠﻴل
ﺇﺫﺍ ﻜﺎﻥ
)
C
(
،ﺍﻟﺴﺭﻋﺔ
(L)
،ﺴﺎﻓﺔـﻤﻟﺍ ﻭﺍ ﺔـﺤﺍﺯﻻﺍ
(t)
،ﺯﻤﻥـﻟﺍ
ﻓﺴﻴﻜﻭﻥ
:
4- Shaft W.
ﺸﻐل ﺍﻟﻌﻤﻭﺩ
kW
1
.
11
s
20
2
.
222
t
Wa
W
kJ
2
.
222
s
/
m
1000
kg
/
kJ
0
3600
80000m
.
kg
900
2
1
)
c
c
(
m
2
1
cdc
m
(Cdt)
.
)
dt
dc
m
(
FdL
W
)
dt
dL
c
(
Cdt
dL
)
dt
dc
a
(
dt
dc
m
ma
F
a
2
2
2
2
2
1
2
2
2
1
2
1
2
1
a
=
=
∆
=
=
⎟
⎠
⎞
⎜
⎝
⎛
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
×
=
−
=
=
=
=
=
=
=
=
=
•
∫
∫
∫
Q
Q
kW
83.7
)
m
.
N
1000
kJ
1
)(
s
60
min
1
)(
m
.
N
200
)(
min
1
(4000
2
NT
2
W
(kJ)
NT
2
rN)
2
(
r
T
L
F
W
rN
2
L
F.r)
T
(
r
T
F
sh.
sh.
=
π
=
=
π
=
π
=
π
=
×
=
π
=
=
=
•
Q
∆t=208
M=900kg
0
h
Km →80
h
Km
N=4000rpm
T=200 N.M
r
F
W=2
πNT
sh.
N

)
63
(
5- Spring W.
ﺸﻐل ﺍﻟﻨﺎﺒﺽ
K … Spring Constant
X … Displacement
F =K . X
)
3.6
(
-
ﺍﻟﻤﻔﻬﻭﻡ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻲ ﻟﻠﺤﺭﺍﺭﺓ
Thermodynamic Concept of Heat
ﻫﻲ ﻨﻭﻉ ﻤﻥ ﺍﻨﻭﺍﻉ ﺍﻟﻁﺎﻗﺔ ﺘﻨﺘﻘل ﻤﻥ ﺠﺴﻡ ﺍﻟﻰ ﺍﺨﺭ ﺍﻭ ﺘﺘﺩﻓﻕ ﻤﻥ ﺍﻟﺠﺯﻴﺌ
ﺎﺕ
ﻰـﻟﺍ ﺎﻁﺎﺸـﻨ ﺭﺜﻜﻷﺍ
ﺍﻟﺠﺯﻴﺌﺎﺕ ﺍﻻﻗل ﻨﺸﺎﻁﺎﹰ ﺒﺴﺒﺏ ﺍﻟﻔﺭﻕ ﺒﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ
.
ﻴﺘﻭﻗﻑ ﺍﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﻋﻨﺩﻤ
ﺎﺭﺩـﺒ ﺭـﺨﻵﺍﻭ ﻥﺨﺎﺴ ﺎﻤﻫﺩﺤﺃ ﻥﺎﻤﺴﺠ ﺱﻤﻼﺘ ﺍﺫﺄﻓ ،ﺀﺍﺭﺠﻹﺍ ﻑﻗﻭﺘﻴ ﺎ
ﺔـﻟﺎﺤ لﺼﺤﺘ ﻰﺘﺤ لﺎﻘﺘﻨﻻﺍ ﺍﺫﻫ ﺭﻤﺘﺴﻴﻭ ﺩﻭﺩﺤﻟﺍ ﺩﺒﻋ ﺎﺭﺩﺒﻟﺍ ﻡﺴﺠﻟﺍ ﻰﻟﺍ ﻥﺨﺎﺴﻟﺍ ﻡﺴﺠﻟﺍ ﻥﻤ ﺓﺍﺭﺤﻟﺍ لﻘﺘﻨﺘﺴ
ﺍﻻﺘﺯﺍﻥ ﺍﻟﺤﺭﺍﺭﻱ ﺃﻱ ﺘﺴﺎﻭﻱ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺍﻟﺠﺴﻤﻴﻥ ﻭﺒﺫﻟﻙ ﻴﺘﻭﻗﻑ ﺍﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﺒﺘﻭﻗﻑ ﺍﻻﺠﺭﺍﺀ
.
ﺘﻨﺘﺞ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ
ﻲـﻓ ﺕﺎـﺌﻴﺯﺠﻟﺍ ﻩﺫـﻫ ﻥﺃ ﺫﺍ ،ﺓﺩﺎﻤﻠﻟ ﺔﻨﻭﻜﻤﻟﺍ ﺓﺭﻴﻐﺼﻟﺍ ﺕﺎﺌﻴﺯﺠﻟﺍ ﺔﻜﺭﺤ ﻥﻤ
ﺏﻌﺼـﺘﻭ ،ﺔﺒﻠﺼ ﻡﺍ ﺔﻠﺌﺎﺴ ﻡﺍ ﺔﻴﺯﺎﻏ ﺓﺩﺎﻤﻟﺍ ﺕﻨﺎﻜ ﺀﺍﻭﺴ ،ﺓﺩﺎﻤﻟﺍ لﺨﺍﺩ ﺕﺎﻫﺎﺠﺘﻻﺍ ﻑﻠﺘﺨﻤ ﻲﻓ ﺔﻤﺌﺍﺩ ﺔﻜﺭﺤ
ﺓﺭﺍﺭـﺤ ﻡﺴﺠ ﺏﺴﺘﻜﺍ ﺍﺫﺍﻭ ﻑﻭﺭﻌﻤ ﺭﻬﺠﻤ ﻕﺩﺍ ﻙﻟﺫ ﻲﻓ ﻡﺩﺨﺘﺴﺍ ﻭﻟﻭ ﻰﺘﺤ ﺕﺎﺌﻴﺯﺠﻟﺍ ﻩﺫﻫ ﺔﻜﺭﺤ ﺔﻅﺤﻼﻤ
ﻤﺎ ﻓﺄﻥ ﻫﺫﺍ ﻴﻌﻨﻲ ﺘﺯﻭ
ﻓﺘﺯﺩﺍﺩ ﺘﺒﻌﺎ ﻟﺫﻟﻙ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﻭﻋﻠﻰ،ﺎﻬﺘﻋﺭﺴ ﺓﺩﺎﻴﺯ ﻰﻠﻋ لﻤﻌﺘ ﺔﻗﺎﻁﺒ ﻪﺘﺎﺌﻴﺯﺠ ﺩ
ﻙﺭـﺤﺘ ﺔﻋﺭﺴ ﺓﺩﺎﻴﺯﻟ ﺔﻨﻭﺨﺴ ﺩﺍﺩﺯﺘ ﺎﻬﻨﺎﻓ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻤ ﺔﻴﻤﻜ ﻙﺭﺤﻤ ﺔﻨﺍﻭﻁﺴﺍ ﺕﺎﻴﻭﺘﺤﻤ ﺕﺒﺴﺘﻜﺍ ﺍﺫﺍ ﺍﺫﻫ
ﻰـﻨﻌﻤﺒﻭ ،ﺎـﻬﺘﺭﺍﺭﺤ ﺔﺠﺭﺩ ﻲﻓ ﺎﻋﺎﻔﺘﺭﺍ لﺠﺴﻴ ﻪﻨﺈﻓ ﺎﻬﻨﻤ ﺍﺭﺍﺭﺤﻤ ﺎﻨﺒﺭﻗ ﺍﺫﺇ ﺱﺎﺴﻻﺍ ﺍﺫﻫ ﻰﻠﻋﻭ ،ﺎﻬﺘﺎﺌﻴﺯﺠ
ﺁﺨﺭ ﻓﺄ
ﻥ ﺍﺭﺘﻔﺎﻉ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺠﺴﻡ ﻤﺎ ﻴﻌﻨﻲ ﺍﺯﺩﻴﺎﺩ ﺴﺭﻋﺔ ﺘﺤﺭﻙ ﺠﺯﻴﺌﺎﺘﻪ
.
ﻜلـﺸ ﺫـﺨﺘﺘ ﺔﻌﺌﺎﻤ ﺎﻬﻨﺃ ﺕﺍﺯﺎﻐﻟﺍ ﺹﺍﻭﺨ ﻥﻤ ﻥﺎﻓ ﺔﻴﺠﺭﺎﺨﻟﺍ ﺎﻬﻟﺎﻜﺸﺎﺒ ﺔﺒﻠﺼﻟﺍ ﺩﺍﻭﻤﻟﺍ ﻅﻔﺘﺤﺘ ﺎﻤﻨﻴﺒﻭ
ﺔـﻨﻴﻌﻤ ﺓﻭﻘﺒ ﺔﻴﻋﻭﻻﺍ ﻙﻠﺘ ﻥﺍﺭﺩﺠ ﺔﻴﻟﺎﻋ ﺔﻋﺭﺴﺒ ﺔﻜﺭﺤﻟﺍ ﺔﻤﺌﺍﺩﻟﺍ ﺎﻬﺘﺎﺌﻴﺯﺠ ﻕﺭﻁﺘﻭ ،ﺎﻬﻴﻭﺘﺤﺘ ﻲﺘﻟﺍ ﺔﻴﻋﻭﻻﺍ
ﻴﻤﻜﻥ ﻗﻴﺎﺴﻬﺎ ﻭﺘﺴﻤﻰ ﻀﻐ
ﻁ ﺍﻟﻐﺎﺯ
.
ـﻪ ﻓﺘﺭﺘﻔـﺘﺎﺌﻴﺯﺠ ﺔﻋﺭﺴ ﺕﺍﺩﺯﺍ ﺓﺭﺍﺭﺤ ﺯﺎﻐﻟﺍ ﺏﺴﺘﻜﺍ ﺍﺫﺍﻭ
ﺔـﺠﺭﺩ ﻊ
ﻓﺎﺫﺍ ﻜﺎﻥ ﺍﻟﺤﻴﺯ ﺍ،ﻪﺘﺭﺍﺭﺤ
ﻓﺎﻥ ﻫﺫﻩ ﺍﻟﺤﺭﺍﺭﺓ ﺘﺯﻴﺩ ﻤﻥ ﺸﺩﺓ ﻁﺭﻕ،ﻼﺜﻤ ﻕﻠﻐﻤ ﺀﺎﻋﻭﻜ ،ﺍﺩﻭﺩﺤﻤ ﻪﻴﻭﺘﺤﻴ ﻱﺫﻟ
ﺠﺯﻴﺌﺎﺕ ﺍﻟﻐﺎﺯ ﻋﻠﻰ ﺠﺩﺭﺍﻥ ﺍﻟﻭﻋ
ﺎ
ﺀ ﻨﺘﻴﺠﺔ ﻻﺯﺩﻴﺎﺩ ﺴﺭﻋﺔ ﺘﺤﺭﻜﺎﺘﻬﺎ ﻓﻴﺯﺩﺍﺩ ﻟﺫﻟﻙ ﻀﻐﻁ ﺍﻟﻐﺎﺯ
.
ﻭﻫﺫﺍ ﻫﻭ ﻤﺎﻴﺤﺩﺙ ﻋﻨﺩ ﺍ
ﻻﻥ ﺍﺤﺘﺭﺍﻕ ﺍﻟﻭﻗﻭﺩ ﻴﻌﻁﻲ ﻜﻤﻴﺔ،ﹰﻼﺜﻤ ﻙﺭﺤﻤ ﺔﻨﺍﻭﻁﺴﺍ ﻲﻓ ﺩﻭﻗﻭﻟﺍ ﻕﺍﺭﺘﺤ
ﺔـﺠﺭﺩ ﻊﻔﺘﺭﺘ ﻙﻟﺫﺒﻭ ،ﻕﺍﺭﺘﺤﻻﺍ ﺔﻓﺭﻏ ﻰﻤﺴﻤﻟﺍ ﺩﻭﺩﺤﻤﻟﺍ ﺯﻴﺤﻟﺍ ﻲﻓ ٍﺫﺌﻨﻴﺤ ﺓﺩﻭﺠﻭﻤﻟﺍ ﺕﺍﺯﺎﻐﻠﻟ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻤ
ﺤﺭﺍﺭﺓ ﻫﺫﻩ ﺍﻟﻐﺎﺯﺍﺕ ﻭﻴﺯﺩﺍﺩ ﻀﻐﻁﻬﺎ ﺍﻟﺫﻱ ﻴﺅﺜﺭ ﺒﺩﻭﺭﻩ ﻓﻲ ﺍﻟﺠﺩﺭﺍﻥ ﺍﻟﻤﺤﻴﻁﺔ ﺒﻪ
.
ﺴﻁﺢـﻟﺍ ﻥﺎـﻜ ﺎـﻤﻟﻭ
⎟
⎠
⎞
⎜
⎝
⎛
m
KN
)
(
2
1
2
1
2
2
.
X
X
k
W
sp
=
Rest Position
X
1
=1mm
F
1
=300N
F
2
=600N
X
2
=2mm
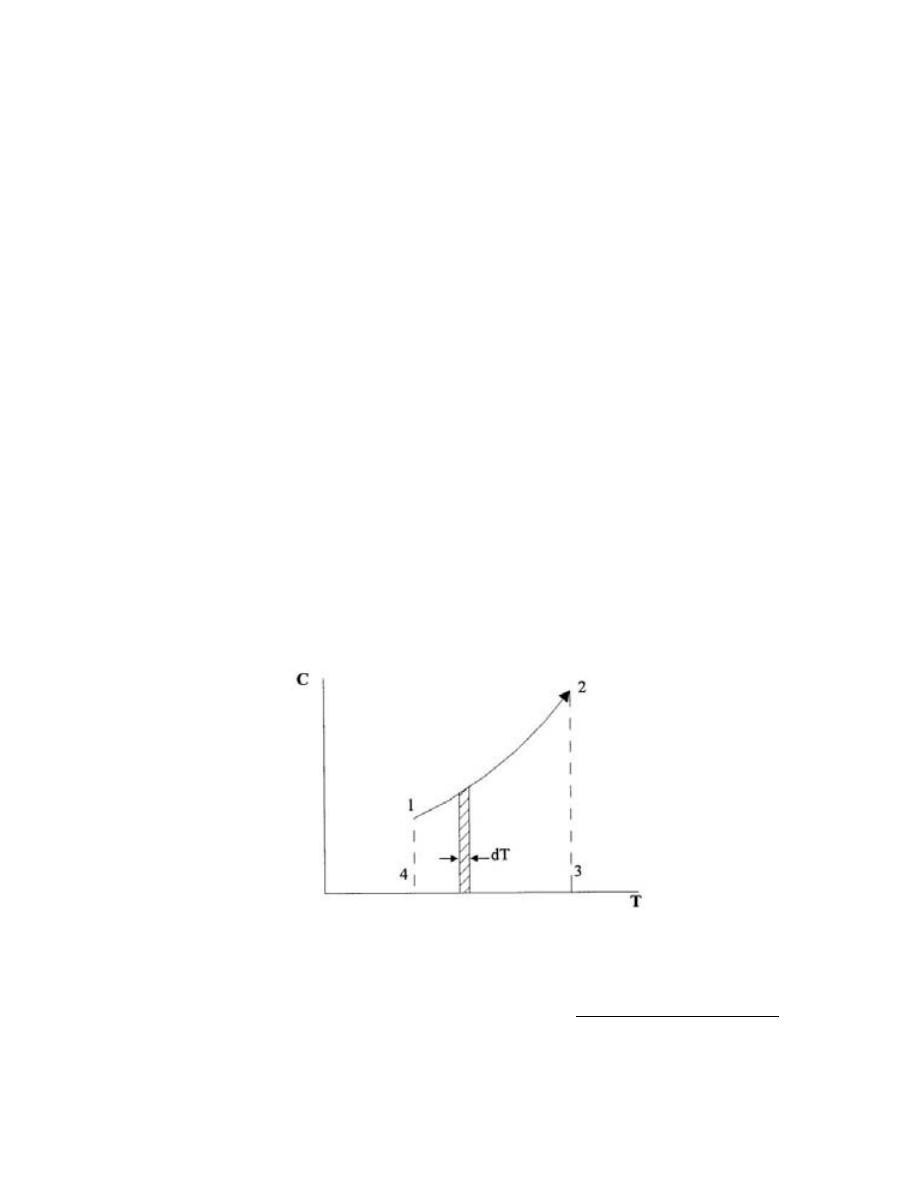
)
64
(
ﺍﻟﻌﻠﻭﻱ ﻟﻠﻤﻜﺒﺱ ﻫﻭ
ﻜﻤﺎ ﺍﻨﻪ ﺍﻟﻭﺤﻴﺩ ﺍﻟﻘﺎﺒل ﻟﻠﺘﺤﺭﻙ ﻓﺎﻨﻪ ﻴﻨﺩﻓﻊ ﺍﻟﻰ ﺍﻻﺴﻔل ﻤﻨﺘﺠﺎ ﺸﻐﻼﹰ،ﻥﺍﺭﺩﺠﻟﺍ ﻙﻠﺘ ﺩﺤﺃ
ﻤﻴﻜﺎﻨﻴﻜﻴﺎ
.
ﺍﻥ ﺍﻟﺤﺭﺍﺭﺓ
ﻟﻴﺴﺕ
ﺨﺎﺼﻴ
ﺔ
ﻻﻨﻬﺎ ﻟﻴﺴﺕ ﻤﺎﺩﺓ ﻴﻤﻜﻥ ﺍﻥ ﺘﺨﺯﻥ ﻜﻤﺎ ﺘﺼﻭﺭ ﺍﻟﺒﺎﺤﺜﻭﻥ ﺍﻻﻭﺍﺌل،ﻡﺎﻅﻨﻠﻟ
.
ﻭﺤﺩﺍﺘﻬﺎ ﻨﻔﺱ ﻭﺤﺩﺍﺕ ﺍﻟﺸﻐل ﻭﻫﻲ ﺍﻟﺠﻭل
)J
(
ﺸﻐﻠﻭﺭﻤﺯﻫﺎـﻟﺍ ﺓﺭﺎﺸﺍ ﺱﻜﻋ ﺎﻬﺘﺭﺎﺸﺍﻭ ﻪﺘﺎﻘﺘﺸﻤﻭ
)
Q
(
ﻭﺍﺫﺍ
ﻜﺎﻨﺕ ﻟﻜل
)
kg
1
(
ﻤﻥ ﺍﻟﻤﺎﺩﺓ ﻓﺭﻤﺯﻫﺎ
)
q
.(
ﺎﺭـﻴﺘﻟﺍ ﺭﻭﺭـﻤ ،ﻲﻜﻴﻨﺎـﻜﻴﻤﻟﺍ ﻙﺎـﻜﺘﺤﻻﺍ ،ﺭﺸﺎﺒﻤﻟﺍ ﻥﻴﺨﺴﺘﻟﺍ ﺔﻁﺴﺍﻭﺒ ﺓﺭﺍﺭﺤ ﻰﻠﻋ ﻡﺎﻅﻨﻟﺍ لﺼﺤﻴ
ﺍﻟﺘﻔﺎﻋل ﺍﻟﻜﻤﻴﺎﻭﻱ،ﻲﺌﺎﺒﺭﻬﻜﻟﺍ
.
)
3.7
(
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ
The Specific Heat Capacity
ﻫﻲ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﺭﻓﻊ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﻜﻴﻠﻭ ﻏﺭﺍﻡ
ﻭﺍﺤﺩ
(1kg)
ﻤﻥ ﺍﻟﻤﺎﺩﺓ ﺩﺭﺠﺔ ﻭﺍﺤﺩﺓ
∗
.
ﺭﻤﺯﻫﺎ
(C)
ﻭﺤﺩﺍﺘﻬﺎ،
(kJ/kg.K)
.
ﺃﻱ ﺘﺨﻀﻊ ﻟﻠﻌﻼﻗﺔ،ﻁﻘﻓ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻟ ﺔﻟﺍﺩ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺇ
:
C =
φ (T)
ﺃﻱ ﺍﻨﻪ ﻋﻨﺩ،ﺩﺍﻭﻤﻟﺍ ﺭﻴﻐﺘﺒ ﺭﻴﻐﺘﺘﺴﻭ ﺔﺘﺒﺎﺜ ﺎﻬﺘﻤﻴﻗ ﻥﻭﻜﺘﺴ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺄﻓ ﺓﺭﺍﺭﺤﻟﺍ لﻘﺘﻨﺘ ﺎﻤﺩﻨﻌﻓ
ﺘﺴﺨﻴﻥ ﻤﻭﺍﺩ ﻤﺨﺘﻠﻔﺔ ﻟﻨﻔﺱ ﺩﺭﺠﺎﺕ
ﻭﻫﺫﺍ،ﻯﺭﺨﻷ ﺓﺩﺎﻤ ﻥﻤ ﺭﺍﺩﻘﻤﻟﺎﺒ ﻑﻠﺘﺨﺘ ﺔﻤﺯﻼﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺈﻓ ﺓﺭﺍﺭﺤﻟﺍ
ﺸﻜلـﻟﺍ ﻥﺈـﻓ ﻙﻟﺫﻜ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻰﻤﺴﺘ ﺔﻨﻴﻌﻤ ﺔﻴﺭﺍﺭﺤ ﺔﻴﺼﺎﺨ ﺎﻬﻟ ﺓﺩﺎﻤ لﻜ ﻥﺍ ﻰﻟﺍ ﻊﺠﺭﻴ
)
3.13
(
ﺭﻯـﺨﺍ ﻰـﻟﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩ ﻥﻤ ﻑﻠﺘﺨﺘ ﺔﻤﺯﻼﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺄﻓ ﺔﻨﻴﻌﻤ ﺓﺩﺎﻤ ﻥﻴﺨﺴﺘ ﺩﻨﻋ ﻪﻨﺍ ﻥﻴﺒﻴ
.
ﺜﻼﹰـﻤﻓ
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﺭ
ﻓﻊ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﻜﻤﻴﺔ ﻤﻌﻴﻨﺔ ﻤﻥ ﺍﻟﻬﻭﺍﺀ ﻤﻥ
(300K)
ﺍﻟﻰ
(800K)
ﺴﻴﻜﻭﻥ ﻤﺨﺘﻠﻔﺎﹰ
ﺸﻜل
)
3.13
(
-
ﺘﻐﻴﺭ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺒﺘﻐﻴﺭ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
∗
ﺤﻴﺙ ﺍﻥ ﻟﻠﻐﺎﺯﺍﺕ ﺤﺭﺍﺭﺘﻴﻥ ﻨﻭﻋﻴﺘﻴﻥ،لﻜﺎﺸﻤﻟﺍ ﺽﻌﺒ ﺭﻴﺜﻴ ﺎﻨﻫ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻑﻴﺭﻌﺘ ﻥﺍ ﻊﻗﺍﻭﻟﺍ ﻲﻓ
ﺍﺫﻥ ﻫﻨﺎ ﺍ،ﹰﺎﻘﺤﻻ ﺩﺭﻴﺴ ﺎﻤﻜ
ﻟﺘﻌﺭﻴﻑ ﻴﺸﻤل ﺍﻟﻤﻭﺍﺩ ﻏﻴﺭ ﺍﻟﻐﺎﺯﻴﺔ
.
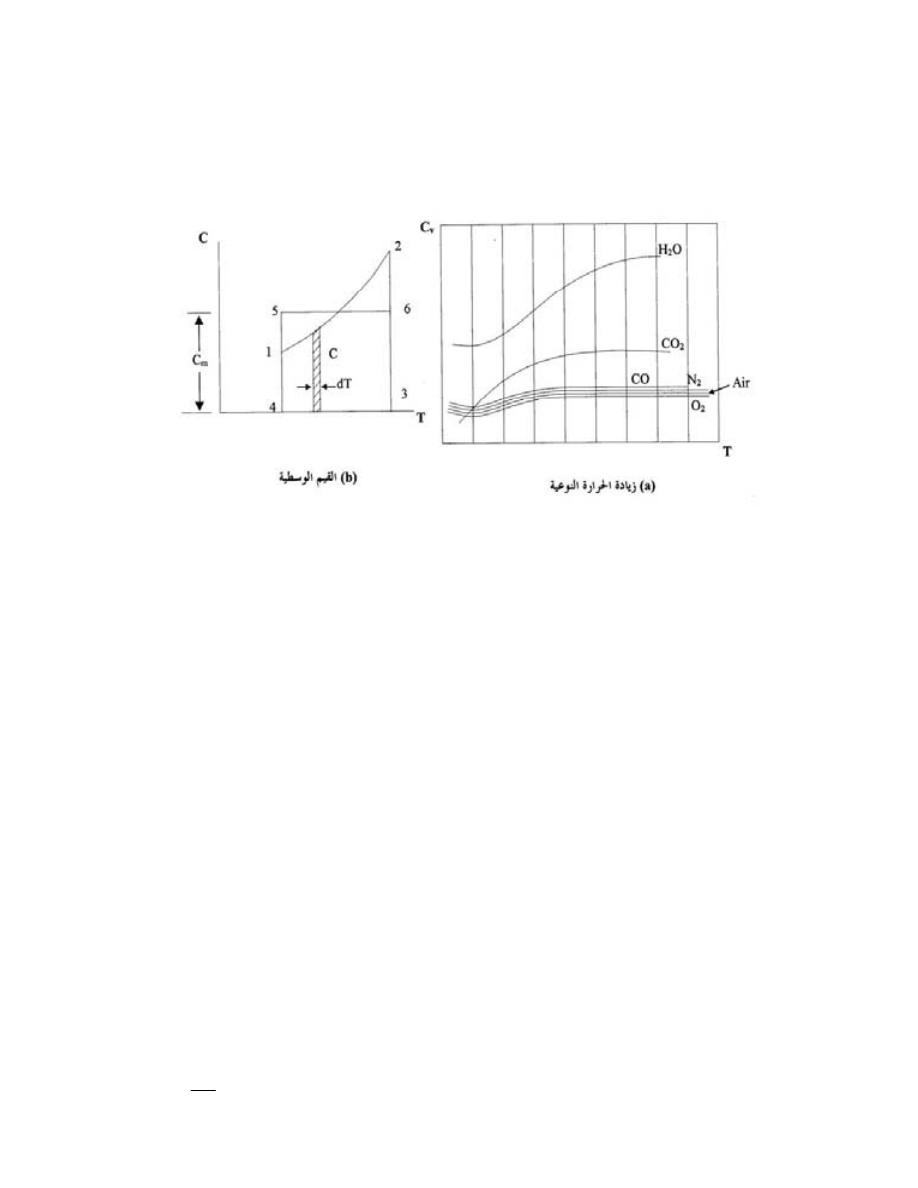
)
65
(
ﻥـﻤ ﻪـﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩ ﻊـﻓﺭﻟ ﺔﻤﺯﻼﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻋ
(3000K)
ﻰـﻟﺍ
(3500K)
ﻲـﻓ ﺎـﻤﻜ ،
ﺸﻜل
(3.14-a)
.
ـﻓﺒﺭﻏﻡ ﺍﻥ ﺍﻟ
(
∆T)
ﺜﺎﺒﺕ ﺍﻻ ﺍﻥ
(Q)
ﻤﺘﻐﻴﺭﺓ ﻭﺒﺎﻟﺘﺎﻟﻲ
ﻓﺈﻥ
(C)
ﻤﺘﻐﻴﺭﺓ ﺍﻴﻀﺎﹰ
.
ﺸﻜل
)
3.14
(
-
ﺯﻴﺎﺩﺓ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺒﺯﻴﺎﺩﺓ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
ﻴﻥـﻴﻌﺘ ﺏﺠﻴ ﺔﻟﺎﺤﻟﺍ ﻩﺫﻫ ﻲﻓﻭ ،ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻡﻴﻗ ﻥﻤ ﻲﺌﺎﻬﻨ ﻻ ﺩﺩﻋ ﺓﺩﺎﻤﻠﻟ ﻥﻭﻜﻴﺴ ﺱﺎﺴﻻﺍ ﺍﺫﻫ ﻰﻠﻋﻭ
ﺍﻟﻘﻴﻤﺔ ﺍﻟﻭﺴﻁﻴﺔ ﺍﻭ ﺍﻟﻤﻌﺩل
(Cm)
ﻟﻤﺩﻯ ﺩﺭﺠﺎﺕ ﺤﺭﺍﺭﺓ ﻤﻥ
(T1)
ﺍﻟﻰ
(T2)
ﺩلـﻌﻤﻟﺍ ﺍﺫـﻫ ﺭﺎﺒﺘﻋﺍﻭ ،
ﻜﻤﺎ ﻤﻭﻀﺢ ﻓﻲ ﺸﻜل،ﺔﺘﺒﺎﺜ ﺔﻤﻴﻘﻜ
(3.14-b)
ﺤﻴﺙ ﺍﻥ ﺍﻟﻤﺴﺎﺤﺔ
)
1234
(
ﻤﺴﺎﻭﻴﺔ ﻟﻠﻤﺴﺎﺤﺔ
)
3456
.(
ﻼلـﺨ ﻥـﻤ ﻅﺤﻼﻨﺴ ﺎﻤﻜ ،ﺔﻴﻜﻴﻤﺎﻨﻴﺩﻭﻤﺭﺜﻟﺍ ﺕﺎﺒﺎﺴﺤﻟﺍ ﻲﻓ ﻥﺎﺒﺴﺤﻟﺎﺒ ﺫﺨﺅﺘ ﺔﺘﺒﺎﺜ ﺔﻤﻴﻗ ﻭﻫ لﺩﻌﻤﻟﺍ ﺍﺫﻫ ﻥﺇ
ﺜﻭﺍﺒﺕ ﺒﻌﺽ ﺍﻟﻘﻴﻡ ﻟﺒﻌﺽ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﺘﻲ ﺴﺘﺭﺩ ﻓﻲ ﺠﺩﻭل ﻻﺤﻕ
.
ﻋﻨﺩ ﺘﺴﺨﻴﻥ ﻏﺎﺯ ﻤﻭﺠﻭﺩ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ
ﻤﻐﻠﻘﺔ ﺒﻤﻜﺒﺱ ﻜﻤﺎ ﻓﻲ ﺸﻜل
)
3.15
(
ﺭﺍﺭﺓـﺤﻟﺍ ﺔـﻴﻤﻜ ﻥﺈﻓ ،
ﻓﻌﻨﺩ ﺘﺜﺒﻴﺕ ﺍﻟﻤﻜﺒﺱ ﺴﻭﻑ ﻴﺴﺨﻥ ﺍﻟﻐﺎﺯ ﺒﺤﺠﻡ ﺜﺎﺒﺕ،ﺱﺒﻜﻤﻠﻟ ﺙﺩﺤﻴ ﺎﻤ ﻰﻠﻋ ﺩﻤﺘﻌﺘ
.
ﺒﺱـﻜﻤﻟﺍ ﻙﺭﺤﺘ ﺍﺫﺇﻭ
ﻭﺃﻨﺠﺯ ﺸﻐﻼﹰ ﻓﺴﻴﻜﻭﻥ ﺒﺴﺒﺏ ﺘﺴﺨﻴﻥ ﺍﻟﻐﺎﺯ ﺘﺤﺕ ﻀﻐﻁ ﺜﺎﺒﺕ
)
ﻭﺯﻥ ﺍﻟﻤﻜﺒﺱ
(
ﺎﻥـﻴﻟﺎﺘ ﺎﻥﻋﻭﻨ ﻙﺎﻨﻫ ﻙﻟﺫﻟ ،
ﻟﻠﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﻟﻠﻐﺎﺯ
:
1
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍ
ﻟﻨﻭﻋﻴﺔ ﻋﻨﺩ ﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
The Specific Heat at Constant Volume
ﻫﻲ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﺭﻓﻊ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(1kg)
ﻡـﺠﺤﻟﺍ ﺕﻭـﺒﺜ ﻁﺭـﺸ ،ﺓﺩﺤﺍﻭ ﺔﺠﺭﺩ ﺯﺎﻐﻟﺍ ﻥﻤ
.
ﺭﻤﺯﻫﺎ
(Cv)
ﺘﻐﻴﺭﻫﺎ ﻴﻌﺘﻤﺩ ﻋﻠﻰ،
(T)
ﺃﻱ ﺍﻥ،
:
Cv =
φ (T)
(3.19)
........
)
dT
(
Cv
)
u
(d
OR
T
Cv
ν
ν
ν
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
µ
∂
=
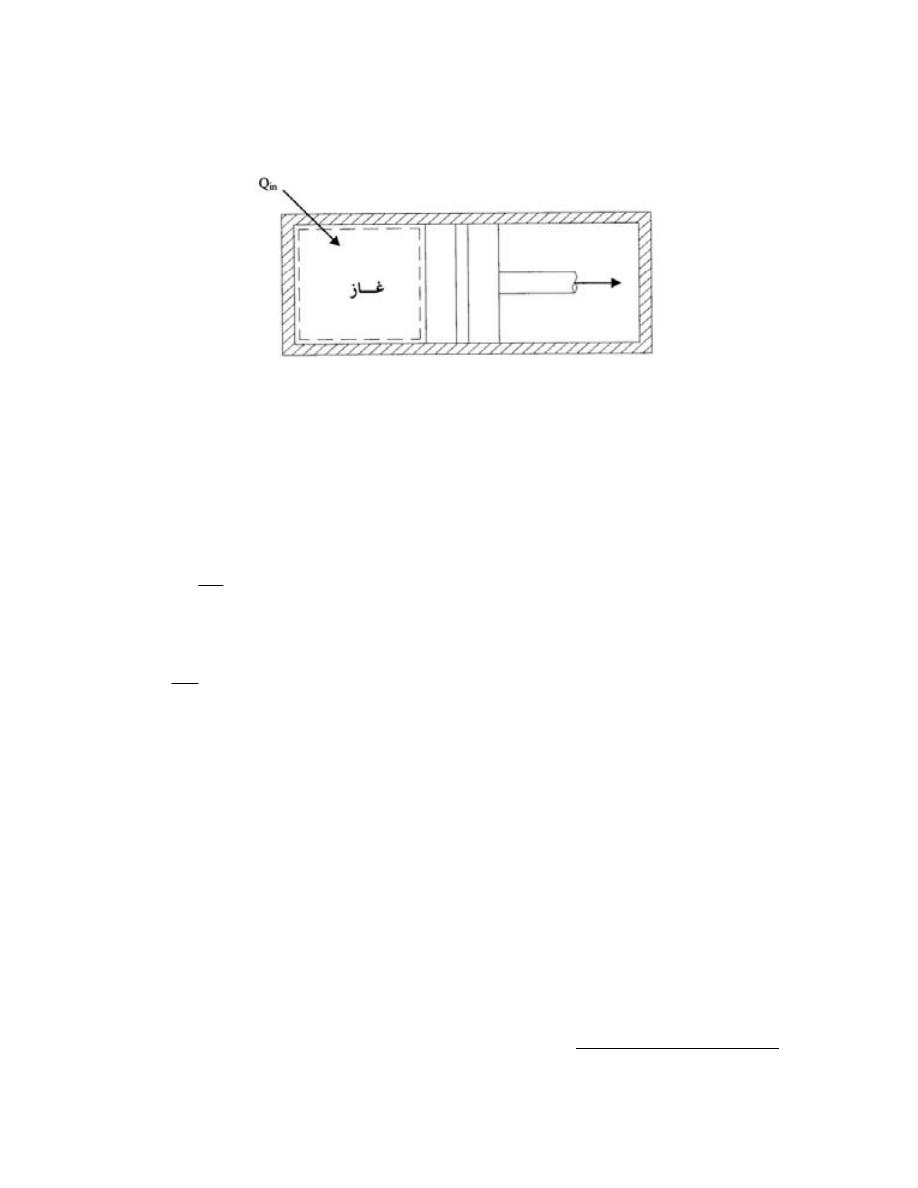
)
66
(
ﺸﻜل
)
3.15
(
-
ﺘﺴﺨﻴﻥ ﺍﻟﻐﺎﺯ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺍﻭ ﺍﻟﻀﻐﻁ
2
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨ
ﻭﻋﻴﺔ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
The Specific Heat at Constant Pressure
ﻫﻲ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﺭﻓﻊ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(1kg)
ﻭﺕـﺒﺜ ﻁﺭـﺸ ،ﺓﺩـﺤﺍﻭ ﺔﺠﺭﺩ ﺯﺎﻐﻟﺍ ﻥﻤ
ﺍﻟﻀﻐﻁ
.
ﺭﻤﺯﻫﺎ
(Cp)
.
ﻜﺫﻟﻙ ﻓﺈﻥ ﺘﻐﻴﺭﻫﺎ ﻴﻌﺘﻤﺩ ﻋﻠﻰ
(T)
ﺃﻱ ﺍﻥ
:
Cp =
φ (T)
*
ﺘﻌﺩ ﻨﺴﺒﺔ
(Cp)
ﺍﻟﻰ
(Cv)
ﻨﺴﺒﺔ ﻤﻬﻤﺔ ﻓﻲ ﻋﻠﻡ ﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤ
ـﺭﺍﺭﺓ ﻴﺭﻤﺯ ﻟﻬﺎ ﺒ
)
γ
(
ﺍﻤﺎ ﺍﻟﻔﺭﻕ ﺒﻴﻥ
(Cp)
ﻭ
(Cv)
ﻭﻟﻜﻥ ﻴﻜﻭﻥ ﺼﻐﻴﺭﺍﹰ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻤﻭﺍﺩ،ﻪﻟﺎﻤﻫﺍ ﻥﻜﻤﻴ ﻻ ﹰﺍﺭﻴﺒﻜ ﺕﺍﺯﺎﻐﻠﻟ
ﺎﻬﺴـﻔﻨ ﻲـﻫ ﹰﻼﺜـﻤ ﺀﺎﻤﻠﻟ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺍ لﺎﻘﻴ ﻙﻟﺫﻟ ،ﺀﻲﻁﺒﻟﺍ ﺩﺩﻤﺘﻟﺍ لﻤﺎﻌﻤ ﺏﺒﺴﺒ ﺔﻠﺌﺎﺴﻟﺍﻭ ﺔﺒﻠﺼﻟﺍ
ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺍﻭ ﺍﻟﻀﻐﻁ ﻭﺘﺴﺎﻭﻱ
:
Cw = 4.2 kJ / kg . K
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
:
)
3.1
(
*
ﺃﻥ
)
h
(
ﺭﻤﺯ ﻟﻼﻨﺜﺎﻟﺒﻲ ﺍﻟﺫﻱ ﺴﻴﺭﺩ ﺫﻜﺭﻩ ﻓﻴﻤﺎ ﺒﻌﺩ
(3.21)
.
..........
Cv
Cp
=
γ
(3.20)
..........
)
dT
(
Cp
dh)
OR
T
h
Cp
p
*
p
*
p
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=

)
67
(
ﻴﺴﻘﻁ ﻤﺎﺀ ﻓﻲ ﺸﻼل ﻤﻥ ﺇﺭﺘﻔﺎﻉ
(50m)
ﻓﺘﺘﺤﻭل ﺠﻤﻴﻊ ﻁﺎﻗﺘﻪ ﺍﻟﻰ ﺤﺭﺍﺭﺓ
.
ﺔـﺠﺭﺩ ﻲﻓ ﻉﺎﻔﺘﺭﻻﺍ ﺏﺴﺤﺍ
ﺤﺭﺍﺭﺓ ﺍﻟﻤﺎﺀ ﺍﺫﺍ ﺍﻓﺘﺭﻀﺕ ﻋﺩﻡ ﺘﺒﺎﺩل ﺍﻴﺔ ﺤﺭﺍﺭﺓ ﻤﻊ ﺍﻟﻤﺤﻴﻁ
.
ﺎﺀـﻤﻠﻟ ﺔـﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭـﺤﻟﺍ ﻥﺄـﺒ ﹰﺎـﻤﻠﻋ
(4.2 kJ/kg.K)
.
PE = Q
m g z = m c
∆T
∆T =
)
3.2
(
ﻴﺴﻘﻁ ﻤﺎﺀ ﻤﻥ
ﺸﻼل ﻋﻠﻰ ﺇﺭﺘﻔﺎﻉ
(100m)
.
ﻪـﺘﻗﺎﻁ لﻭـﺤﺘﺘ ﻪﻀﻌﺒ ﻊﻤ ﺽﺭﻻﺍ ﻊﻤ ﺀﺎﻤﻟﺍ ﻡﺍﺩﻁﺼﺍ ﺩﻨﻋ
ﺍﻟﻰ ﻁﺎﻗﺔ ﻴﻨﺘﻘل
(80%)
ﻤﻨﻬﺎ ﺍﻟﻰ ﺍﻟﻤﺎﺀ ﻭﺍﻟﺒﺎﻗﻲ ﻴﺫﻫﺏ ﺍﻟﻰ ﺍﻟﻤﺤﻴﻁ
.
ﺭﺍﺭﺓـﺤﻟﺍ ﺔـﺠﺭﺩﺒ ﻉﺎﻔﺘﺭﻻﺍ ﺏﺴﺤﺍ
ﻋﻠﻤﺎﹰ ﺒﺄﻥ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﻟﻠﻤﺎﺀ
(4.2 kJ/kg. K)
.
0.8 PE = Q
0.8
×m g z = m c ∆T
∆T =
)
3.3
(
ﻤ
ﺴﺨﻨﺔ ﻤﺎﺀ ﻜﻬﺭﺒﺎﺌﻴﺔ ﻗﺩﺭﺘﻬﺎ
(1200W)
ﺘﺴﺨﻥ ﻤﺎﺀ ﻜﺘﻠﺘﻪ
(3kg)
ﺭﺍﺭﺓـﺤ ﺔـﺠﺭﺩ ﻥﻤ
(20
°C)
ﻰـﻟﺍ
(100
°C)
.
ﻋﻠﻤﺎﹰ ﺒﺄﻥ،ﻙﻟﺫﻟ ﻡﺯﻼﻟﺍ ﺕﻗﻭﻟﺍ ﻭﻫ ﺎﻤ
(Cw = 4.2 kJ / kg.K)
ﻭﻻ ﻴﻭﺠﺩ ﻓﻘﺩ ﻟﻠﺤﺭﺍﺭﺓ،
.
)
3.4
(
ﻴﺴﻘﻁ ﻤﺎﺀ ﻤﻥ ﺍﺭﺘﻔﺎﻉ
(1200m)
ﺍﻟﻰ ﺇﺭﺘﻔﺎﻉ
(520m)
.
ﺇﺫﺍ ﻋﻠﻤﺕ،ﻁﻗﺎﺴﻟﺍ ﺀﺎﻤﻟﺍ ﺔﻴﻤﻜ ﺏﺴﺤﺍ
ﺍﻥ ﻤﻘﺩﺍﺭ
ﺍﻟﻔﻘﺩ ﻟﻁﺎﻗﺔ ﺍﻟﻭﻀﻊ ﻫﻭ
(7kJ)
.
PE = m g
∆ Z = 7
)
3.5
(
ﻤﺼﻌﺩ ﻜﺘﻠﺘﻪ
(585 kg)
ﺇﺭﺘﻔﻊ ﻤﺴﺎﻓﺔ
(32m)
.
ﺍﺤﺴﺏ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ
.
K
117
.
0
10
4.2
50
1
8
.
9
c
z
g
3
=
×
×
=
×
K
187
.
0
10
4.2
100
9.81
8
.
0
3
=
×
×
×
s
840
1.2
20)
-
(100
2
.
4
3
P
T
c
m
P
W
time
=
×
×
=
∆
=
=
kg
05
.
1
10
520)
-
(1200
81
.
9
7
g
7
m
3
-
=
×
=
∆
=
Z

)
68
(
PE = W = m g z = 585
× 9.81 × 32 = 183.6 J
)
3.6
(
ﺭﻓﻌﺕ ﻜﺘﻠﺔ
(210kg)
ﻤﺴﺎﻓﺔ
(24.5m)
ﻓﻲ
(1min.)
ﻭ
(34s)
ﺍﺤﺴﺏ ﺍﻟﻘﺩﺭﺓ ﺍﻟﻼﺯﻤﺔ
.
PE = W = m g z = 210
× 9.81 × 24.5 = 50.5 J
)
3.7
(
ﻨﻅﺎﻡ
ﻴﺘﺄﻟﻑ ﻤﻥ ﺨﻠﻴﺔ ﺸﻤﺴﻴﺔ ﺘﻨﺘﺞ
(1050 kWh)
ﻓﻲ ﺍﻟﺸﻬﺭ
.
ﻭﻤﻌﺩل ﺍﻻﻨﺘﺎﺝ ﻴﺴﺎﻭﻱ
(15%)
ﻤﻥ ﻗﺩﺭﺓ
ﺍﻟﻤﻨﻅﻭﻤﺔ
.
ﺍﺤﺴﺏ ﻤﻌﺩل ﺍﻟﻘﺩﺭﺓ
.
)
3.8
(
ﺘﺞـــﻨﻴ ﻱﺭﺎـــﺨﺒ ﻲﻨﻴﺒﺭﻭـــﺘ ﺩـــﻟﻭﻤ
(750kW)
ﺩلـــﻌﻤﺒ ﺭﺎـــﺨﺒﻟﺍ ﻕﻓﺩـــﺘﻴ ﺎﻤﺩـــﻨﻋ
(2.250 . 10
3
kg/h)
.
ﺍﺤﺴﺏ ﺍﻟﺸﻐل
ﺍﻟﻤﻨﺠﺯ ﻟﻜل
(1Kg)
ﻤﻥ ﺍﻟﺒﺨﺎﺭ
.
)
3.9
(
ﺍﻟﻘﺩﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﻁﺎﺌﺭﺓ ﺘﻁﻴﺭ ﺒﺴﺭﻋﺔ
(545 km/h)
ﻫﻲ
(1800kW)
.
ﺔـﻤﻭﺎﻘﻤﻟﺍ ﺓﻭـﻗ ﻁﺴﻭﺘﻤ ﺏﺴﺤﺍ
ﺒﻭﺤﺩﺍﺕ
(N)
.
W
537
.
0
94
5
50
t
W
P
=
×
=
=
kW
72
.
9
15
.
0
458
.
1
P
kW
458
.
1
24
30
1050
t
W
P
=
=
∴
=
×
=
=
•
J/kg
1200
625
.
0
750
m
W
w
kg/s
625
.
0
3600
10
250
.
2
m
s
3
s
=
=
=
=
×
=
•
•
•
N
89
.
11
3600
1000
545
1000
1800
a
P
a
W
F
a
F
W
=
×
×
=
=
=
×
=
•
•

)
69
(
)
3.10
(
ﺴﻴﺎﺭﺓ ﻗﺩﺭﺓ ﻤﺤﺭﻜﻬﺎ
(23kW)
ﻭﺘﺴﻴﺭ ﺒﺴﺭﻋﺔ
(64 km/h)
ﺍﺫﺍ ﺍﻫﻤﻠﺕ ﺍﻟﺨﺴﺎﺌﺭ
.
ﺔـﻤﻭﺎﻘﻤﻟﺍ ﺓﻭﻗ ﺏﺴﺤﺇ
ﺍﻟﺘﻲ ﺘﺘﻌﺭﺽ ﻟﻬﺎ ﺍﻟﺴﻴﺎﺭﺓ ﺒﺴ
ﺒﺏ ﺍﻻﺤﺘﻜﺎﻙ ﻤﻊ ﺍﻟﻬﻭﺍﺀ ﻭﺍﻻﺭﺽ
.
)
3.11
(
ﻤﺎ ﻫﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ ﺒﻭﺤﺩﺍﺕ
(kcal)
،
(kWh)
ﻟﻜﺘﻠﺔ ﻤﻥ ﺍﻟﻤﺎﺀ ﻤﻘﺩﺍﺭﻫﺎ
(1kg)
ﻤﻭﻀﻭﻋﺔ ﻋﻠﻰ ﺇﺭﺘﻔﺎﻉ
(1200m)
.
PE = F × z = mgz = 1
× 9.81 × 1200 = 11.772 kJ
)
3.12
(
(1kg)
ﺴﺭﻋﺔــﺒ ﻕﻭــﺒ ﺔــﻫﻭﻓ ﻥــﻤ ﺏﺎﺴــﻨﻴ ﺭﺎــﺨﺒ
(300m/s)
.
ﺔ ﺍــﻗﺎﻁﻟﺍ ﺩــﺠﻭﺍ
ﺔــﻴﻜﺭﺤﻟ
ﺒﻭﺤﺩﺍﺕ
(kcal)
.
)
3.13
(
ﻤﺴﺨﻥ ﻜﻬﺭﺒﺎﺌﻲ ﻗﺩﺭﺘﻪ
(0.08 MW)
ﻜﻔﺎﺀﺘﻪ ﻓﻲ ﺍﻟﺘﺴﺨﻴﻥ
(85%)
.
ﺭﺍﺭﺓـﺤ ﺔﺠﺭﺩ ﻲﻓ ﻉﺎﻔﺘﺭﻻﺍ ﺏﺴﺤﺍ
ﺇﺫﺍ ﻋﻠﻤﺕ ﺍﻥ ﻜﻤﻴﺔ ﺍﻟﻤﺎﺀ ﺍﻟﻤﺎﺭ،ﺀﺎﻤﻟﺍ
(63 kg/min.)
.
)
3.14
(
ﻴﺘﺤﻭل
(82%)
ﻤﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ ﺍﻟﻰ ﺤﺭﻜﻴﺔ ﻟﻤﺎﺌﻊ ﺤﺠﻤﻪ
(30L)
ﻭﺴﺭﻋﺘﻪ
(496 m/min.)
.
ﺍ
ﺤﺴﺏ
ﻤﻘﺩﺍﺭ ﻁﺎﻗﺔ ﺍﻟﻭﻀﻊ
.
ﻋﻠﻤﺎﹰ ﺍﻥ ﻜﺜﺎﻓﺔ ﺍﻟﻤﺎﺀ
(10
3
kg/m
3
)
.
kN
m
1
s
s
m
.
kN
m
1
s
s
kJ
kN
29
.
1
1000
64
3600
23
C
P
F
C
F
t
a
F
t
W
P
=
×
×
=
⎟
⎠
⎞
⎜
⎝
⎛
×
×
=
×
×
=
=
×
=
×
=
=
kWh
0033
.
0
3600
11.772
kcal
812
.
2
1868
.
4
772
.
11
=
=
=
=
kcal
748
.
10
4.1868
45
kJ
45
2
300
1
2
mc
KE
2
2
=
=
=
×
=
=
K
10
3
.
4
60
63
2
.
4
10
0.08
85
.
0
mc
P
T
P
T
mc
P
Q
P
Q
3
-
3
×
=
×
×
×
×
=
η
=
∆
η
=
∆
⇒
η
=
⇒
=
η
kg
25
.
1
1640
13
.
2050
PE
2000
60
396
30
2
mc
KE
PE
82
.
0
2
2
=
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
=
=

)
70
(
)
3.15
(
ﺩﺍﺕــﺤﻭﺒ ﻡﺯﻼــﻟﺍ لﻐﺸــﻟﺍ ﺭﺍﺩــﻘﻤ ﺏﺴــﺤﺍ
(kJ)
ﻪــﻤﺠﺤ ﺀﺍﻭــﻫ ﻥﻭﻟﺎــﺒ ﻸــﻤﻟ ﻡﺯﻼــﻟﺍ
(0.568 m
3
)
ﻋﻨﺩ ﻀﻐﻁ ﻤﻘﺩﺍﺭﻩ
(0.75 mmHg)
.
ﻭﺍﺤﺴﺏ ﻤﻘﺩﺍﺭ ﺍﻟﺸﻐل ﺒﻭﺤﺩﺍﺕ
(Lb
f
. ft)
.
W
Flow
= P
∆V = 0.75
× 13600 × 9.81 × (0.568)
= 56.8 kJ
= 41800 Lb
f
. ft
)
3.16
(
ﻤﺎ ﺍﻟﺴﺭﻋﺔ ﺍﻟﺘﻲ ﻴﺠﺏ ﺍﻥ ﺘﻜﺘﺴﺒﻬﺎ ﻜﺘﻠﺔ ﻗﺩﺭﻫﺎ
(1kg)
ﺤﺘﻰ ﺘﻜﺘﺴﺏ ﻁﺎﻗﺔ ﺤﺭﻜﻴﺔ ﻤﻘﺩﺍﺭﻫﺎ
(100J)
.
)
3.17
(
ﻴﻨﺴﺎﺏ ﻤﺎﺀ ﻤﻥ ﻓﻭﻕ ﺸﻼل ﺍﺭﺘﻔﺎﻋﻪ
(100m)
.
ﺍﻓﺘﺭﺽ ﻋﺩﻡ ﺤﺩﻭﺙ ﺘﺒﺎﺩل ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺒﻴﻥ ﺍﻟﻤﺎﺀ ﻭﺍﻟﻭﺴﻁ
ﺍﻟﺨﺎﺭﺠﻲ
.
ﺍﺤﺴﺏ ﻟﻜل
(1kg)
:
ﺃ
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ ﻟﻠﻤﺎﺀ ﻋﻨﺩ ﻗﻤﺔ ﺍﻟﺸﻼل ﺒﺎﻟﻨﺴﺒﺔ ﺍﻟﻰ ﻗﺎﻋﺩﺘﻪ
.
ﺏ
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ ﻟﻠﻤﺎﺀ ﻗﺒل ﺍﻥ ﻴﺼﻁﺩﻡ ﻤﺒﺎﺸﺭﺓﹰ ﺒﺎﻟﻘﺎﻉ
.
ـﺠ
-
ﻔلـﺴﺍ ﺩﻭـﺠﻭﻤﻟﺍ ﺭﻬﻨﻟﺍ ﻲﻓ ﺀﺎﻤﻟﺍ ﻥﻤ ﺔﻴﻤﻜﻟﺍ ﻩﺫﻫ لﻭﺨﺩ ﺩﻌﺒ ﺀﺎﻤﻟﺍ ﺔﻟﺎﺤ ﻲﻓ ﺙﺩﺤﻴ ﻱﺫﻟﺍ ﺭﻴﻐﺘﻟﺍ ﺎﻤ
ﺍﻟﺸﻼل
.
a- PE = mgz = 1
× 9.81 × 100 = 981 J/kg
b- KE = PE = 981 J/kg
c- ∆U = ∆KE = 981 J/kg = m c ∆T
)
3.18
(
ﺴﻴﺎﺭﺓ ﺴﺭﻋﺘﻬﺎ
(50 km/h)
.
ﻭﻜﺎﻨﺕ ﺍﻟﻤﻘﺎﻭﻤﺔ ﻀﺩ ﺤﺭﻜﺔ ﺍﻟﺴﻴﺎﺭﺓ
(900N)
.
ﺩـﻨﻋ ﻙﺭﺤﻤﻟﺍ ﺓﺭﺩﻗ ﺩﺠﻭﺍ
ﻭﺍﻫﻤل ﺒﻘﻴﺔ ﺍﻟﺨﺴﺎﺌﺭ،ﺔﻋﺭﺴﻟﺍ ﻩﺫﻫ
.
)
3.19
(
ﺍﻟﻰ ﺃﻱ ﺍﺭﺘﻔﺎﻉ ﻴﺠﺏ ﺍﻥ ﺘﺭﻓﻊ ﻜﺘﻠﺔ ﻤﻘﺩﺍﺭﻫﺎ
(1kg)
ﺤﺘﻰ ﺘﺼﺒﺢ ﻁﺎﻗﺘﻬﺎ ﺍﻟﻭﻀﻌﻴﺔ
(1000J)
.
PE = m g z
1000 = 1
× 9.81 × z
z = 101.9 m
m/s
14
.
14
C
2
C
1
100
2
mC
KE
2
2
=
×
=
=
K
234
.
0
4186
981
mc
U
T
=
=
∆
=
∆
kW
5
.
12
3600
10
10
50
900
t
a
F
t
W
P
-3
3
=
×
×
×
=
×
=
=

)
71
(
ﻤﺴﺎﺌل
ﻜﻤﻴﺔ ﻤﻥ ﺍﻟﻤﺎﺀ ﻜﺘﻠﺘﻬﺎ
(2kg)
ﺍﺭﺩﻨﺎ ﺘﺴﺨﻴﻨﻬﺎ ﺒﻭﺴﺎﻁﺔ ﻤﺴﺨﻥ ﻜﻬﺭﺒﺎﺌﻲ ﻤﻥ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(10
°C)
ﻰـﻟﺍ
(100
°C)
ﺩـﺠﻭﺘ ﻪـﻨﺍ ﹰﺎﻤﻠﻋ ،ﺔﻋﺎﺴ ﻊﺒﺭ ﻥﻴﺨﺴﺘﻟﺍ ﺓﺭﺘﻓ ﺯﻭﺎﺠﺘﺘ ﻻ ﻥﺍ ﺩﻴﺭﺍ ﺍﺫﺍ ،ﻥﺨﺴﻤﻟﺍ ﺓﺭﺩﻗ ﻲﻫ ﻡﻜﻓ
ﺨﻼل ﻫﺫﻩ ﺍﻟﻔﺘﺭﺓ ﺨﺴﺎﺌﺭ ﺤﺭﺍﺭﻴﺔ ﻤﻥ ﺍﻟﻤﺎﺀ ﺍﻟﻰ
ﺍﻟﻤﺤﻴﻁ ﻤﻘﺩﺍﺭﻫﺎ
(45kJ)
ﻋﻠﻤﺎﹰ ﺍﻥ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﻟﻠﻤﺎﺀ
(4.2 kJ/kg.K)
.
ﺝ
) :
0.89 kW
.(
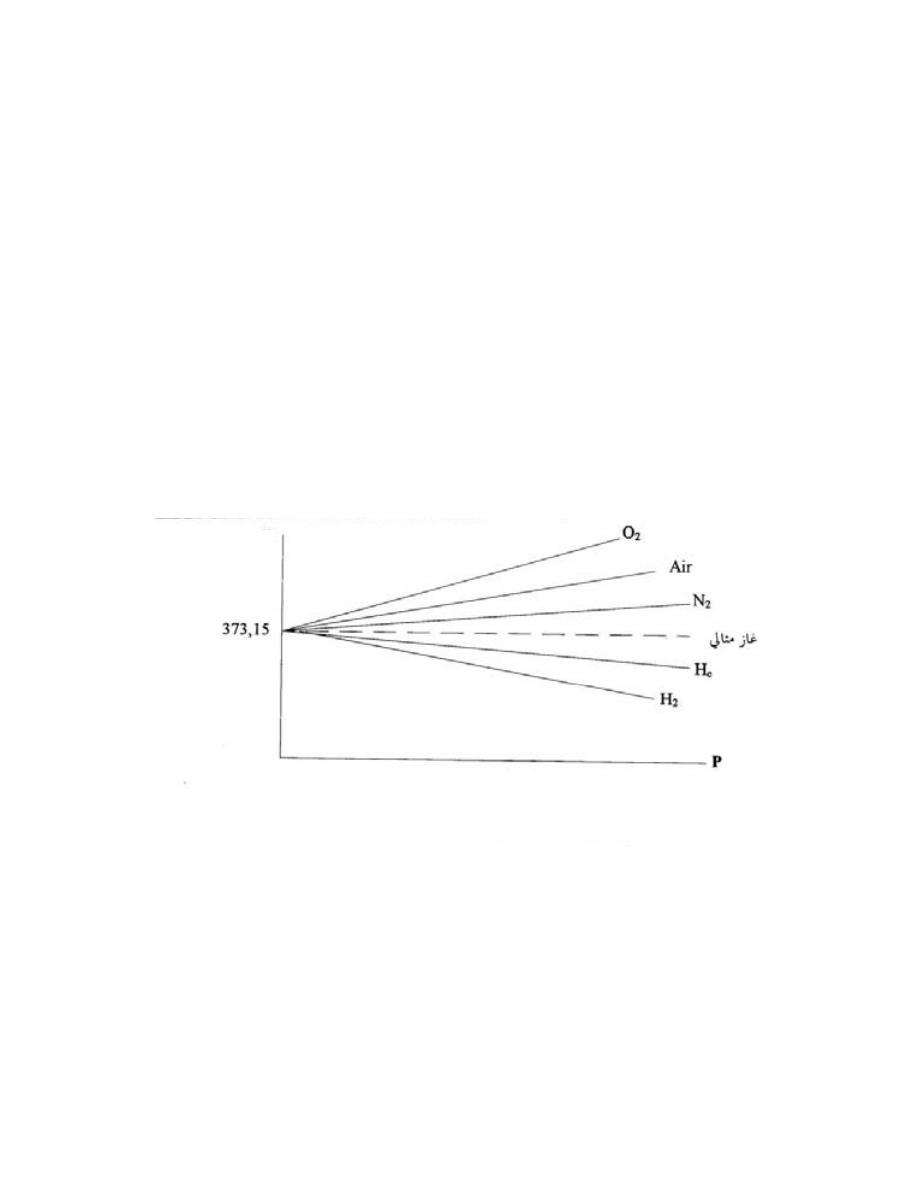
)
72
(
ﺍﻟﻔﺼﻞ ﺍﻟﺮﺍﺑﻊ
-
ﺧﻮﺍﺹ ﺍﻟﻐﺎﺯﺍﺕ
)
4.1
(
-
ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﻤﺜﺎﻟﻴﺔ ﻭﺍﻟﺤﻘﻴﻘﻴﺔ
∗
Real or Ideal and Perfect Gases
ﻀﻊـﺨﻴ ﺔـﻴﻟﺎﺜﻤ ﺔـﻟﺎﺤ ﻭـﻬﻓ ﺍﺫـﻟ ،ﺔـﻌﻴﺒﻁﻟﺍ ﻲﻓ ﺩﻭﺠﻭﻤ ﺭﻴﻏ ﻲﻠﻴﺨﺘ ﺯﺎﻏ ﻭﻫ ﻲﻟﺎﺜﻤﻟﺍ ﺯﺎﻐﻟﺍ ﻥﺇ
ﻟﻸﻓﺘﺭﺍﻀﺎﺕ ﺍﻵﺘﻴﺔ
:
1
-
ﻴﺨﻀﻊ ﻟﻘﻭﺍﻨﻴﻥ ﺒﻭﻴل ﻭﺸﺎﺭل ﻭﻏﺎﻴﻠﻭﺴﺎﻙ
.
ـﻰ ﺍﻟﻐـﻠﻋ ﻕـﺒﻁﻨﺘ ﻥﻴﻨﺍﻭﻘﻟﺍ ﻩﺫﻫ ﻥﺇ
ﺔـﻴﻟﺎﺜﻤﻟﺍ ﺕﺍﺯﺎ
ﺓﺭﺍﺭﺤﻟﺍ ﺕﺎﺠﺭﺩﻭ ﺔﻀﻔﺨﻨﻤﻟﺍ ﻁﻭﻐﻀﻟﺍ ﺩﻨﻋ ﹰﺎﺼﻭﺼﺨﻭ ﹰﺎﺒﻴﺭﻘﺘ ﻪﺴﻔﻨ ﻙﻭﻠﺴﻟﺍ ﺎﻤﻬﻟ ﻥﻷ ،ﺔﻴﻘﻴﻘﺤﻟﺍﻭ
ﺍﻟﻌﺎﻟﻴﺔ
.
ﻓﺴﻠﻭﻙ ﺍﻟﻜﺜﻴﺭ ﻤﻥ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﺤﻘﻴﻘﻴﺔ
)
ﺍﻟﺩﺍﺌﻤﻴﺔ
(
(Permanent Gas)
ﺴﺠﻴﻥـﻜﻭﻻﺍ لﺜﻤ
ﻭﺍﻟﻬﻭﺍﺀ ﻭﺍﻟﻨﺘﺭﻭﺠﻴﻥ ﻭﺍﻟﻬﻴﺩﺭﻭﺠﻴﻥ
…
ﻲـﻓ ﺢـﻀﻭﻤ ﺎﻤ ﺏﺴﺤﺒ ﻲﻟﺎﺘﻟﺍ ﺯﺎﻐﻟﺍ ﻙﻭﻠﺴ ﻪﺒﺸﺘ ،ﺦﻟﺍ
ﺍﻟﺸﻜل
)
4.1
(
ﻀﻐﻭﻁـﻟﺍ ﺩـﻨﻋ ﺔﻘﺒﺎﻁﺘﻤ ﻥﻭﻜﺘ ﺔﻴﻟﺎﺜﻤﻟﺍﻭ ﺔﻴﻘﻴﻘﺤﻟﺍ ﺕﺍﺯﺎﻐﻟﺍ ﻙﻭﻠﺴ ﻥﺍ ﻥﻴﺒﻴ ﻱﺫﻟﺍ ،
ﺍﻟﻤﻨﺨﻔﻀﺔ ﻭﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻌﺎﻟﻴﺔ
(373.15K)
.
2
-
ﻟﻪ ﺤﺭﺍﺭﺓ ﻨﻭﻋﻴﺔ ﺜﺎﺒﺘﺔ
(C = Const.)
.
ﻭﻥـﻜﺘ ﻲـﻘﻴﻘﺤﻟﺍ ﺯﺎـﻐﻠﻟ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺍ ﻥﻴﺤ ﻲﻓ
ﻤﺘﻐﻴﺭﺓ ﺒﺘﻐﻴﺭ ﺩﺭﺠﺔ ﺍ
ﺃﻱ،ﺓﺭﺍﺭﺤﻟ
C =
∅ (T)
.
ـــــــــــــــــ
∗
ﺍﻥ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﺤﻘﻴﻘﻴﺔ ﻫﻲ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﻌﺎﺩﻴﺔ ﺍﻭ ﺍﻟﺩﺍﺌﻤﺔ ﻜﺎﻻﻭﻜﺴ
ﺎـﻫﺭﻴﻏﻭ ﻥﻴﺠﻭﺭﺘﻨﻟﺍﻭ ﻥﻴﺠﻭﺭﺩﻴﻬﻟﺍﻭ ﻥﻴﺠ
.
ﺍﻤﺎ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﻤﺜﺎﻟﻴﺔ ﻭﺍﻟﺘﻲ ﺘﺴﻤﻰ ﺍﻴﻀﺎﹰ ﺒﺎﻟﻐﺎﺯﺍﺕ ﺍﻟﻜﺎﻤﻠﺔ
(Perfect or Ideal Gases)
ﻓﻬﻲ ﺍﻟﻐﺎﺯﺍﺕ
ﺍﻟﻤﺜﺎﻟﻴﺔ ﺍﻻﻓﺘﺭﺍﻀﻴﺔ
.
T(K)
ﺸﻜل
)
4.1
(
-
ﺘﺸﺎﺒﻪ ﺴﻠﻭﻙ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﺤﻘﻴﻘﻴﺔ ﻭﺍﻟﻤﺜﺎﻟﻴﺔ
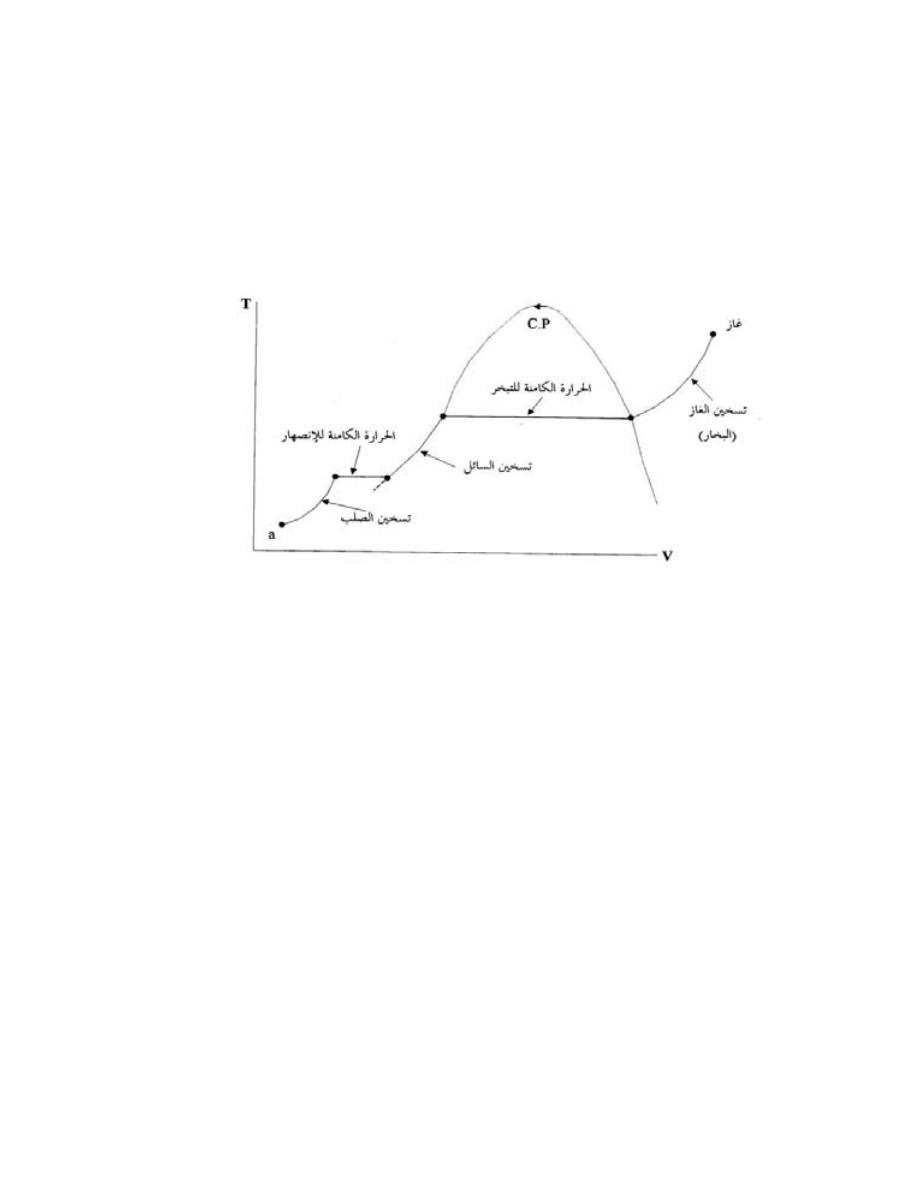
)
73
(
3
-
ﻴﺒﻘﻰ ﻓﻲ ﺤﺎﻟﺘﻪ ﺍﻟﻐﺎﺯﻴﺔ ﺘﺤﺕ ﺠﻤﻴﻊ ﺍﻟﻅﺭﻭﻑ ﺤﺘﻰ ﻋﻨﺩ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺍﻟﺼﻔﺭ ﺍﻟﻤﻁﻠﻕ
.
ﻴﻥـﺤ ﻲﻓ
ﺔـﺠﺭﺩﻭ ﻪﻁﻐﻀ ﺽﻔﺨﻨﺍ ﺎﻤﻠﻜ ،ﺏﻠﺼ ﻭﺍ لﺌﺎﺴ ﻭﺍ ﺭﺎﺨﺒ ﻰﻟﺍ لﻭﺤﺘﻴ ﻥﺍ ﻥﻜﻤﻴ ﻲﻘﻴﻘﺤﻟﺍ ﺯﺎﻐﻟﺍ ﻥﺍ
ﺤﺭﺍﺭﺘﻪ ﻜﺜﻴﺭﺍﹰ ﻋﻥ ﺍﻟﻨﻘﻁﺔ ﺍﻟﺤﺭﺠﺔ
(C.P)
ﺴـﻟﺍ ﻰـﻟﺍ ﺔـﻴﺯﺎﻐﻟﺍ ﺔﻟﺎﺤﻟﺍ ﻥﻤ لﻭﺤﺘﻟﺍ ﺔﻁﻘﻨ ﻱﺃ
ﺎﺌﻠﺔ
ﻭﺒﺎﻟﻌﻜﺱ ﻭﻭﺼﻭل ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻟﻰ ﺍﻟﺼﻔﺭ ﺍﻟﻤﻁﻠﻕ
(a)
ﻜﻤﺎ ﻓﻲ ﺸﻜل،
)
4.2
(
ﺍﻟﺫﻱ ﻴﺒﻴﻥ ﺍﻨﻪ
ﻋﻨﺩ ﺘﺒﺭﻴﺩ ﺍﻟﻐﺎﺯ
)
ﺍﻟﺒﺨﺎﺭ
(
ﻭﻋﻨﺩ ﺘﺒﺭﻴﺩ ﺍﻟﺴﺎﺌل ﻴﺘﺤﻭل ﺍﻟﻰ ﺼﻠﺏ،لﺌﺎﺴ ﻰﻟﺍ لﻭﺤﺘﻴ
)
ﺍﻟﻨﻘﻁﺔ
a
(
،
ﻭﺍﻟﻌﻜﺱ ﺼﺤﻴﺢ ﺍﻴﻀﺎﹰ
.
ﻭﻤﻊ ﺫﻟﻙ ﻨﻘﻭل ﻋﻨﺩ ﺘﻁﺒﻴﻕ ﻗﻭﺍﻨﻴﻥ ﺍﻟﻐﺎﺯ
ﻭﻥـﻜﻴ ﺞﺌﺎﺘﻨﻟﺍ ﻲﻓ ﻕﺭﻔﻟﺍ ﻥﺄﻓ ﺔﻴﻘﻴﻘﺤﻟﺍ ﺕﺍﺯﺎﻐﻟﺍ ﻰﻠﻋ ﺔﻴﻟﺎﺜﻤﻟﺍ ﺕﺍ
ﺼﻐﻴﺭﺍﹰ ﺠﺩﺍﹰ ﻴﻤﻜﻥ ﺍﻫﻤﺎﻟﻪ ﻓﻲ ﺍﻟﺤﺴﺎﺒﺎﺕ ﺍﻟﻌﺎﻤﺔ
.
ﻤﺜﺎل
)
4.1
(
ﺍﺤﺴﺏ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﺘﺤﻭﻴل
(20kg)
ﻤﻥ ﺍﻟﺠﻠﻴﺩ ﻭﻫﻭ ﺒﺩﺭﺠﺔ
(-10
°C)
ﺎﺀـﻤ ﺭﺎﺨﺒ ﻰﻟﺍ
ﻭﻫﻭ ﻓﻲ ﺩﺭﺠﺔ
(120
°C)
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﻟﻠﺠﻠﻴﺩ
=
2.1 kJ/kg.K
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻜﺎﻤﻨﺔ ﻷﻨﺼﻬﺎﺭ ﺍﻟﺠﻠﻴﺩ
(h
s
L)
*
=
336 kJ/kg
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﻟﻠﺒﺨﺎﺭ
=
1.95 kJ/kg.K
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻜﺎﻤﻨﺔ ﻟﻠﺘﺒﺨﺭ
(h
f
g)
*
=
2256 kJ/kg
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﻟﻠﻤﺎﺀ
=
4.2 kJ/kg.K
ـــــــــــــــــ
*
ـﺍﻥ ﺍﻟ
)
hsL
(
ﺘﻌﻨﻲ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻜﺎﻤﻨﺔ ﻟﻼﺘﺼﻬﺎﺭ
)
Latent Heat of Liquidization
(
ـﻭﺍﻥ ﺍﻟ
)s
(
ﺘﻌﻨﻲ
)
Solid
(
ـﻭﺍﻟ
)
L
(
ﺘﻌﻨﻲ
)
liquid
.(
*
ـﺍﻥ ﺍﻟ
)
h
f
g
(
ﺘﻌﻨﻲ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻜﺎﻤﻨﺔ ﻟﻠﺘﺒﺨﺭ
)
Latent Heat of Evaporation
(
ـﻭﺍﻥ ﺍﻟ
)f
(
ﺘﻌﻨﻲ
)
fluid
(
ـﻭﺍﻟ
)
g
(
ﺘﻌﻨﻲ
)
Gas
(
ﻫﺫﻩ ﺍﻟﻘﻴﻡ ﺘﺴﺘﺨﺭﺝ ﻤﻥ ﺠﺩﺍﻭل ﺍﻟﺒﺨﺎﺭ
.
m.hs
mc
∆
mc
∆
mc
∆
m.h
f
g
ﺸﻜل
)
4.2
(
-
ﺘﻐﻴﺭ ﺍﻟﺤﺎﻟﺔ ﺍﻟﻐﺎ
ﺯ
)
ﺍﻟﺒﺨﺎﺭ
(
ﺍﻟﺤﻘﻴﻘﻲ
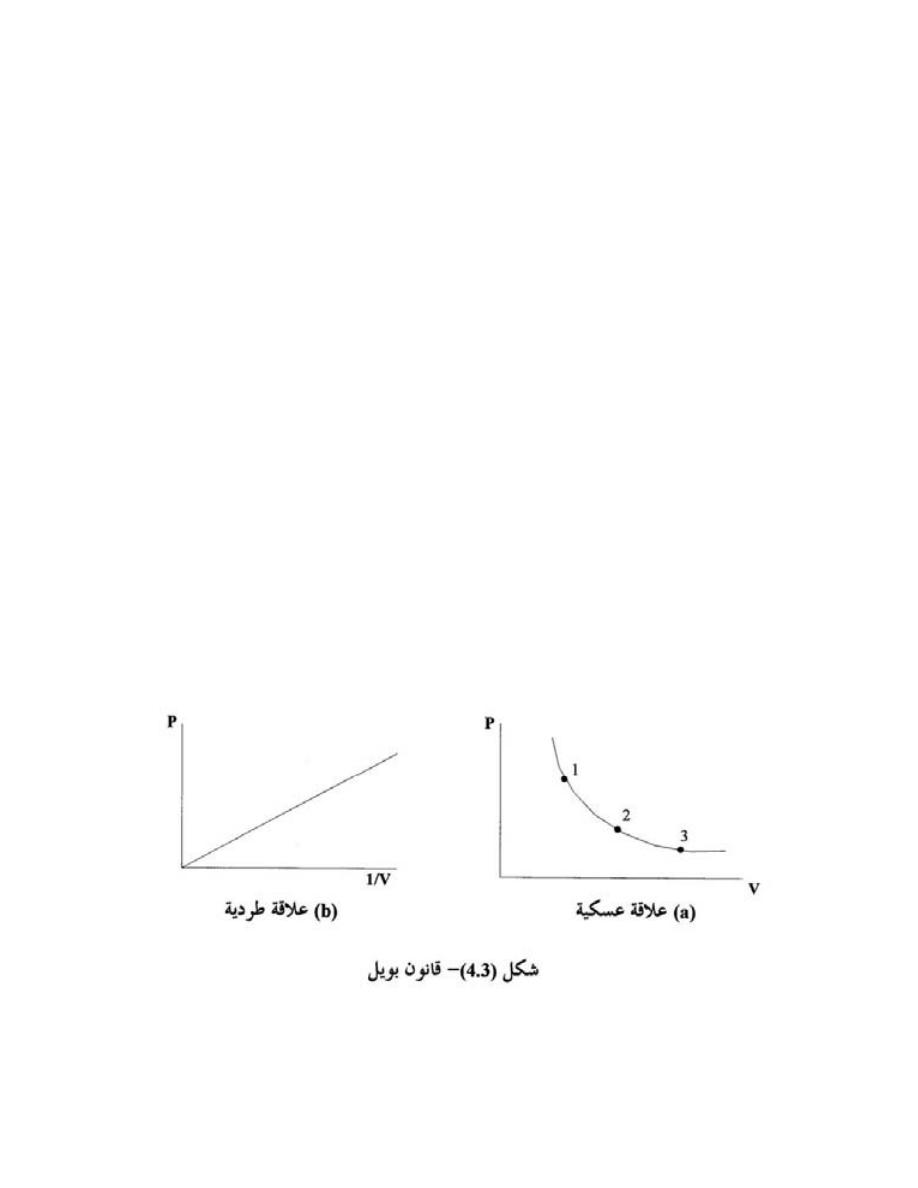
)
74
(
Q
T
= Q
12
+ Q
23
+ Q
34
+ Q
45
+ Q
56
= 20 2
× .1× [0–(-10)]+20.336+20×4.2× (100-0)+20.2256+20×1.95× (120-100)
= 420 + 6720 + 8400 + 45120 + 780 = 62220 J
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻜﺎﻤﻨﺔ ﻟﻸﻨﺼﻬﺎﺭ
Latent Heat of Liquidization
ﻫﻲ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﺘﺤﻭﻴل
(1kg)
ﺩﺘﻬﺎـﺤﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺕﻭﺒﺜﺒ ﺔﻠﺌﺎﺴ ﻰﻟﺍ ﺔﺒﻠﺼﻟﺍ ﺓﺩﺎﻤﻟﺍ ﻥﻤ
(kJ/kg)
.
ﻭﺭﻤﺯﻫﺎ
)
h
s
L
) . (
1kg
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻜﺎﻤﻨﺔ ﻟﻠﺘﺒﺨﺭ
Latent Heat of Evaporation
ﻫﻲ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻼﺯﻤﺔ ﻟﺘﺤﻭﻴل
(1kg)
ﻤﻥ ﺴﺎﺌل ﺍﻟﻰ ﺒﺨﺎﺭ ﺒﺜﺒﻭﺕ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺤﺩﺘﻬﺎ
(kJ/kg)
ﻭﺭﻤﺯﻫﺎ
)
h
f
g
(
)
4.2
(
-
ﻗﺎﻨﻭﻥ ﺒﻭﻴل
Boyle’s Law
ﻟﻭﺤﻅ ﺘﻐ،ﺔﺘﺒﺎﺜ ﻪﺘﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ ﻪﺘﻠﺘﻜ ﺔﻨﺍﻭﻁﺴﺍ ﻲﻓ ﺭﻭﺼﺤﻤ ﺯﺎﻏ ﻰﻠﻋ ﺔﺒﺭﺠﺘ لﻼﺨ ﻥﻤ
ﻲـﻓ ﺭـﻴ
ﺍﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﻴﻤﺜل ﺒﻤﻨﺤﻨﻲ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
ﺸﻜل
(4.3-a)
.
ﺭﺏـﻀ لـﺼﺎﺤ ﻥﺍ ﻅﺤﻭـﻟ ﺎﻤﻜ
ﺍﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﻷﻱ ﻨﻘﻁﺔ ﻋﻠﻰ ﺍﻟﻤﻨﺤﻨﻲ ﺴﻭﻑ ﻴﻜﻭﻥ ﻋﺩﺩ ﻤﺎ ﻤﺘﺴﺎﻭﻴﺎﹰ ﺍﻭ ﺜﺎﺒﺘﺎﹰ
(Const.)
.
ﺫﻨﺎـﺨﺃ ﺍﺫﺈـﻓ
ﺍﻟﻨﻘﺎﻁ
)
1
،
2
،
3
(
ﻋﻠﻰ ﺍﻟﻤﻨﺤﻨﻲ ﻓﺴﻴﻜﻭﻥ
:
P
1
V
1
= P
2
V
2
= P
3
V
3
= PV = Const.
………… (4.1)

)
75
(
ﻫﺫﻩ ﺍﻟﺘﺠﺭﺒﺔ ﻗﺎﻡ ﺒﻬﺎ ﺍﻟﻌﺎﻟﻡ ﺍﻻﻨﻜﻠﻴﺯﻱ ﺭﻭﺒﺭﺕ ﺒﻭﻴل
)
1627
-
91
(
ﻭﺘﻭﺼل ﺍﻟﻰ ﻨﺹ ﻗﺎﻨﻭﻨﻪ ﺍﻟﻤﺸﻬﻭﺭ ﻋﺎﻡ
)
1660
:(
ﺭﺍﺭﺓـﺤﻟﺍ ﺔـﺠﺭﺩ ﺕﻭﺒﺜ ﻁﺭﺸ ﻪﻤﺠﺤ ﻊﻤ ﹰﺎﻴﺴﻜﻋ ﺏﺴﺎﻨﺘﺘ ﺯﺎﻏ ﻥﻤ ﺔﻨﻴﻌﻤ ﺔﻴﻤﻜ ﻁﻐﻀ
.
ﻲـﻓﻭ
ﹰﻼﻘﺘﺴـﻤ لـﻤﻌﻴ ﻥﺎـﻜ ﻱﺫﻟﺍ ﺕﻭﻴﺭﺎﻤ ﻡﺩﺁ ﻲﺴﻨﺭﻔﻟﺍ ﻡﻟﺎﻌﻟﺍ ﻭﻫﻭ ﺭﺨﺁ ﺹﺨﺸ ﻥﻭﻨﺎﻘﻟﺍ ﺍﺫﻫ ﻑﺸﺘﻜﺍ ﺔﻘﻴﻘﺤﻟﺍ
ﺒﺎﻟﻭﻗﺕ ﻨﻔﺴﻪ ﻋﻥ ﺍﻟﻌﺎﻟﻡ ﺍﻻﻨﻜﻠﻴﺯﻱ
.
ﻭﺍﺫﺍ ﺭﺴﻤﻨﺎ ﻤﺨﻁﻁ
(P . 1/V)
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل
(4.3-b)
ﻓﺎﻥ ﺍﻟﻌﻼﻗﺔ ﺴﺘﻤﺜل ﺒﺨﻁ ﻤﺴﺘﻘﻴﻡ ﻴﻤﺭ ﻤﻥ
ﻨﻘﻁﺔ ﺍﻻﺼل ﻭﺒﻤﻴل ﺜﺎﺒﺕ
(Const.)
.
4.3
ﻗﺎﻨﻭﻥ ﺸﺎﺭل ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ
Charle’s Law and Absoulte Temperature
ﻤﻥ ﺨﻼل ﺘﺠﺭﺒﺔ ﻋﻠﻰ ﻏﺎﺯ ﻤﺤﺼﻭﺭ ﻓ
ﻡـﺠﺤﻟﺍ ﻲﻓ ﺭﻴﻐﺘ ﻅﺤﻭﻟ ،ﺕﺒﺎﺜ ﻪﻁﻐﻀﻭ ﻪﺘﻠﺘﻜ ﺔﻨﺍﻭﻁﺴﺍ ﻲ
ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻴﻤﺜل ﺒﺨﻁ ﻤﺴﺘﻘﻴﻡ ﻋﻠﻰ ﻤﺨﻁﻁ
(V-t)
ﺍﻟﻤﺒﻴﻥ ﻓﻲ ﺸﻜل
(4.4-a)
.
ﻓﺈﺫﺍ ﻜﺎﻥ
(V)
لـﺜﻤﻴ
،ﺍﻟﺤﺠﻡ
(t)
، ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
(C)
، ﺍﻟﻤﻴل ﻭﻫﻭ ﻗﻴﻤﺔ ﺜﺎﺒﺘﺔ
(Vo)
ﻓﺴﻴﻌﺒﺭ ﻋﻥ،ﻱﻭﺌﻤﻟﺍ ﺭﻔﺼﻟﺍ ﺩﻨﻋ ﻡﺠﺤﻟﺍ
ﻫﺫﻩ ﺍﻟﺘﺠﺭﺒﺔ ﺭﻴﺎﻀﻴﺎﹰ ﻜﻤﺎ ﻴﺄﺘﻲ
:
V = C t + V
o
…………. (4.2)
ﺼﺒﺢـﻴ ﺎﻫﺩـﻨﻋﻭ ﺕﺎﻨﻴﺴﻟﺍ ﺭﻭﺤﻤ ﻰﻠﻋ ﺓﺩﻴﺩﺠ ﺔﻁﻘﻨ ﺩﻨﻋ ﻲﻘﺘﻠﻴ ﻡﻴﻘﺘﺴﻤﻟﺍ ﻁﺨﻟﺍ ﺩﺍﺩﺘﻤﺍ ﻥﺍ ﻅﺤﻭﻟ ﺎﻤﻜ
ﺍﻟﻘﺎﻨﻭﻥ
:
V = C T
………… (4.3)
ﺩـﻨﻋ ﺎﻬﻌﻴﻤﺠ ﻲﻘﺘﻠﺘ ﺔﻤﻴﻘﺘﺴﻤ ﻁﻭﻁﺨ ﺓﺩﻋ ﻙﺎﻨﻫ ﻥﻭﻜﻴﺴﻓ ﺔﻔﻠﺘﺨﻤ ﺕﺍﺯﺎﻏ ﻰﻠﻋ ﺔﺒﺭﺠﺘﻟﺍ ﺀﺍﺭﺠﺍ ﺩﻨﻋﻭ
ﺍﻟﻨﻘﻁﺔ ﺍﻟﺠﺩﻴﺩﺓ ﻨﻔﺴﻬﺎ ﻋﻠﻰ ﻤﺤﻭﺭ ﺍﻟ
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﺕﺎﻨﻴﺴ
(4.4-b)
.
ﻕـﻠﻁﻤﻟﺍ ﺭﻔﺼـﻟﺍ لﺜﻤﺘ ﺔﻁﻘﻨﻟﺍ ﻩﺫﻫ
ﺍﻟﺫﻱ ﻗﻴﻤﺘﻪ
(-273
°C)
ﻜﻤﺎ ﻓﻲ ﺸﻜل،
(4.4-c)
ﻟﺫﻟﻙ ﻅﻬﺭ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﺠﺩﻴﺩ ﻟﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻴﺴﻤﻰ ﺒﺩﺭﺠﺔ
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ ﺭﻤﺯﻩ
(T)
ﻭﻭﺤﺩﺘﻪ ﻜﻠﻔﻥ
(K)
.
ﺇﻥ
(T)
ﻫﻲ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﺴﺠﻠﺔ ﻤﻥ ﻨﻘﻁﺔ ﺍﻻﺼل
ﺍﻟﺠﺩﻴﺩﺓ ﻭ
(t)
ﺘﻤﺜل ﻗﺭﺍﺀﺓ
ﻟﺫﻟﻙ ﻓﺈﻥ،ﺭﺍﺭﺤﻤﻟﺍ
:
T = t + 273
….. (4.4)
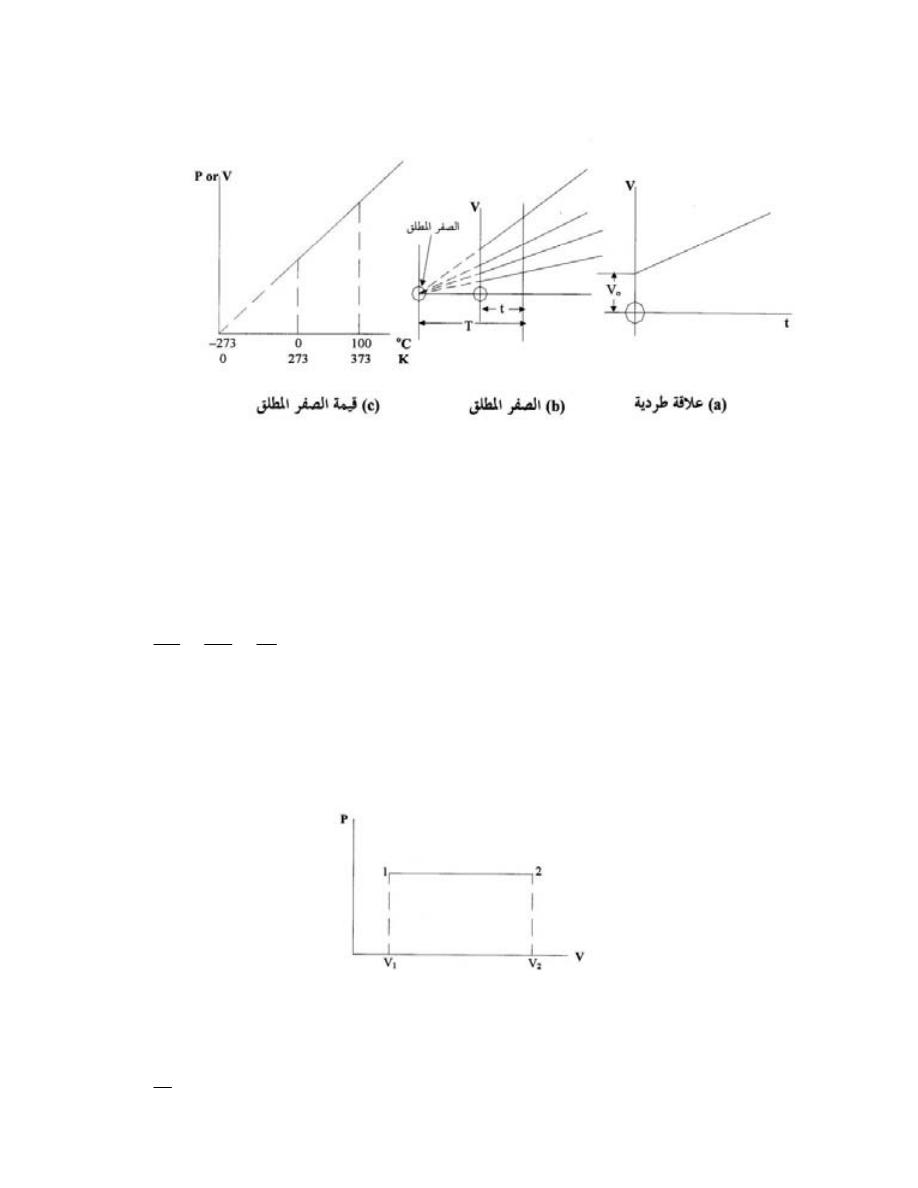
)
76
(
ﻫﺫﺍ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ ﻷﻨﻪ ﻴﺒﻘﻰ،ﻕﻠﻁﻤﻟﺍ ﺭﻔﺼﻟﺍ ﺩﻨﻋ ﹰﺍﺭﻔﺼ ﺕﺤﺒﺼﺍ ﻡﻭﺠﺤﻟﺍ ﻊﻴﻤﺠ ﻥﺍ ﻅﺤﻭﻟﻭ
ﻩﺫـﻫ ﻲـﻓ لﻭﺤﺘﺘ ﺔﻴﻘﻴﻘﺤﻟﺍ ﺕﺍﺯﺎﻐﻟﺍ ﻥﺍ ﻥﻴﺤ ﻲﻓ ،ﺔﺌﻁﺍﻭﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺕﺎﺠﺭﺩ ﺩﻨﻋ ﻰﺘﺤ ﺔﻴﺯﺎﻐﻟﺍ ﻪﺘﻟﺎﺤ ﻲﻓ
ﺸﻜل،ﺏﻠﺼ ﻡﺜ لﺌﺎﺴ ﻰﻟﺍ ﺔﺠﺭﺩﻟﺍ
)
4.2
.(
ﻴﻤﻜﻥ ﺍﻥ ﻨﻠﺨﺹ ﻤﺎ ﻭﺭﺩ ﺁﻨﻔﺎﹰ ﺒﻤﺎ ﻴﺄﺘﻲ
:
ﻀﻐﻁـﻟﺍ ﺕﻭﺒﺜ ﻁﺭﺸ ﺔﻘﻠﻁﻤﻟﺍ ﻪﺘﺭﺍﺭﺤ ﺔﺠﺭﺩ ﻊﻤ ﹰﺎﻴﺩﺭﻁ ﺏﺴﺎﻨﺘﺘ ﺯﺎﻏ ﻥﻤ ﺔﻨﻴﻌﻤ ﺔﻴﻤﻜ ﻡﺠﺤ
.
ﺈﺫﺍـﻓ
ﺘﻐﻴﺭ ﺍﻟﻐﺎﺯ ﻤﻥ ﺍﻟﺤﺎﻟﺔ
)
1
(
ﺍﻟﻰ
)
2
(
ﻜﻤﺎ ﻓﻲ ﺸﻜل
)
4.5
(
ﻓﺴﻴﻜﻭﻥ
:
ﻫﺫﻩ ﺍﻟﺤﻘﻴﻘﺔ ﺘﻭﺼل ﺍﻟﻴﻬﺎ ﺍﻟﻔﺭﻨﺴﻲ ﺠﺎﻜﻴﻭﺱ ﺁﻱ
.
ﺴﻲ
.
ﺸﺎﺭل
)
1746
-
1823
(
ﺤﻴﺙ ﺍﻜﺘﺸﻑ ﺜﺎﺒﺕ
ﻤﻌﺎﻤل ﺍﻟﺘﻤﺩﺩ ﻟﻠﻐﺎﺯﺍﺕ ﺍﻟﺫﻱ ﻗﺎﺩﻩ ﺍﻟﻰ ﻫﺫﺍ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺫﻱ ﺴﻤﻲ ﺒﺄﺴﻤﻪ
.
ﺴﻴﺎﹰـﻨﺭﻓ ﻥﺍ ﺔﻅﺤﻼﻤﻟﺎﺒ ﺭﻴﺩﺠﻟﺍ ﻥﻤﻭ
ﺁﺨﺭ ﻭﻫﻭ ﺠﻭﺯﻴﻑ ﻜﺎﻱ
–
ﻟﻭﺴﺎﻙ
)
1778
-
1850
(
ﻗﺩ ﺍﻜﺘﺸﻑ ﻫﺫﺍ ﺍﻻﻜﺘﺸﺎﻑ ﻨﻔﺴﻪ ﻭﻓﻲ ﺍﻟﻔﺘﺭﺓ ﺍﻟﺯﻤﻨﻴﺔ،
ﺤﻴﺙ ﻭﻀﻊ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻟﺘﺎﻟﻲ،ﻡﺠﺤﻟﺍ ﺕﻭﺒﺜﺒ ﻥﻜﻟﻭ ﹰﺎﺒﻴﺭﻘﺘ ﺎﻬﺴﻔﻨ
:
ﻀﻐﻁ ﻜﻤﻴﺔ ﻤﻌﻴﻨﺔ ﻤﻥ
ﻏﺎﺯ ﺘﺘﻨﺎﺴﺏ ﻁﺭﺩﻴﺎﹰ ﻤﻊ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻟﻤﻁﻠﻘﺔ ﺸﺭﻁ ﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
.
ﺃﻱ ﺍﻥ
:
(4.5)
.......
.
Const
T
V
T
V
T
V
2
2
1
1
=
=
=
(4.6)
.......
.
Const
T
P =
t
ﺸﻜل
)
4.4
(
-
ﻗﺎﻨ
ﻭ
ﻥ ﺸﺎﺭل ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ
ﺸﻜل
)
4.5
(
-
ﻗﺎﻨ
ﻭ
ﻥ ﺸﺎﺭل
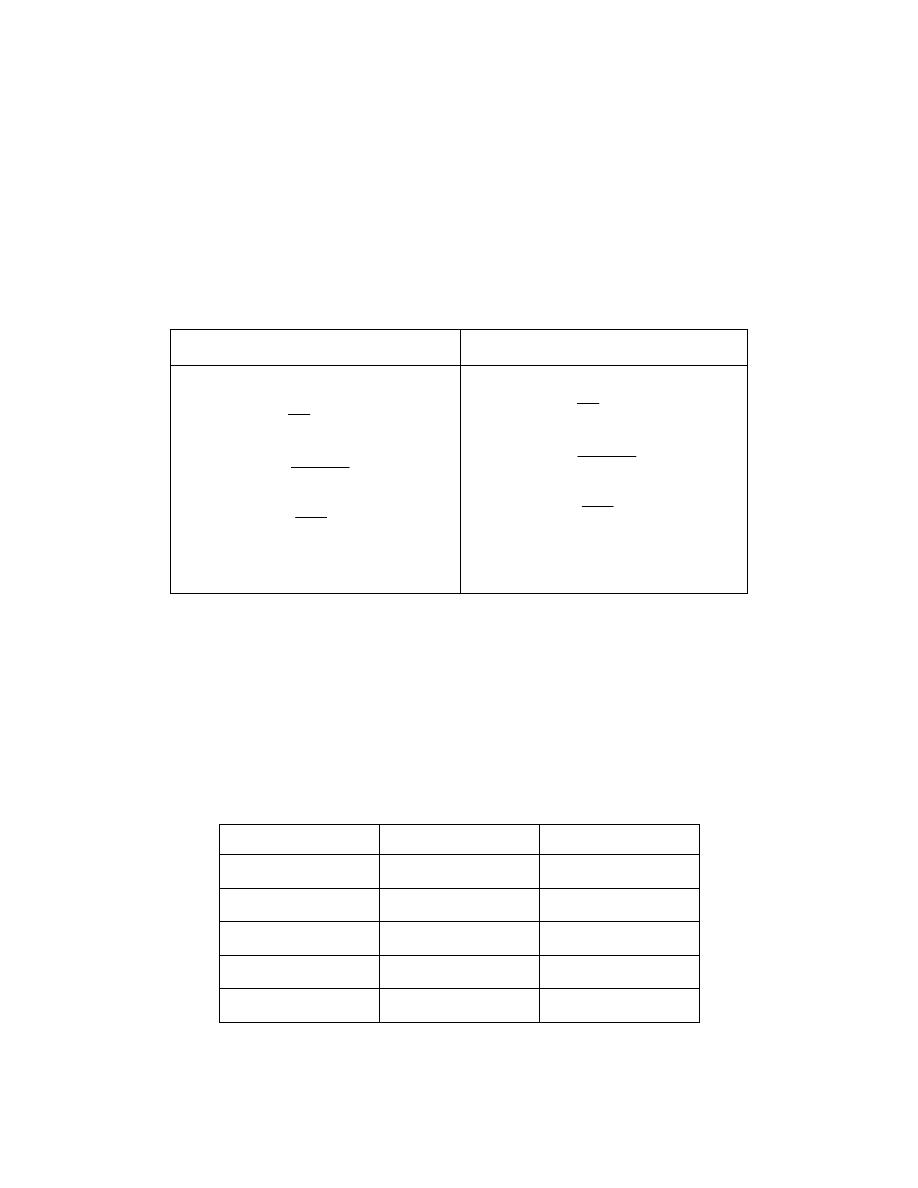
)
77
(
)
4.4
(
-
ﺍﻟﻤﺤﺭﺍﺭ ﺍﻭ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻐﺎﺯﻱ ﺫﻭ ﺍﻟﻀﻐﻁ ﺍﻭ ﺍﻟﺤﺠﻡ ﺍﻟﺜﺎﺒﺕ
ﻴﺯﺩﺍﺩ ﻀﻐﻁ ﺍﻟﻐﺎﺯ
)
ﺍﻭ ﺤﺠﻤﻪ
(
ﺒﻤﻘﺎﺩﻴﺭ ﻤﺘﺴﺎﻭﻴﺔ ﻟﻤﻘﺎﺩﻴﺭ ﻤﺘﺴﺎﻭﻴﺔ ﻤﻥ ﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ
.
ﻤﺎﺫﺍ ﻴﻘﺼﺩ
ﺒﺫﻟﻙ
.
ﺍﺫﺍ ﺴﺨﻥ ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
)
ﺍﻭ ﺜﺒﻭﺕ
ﺍﻟﺤﺠﻡ
(
ﺈﻥـﻓ ﻥﺎﻴﻠﻐﻟﺍ ﺔﻁﻘﻨ ﻰﻟﺍ ﺩﺎﻤﺠﻨﻻﺍ ﺔﻁﻘﻨ ﻥﻤ
ـﺩﺭﺠﺔ ﻭﺍﺤﺩﺓ ﻋﻠﻰ ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻤﺌﻭﻱ ﺴﺘﻤﺜل ﺒ
(1/100)
ﻤﻥ ﺘﻐﻴﺭ ﺍﻟﺤﺠﻡ ﺍﻭ ﺍﻟﻀﻐﻁ
.
ﻭﻫﻜﺫﺍ ﻴﻤﻜﻥ ﺍﺴﺘﻌﻤﺎل ﺍﻟﻤﻘﻴﺎﺱ ﺍﻟﻐﺎﺯﻱ ﺫﻭ ﺍﻟﻀﻐﻁ
)
ﺍﻭ ﺍﻟﺤﺠﻡ
(
ﺍﻟﺜﺎﺒﺕ ﻜﻤﻘﻴﺎﺱ ﻟﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
.
ﺇﻥ
ﻗﻭﺍﻨﻴﻥ ﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﺍﻜﺘﺸﻔﻬﺎ ﺸﺎﺭل ﻭﻗﻭﺍﻨﻴﻥ ﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺍﻜﺘﺸ
ﻔﻬﺎ ﻏﺎﻴﻠﻭ ﺴﺎﻙ
.
ﻨﻭﻀﺢ ﻤﺎ ﻴﺄﺘﻲ
:
V = Const.
ﻗﺎﻨﻭﻥ ﻏﺎﻴﻠﻭﺴﺎﻙ
P
=
Const.
ﻗﺎﻨﻭﻥ ﺸﺎﺭل
ﺇﻥ ﺍﻻﺸﺎﺭﺓ
(
o
)
ﺘﻌﻨﻲ ﺍﻟﻘﻴﻤﺔ ﻋﻨﺩ
(0
°C)
.
ﻭﺍﻥ
(
β)
، ﺘﻤﺜل ﻤﻌﺎﻤل ﺍﻟﺯﻴﺎﺩﺓ ﻓﻲ ﺍﻟﻀﻐﻁ
(
α)
ﻤﻌﺎﻤل
ﺍﻟﺯﻴﺎﺩﺓ ﻓﻲ ﺍﻟﺤﺠﻡ
.
ﻭﺘﺒﻴﻥ ﺍﻥ
(
β)
ﻭ
(
α)
ﺜﺎﺒﺘﺔ ﻭﻤﺘﺴﺎﻭﻴﺔ ﻟﺠﻤﻴﻊ ﺍﻟﻐﺎﺯﺍﺕ ﻜﻤﺎ ﻤﻭﻀﺤﺔ ﻓﻲ ﺠﺩ
ﻡـﻗﺭ لﻭ
)
4.1
(
ﻭﻫﻲ ﺘﺴﺎﻭﻱ
(1/273)
.
ﻤﻥ ﺍﻟﻤﻌﺎﺩﻻﺕ ﺍﻋﻼﻩ ﺘﺒﻴﻥ ﺍﻨﻪ ﻋﻨﺩ ﻀﻐﻁ
)
ﺍﻭ ﺤﺠﻡ
(
ﺜﺎﺒﺕ ﻓﺈﻥ ﺤﺠﻡ
)
ﺍﻭ
ﻀﻐﻁ
(
ﺍﻟﻐﺎﺯ ﻴﺘﻐﻴﺭ ﺒﻨﺴﺒﺔ
(1/273)
ﻋﻨﺩﻤﺎ ﺘﺯﺩﺍﺩ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺩﺭﺠﺔ ﻭﺍﺤﺩﺓ
.
ﺠﺩﻭل
)
4.1
(
ﻤﻌﺎﻤل ﺘﻤﺩﺩ ﺍﻟﻐﺎﺯﺍﺕ ﻟﻜل ﺩﺭﺠﺔ ﻤﺌﻭﻴﺔ
β
α
ﺍﻟﻐﺎﺯ
0.00367
0.00367
ﺍﻟﻬﻭﺍﺀ
0.00366
0.00366
ﺍﻟﻬﻴﺩﺭﻭﺠﻴﻥ
0.00367
0.00367
ﺍﻻﻭﻜﺴﺠﻴﻥ
0.00367
0.00367
ﺍﻟﻨﺘﺭﻭﺠﻴﻥ
0.00373
0.00374
ﺜﺎﻨﻲ ﺍﻭﻜﺴﻴﺩ ﺍﻟﻜﺎﺭﺒﻭﻥ
1)
t
(
.
P
1
t
273
1
.
P
273
273
t
.
P
T
T
.
P
P
o
o
o
o
o
+
β
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
=
=
(4.8)
.....
1)
t
(
.
V
1
t
273
1
.
V
273
273
t
.
V
(4.7)
......
T
T
.
V
V
o
o
o
o
o
+
α
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
=
=
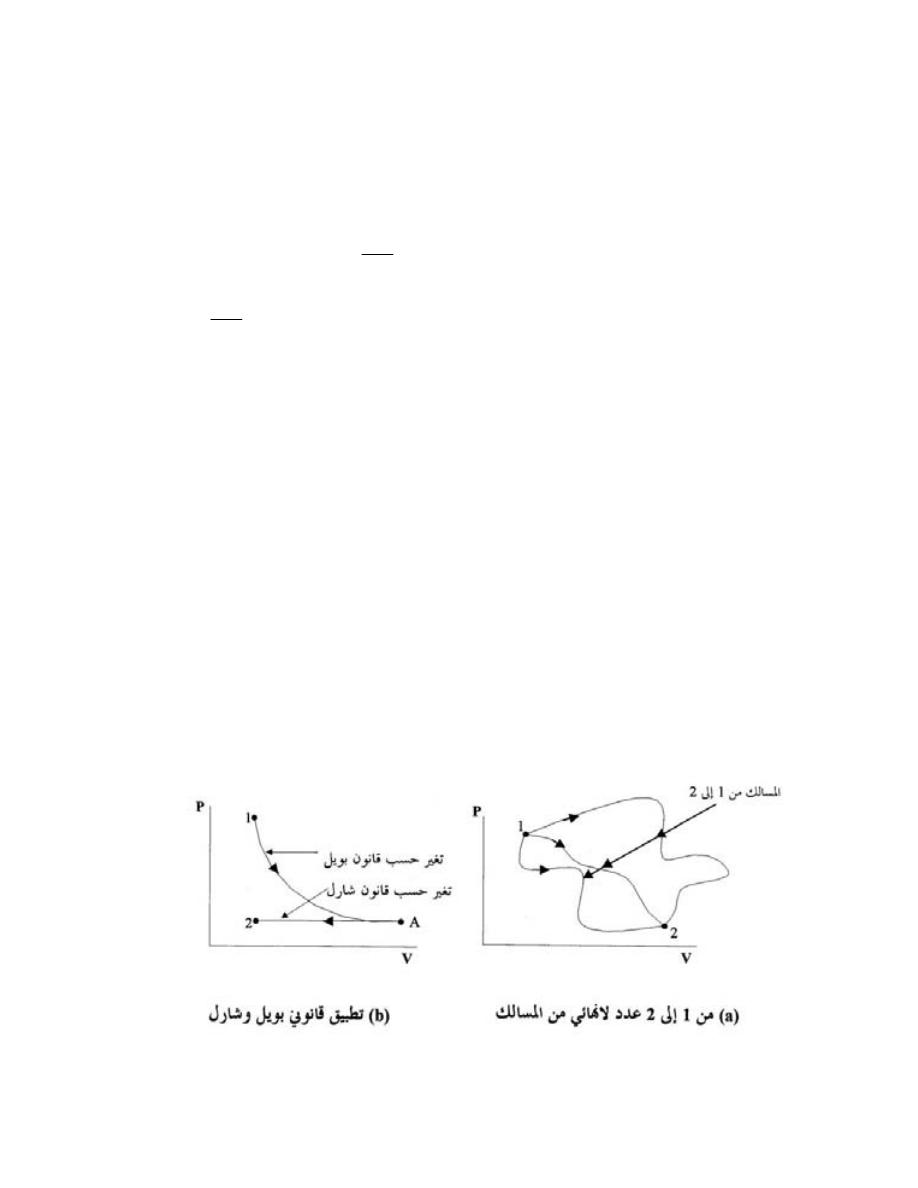
)
78
(
ﻟﺫﻟﻙ ﻴﻤﻜﻥ ﺍﺴﺘﻌﻤﺎل ﺃﻱ ﻗﺎﻨﻭﻥ ﻤﻥ ﻫﺫﻴﻥ ﺍﻟﻘﺎﻨﻭﻨﻴﻥ ﻟﻌﻤل ﻤﺤﺭﺍﺭ ﻏﺎﺯﻱ ﺴﻭﺍﺀ ﺒﻀﻐﻁ
)
ﻡـﺠﺤﺒ ﻭﺍ
(
ﺜﺎﺒﺕ
.
ﺇﻥ ﺍﻟﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ ﻴﺒﻘﻰ ﻏﺎﺯﻴﺎﹰ ﺘﺤﺕ ﺠﻤﻴﻊ ﺍﻟﻅﺭﻭﻑ
.
ﻭﻗﺩ ﻭﺠﺩ ﺍﻥ ﺤﺠ
ﺼﻔﺭـﻟﺍ ﺩﻨﻋ ﹰﺍﺼﻔﺭ ﻥﻭﻜﻴ ﻪﻤ
ﺍﻟﻤﻁﻠﻕ
(t=-273)
ﺃﻱ
:
ﻭﺍﻟﺤﺠﻡ ﺍﻟﺠﺩﻴﺩ ﻋﻥ ﺘﺴﺨﻴﻥ ﺍﻟﻐﺎﺯ ﻴﺴﺎﻭﻱ
:
ﺍﻤﺎ ﺍﻟﺤﺠﻡ ﺍﻟﺠﺩﻴﺩ ﻋﻨﺩ ﺘﺒﺭﻴﺩ ﺍﻟﻐﺎﺯ ﻓﻴﺴﺎﻭﻱ
:
)
4.5
(
-
ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ
The General Equation of Perfect Gas
ﺘﺴﻤﻰ ﺍﻴﻀﺎﹰ ﺒﻤﻌﺎﺩﻟﺔ ﺍﻟﺤﺎﻟﺔ
(Equation of State)
.
ﻗﺩ ﺘﺘ
ﺭـﻴﻐﺘ ﻰﻟﺍ ﺯﺎﻏ ﻥﻤ ﺔﻨﻴﻌﻤ ﺔﻠﺘﻜ ﺽﺭﻌ
ﻓﻲ ﺍﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ ﻭﻗﺕ ﻭﺍﺤﺩ
.
ﺸﺘﺭﻁـﻴ ﻱﺫـﻟﺍ لﻴﻭﺒ ﻥﻭﻨﺎﻗ ﻕﻴﺒﻁﺘ ﻥﻜﻤﻴ ﻻ ﻙﻟﺫﻟ
ﻭﻻ ﻗﺎﻨﻭﻥ ﺸﺎﺭل ﺍﻟﺫﻱ ﻴﺸﺘﺭﻁ ﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ،ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺕﻭﺒﺜ
.
ﺔـﻟﺩﺎﻌﻤ ﻭﺍ ﻥﻭﻨﺎﻗ ﻰﻟﺍ ﺝﺎﺘﺤﻨ ٍﺫﺌﺩﻨﻋ
ﺠﺩﻴﺩﺓ ﺘﺭﺒﻁ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﻫﺫﻩ ﺍﻟﻤﺘﻐﻴﺭﺍﺕ
.
ﻓﻌﻨﺩﻤﺎ ﺘﺘﻐﻴﺭ
ﺤﺎﻟﺔ ﺍﻟﻐﺎﺯ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻜﻤﺎ ﻓﻲ ﺸﻜل
(4.6-a)
ﺎﹰـﻴﺌﺎﻬﻨ ﻻ ﹰﺍﺩﺩﻋ ﻙﺎﻨﻫ ﻥﺍ ﻥﻴﺒﺘﻴ
ﻤﻥ ﺍﻟﻤﺴﺎﻟﻙ ﻴﺭﺒﻁ ﺒﻴﻥ ﺍﻟﺤﺎﻟﺘﻴﻥ
.
[
]
(4.9)
......
)
273
(
0
(
273
1
1
)
t
t
(
1
V
o
o
⎥⎦
⎤
⎢⎣
⎡
−
−
=
−
α
−
=
(4.10)
.......
0
1
1
273
273
1
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛ +
−
=
[
]
(4.11)
......
)
t
(t
1
V
V
0
1
o
1
+
α
+
=
[
]
(4.12)
......
)
t
(t
1
V
V
1
0
o
2
−
α
−
=
ﺸﻜل
)
4.6
(
-
ﺍﺸﺘﻘﺎﻕ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ
)
79
(
ﻭﻟﻜﻥ ﻴﺠﺏ ﺍﻥ ﻨﺨﺘﺎﺭ ﻤﺴﻠﻜﺎﹰ ﻴﺴﺘﻨﺩ ﺍﻟﻰ ﻗﺎﻨﻭﻨﻲ ﺒﻭﻴل ﻭﺸﺎﺭل ﻜﻤﺎ ﻓﻲ ﺸﻜل
(4.6-b)
.
ﺭﺽ ﺍﻥـﺘﻔﻨ
ﺨﻭﺍﺹ ﺍﻟﺤﺎﻟﺔ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ ﻟﻜﺘﻠﺔ ﻤﻌﻴﻨﺔ ﻤﻥ ﻏﺎﺯ
)
P
1
،
V
1
،
T
1
(
ﻭﺍﻟﺤﺎﻟﺔ ﺍﻟ
ﻨﻬﺎﺌﻴﺔ
)
P
2
،
V
2
،
T
2
(
ﻭﺤﺼﻭل
ﺍﻟﺘﻐﻴﺭ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻴﻜﻭﻥ ﻋﻠﻰ ﻤﺭﺤﻠﺘﻴﻥ ﻤﺘﻌﺎﻗﺒﺘﻴﻥ ﺒﻴﻨﻬﻤﺎ ﺤﺎﻟﺔ ﻤﺘﻭﺴﻁ ﻤﺜل
(A)
.
ﺎﻥـﺘﻠﺤﺭﻤﻟﺍ ﺎـﻤﺍ
ﻓﻬﻤﺎ
:
-
1
-
ﺘﻐﻴﺭ ﺍﻟﺤﺎﻟﺔ ﻤﻥ
)
1
(
ﺍﻟﻰ
(A)
ﺒﺜﺒﻭﺕ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
.
ﺒﻤﻭﺠﺏ ﻗﺎﻨﻭﻥ ﺒﻭﻴل ﻴﻜﻭﻥٍﺫﺌﺩﻨﻋ
:
P
1
V
1
= P
A
V
A
= P
2
V
A
2
-
ﺘﻐﻴﺭ ﺍﻟﺤﺎﻟﺔ ﻤﻥ
(A)
ﺍﻟﻰ
)
2
(
ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
.
ﺒﻤﻭﺠﺏ ﻗﺎﻨﻭﻥ ﺸﺎﺭل ﻴﻜﻭﻥٍﺫﺌﺩﻨﻋ
:
-
ﻭﺒﺘﻌﻭﻴﺽ ﺍﻟﻤﻌﺎﺩﻟﺔ
)
4.14
(
ـﺒ
)
4.13
(
ﻴﻜﻭﻥ
:
ﻭﺒﺄﻋﺎﺩﺓ ﺘﺭﺘﻴﺏ ﻫﺫﻩ ﺍﻟﻤﻌﺎﺩﻟﺔ ﻭﻋﻨﺩ ﻭﺠﻭﺩ ﺘﻐﻴﺭﺍﺕ ﺍﺨﺭﻯ ﻟﻨﻔﺱ ﻜﺘﻠﺔ ﺍﻟﻐﺎﺯ ﻤﺜل
)
3
،
4
،
…
ﺍﻟﺦ
(
ﻓﻴﻜﻭﻥ
:
ﻭﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ
(ν)
ﺘﻤﺜل ﺤﺠﻡ
(1Kg)
ٍ ﺃﻱ ﺍﻟﺤﺠﻡ ﺍﻟﻨﻭﻋﻲ ﻋﻨﺩﺌﺫ،ﺯﺎﻐﻟﺍ ﻥﻤ
ﻴﻜﻭﻥ
:
ﻴﺭﻤﺯ ﻟﻬﺫﺍ ﺍﻟﺜﺎﺒﺕ
(Const.)
ﺒﺎﻟﺭﻤﺯ
(R)
ﻭﻨﺴﻤﻴﻪ ﺜﺎﺒﺕ ﺍﻟﻐﺎﺯ ﺍﻟﺫﻱ ﻴﺨﺘﻠﻑ ﻤﻥ ﻏﺎﺯ ﻵﺨﺭ ﻋﻠﻴﻪ ﻴﻜﻭﻥ
:
ﺍﻤﺎ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻜﺘﻠﺔ
(m)
ﻤﻥ ﺍﻟﻐﺎﺯ ﻓﻴﻜﻭﻥ
:
PV = m R T
………. (4.19)
ﺔـﻟﺎﺤﻟﺍ ﺔﻟﺩﺎﻌﻤ ﻭﺍ ﺕﺍﺯﺎﻐﻠﻟ ﻡﺎﻌﻟﺍ ﻥﻭﻨﺎﻘﻟﺍ ﻭﺍ ﺔﻤﺎﻌﻟﺍ ﺔﻟﺩﺎﻌﻤﻟﺎﺒ ﻰﻤﺴﺘ ﺔﻟﺩﺎﻌﻤﻟﺍ ﻩﺫﻫ
.
ﺏـﺠﻴ ﺎـﻬﻴﻓﻭ
ﺍﺴﺘﻌ
ﻤﺎل ﺍﻟﻀﻐﻭﻁ ﺍﻟﻤﻁﻠﻘﺔ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻘﺔ
.
ﺔـﻴﻟﺎﺜﻤﻟﺍ ﺕﺍﺯﺎﻐﻠﻟ لﺭﺎﺸﻭ لﻴﻭﺒ ﻲﻨﻭﻨﺎﻗ ﻥﻤ لﻜ ﺢﻀﻭﺍ ﺎﻤﻜ ﹰﺎﻤﺎﻤﺘ ﺔﻠﻬﺴ ﺕﺴﻴﻟ ﺕﺍﺯﺎﻐﻟﺍ ﻥﻴﻨﺍﻭﻗ ﻥﺇ
.
ﻭﻟﻠﻐﺎﺯﺍﺕ ﺍﻟﺤﻘﻴﻘﻴﺔ ﻤﻌﺎﺩﻻﺕ ﺤﺎﻟﺔ ﺍﻜﺜﺭ ﺘﻌﻘﻴﺩﺍﹰ ﻤﻥ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﻜﻤﻌﺎﺩﻟﺔ ﺒﻴﺘﻲ
–
ﺭـﺘﻴﺩ ،ﻥﺎﻤﻜﺭﺒ
(4.13)
.
..........
P
V
P
V
2
1
1
A
=
(4.14)
..........
T
T
V
V
T
V
T
V
T
V
2
1
2
A
1
A
2
2
A
A
=
∴
=
=
(4.15)
.........
T
T
V
P
V
P
2
1
2
2
1
1
=
(4.16)
......
.
Const
T
PV
T
V
P
T
V
P
T
V
P
3
3
3
2
2
2
1
1
1
=
=
=
=
(4.17)
.........
.
Const
T
P
=
ν
(4.18)
.........
R
T
P
=
ν

)
80
(
ﻭﻤﻌﺎﺩﻟﺔ ﻓﺎﻥ ﺩ،ﺕﻭﻠﻴﺜ ﺭﻴﺒ ،ﻲﺸﻴ
ﻴﺭ ﻭﺍﻟﺯ
.
ﺎﺯـﻐﻟﺍ ﻥﻴﻨﺍﻭـﻗ ﺭـﻴﻏ ﹰﺎـﻨﻴﻨﺍﻭﻗ ﻙﺎﻨﻫ ﻥﺍ ﻥﻴﺒﺘ ﺕﻻﺩﺎﻌﻤﻟﺍ ﻩﺫﻫ
ﺍﻟﻤﺜﺎﻟﻲ
.
ﺎﻟﻲـﺜﻤﻟﺍ ﺯﺎﻐﻠﻟ ﺔﻟﺎﺤﻟﺍ ﺔﻟﺩﺎﻌﻤ ﻰﻟﺍ لﻭﺤﺘﺘ ﺕﻻﺩﺎﻌﻤﻟﺍ ﻩﺫﻫ لﻜ ﻁﻴﺴﺒﺘ ﺩﻌﺒ ﻥﻜﻟﻭ
.
ﺴﺒﺔـﻨﻟﺎﺒ ﹰﻼﺜـﻤﻓ
ﻟﻤﻌﺎﺩﻟﺔ ﻓﺎﻥ ﺩﻴﺭ ﻭﺍﻟﺯ
:
ﻭﻋﻨﺩ
(a)
ﻭ
(b)
ﺘﺴﺎﻭﻱ ﺼﻔﺭﺍﹰ ﻓﺘﺼﺒﺢ ﺍﻟﻤﻌﺎﺩﻟﺔ
:
(P + O) (
ν - O) = RT
P
ν = RT
………. (4.21)
ﺇﻥ
(R)
ﻫﻭ ﺜﺎﺒﺕ ﺍﻟﻐﺎﺯ ﻜﻤﺎ ﺍﺸﺭﻨﺎ
(Gas Constant)
ﻗﻴﻤﺘﻪ،ﺯﺎﻐﻠﻟ ﺯﻴﻤﻤﻟﺍ ﺕﺒﺎﺜﻟﺎﺒ ﹰﺎﻀﻴﺍ ﻰﻤﺴﻴﻭ
ﺘﺨﺘﻠﻑ ﺒﺎﺨﺘﻼﻑ ﺍﻟﻐﺎﺯﺍﺕ
.
ﻭﻋﻨﺩﻤﺎ ﺘﻜﻭﻥ
(mkg)
ﻓﺴﺘﻜﻭﻥ ﻭﺤﺩﺍﺕ
(R)
ﻜﺎﻟﺘﺎﻟﻲ
:
)
4.6
(
-
ﺍﻻﻨﺜﺎﻟﺒﻲ
Enthalpy
ﺃﺴﺘﺒﺩﻟﺕ ﺘﺴﻤﻴﺘﻪ ﺒﺎﻟﻤﺤﺘﻭﻯ ﺍﻟﺤﺭﺍﺭﻱ ﺍﻭ،ﺔﻴﻠﻜﻟﺍ ﺓﺭﺍﺭﺤﻟﺎﺒ ﻰﻋﺩﻴ ﻥﺎﻜ
ﺎﻟﺒﻲـﺜﻨﻻﺍ ﻭﺍ ﺔﻠﻤﺤﻤﻟﺍ ﺔﻗﺎﻁﻟﺍ
.
ﺍﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
(
µ)
ﻭﺍﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﺍﻟﺫﻱ ﻴﻜﻭﻥ ﺤﺎﺼل ﻀﺭﺒﻬﻤﺎ ﺍﻟﺸﻐل
(P
ν)
ﻭﺍﺹـﺨ ﻥـﻤ ﻲﻫ
ﻭﻋﻨﺩ ﺠﻤﻊ ﻫﺫﻩ ﺍﻟﺨﻭﺍﺹ ﺘﻅﻬﺭ ﺨﺎﺼﻴﺔ ﺠﺩﻴﺩﺓ ﺘﺴﻤﻰ ﺒﺎﻻﻨﺜﺎﻟﺒﻲ ﺭﻤﺯﻩ،ﺓﺩﺎﻤﻟﺍ
)
H
(
ﻪـﺘﺩﺤﻭﻭ
)
kJ
(
ﺎـﻤﺍ
.
ﺍﻻﻨﺜﺎﻟﺒﻲ ﺍﻟﻨﻭﻋﻲ ﻓﺭﻤﺯﻩ
)
h
(
ﺒﻭﺤﺩﺍﺕ
(kJ/kg)
ﻋﻠﻴﻪ ﻴﻜﻭﻥ
:
h =
µ + Pν
………… (4.23)
ﻭﺒﺼﻭﺭﺓ ﺘﻔﺎﻀﻠﻴﺔ ﻴﻜﻭﻥ
:
dh = d
µ + dPν
= d
µ + dPν + νdP
ﻭﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ
(P = Const.)
ﻓﺈﻥ
(dP = 0)
ﻭﺒﺎﻟﺘﺎﻟﻲ ﻴﻜﻭﻥ
:
dh = d
µ + Pdν
ﻭﺒﺘﻜﺎﻤل ﺍﻟﻤﻌﺎﺩﻟﺔ ﻴﻜﻭﻥ
:
∫dh = ∫d
µ + ∫Pdν
ﻭﺒﺎﻟﺘﺎﻟﻲ ﻓﺄﻥ
:
∆h = ∆µ + P∆ν
……….. (4.24)
(
)
(4.20)
..........
RT
b
a
P
2
=
−
ν
⎟
⎠
⎞
⎜
⎝
⎛
ν
+
(4.22)
......
...
K
.
kg
/
kJ
K
.
Kg
m
.
kN
K
1
kg
1
m
m
kN
mT
PV
R
3
2
=
=
×
×
×
=
=

)
81
(
)
4.7
(
-
ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺍﻟ
ﺤﺭﺍﺭﺘﻴﻥ ﺍﻟﻨﻭﻋﻴﺘﻴﻥ
Relationship between the Specific Heats
ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ ﺤﺭﺍﺭﺘﺎﻥ ﻨﻭﻋﻴﺘﺎﻥ ﻫﻤﺎ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﻭﺭﻤﺯﻫﺎ
(Cv)
ﺎـﻫﺯﻤﺭﻭ ﻁﻐﻀـﻟﺍ ﺕﻭـﺒﺜﺒﻭ
(Cp)
.
ﻓﻌﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻻﺠﺭﺍﺀ ﻤﺘﻨﺎﻫﻲ ﺍﻟﺼﻐﺭ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﻓﺄﻥ
:
or
(d
µ)
ν
= Cv (dT)
ν
or
d
µ = Cv d T
ﺒﺘﻜﺎﻤل ﺍﻟﻤﻌﺎﺩﻟﺔ ﻴﻨﺘﺞ
:
∆ µ = Cv ∆ T
……….. (4.26)
ﻭﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻻﺠﺭﺍﺀ ﻤﺘﻨﺎﻫﻲ ﺍﻟﺼﻐﺭ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﻓﺈﻥ
:
or
(dh)
p
= Cp (dT)
p
or
dh = Cp dT
ﻭﺒﺘﻜﺎﻤل ﺍﻟﻤﻌﺎﺩﻟﺔ ﻴﻨﺘﺞ
:
∆h = Cp ∆T
……….. (4.28)
ﺍﻤﺎ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺍﻟﺤﺭﺍﺭﺘﻴﻥ ﺍﻟﻨﻭﻋﻴﺘﻴﻥ ﻓﺘﺸﺘﻕ ﻜﻤﺎ ﻴﺄﺘﻲ
:
h =
µ + Pν
∆ h = ∆ µ + P ∆ ν
Cp
∆T = Cv ∆ T + R ∆T
R = Cp – Cv
………….. (4.29)
ﺒﻤﺎ ﺍﻥ
(R)
ﻟﺫﺍ ﻴﺠﺏ ﺍﻥ ﺘﻜﻭﻥ،ﺔﺒﺠﻭﻤ ﺔﻴﻤﻜ
Cp > Cv
ـ ﺃﻱ ﻋﻨﺩﻤﺎ ﺘﺘﻐﻴﺭ ﺍﻟ،ﹰﺎﻤﺌﺍﺩ
(Cp)
ـ ﻭﺍﻟ
(Cv)
ﺒﺘﻐﻴﺭ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻴﺒﻘﻰ ﺍﻟﻔﺭﻕ ﺒﻴﻨﻬﻤﺎ ﺜﺎﺒﺘﺎﹰ
.
(4.25)
.
..........
T
Cv
υ
⎟
⎠
⎞
⎜
⎝
⎛
∂
µ
∂
=
(4.27)
.
..........
T
h
Cp
p
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
)
82
(
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
)
4.2
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.9 m
3
)
ﻭﻀﻐﻁﻪ
(1 bar)
ﻀﻐﻁ ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ
ﺍﻟﻰ
(0.3m
3
)
ﺍﺤﺴﺏ
)
1
(
ﺍﻟﻀﻐﻁ ﺍﻟﻨﻬﺎﺌﻲ
)
2
(
ﻜﻡ ﻴﺼﺒﺢ ﻀﻐﻁ ﺍﻟﻐﺎﺯ ﺇﺫﺍ ﻜﺎﻨﺕ ﺍﻟﺯﻴﺎﺩﺓ ﺒﻤﻘﺩﺍﺭ،ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺎﻨﺩﺯ ﻭﻟ
(1.2/1)
.
)
4.3
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(40kN/m
2
)
ﻭﺤﺠﻤﻪ
(0.1m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(25
°C)
ﻋﻠﻰ ﺍﻟﺘﻭﺍﻟﻲ
.
ﻀﻐﻁ ﺍﻟﻐﺎﺯ ﺍﻟﻰ
(700kN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(60
°C)
ﺍﺤﺴﺏ ﺍﻟﺤﺠﻡ ﺍﻟﺠﺩﻴﺩ،
.
)
4.4
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(350kN/m
2
)
ﻭﺤﺠﻤﻪ
(0.03m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(35
°C)
ﺍﺭﺘﻔﻊ ﻀﻐﻁﻪ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
ﺍﻟﻰ
(1.05 MN/m
2
)
.
ﺇﺫﺍ ﻜﺎﻥ،ﺓﺩﻴﺩﺠﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺏﺴﺤﺍ
:
R = 0.29 kJ/kg . K
ﻭﺍﺤﺴﺏ ﺍﻴﻀﺎﹰ ﻜﺘﻠﺔ ﺍﻟﻐﺎﺯ
.
)
4.5
(
(4.2kg)
ﺎﺯــﻏ ﻥــﻤ
(CO
2
)
ﻐﻁﻪــﻀ
(12bar)
ﻪــﺘﺭﺍﺭﺤ ﺔــﺠﺭﺩﻭ
(92
°C)
ﺎﻥــﻜ ﺍﺫﺈــﻓ
R = 0.189 kJ/kg . K
.
ﺍﺤﺴﺏ ﺤﺠﻡ
(CO
2
)
.
)
4.6
(
ﺍﻭﻜﺴﺠﻴﻥ ﻀﻐﻁﻪ
(15.5 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(410
°C)
ﻭﻜﺎﻥ
R=0.26 kJ/kg.K
.
ﺍﺤﺴﺏ ﺍﻟﻜﺜﺎﻓﺔ
.
bar
3.6
1
1.2
0.3
0.9
1
T
T
V
V
P
P
-
2
bar
3
0.3
0.9
1
V
V
P
P
1
1
2
2
1
1
2
2
1
1
2
=
×
×
=
×
=
=
×
=
=
−
3
1
1
2
2
1
2
m
0.0223
0.1
298
333
700
140
V
T
T
P
P
V
=
×
×
=
×
×
=
C
651
K
924
35
.
0
05
.
1
308
P
P
T
T
kg
118
.
0
308
0.29
0.03
350
RT
PV
m
1
2
1
2
o
=
=
=
×
=
=
×
×
=
=
3
m
2414
.
0
100
12
0.189
365
2
.
4
P
mTR
V
=
×
×
×
=
=
3
2
kg/m
728
.
8
0.26
683
10
5
.
15
TR
P
=
×
×
=
=
ρ

)
83
(
)
4.7
(
ﻭﻋﺎﺀ ﺤﺠﻤﻪ
(0.2m
3
)
ﻴﺤﺘﻭﻱ ﻋﻠﻰ ﻨﻴﺘﺭﻭﺠﻴﻥ ﻋﻨﺩ ﻀﻐﻁ
(1.013bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(15
°C)
.
ﻡـﺘ
ﻀﺦ
(0.2kg)
ﻤﻥ ﺍﻟﻨﺘﺭﻭﺠﻴﻥ ﺒﻭﺍﺴﻁﺔ ﻤﺨﻀﺔ ﺨﺎﺼﺔ
ﺍﻟﻰ ﺍﻟﺨﺯﺍﻥ
.
ﺩـﻨﻋ ﺯﺎـﻐﻠﻟ ﺩﻴﺩﺠﻟﺍ ﻁﻐﻀﻟﺍ ﺏﺴﺤﺍ
ﺔــﻴﺌﺍﺩﺘﺒﻻﺍ ﻪــﺘﺭﺍﺭﺤ ﺔــﺠﺭﺩ ﻰــﻟﺍ ﻥﺍﺯــﺨﻟﺍ ﻉﻭــﺠﺭ
.
،ﺎﻟﻲــﺜﻤ ﺯﺎــﻏ ﻥﻴﺠﻭﺭــﺘﻨﻟﺍ ﺭــﺒﺘﻋﺍ
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R = 296.9 J/kg . K
m
2
= m
1
+ 0.2 = 0.337 + 0.2 = 0.437 kg
)
4.8
(
(0.01Kg)
ﻤﻥ ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻴﺸﻐل ﺤﺠﻡ ﻤﻘﺩﺍﺭﻩ
(0.003m
3
)
ﻐﻁـﻀ ﺩـﻨﻋ
(7bar)
ﻭﺩﺭ
ﺭﺍﺭﺓـﺤ ﺔـﺠ
(131
°C)
.
ﻋﻨﺩﻤﺎ ﺴﻤﺢ ﻟﻠﻐﺎﺯ ﺒﺎﻟﺘﻤﺩﺩ ﺍﻟﻰ ﻀﻐﻁ
(1bar)
ﺎﺌﻲـﻬﻨﻟﺍ ﻪﻤﺠﺤ ﺢﺒﺼﺍ
(0.02m
3
)
.
ﺴﺏـﺤﺇ
ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺍﻟﻐﺎﺯ ﺍﻟﻨﻬﺎﺌﻴﺔ
.
)
4.9
(
ﻗﻨﻴﻨﺔ ﺤﺩﻴﺩﻴﺔ ﺤﺠﻤﻬﺎ
(12L)
ﺘﺤﺘﻭﻱ ﻋﻠﻰ
(CO
2
)
ﺭﺍﺭﺓـﺤ ﺔـﺠﺭﺩﺒ
(20
°C)
ﻐﻁـﻀﻭ
(73.5 bar)
.
ﺍﺤﺴﺏ ﻜﺘﻠﺔ
(CO
2
)
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R
CO2
= 0.189 kJ/kg . K
kg
237
.
0
288
0.2969
0.2
10
013
.
1
RT
V
P
m
2
1
1
1
1
=
×
×
×
=
=
bar
87
.
1
0.2
288
0.2969
437
.
0
V
mRT
P
2
2
2
=
×
×
=
=
C
111.52
K
5
.
384
0.52
0.01
0.02
100
mR
V
P
T
K
.
kg
/
J
k
52
.
0
404
0.01
0.003
10
7
mT
V
P
R
2
2
2
2
1
1
1
o
=
=
×
×
=
=
=
×
×
×
=
=
kg
593
.
1
293
0.189
0.012
10
5
.
73
RT
V
P
m
2
1
1
1
=
×
×
×
=
=
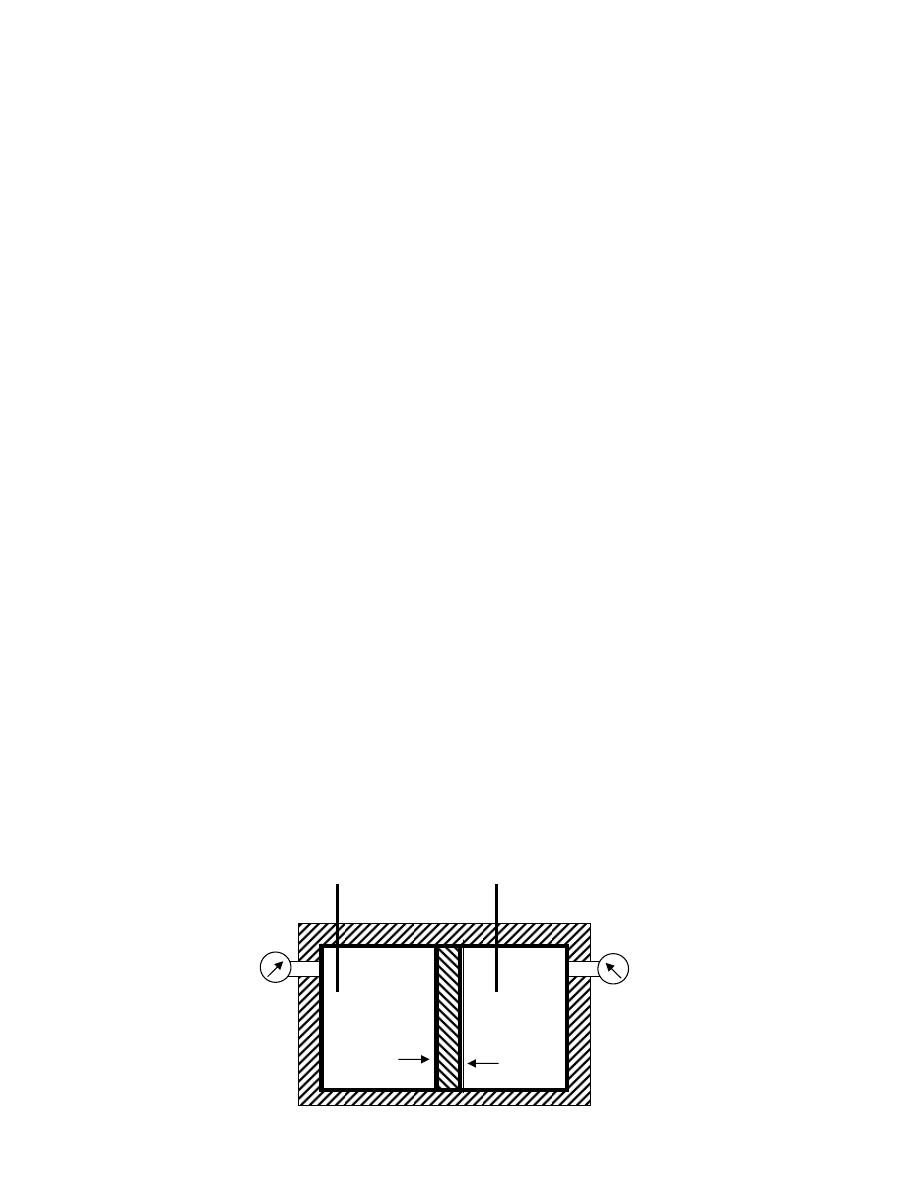
)
84
(
ﻤﺴﺎﺌ
ـ
ل
)
4.1
(
ﻨﻅﺎﻡ ﻤﻌﺯﻭل ﺤﺭﺍﺭﻴﺎﹰ ﻴﺘﻜﻭﻥ ﻤﻥ ﺠﺯﺌﻴﻥ
)
a
ﻭ
b
(
ﺎﺯـﻐﻟﺍ ﻰﻠﻋ ﻥﺎﻴﻭﺘﺤﻴ ﻱﺭﺍﺭﺤ لﺎﺯﻋ ﻭﺫ ﺯﺠﺎﺤ ﺎﻤﻬﻨﻴﺒ
ﺯﺀـــﺠﻟﺍ ﻡـــﺠﺤ ،ﻪﺴـــﻔﻨ
(a)
(10L)
ﻪـــﺘﺭﺍﺭﺤ ﺔـــﺠﺭﺩﻭ
(100
°C)
ﻐﻁﻪـــﻀﻭ
(10 bar)
ﻭﺤﺠﻡ ﺍﻟﺠﺯﺀ
(b)
(20L)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﻭﻀﻐﻁﻪ
(5 bar)
.
ﺎﺠﺯـﺤﻟﺍ لﻴﺯﺃ ﺍﺫﺈﻓ
ﺒﻴﻥ ﺍﻟﺠﺯﺌﻴﻥ ﺒﺤﻴﺙ ﺘ
ﺴﺎﻭﻱ ﺍﻟﻀﻐﻁ ﻓﻲ ﺠﻤﻴﻊ ﺍﺠﺯﺍﺌﻪ
.
ﺃﻭﺠﺩ ﺍﻟﻀﻐﻁ ﺍﻟﻨﻬﺎﺌﻲ ﻭﺃﻫﻤل ﺤﺠﻡ ﺍﻟﺤﺎﺠﺯ
.
ﻋﻠﻤﺎﹰ
ﺃﻥ
:
R=0.25 kJ/kg.K
.
ﺝ
) :
6.658 bar
(
)
4.2
(
ﺨﺯﺍﻥ ﻤﻐﻠﻕ
.
ﺤﺠﻤﻪ
(0.5m
3
)
ﻴﺤﺘﻭﻱ ﻋﻠﻰ ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(0.75kg)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(25
°C)
.
ﻓﺈﺫﺍ ﻜﺎﻨﺕ
ﻗﺭﺍﺀﺓ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ ﻫﻲ
(1bar)
.
ﺍﻭﺠﺩ ﻤﺎ ﻴﻠﻲ
) :
1
(
ﺎﻨﻭﻤﻴﺘـﻤﻟﺍ ﺓﺀﺍﺭـﻗ
ﺩﺍﺕـﺤﻭﺒ ﺭ
(mmHg)
) .
2
(
ﺇﺫﺍ
ﺃﻀﻴﻑ ﻟﻠﻐﺎﺯ ﺤﺭﺍﺭﺓ ﻤﻘﺩﺍﺭﻫﺎ
(15kJ)
ﻜﻡ ﺴﺘﺼﺒﺢ ﻗﺭﺍﺀﺓ ﺍﻟﻤﺎﻨﻭﻤﻴﺘﺭ ﺒﻭﺤﺩﺍﺕ
(mmHg)
ﺍﻴﻀﺎﹰ
.
ﺎﹰـﻤﻠﻋ
ﺒﺄﻥ
:
Cp = 1.005 kJ/kg.K. Cv = 0.717 kJ/kg.K.
ρHg = 13600 kg/m
3
ﺝ
) :
215 mmHg
305 mmHg.
(
)
4.3
(
ﺍﻟﻨﻅﺎﻡ ﺍﻟﻤﺒﻴﻥ ﻓﻲ ﺍﻟﺸﻜل ﺍﻟﻤﻌﺯﻭل ﺤﺭﺍﺭﻴﺎﹰ ﻭﻴﺤﻭﻱ ﻋﻠﻰ
ﻏﺎﺯ ﺍﻻﻭﻜﺴﺠﻴﻥ
(O
2
)
ﻓﻲ ﺍﻟﺤﻴﺯ
(A)
ﻪـﺘﻠﺘﻜﻭ
(1.5kg)
ﻭﻏﺎﺯ ﺍﻟﻨﺘﺭﻭﺠﻴﻥ
(N
2
)
ﻓﻲ ﺍﻟﺤﻴﺯ
(B)
ﻭﻜﺘﻠﺘﻪ
(5.2 kg)
ﺔـﻨﻴﺒﻤﻟﺍ ﺕﺍﺀﺍﺭـﻘﻟﺍ ﻥﻴﺯﻴﺤﻟﺍ ﻼﻜﻟﻭ
ﺒﺎﻟﺸﻜل
.
ﺒﺤﺕـﺼﺍ ﺙـﻴﺤﺒ ﹰﺎﻴﺭﺍﺭﺤ ﻥﺯﺘﺇ ﻥﺍ ﻰﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻙﺭﺘﻭ ﻥﻴﺯﻴﺤﻟﺍ ﻥﻴﺒ ﻱﺭﺍﺭﺤﻟﺍ لﺯﺎﻌﻟﺍ ﻊﻓﺭ ﺍﺫﺈﻓ
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ ﺍﻟﺤﻴﺯ
(A)
ﻭﺍﻟﺤﻴﺯ
(B)
(60.19
°C)
.
ﻀﻐﻁـﻟﺍ ﺕﻭﺒﺜﺒ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺩﺠ
(Cp)
ﺎﹰ ﺍﻥـﻤﻠﻋ ﻥﻴﺠﻭﺭﺘﻴﺎـﻨﻟﺍﻭ ﻥﻴﺠﺴـﻜﻭﻻﺍ ﺯﺎﻐﻟ
)
ﺎﺭﻭﻤﻴﺘﺭـﺒﻟﺍ ﺓﺀﺍﺭـﻗ
(760mmHg)
ﻕـﺒﺌﺯﻟﺍ ﺔـﻓﺎﺜﻜﻭ
(13600 kg/m
3
)
،
(Cv N
2
= 0.744 kJ/kg.K)
.
ﺃﻫﻤل ﺤﺠﻡ ﺍﻟﻌﺎﺯل ﺍﻟﺤﺭﺍﺭﻱ
t=50
0
C
t=100
0
C
P
g
=4bar
(B)
V=0.992m
3
ﻋﺎﺯل ﺤﺭﺍﺭﻱ
(A)
V=0.483m
3
ﺤﺎﺠﺯ
P
g
=2bar

)
85
(
ﺍﻟﻔﺼﻞ ﺍﻟﺨﺎﻣﺲ
–
ﺍﻟﻘﺎﻧﻮﻥ ﺍﻷﻭﻝ ﻟﺪﻳﻨﺎﻣﻴﻚ ﺍﻟﺤﺮﺍﺭﺓ
)
5.1
(
-
ﺍﻟﻘﺎﻨﻭﻥ ﺍﻷﻭل ﻟﺩﻴﻨﺎﻤﻴﻙ ﺍﻟﺤﺭﺍﺭﺓ
The First Law of Thermodynamics
ﻥـﻤ ﺩﺠﻭ ﻱﺫﻟﺍ ،لﻭﻷﺍ ﻥﻭﻨﺎﻘﻟﺍ ﻭﻫ ﺓﺭﺍﺭﺤﻟﺍ ﻙﻴﻤﺎﻨﻴﺩ لﻜﻴﻫ ﺎﻬﻴﻠﻋ ﺩﻤﺘﻌﻴ ﻲﺘﻟﺍ ﺔﻤﻬﻤﻟﺍ ﻥﻴﻨﺍﻭﻘﻟﺍ ﻥﻤ
ﻴﺘﻨﺎﻭل ﻜل ﺃﺸﻜﺎل ﺍﻟﻁﺎﻗﺔ،ﻪﺘﺭﺒﺨﻭ ﻥﺎﺴﻨﻻﺍ ﺔﺒﺭﺠﺘ لﻼﺨ
ﺭﺍﺭﺓـﺤﻟﺍ ﺎﻬﻴﻠﻜﺸﺒ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺔﻗﺎﻁﻟﺎﻜ ،ﺔﻌﻴﺒﻁﻟﺍ ﻲﻓ
ﻭﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﺨﺯﻭﻨﺔ ﺒﻜل ﺃﺸﻜﺎﻟﻬﺎ،لﻐﺸﻟﺍﻭ
.
ﻰ ﻭﻻـﻨﻔﺘ ﻻ ﺔﻗﺎﻁﻟﺍ ،ﺔﻗﺎﻁﻟﺍ ﻅﻔﺤ ﻥﻭﻨﺎﻗ ﻎﻴﺼ ﻥﻤ ﺔﻐﻴﺼ ﻭﻫ
ﻓﻤﺘﻰ ﻤﺎ ﺍﺨﺘﻔﻰ ﺸﻜل ﻤﻥ ﺃﺸﻜﺎل ﺍﻟﻁﺎﻗﺔ ﻅﻬﺭ،ﺙﺩﺤﺘﺴﺘ
ﺒ
ﺸﻜل ﺁﺨﺭ
.
ﺸﻐلـﻟﺍ ﺕﺎـﻴﻤﻜ ﺏﺴﺤﻨ ﻪﺘﻁﺎﺴﻭﺒ
ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻋﺒﺭ ﺤﺩﻭﺩ ﺍﻟﻨﻅﺎﻡ ﻋﻨﺩﻤﺎ
ﻤﺜﻼﹰ ﺍﻟﺸﻐل ﺍﻟﻨﺎﺘﺞ ﻤﻥ ﺘﻤﺩﺩ،ﺔﻟﺎﺤﻟﺍ ﻲﻓ ﺔﻨﻴﻌﻤ ﺕﺍﺭﻴﻐﺘ ﺙﺩﺤﺘ
ﻁﻐـﻀ ﺩﻨﻋ ﺭﺎﺨﺒ ﺩﻴﻟﻭﺘﻟ ﺔﻤﺯﻼﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻭﺍ ،ﻁﻏﺎﻀ ﻲﻓ ﺀﺍﻭﻫ ﻁﻐﻀﻟ ﻡﺯﻼﻟﺍ لﻐﺸﻟﺍ ،ﻥﻴﺒﺭﻭﺘ ﻲﻓ ﺭﺎﺨﺒ
ﻤﻌﻴﻥ ﺩﺍﺨل ﺍﻟﻤﺭﺠل
.
ﻰـﻟﺍ ﹰﺎـﻴﻠﻜ لﻐﺸـﻟﺍ لﻴﻭﺤﺘ ﻥﻜﻤﻴ ﻪﻨﺍ ﺢﻀﻭﺍ ﺫﺇ ،ﻩﺎﺠﺘﻻﺍﻭ لﻭﺤﺘﻟﺍ ﺔﺒﺴﻨ لﻭﻻﺍ ﻥﻭﻨﺎﻘﻟﺍ لﻤﻫﺍ ﺩﻘﻟ
ﺤﺭﺍﺭﺓ ﺒﺎﻻ
ﺘﻨﺎـﺴﺍﺭﺩ ﺩـﻨﻋ ﻅﺤﻼﻨـﺴ ﺎـﻤﻜ ،لﻐﺸ ﻰﻟﺍ ﹰﺎﻴﻠﻜ ﺓﺭﺍﺭﺤﻟﺍ لﻴﻭﺤﺘ لﻴﺤﺘﺴﻤﻟﺍ ﻥﻤ ﻥﻜﻟﻭ ﻙﺎﻜﺘﺤ
ﻟﻠﺩﻭﺭﺍﺕ ﺍﻟﺤﺭﺍﺭﻴﺔ
.
)
5.2
(
-
ﺘﺠﺭﺒﺔ ﺠﻭل
Joule’s Experiment
ﺭﺍﺭﺓـﺤﻟﺍ ﻥﻴـﺒ ﺔـﻴﻤﻜﻟﺍ ﺔـﻗﻼﻌﻟﺍ ﺩﺎﺠﻴﻷ لﻭﺠ ﺔﺒﺭﺠﺘ ﻲﻫ ﻥﻭﻨﺎﻘﻟﺍ ﺍﺫﻫ ﺕﺭﻗﺍ ﻲﺘﻟﺍ ﺏﺭﺎﺠﺘﻟﺍ ﻥﻤ
ﻭﺍﻟﺘﻲ ﺘﻠﺨﺹ ﻜﻤﺎ ﻴﺄﺘﻲ،لﻐﺸﻟﺍﻭ
:
ﻴﺘﻜﻭﻥ ﺍﻟﺠﻬﺎﺯ ﻜﻤ
ﺎ ﻓﻲ ﺸﻜل
)
5.1
(
ﻤﻥ ﻭﻋﺎﺀ ﻤﻐﻠﻕ ﻤﻌﺯﻭل ﻴﺤﺘﻭﻱ ﻋﻠﻰ ﻤﺎﺌﻊ
.
ﻓﺈﺫﺍ ﻫﺒﻁ ﺍﻟﻭﺯﻥ
(m)
ﻤﺴﺎﻓﺔ
(Z)
ﻓﺄﻥ ﺸﻐﻼﹰ ﻤﺎ
(W
in
)
ﺴﻭﻑ ﻴﻨﺠﺯ ﻋﻠﻰ ﺍﻟﻤﺎﺌﻊ ﻴﺤﺴﺏ ﺒﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(mgz)
ﻓﺴﺘﺭﺘﻔﻊ،
ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺍﻟﻤﺎﺌﻊ
.
ﺎﺌﻊـﻤﻟﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩ ﺕﺩﺎﻌﻓ ،ﺀﺎﻤ ﺽﻭﺤ ﻲﻓ ﺀﺎﻋﻭﻟﺍ ﻊﻀﻭﻭ ﺔﻟﺯﺎﻌﻟﺍ ﺓﺩﺎﻤﻟﺍ ﺕﺩﻌﺒﺍ
ﺸﻜل
)
5.1
(
-
ﺘﺠﺭﺒﺔ ﺠﻭل
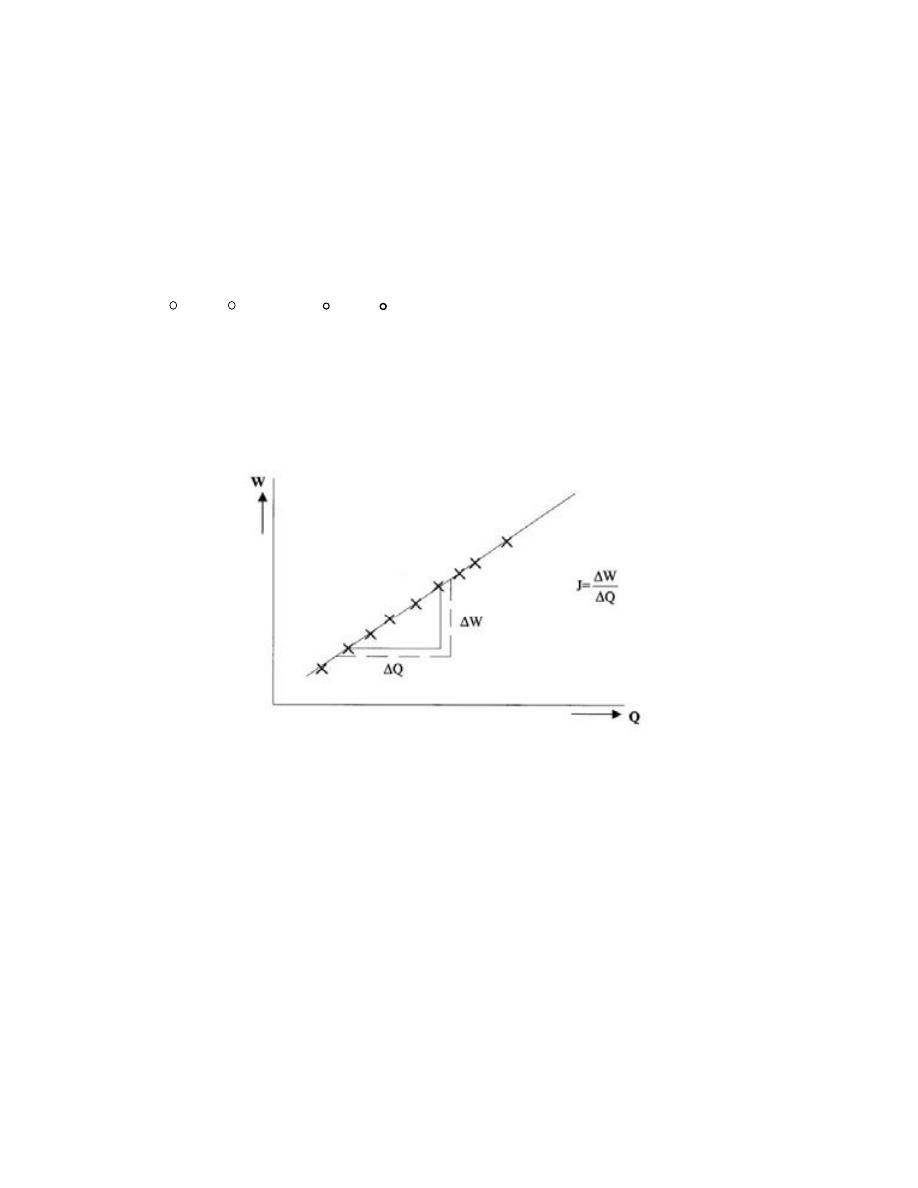
)
86
(
ﺍﻟﻰ ﻗﻴﻤﺘﻬﺎ ﺍﻻﺼﻠﻴ
ﺔ ﺒﻌﺩ ﺇﻨﺘﻘﺎل ﻜﻤﻴﺔ ﻤﻥ ﺍﻟﺤﺭﺍﺭﺓ
(Q
out
)
ﺩﺍﺭـﻘﻤ لﻼﺨ ﻥﻤ ﺏﺴﺤﺘ ﺀﺎﻤﻟﺍ ﻰﻟﺍ ﻊﺌﺎﻤﻟﺍ ﻥﻤ
ﺇﺭﺘﻔﺎﻉ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺍﻟﻤﺎﺀ
.
ﺒﺫﻟﻙ ﻴﻜﻭﻥ ﺍﻟﻨﻅﺎﻡ ﻗﺩ ﻤﺭ ﺒﺩﻭﺭﻩ
.
ﺍﻜﺘﺸﻑ ﺠﻭل ﺍﻥ ﺍﻟﺸﻐل
(W
in
)
ﻴﺘﻨﺎﺴﺏ ﻤﻊ
ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ
(Q
out
)
ﺃﻱ،
:
Q
out
α W
in
Q
out
= W
in
ﻭﻟﻠﻭﺤﺩﺍﺕ ﻨﻔﺴﻬﺎ
.
ﻭﺒﺼﻭﺭﺓ ﻋﺎﻤﺔ ﻟﻸﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ
ﻋﻨﺩﻤﺎ ﺘﻤﺭ ﺒﺩﻭﺭﻩ ﻓﺈﻥ
:
ﺘﻤﺜل ﺍﻟﻤﻌﺎﺩﻟﺘﺎﻥ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺍﻨﻔﺎﹰ ﺍﻟﺘﻌﺒﻴﺭ ﺍﻟﺭﻴﺎﻀﻲ ﻟﻠﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻟﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻴﻤﺭ ﺒﺩﻭﺭﻩ
.
ﻭﻟﻭﺤﻅ ﺍﻥ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ
(W)
ﻭ
(Q)
ﻁﺭﺩﻴﺔ ﺒﺤﺴﺏ ﺍﻟﺸﻜل
)
5.2
.(
ﺤﻴﺙ ﺘﻤﺜل
(J)
ﺔـﺘﺒﺎﺜ ﺔﻤﻴﻗ
ﺘﺴﻤﻰ ﺒﻤﻜﺎﻓﺊ ﺠﻭل ﻭﺘﺴﺎﻭﻱ
(4.2kJ/kcal)
ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﺸﻐل ﺒﻭﺤﺩﺍﺕ ﺍﻟﺠﻭل
ﺩﺍﺕـﺤﻭﺒ ﺓﺭﺍﺭـﺤﻟﺍﻭ
(kcal)
ﻜﻤﺎ ﻜﺎﻥ ﺴﺎﺒﻘﺎﹰ،
.
)
5.3
(
-
ﺼﻴﻎ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
The First Law Statement
ﺔـﻘﻠﻐﻤﻟﺍ ﺔـﻤﻅﻨﻻﺍ ﻲﻓ لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻴﺒ ﺔﻗﻼﻌﻟﺍ ﺕﺤﻀﻭﺍ لﻭﺠ ﺎﻬﻴﻟﺍ لﺼﻭﺘ ﻲﺘﻟﺍ ﺞﺌﺎﺘﻨﻟﺍ ﻥﺍ
ﻴﻌﺒﺭ ﻋﻨﻬﺎ ﺒﺎﻟﺼﻴﻎ ﺍﻟﺘﺎﻟﻴﺔ
:
ﻋﻨﺩﻤﺎ ﻴﻤﺭ ﺍﻟﻨﻅﺎﻡ ﺒﺩﻭﺭﻩ ﺃﻱ ﻴﻌﻭﺩ ﺍﻟﻰ ﺤﺎﻟﺘﻪ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ ﺒﻌﺩ
ﻤﺭﻭﺭﻩ ﺒﺴﻠﺴﻠﺔ ﻤﻥ ﺍﻻﺠﺭﺍﺀﺍﺕ ﻓﺈﻥ
:
ﺃ
-
ﺘﺘﺤﻭل ﺍﻟﺤﺭﺍﺭﺓ ﻜﻠﻴﺎﹰ ﺍﻟﻰ ﺸﻐل
.
ـﻓﻠﻨﻔﺱ ﺍﻟﻭﺤﺩﺍﺕ ﻴﻌﺒﺭ ﻋﻨﻬﺎ ﺭﻴﺎﻀﻴﺎﹰ ﺒ
(Q=W)
.
∫
∫
∑
∑
=
⇒
=
(5.1)
......
W
Q
dW
dQ
ﺸﻜل
)
5.2
(
-
ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ
)
ﻤﻜﺎﻓﺊ ﺠﻭل
J
(
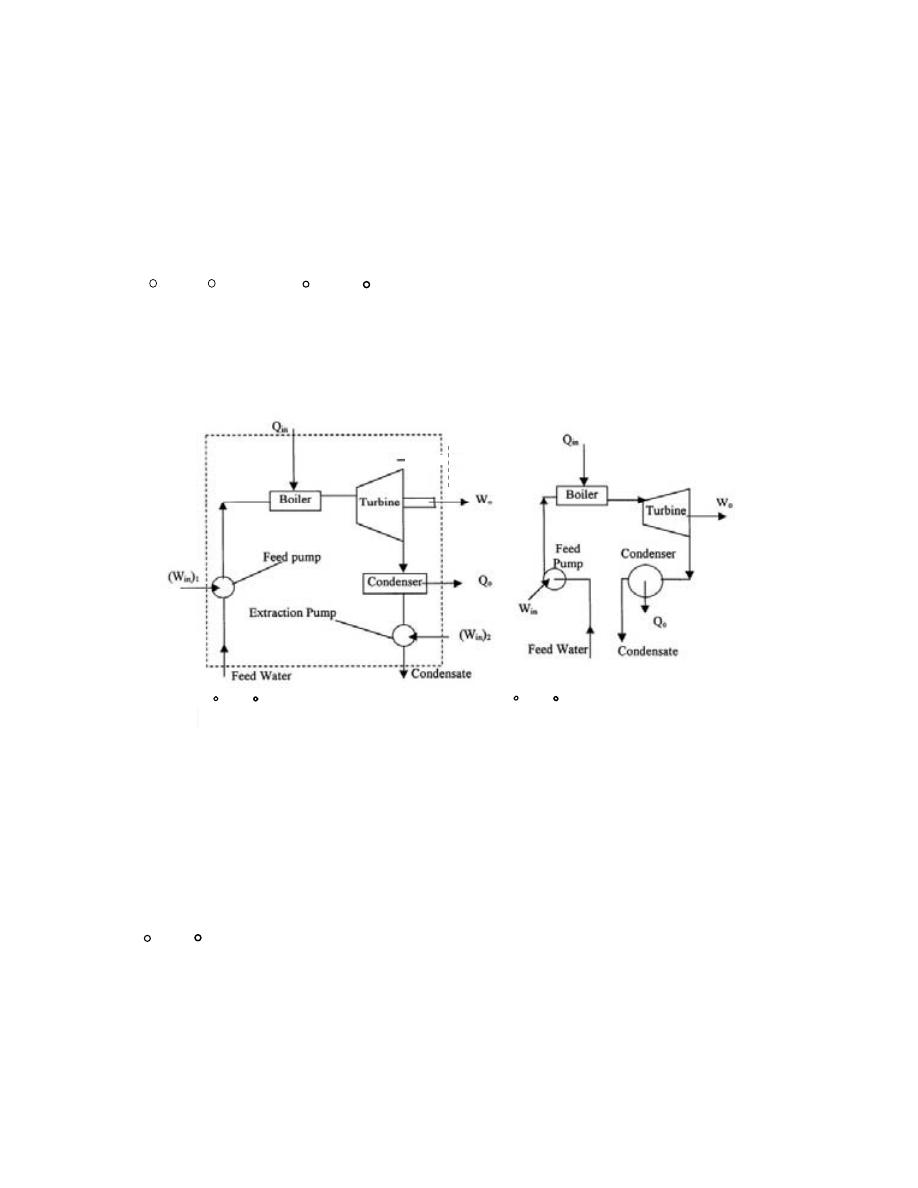
)
87
(
ﺏ
-
ﺍﻟﺤﺭﺍﺭﺓ ﻫﻲ ﺍﺤﺩﻯ ﺼﻭﺭ ﺍﻟﻁﺎﻗﺔ
.
ﺎـﻬﻠﻴﻭﺤﺘ ﻭﺍ ﻲﻜﻴﻨﺎﻜﻴﻤﻟﺍ لﻐﺸﻟﺍ ﻥﻤ ﺎﻬﻴﻠﻋ لﻭﺼﺤﻟﺍ ﻥﻜﻤﻤﻟﺍ ﻥﻤ
ﺍﻟﻴﻪ
.
ﺃﻱ
(Q
⇔W)
.
ـﺠ
-
ﺍﻟﺘﻜﺎﻤل ﺍﻟﺩﻭﺭﻱ ﻟﻠﺤﺭﺍﺭﺓ ﺘﺘﻨﺎﺴﺏ ﻁﺭﺩﻴﺎﹰ ﻤﻊ ﺍﻟﺘﻜﺎﻤل ﺍﻟﺩ
ﻭﺭﻱ ﻟﻠﺸﻐل ﺍﻭ ﺍﻟﻤﺠﻤﻭﻉ ﺍﻟﺠﺒﺭﻱ ﻟﻠﺤﺭﺍﺭﺓ
ﻴﺴﺎﻭﻱ ﺍﻟﻤﺠﻤﻭﻉ ﺍﻟﺠﺒﺭﻱ ﻟﻠﺸﻐل
.
لـﻘﺘﻨﻤﻟﺍ ﻲﻓﺎﺼﻟﺍ لﻐﺸﻟﺍ ﻥﺈﻓ ﻩﺭﻭﺩﺒ ﻕﻠﻐﻤ ﻡﺎﻅﻨ ﻱﺃ ﺭﻤﻴ ﺎﻤﺩﻨﻋ ﻪﻨﺍ ﻱﺃ
ﺍﻟﻰ ﺍﻟﻤﺤﻴﻁ ﻴﺘﻨﺎﺴﺏ ﻤﻊ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﺼﺎﻓﻴﺔ ﺍﻟﻤﺄﺨﻭﺫﺓ ﻤﻥ ﺍﻟﻤﺤﻴﻁ
.
ﺃﻱ
:
ﻭﻜﻤ،ﺔﻗﺎﻁﻟﺍ ﺩﻴﻟﻭﺘﻟ ﺔﻴﺭﺎﺨﺒﻟﺍ ﺔﻁﺤﻤﻟﺍ ﻭﻫ ﺔﻟﺎﺤﻟﺍ ﻩﺫﻬﻟ لﺎﺜﻤ ﻁﺴﺒﺍ
ﻜلـﺸ ﻲـﻓ ﺎ
)
5.3
(
ﺙ ﺍﻥـﻴﺤ
ﺍﻟﻤﻀﺨﺔ ﺘﺤﺘﺎﺝ ﺸﻐل
(W
in
)
.
ﻟﺘﺩﻓﻊ ﺍﻟﻤﺎﺀ ﺍﻟﻰ ﺍﻟﻤﺭﺠل ﺍﻟﺫﻱ ﻴﺤﺘﺎﺝ ﺍﻟﻰ ﺤﺭﺍﺭﺓ
(Q
in
)
ﻟﻴﺘﺒﺨﺭ ﺍﻟﻤﺎﺀ ﻭﻴﺘﻤﺩﺩ ﻓﻲ ﺍﻟﺘﻭﺭﺒﻴﻥ ﺍﻟﺫﻱ ﻴﻌﻁﻲ ﺸﻐﻼﹰ
(W
out
)
ﻟﺘﺩﻭﻴﺭ ﻤﻭﻟﺩ ﻜﻬﺭﺒﺎﺌﻲ ﻤﺜﻼﹰ
.
ﻭﻓﻲ ﺍﻟﻤﻜﺜﻑ ﺘﻁﺭﺩ ﺤﺭﺍﺭﺓ
(Q
o
)
ﻟﻴﺘﻜﺜﻑ ﺍﻟﺒﺨﺎﺭ ﻭﺘﺩﻓﻌﻪ ﺍﻟﻤﻀﺨﺔ ﺜﺎﻨﻴﺔﹰ
ﺍﻟﻰ ﺍﻟﻤﺭﺠل ﻭﻫ
ﻜﺫﺍ
.
ﻓﺈﺫﺍ ﺍﻋﺘﺒﺭﻨﺎ ﻫﺫﻩ ﺍﻻﺠﺭﺍﺀﺍﺕ ﺩﻭﺭﺓ ﻓﺴﺘﻜﻭﻥ ﺼﻴﻐﺔ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻜﻤﺎ ﻴﺄﺘﻲ
:
∑Q = ∑W
Q
in
+ (–Q
o
) = W
o
+ (–W
in
)
Q
in
– Q
o
= W
o
– W
in
………..
(5.3)
ﺍﻥ
:
W
in
= (W
p
)
1
+ (W
p
)
2
∫
∫
∑
∑
=
⇒
=
(5.2)
......
W
Q
dW
dQ
∑Q = ∑W
(Q
in
) + (–Q
o
) = W
o
+ (–W
in
) = W
o
– W
in
Q
in
– Q
o
= W
o
– [(W
in
)
1
+ (W
in
)
2
]
Q
in
– Q
o
= W
o
– W
in
∑Q = ∑W
(Q
in
) + (–Q
o
) = W
o
+ (–W
in
)
Q
in
– Q
o
= W
o
– W
in
ﺸﻜل
)
5.3
(
-
ﻤﺤﻁﺔ ﺒﺨﺎﺭﻴﺔ
–
ﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
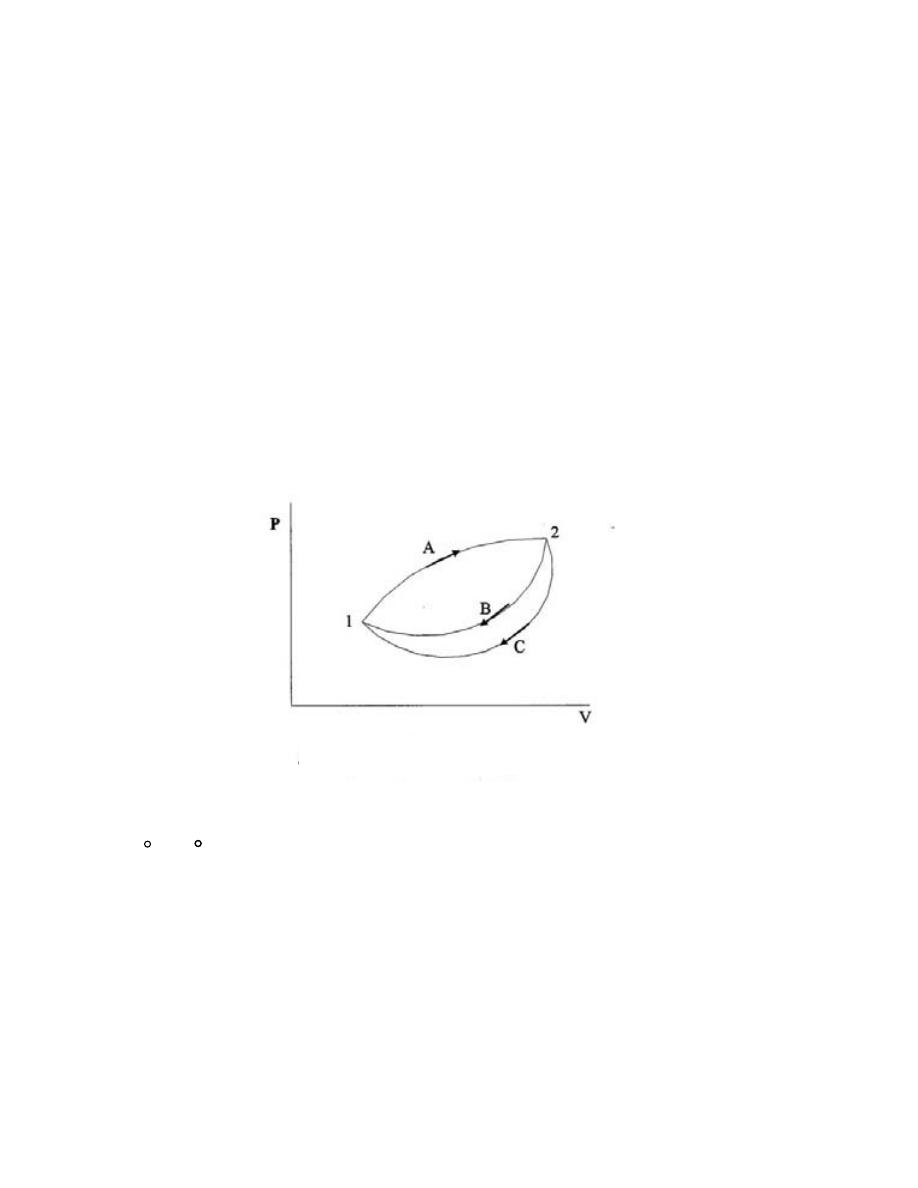
)
88
(
ﺔ ﺫﺍﺕـﻨﻜﺎﻤﻟﺎﺒ ﻰﻤﺴﺘﻓ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻤ ﺭﺜﻜﺍ لﻐﺸ ﻲﻁﻌﺘ ﻭﺍ ﺊﺸ ﻻ ﻥﻤ لﻐﺸ ﻲﻁﻌﺘ ﺔﻨﻜﺎﻤ ﺕﺭﻬﻅ ﺍﺫﺍ
ﺍﻟﺤﺭﻜﺔ
ﺎﻨﻭﻥ ﺍﻻﻭلـﻘﻟﺍ ﻊﻤ ﺽﺭﺎﻌﺘﺘ ﺎﻬﻨﻷ ،ﻊﻨﺼﻟﺍ ﺔﻠﻴﺤﺘﺴﻤﻟﺍ لﻭﻻﺍ ﻉﻭﻨﻟﺍ ﻥﻤ ﺔﻴﺩﻤﺭﺴﻟﺍ ﻭﺍ ﺔﻴﺩﺒﻻﺍ
.
ﺫﻟﻙـﻟ
ﻅﻬﺭﺕ ﺍﻟﺼﻴﻐﺔ ﺍﻟﺘﺎﻟﻴﺔ ﻟﻠﻘﺎﻨﻭﻥ ﺍﻻﻭل
:
"
ﻻ ﻭﺠﻭﺩ ﻟﻤﺎﻜﻨﺔ ﺫﺍﺕ ﺤﺭﻜﺔ ﺍﺒﺩﻴﺔ ﻤﻥ ﺍﻟﻨﻭﻉ ﺍﻻﻭل
."
)
5.4
(
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ
Energy Equation
ﻤﻌﺎﺩﻟﺔ ﻤﻬﻤ،لﻭﻻﺍ ﻥﻭﻨﺎﻘﻟﺍ ﻥﻋ ﻲﻀﺎﻴﺭﻟﺍ ﺭﻴﺒﻌﺘﻟﺍ ﻲﻫ
ﻊـﻴﻤﺠ ﻲـﻓ ﺔـﻤﺎﻋ ﺓﺭﻭﺼـﺒ لﻤﻌﺘﺴﺘ ﹰﺍﺩﺠ ﺔ
ﺍﻟﻌﻤﻠﻴﺎﺕ ﺍﻟﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﺍﻟﺘﻲ ﺘﻤﺭ ﺒﺠﺯﺀ ﻤﻥ ﺩﻭﺭﻩ
)
ﻋﻤﻠﻴﺔ ﺴﺎﻜﻨﺔ
.(
ﻼلـﺨ ﻥﻤ ﻡﺎﻅﻨﻟﺍ ﺹﺍﻭﺨ ﺕﺭﻴﻐﺘ ﺍﺫﺈﻓ
ﺔـﻨﻭﺯﺨﻤ ﺔـﻗﺎﻁ لﻜﺸ ﻰﻠﻋ ﻡﺎﻅﻨﻠﻟ ﺓﺩﻴﺩﺠ ﺔﻴﺼﺎﺨ ﺭﻬﻅﺘﺴﻓ ،ﻪﻌﻀﻭﻤ ﺭﻴﻐﺘ ﻭﺍ ﻪﻜﺭﺤﺘ
(Stored Energy)
ﻜﻤﻴﺘﻬﺎ ﺜﺎﺒﺘﺔ ﻴﺭﻤﺯ ﻟﻬﺎ ﺒﺎﻟﺭﻤﺯ
(
∆E
se
)
.
ﻭﻟﻐﺭﺽ ﺘﻭﻀﻴ
ﺢ ﺫﻟﻙ ﻨﻔﺘﺭﺽ ﻭﺠﻭﺩ ﻨﻅﺎﻡ ﺘﺘﻐﻴﺭ ﺤﺎﻟﺘﻪ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﺴﺎﺭـﻤﻟﺍ ﺭﺒﻋ
(A)
ﻡـﺜ ،
ﻴﻌﻭﺩ ﺍﻟﻰ ﺤﺎﻟﺘﻪ ﺍﻻﺼﻠﻴﺔ ﻤﻥ
)
2
(
ﺍﻟﻰ
)
1
(
ﻋﺒﺭ ﺍﻟﻤﺴﺎﺭ
(B)
ﺍﻭ
(C)
.
ﻭﻜﻤﺎ ﻓﻲ ﺸﻜل
)
5.4
.(
ﺍﺴﺘﻨﺎﺩﺍﹰ ﺍﻟﻰ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻓﻲ ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﺩﻭﺭﻴﺔ ﻓﺈﻥ
:
∑Q = ∑W
ﻭﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻌﻤﻠﻴﺔ ﺍﻟﺩﻭﺭﻴﺔ
1A2B1
ﻓﺈﻥ
:
(Q
12
)
A
+ (Q
21
)
B
= (W
12
)
A
+ (W
21
)
B
…. (1)
ﻭﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻌﻤﻠﻴﺔ ﺍﻟﺩﻭﺭﻴﺔ
1A2C1
ﻓﺈﻥ
:
± (Q
12
)
A
± (Q
21
)
C
=
± (W
12
)
A
± (W
21
)
C
….
(2)
ﺒﻁﺭﺡ
)
1
(
ﻤﻥ
)
2
(
ﻴﻨﺘﺞ
:
(Q
21
)
B
– (Q
21
)
C
= (W
21
)
B
– (W
21
)
C
∴ (W
21
)
B
– (W
21
)
B
= (Q
21
)
C
– (W
21
)
C
…. (5.4)
ﺸﻜل
)
5.4
(
-
ﻤﺴﺎﺭ
ﺍﺕ
ﺍﻟﻌﻭﺩﺓ ﺜﺎﺒﺘﺔ

)
89
(
ﻴﺘﻀﺢ ﻤﻥ ﺨﻼل ﻫﺫﻩ ﺍﻟﻤﻨﺎﻗﺸﺔ ﺍﻟﺭﻴﺎﻀ
ﻴﺔ ﺍﻥ ﺍﻟﻘﻴﻤﺔ
(Q-W)
ﺜﺎﺒﺘﺔ ﻋﺒﺭ ﻤﺴﺎﺭﺍﺕ ﺍﻟﻌﻭﺩﺓ
(B)
ﺍﻭ
(C)
ﺍﻭ ﺃﻱ ﻤﺴﺎﺭ ﺁﺨﺭ
.
ﺍﺫﻥ ﻋﻨﺩﻤﺎ ﺘﺘﻐﻴﺭ ﺤﺎﻟﺔ ﺍﻟﻨﻅﺎﻡ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻓﺈﻥ
(Q-W)
ﺭـﺒﻋ ﺔﺘﺒﺎﺜ ﻥﻭﻜﺘ
ﺍﻟﻤﺴﺎﺭ
(A)
ﻷﻥ ﻁﺭﻴﻕ ﺍﻟﻌﻭﺩﺓ ﺜﺎﺒﺕ ﻤﻬﻤﺎ ﺍﺨﺘﻠﻔﺕ ﺍﻟﻤﺴﺎﺭﺍﺕ،ﺭﺨﺁ ﺭﺎﺴﻤ ﻱﺃ ﻭﺍ
.
ﺔـﺘﺒﺎﺜﻟﺍ ﺔﻤﻴﻘﻟﺍ ﻥﺎﻓ ﺍﺫﻟ
(Q-W)
ﺘﻤﺜل ﺨﺎﺼﻴﺔ ﺠﺩﻴﺩﺓ ﻟﻠ
ﺘﻌﺭﻑ،ﺔﻴﺌﺎﻬﻨﻟﺍﻭ ﺔﻴﺌﺍﺩﺘﺒﻻﺍ ﺔﻟﺎﺤﻟﺍ ﻰﻠﻋ ﺎﻤﻨﺇﻭ ﺭﺎﺴﻤﻟﺍ ﻰﻠﻋ ﻑﻗﻭﺘﺘ ﻻ ﻡﺎﻅﻨ
ـ ﻴﺭﻤﺯ ﻟﻬﺎ ﺒ،ﻡﺎﻅﻨﻠﻟ ﺔﻴﻠﻜﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻭﺍ ﺔﻨﻭﺯﺨﻤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻲﻓ ﺭﻴﻐﺘﻟﺎﺒ
(
∆E
se
)
ﺭـﻴﻐﺘﺒ ﺭﻴﻐﺘﺘ
(Q-W)
ﺃﻱ،
ﺍﻥ
:
Q – W =
∆E
se
………… (5.5)
ﻟﺫﺍ ﻓﺈﻥ ﺍﻟﻘﻴﻤﺔ ﺍﻟﺜﺎﺒﺘﺔ
(Q-W)
ﺘﻤﺜل ﺨﺎﺼﻴﺔ ﺠﺩﻴﺩﺓ ﻟﻠﻨﻅﺎﻡ ﻻ ﺘﺘﻭﻗﻑ ﻋﻠ
ﻰـﻠﻋ ﺎـﻤﻨﺇﻭ ﺭﺎﺴﻤﻟﺍ ﻰ
ﺘﻌﺭﻑ ﺒﺎﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﺨﺯﻭﻨﺔ ﺍﻭ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻠﻴﺔ ﻟﻠﻨﻅﺎﻡ،ﺔﻴﺌﺎﻬﻨﻟﺍﻭ ﺔﻴﺌﺍﺩﺘﺒﻻﺍ ﺔﻟﺎﺤﻟﺍ
.
ــﺎ ﺒـﻬﻟ ﺯﻤﺭﻴ
(
∆E
se
)
ﺘﺘﻐﻴﺭ ﺒﺘﻐﻴﺭ
(Q-W)
ﺃﻱ
:
Q – W =
∆E
se
=
∆U + ∆KE + ∆PE ……….. (5.6)
ﺔـﻗﺎﻁﻠﻟ ﺔﻤﺎﻌﻟﺍ ﺔﻟﺩﺎﻌﻤﻟﺍ ﻡﺴﺍ ﺔﻟﺩﺎﻌﻤﻟﺍ ﻩﺫﻫ ﻰﻠﻋ ﻕﻠﻁﻴ
(The General Energy Equation)
.
ﻓﺈﺫﺍ ﻁﺒﻘﺕ ﻋﻠﻰ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ ﺍﻟﺘﻲ ﺘﻤﺭ ﺒﺠﺯﺀ ﻤﻥ ﺩﻭﺭﺓ
)
ﺃﻱ ﺍﻟﻌﻤﻠﻴﺎﺕ ﺍﻟﺴﺎﻜﻨﺔ
(
ﺎﻗﺘﻴﻥـﻁﻟﺍ لﻤﻬﺘﺴـﻓ
ﺍﻟﺤﺭﻜﻴﺔ ﻭﺍﻟﻜﺎﻤﻨﺔ ﻭﺘﺼﺒﺢ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ ﻜﺎﻵﺘﻲ
:
Q – W =
∆U
………. (5.7)
ﻭﺍﻨﻤﺎ ﻴﺘﺤﻭل ﺠﺯﺀ ﻤﻨﻬﺎ ﻟﺯﻴﺎﺩﺓ ﺍﻟﻁﺎﻗﺔ،لﻐﺸ ﻰﻟﺍ ﹰﺎﻴﻠﻜ لﻭﺤﺘﺘ ﻻ ﺔﻠﺨﺍﺩﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺍ ﻱﺃ
ﺍﻟﺩﺍﺨﻠﻴﺔ
ﻟﻠﻨﻅﺎﻡ
.
ﻫﺫﻩ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺘﺴﻤﻰ ﺒﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻼﺠﺭﻴﺎﻨﻴﺔ
(Non-Flow Energy Equation)
ﺎـﻬﻟ ﺯﻤﺭﻴ
(NFEE)
.
ـﺍﻤﺎ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻌﻤﻠﻴﺎﺕ ﺸﺒﻪ ﺍﻟﺴﺎﻜﻨﺔ ﻓﺘﺼﺒﺢ ﺍﻟ
(NFEE)
ﻜﻤﺎ ﻴﻠﻲ
:
dQ – dW = dU
……… (5.8)
ﻭﻋﻨﺩﻤﺎ ﻴﻤﺭ ﺍﻟﻨﻅﺎﻡ ﺒﺩﻭﺭﻩ ﻓﺈﻥ
(
∆U=0)
ـ ﻟﺫﺍ ﺴﺘﺘﺤﻭل ﺍﻟ،
(NFEE)
ﺍﻟﻰ ﻗ
ﺃﻱ،لﻭﺠ ﻥﻭﻨﺎ
:
Q = W
………. (5.9)
)
5.5
(
-
ﺍﻟﻌﻤﻠﻴﺎﺕ ﺸﺒﻪ ﺍﻟﺴﺎﻜﻨﺔ
ﺎﻜﻨﺔـﺴ ﻪﺒﺸ ﻭﺍ ﺎﻜﻨﺔﺴ ﻥﻭﻜﺘ ﻥﺍ ﺎﻤﺍ ﺔﻴﻠﻤﻋ ﻲﻓ ﺓﺭﻭﺩ ﻥﻤ ﺀﺯﺠﺒ ﺔﻤﻅﻨﻻﺍ ﺭﻤﺘ
.
ﻭﻥـﻜﺘ ﺔﻨﻜﺎﺴـﻟﺎﻓ
ﻤﺤﺩﺩﺓ ﺒﻴﻥ ﺍﻟﺤﺎﻟﺘﻴﻥ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ ﻭﺍﻟﻨﻬﺎﺌﻴﺔ ﻤﺜﻼﹰ
)
U
،
W
،
Q
(
ﺔـﻟﺎﺤﻟﺍ ﺭـﻴﻐﺘ ﺎﻬﻴﻓ ﻥﻭﻜﻴﻓ ﺔﻨﻜﺎﺴﻟﺍ ﻪﺒﺸ ﺎﻤﺍ ،
ﺼﻐﻴﺭ ﺠﺩﺍﹰ ﻭﻴﺘﻡ ﺒﻐﺎ
ﺜﻼﹰـﻤ ﺔﻴﻠـﻀﺎﻔﺘ ﺔﻐﻴﺼﺒ ﺎﻬﻨﻋ ﺭﺒﻌﻴ ﺔﻗﺎﻁﻟﺍ ﻲﻓ ﻉﺎﻴﻀ ﺎﻬﺒﺤﺎﺼﻴ ﻥﺍ ﻥﻭﺩ ﻥﻤ ﺄﻁﺒﻟﺍ ﺔﻴ
)
dU
،
dW
،
dQ
.(
ﺔ ﺍﻭـﻤﺎﺘ ﺭﻴﺒﺎـﻌﺘﺒ لـﺜﻤﻴ ﺔﻴـﺼﺎﺨﻠﻟ ﻥﻴﺘﻤﻴﻗ ﻥﻴﺒ ﹰﺍﺩﺩﺤﻤ ﹰﺎﻗﺭﻓ ﻲﻁﻌﻴ ﺔﻴﺼﺎﺨﻟﺍ لﻀﺎﻔﺘ لﻤﺎﻜﺘ ﻥﺇ
ﻤﻀﺒﻭﻁﺔ
(Exact)
ﻤﺜﻼﹰ
:

)
90
(
ﺍﻤﺎ ﺘﻜﺎﻤل ﺘﻔﺎﻀل ﺍﻟﻜﻤﻴﺔ ﻓﻴﻌﻁﻲ ﻜﻤﻴﺔ ﻤﺤﺩﺩﺓ ﻟﻠﺤﺭﺍﺭﺓ ﺍﻭ ﺍﻟﺸﻐل ﻴﻤﺜل
ﺒﺘﻌﺎﺒﻴﺭ ﻏﻴﺭ ﺘﺎﻤﺔ ﺍﻭ ﻏﻴﺭ
ﻤﻀﺒﻭﻁﺔ
(Inexact)
ﻓﻤﺜﻼﹰ،
:
∫dQ = Q
and
∫dW = W
…….. (5.11)
ﺘﺩل ﺍﻻﺸﺎﺭﺓ
(d)
ﻋﻠﻰ ﺍﻟﻜﻤﻴﺎﺕ ﺍﻟﻤﺘﻨﺎﻫﻴﺔ ﻓﻲ ﺍﻟﺼﻐﺭ
.
ﻓﻔﻲ ﺍﻟﻌﻤﻠﻴﺎﺕ ﺍﻟﺘﻲ ﻴﻜﻭﻥ ﻓﻴﻬﺎ ﺘﻐﻴﺭ ﺍﻟﺤﺎﻟﺔ
ﺃﻱ،ﺔﻴﻠﻀﺎﻔﺘ ﺓﺭﻭﺼﺒ ﺔﻟﺩﺎﻌﻤﻟﺍ ﺏﺘﻜﺘﻓ ،ﻉﺎﻴﻀ ﺎﻬﺒﺤﺎﺼﻴ ﻻﻭ لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﻲﻓ ﹰﺍﺩﺠ ﺭﻴﻐﺼ
:
dQ – dW = dU
ﺃﻱ،ﺔﻗﺎﻁﻟﺍ ﺔﻟﺩﺎﻌﻤ ﻰﻠﻋ لﺼﺤﻨ ﺔﻟﺩﺎﻌﻤﻟﺍ ﻩﺫﻫ لﻤﺎﻜﺘ ﺩﻨﻋﻭ
:
∫dQ - ∫dW = ∫dU
∴ Q – W = ∆U
…….
(5.12)
،ﺩﺍﺕـﻌﻤﻟﺍ ﺽﻌﺒ ﻡﻴﻤﺼﺘ ﻲﻓ ﺎﻬﺘﻓﺭﻌﻤﻟ ﺝﺎﺘﺤﻨ ﻲﺘﻟﺍ ﺔﺴﻴﺌﺭﻟﺍ ﻡﻴﻘﻟﺍ ﻥﻤ لﻐﺸﻟﺍ ﻭﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺔﻴﻤﻜ ﻥﺇ
ﺔــﻴﺭﺍﺭﺤﻟﺍ ﺕﻻﺩﺎــﺒﻤﻟﺍ لــﺜﻤ
(Heat Exchangers)
ﺭﺍﺕــﺨﺒﻤﻟﺍ ،
(Evaporators)
ﻀﻭﺍﻏﻁــﻟﺍ ،
(Compressors)
ﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ،
(Turbines)
ﻭﺍﻟﻤﺤﺭﻜﺎﺕ
(Engines)
ﻭﻏﻴﺭﻫﺎ
.
)
5.6
(
-
ﻨﺘﺎﺌﺞ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
1
-
ﺍﺜﻨﺎﺀ،لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻴﺒ ﻕﺭﻔﻠﻟ ﻱﻭﺎﺴﻴ ﺎﻬﺘﻤﻴﻗ ﻲﻓ ﺭﻴﻐﺘ ﻱﺃ ﻥﺍ ﺙﻴﺤﺒ ﻕﻠﻐﻤﻟﺍ ﻡﺎﻅﻨﻠﻟ ﺔﻴﺼﺎﺨ ﺩﺠﻭﺘ
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل،ﺔﻟﺎﺤﻟﺍ ﻲﻓ ﺭﻴﻐﺘ ﻱﺃ
)
5.4
(
ﻓﺈﺫﺍ ﺭﻤﺯﻨﺎ ﻟﻠﺨﺎﺼﻴﺔ ﺍﻟﺘﻲ
ـ ﺍﻜﺘﺸﻔﺕ ﺒ
(U)
ﺭـﺒﻌﺘ ﻲﺘﻟﺍﻭ
ﻋﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻠﻨﻅﺎﻡ ﻓﺴﻴﻜﻭﻥ
:
dQ – dW = dU
∫dQ -∫dW = ∫dU
Q – W =
∆U
or
∑ (dQ – dW) = ∆U
……. (5.13)
ﺭـﻬﻅﺘﻓ ﻱﺭﻭﺩ ﺭـﻴﻏ ﺀﺍﺭـﺠﺍ ﻲـﻓ ﻕﻠﻐﻤ ﻡﺎﻅﻨ ﺩﻭﺩﺤ ﺭﺒﻋ لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺇ ﺩﻨﻋ ﻪﻨﺍ ﻱﺃ
ﺔــﻴﻠﺨﺍﺩﻟﺍ ﺔــﻗﺎﻁﻟﺎﺒ ﻰﻤﺴــﺘ ﺔﻴــﺼﺎﺨ
.
ﺫﻩ ﺍﻟﻤﻌﺎﺩــﻫ ﻰﻤﺴــﺘ
ﺩﻓﻕــﺘﻟﺍ ﺔــﻤﻴﺩﻋ ﺔــﻗﺎﻁﻟﺍ ﺔــﻟﺩﺎﻌﻤﺒ ﺔــﻟ
(Non-Flow Energy Equation)
.
2
-
ﻫﺫﻩ ﺍﻟﻨﺘﻴﺠﺔ ﺘﺴﻤﻰ ﻏﺎﻟﺒﺎﹰ،ﻪﻁﻴﺤﻤ ﻥﻋ ﹰﻻﻭﺯﻌﻤ ﻡﺎﻅﻨﻟﺍ ﻥﺎﻜ ﺍﺫﺍ ﺔﺘﺒﺎﺜ ﻰﻘﺒﺘ ﻕﻠﻐﻤ ﻡﺎﻅﻨﻟ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ
ﺒﻘﺎﻨﻭﻥ ﺤﻔﻅ ﺍﻟﻁﺎﻗﺔ
.
3
-
ﺇﻥ ﺁﻟﺔ ﺍﻟﺤﺭﻜﺔ ﺫﺍﺘﻴﺔ ﺍﻟﻁﺎﻗﺔ ﻤﻥ ﺍﻟﻨﻭﻉ ﺍﻻﻭل ﻤﺴﺘﺤﻴﻠﺔ
.
ﺃﻱ ﺍﻥ ﺍﻵﻟﺔ ﺍﻟﺘﻲ ﺘﻨﺘﺞ ﺸﻐﻼﹰ ﺒﺼﻭﺓ
ﺴﺘﻤﺭﺓـﻤ
ﺒﺩﻭﻥ ﺍﻥ ﺘﻤﺘﺹ ﻁﺎﻗﺔ ﻤﻥ ﻤﺤﻴﻁﻬﺎ ﻭﺘﺴﻤﻰ ﺁﻟﺔ ﺍﻟﺤﺭﻜﺔ ﺫﺍﺘﻴﺔ ﺍﻟﻁﺎﻗﺔ ﺘﻜﻭﻥ ﻤﺴﺘﺤﻴﻠﺔ ﺍﻟﺼﻨﻊ
.
∫
∫
∆
=
−
=
∆
=
−
=
2
1
2
1
T
T
U
U
1
2
1
2
(5.10)
..........
U
U
U
dU
and
T
T
T
dT
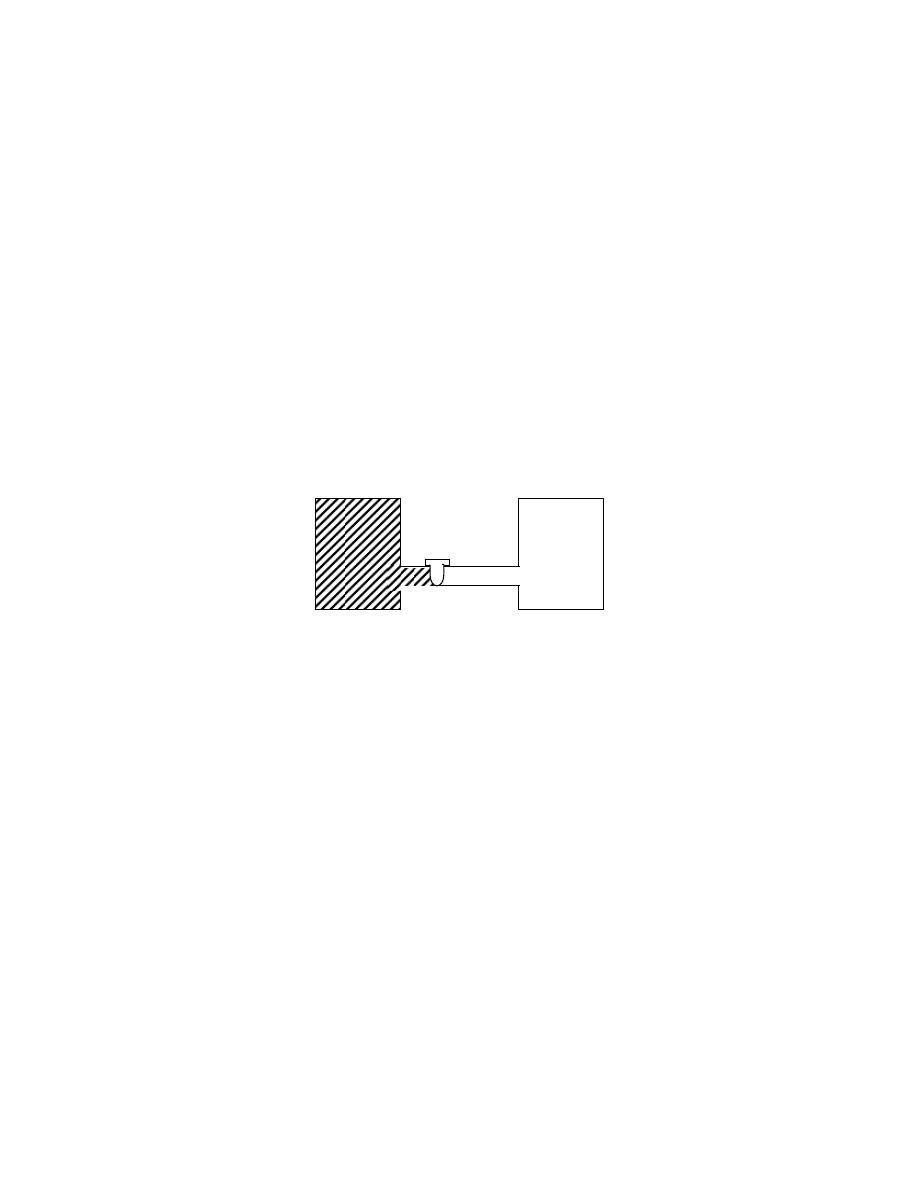
)
91
(
)
5.7
(
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺍﻭ ﻗﺎﻨﻭﻥ ﺠﻭل
Internal Energy or Joule's Law
ﺔـﻗﻼﻌﻠﻟ ﻊﻀـﺨﺘ ﻱﺃ ،ﻁﻘﻓ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻟ ﻊﺒﺎﺘ ﻲﻟﺎﺜﻤﻟﺍ ﺯﺎﻐﻠﻟ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ
[
µ = ∅ (T)]
،
ﻭﻫﺫﺍ ﻤﺎ ﺤﻘﻘﻪ ﺠﻭل
ﻟﺫﺍ ﺘﺴﻤﻰ ﻫﺫﻩ ﺍﻟﻌﻼﻗﺔ ﺒﻘﺎﻨﻭﻥ ﺠﻭل،ﺔﻴﻟﺎﺘﻟﺍ ﻪﺘﺒﺭﺠﺘ لﻼﺨ ﻥﻤ
.
ﺔـﺒﺭﺠﺘﻟﺍ ﺡﺭﺸـﻨﺴﻭ
ﻭﻨﺘﺎﺌﺠﻬﺎ ﺒﺎﻟﻨﻘﺎﻁ ﺍﻵﺘﻴﺔ
:
-
1
-
ﺎـﻤﻬﻨﻴﺒ ﻍﺭﻔﻤ ﻲﻨﺎﺜﻟﺍﻭ ﻪﺼﺍﻭﺨ ﺔﺴﺍﺭﺩ ﺩﺍﺭﻤﻟﺍ ﺯﺎﻐﻟﺍ ﻰﻠﻋ ﺎﻤﻫﺩﺤﺍ ﻱﻭﺘﺤﻴ ﻥﻴﻀﻭﺤ ﻥﻤ ﺯﺎﻬﺠﻟﺍ ﻑﻟﺄﺘﻴ
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﻡﺎﻤﺼ
)
5.5
.(
2
-
ﺘﻘﺎﺱ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺍﻟﻐﺎﺯ
.
3
-
ﻴﺴﻤﺢ ﻟﻠﻐﺎﺯ ﺒﺎﻟﺘﻤﺩﺩ ﺍﻻﺩﻴﺎﺒ
ﺎﺘﻲ ﻋﻥ ﻁﺭﻴﻕ ﻓﺘﺢ ﺍﻟﺼﻤﺎﻡ ﺒﺤﻴﺙ ﻴﻤﻸ ﺍﻟﻐﺎﺯ ﺍﻟﺤﻭﺽ ﺍﻟﻤﻔﺭﻍ
.
4
-
ﻭﻋﻨﺩﻤﺎ ﻴﺤﺩﺙ ﺍﻟﺘﻭﺍﺯﻥ ﺍﻟﺠﺩﻴﺩ ﺘﻘﺎﺱ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻤﺭﺓ ﺜﺎﻨﻴﺔ
.
5
-
ﺇﺫﻥ،ﺭﺤ ﺩﺩﻤﺘﻟﺍ ﻥﺃ ﺎﻤﺒﻭ
(W = 0)
ﺇﺫﻥ،ﻲﺘﺎﺒﺎﻴﺩﺍ ﺩﺩﻤﺘﻟﺍﻭ ،
(Q = 0)
ﺎﻨﻭﻥ ﺍﻻﻭلـﻘﻟﺍ ﻥﻤ ﺞﺘﻨﺘﺴﻨ ﺍﺫﻟ
ﺍﻥ
:
Q – W =
∆U
∆U = 0
ﺸﻜل
)
5.5
(
-
ﺘﺠﺭﺒﺔ ﺠﻭل ﺍﻟﻁﺎﻗﺔ ﺍ
ﻟﺩﺍﺨﻠﻴﺔ
ﺃﻱ ﺍﻨﻪ ﻻ ﻴﺤﺩﺙ ﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺒﻴﻥ ﺍﻟﺤﺎﻟﺘﻴﻥ
)
1
(
ﻭ
)
2
(
ﺒﺭﻏﻡ ﺘﻐﻴﺭ ﺍﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﺍﻟﻨﻭﻋﻲ
.
6
-
ﻴﻤﻜﻨﻨﺎ ﺍﻥ ﻨﺴﺘﻨﺘﺞ ﺍﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺘﺎﺒﻌﻪ ﻟﺩﺭﺠﺔ،ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﺒ ﺭﻴﻐﺘ ﻱﺃ ﺙﺩﺤﻴ ﻡﻟ ﻪﻨﺍ ﺎﻨﺩﺠﻭ ﺍﺫﺈﻓ
ﺍﻟﺤﺭﺍﺭﺓ ﻓﻘﻁ
.
ﺃﻱ ﺍﻨﻪ ﺒﺼﺭﻑ ﺍﻟﻨﻅﺭ ﻋﻤﺎ ﻴﺤﺩﺙ ﻟﻠﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﻤﻥ ﺘﻐﻴﺭﺍ
ﺘﺒﻘﻰ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ،ﺕ
ﺜﺎﺒﺘﺔ ﻤﺎ ﻟﻡ ﺘﺘﻐﻴﺭ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
.
7
-
،ﺩﻩـﻌﺒﻭ ﺩﺩـﻤﺘﻟﺍ لـﺒﻗ ﺀﺎﻤﻟﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩ ﺱﺎﻗ ﻡﺜ ،ﺀﺎﻤ ﻉﺩﻭﺘﺴﻤ ﻲﻓ ﻥﻴﻀﻭﺤﻟﺍ ﺱﻴﻁﻐﺘﺒ لﻭﺠ ﻡﺎﻗ
ﻭل ﺍﻥـﻘﻟﺍ ﻥـﻤ ﻪـﻨﻜﻤ ﺎﻤﻤ ،ﹰﺎﻀﻴﺍ ﺭﻴﻐﺘﺘ ﻡﻟ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻥﺍ ﺞﺘﻨﺘﺴﺍ ،ﺭﻴﻴﻐﺘ ﻱﺃ ﻅﺤﻼﻴ ﻡﻟ ﺎﻤﺩﻨﻋﻭ
[
µ = ∅ (T)]
ﻭﺘﺴﻤﻰ ﻫﺫﻩ ﺍﻟﻌﻼﻗﺔ ﺒﻘﺎ
ﻨﻭﻥ ﺠﻭل
.
ــﻭﻤﻥ ﺘﻌﺭﻴﻑ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﻟ
(1 kg)
ﻤﻥ ﻏﺎﺯ ﻓﺈﻥ
:
d
µ = Cv dT
ﻭﺒﺼﻴﻐﺔ ﺘﻜﺎﻤﻠﻴﺔ ﻴﻜﻭﻥ
:
∆µ = Cv ∆T
………. (5.14)
ﻨﺴﺘﻨﺘﺞ ﻤﻥ ﺫﻟﻙ ﺍﻨﻪ ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﻤﺎﺌﻊ ﻏﺎﺯﺍﹰ ﻜﺎﻤﻼﹰ ﻓﺈﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺘﺎﺒﻌ
ﺔ
ﺭﺍﺭﺓـﺤﻟﺍ ﺔـﺠﺭﺩﻟ
ﻓﻘﻁ
.

)
92
(
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
)
5.1
(
(0.5kg)
ﻤﻥ ﻤﺎﺌ
ﻊ ﺘﻤﺩﺩ ﺍﺩﻴﺒﺎﺘﻴﺎﹰ ﻓﺄﻨﺘﺞ ﺸﻐﻼﹰ ﻤﻘﺩﺍﺭﻩ
(43.5kJ)
.
ﺍﻭﺠﺩ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺍﻟﻨﻭﻋﻴﺔ
ﻟﻠﻤﺎﺌﻊ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻻﺠﺭﺍﺀ
.
∆U = − W = − 43.5 kJ
)
5.2
(
ﺨﺯﺍﻥ ﻴﺤﺘﻭﻱ ﻋﻠﻰ ﻤﺎﺌﻊ ﻴﻘﻠﺏ ﺒﻭﺴﺎﻁﺔ ﻋﺠﻠﺔ ﻗﻼﺒﺔ
.
ﻼﺏـﻘﻟﺍ ﺔﻠﺠﻌﻟ ﻑﻭﺭﺼﻤﻟﺍ لﻐﺸﻟﺍ
(5283 kJ/hr)
،
ﺘﻨﺘﻘل ﺍﻟﺤﺭﺍﺭﺓ ﻤﻥ ﺍﻟﺨﺯﺍﻥ ﺒﻤﻌﺩل
(1672 kJ/hr)
ﻤﻌﺘﺒﺭﺍﹰ ﺍﻟﻤﻨﻅﻭﻤﺔ ﻫﻲ ﺍﻟﺨﺯﺍﻥ ﻭﺍﻟﻤﺎﺌﻊ
.
ﺍﺤﺴﺏ ﺍﻟﺘﻐﻴﺭ
؟ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻠﻤﻨﻅﻭﻤﺔ ﺨﻼل ﺴﺎﻋﺔ ﻭﺍﺤﺩﺓ
∆U = Q – W = – 1672 – (–5283) = 3611 kJ/hr
)
5.3
(
ﺎـﻬﻌﻁﻘﻤ ﺔﺤﺎﺴﻤ ﺔﻨﺍﻭﻁﺴﺍ لﺨﺍﺩ ﺩﻭﺠﻭﻤ ﻙﺭﺤﺘﻤ ﺱﺒﻜﻤ
(0.1m2)
ﻐﻁﻪـﻀ ﺭﻭﺼـﺤﻤ ﺀﺍﻭـﻫ ﺎـﻬﻴﻓ
(1.5bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(17
°C)
.
ﺴﺨﻥ ﺍﻟﻬﻭﺍﺀ ﻭﺍﺭﺘﻔﻊ ﺍﻟﻤﻜﺒﺱ ﺒﻌﺩ ﺍﻥ ﺍﺼﻁﺩﻡ ﺒﻤﻨﺎﻁﻕ ﺍﻟﺼﺩﺍﻡ
.
ﺜﻡ
ﺴﺨﻥ ﺒﻌﺩ ﺫﻟﻙ ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺢ ﻀﻐﻁﻪ ﻀﻌﻑ ﺍﻟﻀﻐﻁ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﻓﺈﺫﺍ ﺍﻫﻤﻠﻨﺎ ﺴﻤﻙ ﺍﻟﻤﻜﺒﺱ
.
ﺍﺤﺴﺏ ﺩﺭﺠﺔ
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻬﺎﺌﻴﺔ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل
.
)
5.4
(
ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﺘﻐﻴﺭﺕ ﺤﺎﻟﺘﻪ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
.(
ﻓﻲ ﺍﺜﻨﺎﺀ ﺫﻟﻙ ﺍﺴﺘﻠﻡ ﺤﺭﺍﺭﺓ ﻤﻘﺩﺍ
ﺭﻫﺎ
(100kJ)
ﻭﺍﻋﻁﻰ ﺸﻐل
ﻤﻘﺩﺍﺭﻩ
(150 kJ)
.
ﻋﻨﺩ ﺇﻋﺎﺩﺓ ﺍﻟﻨﻅﺎﻡ ﻤﻥ
)
2
(
ﺍﻟﻰ
)
1
(
ﺒﺫل ﻋﻠﻴﻪ ﺸﻐل ﻤﻘﺩﺍﺭﻩ
(80kJ)
.
ﺍﺤﺴﺏ ﺍﻟﺤﺭﺍﺭﺓ
ﺍﻟﻤﻨﺘﻘﻠﺔ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻻﺠﺭﺍﺀ ﻤﻥ
)
2
(
ﺍﻟﻰ
)
1
(
؟ ﻭﺒﻴﻥ ﺇﺘﺠﺎﻫﻬﺎ؟
∑ Q = ∑ W
Q
12
+ Q
21
= W
12
+ W
21
100 + Q
21
= 150 + (-80)
Q
21
= -30 kJ
kJ
87
5
.
0
5
.
43
m
U
−
=
=
∆
=
µ
∆
kJ/kg
30
0.1)
-
150(0.3
)
V
P(V
W
K
870
0.1
1
0.1
3
290
V
V
T
T
1
2
1
2
1
2
=
=
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
×
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
∑
=
+
=
=
×
=
=
=
kJ
30
0
30
W
K
1740
870
2
T
P
2P
T
.
P
P
T
2
1
1
2
2
3
3

)
93
(
)
5.5
(
ﺇﺫﺍ ﻜﺎﻥ ﻤ
ﻘﺩﺍﺭ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺍﻟﻨﻭﻋﻴﺔ
(250 kJ/kg)
ﻋﻨﺩﻤﺎ ﺘﻨﺘﻘل،
(700kJ)
ﻥـﻤ ﺓﺭﺍﺭـﺤ
ﺍﻟﻤﺤﻴﻁ ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ ﻤﻊ ﺇﻨﺘﺎﺝ ﺸﻐل ﻤﻘﺩﺍﺭﻩ
(200kJ)
لـﻤﻫﺍﻭ ﻡﺎـﻅﻨﻟﺍ ﻲﻓ ﺓﺩﻭﺠﻭﻤﻟﺍ ﻊﺌﺎﻤﻟﺍ ﺔﻠﺘﻜ ﺏﺴﺤﺍ
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ ﻭﺍﻟﻜﺎﻤﻨﺔ
.
∆U
12
= Q
12
– W
12
= 700 – 200 = 500 kJ
)
5.6
(
ﻤﻜﺒﺱ
ﻴﺘﺤﺭﻙ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﺘﺤﺘﻭﻱ ﻋﻠﻰ ﻏﺎﺯ ﻀﻐﻁﻪ
(690kN/m
2
)
ﻥـﻤ ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ ﻡﺠﺤﻟﺍ ﺩﺍﺩﺯﺇ
(0.003m
3
)
ﺍﻟﻰ
(0.024m
3
)
ﺍﻭﺠﺩ ﻤﻘﺩﺍﺭ ﺍﻟﺘﻐﻴﺭ ﺒﺎﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻤﺤﺘﻭﻴﺎﺕ ﺍﻻﺴﻁﻭﺍﻨﺔ ﺇﺫﺍ ﻜﺎﻨﺕ ﺘﺸﻊ
ﺍﻟﻰ ﺍﻟﻤﺤﻴﻁ ﻁﺎﻗﺔ ﺤﺭﺍﺭﻴﺔ ﻤﻘﺩﺍﺭﻫﺎ
(6 kJ)
.
∆U
12
= Q – W = Q - P
∆V
12
= (–6) –[690 (0.024 – 0.003)
] = –20.49 kJ
)
5.7
(
ﺎﺯـﻐﻟﺍ ﺩﻘﻔﻴ ﻥﻴﻌﻤ ﺀﺍﺭﺠﺍ ﺀﺎﻨﺜﺍ ﻲﻓ ،ﺎﺯﻏ ﻰﻠﻋ ﻱﻭﺘﺤﺘ ﻙﺭﺤﺘﻤ ﺱﺒﻜﻤﺒ ﺔﻘﻠﻐﻤ ﺔﻨﺍﻭﻁﺴﺍ
(1055kJ)
ﻥـﻤ
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺘﺯﺩﺍﺩ ﻁﺎﻗﺘﻪ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺒﻤﻘﺩﺍﺭ
(210kJ)
ﺍﺤﺴﺏ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل ﻭﻤﺎ ﻫﻭ ﺍﺘﺠﺎﻫﻪ
.
ﺭﺍﺀـﺠﻻﺍ لﻫﻭ
ﺍﻟﻤﺫﻜﻭﺭ ﺘﻤﺩﺩ ﺍﻡ ﺍﻨﻀﻐﻁ
.
Q – W =
∆U
–1055 – W = 210
⇒ ∴ W = –1265 kJ
)
5.8
(
ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻴﺘﻡ ﺘﺒﺭﻴﺩ
(0.5kg)
ﻡـﺠﺤ ﻥـﻤ ﺕـﺒﺎﺜ ﻁﻐـﻀ ﺕـﺤﺘ ﺀﺎﻤﻟﺍ ﺭﺎﺨﺒ ﻥﻤ
(3m
3
)
ﻰـﻟﺍ
(0.028m
3
)
.
ﺩﺍﺭـﻘﻤﺒ ﺀﺍﺭـﺠﻻﺍ ﺀﺎﻨﺜﺍ ﻲﻓ ﺔﻗﺎﻁﻟﺎﺒ لﺎﻘﺘﻨﻻﺍ ﻥﺎﻜ ﻭﻟ
(900kJ)
ﺭﺍﺭﺓـﺤ لﻜـﺸ ﻰـﻠﻋ
ﻭ
(81.6kJ)
ﻋﻠﻰ ﺸﻜل ﺸﻐل
.
ـﺍﻭﺠﺩ ﺍﻟﻀﻐﻁ ﺒﻭﺤﺩﺍﺕ ﺍﻟ
(bar)
ﺔـﻴﻠﺨﺍﺩﻟﺍ ﺔـﻗﺎﻁﻟﺎﺒ ﺭـﻴﻐﺘﻟﺍ ﺏﺴﺤﺍﻭ
ﺍﻟﻨﻭﻋﻴﺔ
.
∆U
12
= Q
12
– W
12
= (–900) – (–81.6)
= –818.4 kJ
W
12
= P
∆V
12
kg
2
250
500
U
m
12
12
=
=
µ
∆
∆
=
kJ/kg
8
.
1636
5
.
0
4
.
818
m
U
12
12
−
=
−
=
∆
=
µ
∆
bar
2746
.
0
3
028
.
0
6
.
31
V
W
P
12
12
=
−
−
=
∆
=

)
94
(
)
5.9
(
(2 kg)
ﻥـﻤ ﺔﻴﻋﻭﻨﻟﺍ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻪﻟﻼﺨ ﺩﺍﺩﺯﺘ ﻡﺠﺤﻟﺍ ﺕﻭﺒﺜ ﺔﻴﻠﻤﻌﻟ ﺽﺭﻌﺘﻴ ﻕﻠﻐﻤ ﻡﺎﻅﻨ ﻲﻓ ﻊﺌﺎﻤ ﻥﻤ
(120 kJ/kg)
ﺍﻟﻰ
(180 kJ/kg)
.
ﺍﺤﺴﺏ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺒﻭﺤﺩﺍﺕ
(kJ)
.
q =
∆ µ = 180 – 120 = 60kJ/kg
Q = m×q = 2×60 =120 kJ
)
5.10
(
ﻜﺎﻥ ﻤﻘﺩﺍﺭ ﺍﻟﺸﻐل ﺍﻟﻤﺒﺫﻭل ﻋﻠﻰ ﻀﻐﻁ ﺸﺤﻨﻪ ﺩﺍﺨل ﺍﺴﻁﻭﺍﻨﺔ ﻤﺤﺭﻙ ﻫﻭ
(75 kJ/kg)
ﺭﺍﺭﺓـﺤﻟﺍ ﺭﺍﺩﻘﻤﻭ
ﺍﻟﻤﻁ
ﺭ
ﻭﺩﺓ ﺍﻟﻰ ﺍﻟﻤﺤﻴﻁ
(42 kJ/kg)
.
ﺍﻭﺠﺩ ﻤﻘﺩﺍﺭ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
∆ µ = Q - w = (-42) – (-75) = 33 kJ/kg
)
5.11
(
ﺍﺴﻁﻭﺍﻨﺔ ﺘﺤﺘﻭﻱ ﻋﻠﻰ ﻏﺎﺯ ﻤﻐﻠﻕ ﺒﻤﻜﺒﺱ ﻻ ﺇﺤﺘﻜﺎﻜﻲ ﻭﺯﻨﻪ ﻴﺤﺩﺙ ﻀﻐﻁ ﻤﻘﺩﺍﺭﻩ
(3 bar)
.
ﺭﺩـﺒﻴ ﺎﻤﺩﻨﻋ
ﻥــﻤ ﻪــﻤﺠﺤ لــﻘﻴ ﺯﺎــﻐﻟﺍ
(0.1 m
3
)
ﻰــﻟﺍ
(0.03 m
3
)
ﻥــﻤ ﺔــﻴﻠﺨﺍﺩﻟﺍ ﻪــﺘﻗﺎﻁ ﺩﺍﺩﺯــﺘﻭ
(4.18 kJ)
ﺍﻟﻰ
(16.72 kJ)
.
ﺍﺤﺴﺏ ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺘﻴﻥ
.
W = P
∆V = 300 (0.03 – 0.1) = -21 kJ
Q =
∆U + W = (16.72 – 4.18) + (-21) = -8.46 kJ
)
5.12
(
ﺨﺯﺍﻥ ﻤﻌﺯﻭل ﻤﻜﻭﻥ ﻤﻥ ﺠﺯﺌﻴﻥ ﻴﻔﺼل ﺒﻴﻨﻬﻤﺎ ﺤﺎﺠﺯ
.
ﺍﺤﺩ ﺍﻟﺠﺯﺌﻴﻥ ﺒﺤﺠﻡ
(2m
3
)
ﻀﻐﻁـﺒ ﺀﺍﻭﻫ ﻱﻭﺤﻴ
(5 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(300K)
ﻭﺍﻟﺠﺯﺀ ﺍﻟﺜﺎﻨﻲ ﻤﻥ ﺍﻟﺨﺯﺍﻥ ﺒﺤﺠﻡ
(5m
3
)
ﺭﻓﻊ ﺍﻟﺤﺎﺠﺯ ﺒﻴﻥ ﺍﻟﺠﺯﺌﻴﻥ،
ﻭﺘﻤﺩﺩ ﺍﻟﻬﻭﺍﺀ ﻟﻤلﺀ ﺍﻟﺨﺯﺍﻥ ﺒﺄﻜﻤﻠﻪ
.
ﺍﻋﺘﺒﺭ ﺍﻟﻬ
ﻭﺍﺀ ﻨﻅﺎﻡ ﺤﺭﺍﺭﻱ
.
ﺍﺤﺴﺏ
) :
1
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ ﻋﻠﻰ ﺍﻟﻬﻭﺍﺀ
.
)
2
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻤﻥ ﺍﻟﻨﻅﺎﻡ
) .
3
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
) .
4
(
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﻀﻐﻁ ﻓﻲ ﻨﻬﺎﻴﺔ
ﺍﻻﺠﺭﺍﺀ
.
(1) W = 0
(2) Q = 0
bar
43
.
1
7
2
5
V
V
P
P
(4)
0
U
W
-
Q
0
T
300
T
T
)
3
(
2
1
1
2
2
1
=
×
=
=
=
∆
=
∴
=
∆
∴
=
=
Q
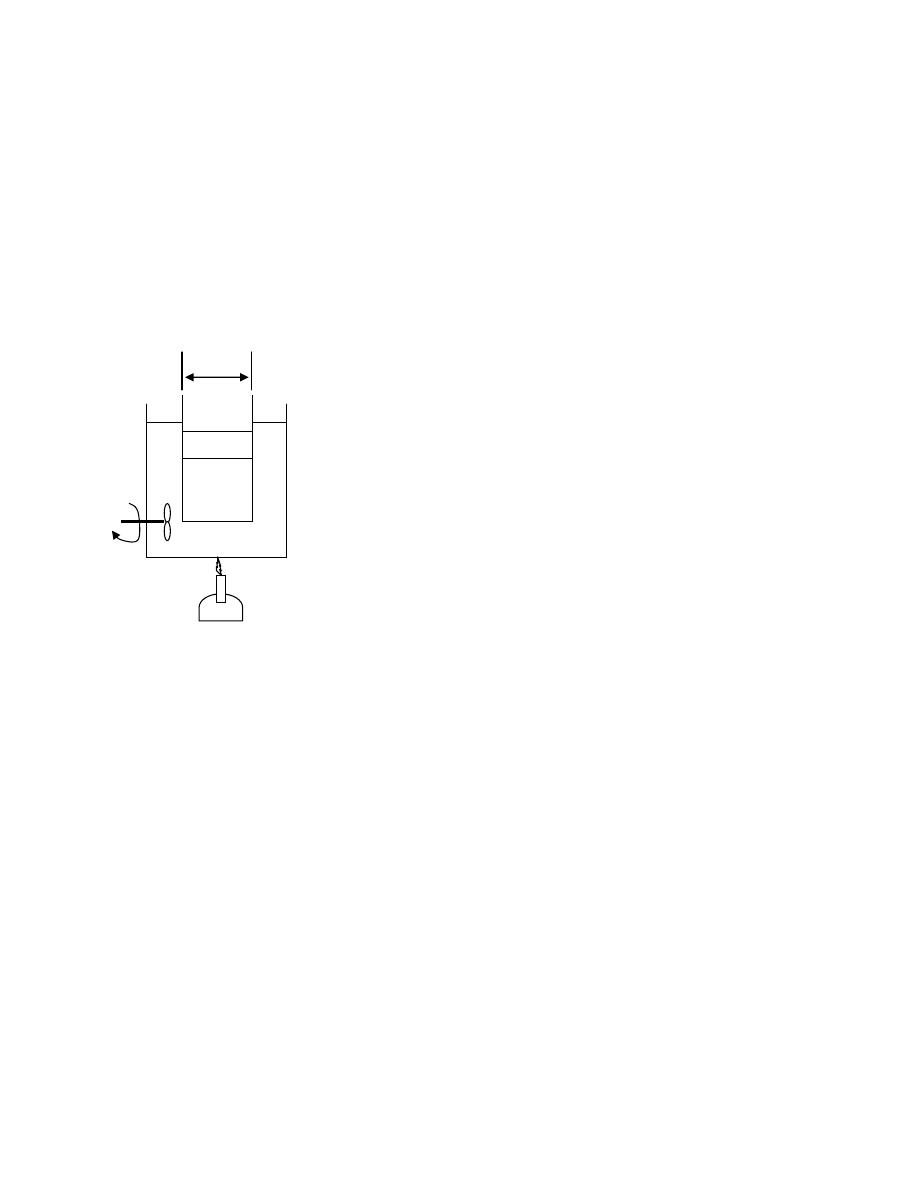
)
95
(
ﻤﺎﺀ
D=20cm
ﻏ
ﺎﺯ
ﻤﻜﺒﺱ
ﻤﺭﻭﺤﺔ
D=20cm
ﻤﺴﺎﺌل
)
5.1
(
ﻏﺎﺯ ﻴﺘﻤﺩﺩ ﻋﻨﺩ ﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﺤﻴﺙ ﻴﻨﺠﺯ ﻓﻲ ﺍﺜﻨﺎﺀ ﺫﻟﻙ ﺸﻐﻼﹰ ﻤﻘﺩﺍﺭﻩ
(5kJ)
.
ﻓﺈﺫﺍ ﻋﻠﻤﺕ ﺍﻥ
(
γ=1.66)
.
ﺍﺤﺴﺏ
:
)
1
(
ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻟﺘﻤﺩﺩ ﻭﺍﺘﺠﺎﻫﻬﺎ
)
2
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻠﻐﺎﺯ
.
ﺝ
) :
12.57 kJ
،
7.57
(
)
5.2
(
ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(0.5kg)
ﻤﻭﺠﻭﺩ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﻋﻤﻭﺩﻴﺔ ﻓﻭﻗﻪ ﻤﻜﺒﺱ ﻋﺩﻴﻡ ﺍﻻﺤﺘﻜﺎﻙ
ﻜﺘﻠﺘﻪ
(1kg)
.
ﺍﻻﺴﻁﻭﺍﻨﺔ ﻤﻭﻀﻭﻋﺔ ﻓﻲ ﺨﺯﺍﻥ ﻤ
ﺸﻜلـﻟﺍ ﻲﻓ ﺢﻀﻭﻤ ﺎﻤﻜ ﺀﺎ
.
ﺍﻟﺴﺨﺎﻥ ﻴﻌﻁﻲ ﻗﺩﺭﺓ ﺤﺭﺍﺭﻴﺔ ﻟﻠﻤﺎﺀ ﺒﻤﻌﺩل
(1kW)
ﺎﺀـﻤﻟﺍ ﻙـﻴﺭﺤﺘ ﺔﺤﻭﺭﻤﻭ
ﺘﻌﻤل ﺒﻘﺩﺭﺓ ﻤﻘﺩﺍﺭﻫﺎ
(0.1kW)
.
ﺴﺎﻭﻱـﺘ ﻭﺠﻠﻟ ﺀﺎﻤﻟﺍ ﻥﻤ ﺔﺤﻭﺭﻁﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ
(10%)
ﻤﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﻀﺎﻓﺔ
.
ﺩـﻌﺒ ﺀﺎـﻤﻠﻟ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻲﻓ ﺓﺩﺎﻴﺯﻟﺍ ﻲﻫ ﺎﻤ
ﺩﺓـﻤﻟ ﺔﺤﻭﺭﻤﻟﺍﻭ ﻥﺎﺨﺴﻟﺍ لﻴﻐﺸﺘ
(20 min.)
ﻭﺍﺫ
ﺎـﻬﻟﻼﺨ ﺱﺒـﻜﻤﻟﺍ ﻊـﻔﺘﺭﺍ ﺍ
)
20cm
(
ﻭﺇﺯﺩﺍﺩﺕ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻠﻐﺎﺯ ﺒﻤﻘﺩﺍﺭ
(10kJ)
.
ﺭﺍﺀﺓـﻗ ﻥﺃ ﹰﺎـﻤﻠﻋ
ﺍﻟﺒﺎﺭﻭﻤﺘﺭ
(1.01 bar)
.
ﺝ
) :
1177.364 kJ
(
)
5.3
(
ﻏﺎﺯ ﻴﻤﺭ ﻓﻲ ﺩﻭﺭﺓ ﺘﺘﻜﻭﻥ ﻤﻥ
)
3
(
ﺇﺠﺭﺍﺀﺍﺕ
) :
1
(
ﺩﺍﺭﻫﺎـﻘﻤ ﺓﺭﺍﺭـﺤ ﺯﺎﻐﻟﺍ ﻪﻴﻓ ﻡﻠﺘﺴﻴ ﺀﺍﺭﺠﺇ
(500kJ)
ﻭﻴﻌﻁﻲ ﺸﻐل ﻤﻘﺩﺍﺭﻩ
(320kJ)
) .
2
(
ﺇﺠﺭ
ﺍﺀ ﻴﺴﺘﻠﻡ ﻓﻴﻪ ﺍﻟﻐﺎﺯ ﺸﻐل ﻤﻘﺩﺍﺭﻩ
(140kJ)
ﺭﺍﺭﺓـﺤ ﻲـﻁﻌﻴﻭ
ﻤﻘﺩﺍﺭﻫﺎ
(200kJ)
) .
3
(
ﺇﺠﺭﺍﺀ ﺍﺩﻴﺎﺒﺎﺘﻲ
.
ﺠﺩ ﺍﻟﺘﻐﻴﺭ ﻟﻠﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻓﻲ ﺍﻻﺠﺭﺍﺀ ﺍﻻﺩﻴﺎﺒﺎﺘﻲ
.
ﺝ
) :
-120kJ
(
)
5.4
(
ﻭﺭﺸﺔ ﺘﺤﺘﺎﺝ ﻟﻠﺘﺩﻓﺌﺔ ﻓﻲ ﺍﻟﺸﺘﺎﺀ ﺤﻴﺙ ﺘﻜﻭﻥ ﺍﻟﺨﺴﺎﺌﺭ ﺍﻟﺤﺭﺍﺭﻴﺔ ﻨﺤﻭ ﺍﻟﻤﺤﻴﻁ
(320 000 kJ/hr)
.
ﺍﻟﻘﺩﺭﺓ
ﺍﻟﻼﺯﻤﺔ ﻟﺘﺸ
ﻐﻴل ﺍﻟﻤﻜﺎﺌﻥ ﻓﻲ ﺍﻟﻭﺭﺸﺔ
(25kW)
.
ﻭﻴﻭﺠﺩ ﻜﺫﻟﻙ
)
20
(
ﺎـﻬﻨﻤ لـﻜ ﺓﺭﺩـﻗ ًﺀﺎﻀﻤ ﹰﺎﺤﺎﺒﺼﻤ
(100W)
.
ﺍﺤﺴﺏ ﻜﺘﻠﺔ ﺍﻟﻭﻗﻭﺩ ﺍﻟﻼﺯﻡ ﺤﺭﻗﻪ ﻓﻲ ﺍﻟﺴﺎﻋﺔ ﻟﻠﺤﻔﺎﻅ ﻋﻠﻰ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺩﺍﺨل ﺍﻟﻭﺭﺸﺔ ﺜﺎﺒﺘﺔ
.
ﺇﺫﺍ ﻋﻠﻤﺕ ﺍﻥ
(85%)
ﻤﻥ ﻁﺎﻗﺔ ﺍﻟﻭﻗﻭﺩ ﺘﺩﺨل ﺍﻟﻭﺭﺸﺔ ﻟﺘﺩﻓﺌﺘﻬﺎ
.
ﺴﺘﻌﻤلـﻤﻟﺍ ﺩﻭـﻗﻭﻠﻟ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺔﻤﻴﻘﻟﺍ ﻥﺇ
(40 MJ/kg)
.
ﺝ
) :
6.553 kg/hr
(

)
96
(
)
5.5
(
ﺍﺴﻁﻭﺍﻨﺔ ﻤﺯﻭﺩﺓ ﺒﻤﻜﺒﺱ ﻓﻴﻬﺎ ﻨﺘﺭﻭﺠﻴﻥ ﺒﺤﺠﻡ
(0.1m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(25
°C)
ﻭﻀﻐﻁ
(150 kPa)
.
ﺘﺤﺭﻙ ﺍﻟﻤﻜﺒﺱ ﻀﺎﻏﻁﺎﹰ ﺍﻟﻨﺘﺭﻭﺠﻴﻥ ﺤﺘﻰ ﻭﺼل ﺍﻟﻀﻐﻁ
(1MPa)
ﺭﺍﺭﺓـﺤ ﺔﺠﺭﺩﻭ
(150
°C)
.
ﺫلـﺒﻭ
ﺸﻐل ﻋﻠﻰ ﺍﻟﻐﺎﺯ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻻﻨﻀﻐﺎﻁ ﻤﻘﺩﺍﺭﻩ
(27.8 kJ)
.
ﺍﺤﺴﺏ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍ
ﻀﻐﺎﻁـﻨﻻﺍ ﺀﺎﻨﺜﺍ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭ
ﻭﺍﺘﺠﺎﻫﻬﺎ ﻭﻜﺫﻟﻙ ﺍﺤﺴﺏ ﺤﺠﻡ ﺍﻟﻐﺎﺯ ﺍﻟﻨﻬﺎﺌﻲ
.
ﻋﻠﻤﺎﹰ ﺒﺄﻥ
:
Cp = 1.04 kJ/kg . K
γ = 1.4
ﺝ
) :
0.0213 m
3
،
-12.06 kJ
(
)
5.6
(
ﺔـﻗﻼﻌﻟﺍ ﺏـﺠﻭﻤﺒ ﻪﻤﺠﺤﻭ ﻪﻁﻐﻀ ﺭﻴﻐﺘ ﺩﻗﻭ ،ﻙﺎﻜﺘﺤﺇ ﻥﻭﺩﺒ ﺀﺍﺭﺠﻷ ﺽﺭﻌﺘ ﺱﺒﻜﻤﻭ ﺔﻨﺍﻭﻁﺴﺍ ﻲﻓ ﻊﺌﺎﻤ
(P = a + bV)
ﺤﻴﺙ ﺍﻥ
a)
،
(b
ﺜﻭﺍﺒﺕ
.
ﺴﺏـﺤ ﺀﺍﺭـﺠﻻﺍ لﻼﺨ ﺔﻤﻭﻅﻨﻤﻠﻟ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺕﺭﻴﻐﺘﻭ
ﺍﻟﻌﻼﻗﺔ
(U = 34 + 3.15 PV)
ﺤﻴﺙ
(U
≡ kJ)
،
(P
≡ kN/m
2
)
،
(V
≡ m
3
)
.
ﻀﻐﻁـﻟﺍ ﻥﺎـﻜ ﺍﺫﺇ
ﻭﺍﻟﺤﺠﻡ ﻓﻲ ﺒﺩﺍﻴﺔ ﺍﻻﺠﺭﺍﺀ
(170 kPa)
،
(0.03 m
3
)
ﺭﺍﺀـﺠﻻﺍ ﺔﻴﺎﻬﻨ ﻲﻓﻭ
(400 kPa)
،
(0.06 m
3
)
ﻋﻠﻰ ﺍﻟﺘﻭﺍﻟﻲ
.
ﺍﺭﺴﻡ ﺍﻻﺠﺭﺍﺀ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
ﻭ
ﻼلـﺨ لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﻥﻤ لﻜ ﻩﺎﺠﺘﺍﻭ ﺔﻤﻴﻗ ﺏﺴﺤﺍ
ﺍﻻﺠﺭﺍﺀ
.
ﺝ
) :
8.55 kJ
،
68.05 kJ
(
)
5.7
(
ﻴﺤﺘﻭﻱ ﺍﻟﺤﻴﺯ، ،ﹰﺎﻴﺭﺍﺭﺤ لﻭﺯﻌﻤ ﻡﺎﻅﻨ ﻲﻓ
(a)
ﻭﺍﻟﺫﻱ ﺤﺠﻤﻪ
(0.5m
3
)
ﻪـﺘﻠﺘﻜ ﺀﺍﻭـﻫ ﻰـﻠﻋ
(0.5kg)
ﻭﻀﻐﻁﻪ
(1.35bar)
ﻭﻴﺤﺘﻭﻱ ﺍﻟﺤﻴﺯ
(b)
ﺍﻟﺫﻱ ﺤﺠﻤﻪ
(0.25m
3
)
ﻋﻠﻰ ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(1kg)
ﻐﻁﻪـﻀﻭ
(4.25 bar)
.
ﻓﺈﺫﺍ ﺭﻓﻊ ﺍﻟﺤﺎﺠﺯ
(c)
)
ﺍﻫﻤل ﺤﺠﻡ ﺍﻟﺤﻴﺯ
(
ﻭﺘﺭﻙ ﺍﻟﻨﻅﺎﻡ ﺍﻟﻰ ﺍﻥ ﻴﺼل ﺍﻟﻰ ﺤﺎﻟﺔ ﺍﻻﺴﺘﻘﺭﺍﺭ
.
ﺇﺫﺍ ﻋﻠﻤﺕ ﺍﻥ،ﻡﺎﻅﻨﻟﺍ ﻲﻓ ﻲﺌﺎﻬﻨﻟﺍ ﻁﻐﻀﻟﺍﻭ ﺔﻴﺌﺎﻬﻨﻟﺍ ﺀﺍﻭﻬﻟﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩ ﻥﻭﻜﺘﺴ ﺍﺫﺎﻤ
:
Cp = 1.005 kJ/kg . K
.
Cv = 0.717 kJ/kg .K
ﺝ
) :
402.18 K
،
2.316 bar
(
)
5.8
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(2kg)
ﻓﻲ ﻨﻅ
ﺎﻡ ﻤﻐﻠﻕ
.
ﺍﻀﻴﻔﺕ ﺍﻟﻴﻪ ﻁﺎﻗﺔ ﺤﺭﺍﺭﻴﺔ ﻭﺍﻨﺘﺞ ﺍﻟﻨﻅﺎﻡ ﺸﻐﻼﹰ
.
ﺸﻐلـﻟﺍ ﻥﺎـﻜ ﺍﺫﺈـﻓ
ﻙـﻟﺫ ﺀﺎﻨﺜﺍ ﻲﻓ ﺕﻌﻔﺘﺭﺍ ﻡﺎﻅﻨﻟﺍ ﻲﻓ ﺀﺍﻭﻬﻟﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ ﺔﻓﺎﻀﻤﻟﺍ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻑﺼﻨ ﻱﻭﺎﺴﻴ ﺞﺘﺎﻨﻟﺍ
ﺒﻤﻘﺩﺍﺭ
(600K)
.
ﻋﻠﻤﺎﹰ ﺒﺄﻥ،ﺞﺘﺎﻨﻟﺍ لﻐﺸﻟﺍﻭ ﺔﻓﺎﻀﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺭﺍﺩﻘﻤ ﺩﺠﻭﺃ
:
Cp = 1.005 kJ/kg.K
.
Cv = 0.718 kJ/kg.K
ﺝ
) :
1723.2 kJ
،
861.6 kJ
(

)
97
(
)
5.9
(
ﺍﺴﻁﻭﺍﻨﺔ ﺸﺎﻗﻭﻟﻴﺔ ﺘﺤﺘﻭﻱ ﻋﻠﻰ
(100g)
ﻫﻭﺍﺀ ﻤﻐﻠﻘﺔ ﺒﻤﻜﺒﺱ ﺤﺭ ﺍﻟﺤﺭﻜﺔ
)
ﺒﺩﻭﻥ ﺇﺤﺘﻜﺎﻙ
(
ﺎﻉـﻔﺘﺭﺇ ﻰﻠﻋ
(50cm)
.
ﻜﺎﻨﺕ ﻗﺭﺍﺀﺓ ﺍﻟﺒﺎﺭﻭﻤﺘﺭ
(1 bar)
:
ﺃ
-
ﺍﻀﻴﻔﺕ ﺤﺭﺍﺭﺓ ﻤﻘﺩﺍﺭﻫﺎ
(5.95kJ)
ﻭﺃﺼﺒﺤﺕ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
(103
°C)
ﻰـﻠﻋ ﺱﺒـﻜﻤﻟﺍ ﺢﺒﺼﺍﻭ
ﻭﺸﻙ ﺍﻟﺤﺭﻜﺔ
.
ﺍﺤﺴﺏ
ﻀﻐﻁ ﺍﻟﻬﻭﺍﺀ ﻗﺒل ﺇﻀﺎﻓﺔ ﺍﻟﺤﺭﺍﺭﺓ
.
ﺏ
-
ﺍﺫﺍ ﺍﺴﺘﻤﺭﻴﻨﺎ ﻓﻲ ﺇﻀﺎﻓﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻰ ﺍﻥ ﻴﺭﺘﻔﻊ ﺍﻟﻤﻜﺒﺱ
(50cm)
.
،ﺍﺤﺴﺏ ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻀﺎﻓﺔ
ﺍﻟﻀﻐﻁ ﺍﻟﻤﻘﺎﺱ ﻟﻠﻬﻭﺍﺀ،ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻲﻓ ﻕﺭﻔﻟﺍ ،لﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍ
.
ﻁـﻁﺨﻤ ﻰﻠﻋ ﺕﺍﺀﺍﺭﺠﻹﺍ ﻡﺴﺭﺍ
(P-V)
ﻋﻠﻤﺎﹰ ﺒﺄﻥ
:
Cp = 1.005 kJ/kg.K
.
Cv = 0.717 kJ/kg.K
ﺝ
) :
0.861 bar
،
37.79 kJ
،
10.829 kJ
،
26.96 kJ
(
)
5.10
(
ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻴﺤﺘﻭﻱ ﻋﻠﻰ
(0.2kg)
ﻤﻥ ﻏﺎﺯ ﻤﺜﺎﻟﻲ
.
ﻰـﻟﺍ ﹰﺎﻴﺒﻭﺭﺘﻟﻭﺒ ﻁﻐﻀ
(100
°C)
ﺎﺀـﻨﺜﺍ ﻑﻴـﻀﺍﻭ
ﺍﻻﻨﻀﻐﺎﻁ ﺸﻐﻼﹰ ﻤﻘﺩﺍﺭﻩ
(19.7kJ)
.
ﻭﻁﺭﺤﺕ ﺤﺭﺍﺭﺓ ﻤﻘﺩﺍﺭﻫﺎ
(5.3kJ)
.
ﺕـﻨﺎﻜ ﺍﺫﺈﻓ
(
γ=1.4)
ﺩـﺠﻭﺍ
ﻗﻴﻤ
ﺔ
(R)
.
ﺝ
) :
0.295 kJ/kg.K
(

)
98
(
)
5.8
(
-
ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﻼﺠﺭﻴﺎﻨﻴﺔ
)
ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ
(
Non-Flow Processes (Closed System)
ﻲـﻓ ﺙﺩـﺤﺘ ﻲﺘﻟﺍ ﺕﺎﻴﻠﻤﻌﻟﺍ ﻲﻫ ﺔﻘﻠﻐﻤﻟﺍ ﺔﻤﻅﻨﻷﺍ ﺕﺍﺀﺍﺭﺠﺇ ﺎﻨﻟ ﺢﻀﻭﺘ ﻲﺘﻟﺍ ﺔﻴﻌﻗﺍﻭﻟﺍ ﺔﻠﺜﻤﻻﺍ ﻥﻤ
ﻓﻴﺩﺨل ﺍﻟﻤﺎﺌﻊ ﺍﻟﻰ ﺩﺍﺨل ﺍﻻﺴﻁﻭﺍﻨﺔ ﻴﺒﻘﻰ ﻓﻴﻬﺎ ﺤﺒﻴ،ﻲﻠﺨﺍﺩﻟﺍ ﻕﺍﺭﺘﺤﻻﺍ ﻙﺭﺤﻤ ﺔﻨﺍﻭﻁﺴﺍ
ﺴ
ﺎﹰ ﻟﻔﺘﺭﺓ ﻴ
ﺘﻡ ﺨﻼﻟﻬﺎ
ﻀﻐﻁ ﺍﻟﻤﺎﺌﻊ ﺒﻭﺴﺎﻁﺔ ﺍﻟﻤﻜﺒﺱ
.
ﻭﺒﻌﺩ ﺫﻟﻙ ﺘﺘﻭﻟﺩ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ ﻓﻴﺘﻤﺩﺩ ﺍﻟﻤﺎﺌﻊ ﺩﺍﻓﻌﺎﹰ ﺍﻟﻤﻜﺒﺱ ﻓﻴﻨﺠﺯ ﺸﻐﻼﹰ
ﺨﺎﺭﺠﻴﺎﹰ
.
ﻟﻭﺤﻅ ﻓﻲ ﺍﺜﻨﺎﺀ ﻀﻐﻁ ﺍﻟﻤﺎﺌﻊ ﻭﺘﻤﺩﺩﻩ ﺘﺘﺤﻘﻕ ﺍﻟﻌﻤﻠﻴﺔ ﺍﻟﻼﺠﺭﻴﺎﻨﻴﺔ ﺍﻟﺘﻲ ﻴﻤﻜﻥ ﺍﻥ ﺘﻜﻭﻥ ﻓﻴﻬﺎ ﺍﻟﺤﺩﻭﺩ
ﺍﻟﺘﻲ ﺘﻔﺼل ﺍﻟﻨﻅﺎﻡ ﺍﻟﻤﻐﻠﻕ ﻋﻥ ﻤﺤﻴﻁﻪ ﻟﻴﺴﺕ ﺒﺎﻟﻀﺭﻭﺭﺓ ﺜﺎﺒﺘ
ﺘﻘﻠﺹـﺘ ﻭﺍ ﺩﺩـﻤﺘﺘ ﺎﻤﺩـﻨﻋ ﺓﺭـﻴﻐﺘﻤ لﺒ ،ﺔ
ﻟﺘﺴﺘﻭﻋﺏ ﺍﻟﺘﻐﻴﺭﺍﺕ ﻓﻲ ﺤﺠﻡ ﻜﻤﻴﺔ ﺍﻟﻤﺎﺌﻊ ﺍﻟﺜﺎﺒﺘﺔ
.
ﺇﻥ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻓﻲ ﻫﺫﻩ ﺍﻟﻌﻤﻠﻴﺔ ﻫﻲ
:
Q – W =
∆U
ـﻭﺒﺎﻟﻨﺴﺒﺔ ﻟ
(1kg)
ﻤﻥ ﻏﺎﺯ ﻓﺈﻥ
:
q – w =
∆µ
……..
(5.15)
ﻫﺫﻩ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﺘﻲ ﺴﻨﻌﺘﻤﺩ ﻋﻠﻴﻬﺎ ﻓﻲ ﺍﻏﻠﺏ ﺍﻟﻔﺼﻭل ﺍﻟﻘﺎﺩﻤﺔ ﺘﺘﻐﻴﺭ ﺒﺤﺴﺏ ﻨﻭﻋﻴﺔ ﺍﻻ
ﺠﺭﺍﺀﺍﺕ ﺍﻟﺘﻲ
ﺘﺘﻤﻴﺯ ﺒﻤﺎ ﻴﺄﺘﻲ
:
1
-
ﻤﻊ ﺇﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﻋﺒﺭ ﺍﻟﺤﺩﻭﺩ،ﺔﺘﺒﺎﺜ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻭﺍ ﻁﻐﻀﻟﺍ ﻭﺍ ﻡﺠﺤﻟﺍ ﺀﺎﻘﺒ
.
2
-
ﺇﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﻴﺴﺎﻭﻱ ﺼﻔﺭﺍﹰ
.
3
-
ﺒﺤﻴﺙ ﻴﻜﻭﻥ ﺨﺎﻀﻌﺎﹰ ﻟﻠﻌﻼﻗﺔ،ﻡﺠﺤﻟﺍﻭ ﻁﻐﻀﻟﺍ ﺭﻴﻐﺘ
(P
ν
n
= C.)
.
ﺇﻥ ﺃﻏﻠﺏ ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﻼﺠﺭﻴﺎﻨﻴﺔ ﺍﻟﻌﻤﻠﻴﺔ ﺘﻘﺘﺭﺏ ﻤﻥ ﺍﺤﺩ ﻫﺫﻩ ﺍﻻﺠﺭﺍﺀﺍﺕ
.
ﻭﻴﻌﺎ
ﺭﺍﺀـﺠﺍ لـﻜ ﺞﻟ
ﻋﻠﻰ ﻓﺭﺽ ﺍﻥ ﺍﻟﻤﺎﺌﻊ ﺍﻤﺎ ﺍﻥ ﻴﻜﻭﻥ ﺒﺨﺎﺭﺍﹰ ﺍﻭ ﻏﺎﺯﺍﹰ ﻜﺎﻤﻼﹰ
.
ﺩﺍﻭلـﺠ لﺎﻤﻌﺘـﺴﺍ ﺏـﺠﻴ ﺭﺎـﺨﺒﻠﻟ ﺔﺒﺴﻨﻟﺎﺒﻭ
ﻭﻤﻊ ﺫﻟﻙ ﺘﺅﺠل ﺩﺭﺍﺴﺘﻪ ﺍﻟﻰ ﺍﻟﻤﺭﺤﻠﺔ ﺍﻟﺜﺎﻨﻴﺔ،ﺹﺍﻭﺨﻟﺍ
.
لـﻴﻠﺤﺘﻟﺍ ﺎـﻨﻨﻜﻤﻴﻓ لـﻤﺎﻜﻟﺍ ﺯﺎـﻐﻠﻟ ﺔﺒﺴﻨﻟﺎﺒ ﺎﻤﺍ
ﻭﺴﻨﺴﺘﻌﻤل ﺍﻟﻬﻭﺍﺀ ﻜﻤﺜﺎل ﻋﻠﻰ ﺍﻟﻐﺎﺯ ﺍﻟﻜﺎﻤل،ﺔﻴﺭﺒﺠﻟﺍ ﺕﺎﻗﻼﻌﻟﺍ لﺎﻤﻌﺘﺴﺎﺒ
ﻤﻊ ﺍﺴﺘﻌﻤﺎل ﺍﻟﺜﻭﺍﺒﺕ ﺍﻵﺘﻴﺔ
:
R=0.287 kJ/kg.K
، Cv=0.718 kJ/kg.K ، Cp = 1.005 kJ/kg.K
ﺔـﻴﻨﺎﻴﺭﺠ ﻻ ﻭﺍ ﻕﻓﺩـﺘﻟﺍ ﺔـﻤﻴﺩﻋ ﺕﺍﺀﺍﺭـﺠﺍ ﻰﻤﺴـﺘ ﻕـﻠﻐﻤﻟﺍ ﻡﺎﻅﻨﻟﺍ ﻲﻓ ﻊﺌﺎﻤﻟﺍ ﺕﺍﺀﺍﺭﺠﺍ ﻥﺍ
(Non-Flow Processes)
.
ﺜﻡ ﻁﺒﻘﺕ ﺍﻟﻨﺘﺎﺌﺞ ﺒﻌﺩ،ﺔﻘﻠﻐﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﺕﺍﺀﺍﺭﺠﺇ ﻰﻠﻋ لﻭﻻﺍ ﻥﻭﻨﺎﻘﻟﺍ ﻕﺒﻁ
ﺫﻟﻙ ﻋﻠﻰ
ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ ﺍﻟﺘﻲ ﺴﻴﺭﺩ ﺫﻜﺭﻫﺎ ﻻﺤﻘﺎﹰ
.
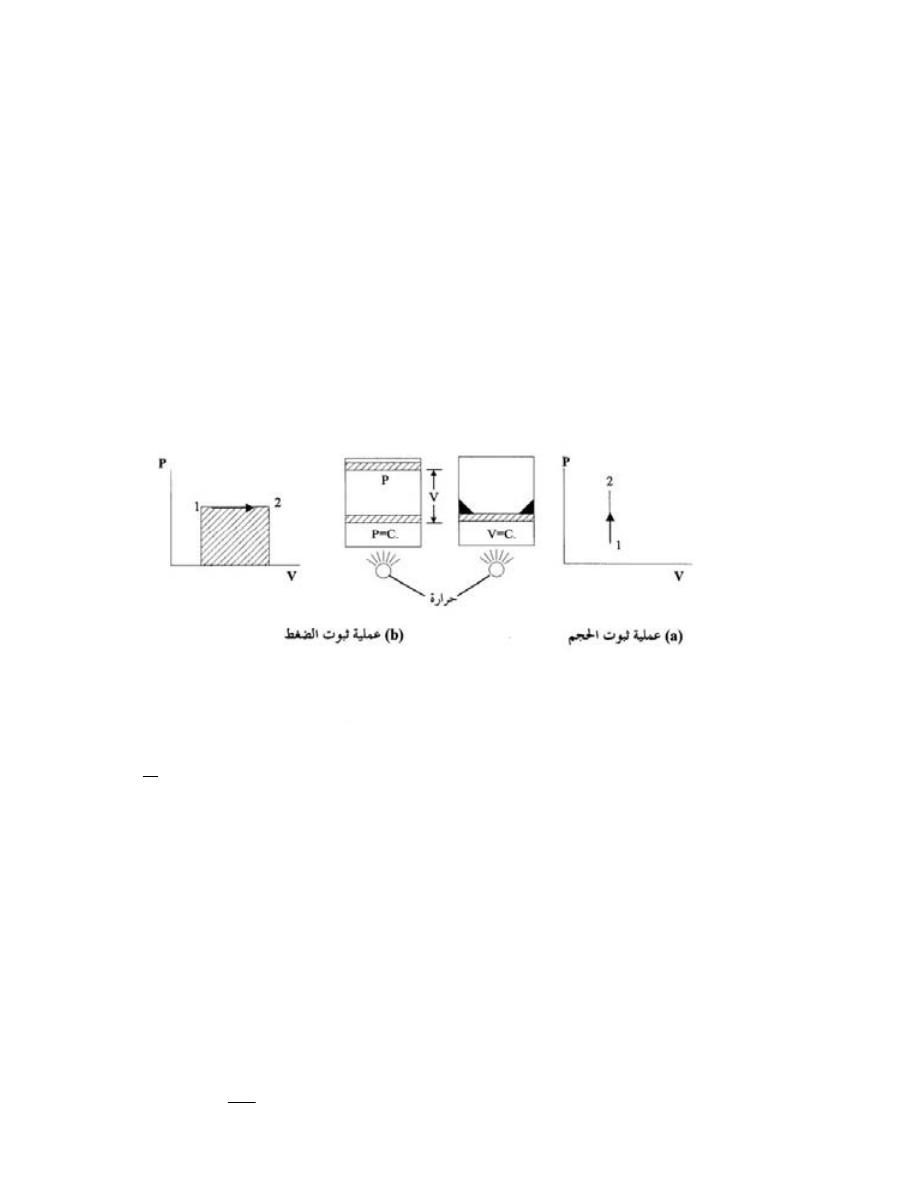
)
99
(
)
5.9
(
-
ﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻋﻠﻰ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ
Application of the First Law of Thermodynamics on the Closed System
ﺭﺍﺀﺍﺕـﺠﻸﻟ ﺔـﺼﺎﺨ ﺕﻻﺎـﺤ ﺭـﺒﺘﻌﺘ ﺕﺎﻴﻠﻤﻋ ﻲﻓ ﻕﻠﻐﻤ ﻡﺎﻅﻨ ﻲﻓ ﺩﻭﺠﻭﻤﻟﺍ ﺯﺎﻐﻟﺍ ﺔﻟﺎﺤ ﺭﻴﻐﺘﺘ
ﺍﻟﻼﺠﺭﻴﺎﻨﻴﺔ ﻭﻫﺫﻩ ﺍﻟﻌ
ﻤﻠﻴﺎﺕ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻭﺤﺩﺓ ﻜﺘﻠﺔ ﻤﻥ ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻫﻲ
:
)
5.9.1
(
-
ﻋﻤﻠﻴﺔ ﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
Constant Volume Process
ﺘﺴﻤﻰ ﺍﻴﻀﺎﹰ ﺒﺎﻷﺠﺭﺍﺀ ﺍﻻﻴﺯﻭﻤﻴﺭﻱ ﺍﻭ ﺍﻻﻴﺯﻭﻜﻭﺭﻱ
(Iso-Choric)
ﻰـﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺇ ﺩﻌﺒﻓ
ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻤﺘﻜﻭﻥ ﻤﻥ ﻭﻋﺎﺀ ﻤﻌﺩﻨﻲ ﻤﻤﻠﻭﺀ ﺒﻐﺎﺯ ﻤﺜﺎﻟﻲ ﺤﺭﺍﺭﺘﻪ ﺍﻟﻨﻭﻋﻴﺔ
(Cv)
ﻓﺴﻴﻜﻭﻥ ﻤﺴﺎﺭ،
ﺔـﻴﻠﻤﻌﻟﺍ
ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
ﻋﺒﺎﺭﺓ ﻋﻥ ﻤﺴﺘﻘﻴﻡ ﻋﻤﻭﺩﻱ ﻜﻤﺎ ﻓﻲ ﺸﻜل
(5.6-a)
.
ﻭﺤﻴﺙ ﺍﻥ ﺤﺠﻡ ﺍﻟﻭﻋﺎﺀ ﺜﺎﺒﺕ ﻓﺈﻥ
(V
1
-V
2
)
ﻭﺒﺎﻟﺘﺎﻟﻲ ﻓﺈﻥ
(dV=0)
ﻟﺫﺍ ﻴﻜﻭﻥ،
:
ﺃ
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﺤﺎﻟﺔ
:
ﺏ
-
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
:
ﺝ
-
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠ
ﻴﺔ
:
ﺩ
-
ﻋﻨﺩ ﺘﻁﺒﻴﻕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
:
(5.16)
.........
0
Pd
w
2
1
12
∫
=
ν
=
(
)
∫
−
=
=
µ
∆
2
1
1
2
(5.17)
.........
kJ/kg
)
T
T
(
Cv
dT
Cv
(
)
T
Cv
(5.18)
.........
kJ/kg
)
T
(T
Cv
q
w
q
1
2
∆
µ
∆
=
∴
−
=
µ
∆
=
µ
∆
=
−
ﺸﻜل
)
5.6
(
-
ﺘﻐﻴﺭ ﺤﺎﻟﺔ ﺍﻟﻐﺎﺯﺍﺕ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺃﻭ ﺍﻟﻀﻐﻁ
.
Const
T
P =

)
100
(
ﻑـﻗﻭﺘﻴ ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻲﻓ ﺭﻴﻐﺘﻟﺍ ﻥﺍ ﻙﻟﺫﻭ ،ﻪﻤﺴﺄﺒ ﹰﺎﻨﻭﻨﺎﻗ ﺎﻫﺎﻤﺴﻭ لﻭﺠ ﺎﻫﺩﺠﻭﺍ ﺔﻘﻴﻘﺤﻟﺍ ﻩﺫﻫﻭ
ﻋﻠﻰ ﺍﻟﺘﻐﻴﺭ ﺒﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ ﻋﻨﺩ ﺜﺒﻭﺕ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ
.
)
5.9.2
(
-
ﻋﻤﻠﻴﺔ ﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
Constant Pressure Process
ﺘﺴﻤﻰ ﺍﻴﻀﺎﹰ ﺒﺎﻻﺠﺭﺍﺀ ﺍﻻﻴﺯﻭ
ﺒﺎﺭﻱ
(Iso-baric)
.
ﻭﻥـﻜﺘﻤ ﻕﻠﻐﻤ ﻡﺎﻅﻨ ﻰﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺍ ﺩﻌﺒﻓ
ﻤﻥ ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﺤﺭﺍﺭﺘﻪ ﺍﻟﻨﻭﻋﻴﺔ
(Cp)
ﻴﺔـﺴﺃﺭ ﺔﻨﺍﻭﻁﺴﺍ لﺨﺍﺩ ﺱﺒﻜﻤﻟﺍ ﻙﺭﺤﺘﻴﻭ ،ﺕﺒﺎﺜ ﻁﻐﻀﺒ ﻅﻔﺘﺤﻴﻭ
.
ﻓﺴﻴﻜﻭﻥ ﻤﺴﺎﺭ ﺍﻟﻌﻤﻠﻴﺔ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
ﻜلـﺸ ﻲـﻓ ﺎﻤﻜ ،ﻲﻘﻓﺍ ﻡﻴﻘﺘﺴﻤ ﻥﻋ ﺓﺭﺎﺒﻋ
(5.6-b)
.
ﻭﺤﻴﺙ ﺍﻥ ﺍﻟﻀﻐﻁ ﺜﺎﺒﺕ
(P
1
=P
2
)
ﻟﺫﺍ ﺴﻴﻜﻭﻥ،
:
ﺃ
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﺤﺎﻟﺔ
:
ﺏ
-
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
:
ﺝ
-
ﻋﻨﺩ ﺘﻁﺒﻴﻕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
:
1
-
ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ
)
q
(
q =
∆µ + w
= Cv (T
2
– T
1
) + R(T
2
– T
1
)
= Cp (T
2
– T
1
)
…….
(5.20)
2
-
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻻﻨﺜﺎﻟﺒﻲ
)
∆h
(
d q = d
µ + d w
…… (5.21)
ﻭﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﻀﻐﻁ ﺜﺎﺒﺕ ﺘﺼﺒﺢ
:
= d
µ + d P ν
= d (
µ + Pν)
∴dq = dh
ﻭﺒﺼﻴﻐﺔ ﺘﻜﺎﻤﻠﻴﺔ ﻴﻜﻭﻥ
:
q =
∆h
∴ q = ∆h = Cp ∆T ……..
(5.22)
ﺎﻟﺒﻲـﺜﻨﻻﺍ ﻲﻓ ﺓﺩﺎﻴﺯﻟﺍ ﻱﻭﺎﺴﺘ ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜ ﺀﺍﺭﺠﺍ ﺀﺎﻨﺜﺍ ﺔﻓﺎﻀﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻥﺍ ﻱﺃ
.
ﺫﻩـﻫ ﻥـﻤﻭ
ـﺍﻟﻤﻌﺎﺩﻟﺔ ﻨﺘﻌﺭﻑ ﻋﻠﻰ ﺍﻟ
(Cp)
Cp =
∆h / ∆T
…….. (5.23)
3
-
ﺜﺎﺒﺕ ﺍ
ﻟﻐﺎﺯ
)
R
(
q =∆µ+w
C
p∆T
= C
v∆T
+R∆T
R = C
p
-C
v
.
Const
T
=
ν
(
)
(5.19)
........
kJ/kg
)
T
T
(
R
)
(
P
Pd
w
2
1
1
2
1
2
12
∫
−
=
ν
−
ν
=
ν
=

)
101
(
)
5.9.3
(
-
ﻋﻤﻠﻴﺔ ﺜﺒﻭﺕ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
Constant Temperature Process
ﺘﺴﻤﻰ ﺍﻴﻀﺎﹰ ﺒﺎﻻﺠﺭﺍﺀ ﺍﻻﻴﺯﻭﺜﺭﻤﻠﻲ
(Isothermal)
.
ﻕـﻠﻐﻤ ﻡﺎـﻅﻨ ﻰـﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﺇ ﺩﻌﺒﻓ
ﻤﺘﻜﻭﻥ ﻤﻥ ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻴﺤﺘﻔﻅ ﺒﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ ﺜﺎﺒﺘﺔ ﺒﻭﺍﺴﻁﺔ ﺤﺭﻜﺔ ﺍﻟﻤﻜﺒﺱ ﺍﻟﺒﻁﻴﺌﺔ
ﺠﺩﺍﹰ ﺩﺍﺨل ﺍﻻﺴﻁﻭﺍﻨﺔ
.
ﻴﻥـﺒ ﻥﺎـﻜﻤ لﻜ ﻲﻓ ﺭﺸﺘﻨﺘﻭ ﺔﻨﺍﻭﻁﺴﻻﺍ ﻥﺍﺭﺩﺠ لﻼﺨ ﻥﺎﻴﺭﺴﻟﺎﺒ ﺓﺭﺍﺭﺤﻠﻟ ﻑﺎﻜ ﺕﻗﻭ ﻙﺎﻨﻫ ﻥﻭﻜﻴ ﺍﺫﻜﻫﻭ
ﺍﻟﻐﺎﺯ
.
ﺭﻋﺔـﺴ ﻥﺍ ﺙﻴﺤ ،ﺔﺜﻴﺩﺤﻟﺍ ﻲﻠﺨﺍﺩﻟﺍ ﻕﺍﺭﺘﺤﻻﺍ ﺕﺎﻜﺭﺤﻤ ﻰﻠﻋ ﺀﺍﺭﺠﻻﺍ ﺍﺫﻫ ﻕﺒﻁﻨﻴ ﻻ ﺏﺒﺴﻟﺍ ﺍﺫﻬﻟﻭ
ﻫﺫﻩ ﺍﻟﻤﺤﺭﻜﺎﺕ ﻋﺎﻟﻴﺔ ﺠﺩﺍﹰ
.
ﺇﻥ ﻤﺴﺎﺭ ﺍﻟﻌﻤﻠﻴﺔ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻋﻠﻰ ﻤ
ﺨﻁﻁ
(P-V)
ﻲـﻓ ﺢـﻀﻭﻤ ﺎﻤﻜ ،ﻲﻨﺤﻨﻤ ﻥﻋ ﺓﺭﺎﺒﻋ
ﺸﻜل
(5.7-a)
.
ﻭﺒﻤﺎ ﺍﻥ
(T
1
=T
2
)
ﻓﺴﻴﻜﻭﻥ
:
ﺃ
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﺤﺎﻟﺔ
:
P
ν = Const.
ﺏ
-
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
:
Or
1
2
1
1
1
2
Ln
P
RTLn
d
RT
Pdv
w
ν
ν
ν
=
ν
ν
=
ν
ν
=
=
∫
∫
ﺝ
-
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
:
ﺩ
-
ﻋﻨﺩ ﺘﻁﺒﻴﻕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
:
)
5.9.4
(
-
ﺍﻟﻌﻤﻠﻴﺔ ﺍﻻﺩﻴﺎﺒﺎﺘﻴﺔ
Adiabatic Process
، ﻭﺘﺘﻡ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﻤﺤﺭﻙ ﻤﻌﺯﻭﻟﺔ،ﻱﺭﺍﺭﺤ لﺩﺎﺒﺘ ﻥﻭﺩ ﺯﺎﻐﻟﺍ ﺔﻟﺎﺤ ﺎﻬﻴﻓ ﺭﻴﻐﺘﺘ ﻲﺘﻟﺍ ﺔﻴﻠﻤﻌﻟﺍ ﻲﻫ
ﺎـﻤﻨﻴﺒ ،ﻲﻜﺎﻜﺘﺤﺇ ﻻ لﻭﺯﻌﻤ ﺱﺒﻜﻤﺒ ﺓﺯﻬﺠﻤﻟﺍﻭ ﺔﻟﻭﺯﻌﻤﻟﺍ ﺔﻨﺍﻭﻁﺴﻻﺍ ﻥﺍﺭﺩﺠ لﻼﺨ ﺓﺭﺍﺭﺤ لﻘﺘﻨﺘ ﻻ ﺙﻴﺤﺒ
ﻴﺘﻤﺩﺩ ﺍﻟﻐﺎﺯ ﻭﻴﻘﻭﻡ ﺒﻌﻤل ﺨﺎﺭﺠﻲ
.
ﻫﺫﻩ ﺍﻟﺤﺎﻟﺔ ﻏﻴﺭ ﻤﻭﺠﻭﺩﺓ ﻓﻌﻼﹰ ﻭﻟﻜﻥ ﻋﻨﺩﻤﺎ ﻴﺤﺩﺙ
ﺎﺩلـﺒﺘﻠﻟ ٍﻑﺎﻜ ﺕﻗﻭ ﺩﺠﻭﻴ ﻻ ﹰﺎﻌﻴﺭﺴ ﺀﺍﺭﺠﻻﺍ
ﺍﻟﺤﺭﺍﺭﻱ ﺒﻴﻥ ﺍﻟﻐﺎﺯ ﻭﺍﻟﻤﺤﻴﻁ ﻋﺒﺭ ﺠﺩﺭﺍﻥ ﺍﻻﺴﻁﻭﺍﻨﺔ
.
ﺩﺩـﻤﺘﻟﺍﻭ ﻁﺎﻐﻀﻨﻻﺍ ﺔﻴﻠﻤﻋ ﻭﻫ ﻙﻟﺫ ﻰﻠﻋ لﺎﺜﻤﻜﻭ
ﺔـﻴﻨﻤﺯﻟﺍ ﺓﺭـﺘﻔﻟﺍ لﻼـﺨ ﻲﻔﻓ ،ﺔﻴﺘﺎﺒﺎﻴﺩﺍ ﺔﻴﻠﻤﻋ ﹰﺎﺒﻴﺭﻘﺘ ﺎﻫﺭﺎﺒﺘﻋﺍ ﻥﻜﻤﻴ ﻲﺘﻟﺍ ﻲﻠﺨﺍﺩﻟﺍ ﻕﺍﺭﺘﺤﻻﺍ ﻙﺭﺤﻤ ﻲﻓ
(5.24)
.......
PV
C
V
C
P
or
C
mRT
PV
=
⇒
=
=
=
Q
(5.25)
..
..........
..........
..........
..........
..........
Ln
P
kg
kJ
V
V
RTLn
V
V
Ln
V
P
V
V
CLn
V
dV
C
dV
V
C
PdV
w
1
2
1
1
1
2
2
1
2
1
1
2
1
1
1
2
ν
ν
ν
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
=
=
∫
∫
∫
∫
=
=
µ
∆
2
1
0
dT
Cv
(5.26)
.
..........
w
q
w
q
=
∴
µ
∆/
=
−
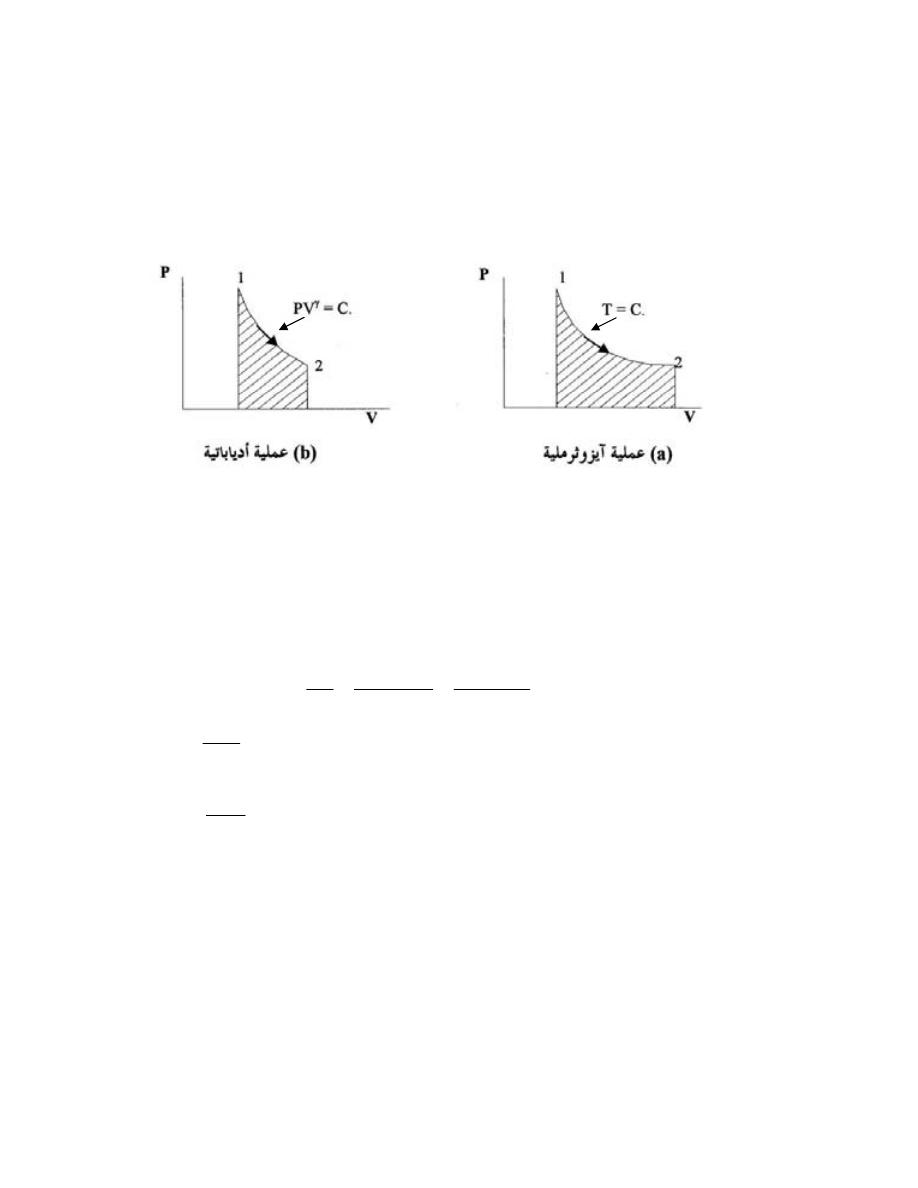
)
102
(
ﺍﻟﻘﺼﻴﺭﺓ ﺍﻟﺘﻲ ﺘﺘﻡ ﻓﻴﻬﺎ ﻫﺫﻩ ﺍﻟﻌﻤﻠﻴﺎﺕ
ﺭﻋﺔـﺴ ﺏﺒﺴـﺒ ﻁﻴﺤﻤﻟﺍﻭ ﺯﺎﻐﻟﺍ ﻥﻴﺒ ﻱﺭﺍﺭﺤﻟﺍ لﺩﺎﺒﺘﻟﺍ لﺎﻤﻫﺇ ﻥﻜﻤﻴ
ﺃﻱ،ﺔﻴﻟﺎﻌﻟﺍ ﻙﺭﺤﻤﻟﺍ
(q=0)
.
ﻤﺴﺎﺭﻫﺎ ﻤﻥ،ﻡﺎﻌﻟﺍ ﺀﺍﺭﺠﻻﺍ ﻥﻤ ﺔﺼﺎﺨ ﺔﻟﺎﺤ ﻲﻫ ﺔﻴﻠﻤﻌﻟﺍ ﻩﺫﻫ
)
1
(
ﺍﻟﻰ
)
2
(
ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
ﻋﺒﺎﺭﺓ ﻋﻥ ﻤﻨﺤﻨﻲ ﻜﻤﺎ ﻓﻲ ﺸﻜل
(5.7-b)
ﻟﺫﻟﻙ ﺴﻴﻜﻭﻥ
:
ﺃ
-
ﺍﻻﺱ ﺍﻻﺩﻴﺎﺒﺎﺘﻲ ﻜﺎﻤﺎ
(
γ)
ﻭﻴﺴﺎﻭﻱ
:
γ = Cp / Cv
ـﺍﻤﺎ ﺍﻟ
)
Cv
،
Cp
(
ﻓﺘﺸﺘﻕ ﻜﻤﺎ ﻴﻠﻲ
:
ﻭﻜﺫﻟﻙ
:
R = Cp – Cv =
γ Cv – Cv = Cv (γ– 1)
ﺍﻟﻌﻼﻗﺎﺕ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﺘﺼﺢ ﻟﻠﻐﺎﺯ ﺍﻟﺤﻘﻴﻘﻲ ﻭﺍﻟﻤﺜﺎﻟﻲ
.
ﺇﻥ ﺍﻟﺜﻭﺍﺒﺕ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﻭﺜﻭﺍﺒﺕ ﺍﺨﺭﻯ ﻤﻭﻀﺤﺔ
ﻓﻲ ﺠﺩﻭل
)
5.1
.(
(5.27)
..........
1
R
Cp
)
1
(
Cp
Cp
Cp
Cp
Cp
Cv
Cp
R
−
γ
γ
=
∴
γ
−
γ
=
γ
−
γ
=
γ
−
=
−
=
(5.28)
..........
1
R
Cv
−
γ
=
∴
ﺸﻜل
)
5.7
(
-
ﺘﻐﻴﺭ ﺤﺎﻟﺔ ﺍﻟﻐﺎﺯ ﺤﺎﻟﺔ ﺁﻴﺯﻭﺜﺭﻭﻤﻠﻴﺎ ﺃﻭ ﺍﺩﻴﺎﺒﺎﺘﻴﺎ
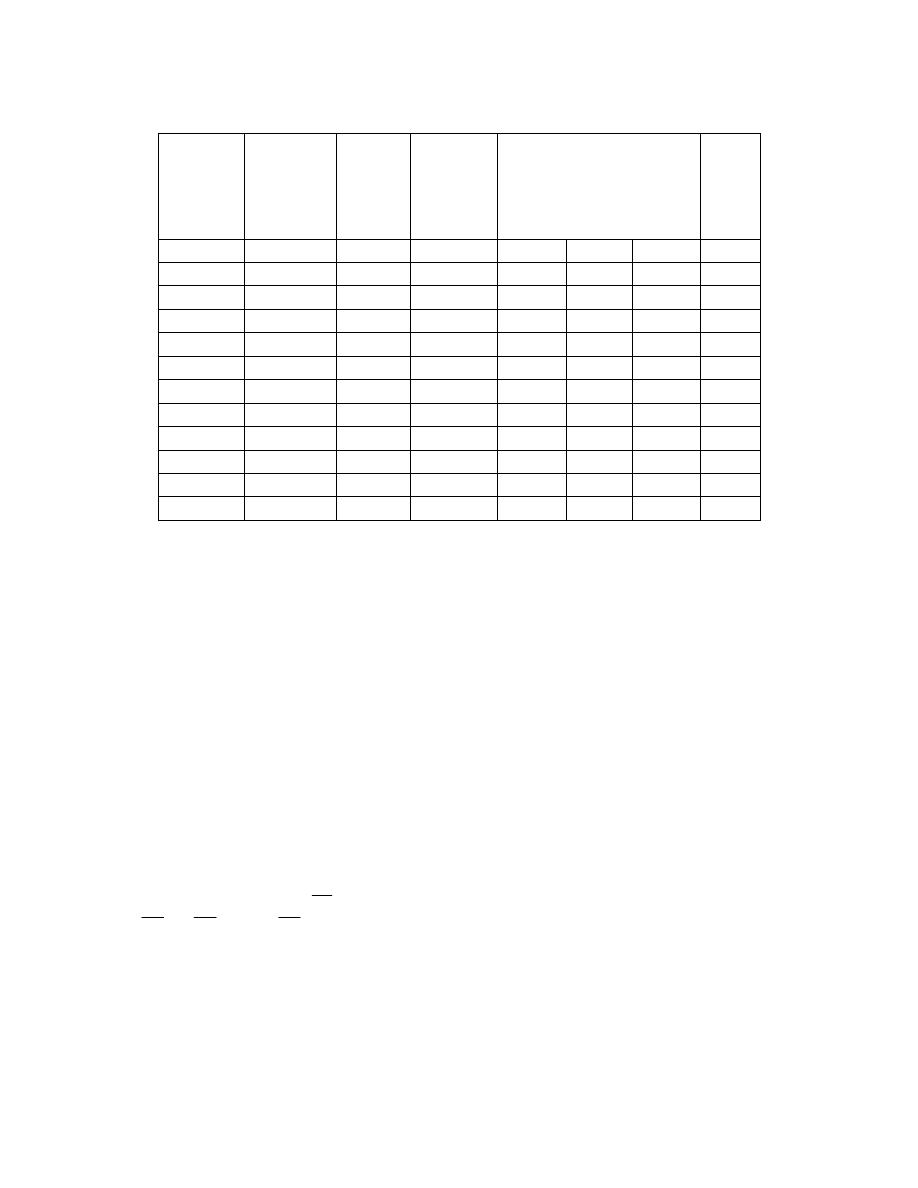
)
103
(
ﺠﺩﻭل
)
5.1
(
ﺼﻔﺎﺕ ﺍﻟﻐﺎﺯﺍﺕ ﺍﻟﺤﻘﻴﻘﻴﺔ
ﻐﺎﺯ
ﺍﻟ
Gas
ﻓﻲ
ﺍﺕ
ﺍﻟﺫﺭ
ﺩﺩ
ﻋ
ﺍ
ﻟﺠﺯﻴﺊ
N
ﻲ
ﻟﺠﺯﻴﺌ
ﻭﺯﻥ ﺍ
ﺍﻟ
M
ﺍﻟﻜﺜﺎﻓﺔ
(S.T.P)
ρ kg/m
3
kJ/kg
.K
γ
Cp
Cv
R
Air - 29
1.293
1.01
0.72
0.287
1.4
He
1
4
0.179 5.19 3.11 2.08 1.67
H2 2 2
0.09
14.20
10.08
4.12
1.41
N2 2 28
1.253
1.04
0.74
0.297
1.4
O2 2 32
1.430
0.92
0.66
0.260
1.4
CO 2 28
1.151
1.04
0.74
0.297
1.4
CO2 3 44
1.975
0.82
0.63
0.189
1.31
SO2
3
61
2.90 0.61 0.48 0.13 1.26
CH4
5
16 0.718 2.23 1.71 0.52 1.31
C2H6 8 30
1.358
1.75
1.47
0.277
1.19
ﻨﺘﺭﻭﺠﻴﻥ ﺠﻭﻱ
28.15 1.03
0.74
0.295
1.4
ﻤﺭﻜﺒﺎﺕ ﺍﻟﻬﻭﺍﺀ
:
ﺍﻟﻨﺴﺒﺔ ﺍﻟﺤﺠﻤﻴﺔ
:
(79% N
2
)
،
(21%O
2
)
ﺍﻟﻨﺴﺒﺔ ﺍﻟﻭﺯﻨﻴﺔ
:
(76.8% N
2
)
،
(23.2%O
2
)
N
2
…
ﻨﻴﺘﺭﻭﺠﻴﻥ ﺠﻭﻱ
.
ﺏ
-
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺍﻟﻨﻭﻋﻴﺔ
:
∆µ = Cv ∫dT = Cv (T
2
– T
1
)
……. (5.29)
ﺝ
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﺤﺎﻟﺔ
)
ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ
(
ﺍﻟﺘﻲ ﺘﻌﺒﺭ ﻋﻥ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ
(P)
ﻭ
(
ν)
:
P
ν
γ
=
Const.
……..
(5.30)
ﺩ
-
ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ ﺍﻟﺘﻲ ﺘﺭﺒﻁ ﺍﻟﻌﻼﻗﺔ ﺒﻴﻥ
)
P
،
ν
،
T
:(
(5.31)
..........
P
P
T
T
1
1
2
1
2
1
1
2
γ
−
γ
−
γ
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
ν
ν
=
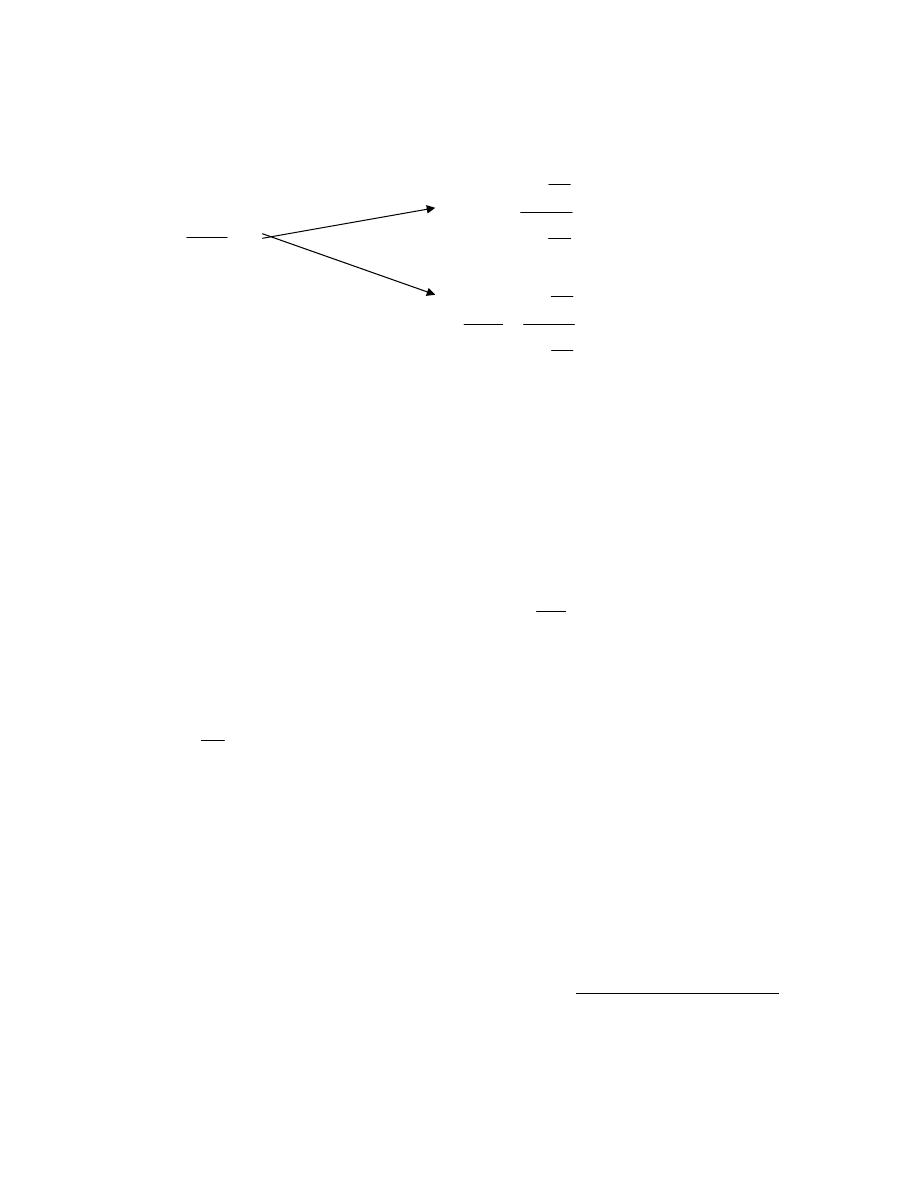
)
104
(
ﻭﺍﺫﺍ ﻜﺎﻥ ﺍﻟﻤﻁﻠﻭﺏ ﺍﻴﺠﺎﺩ ﻗﻴﻤﺔ ﺍﻻﺱ ﻓﻲ ﺍﻟﻤﻌﺎﺩﻟﺔ
)
5.31
(
ﻓﻨﺴﺘﻌﻴﻥ ﺒﺎﻟﻌﻼﻗﺔ ﺍﻟﺭﻴﺎﻀﻴﺔ ﺍﻵﺘﻴﺔ
:
y = x
a
Ln y = a Ln x
ﺤﻴﺙ ﺍﻥ
(Ln)
∗
ﻫﻭ ﺍﻟﻠﻭﻏﺎﺭﻴﺘﻡ
ﺍﻟﻁﺒﻴﻌﻲ
.
ﺍﻤﺎ ﺍﺫﺍ ﺼﺎﺩﻓﻨﺎ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻟﺤﺴﺎﺒﺎﺕ ﺍﻟﻌﻼﻗﺔ
(Ln y = x)
ﻓﻨﺴﺘﻌﻴﻥ ﺒﺎﻟﻌﻼﻗﺔ ﺍﻟﺭﻴﺎﻀﻴﺔ ﺍﻵﺘﻴﺔ
:
Ln y = x
∴ y = e
x
ﻭﺒﺎﻟﻨﺴﺒﺔ ﻟﻐﺎﺯ ﻤﺜﺎﻟﻲ ﺫﻱ ﺤﺭﺍﺭﺓ ﻨﻭﻋﻴﺔ ﺜﺎﺒﺘﺔ ﻴﻘﻊ ﺘﺤﺕ ﺘﺄﺜﻴﺭ ﻋﻤﻠﻴﺔ ﺇﻨﻀﻐﺎﻁ ﺍﻭ ﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻲ
ﻓﺈﻥ ﺍﻟﻤﻌﺎﺩﻻﺕ ﻓﻲ،ﻲﺴﺎﻜﻌﻨﺍ
)
ﺝ
(
ﻭ
)ﺩ
(
ﺘﺸﺘﻕ ﻜﻤﺎ ﻴﺄﺘﻲ
:
∗
ـ ﻴﻘﺼﺩ ﺒ
(Ln)
ﻟﻭﻏﺎﺭﻴﺘﻤﺎﺕ ﻁﺒﻴﻌﻴﺔ ﻭﺍﻟﺘﻲ ﺍﺴﺎﺴﻬﺎ
(e)
.
ـﺍﻤﺎ ﺍﻟ
(Log)
ﺸﺭﻴﺔـﻋ ﺕﺎﻤﺘﻴﺭﺎﻏﻭﻟ ﻲﻬﻓ
ﻭ
ﺍﻟﺘﻲ ﺍﺴﺎﺴﻬﺎ
(10)
ﻭﺍﻟﻌﻼﻗﺔ ﺒﻴﻨﻬﻤﺎ ﻫﻲ
:
Ln = 2. 3 log
x
n
L
y
Ln
a
=
∴
∫
∫
∫
∫
=
ν
ν
−
=
−
µ
∆
=
−
µ
∆
=
−
2
1
2
1
2
1
2
1
dt
Cv
d
RT
CvdT
Pdv
w
w
q
1
2
1
2
v
v
Ln
T
T
Ln
1
=
−
γ
∴
1
2
1
2
P
P
Ln
T
T
Ln
1 =
γ
−
γ
∴
)
1
(
Cv
R
v
RT
P
−
γ
=
=
Q
Q
)
105
(
ﻭﺍﻟﻘﺴﻤﺔ ﻋﻠﻰ
(T)
ﻴﻨﺘﺞ
:
ﻨﻌﻭﺽ
(5.33)
ـ ﺒ
(5.32)
ﻴﻨﺘﺞ
:
ﻭﻤﻥ ﻫﺫﻩ ﺍﻟﻤﻌﺎﺩﻟﺔ ﻨﻭﺠﺩ ﺍﻟﻌﻼﻗﺔ ﺍﻵﺘﻴﺔ
:
P
1
ν
1
γ
= P
2
ν
2
γ
= P
ν
γ
= Const.
……. (5.35)
ـﻴﺭﻤﺯ ﻟﻠﺜﺎﺒﺕ ﺒ
(Const.)
ﺍﻭ
(C.)
.
(5.32)
.......
T
T
T
T
Ln
Ln
T
T
Ln
Ln
)
1
(
T
dT
Cv
d
)
1
(
Cv
1
2
1
2
1
1
2
)
1
(
1
2
1
2
1
2
2
1
2
1
=
⎟
⎠
⎞
⎜
⎝
⎛
ν
ν
=
⎟
⎠
⎞
⎜
⎝
⎛
ν
ν
=
ν
ν
−
γ
−
=
ν
ν
−
γ
−
−
γ
−
γ
−
∫
∫
(5.33)
.........
P
P
T
T
P
P
T
T
P
P
T
T
.
T
T
T
T
.
P
P
T
T
1
1
2
1
2
1
1
2
1
2
1
1
2
1
1
2
1
2
1
1
2
1
1
2
1
2
γ
−
γ
−
γ
γ
−
γ
−
γ
−
γ
−
γ
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=
(5.34)
.........
P
P
T
T
1
1
2
1
2
1
1
2
γ
−
γ
−
γ
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
ν
ν
=
Lny
aLnX
Lny
LnX
y
X
a
a
=
=
=
2
1
1
2
2
1
T
P
T
P
v
v =
Q
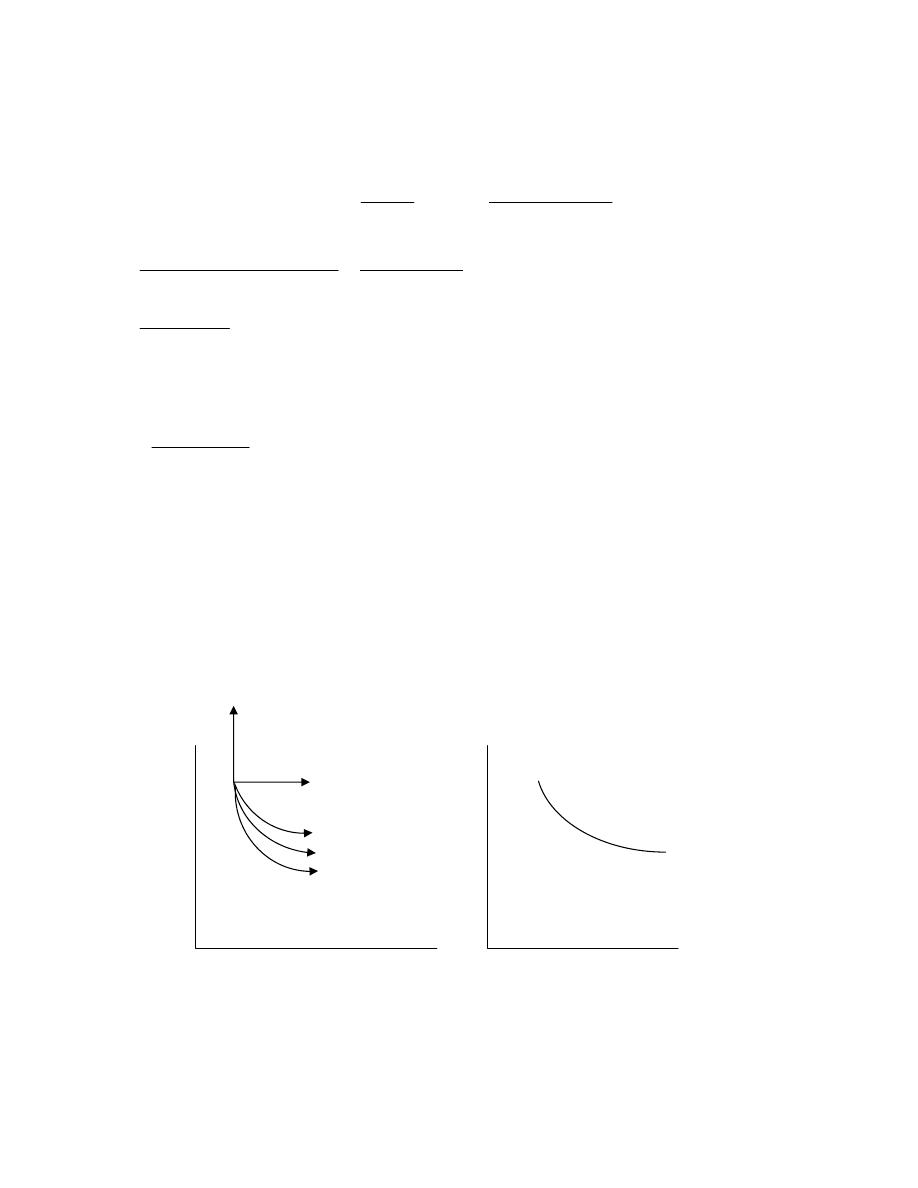
)
106
(
ـﻫ
-
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
ﻭ
-
ﻋﻨﺩ ﺘﻁﺒﻴﻕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل
:
)
5.9.5
(
-
ﺍﻟﻌﻤﻠﻴﺔ ﺍﻟﺒﻭﻟﺘﺭﻭﺒﻴﺔ
Polytropic Process
ﺘﺴﻤ
ﺎﻡـﻅﻨﻟﺍ ﺹﺍﻭﺨ ﻥﻭﻜﺘ ﺎﻤﺩﻨﻋ ﺙﺩﺤﻴ ،ﻲﺨﺎﻨﻤﻟﺍ ﻭﺍ ﺀﺎﻨﺤﻨﻻﺍ ﺩﺩﻌﺘﻤ ﻭﺍ ﺎﻡﻌﻟﺍ ﺀﺍﺭﺠﻷﺎﺒ ﹰﺎﻀﻴﺍ ﻰ
ﻜﺎﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻤﺘﻐﻴﺭﺓ
.
ﻴﻤﺜل ﺒﻤﻨﺤﻨﻲ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-v)
ﻜلـﺸ ﻲﻓ ﺎﻤﻜ ،
(5.8-a)
.
ﻭﻕـﻓ ﻊـﻘﻴ ﻲﻠﻤﺭﺜﻭﺯﻴﻻﺍ ﺀﺍﺭﺠﻻﺍ ﻲﻨﺤﻨﻤ ﻥﺍ ﺫﺇ ،ﻲﺘﺎﺒﺎﻴﺩﻻﺍﻭ ﻲﻠﻤﺭﺜﻭﺯﻴﻻﺍ ﻥﻴﺌﺍﺭﺠﻻﺍ ﻥﻴﺒ ﻊﻘﻴ ﺀﺍﺭﺠﺇ ﻭﻫ
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﺩﺩﻤﺘﻟﺍ ﺔﻟﺎﺤ ﻲﻓ ﺎﻤﻬﻨﻴﺒ ﻲﺒﻭﺭﺘﻟﻭﺒﻟﺍﻭ ﻲﺘﺎﺒﺎﻴﺩﻻﺍ ﺀﺍﺭﺠﻻﺍ ﻲﻨﺤﻨﻤ
(5.8-b)
.
ﺔـﻟﺎﺤ ﻲـﻓ ﺎﻤﺍ
ﺍﻻﻨﻀﻐﺎﻁ ﻓﻴﻜﻭﻥ ﺍﻟﻌﻜﺱ
.
ﺇﻥ ﺨﻁﻭﻁ ﻭﻤﻨﺤﻨﻴﺎﺕ ﺍﺠﺭﺍﺀﺍﺕ ﺍﻟﺘﻤﺩﺩ ﻓﻲ ﺸﻜل
(5.8-b)
ﺭﺍﺀﺍﺕـﺠﺍ ﺱـﻜﻋ
ﺍﻻﻨﻀﻐﺎﻁ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
.
(5.37)
........
(kJ/kg)
1
)
T
T
(
R
1
V
P
V
P
1
V
V
P
V
V
P
1
V
V
C
1
V
C
dV
CV
PdV
W
(5.36)
.......
V
P
V
P
C
CV
P
C
PV
2
1
2
2
1
1
1
1
1
1
1
2
2
2
1
1
1
2
V
V
1
-
2
2
1
1
-
2
1
−
γ
−
=
−
γ
−
=
+
γ
−
−
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
γ
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
γ
−
=
=
=
=
=
⇒
=
⇒
=
+
γ
−
γ
+
γ
−
γ
+
γ
−
+
γ
−
+
γ
−
γ
γ
γ
γ
γ
∫
∫
Q
(
)
(5.38)
........
T
T
Cv
1
P
P
w
w
q
1
2
2
2
1
1
−
=
−
γ
ν
−
ν
−
µ
∆
=
−
µ
∆
=
−
1
2
PV = Const.
)
ِ
(a
ﻋﻤﻠﻴﺔ ﺒﻭﻟﺘﺭﻭﺒﻴﺔ
)
ِ
(b
ﺇﺠﺭﺍﺀﺍﺕ ﻋﺎﻤﺔ
P
V
V
P
PV
n
= Const.
PV
γ
= Const.
PV
0
= Const.
PV
∞
= Const.
PV
n
= Const.
ﺸﻜل
)
5.8
-(
ﻤﻨﺤﻨﻴﺎﺕ ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﻌﺎﻤﺔ

)
107
(
ﺃ
-
ﺍﻻﺱ ﺍﻟﺒﻭﻟﺘﺭﻭﺒﻲ
(n)
:
ﻴﻌﺘﻤﺩ
ﻀﻐﺎﻁـﻨﻻﺍ ﺔﺒﺴﻨ ،ﺕﺍﺯﺎﻐﻟﺍ ﻁﻴﻠﺨ لﺜﻤ ﺔﻨﺍﻭﻁﺴﻻﺍ ﻑﻭﺭﻅ ﻰﻠﻋ
…
ﺍﻟﺦ
.
ﻗﻴﻤﺘﻪ ﻋﺎﺩﺓﹰ ﺘﻜﻭﻥ ﻭﺍﻗﻌﺔ ﺒﻴﻥ
)
1
،
γ
(
ﻭﻟﻜﻥ ﺒﺸﻜل ﻋﺎﻡ ﺘﺘﺤﺩﺩ ﻗﻴﻤﺘﻪ ﺒﻴﻥ
)
∞
-
0
.(
ﻰـﻟﺍ ﹰﺍﺩﺎﻨﺘﺴﺇﻭ
ﺸﻜل
(5.8-b)
ﻓﺈﻨﻪ
:
1
.
ﺇﺫﺍ ﻜﺎﻨﺕ
(n=0)
ﺃﻱ،ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜ ﺀﺍﺭﺠﻻﺍ ﻥﻭﻜﻴﺴﻓ
:
PV
0
= Const.
∴ P = Const.
2
.
ﺇﺫﺍ ﻜﺎﻨﺕ
(n=
∞)
ﻓﺴﻴﻜﻭ
ﺃﻱ،ﻡﺠﺤﻟﺍ ﺕﻭﺒﺜ ﺀﺍﺭﺠﻷﺍ ﻥ
:
-
3
.
ﺍﺫﺍ ﻜﺎﻨﺕ
(n=1)
ﺃﻱ،ﻲﻠﻤﺭﺜﻭﺯﻴﺍ ﺀﺍﺭﺠﻹﺍ ﻥﻭﻜﻴﺴﻓ
:
PV = Const.
4
.
ﺍﺫﺍ ﻜﺎﻨﺕ
(n=
γ)
ﺃﻱ،ﻲﺘﺎﺒﺎﻴﺩﺍ ﺀﺍﺭﺠﻻﺍ ﻥﻭﻜﻴﺴﻓ
:
PV
γ
= Const.
ﻟﺫﻟﻙ ﺘﻌﺩ ﺍﻟﺤﺎﻻﺕ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﺤﺎﻻﺕ ﺨﺎﺼﺔ ﻭﺍﻟﺒﻭﻟﺘﺭﻭﺒﻲ ﻫﻭ ﺍﻟﺤﺎﻟﺔ ﺍﻟﻌﺎﻤﺔ ﻟﺘﻤﺩﺩ ﺍﻟﻤﺎﺩﺓ ﺍﻭ
ﺇﻨﻀﻐﺎﻁﻬﺎ
.
ﺏ
-
ﺍﻟﻘﺎﻨﻭ
ﻥ ﺍﻭ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ ﺍﻟﺫﻱ ﻴﺭﺒﻁ ﺒﻴﻥ ﺍﻟﺨﺎﺼﻴﺘﻴﻥ
(
ν. P)
ﻫﻭ
:
P
ν
n
= Const.
……… (5.39)
ﻓﺈﺫﺍ ﻋﻠﻤﺕ ﺨﻤﺴﺔ ﺨﻭﺍﺹ ﻓﺴﺘﻜﻭﻥ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ ﻫﻲ
:
ﻭﻋﻨﺩ ﻋﺩﻡ ﻤﻌﺭﻓﺔ ﺨﻤﺴﺔ ﺨﻭﺍﺹ ﻓﺴﺘﻜﻭﻥ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻌﺎﻤﺔ
:
ﺝ
-
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
:
Const.
V
.
Const
V
P
.
Const
V
P
.
Const
PV
0
/
1
=
∴
=
⇒
=
⇒
=
∞
∞
(5.40)
.........
.
Const
T
P
T
P
2
2
2
1
1
1
=
ν
=
ν
(5.41)
.
..........
P
P
V
V
T
T
n
1
n
1
2
1
n
2
1
1
2
−
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
(5.42)
........
(kJ/kg)
)
T
(T
Cv
dT
Cv
1
2
2
1
−
=
=
µ
∆
∫

)
108
(
ﺩ
-
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
:
ـﻫ
-
ﺒﺘﻁﺒﻴ
ﻭﻜﺎﻟﺘﺎﻟﻲ،ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﻕﺎﻘﺘﺸﺍ ﻥﻜﻤﻴ ،لﻭﻻﺍ ﻥﻭﻨﺎﻘﻟﺍ ﻕ
:
ﻤﻥ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﻨﺴﺘﻨﺘﺞ ﻤﺎ ﻴﺄﺘﻲ
:
1
-
ﺍﺫﺍ ﻜﺎﻨﺕ
(n=γ)
ﻓﺘﻜﻭﻥ ﻭﻴﻜﻭﻥ
(q=0)
ﻓﺎﻻﺠﺭﺍﺀ ﺍﺩﻴﺎﺒﺎﺘﻲ
.
2
-
ﺍﺫﺍ
ﻜﺎﻨﺕ
(n=1)
ﻓﺘﻜﻭﻥ
ﻭﻴﻜﻭﻥ
(q=w)
ﻓﺎﻻﺠﺭﺍﺀ ﺍﻴﺯﻭﺜﺭﻤﻠ
ﻲ
.
ﺍﺫﻥ ﺍﻟﻌﻤﻠﻴﺔ ﺍﻟﺤﻘﻴﻘﻴﺔ ﻫﻲ ﺍﻟﻌﻤﻠﻴﺔ ﺍﻟﻭﺍﻗﻌﺔ ﺒﻴﻥ ﺍﻻﺠﺭﺍﺌﻴﻥ ﺍﻻﻴﺯﻭﺜﺭﻤﻠﻲ ﻭﺍﻻﺩﻴﺒﺎﺘﻲ
.
(5.44)
.
..........
(kJ/kg)
1
n
)
T
T
(
R
1
n
V
P
V
P
1
n
V
V
P
V
V
P
1
n
V
V
C
1
n
V
C
dV
CV
PdV
W
(5.43)
........
V
P
V
P
C
CV
P
C
PV
2
1
2
2
1
1
1
n
1
n
1
1
1
n
2
n
2
2
1
n
1
1
n
2
V
V
1
n
n
-
n
2
2
n
1
1
-n
n
2
1
−
−
=
−
−
=
+
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
=
=
=
=
=
⇒
=
⇒
=
+
−
+
−
+
−
+
−
+
−
∫
∫
Q
(5.45)
.........
(kJ/kg)
w
.
1
-
n
-
q
(5.45)
.........
1
n
)
T
T
(
R
.
1
-
n
-
)
T
T
(
R
1)
-
1)(
-
(n
1)
-
(n
-
1)
-
(
)
T
T
(
R
1
-
1
1
-
n
1
)
T
T
(
1
-
R
)
T
T
(
1
-
n
R
)
T
T
(
1
-
n
R
)
T
T
(
1
-
R
1
-
R
Cv
1
n
)
T
T
(
R
)
T
(T
Cv
w
q
2
1
2
1
2
1
2
1
1
2
2
1
1
2
2
1
1
2
γ
γ
=
−
−
γ
γ
=
−
⎥
⎦
⎤
⎢
⎣
⎡
γ
γ
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
γ
−
=
−
γ
−
−
=
−
+
−
γ
=
γ
=
−
−
+
−
=
+
µ
∆
=
Q
(
)
0
1
=
−
γ
γ
−
γ
(
)
0
1
1
=
−
γ
−
γ

)
109
(
ﻭ
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ
(Cn)
:
ﺇﺴﺘﻨﺎﺩﺍﹰ ﺍﻟﻰ ﺍﻟﻤﻌﺎﺩﻟﺔ
)
5.45
(
ﻓﻴﻜﻭﻥ
:
ﻴﺘﺒﻴﻥ ﺍﻥ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺘﺴﺎﻭﻱ
:
ﺇﻥ ﺨﻼﺼﺔ ﻤﺎ ﺫﻜﺭ ﻓﻲ ﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻟﻠﻤﻌﺎﺩﻻﺕ ﺍﻟﺨﺎﺼﺔ ﺒﺄﺠﺭﺍﺀﺍﺕ ﺍ
،ﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ
ﻤﻭﻀﺤﺔ ﻓﻲ ﺠﺩﻭل ﺭﻗﻡ
)
5.2
.(
(5.47)
.
..........
)
T
(T
Cn
q
)
T
(T
)
1
n
(
)
n
(
Cv
1
n
T
T
)
1
(
Cv
.
)
1
(
)
n
(
)
1
(
Cv
R
)
1
n
(
)
T
(T
R
.
)
1
(
)
n
(
q
2
1
2
1
2
1
2
1
−
=
−
−
−
γ
=
−
−
−
γ
−
γ
−
γ
=
−
γ
=
−
−
−
γ
−
γ
=
Q
(5.48)
..........
)
1
n
(
)
n
(
Cv
Cn
−
−
γ
=
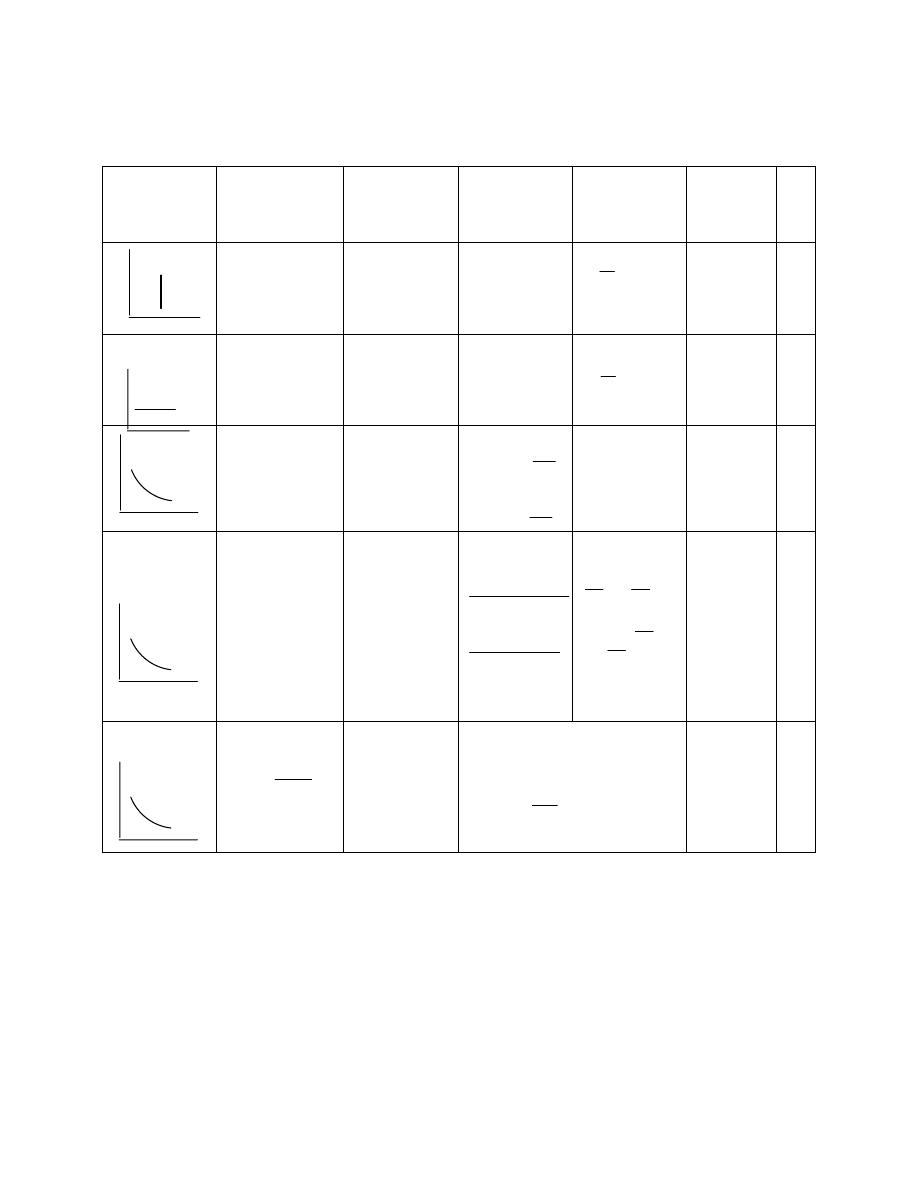
)
110
(
ﺠﺩﻭل
)
5.2
" (
ﻤﻌﺎﺩﻻﺕ ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ
"
ﺕ
ﺍﻻﺠﺭﺍﺀ
ﻤﻌﺎﺩﻟﺔ ﺍﻟﺤﺭﺍﺭﺓ
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ
w
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ
ﺍﻟﺩﺍﺨﻠﻴﺔ
(
∆µ)
ﻋﻨﺩ ﺘﻁﺒﻴﻕ ﺍﻟﻘﺎﻨﻭﻥ
ﺍﻻﻭل
w
=0
ﺍﻻﺸﻜﺎل
1
.
ﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
0
Cv(T
2
-T
1
)
2
.
ﺜ
ﺒﻭﺕ ﺍﻟﻀﻐﻁ
P
∆V=R∆T
Cv(T
2
-T
1
)
q=
∆µ+w
=(
µ
2
+P
2
ν
2
) -
(
µ
1
+P
1
ν
1
)
q=
∆h
12
=Cp
∆T
R=Cp-Cv
3
.
ﺍﻻﻴﺯﻭﺜﺭﻤﻠﻲ
P
ν=C
.
0
4
.
ﺍﻻﺩﻴﺎﺒﺎﺘﻲ
Cv (T
2
-T
1
)
γ=Cp/Cv ,
Cv=R/
γ-1
Cp= R
γ/γ-1
5
.
ﺍﻟﺒﻭﻟﺘﺭﻭﺒﻲ
ﺘﺴﺘﺒﺩل
)
γ
(
ـﺒ
(n)
.
C
T
P =
ν
Cv (T
2
-T
1
)
Cn=Cv(
γ-n)
/(n-1)
.
C
T
P =
µ
∆
=
/
−
=0
w
q
1
2
1
1
2
1
1
Ln
RT
Ln
P
ν
ν
ν
ν
ν
0
w
q
=
µ
∆
+
=
γ
−
γ
−
γ
γ
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
ν
ν
=
=
ν
1
1
2
1
2
1
1
2
P
P
T
T
.
C
P
1
)
T
T
(
R
1
P
P
2
1
2
2
1
1
−
γ
−
−
γ
ν
−
ν
µ
∆
=
−
=
w
q
0
.
C
T
=
ν
w
.
1
-
n
-
w
q
γ
γ
=
+
µ
∆
=
P
V
P
V
P
V
P
V
P
V
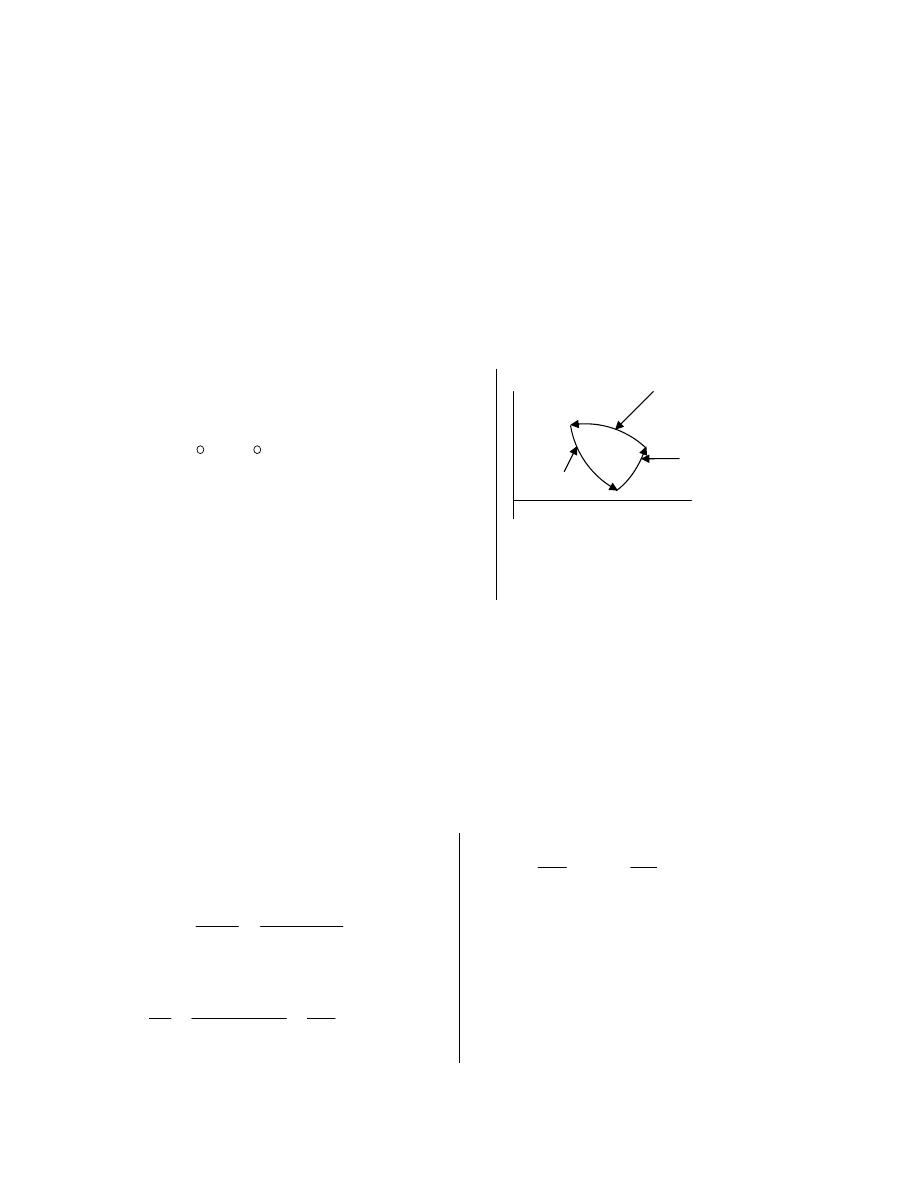
)
111
(
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟﺔ
)
5.13
(
ـﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻴﻤﺭ ﺒ
)
3
(
ﺍﺠﺭﺍﺀﺍﺕ
) :
1
(
ﺍﻨﺘﻘﺎل ﺤﺭﺍﺭﺓ
(8 kJ)
ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ ﻤﻊ ﺇﻨﺘﺎﺝ ﺸﻐل
(2 kJ)
) .
2
(
ﺍﺠﺭﺍﺀ ﺍﺩﻴﺎﺒﺎﺘﻲ
) .
3
(
ﺩﺍﺭﻩـﻘﻤ ﻡﺎﻅﻨﻟﺍ ﻰﻠﻋ لﻐﺸ لﺫﺒ
(3kJ)
ــﻀﺕ ﺍﻟـﻔﺨﻨﺇ ﺙـﻴﺤﺒ
(
∆U)
ﺩﺍﺭـﻘﻤﺒ
(2 kJ)
.
ﺍﺤﺴﺏ
:
1
-
∆U
ﻟﻸﺠﺭﺍﺌﻴﻥ ﺍﻻﻭﻟﻴﻴﻥ
.
2
-
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻓﻲ ﺍﻻﺠﺭﺍﺀ ﺍﻻﺨﻴﺭ
.
3
-
ﺍﻟﺸﻐل ﻓﻲ ﺍﻻﺠﺭﺍﺀ ﺍﻟﺜﺎﻨﻲ
.
∆U
12
= Q
12
– W
12
= 8-2 = 6 kJ
Q
31
= W
31
+
∆U
31
= -3 + (-2) = - 5 kJ
Q
12
+ Q
23
+ Q
31
= W
12
+ W
23
+ W
31
8 + 0 + (-5) = 2 + W
23
+ (-3)
∴ W
23
= -4 kJ
∆U
23
= Q
23
– W
23
= 0-4 = -4 kJ
ﺘﻨﺨﻔﺽ
)
5.14
(
ﺍﺴﻁﻭﺍﻨﺔ ﺴﻌﺘﻬﺎ
(0.85 m
3
)
ﺘﺤﺘﻭﻱ ﻋﻠﻰ ﻏﺎﺯ ﻀﻐﻁﻪ
(275 kN/m
2
)
ﻪـﺘﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ
(15
°C)
.
ﺇﺫﺍ
ﺍﻀﻴﻑ
(1.6kg)
ﻤﻥ ﺍﻟﻐﺎﺯ ﻨﻔﺴﻪ ﺍﻟﻰ ﺍﻻﺴﻁﻭﺍﻨﺔ
.
ﺭﺍﺭﺓـﺤﻟﺍ ﺔـﺠﺭﺩ ﺢﺒﺼﺘ ﺎﻤﺩﻨﻋ ﻁﻐﻀﻟﺍ ﺢﺒﺼﻴﺴ ﺍﺫﺎﻤ
(15
°C)
ﺇﺤﺴﺏ ﻜﺫﻟﻙ ﺍﻟﻤ؟ ﻯﺭﺨﺍ ﺓﺭﻤ
ﺔـﻴﺌﺎﻬﻨﻟﺍﻭ ﺔـﻴﺌﺍﺩﺘﺒﻻﺍ ﺔﻟﺎﺤﻟﺍ ﻲﻓ ﺯﺎﻐﻠﻟ ﻲﻋﻭﻨﻟﺍ ﻱﺭﺍﺭﺤﻟﺍ ﻯﻭﺘﺤ
.
ﻓﻭﻕ ﺍﻟﺼﻔﺭ ﺍﻟﻤﺌﻭﻱ
(0
°C)
،ﻔﺭﺍﹰـﺼ ﺔـﻗﺎﻁﻟﺍ ﺎﻫﺩـﻨﻋ ﻥﻭﻜﺘ ﻲﺘﻟﺍ ﺔﻴﺴﺎﺴﻻﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻲﻫ ﻲﺘﻟﺍﻭ
ﺍﺴﺘﻌﻤل
:
Cv = 0.715 kJ/kg. K
، Cp = 1.005 kJ/kg.K
R = Cp – Cv = 1.005 – 0.715
= 0.29 kJ/kg.K
m
2
= 2.8 + 1.7 = 4.5 kg
1
2
1
1
1
2
2
2
1
2
m
m
V
/
RT
m
V
/
RT
m
P
P
=
=
∆h = Cp (T
2
– T
1
)
=1.005(288 - 273)
= 15.075 kJ/kg
∫
∫
∫
∫
∫
∫
∫
∫
+
+
=
+
+
=
2
1
3
2
1
3
2
1
3
2
1
3
dW
dW
dW
dQ
dQ
dQ
dW
dQ
2
1
2
1
2
m
/
kN
442
8
.
2
5
.
4
275
m
m
P
P
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
1
2
3
Q
o
=?
W
in
=3kJ
∆u=-2kJ
Wo=?
∆u=?
Q
in
=8kJ
W
in
=2kJ
∆u= ?
kg
8
.
2
288
29
.
0
85
.
0
275
RT
V
P
m
1
1
1
1
=
×
×
=
=

)
112
(
)
5.15
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(5 kg)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﻭﻀﻐﻁﻪ
(3 bar)
.
ﺩﺍﺭﻫﺎـﻘﻤ ﺕـﺒﺎﺜ ﻡﺠﺤﺒ ﺓﺭﺍﺭﺤﺒ ﺩﻭﺯ
(500 kJ)
) .
ﺃ
(
ﻜﻴﻑ ﺴﺘﻜﻭﻥ ﺤﺎﻟﺘﻪ ﺍﻟﻨﻬﺎﺌﻴﺔ ﺒﻌﺩ ﺍﻟﺘﺴﺨﻴﻥ
) .
ﺏ
(
ﻭﻟﻭ ﺍﺭ
ﺩﻨﺎ ﺒﻌﺩ ﺫﻟﻙ ﺍﻥ ﻨﺒﺭﺩ ﺍﻟﻐﺎﺯ ﺒﻀﻐﻁ
ﺜﺎﺒﺕ ﻟﻜﻲ ﻴﺭﺠﻊ ﺍﻟﻰ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ ﻓﻜﻡ ﻫﻲ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺘﻲ ﻴﺠﺏ ﺍﻥ ﻨﺄﺨﺫﻫﺎ ﻤﻥ ﺍﻟﻬﻭﺍﺀ
.
ﻋﻠﻤﺎﹰ
ﺒﺄﻥ
:
Cv = 0.715 kJ/kg.K
،
R = 0.29 kJ/kg.K
ﺇﻥ ﻋﺒﺎﺭﺓ
)
ﻜﻴﻑ ﺴﺘﻜﻭﻥ ﺤﺎﻟﺘﻪ ﺍﻟﻨﻬﺎﺌﻴﺔ
(
ﻲـﻨﻌﺘ
ﺍﻴﺠﺎﺩ ﻗﻴﻡ
T
2
،
V
2
،
P
2
.
T
2
=
∆T + T
1
= 139.86 + 20
= 159.86
°C
Cp = R + Cv = 0.29 + 0.715
= 1.005 kJ/kg.K
Q
23
= m Cp (T
3
-T
2
)
= 5×1.005 (20-159.86)
= - 702.796 kJ
)
5.16
(
ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(2kg)
ﻭﺤﺠﻤﻪ
(0.7m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
ﺒﺤﺕـﺼﺍ ﺙـﻴﺤﺒ ﻡﺠﺤﻟﺍ ﺕﻭﺒﺜﺒ ﻥﺨﺴ
ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(135
°C)
.
ﺍﺤﺴﺏ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﺍﻟﻰ ﺍﻟﻐﺎﺯ ﻭﺍﻟﻀﻐﻁ ﺍﻟﻨﻬﺎﺌﻲ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R = 0.29 kJ/kg.K
،
Cv = 0.72 kJ/kg.K
Q = m Cv (T
2
– T
1
) = 2 × 0.72 (135 – 15) = 172.8 kJ
K
86
.
139
0.715
5
500
mCv
Q
T
=
×
=
=
∆
2
1
2
1
2
kN/m
2
.
443
293
432.86
300
T
T
P
P
=
×
=
=
2
1
2
1
2
2
1
1
1
kN/m
1
.
338
288
408
6
.
238
T
T
P
P
kN/m
6
.
238
0.7
288
0.29
2
V
mRT
P
=
=
=
=
×
×
=
=
3
1
1
1
m
42
.
1
300
293
0.29
5
P
mRT
V
=
×
×
=
=

)
113
(
)
5.17
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(2bar)
ﻭﺤﺠﻤﻪ
(0.9m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(30
°C)
ﺯﻭﺩ ﺒﺤﺭﺍﺭﺓ ﺒﻀﻐﻁ ﺜﺎﺒﺕ ﻭﺍﺼﺒﺤﺕ
ﺩﺭﺠﺔ ﺤﺭﺍ
ﺭﺘﻪ
(180
°C)
.
ﺍﺤﺴﺏ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘﻠﻴﻥ ﻋﻠﻤﺎﹰ ﺍﻥ
:
Cp = 1.005 kJ / kg.K
،
R = 0.29 kJ/kg.K
Q
12
= m Cp
∆T
= 2.11 × 1.005 (180-20)
= 339.29 kJ
W
12
= P (V
2
– V
1
)
= 2 (1.39 – 0.9)
= 98.2 kJ
)
5.18
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(275 kN/m
2
)
ﻭﺤﺠﻤﻪ
(0.09 m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(18.5
°C)
.
ﻀﻐﻁـﺒ ﻪﺘﻟﺎﺤ ﺕﺭﻴﻐﺘ
ﺜﺎﺒﺕ ﻭﺍﺼﺒﺤﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
.
ﺎﺀـﻨﺜﺍ ﻲـﻓ ﺯﺠﻨﻤﻟﺍ لﻐﺸﻟﺍﻭ ﺯﺎﻐﻟﺍ ﻥﻤ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺏﺴﺤﺇ
ﺍﻻﺠﺭﺍﺀ
.
ﻋﻠﻤﺎﹰ ﺍﻥ
:
Cv = 1.005 kJ/kg.K
،
R = 0.29 kJ/kg.K
Q = m Cp (T
2
– T
1
)
= 0.186 × 1.005 (288 – 458)
= -31.78 kJ
W = P(V
2
– V
1
) = 275 (0.0566 – 0.09)
= - 9.19 kJ
)
5.19
(
ﻤﺎﺌﻊ ﻜﺘﻠﺘﻪ
(2.25 kg)
ﻭﺤﺠﻤﻪ
(0.1m
3
)
ﻭﻀﻐﻁﻪ
(7bar)
ﻤﻭﻀﻭﻉ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﻓﻴﻬﺎ ﻤﻜﺒﺱ ﻤﺘﺤﺭﻙ،
ﺒﺤﻴﺙ ﻴﺒﻘﻰ ﺍﻟﻀﻐﻁ ﺜﺎﺒﺘﺎﹰ
.
ﺒﻌﺩ ﺘﺴﺨﻴﻨﻪ ﻴﺘﻤﺩﺩ ﺍﻟﻰ ﺤﺠﻡ
(0.2 m
3
)
.
ﻓﻠﻭ ﻋﻠﻤﺕ ﺍﻥ ﺍﻻﻨﺜﺎﻟﺒﻲ ﺍﻟﻨﻭﻋﻲ ﻟﻠﻤ
ﺎﺌﻊ
ﻋﻨﺩ ﺍﻟﺒﺩﺍﻴﺔ
(210kJ/kg)
ﻭﺍﻟﻨﻬﺎﻴﺔ
(280kJ/kg)
.
ﺍﺤﺴﺏ
:
)ﺃ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
) .
ﺏ
(
ﻤﻘﺩﺍﺭ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻠﻤﺎﺌﻊ
.
Q =
∆H = m (h
2
– h
1
)
= 2.25 (280 – 210)
= 157.5 kJ
∆U = Q - P∆V
= 157.5 – [700 (0.2 – 0.1)]
= 87.5 kJ
kg
186
.
0
458
0.29
0.09
275
RT
V
P
m
1
1
1
=
×
×
=
=
kg
11
.
2
293
0.29
0.9
200
RT
V
P
m
1
1
1
=
×
×
=
=
3
1
2
1
2
m
39
.
1
293
453
9
.
0
T
T
V
V
=
×
=
=
3
1
2
1
2
m
0566
.
0
458
288
09
.
0
T
T
V
V
=
=
=
)
114
(
)
5.20
(
ﻏﺎﺯ ﻴﺘﻤﺩﺩ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﻭﻴﻨﺠﺯ ﺸﻐﻼﹰ ﻤﻘﺩﺍﺭﻩ
(5 kJ)
.
ﻓﺈﺫﺍ ﻜﺎﻨﺕ
(
γ =1.66)
.
ﺍﺤﺴﺏ
:
)
1
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
)
2
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
∆U = Q – W = 12.575 – 5 = 7.575 kJ
)
5.21
(
ﻏﺎﺯ ﻤﻭﺠﻭﺩ ﻓﻲ ﺨﺯﺍﻥ ﻀﻐﻁﻪ
(0.4 MN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(14
°C)
ﻭﺤﺠﻤﻪ
)
L
3000
.(
ﺍﻀﻴﻔ
ﺕ
ﺍﻟﻴﻪ ﻜﻤﻴﺔ ﺍﺨﺭﻯ ﻤﻥ ﻨﻔﺱ ﺍﻟﻐﺎﺯ ﺒﺤﻴﺙ ﺘﻀﺎﻋﻑ ﻀﻐﻁﻪ
.
ﺍﺤﺴﺏ
:
)
ﺃ
(
ﺍﻟﻜﺜﺎﻓﺔ
)
ﺏ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
)
ﺝ
(
ﻋﻠﻤﺎﹰ ﺒﺄﻥ،ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ ﻲﻓ ﺭﻴﻐﺘﻟﺍ
:
Cp = 1.005 kJ/kg.K
،
R = 0.26 kJ/kg.K
∆m = m
2
– m
1
= 30.66 – 16.08
= 14.59 kg
Cv = Cp – R
= 1.005 – 0.26 = 0.745 kJ/kg.K
Q
12
= m Cv
∆T
= 14.59 × 0.745 (28-14)
= 152.17 kJ
Q
12
=
∆U
12
= 152.17 kJ
kJ
575
.
12
1
-
1.66
1.66
5
Q
1
W
1
V
P
T
1
-
R
m
T
Cp
m
Q
=
×
=
∴
−
γ
γ
=
−
γ
γ
∆
=
∆
γ
γ
=
∆
=
kg
66
.
30
287
0.26
3
400
2
RT
V
P
m
kg
08
.
16
287
0.26
3
400
RT
V
P
m
2
2
2
2
1
1
1
1
=
×
×
×
=
=
=
×
×
=
=
3
kg/m
86
.
4
3
59
.
14
V
m
=
=
=
ρ

)
115
(
)
5.22
(
ﺎﺒﺘﺘﻴﻥـﺜ ﺓﺭﺍﺭـﺤ ﺔـﺠﺭﺩﻭ ﻁﻐﻀ ﺕﺤﺘ ﺯﺎﻐﻟﺍ ﻪﻴﻓ ﻅﻔﺤﻴ ﺯﺎﻐﻠﻟ ﻉﺩﻭﺘﺴﻤﺒ ،ﻡﺎﻤﺼﺒ ﻁﻭﺒﺭﻤ ،ﻁﻐﻀﻠﻟ ﺀﺎﻋﻭ
ﻗﻴﻤﺘﻬﻤﺎ
(1.4 MN/m
2
)
ﻭ
(85
°C)
ﻋﻠﻰ ﺍﻟﺘﻭﺍﻟﻲ
.
ﻭﻋﺎﺀ ﺍﻟﻀﻐﻁ
ﻜﺎﻥ ﻤﻔﺭﻏﺎﹰ ﻓﻲ ﺍﻟﺒﺩﺍﻴﺔ
.
ﺼﻤﺎﻡـﻟﺍ ﺢﺘﻓ
ﻷﺘﺎﺤﺔ ﺍﻟﻤﺠﺎل ﻟﻜﺘﻠﺔ ﻤﻥ ﺍﻟﻐﺎﺯ ﻤﻘﺩﺍﺭﻫﺎ
(2.7kg)
ﺼﻤﺎﻡـﻟﺍ ﻕـﻠﻏﺍ ﻡـﺜ ﻥﻤﻭ ﻁﻐﻀﻟﺍ ﺼﻤﺎﻡ ﻰﻟﺍ ﺭﻭﺭﻤﻠﻟ
ﻀﻐﻁـﻟﺍ ﺀﺎـﻋﻭ ﻲﻓ ﺯﺎﻐﻟﺍ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ ﻀﻐﻁﻟﺍ ﻥﻤ لﻜ ﺢﺒﺼﺍﻭ
(700kN/m
2
)
ﻭ
(60
°C)
ﻰـﻠﻋ
ﺍﻟﺘﻭﺍﻟﻲ
.
ﺍﺤﺴﺏ ﻤﻘﺩﺍﺭ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﺍﻟﻰ ﺍﻟﻐﺎﺯ ﻓﻲ ﺍﻟﻭﻋﺎﺀ ﺍﻭ ﻤﻨ
ﻪ
.
ﻀﻐﻁـﻟﺍ ﺀﺎﻋﻭ ﻡﺠﺤ ﻙﻟﺫﻜ ﺏﺴﺤﺍ
ﻭﺤﺠﻡ ﺍﻟﻐﺎﺯ ﻗﺒل ﺍﻻﻨﺘﻘﺎل
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cv = 0.67 kJ/kg.K
،
Cp = 0.88 kJ/kg.K
q =
∆µ – w
= Cv (T
2
– T
1
) – RT
1
= Cv (T
2
– T
1
) – (Cp – Cv) T
1
= 0.67×(333-358)–(0.88 – 0.67) 358
= – 91.93 kJ/kg
Q = q × m
= 91.93 × 2.7
= 248.2 kJ
P
1
ν
1
= RT
1
V
1
=
ν
1
×m = 0.0537×2.7 = 0.145m
3
)
5.23
(
ﻤﺎﺌﻊ ﻀﻐﻁﻪ
(7 bar)
ﻭﺤﺠﻤﻪ
(0.1 m
3
)
ﻭﻜﺘﻠﺘﻪ
(2.25 kg)
ﺒﺱـﻜﻤﺒ ﺔـﻘﻠﻐﻤ ﺔﻨﺍﻭﻁﺴﺍ ﻲﻓ ﻉﻭﻀﻭﻤ
ﻴﺘﺤﺭﻙ ﺒﺤﻴﺙ ﻴﺒﻘﻰ ﺍﻟﻀﻐﻁ ﺜﺎﺒﺘﺎﹰ
.
ﻴﺠﻬﺯ ﺒﻁﺎﻗﺔ ﺤﺭﺍﺭﻴﺔ ﻓﻴﺘﻤﺩﺩ ﺤﺘﻰ
(0.2 m
3
)
.
ﺎﻟﺒﻲـﺜﻨﻻﺍ ﺕـﻨﺎﻜ ﺍﺫﺈﻓ
ﺍﻟﻨﻭﻋﻲ ﺍﻻ
ﺒﺘﺩﺍﺌﻲ
(210 kJ/kg)
ﻭﺍﻟﻨﻬﺎﺌﻲ
(280 kJ/kg)
ﺍﻭﺠﺩ
) :
ﺃ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
)
ﺏ
(
ﻲـﻓ ﺭﻴﻐﺘﻟﺍ
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
Q =
∆H = m (h
2
– h
1
)
= 2.25 (280 – 210)
= 157.5 kJ
W = P (V
2
– V
1
)
= 700 (0.2 – 0.1)
= 70 kJ
∆U = Q – W
= 157.5 – 70
= 87.5 kJ
kg
m
0537
.
0
1400
0.67)358
-
(0.88
P
T
)
Cv
Cp
(
3
1
1
1
=
=
−
=
υ
3
1
2
2
1
2
m
27
.
0
358
700
0.145
333
1400
V
T
P
T
P
V
=
×
×
×
=
×
=

)
116
(
)
5.24
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(1 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
ﻭﻜﺜﺎﻓﺘﻪ
(1.855 kg/m
3
)
.
ﺔـﻤﻴﻗ ﺏﺴﺤﺍ
(R)
.
ﺩـﻨﻋ
ﺘﺴﺨﻴﻥ
(0.9 kg)
ﻤﻥ ﻫﺫﺍ ﺍﻟﻐﺎﺯ ﻤﻥ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(15
°C)
ﻰـﻟﺍ
(250
°C)
ﺕـﻨﺎﻜ ،ﺕـﺒﺎﺜ ﻁﻐﻀـﺒ
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻁﻠﻭﺒﺔ
(175 kJ)
.
ﺍﺤﺴﺏ
(Cp)
ﻭ
(Cv)
.
ﺔـﻴﻠﺨﺍﺩﻟﺍ ﺔـﻗﺎﻁﻟﺍ ﻲـﻓ ﺭـﻴﻐﺘﻟﺍ ﺭﺍﺩﻘﻤ ﺏﺴﺤﺍﻭ
ﻭﺍ
ﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل
.
= 0.828 kJ/kg . K
Cv = Cp–R
= 0.828 – 0.185
= 0.643 kJ/kg.K
∆U = m Cv (T
2
– T
1
)
= 0.9 × 0.643 (250 – 15)
= 136 kJ
W = Q -
∆U
= 175 – 136
= 39 kJ
)
5.25
(
ﺍﺴﻁﻭﺍﻨﺔ ﻋﺩﻴ
ﻤﺔ ﺍﻟﺘﻭﺼﻴل ﺍﻟﺤﺭﺍﺭﻱ ﻗﻁﺭﻫﺎ
(100mm)
ﻪـﺘﺭﺍﺭﺤ ﺔﺠﺭﺩ ﺀﺍﻭﻫ ﻰﻠﻋ ﻱﻭﺘﺤﺘ
(15.5
°C)
ﻤﻐﻠﻘﺔ ﺒﻤﻜﺒﺱ ﻋﺩﻴﻡ ﺍﻟﺘﻭﺼﻴل ﺍﻟﺤﺭﺍﺭﻱ ﻭﻋﺩﻴﻡ ﺍﻻﺤﺘﻜﺎﻙ ﻭﺯﻨﻪ
(15N)
.
ﺎﻉـﻔﺘﺭﺇ ﻰـﻠﻋ ﺱﺒـﻜﻤﻟﺍ ﻥﺎﻜﻭ
(150mm)
ﻤﻥ ﻗﺎﻋﺩﺓ ﺍﻻﺴﻁﻭﺍﻨﺔ
.
ﻋﻨﺩ ﺘﺴﺨﻴﻥ ﺍﻟﻬﻭﺍﺀ ﺍﺭﺘﻔﻊ ﺍﻟﻤﻜﺒﺱ
(150mm)
ﺎﻥـﻜ ﺍﺫﺈـﻓ ﺔﻴﻓﺎﻀﺍ
ﺍﻟﻀﻐﻁ ﺍﻟﺠﻭﻱ
(1.013 bar)
ﻭﻜﺎﻥ،
R = 0.287 kJ/kg.K
،
Cp = 1 kJ/kg.K
ﺍﻭﺠﺩ
) :
1
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
)
2
(
ﺍﻟﺘﻐﻴﺭ ﺒﺎﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
15
250
(
9
.
0
175
)
T
m(T
Q
Cp
kJ/kg.K
185
.
0
278
1.875
1
100
mT
PV
R
1
2
−
=
−
=
=
×
×
=
=

)
117
(
ﻓﺎﻟﻌﻤﻠﻴﺔ ﺘﻤﺕ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ،ﺕﺒﺎﺜ ﺱﺒﻜﻤﻟﺍ ﻥﺯﻭ
V
1
=A×L
1
=0.007854 × 0.15=0.00118m
3
V
2
= A×L
2
= 0.007854 × 0.3 = 0.00236 m
3
A
F
P
g
=
Q
Pabs = Patm + Pg
Q = m Cp (T2 – T1)
= 0.00147 × 1 × (577 – 288.15)
= 0.425 kJ
W = P (V2 – V1)
= 1.032×10
2
(0.00236–0.06118)
= 0.122kJ
∆U = Q – W
= 0.424 – 0.122
= 0.3021 kJ
)
5.26
(
ﺍﺴﻁﻭﺍﻨﺔ ﺍﻭﻜﺴﺠﻴﻥ ﺴﻌﺘﻬﺎ
(300Litre)
ﻭﺘﺤﺘﻭﻱ ﻋﻠﻰ ﺍﻻﻭﻜﺴﺠﻴﻥ ﺘﺤﺕ ﻀﻐﻁ
(3.1MN/m
2
)
ﻭﺩﺭﺠﺔ
ﺤﺭﺍﺭﺓ
(18
°C)
.
ﻓﺘﺢ ﺍﻟﺼﻤﺎﻡ ﻭﺍﺴﺘﻌﻤل ﻗﺴﻡ ﻤﻥ ﺍﻟﻐﺎﺯ
.
ﺇﺫﺍ ﻜﺎﻥ ﻀﻐﻁ ﺍﻻﻭﻜﺴﺠﻴﻥ ﺍﻟﺒﺎﻗﻲ ﻓﻲ ﺍﻻﺴﻁﻭﺍﻨﺔ
(1.7MN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
.
ﻲـﻓ ﻲﻗﺎـﺒﻟﺍ ﻥﻴﺠﺴـﻜﻭﻻﺍ ﻊﺠﺭ ﻡﺎﻤﺼﻟﺍ ﻕﻼﻏﺇ ﺓﺩﺎﻋﺇ ﺩﻌﺒ
ﺍﻻﺴﻁﻭﺍﻨﺔ
ﺍﻟﻰ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
.
ﺩـﻨﻋ ﻥﻴﺠﺴﻜﻭﻻﺍ ﺔﻓﺎﺜﻜ ﻥﺍ ﺕﻤﻠﻋ ﺍﺫﺇ ،ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺏﺴﺤﺍ
ﺩﺭﺠﺔ
(0
°C)
ﻭﻀﻐﻁ
(0.101325MN/m
2
)
ﻫﻲ
(1.429kg/m
3
)
ﻭﺍﻥ
γ=1.4
.
12.3 – 6.8 = 5.5 kg
Q =
∆U = m Cv (T
2
– T
1
)
= 5.5 . 0.65 (291 – 288)
= 10.725 kJ
2
2
2
m
007854
.
0
4
(0.1)
4
D
.
A
=
×
π
=
π
=
bar
03
.
1
007854
.
0
15
10
013
.
1
5
=
+
×
=
kg
00147
.
0
288.5
0.287
0.00118
10
032
.
1
RT
PV
m
2
=
×
×
×
=
=
K
577
0.00118
0.0236
15
.
288
V
V
.
T
T
1
2
1
2
=
×
=
=
kg
8
.
6
288
26
.
0
10
300
10
7
.
1
RT
V
P
m
kg
3
.
12
291
26
.
0
10
300
10
1
.
3
RT
V
P
m
kJ/kg.K
26
.
0
273
429
.
1
1
10
101325
.
0
mT
PV
R
3
-
3
2
2
2
2
3
3
1
1
1
1
3
=
×
×
×
×
=
=
=
×
×
×
×
=
=
=
×
×
×
=
=
−
kJ/kg.K
65
.
0
4
.
0
26
.
0
1
R
Cv
=
=
−
γ
=

)
118
(
)
5.27
(
(0.05 kg)
ﻐﻁﻪـﻀ ﻊﺌﺎﻤ ﻥﻤ
(2 bar)
ﻪـﻤﺠﺤﻭ
(0.8856 m
3
/kg)
ﻰـﻟﺍ ﺕـﺒﺎﺜ ﻁﻐﻀـﺒ ﺩﺩـﻤﺘ
(0.0658 m
3
)
.
ﺇﺤﺴﺏ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘﻠﻴﻥ ﺇﺫﺍ ﻜﺎﻥ
:
)ﺃ
(
ﺍﻟﻤﺎﺌﻊ ﺒﺨﺎﺭ ﻭﺤﺎﻟﺘﻪ ﺍﻟﻨﻬﺎﺌﻴﺔ ﺠﺎﻑ ﻤﺸﺒﻊ ﺤﺭﺍﺭﺓ ﺍﻟﺒﺨﺎﺭ
(300
°C)
.
)
ﺏ
(
ﺍﻟﻤﺎﺌﻊ ﻫﻭﺍﺀ ﺘﺼل ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(130
°C)
ﻋﻠﻤﺎﹰ ﺃﻥ
:
ﺍﻻﻨﺜﺎﻟﺒﻲ ﺘﺤﺕ ﻀﻐﻁ
(2 bar)
ﻫﻭ
(2707 kJ/kg.K)
.
ﺍﻻﻨﺜﺎﻟﺒﻲ ﺒﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(300
°C)
ﻫﻭ
(307 kJ/kg.K)
.
(a)
Q
in
= m (h
2
– h
1
)
= 0.05 (3072 – 2707)
= 18.25 kJ
w = P
∆ν = P (ν
2
-
ν
1
)
= 200 (1.316 – 0.8856)
= 86.08 kJ/kg
W = m× w = 0.05 × 86.08
= 4.304 kg
(b)
Q = m Cp
∆T
= 0.05 × 1.005 (917 – 403)
= 25.83 kJ
w = R (T
2
– T
1
)
= 0.287 (917 – 403)
= 147.52 kJ/kg
W = m ×w
= 0.05 × 147.52 = 7.38 kJ
kg
/
m
316
.
1
05
.
0
0658
.
0
m
V
3
2
2
=
=
=
ν
K
917
0.287
0.05
0.0658
200
mR
V
P
T
2
2
2
=
×
×
=
=

)
119
(
)
5.28
(
ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻤﻭﺠﻭﺩ ﺩﺍﺨل ﺍﺴﻁﻭﺍﻨﺔ ﻤﺯﻭﺩﺓ ﺒﻤﻜﺒﺱ ﻋﺩﻴﻡ ﺍﻻﺤﺘﻜﺎﻙ ﺤﺠﻤﻪ
(23.7 L)
ﻪـﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩﻭ
(16
°C)
ﻭﻀﻐﻁﻪ
(1.013 bar)
.
ﻴﻁﻠﺏ ﺭﻓﻊ ﻀﻐﻁﻪ ﺍﻟﻰ
(5 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(16
°C)
ﺒﺄﺠﺭﺍﺌﻴﻥ
ﺍﻨﻌﻜﺎﺴﻴﻴﻴﻥ ﻤﺨﺘﻠﻔﻴﻥ ﻫﻤﺎ
:
ﺃ
-
ﺘﺒﺭﻴﺩ ﺒﻀﻐﻁ ﺜﺎﺒﺕ ﻴﺘﺒﻌﻪ ﺘﺴﺨﻴﻥ ﺘﺤﺕ ﺤﺠﻡ ﺜﺎﺒﺕ
.
ﺏ
-
ﺘﺴﺨﻴﻥ ﺘﺤﺕ ﺤﺠﻡ ﺜﺎﺒﺕ ﻴﺘﺒﻌﻪ ﺘﺒﺭﻴﺩ ﺘﺤﺕ ﻀﻐﻁ ﺜﺎﺒﺕ
.
ﺭﺍﺌﻴﻥـﺠﻻﺍ ﻥﻤ لﻜﻟ ﺏﺴﺤﺍ
)
1
(
ﺭﺍﺭﺓـﺤﻟﺍ
ﻭﺍﻟﺸﻐل ﺍ
ﻟﻤﻨﺘﻘﻠﻴﻥ
)
2
(
∆U
،
∆H
ﻋﻠﻤﺎﹰ ﺍﻥ،
:
Cv = 0.21 kJ/kg.K
،
Cp = 0.293 kJ/kg.K
(1)
q
o
=
∆h = Cp∆T
= 0.293 (57.8 – 289)
= – 6.774 kJ/kg
∆µ
12
=
∆h – P∆V
= – 4.855 kJ/kg
∆µ
23
= q
in
= Cv
∆T
= 0.21 (289-578)
= 4.855 kJ/kg
∑q = q
o
+q
in
= –6.774 + 4.855
= –1.92 kJ/kg
∑∆µ = ∆µ
12
+
∆µ
23
= – 4.855 + 4.855 = 0
w = q –
∆µ
= –1.919 – 0
= – 1.919 kJ/kg
(2)
q
in
=
∆µ
12
=Cv.
∆T
=0.21 (1445 – 289)
=24.3kJ
q
o
=
∆h=Cp ∆T
=0.293(289-1445)
=-33.87 kJ
∑q = 24.27 – 33.871
= – 9.611 kJ
∆µ
23
=
∆h - P∆V
∑µ = 24.27 – 24.27 = 0
w = q –
∆µ
= – 9.611 – 0
= -9.601 kJ
K
8
.
57
7
.
23
74
.
4
289
V
V
T
T
L
74
.
4
5
1
7
.
23
P
P
.
V
V
1
2
1
2
2
1
1
.
2
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
×
=
=
⎥⎦
⎤
⎢⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−
=
1000
7
.
23
74
.
4
3
.
101
774
.
6
K
1445
1
5
289
P
P
T
T
1
2
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
KJ
27
.
24
1000
1
.
23
74
.
4
500
871
.
33
=
⎥⎦
⎤
⎢⎣
⎡
−
−
−
=

)
120
(
)
5.29
(
ﺎﻙـﻜﺘﺤﻻﺍ ﻡﻴﺩﻋ ﻙﺭﺤﺘﻤ ﺱﺒﻜﻤﺒ ﺔﻘﻠﻐﻤ ﺔﻨﺍﻭﻁﺴﺍ ﻲﻓ ﺩﻭﺠﻭﻤ ﻊﺌﺎﻤ
.
ﺩﺍﺭﻫﺎـﻘﻤ ﺓﺭﺍﺭـﺤ ﻪـﻴﻟﺍ ﺕﻔﻴـﻀﺃ
(1023.67 kJ/kg)
.
ﺩﺍﺭﻩــﻘﻤ ﺕــﺒﺎﺜ ﻁﻐﻀــﺒ ﺩﺩــﻤﺘﻭ
(1.0133 bar)
ﻥــﻤ ﻪــﻤﺠﺤ ﺭــﻴﻐﺘﻭ
(0.00104 m
3
/kg)
ﺍﻟﻰ
(1.67 m
3
/kg)
.
ﺍﺤﺴﺏ
:
∆µ
،
∆h
.
)
5.30
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(1kg)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(290K)
ﺒﺱـﻜﻤ ﺎﻬﻠﺨﺍﺩﺒ ﻙﺭﺤﺘﻴ ﺔﻨﺍﻭﻁﺴﺍ لﺨﺍﺩ ﺩﻭﺠﻭﻤ
.
ﻐﻁـﻀ
ﺍﻟﻬﻭﺍﺀ ﺒﻌﻤﻠﻴﺔ ﺒﻁﻴﺌﺔ ﻋﺩﻴﻤﺔ ﺍﻻﺤﺘﻜﺎﻙ ﺒﺤﻴﺙ ﺘﻐﻴﺭ ﺤﺠﻤﻪ ﺍﻟﻨﻭﻋﻲ ﻤﻥ
(0.8m
3
/kg)
ﻰـﻟﺍ
(0.2m
3
/kg)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻟﻨﻬﺎﺌﻴﺔ
(500K)
ﻭﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.25
=0.75)
ﺤﻴﺙ ﺍﻥ،
(P)
ﺩﺍﺕـﺤﻭﺒ
(bar)
ﻭ
(v)
ﺒﻭﺤﺩﺍﺕ
(m
3
/kg)
.
ﻋﻠﻤﺎﹰ ﺃﻥ،ﻥﻴﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍﻭ لﻐﺸﻟﺍ ﺏﺴﺤﺍ
:
Cp=0.287 kJ/kg.K
[
]
J/kg
k
67
.
1023
h
q
J/kg
k
55
.
854
)
00104
.
0
67
.
1
(
33
.
101
67
.
1023
P
q
w
q
=
∆
=
=
−
−
=
ν
∆
−
=
−
=
µ
∆
kJ
40.2
168
-
208.2
W
U
Q
kJ
208.2
290)
-
(580
0.718
1
T
Cv
m
kJ
168
m
.
bar
68
.
1
12
.
1
5
.
1
)
12
.
1
237
.
2
(
5
.
1
894
.
0
1
447
.
0
1
5
.
1
8
.
0
1
2
.
0
1
75
.
0
2
8
.
0
2
.
0
2
75
.
0
5
.
0
8
.
0
2
.
0
75
.
0
1
5
.
1
8
.
0
2
.
0
75
.
0
1
1
V
V
mc
1
V
mc
dV
V
.
C
m
V
dV
C
m
PdV
m
W
3
5
.
0
5
.
0
1
5
.
1
1
5
.
1
1
1
1
2
2
.
0
8
.
0
1
V
V
V
V
V
V
2
1
2
1
2
1
=
=
+
∆
=
=
×
=
∆
=
µ
∆
=
−
=
×
=
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
×
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
−
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
γ
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
γ
−
=
=
=
=
−
−
+
−
+
−
+
γ
−
+
γ
−
+
γ
−
γ
−
γ
∫
∫
∫

)
121
(
)
5.31
(
ﻫﻭﺍﺀ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﻭﻀﻐﻁﻪ
(1 bar)
ﻭﺤﺠﻤ
ﻪ
(0.02m
3
)
.
ﻰـﻟﺍ ﻡـﺠﺤﻟﺍ ﺕﻭـﺒﺜﺒ ﻥﺨـﺴ
(5 bar)
.
ﺔـﻴﺌﺍﺩﺘﺒﻻﺍ ﻪﺘﺭﺍﺭﺤ ﻰﻟﺍ ﺩﺎﻋ ﻥﺍ ﻰﻟﺍ ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ ﺩﺭﺒ ﺎﻫﺩﻌﺒﻭ
.
ﺸﻐلـﻟﺍ ﻲﻓﺎـﺼ ﺏﺴـﺤﺍ
ﻭﺍﻟﺤﺭﺍﺭﺓ ﻋﻠﻤﺎﹰ ﺍﻥ
:
R=0.287 kJ/kg.K ، Cp =1.01 kJ/kg.K
W
23
= P
3
(V
3
-V
2
)
=500(0.004 - 0.02) = -8 kJ
Q
23
= m Cp (T
3
-T
2
)
=0.0238×1.01 (20 - 1465)
= - 34.7kJ
∑W=0 + (-8) = -8kJ
∑Q = 20 + (-34.7) = - 14.7 kJ
)
5.32
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(100 kN/m
2
)
ﻭﺤﺠﻤﻪ
(0.056m
3
)
ﻀﻐﻁ ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ ﺍﻟﻰ ﺤﺠﻡ
(0.007m
3
)
.
ﺴﺏـﺤﺇ
؟ ﺍﻟﻀﻐﻁ ﺍﻟﻨﻬﺎﺌﻲ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ ﻋﻠﻰ ﺍﻟﻐﺎﺯ
kJ
19.9
293)
-
(1465
0.723
0.0238
)
T
T
(
Cv
m
Q
K
1465
1
5
293
P
P
.
T
T
kg
0238
.
0
298
0.287
0.02
100
RT
V
P
m
K
.
kg
/
kJ
723
.
0
287
.
0
01
.
1
R
Cp
Cv
1
2
12
1
2
1
2
1
1
1
=
×
×
=
−
=
=
=
=
=
×
×
=
=
=
−
=
−
=
3
2
1
2
3
m
004
.
0
1405
293
02
.
0
T
T
.
V
V
=
×
=
=
kJ
65
.
11
0.056
0.007
n
L
0.056
100
V
V
Ln
V
P
D
.
W
kN/m
800
0.007
0.056
100
V
V
P
P
2
1
1
1
2
2
1
1
2
−
=
×
=
=
=
×
=
=

)
122
(
)
5.33
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(1kg)
ﻤﺤﺼﻭﺭ ﻓﻲ
ﻐﻁﻪـﻀ ﺔﻨﺍﻭﻁـﺴﺍ
(2 bar)
ﻪـﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩﻭ
(427
°C)
ﻐﻁـﻀ
ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ ﺍﻟﻰ
(5 bar)
.
ﺩﺍﺌﻲـﺘﺒﻻﺍ ﻪﻁﻐﻀ ﻰﻟﺍ ﺩﺎﻋ ﻥﺍ ﻰﻟﺍ ﺕﺒﺎﺜ ﻡﺠﺤﺒ ﺩﺭﺒ ﻡﺜ
.
ﺩـﺠﻭﺍ
)
1
(
ﺸﻐلـﻟﺍ
ﺍﻟﻤﻨﺠﺯ ﻓﻲ ﺍﻻﺠﺭﺍﺌﻴﻥ ﻭﺍﻟﺸﻐل ﺍﻟﻜﻠﻲ
) .
2
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻜﻠﻴﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R=0.287 kJ/kg.K ، Cv=0.72 kJ/kg.K
)
5.34
(
ﺍﺴﻁﻭﺍﻨﺔ ﻓﻴﻬﺎ ﻤﻜﺒﺱ ﺘﺤﻭﻱ
(1kg)
ﻤﻥ ﺍﻟﻬﻭﺍﺀ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(300
°C)
.
ﻰ ﺍﻥـﻟﺍ ﹰﺎـﻴﻠﻤﺭﺜﻭﺯﻴﺍ ﺩﺩـﻤﺘ
ﺘﻀﺎﻋﻑ ﺤﺠﻤﻪ
.
ﺘﺭﺠﻊـﺴﺍ ﻥﺍ ﻰﻟﺍ ﺔﻴﻠﻤﻌﻟﺍ ﺀﺎﻨﺜﺍ ﻲﻓ ﹰﺎﺘﺒﺎﺜ ﻁﻐﻀﻟﺍ ﻲﻘﺒ ﺙﻴﺤﺒ لﺨﺍﺩﻟﺍ ﻰﻟﺍ ﺱﺒﻜﻤﻟﺍ ﻊﻓﺩ ﻡﺜ
ﺍﻟﻬﻭﺍﺀ ﺤﺠﻤﻪ ﺍﻻﻭل
.
ﻋﻠﻤﺎﹰ ﺃﻥ،ﺓﺭﺍﺭﺤﻟﺍ ﻲﻓﺎﺼﻭ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺏﺴﺤﺍ
:
Cp=1.01 kJ/kg.K ، R=0.287 kJ/kg.K
Q
23
= mCv (T
3
-T
2
)
= 1 × 1.01 (286.5 – 573)
=-289.37 kJ
∑Q = 114 + (-289.37)
= - 175.4 kJ
K
280
500
700
200
P
T
P
T
kJ
-184.1
5
2
n
L
700
0.287
1
P
P
Ln
mRT
W
Q
2
2
3
3
2
1
1
12
12
=
×
=
=
=
×
×
=
=
=
∑
∑
−
=
−
+
−
=
=
+
=
=
×
=
−
=
kJ
5
.
486
)
4
.
302
(
1
.
184
Q
kJ
-184.1
0
-184.1
W
kJ
-302.4
427)
-
(280
0.72
1
)
T
T
(
Cv
m
Q
2
3
23
K
5
.
286
V
2V
573
V
V
T
T
kJ
114
V
V
Ln
573
0.287
1
V
V
Ln
mRT
Q
1
1
2
3
2
3
1
2
1
2
1
12
=
×
=
×
=
=
×
×
=
=

)
123
(
)
5.35
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(138 kN/m
2
)
ﻭﺤﺠﻤﻪ
(0.112 m
3
)
.
ﻀﻐﻁ ﺍﻟﻰ
(90 kN/m
2
)
ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.4
=C.)
.
ﺍﺤﺴﺏ ﺍﻟ
؟ﺤﺠﻡ ﺍﻟﺠﺩﻴﺩ
)
5.36
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(1.4 MN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(360
°C)
ﻐﻁﻪـﻀ ﺢﺒـﺼﺍ ﻥﺍ ﻰـﻟﺍ ﹰﺎـﻴﺘﺎﺒﺎﻴﺩﺍ ﺩﺩـﻤﺘ
(100kN/m
2
)
ﻐﻁﻪـﻀ ﺢﺒـﺼﺍﻭ ﺔـﻴﺌﺍﺩﺘﺒﻻﺍ ﻪـﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩ ﻰـﻟﺍ ﺩﺎﻋ ﻰﺘﺤ ﺕﺒﺎﺜ ﻁﻐﻀﺒ ﻥﺨﺴﻭ
(200kN/m
2
)
.
ﻭﻀﻐﻁ ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ ﺤﺘﻰ ﻋﺎﺩ ﺍﻟﻰ ﻀﻐﻁﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﻁـﻁﺨﻤ ﻰـﻠﻋ ﺕﺍﺀﺍﺭﺠﻻﺍ ﻡﺴﺭﺍ
(P-v)
ﻭﺍﺤﺴﺏ
)ﺃ
(
ﻗﻴﻤﺔ ﺍﻻﺱ ﺍﻻﺩﻴﺎﺒﺎﺘﻲ
(
γ)
)
ﺏ
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻟﺘﻤﺩﺩ ﺍﻻﺩﻴﺎﺒﺎﺘﻲ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp=1.005 kJ/kg.K
∆U = U
2
- U
1
= m Cv (T
2
-T
1
)
= 0.23 × 0.705 (288-633)
= -55.9 kJ
3
4
.
1
1
1
2
1
1
2
m
0348
.
0
690
138
112
.
0
P
P
V
V
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
γ
425
.
1
36
.
6
Ln
14
Ln
)
36
.
6
(
100
1400
V
V
V
V
P
P
36
.
6
220
1400
V
V
P
P
kJ/kg.K
005
.
1
Cp
1
3
1
2
2
1
1
3
3
1
=
γ
∴
γ
=
⇒
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
=
γ
γ
γ
K
288
633
220
100
T
P
P
T
kJ/kg.K
705
.
0
425
.
1
005
.
1
Cp
Cv
3
3
2
2
=
×
=
=
=
=
γ
=

)
124
(
)
5.37
(
ﻫﻭﺍﺀ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(300 K)
ﻭﻀ
ﻐﻁﻪ
(1 bar)
.
ﺩﺍﺌﻲـﺘﺒﻻﺍ ﻪﻁﻐـﻀ ﻑﻌـﻀ ﻰﻟﺍ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﻁﻐﻀﻴ
ﺒﻭﺴﺎﻁﺔ ﻀﺎﻏﻁ ﻴﺴﺘﻬﻠﻙ ﻗﺩﺭﺓ ﻤﻘﺩﺍﺭﻫﺎ
(200W)
.
ﺔـﻴﻨﺎﺜﻟﺍ ﻲﻓ ﻁﻏﺎﻀﻟﺍ ﻥﻤ ﺝﺭﺎﺨﻟﺍ ﺀﺍﻭﻬﻟﺍ ﻡﺠﺤ ﺏﺴﺤﺇ
ﻭﺍﺤﺴﺏ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
(γ=1.4) .
)
5.38
(
ﻪـﺘﻠﺘﻜ ﺯﺎﻏ ﻰﻠﻋ ﻱﻭﺘﺤﺘ ﺱﺒﻜﻤﺒ ﺔﻘﻠﻐﻤ ﺔﻨﺍﻭﻁﺴﺍ
(0.45kg)
ﻐﻁﻪـﻀﻭ
(6.7bar)
ﻭﺩ
ﺭﺍﺭﺓـﺤ ﺔـﺠﺭ
(185
°C)
ﺘﻤﺩﺩ ﺍﻟﻐﺎﺯ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺢ ﻀﻐﻁﻪ
(138 kN/m
2
)
ﻭﺍﻨﺨﻔﻀﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺒﻤﻘﺩﺍﺭ
(165K)
.
ﺍﺜﻨﺎﺀ ﺍﻟﺘﻤﺩﺩ ﺇﻨﺘﻘل ﺸﻐل ﺒﻭﺴﺎﻁﺔ ﺍﻟﻤﻜﺒﺱ ﻤﻘﺩﺍﺭﻩ
(53 kJ)
.
ﺍﺤﺴﺏ
(Cp)
ﻭ
(Cv)
.
T
2
=
∆T + T
1
= (-165) + 458 = 293 K
W
12
= -
∆U
12
= - m Cv (T
2
-T
1
)
53 = - 0.45 Cv (293-458)
Cv = 0.714 kJ/kg.K
1
-
)
T
-
mR(T
W
K
7
.
365
1
2
300
P
P
T
T
1
2
4
.
1
4
.
0
1
1
2
1
2
γ
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
γ
−
γ
s
/
m
0022
.
0
200
365.7
0012
.
0
P
mRT
V
10
2177
.
1
65.7
04
2
.
0
T
T
)
1
(
W
mR
3
3
-
1
2
=
×
=
=
×
=
×
=
−
−
γ
=
•
kJ/kg.K
0.999
1.4
0.74
.
Cv
Cp
4
.
1
58
.
1
Ln
1
1.565
Ln
138
670
293
458
P
P
T
T
1
1
2
1
2
1
=
×
=
γ
=
=
γ
γ
−
γ
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
γ
−
γ
γ
−
γ

)
125
(
)
5.39
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(0.225kg)
ﺒﻀﻐﻁ ﻤﻘﺩﺍﺭﻩ
(8.3bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(538
°C)
ﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺇﻨﻌﻜﺎﺴﻴﺎﹰ ﺍﻟﻰ
ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(149
°C)
.
ﺍﻭﺠﺩ ﺍﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل ﻋﻠﻤﺎﹰ ﺃﻥ
:
R=0.287 kJ/kg.K
، Cp=1.005 kJ/kg.K
)
5.40
(
ﺘﻤﺩﺩ ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺤﺘﻰ ﺍﺼﺒﺢ ﻀﻐﻁﻪ
( )
5
1
ﺍﻟﻀﻐﻁ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﻲـﻫ ﺔـﻴﺌﺍﺩﺘﺒﻻﺍ ﺓﺭﺍﺭـﺤﻟﺍ ﺔﺠﺭﺩ
(1.5)
ﻤﻥ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻬﺎﺌﻴﺔ
.
ﺇﺫﺍ ﻜﺎﻨﺕ
(R=0.3 kJ/kg.K)
.
ﺍﺤﺴﺏ
(Cp)
ﻭ
(
γ)
.
kPa
3
.
80
811
422
830
T
T
P
P
4
.
1
718
.
0
005
.
1
Cv
Cp
K
.
kg
/
kJ
718
.
0
287
.
0
005
.
1
R
Cp
Cv
1
4
.
1
4
.
1
1
1
2
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
γ
=
−
=
−
=
−
−
γ
γ
kJ
62.799
1
-
1.4
422)
-
(811
0.287
0.225
1
)
T
T
(
mR
W
m
0.33
80.3
422
0.287
225
.
0
P
mRT
V
2
1
12
3
2
2
2
=
×
×
=
−
γ
−
=
=
×
×
=
=
252
.
0
5
1
Ln
5
.
1
1
Ln
P
P
Ln
T
T
Ln
1
P
P
Ln
1
T
T
Ln
P
P
T
T
1
2
1
2
1
2
1
2
1
1
2
1
2
=
=
=
γ
−
γ
γ
−
γ
=
⎟
⎠
⎞
⎜
⎝
⎛
=
γ
−
γ
336
.
1
252
.
0
1
1
K
.
kg
/
kJ
193
.
1
0.336
1.336
3
.
0
1
R
Cp
=
−
=
γ
=
×
=
−
γ
γ
=

)
126
(
)
5.41
(
ﻜﻤﻴﺔ ﻤﻥ ﻏﺎﺯ
(N
2
)
ﻜﺘﻠﺘﻬﺎ
(0.2kg)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭ
ﺘﻬﺎ
(15
°C)
ﺎـﻬﻤﺠﺤ ﺢﺒﺼﺍ ﻰﺘﺤ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﺕﻁﻐﻀ
ﺭﺒﻊ ﻤﺎ ﻜﺎﻥ ﻋﻠﻴﻪ ﻓﻲ ﺍﻟﺒﺩﺍﻴﺔ ﻭﺍﺼﺒﺤﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻬﺎ
(237
°C)
.
لـﻘﺘﻨﻤﻟﺍ لﻐﺸـﻟﺍ ﻥﺎـﻜﻭ
(33kJ)
.
ﺍﺤﺴﺏ
(
γ)
ﻭ
(R)
.
)
5.42
(
ﻏﺎﺯ ﻴﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﻤﻥ ﻀﻐﻁ
(700kN/m
2
)
ﻭﺤﺠﻡ
(0.015 m
3
)
ﺍﻟﻰ
(140 kN/m
2
)
.
ﺍﺤﺴﺏ ﺍﻟﺤﺠﻡ
ﺍﻟﻨﻬﺎﺌﻲ ﻭﺍﻟ
ﺸﻐل ﺍﻟﻤﻨﺘﻘل ﻭﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
ﻋﻠﻤﺎﹰ ﺒﺄﻥ
:
Cv = 0.752 kJ/kg.K
،
Cp = 1.046 kJ/kg.K
kJ/kg.K
2634
.
0
R
1
-
1.412
273)
-
(15
R
2
.
0
33
1
)
T
T
(
mR
W
412
.
1
)
25
.
0
(
Ln
)
1
(
)
5647
.
0
(
Ln
)
25
.
0
(
510
288
V
V
T
T
2
1
12
1
1
1
2
2
1
=
×
=
−
=
−
γ
−
=
=
γ
−
γ
=
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
γ
−
γ
kJ
-9.69
-W
U
kJ
69
.
9
1
-
1.39
0.048
140
-
0.015
700
1
V
P
V
P
W
m
048
.
0
140
700
015
.
0
P
P
V
V
39
.
1
752
.
0
046
.
1
Cv
/
Cp
2
2
1
1
3
39
.
1
1
1
2
1
1
2
=
=
∆
=
×
×
=
−
γ
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
γ
γ

)
127
(
)
5.43
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.3 m
3
)
ﻭﻀﻐﻁﻪ
(100 kN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﻰـﻟﺍ ﺎـﻴﻠﻤﺭﺜﻭﺯﻴﺍ ﻁﻐـﻀ
(500 kN/m
2
)
.
ﻭﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺍﻟﻰ ﺤﺠﻤﻪ ﺍﻻﺼﻠﻲ
.
ﺍﺤﺴﺏ
)ﺍ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘ
،ﻀﻐﺎﻁـﻨﻻﺍ ﺀﺎﻨﺜﺍ ﻲﻓ ﺔﻠﻘ
)
ﺏ
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
ـﺠ
(
ﻜﺘﻠﺔ ﺍﻟﻐﺎﺯ
.
γ = 1.4
،
Cp = 1 kJ/kg.K
) ﺃ
(
ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎ
ً
)
ﺏ
(
ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ
kJ
3
.
48
500
100
n
L
0.3
100
P
P
PVLn
W
Q
m
06
.
0
500
100
3
.
0
P
P
V
V
2
1
3
2
1
1
2
−
=
×
=
=
=
=
=
=
=
kJ
5
.
35
1
-
1.4
0.3)
52.6
-
0.06
(500
-
1
)
V
P
V
P
(
W
U
kN/m
6
.
52
3
.
0
06
.
0
500
V
V
P
P
1
1
2
2
2
4
.
1
3
2
2
3
−
=
×
×
=
−
γ
−
−
=
−
=
∆
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
γ
kg
358
.
0
293
0.286
0.3
100
RT
V
P
m
kJ/kg.K
286
.
0
4
.
1
)
1
4
.
1
(
1
)
1
(
Cp
R
1
1
1
=
×
×
=
=
=
−
=
γ
−
γ
=

)
128
(
)
5.44
(
ﻜﻤﻴﺔ ﻤﻥ ﻏﺎﺯ ﻀﻐﻁﻪ
(5bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
.
ﺘﻤﺩﺩ ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ ﻤﻥ
(0.3m
3
)
ﻐﻁـﻀ ﻰـﻟﺍ
ﻤﻘﺩﺍﺭﻩ
(1bar)
.
ﻓﺈﺫﺍ ﻜﺎﻨ
ﺕ
(
γ=1.4)
ﻭ
(Cp = 1 kJ/kg.K)
.
ﺍﺤﺴﺏ
:
)
ﺃ
(
ﻜﺘﻠﺔ ﺍﻟﻐﺎﺯ
)
ﺏ
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ
)
ـﺠ
(
ﺤﺠﻡ ﺍﻟﻐﺎﺯ
.
)
5.45
(
ﻫﻭﺍﺀ ﺤﺠﻤﻪ
(0.056m
3
)
ﻭﻀﻐﻁﻪ
(1.38 bar)
.
ﻀﻐﻁ ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ ﺍﻟﻰ
(0.014m
3
)
.
ﺸﻐلـﻟﺍ ﺩـﺠﻭﺍ
ﺍﻟﻤﻨﺘﻘل ﻭﻗﺎﺭﻨﻪ ﻤﻊ ﺍﻟﺸﻐل ﻓﻲ ﺤﺎﻟﺔ ﻜﻭﻥ ﺍﻻﻨﻀﻐﺎﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺍﻨﻌ
ﻜﺎﺴﻴﺎ
ﺨﻼل ﺍﻟﻨﺴﺒﺔ
ﺍﻟﺤﺠﻤﻴﺔ ﻨﻔﺴﻬﺎ
.
ﺎﹰـﻤﻠﻋ
ﺃﻥ
:
γ=1.4
،
R=0.287 kJ/kg.K
kg
79
.
1
293
0.286
0.3
500
RT
V
P
m
kJ/kg.K
286
.
0
4
.
1
)
1
4
.
1
(
1
)
1
(
Cp
R
1
1
1
=
×
×
=
=
=
−
=
γ
−
γ
=
3
2
1
1
2
12
2
1
12
m
5
.
1
1
0.3
5
P
V
P
V
kJ
241.41
1
5
n
L
293
0.286
79
.
1
W
P
P
n
L
mRT
W
=
×
=
=
=
×
×
=
=
bar
64
.
9
014
.
0
056
.
0
138
V
V
P
P
kJ
7
.
10
0.056
0.014
n
L
0.056
138
V
V
Ln
V
P
W
4
.
1
2
1
1
2
1
2
1
1
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
×
=
=
γ
kJ
42
.
14
1
-
1.4
0.014
964
0.056
138
1
V
P
V
P
W
2
2
1
1
−
=
×
×
×
=
−
γ
−
=

)
129
(
)
5.46
(
ﻫﻭﺍﺀ ﺤﺠﻤﻪ
(0.2m
3
)
ﻋﻨﺩ ﻀﻐﻁ
(5 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(30
°C)
ﻀﻐﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﻤﻐﻠﻘﺔ
ﺍﻟﻰ ﺤﺠﻡ
(0.1m
3
)
ﺜﻡ ﺒﺭﺩ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺍﻟﻰ ﻀﻐﻁ،
(5 bar)
.
ﻪـﻤﺠﺤ ﻰـﻟﺍ ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ ﻥﺨﺴ ﻡﺜ
ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﺍﺤﺴﺏ ﺼﺎﻓﻲ
:
) ﺃ
(
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ
)
ﺏ
(
ﻋﻠﻤﺎﹰ ﺃﻥ،ﺔﻴﻠﺨﺍﺩﻟﺍ ﺔﻗﺎﻁﻟﺍ
:
R = 0.787 kJ/kg.K . Cp = 1.005 kJ/kg.K
(1)
(2)
kJ
-80.1
303)
-
(400
0.718
1.15
T
-mCv
U
-
W
kg
15
.
1
300
0.787
0.2
500
RT
PV
m
K
400
1
.
0
2
.
0
300
V
V
T
T
399
.
1
718
.
0
/
005
.
1
Cv
/
Cp
K
.
kg
/
kJ
718
.
0
0287
005
.
1
R
Cp
Cv
1
1
4
.
1
2
1
1
2
=
×
−
=
∆
=
∆
=
=
×
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
γ
=
−
=
−
=
γ
kJ
0
)
30
(
30
W
Q
U
KJ
30
175
)
205
(
0
Q
kJ
30
50
0
)
80
(
W
kJ
175
(151.2)
1.005
15
.
1
T
mCp
Q
kJ
205
)
400
5
.
151
(
718
.
0
15
.
1
)
T
T
(
mv
Q
kJ
50
)
1
.
0
2
.
0
(
500
)
V
V
(
P
W
K
1055
1320
500
400
P
P
T
T
kN/m
1320
1
.
0
2
.
0
500
V
V
P
P
T
T
T
T
T
31
2
3
23
3
1
31
2
3
2
3
2
4
.
1
2
1
1
2
=
−
−
−
=
−
=
∆
−
=
+
−
+
=
−
=
+
+
−
=
=
×
=
∆
=
−
=
−
×
=
−
=
=
−
=
−
=
=
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
γ
)
130
(
)
5.47
(
ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻜﺘﻠﺘﻪ
(0.45kg)
ﺯـﺠﻨﺍﻭ ﺔﻴﺍﺩﺒﻟﺍ ﻲﻓ ﻪﻴﻠﻋ ﻥﺎﻜ ﺎﻤ ﻑﺼﻨ ﻪﻁﻐﻀ ﺢﺒﺼﺍ ﻥﺍ ﻰﻟﺍ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﺩﺩﻤﺘ
ﺸﻐﻼﹰ ﻤﻘﺩﺍﺭﻩ
(27kJ)
ﻭﺍﻨﺨﻔﻀﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﻤﻥ
(220
°C)
ﻰـﻟﺍ
(130
°C)
.
ﺔـﻤﻴﻗ ﺏﺴـﺤﺍ
(
γ)
ﻭﻜﺫﻟﻙ
(R)
.
)
5.48
(
ﻫﻭﺍﺀ ﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻋﻨﺩ ﻀﻐﻁ
(6 bar)
ﺍﻟﻰ
(1.48 bar)
.
ﺜﻡ ﺘﺭﻙ ﺍﻟﻰ ﺍﻥ ﻋﺎﺩﺕ ﺩﺭﺠﺔ
ﻰــﻟﺍ ﻪﻁﻐــﻀ ﻊﻔﺘﺭﺄــﻓ ﻡــﺠﺤﻟﺍ ﺕﻭــﺒﺜﺒ ﺔــﻴﺍﺩﺒﻟﺍ ﻲــﻓ ﻪــﻴﻠﻋ ﺕــﻨﺎﻜ ﺎــﻤ ﻰــﻟﺍ ﻪــﺘﺭﺍﺭﺤ
(2.21 bar)
.
ﺍﻭﺠﺩ ﻗﻴﻤﺔ
(R)
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp=1.005 kJ/kg.K
ﻤﻥ
)
1
(
ﻭ
)
2
(
ﻴﻨﺘﺞ
:
( )
kJ/kg.K
273
.
0
)
130
220
(
45
.
0
)
1
41
.
1
(
27
)
T
m(T
1)
-
W(
R
1.41
2
Ln
1
-
1.223
Ln
2
403
493
P
P
T
T
2
1
1
1
2
1
2
1
=
−
−
=
−
γ
=
=
γ
γ
γ
=
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
γ
−
γ
γ
−
γ
....(2)
P
P
T
T
3
2
....(1)
P
P
T
T
2
1
3
2
1
2
1
1
2
1
2
=
⇒
→
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
→
γ
−
γ
kJ/kg.K
325
.
0
68
.
0
005
.
1
Cv
Cp
R
68
.
0
47
.
1
005
.
1
Cp
Cv
47
.
1
21
.
2
Ln
6
Ln
48
.
1
Ln
6
Ln
P
Ln
P
Ln
P
Ln
P
Ln
3
1
2
1
=
−
=
−
=
=
=
γ
=
=
−
−
=
−
−
=
γ

)
131
(
)
5.49
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.12m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﻭﻀﻐﻁﻪ
(1.0133 bar)
.
ﻰـﻟﺍ ﹰﺎـﻴﺘﺎﺒﺎﻴﺩﺍ ﻁﻐـﻀ
(0.024m
3
)
.
ﺍﺤﺴﺏ
)ﺃ
(
ﻜﺘﻠﺔ ﺍﻟﻐﺎﺯ
)
ﺏ
(
،ﻀﻐﺎﻁـﻨﻻﺍ ﺔﻴﺎﻬﻨ ﺩﻨﻋ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ ﻁﻐﻀﻟﺍ
)
ﺝ
(
ﺸﻐلـﻟﺍ
ﺍﻟﻤﻨﺘﻘل
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp = 1.005 kJ/kg.K . Cv=0.718 kJ/kg.K
)
5.50
(
ﻪـﺘﻠﺘﻜ ﺯﺎـﻏ
(1.8 kg)
ﻐﻁﻪـﻀﻭ
(2 bar)
ﻪـﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩﻭ
(27
°C)
.
ﻰـﻟﺍ ﹰﺎـﻴﺘﺎﺒﺎﻴﺩﺍ ﻁﻐـﻀ
(3.5 bar)
.
ﺍﺤﺴﺏ
)
1
(
ﺍﻟﺤﺠﻡ ﺍﻻﺒﺘﺩﺍﺌﻲ ﻭﺍﻟﻨﻬﺎﺌﻲ
)
2
(
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻬﺎﺌﻴﺔ
)
3
(
ﺭﺍﺭﺓـﺤﻟﺍﻭ لﻐﺸـﻟﺍ
ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
)
4
(
ﻤﻘﺩﺍﺭ
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R = 0.3 kJ/kg.K .
γ = 1.4
1
-
1.4
352)
-
(200
0.3
8
.
1
1
)
T
T
(
mR
W
2
1
12
×
×
=
−
γ
−
=
kJ
2
.
70
U
kJ
2
.
70
U
W
kJ
2
.
70
W
12
12
12
12
−
=
∆
=
∆
=
−
−
=
bar
64
.
9
024
.
0
12
.
0
0133
.
1
V
V
P
P
1.4
Cp/Cv
kg
144
.
0
293
0.287
0.12
33
.
101
RT
PV
m
K
.
kg
/
kJ
287
.
0
715
.
0
005
.
1
Cv
Cp
R
4
.
1
2
1
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
γ
=
×
×
=
=
=
−
=
−
=
γ
kJ
-85.283
1
-
1.4
0.024
964
-
0.12
101.33
W
K
557.7
0.12
101.33
0.024
964
293
V
P
V
P
T
T
1
1
2
2
1
2
=
×
×
=
=
×
×
×
=
=
K
352
543
.
0
81
.
0
200
V
V
T
T
m
543
.
0
5
.
3
2
81
.
0
P
P
V
V
m
81
.
0
200
300
0.3
8
.
1
P
mRT
V
1
4
.
1
1
2
1
1
2
3
4
.
1
1
1
2
1
1
2
3
1
1
1
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
×
×
=
=
−
−
γ
γ
)
132
(
)
5.51
(
ﻏﺎﺯ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻀﻐﻁﻪ
(320 kN/m
2
)
.
ﺒﺭﺩ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺤﺘﻰ ﺍﺼﺒﺢ ﻀﻐﻁﻪ
(2.4 bar)
.
ﻡـﺜ
ﻀﻐﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺤﺘﻰ ﺍﺼﺒﺢ ﻀﻐﻁﻪ
(700 kN/m
2
)
ﺔـﻴﺌﺍﺩﺘﺒﻻﺍ ﻪﺘﺭﺍﺭﺤ ﺔﺠﺭﺩ ﻰﻟﺍ ﺩﺎﻋﻭ
.
ﺎﻥـﻜ ﺍﺫﺈـﻓ
(R=0.262 kJ/kg.K)
.
ﺍﺤﺴﺏ ﻗﻴﻤﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻭﻋﻴﺔ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
.
)
5.52
(
ﻫﻭﺍﺀ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(44
°C)
ﻀﻐﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.4
=C.)
ﺍﻟﻰ ﺤﺠﻡ
(450L)
.
ﺭﺩـﺒ ﻡﺜ
ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﺍﻟﻰ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(35
°C)
.
ﻓﺈﺫﺍ ﻜﺎﻥ ﺍﻟﺸ
ﻓﻲ ﺍﻻﺠﺭٍﻭﺎﺴﺘﻤ لﻐ
ﺍﺌﻴ
ﻥ ﺍﺤﺴﺏ ﺍﻟﺤﺠﻡ ﺍﻟﻨﻬﺎﺌﻲ
ـﺒﺎﻟ
(m
3
)
.
P
P
P
P
T
T
....(2)
P
P
T
T
3
2
....(1)
P
P
T
T
2
1
1
3
2
1
2
3
1
1
3
2
3
2
1
2
1
2
γ
−
γ
γ
−
γ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
∴
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⇒
→
=
⇒
→
Q
K
.
kg
/
kJ
97
.
0
1
-
1.37
1.37
262
.
0
1
R
Cp
37
.
1
7
4
.
20
2
.
3
4
.
2
1
=
×
=
−
γ
γ
=
=
γ
⎟
⎠
⎞
⎜
⎝
⎛
=
γ
−
γ
2
2
2
3
2
1
23
12
t
35
4
.
0
t
44
)
T
T
(
mR
1
)
T
T
(
mR
W
W
−
=
−
−
=
−
γ
−
=
3
3
2
2
3
2
m
429
.
0
L
429
308
323
450
T
T
V
V
K
323
C
50
t
=
=
×
=
×
=
=
=
o

)
133
(
)
5.53
(
ﻫﻭﺍﺀ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(538
°C)
ﻭﻀﻐﻁﻪ
(8.3 bar)
ﻭﻜﺘﻠﺘﻪ
(0.225 kg)
.
ﺔـﺠﺭﺩ ﻰـﻟﺍ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﺩﺩﻤﺘ
ﺤﺭﺍﺭﺓ
(149
°C)
.
ﺍﺤﺴﺏ ﺍﻟﻀﻐﻁ ﻭﺍﻟﺤﺠﻡ ﺍﻟﻨﻬﺎﺌﻲ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp = 1.005 kJ/kg.K
،
R=0.287 kJ/kg.K
)
5.54
(
(0.5 kg)
ﻫﻭﺍﺀ ﻀﻐﻁﻪ
(1.2 bar)
ﻭﺤﺠﻤﻪ
(0.4 m
3
)
.
ﻰـﻟﺍ ﹰﺎـﻴﺘﺎﺒﺎﻴﺩﺍ ﻁﻐﻀﻴ ﻡﺜ ،ﹰﺎﻴﻠﻤﺭﺜﻭﺯﻴﺍ ﻁﻐﻀﻴ
(200
°C)
.
ﻋﻠﻤﺎﹰ ﺃﻥ،ﻥﻴﺀﺍﺭﺠﻻﺍ ﻥﻤ ٍلﻜ ﻲﻓ ﻡﺠﺤﻟﺍ ﺏﺴﺤﺍ ،ﻥﻴﺀﺍﺭﺠﻻﺍ ﻲﻓ ٍﻭﺎﺴﺘﻤ لﻐﺸﻟﺍ ﻥﺎﻜ ﺍﺫﺈﻓ
:
Cp=1.005 kJ/kg.K ، Cv=0.718 kJ/kg.K
3
1
4
.
1
1
1
1
2
1
1
2
3
2
1
1
1
1
4
.
1
4
.
1
1
1
2
1
2
m
324
.
0
422
811
063
.
0
T
T
V
V
m
0631
.
0
10
8.3
811
0.287
255
.
0
P
mRT
V
bar
0.839
811
422
3
.
8
T
T
P
P
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
×
×
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−
−
γ
−
−
γ
γ
kJ
9
.
62
422)
-
0.718(811
225
.
0
)
T
T
(
mCv
U
W
2
1
=
×
=
−
=
∆
−
=
0377
.
1
P
P
Ln
2
1
3
2
2
1
1
23
12
1
1
1
e
e
0377
.
1
)
5
.
334
)(
4
.
1
1
(
473
5
.
334
P
P
Ln
1
)
T
T
(
mR
P
P
Ln
mRT
W
W
K
5
.
334
0.287
0.5
0.4
120
mR
V
P
T
2
1
−
=
−
=
−
−
=
−
γ
−
=
=
=
×
×
=
=
3
1
399
.
1
1
1
1
3
2
2
3
3
2
1
1
2
2
2
2
1
m
06
.
0
473
5
.
334
141
.
0
T
T
V
V
m
141
.
0
3.389
0.4
2
.
1
P
V
P
V
bar
389
.
3
P
354
.
0
P
2
.
1
354
.
0
P
P
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
×
=
=
=
=
⇒
=
−
−
γ

)
134
(
)
5.55
(
ﻫﻭﺍﺀ ﻀﻐﻁﻪ
(1 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(300 K)
ﻴﻀﻐﻁ ﻓﻲ ﻀﺎﻏﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺍﻟﻰ
(2 bar)
ﺴﺘﻬﻠﻙـﻴﻭ
ﻓﻲ ﺫﻟﻙ ﻗﺩﺭﺓ
(200 W)
ـ ﺍﺤﺴﺏ ﺤﺠﻡ ﺍﻟﻬﻭﺍﺀ ﺍﻟﺨﺎﺭﺝ ﺒﺎﻟ
(m
3
/s)
ﻋﻠﻤﺎﹰ ﺃﻥ،
:
γ=1.4
)
5.56
(
ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻜﺘﻠﺘﻪ
(0.2 kg)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
.
ﻰـﻟﺍ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﻁﻐﻀ
(1/4)
ﺩﺍﺌﻲـﺘﺒﻻﺍ ﻪـﻤﺠﺤ
ﻭﺇﺭﺘﻔﻌﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭ
ﺘﻪ ﺒﻤﻘﺩﺍﺭ
(222K)
ﻭﺍﻨﺠﺯ ﺸﻐﻼﹰ
ﻤﻘﺩﺍﺭﻩ
(33kJ)
.
ﻀﻐﻁـﻟﺍ ﺕﻭﺒﺜﺒ ﺯﺎﻐﻟﺍ ﺩﺭﺒ ﻡﺜ
ﻭﻋﺎﺩ ﺍﻟﻰ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻻﺼﻠﻴﺔ
.
ﺃﻭﺠﺩ
)
1
(
Cp . Cv
)
2
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل
.
4
.
0
)
300
7
.
365
(
mR
200
1
-
T
mR
W
K
7
.
365
1
2
300
P
P
T
T
4
.
0
1
1
2
1
2
−
=
γ
∆
=
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−
γ
s
m
0022
.
0
200
7
.
365
2177
.
1
P
mRT
V
2177
.
1
mR
3
=
×
=
=
=
kJ/kg.K
304
.
0
)
237
15
(
2
.
0
)
1
41
.
1
(
33
)
T
T
(
m
)
1
(
W
R
41
.
1
4
1
510
288
V
V
T
T
kJ/kg.K
0.74
)
237
15
(
2
.
0
33
)
T
T
(
m
W
Cv
)
T
T
(
mCv
U
W
-
K
510
288
222
T
T
T
:
2
1
2
1
12
1
1
1
2
2
1
2
1
1
2
12
12
1
12
2
=
−
−
−
=
−
−
γ
=
=
γ
⇒
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
−
−
=
−
−
=
−
−
=
∆
−
=
=
+
=
+
∆
=
→
−
γ
−
γ
[
]
kJ
-13.5
46.356)
-(-32.856
(-46.356)
-
32.856
-
-
)
Q
U
(
W
kJ
-32.856
273)
-
(15
0.74
2
.
0
)
T
T
(
mCv
U
kJ
-46.356
237)
-
(15
1.044
0.2
)
T
T
(
mCp
Q
:
3
2
kJ/kg.K
044
.
1
74
.
0
304
.
0
Cv
R
Cp
23
23
23
2
3
23
2
3
23
=
+
=
=
−
∆
−
=
=
×
=
−
=
∆
=
×
=
−
=
→
=
+
=
+
=

)
135
(
)
5.57
(
ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻀﻐﻁﻪ
(1 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(27
°C)
ﻪـﻤﺠﺤﻭ
(3.5m
3
)
ﻰـﻟﺍ ﹰﺎـﻴﻠﻤﺭﺜﻭﺯﻴﺍ ﻁﻐـﻀ
(600kN/m
2
)
.
ﺜﻡ ﺘﻤﺩﺩ ﺍﺩﻴﺎﺒ
ﺎﺘﻴﺎﹰ ﺍﻟﻰ ﺤﺠﻤﻪ ﺍﻻﻭل
.
ﺍﺤﺴﺏ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻭﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
ﻟﻸﺠﺭﺍﺀ ﺍﻻﺨﻴﺭ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
γ=1.4
)
5.58
(
ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(3 kg)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﺩﺍﺭﻩـﻘﻤ لﻐـﺸ لـﻘﺘﻨﻴﻭ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﻕﻠﻐﻤ ﻡﺎﻅﻨ ﻲﻓ ﻁﻐﻀﻴ
(100kJ)
ﺜﻡ ﻴﺘﻤﺩﺩ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﻭﻴﻨﺘﻘل ﺸﻐل ﻤﻘﺩﺍﺭﻩ،
(100 kJ)
.
ﺩـﻌﺒ ﺓﺭﺍﺭـﺤﻟﺍ ﺔـﺠﺭﺩ ﺏﺴـﺤﺍ
ﺍﻻﻨﻀﻐﺎﻁ ﺍﻻﺩﻴﺎﺒﺎﺘﻲ
)
ﺏ
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
γ=1.4
، Cv = 0.72 kJ/kg.K
2
4
.
1
3
2
2
3
3
2
1
1
2
2
1
12
kN/m
84
.
48
5
.
0
083
.
0
600
V
V
P
P
m
083
.
0
600
100
5
.
0
P
P
.
V
V
kJ
6
.
89
600
100
Ln
5
.
0
100
P
P
PVLn
Q
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
−
=
×
=
=
γ
kJ
95
.
63
W
U
kJ
63.95
1
-
1.4
0.5
48.84
-
0.083
600
1
V
P
V
P
W
23
23
3
3
2
2
23
−
=
−
=
∆
=
×
×
=
−
γ
−
=
K
455
T
)
4
.
339
T
(
288
.
0
3
100
)
T
T
(
mR
W
K
4
.
339
T
1
4
.
1
)
T
293
(
288
.
0
3
100
1
)
T
T
(
mR
W
kJ/kg.K
288
.
0
)
1
4
.
1
(
72
.
0
)
1
(
Cv
R
3
3
2
3
23
2
2
2
1
12
=
−
×
=
−
=
=
−
−
×
=
−
γ
−
=
=
−
=
−
γ
=
kJ
350
100
250
W
U
Q
kJ
250
339.3)
-
0.72(455
3
)
T
T
(
mCv
U
23
23
23
2
3
23
=
+
=
+
∆
=
=
×
=
−
=
∆

)
136
(
)
5.59
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.336 m
3
)
ﻭﻀﻐﻁﻪ
(1.03 bar)
ﻪـﺘﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ
(38
°C)
ﻰـﻟﺍ ﹰﺎﻴـﺴﺎﻜﻌﻨﺍ ﻁﻐـﻀ
(16.5 bar)
ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(P
ν
1.3
=C
.
)
.
ﻭﻤﻥ ﺍﻟﻨﻘﻁﺔ ﺍﻻ
ﻰـﻟﺍ ﹰﺎـﻴﺘﺎﺒﺎﻴﺩﺍ ﹰﺎﻴﺴﺎﻜﻌﻨﺍ ﻁﻐﻀ ﺎﻬﺴﻔﻨ ﺔﻴﺌﺍﺩﺘﺒ
ﺍﻟﺤﺠﻡ ﺍﻟﻨﻬﺎﺌﻲ ﻨﻔﺴﻪ
.
ﺍﻭﺠﺩ
) :
1
(
ﺭﺍﺀ ﺍﻻﻭلـﺠﻻﺍ ﻲﻓ ﻥﻴﻠﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩﻭ ﻡﺠﺤﻟﺍ
)
2
(
ﺍﻟﻀﻐﻁ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل ﻓﻲ ﺍﻻﺠﺭﺍﺀ ﺍﻟﺜﺎﻨﻲ
.
ﻋﻠﻤﺎﹰ ﺍﻥ
:
R=0.287 kJ/kg.K
،
Cv=0.718 kJ/kg.K
(1)
(2)
ﻭﺒﻁﺭﻴﻘﺔ ﺍﺨﺭﻯ
:
kJ
26
)
103
(
77
W
U
Q
kJ
77
311)
-
(588
0.718
387
.
0
)
T
T
(
mCv
U
kg
387
.
0
311
0.287
0.336
103
RT
V
P
m
kJ
-103
1
-
1.3
0.0396
1650
-
0.336
103
1
n
V
P
V
P
W
K
588
1.03
0.336
16.5
0.0396
311
V
P
P
V
T
T
m
0396
.
0
5
.
16
03
.
1
336
.
0
P
P
V
V
12
12
12
1
2
12
1
1
1
2
2
1
1
12
1
1
2
2
1
2
3
3
.
1
1
1
2
1
1
2
−
=
−
+
=
+
∆
=
=
×
=
−
=
∆
=
×
×
=
=
=
×
×
=
−
−
=
=
×
×
×
=
×
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
γ
kJ
-115
1
-
1.4
0.0396
20.4
-
0.336
103
1
V
P
V
P
W
K
75
0.336
103
20.4
0.0396
311
V
P
P
V
T
T
bar
4
.
20
0396
.
0
336
.
0
103
V
V
P
P
2
2
1
1
12
1
1
2
2
1
2
4
.
1
2
1
1
2
=
×
×
=
−
γ
−
=
=
×
×
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
γ
-W
kJ
115
(414)
0.718
387
.
0
)
T
T
(
mCv
U
kg
387
.
0
311
0.287
0.336
103
RT
V
P
m
K
725
0396
.
0
336
.
0
311
V
V
T
T
1
2
12
1
1
1
1
2
1
1
2
=
=
×
=
−
=
∆
=
×
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
γ

)
137
(
)
5.60
(
ﻫﻭﺍﺀ ﻀﻐﻁﻪ
(1MN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(45
°C)
ﻭﺤﺠﻤﻪ
(0.3m
3
)
ﻰـﻟﺍ ﺩﺩﻤﺘ
(1.2m
3
)
ﺴﺏـﺤ
ﺍﻟﻌﻼﻗﺔ
(PV
1.25
=C.)
.
ﺍﺤﺴﺏ
)ﺃ
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ
)
ﺏ
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
ﺝ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
γ=1.4
)
5.61
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(1 bar)
ﻭﺤﺠﻤﻪ
(10.7 m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
ﻲـﻓ ﺢﺒﺼﺍ ﺙﻴﺤﺒ ﻪﺘﻟﺎﺤ ﺕﺭﻴﻐﺘ
ﺍﻟﻨﻬﺎﻴﺔ ﻀﻐﻁﻪ
(5 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
.
ﻭﻜﺎﻥ ﻫﺫﺍ ﺍﻟﺘﻐﻴﺭ ﺒﺎﻟﻁﺭﻕ ﺍﻟﺘﺎﻟﻴﺔ
:
-
)
1
(
ﺘﺴﺨﻴﻥ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺜﻡ ﺘﺒﺭﻴﺩ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
.
)
2
(
ﺍﻨﻀﻐﺎﻁ ﺍﻴﺯﻭﺜﺭﻤﻠﻲ
)
3
(
ﺍﻨﻀﻐﺎﻁ ﺍﺩﻴﺎﺒﺎﺘﻲ ﻴﺘﺒﻌﻪ ﺘﺒﺭﻴﺩ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
.
ﺍﺤﺴﺏ ﻟﻜل
ﺍﻟﻤﺴﺎﺭﺍﺕ ﻤﺎ ﻴﻠﻲ
:
)
ﺃ
(
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
)
ﺏ
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
ﺝ
(
،ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻻﻨﺜﺎﻟﺒﻲ
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp = 0.293 kJ/kg.K
، Cv = 0.21 kJ/kg.K
MJ
352
.
0
25
.
0
088
.
0
1
-
1.25
1.2
0.177
0.3
1
1
n
V
P
V
P
W
MN/m
177
.
0
2
.
1
3
.
0
1
V
V
P
P
2
2
1
1
2
25
.
1
25
.
1
2
1
1
2
=
=
×
−
×
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
×
=
⎟
⎠
⎞
⎜
⎝
⎛
=
MJ
132
.
0
352
.
0
22
.
0
W
U
Q
MJ
22
.
0
4
.
0
088
.
0
W
U
=
+
−
=
+
∆
=
−
=
−
=
−
=
∆

)
138
(
(1)
1
→2
2
→3
(2)
(3)
kJ
1
.
15108
288)
-
(1440
0.293
76
.
44
)
T
T
(
mCp
H
kJ
10847.1
288)
-
(1440
0.21
44.76
)
T
T
(
mCv
U
Q
K
1440
0.083
44.7
10.7
500
mR
V
P
T
kg
76
.
44
288
0.083
10.7
100
RT
V
P
m
K
.
kg
/
kJ
083
.
0
Cv
Cp
R
1
2
12
1
2
12
12
2
2
2
1
1
1
=
×
=
−
=
∆
=
×
=
−
=
∆
=
=
×
×
=
=
=
×
×
=
=
=
−
=
kJ
34
.
15134
Q
)
T
T
(
mCp
H
kJ
-10854.34
(-4280)
-
-15134
W
Q
U
kJ
-15134.34
1440)
-
(288
0.293
76
.
44
)
T
T
(
mCp
Q
kJ
4280
)
7
.
10
14
.
2
(
500
)
V
V
(
P
W
m
14
.
2
500
288
0.083
76
.
44
P
mRT
V
23
2
3
23
23
23
23
2
3
23
2
3
2
23
3
3
3
3
−
=
=
−
=
∆
=
=
−
=
∆
=
×
=
−
=
−
=
−
=
−
=
=
×
×
=
=
kJ
-1722
5
1
n
L
288
0.083
44.76
P
P
Ln
mRT
W
Q
0
W
Q
0
H
0
U
2
1
1
12
12
12
12
12
12
=
×
×
=
=
=
=
−
=
∆
=
∆
kJ
8
.
3350
)
T
T
(
mCp
H
kJ
6
.
2401
)
T
T
(
mCv
U
Q
kJ
8
.
3350
)
T
T
(
mCp
H
kJ
2403
W
U
2403
1
)
T
T
(
mR
W
K
5
.
543
P
P
T
T
bar
436
.
9
P
P
1
P
5
P
P
P
P
T
T
T
T
P
P
395
.
1
Cv
/
Cp
2
3
23
2
3
23
23
1
2
12
12
12
2
1
12
3
2
3
2
2
283
.
0
2
2
1
2
1
2
3
2
1
2
3
2
3
−
=
−
=
∆
−
=
−
=
∆
=
=
−
=
∆
=
−
=
∆
−
=
−
γ
−
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
=
γ
γ
−
γ

)
139
(
)
5.62
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(300 kN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘ
ﻪ
(25
°C)
ﺔـﻗﻼﻌﻟﺍ ﺏﺴـﺤ ﻁﻐﻀ ،
(PV
1.4
=C)
ﻰـﺘﺤ
ﺍﺼﺒﺤﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(180
°C)
.
ﺍﺤﺴﺏ ﺍﻟﻀﻐﻁ ﺍﻟﺠﺩﻴﺩ
.
)
5.63
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(2070 kN/m
2
)
ﻭﺤﺠﻤﻪ
(0.04 m
3
)
ﺘﻤﺩﺩ ﺒﻭﻟﺘﺭﻭﺒﻴﺎﹰ ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.35
=C)
ﻰـﻟﺍ
ﻀﻐﻁ
(207 kN/m
2
)
.
ﺍﺤﺴﺏ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ
.
)
5.64
(
ﻤﺎﺌﻊ ﻀﻐﻁﻪ
(1 bar)
ﻭﺤﺠﻤﻪ
(0.06 m
3
)
ﻭﻜﺘﻠﺘﻪ
(0.07 kg)
ﻭﻁﺎﻗﺘﻪ ﺍﻟﺩﺍﺨﻠﻴﺔ
(200 kJ/kg)
.
ﻀﻐﻁ
ﻐﻁﻪــﻀ ﺢﺒــﺼﺍ ﺙــﻴﺤﺒ ﹰﺎــﻴﺒﻭﺭﺘﻟﻭﺒ
(9 bar)
ﻪــﻤﺠﺤﻭ
(0.0111 m
3
)
ﺔــﻴﻠﺨﺍﺩﻟﺍ ﺔــﻗﺎﻁﻟﺍﻭ
(370 kJ/kg)
.
ﺍﺤﺴﺏ
) :
ﺃ
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل
)
ﺏ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
.
Q – W = m (
µ
2
–
µ
1
)
Q – (–13.2) = 0.07 (370 – 200)
Q = – 1.3 kJ
2
2
4
.
0
4
.
1
1
n
n
1
2
1
2
MN/m
299
.
1
kN/m
1299
298
453
300
T
T
P
P
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
kJ
3
.
37
1
-
1.35
0.077
207
-
0.014
2070
1
n
V
P
V
P
W
m
077
.
0
207
2070
014
.
0
P
P
V
V
2
2
1
1
3
35
.
1
1
n
1
2
1
1
2
=
×
×
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
kJ
-13.2
1
-
1.302
0.0111
9
-
0.06
100
1
n
V
P
V
P
W
1.302
n
5.4
n
L
n
9
Ln
0111
.
0
06
.
0
1
9
V
V
P
P
2
2
1
1
n
n
2
1
1
2
=
×
×
=
−
−
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=

)
140
(
)
5.65
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.015 m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(28.5
°C)
.
ﺘﻤﺩﺩ ﺤﺴﺏ ﺍﻟﻘﺎﻨﻭﻥ
(PV
1.35
=C)
ﺤﺘﻰ ﺍﺼﺒﺢ
ﺤﺠﻤﻪ
(0.09 m
3
)
.
ﺍﺤﺴﺏ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﺠﺩﻴﺩﺓ
.
)
5.66
(
ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(0.675 kg)
ﻭﻀﻐﻁﻪ
(1.4 MN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(280
°C)
ﺔـﻗﻼﻌﻟﺍ ﺏﺴـﺤ ﺩﺩﻤﺘ
(PV
1.3
=C)
ﺤﺘﻰ ﺍﺼﺒﺢ ﺤﺠﻤﻪ ﺍﺭﺒﻌﺔ ﺍﻀﻌﺎﻑ ﺤ
ﺠﻤﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﺍﺤﺴﺏ
)
1
(
ﺎﺌﻲـﻬﻨﻟﺍﻭ ﻲﺌﺍﺩﺘﺒﻻﺍ ﻡﺠﺤﻟﺍ
)
ﺏ
(
ﺍﻟﻀﻐﻁ ﺍﻟﻨﻬﺎﺌﻲ
)
ﺝ
(
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻬﺎﺌﻴﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R=0.278 kJ/kg.K
)
5.67
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(0.25 kg)
ﻀﻐﻁﻪ
(140 kN/m
2
)
ﻭﺤﺠﻤﻪ
(0.15 m
3
)
ﻀﻐﻁ ﺍﻟﻰ
(4MN/m
2
)
ﺴﺏـﺤ
ﺍﻟﻘﺎﻨﻭﻥ
(PV
1.25
=C)
.
ﺍﺤﺴﺏ
)
1
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗ
ﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
ﺏ
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل
)
ﺝ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cv = 0.718 kJ/kg.K
، Cp = 1.005 kJ/kg.K
R = Cp – Cv = 1.005 – 0.718 = 0.287 kJ/kg.K
C
25.4
K
4
.
298
09
.
0
015
.
0
558
V
V
T
T
1
35
.
1
1
n
2
1
1
2
o
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−
−
C
92
K
365
553
4
4
.
1
231
.
0
T
.
V
V
.
P
P
T
kN/m
231
MN/m
231
.
0
4
1
4
.
1
V
V
P
P
m
0.306
0.0765
4
V
4
V
m
0675
.
0
10
1.4
553
0.287
675
.
0
P
mRT
V
1
1
2
1
2
2
2
2
3
.
1
n
2
1
1
2
3
1
2
3
3
1
1
1
o
=
=
×
×
=
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
×
=
=
=
×
×
×
=
=
kJ
30.73
292.7)
-
(463.9
0.718
0.25
T
mCv
U
K
9
.
463
140
10
4
.
1
7
.
292
P
P
T
T
K
7
.
292
0.287
0.25
0.15
140
mR
V
P
T
25
.
1
25
.
0
3
n
1
n
1
2
1
2
1
1
1
=
×
=
∆
=
∆
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
×
×
=
=
−
(
)
kJ
-18.37
49.1
-
30.73
W
U
Q
kJ
1
.
49
1
-
1.25
463.9)
-
7
0.287(292.
0.25
1
n
T
T
mR
W
2
1
=
=
+
∆
=
−
=
×
=
−
−
=

)
141
(
)
5.68
(
ﺍﺴﻁﻭﺍﻨﺔ ﺘﺤﺘﻭﻱ ﻋﻠﻰ
(0.75 kg)
ﻤﻥ ﻤﺎﺌﻊ ﻀﻐﻁﻪ
(7 bar)
ﺘﻤﺩﺩ ﺤﺴﺏ ﺍﻟﻘﺎﻨﻭﻥ
(PV
1.37
=C
1
)
ﻰـﺘﺤ
(1.4 bar)
.
ﻓﺈﺫ
ﺍ ﻜﺎﻥ ﺤﺠﻤﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
(0.25 m
3
/kg)
ﻭﻜﺎﻨﺕ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
(33 kJ)
.
ﺍﺤﺴﺏ ﻤﻘﺩﺍﺭ
ﺍﻟﺘﻐﻴﺭ ﺒﺎﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
.
)
5.69
(
ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻜﺘﻠﺘﻪ
(2 kg)
ﺘﻤﺩﺩ ﺒﻭﻟﺘﺭﻭﺒﻴﺎﹰ ﺍﻟﻰ
)
3
(
ﺍﻀﻌﺎﻑ ﺤﺠﻤﻪ ﺍﻻﺼﻠﻲ ﻭﺍﻨﺨﻔﻀﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﻤﻥ
(300
°C)
ﺍﻟﻰ
(60
°C)
ﻭﺍﻨﺠﺯ ﺸﻐﻼﹰ ﻤﻘﺩﺍﺭﻩ
(100 kJ)
ﻭﻜﺎﻨﺕ
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻀﺎﻓﺔ
(20 kJ)
.
ﺴﺏـﺤﺍ
)
1
(
Cv
،
)
2
(
Cp
kJ
140.778
1
37
.
1
66
.
0
140
1875
.
0
700
1
n
V
P
V
P
W
m
66
.
0
4
.
1
7
25
.
0
P
P
V
V
m
1875
.
0
75
.
0
25
.
0
m
.
V
2
2
1
1
12
3
37
.
1
1
n
1
2
1
1
2
3
1
1
=
−
×
−
×
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
×
=
ν
=
kJ
-143.7
75
.
0
778
.
107
m
U
KJ
-107.778
778
.
140
33
W
Q
U
=
−
=
∆
=
µ
∆
=
−
=
−
=
∆
494
.
1
n
3
Ln
)
1
n
(
72
.
1
Ln
V
V
3
333
573
V
V
T
T
kJ/kg.K
0.166
)
573
333
(
2
80
)
T
T
(
m
U
Cv
kJ
80
100
20
W
Q
U
1
n
1
1
1
n
1
2
2
1
1
2
=
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
−
−
=
−
∆
=
−
=
−
=
−
=
∆
−
−
kJ/kg.K
0.27
0.166
0.13
Cv
R
Cp
kJ/kg.K
103
.
0
R
1
494
.
1
)
333
573
(
R
2
100
1
n
)
T
T
(
mR
W
2
1
=
+
=
+
=
=
−
−
=
−
−
=
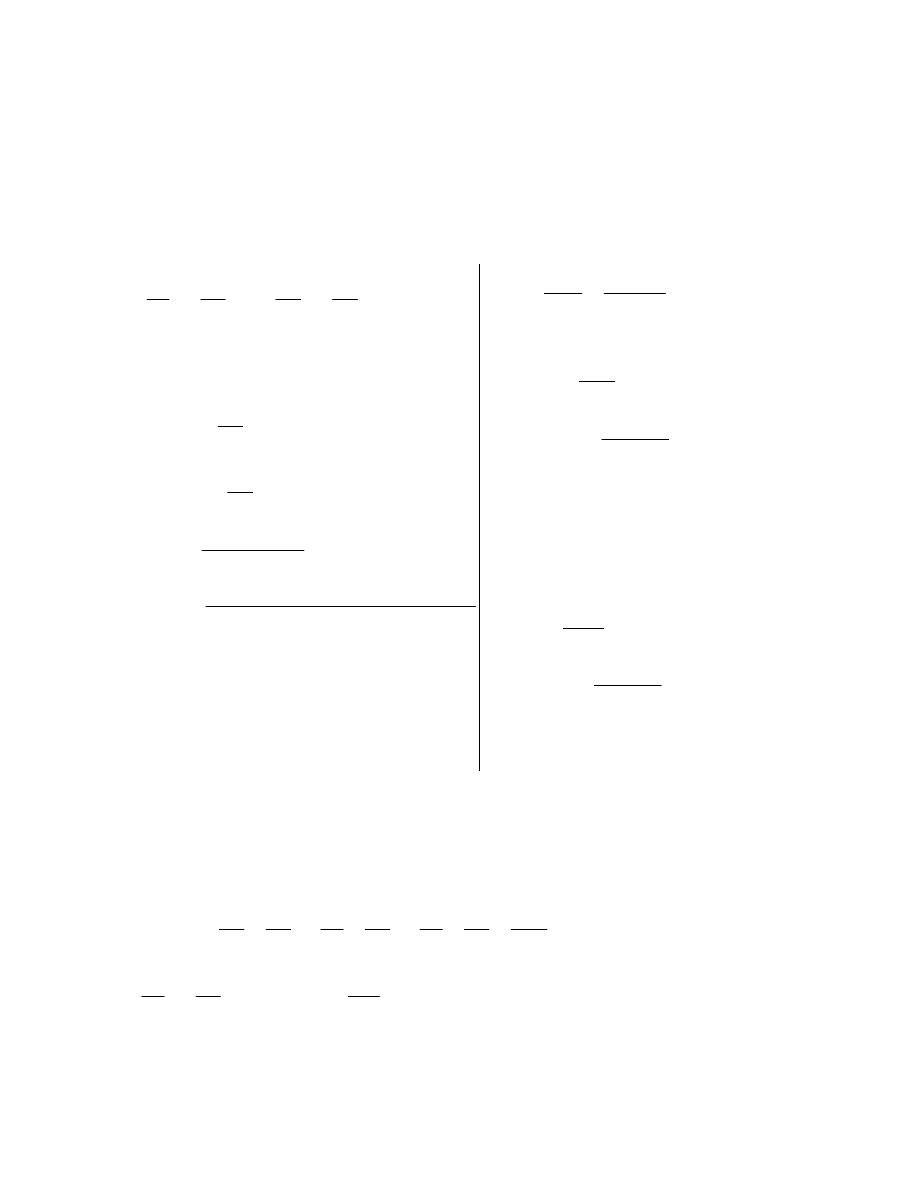
)
142
(
)
5.70
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(1.4 bar)
ﻭﺤﺠﻤﻪ
(12L)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
(100
°C)
.
ﻀﻐﻁ ﺒﻭﻟﺘﺭﻭﺒﻴﺎﹰ ﺒﺤﻴﺙ
ﺍﺼﺒﺢ ﻀﻐﻁﻪ
(28 bar)
ﻭﺤﺠﻤﻪ
(1.2 L)
.
ﺍﺤﺴﺏ
)
1
(
ﺍﻻﺱ ﺍﻟﺒﻭﻟﺘﺭﻭﺒﻲ
(n)
)
2
(
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ
ﻨﻬﺎﻴﺔ ﺍﻻﺠﺭﺍﺀ
)
3
(
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍ
ﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
)
4
(
ﺍﻟﻔﺭﻕ ﺒﺎﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺒﻴﻥ ﺍﻟﻨﻘﻁﺘﻴﻥ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
γ=1.4
،
R=0.287 kJ/kg.K
OR
)
5.71
(
ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﺤﺠﻤﻪ
(470L)
ﻀﻐﻁ ﺒﻭﻟﺘﺭﻭﺒﻴﺎﹰ ﺍﻟﻰ
(200L)
ﺜﻡ ﺒﺭﺩ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﺍﻟﻰ،
(160L)
ﺙـﻴﺤ
ﻋﺎﺩ ﺍﻟﻰ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
.
ﺍﺤﺴﺏ
(n)
.
kJ
6
.
5
1
3
.
1
10
2
.
1
2800
10
12
140
1
n
V
P
V
P
W
K
744
2
.
1
12
373
V
V
T
T
3
.
1
n
1
.
0
Ln
n
05
.
0
Ln
12
2
.
1
28
4
.
1
V
V
P
P
3
3
2
2
1
1
12
1
3
.
1
1
n
2
1
1
2
n
n
1
2
2
1
−
=
−
×
×
−
×
×
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−
−
−
-1.4
373)
-
744
(-0.2393)(
0.0157
)
T
mCn(T
Q
kg.K
-0.2393kJ/
1
3
.
1
4
.
1
3
.
1
718
.
0
1
-
n
-
n
Cv
Cn
kJ/kg.K
718
.
0
1
4
.
10
287
.
0
1
R
Cv
1
2
=
×
=
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
γ
=
=
−
=
−
γ
=
kJ
4.2
(-5.6)
-
-1.4
W
-
Q
U
kJ
4
.
1
1
4
.
1
3
.
1
4
.
1
6
.
5
1
n
W
Q
=
=
=
∆
−
=
−
−
×
−
=
−
γ
−
γ
=
(
)
1.26
n
2.35
Ln
1
-
n
1.25
Ln
200
470
25
.
1
V
V
T
T
25
.
1
16
.
0
2
.
0
V
V
T
T
V
V
T
T
T
V
T
V
3
2
1
n
1
n
2
1
1
2
3
2
1
2
3
2
3
2
3
3
2
2
=
=
⇒
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
⇒
=
⇒
=
⇒
→
−
−

)
143
(
)
5.72
(
ﺴﺭﺏـﺘﻟﺍﻭ ﻙﺎـﻜﺘﺤﻻﺍ ﻡﻴﺩـﻋ ﺱﺒﻜﻤﺒ ﺓﺯﻬﺠﻤ ﺔﻨﺍﻭﻁﺴﺍ لﺨﺍﺩ ﺯﺎﻏ
.
ﻪـﻤﺠﺤ
(0.0135m
3
)
ﻐﻁﻪـﻀﻭ
(27 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(215
°C)
.
ﺔـﻗﻼﻌﻟﺍ ﺏﺴﺤ ﺩﺩﻤﺘ
(P
ν
1.29
=C)
.
لـﻘﺘﻨﻤﻟﺍ لﻐﺸـﻟﺍ ﻥﺎـﻜ
(49 kJ)
ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
(11.9 kJ)
.
ﺍﺤﺴﺏ
)ﺃ
(
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻬﺎﺌﻴﺔ
)
ﺏ
(
γ
)
ﺝ
(
R
)
ﺩ
(
ﺔـﻠﺘﻜ
ﻋﻠ،ﺯﺎﻐﻟﺍ
ﻤﺎﹰ ﺃﻥ
:
Cp=1.03 kJ/kg.K
)
5.73
(
ﻏﺎﺯ ﻀﻐﻁﻪ
(1.032 bar)
ﻭﺤﺠﻤﻪ
(0.085 m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(38
°C)
.
ﺔـﻗﻼﻌﻟﺍ ﺏﺴـﺤ ﻁﻐﻀ
(Pv
1.3
=C)
ﺍﻟﻰ
(5.5 bar)
.
ﻋﻠﻤﺎﹰ ﺃﻥ،ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺩﺠﻭﺍ
:
Cv = 0.715 kJ/kg.K
، R=0.287 kJ/kg.K
1
mR
190
1
.
37
488
298
1
.
37
T
T
U
mCv
kJ
1
.
37
49
9
.
11
W
Q
U
K
298
T
1
29
.
1
488
T
1
0135
.
0
2700
49
1
n
T
T
1
V
P
W
1
n
T
T
V
P
V
P
1
n
V
P
V
P
W
T
T
V
P
V
P
T
V
P
T
V
P
1
2
2
2
1
2
1
1
1
2
1
1
1
1
2
2
1
1
1
2
1
1
2
2
2
2
2
1
1
1
−
γ
=
=
−
−
=
−
∆
=
−
=
−
=
−
=
∆
=
−
⎟
⎠
⎞
⎜
⎝
⎛ −
×
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
−
−
=
−
−
=
=
⇒
=
kg
246
.
0
283
.
0
0746
.
0
R
mR
m
kJ/kg.K
0.283
0.747
-
1.03
Cv
-
Cp
R
kJ/kg.K
747
.
0
38
.
0
103
Cp
Cv
38
.
1
1
0746
.
0
190
37.1
kJ/K
0746
.
0
488
0135
.
0
2700
T
V
P
mR
1
1
1
=
=
=
=
=
=
=
=
γ
=
=
γ
−
γ
=
=
×
=
=
kJ
-3.5
(-13.85)
10.35
W
U
Q
kJ
85
.
13
1
3
.
1
)
458
311
(
287
.
0
0985
.
0
1
n
)
T
mR(T
W
kJ
10.35
311)
-
(458
0.715
0.0985
T
mCv
U
K
0985
.
0
311
287
.
0
085
.
0
5
.
103
RT
V
P
m
K
458
032
.
1
5
.
5
311
P
P
T
T
2
1
1
1
1
3
.
1
1
3
.
1
n
1
n
1
2
1
2
=
+
=
+
∆
=
−
=
−
−
×
=
−
−
=
=
×
=
∆
=
∆
=
×
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−

)
144
(
)
5.74
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.1m
3
)
ﻭﻀﻐﻁﻪ
(120 kN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(25
°C)
ﻀﻐﻁ ﺍﻟﻰ
(1.2MN/m
2
)
ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.2
=C
1
)
.
ﺍﺤﺴﺏ
:
)
ﺃ
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل
)
ﺏ
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
ﺝ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R=0.285 kJ/kg.K
، Cv=0.72 kJ/kg.K
K
438
01
.
0
120
298
0147
.
0
1200
V
P
T
V
P
T
kJ
2
.
28
2
.
0
)
0147
.
0
1200
1
.
0
120
(
10
1
n
V
P
V
P
W
m
0147
.
0
1200
120
1
.
0
P
P
V
V
1
1
1
2
2
2
3
2
2
1
1
3
2
.
1
1
n
1
2
1
1
2
=
×
×
×
=
=
=
×
−
×
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
kJ
-14
28.2
-
14.2
W
U
Q
kJ
14.2
)
298
438
(
72
.
0
141
.
0
)
T
mCv(T
U
kg
141
.
0
298
285
.
0
1
.
0
120
RT
V
P
m
1
2
1
1
1
=
=
+
∆
=
=
−
×
=
−
=
∆
=
×
×
=
=

)
145
(
)
5.75
(
(1kg)
ﻐﻁﻪـﻀ ﻲﻟﺎﺜﻤ ﺯﺎﻏ ﻥﻤ
(1.1 bar)
ﻪـﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩﻭ
(27
°C)
ﺔـﻗﻼﻌﻟﺍ ﺏﺴـﺤ ﻁﻐﻀـﻴ
(PV
1.3
=C
1
)
ﺍﻟﻰ
(6.6 bar)
.
ﺍﺤﺴﺏ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ
:
)ﺃ
(
ﺍﻟﻐﺎﺯ ﺇﻴﺜﺎﻥ
(M=30)
ﻓﺈﻥ
Cp=1.75 kJ/kg.K
)
ﺏ
(
ﺍﻟﻐﺎﺯ ﺁﺭﻜﻭﻥ
(M=40)
ﻓﺈﻥ
:
Cp=0.515 kJ/kg.K
)ﺃ
(
ﺍﻴﺜﺎﻥ
)
ﺏ
(
ﺁﺭﻜﻭﻥ
K
6
.
453
1
.
1
6
.
6
300
P
P
T
T
3
.
1
1
3
.
1
n
1
n
1
2
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−
kJ/kg
5
.
84
1
188
.
1
3
.
1
188
.
1
8
.
141
1
-
n
-
W
Q
kJ/kg
3
.
141
1
3
.
1
)
6
.
453
300
(
277
.
0
1
n
)
T
T
(
R
W
188
.
1
1.473
1.75
Cp/Cv
kJ/kg.K
1.473
0.277
-
1.75
R
-
Cp
Cv
kJ/kg.K
277
.
0
30
314
.
8
M
R
R
2
1
=
−
−
−
=
γ
γ
=
−
=
−
−
=
−
−
=
=
=
=
γ
=
=
=
=
=
=
kJ/kg
4
.
59
1
678
.
1
3
.
1
678
.
1
58
.
106
1
-
n
-
W
Q
kJ/kg
5
.
106
1
3
.
1
)
6
.
453
300
(
208
.
0
1
n
)
T
T
(
R
W
678
.
1
0.307
0.515
Cp/Cv
K
.307kJ/kg.
0
0.208
-
0.515
R
-
Cp
Cv
kJ/kg.K
208
.
0
40
314
.
8
M
R
R
2
1
−
=
−
−
−
=
γ
γ
=
−
=
−
−
=
−
−
=
=
=
=
γ
=
=
=
=
=
=

)
146
(
)
5.76
(
ﺎـﻬﻤﺠﺤ ﺔﻨﺍﻭﻁﺴﺍ ﻲﻓ ﺀﺍﻭﻫ
(45000cm
3
)
ﻐﻁﻬﺎـﻀﻭ
(0.95 bar)
ﺎـﻬﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩﻭ
(121
°C)
.
ﻀﻐﻁﺕ ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
n
=C.)
ﺍﻟﻰ
(9bar)
ﻭﺍﺼﺒﺢ ﺤﺠﻤﻬﺎ
(8000 cm
3
)
.
ﺍﺤﺴﺏ
)
1
(
ﻗﻴﻤﺔ
(n)
.
)
2
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
3
(
ﻋﻠﻤﺎﹰ ﺃﻥ،ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍﻭ لﻐﺸﻟﺍ
:
Cp=1.005 kJ/kg.K
، R=0.287 kJ/kg.K
kJ/kg.K
718
.
0
287
.
0
005
.
1
R
Cp
Cv
K
6
.
678
045
.
0
95
394
008
.
0
900
V
P
T
V
P
T
1.319
n
(5.6)
n
L
n
)
9
(
Ln
008
.
0
045
.
0
1
9
V
V
P
P
1
1
1
2
2
2
n
n
2
1
1
2
=
−
=
−
=
=
×
×
×
=
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
kJ
-1.971
(-9.695)
7.73
W
U
Q
-9.695kJ
1
-
1.319
0.008
900
-
0.045
95
1
n
V
P
V
P
W
kJ
7.73
394)
-
(678.6
0.718
0.0378
)
T
mCv(T
U
kg
0378
.
0
394
0.287
0.045
95
RT
V
P
m
2
2
1
1
1
2
1
1
1
=
+
=
+
∆
=
=
×
×
=
−
−
=
=
×
=
−
=
∆
=
×
×
=
=

)
147
(
)
5.77
(
ﺯل ﺩﺭــﻴﺩ ﻙﺭـﺤﻤ ﺔﻨﺍﻭﻁــﺴﺍ لـﺨﺩ ﺀﺍﻭـﻫ
ﻪـﺘﺭﺍﺭﺤ ﺔـﺠ
(49
°C)
ﻪــﻤﺠﺤﻭ
(0.28 m
3
)
ﻐﻁﻪــﻀﻭ
(110kN/m
2
)
ﻭﻨﺴﺒﺔ ﺍﻻﻨﻀﻐﺎﻁ،
(15/1)
.
ﻴﻀﻐﻁ ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.27
=C.)
.
ﺍﺤﺴﺏ
:
)
1
(
ﺍﻟﻀﻐﻁ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ ﻨﻬﺎﻴﺔ ﺍﻻﻨﻀﻐﺎﻁ
) .
2
(
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ ﻋﻠ
ﻤﺎ
ﺃﻥ
:
Cp=1.0 kJ/kg.K ، Cv=0.71 kJ/kg.K
)
5.78
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(1 kg)
ﻀﻐﻁﻪ
(1 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﻀﻐﻁ ﺍﻟﻰ
(1/4)
ﺩﺍﺌﻲـﺘﺒﻻﺍ ﻪـﻤﺠﺤ
.
ﻀﻐﺎﻁـﻨﻻﺍ ﻡـﺘ ﺍﺫﺇ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ ﻡﺠﺤﻭ ﻁﻐﻀ ﻥﻤ ﺔﻴﺌﺎﻬﻨﻟﺍ ﺀﺍﻭﻬﻟﺍ ﺔﻟﺎﺤ ﺏﺴﺤﺇ
)ﺃ
(
ﻲـﻠﻤﺭﺜﻭﺯﻴﺍ
)
ﺏ
(
ﺒﻭﻟﺘﺭﻭﺒﻲ ﻭﺍﻥ
(n=1.25)
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp=1 kJ/kg.K
، Cv=0.71 kJ/kg.K
R = Cp – Cv
= 1 – 0.71 = 0.29 kJ/kg.K
)ﺃ
(
)
ﺏ
(
kJ/kg.K
29
.
0
71
.
0
1
Cv
Cp
R
kg
33
.
0
322
0.29
0.28
110
RT
V
P
m
K
96
.
668
1
15
322
V
V
T
T
kN/m
163
.
31
1
15
110
V
V
P
P
1
1
1
1
27
.
1
1
n
2
1
1
2
2
27
.
1
n
2
1
1
2
=
−
=
−
=
=
×
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−
kJ
-41.973
1
41
.
1
27
.
1
41
.
1
92
.
122
1
-
n
-
W
Q
1.41
1/0.71
Cp/Cv
kJ
92
.
122
1
-
1.27
395.96)
-
(49
0.29
33
.
0
1
n
)
T
T
(
mR
W
2
1
=
−
−
−
=
γ
γ
=
=
=
=
γ
−
=
×
=
−
−
=
2
2
2
2
3
1
2
3
1
1
1
m
/
kN
400
0.2124
293
0.29
1
V
mRT
P
m
2124
.
0
4
85
.
0
4
V
V
m
85
.
0
100
293
0.29
1
P
mRT
V
=
×
×
=
=
=
=
=
=
×
×
=
=
3
25
.
0
1
1
n
1
2
1
1
2
2
25
.
1
n
2
1
1
2
1
25
.
1
1
1
n
1
2
1
1
2
m
2123
.
0
43
.
414
293
8497
.
0
T
T
V
V
kN/m
7
.
565
)
4
(
100
V
V
P
P
K
427
.
414
)
4
(
293
V
V
T
T
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−
−

)
148
(
)
5.79
(
(0.8 kg)
ﻤﻥ ﺍﻭﻜﺴﺠﻴﻥ ﺘﺤﺕ ﻀﻐﻁ
(1000 kN/m
2
)
ﻭﺤﺠﻡ
(0.06 m
3
)
.
ﻴﻥـﻌﻤ ﺀﺍﺭﺠﺄﺒ ﻡﺎﻴﻘﻟﺍ ﺩﻌﺒ
ﻐﻁﻪــﻀ ﺢﺒــﺼﺍ
(305 kN/m
2
)
ﻪــﻤﺠﺤﻭ
(0.14 m
3
)
.
ﺕــﻨﺎﻜ ﺍﺫﺈــﻓ
Cv=0.65 kJ/kg.K
،
R=0.26 kJ/kg.K
.
ﺍﺤﺴﺏ
)ﺃ
(
ﻨﻭﻋﻴﺔ ﺍﻻﺠﺭﺍﺀ
)
ﺏ
(
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
) .
ﺝ
(
ـﻑ ﺴـﻴﻜ
ﻴ
ﻜﻭﻥ
ﻨﻭﻋﻴﺔ ﺍﻻﺠﺭﺍﺀ ﻟﻭ ﺍﺼﺒﺢ ﺍﻟﻀﻐﻁ
(305 kN/m
2
)
ﻭﺍﻟﺤﺠﻡ
(0.197m
3
)
ﺫﻜﻭﺭﺓـﻤﻟﺍ ﻡﻴـﻘﻟﺍ ﻥـﻤ ﹰﻻﺩـﺒ
ﻭﺍﺤﺴﺏ ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
.
ﻓﻨﺤﺴﺏ،ﻡﻭﻠﻌﻤ ﺭﻴﻏ ﺀﺍﺭﺠﻻﺍ ﻥﺍ ﺎﻤﺒ
n
∴
ﺍﻻﺠﺭﺍﺀ ﺍﻴﺯﻭﺜﺭﻤﻠﻲ
:
0
Q
kJ
43.25
1
-
1.4
0.14
305
-
0.06
1000
1
V
P
W
n
4
.
1
65
.
0
65
.
0
26
.
0
Cv
Cv
R
4
.
1
n
14
.
0
06
.
0
1000
305
V
V
P
P
12
1
1
12
n
n
2
1
1
2
=
=
×
×
=
−
γ
=
=
=
+
=
+
=
γ
=
⇒
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
1
n
197
.
0
06
.
0
1000
305
V
V
P
P
n
n
2
1
1
2
=
⇒
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
′
=
′
kJ
33
.
71
0.06
0.197
n
L
288
0.26
0.8
V
V
n
L
mRT
W
Q
K
46
.
288
0.26
0.8
0.06
1000
mR
V
P
T
2
2
1
2
1
2
1
1
1
1
=
×
×
=
=
=
=
×
×
=
=
′
′
′

)
149
(
)
5.80
(
ﻐﻁﻪــﻀ ﺯﺎــﻏ
(1MN/m
2
)
ﻪــﻤﺠﺤﻭ
(0.003 m
3
)
ﺔــﻗﻼﻌﻟﺍ ﺏﺴــﺤ ﺩﺩــﻤﺘ
(PV
1.3
=C.)
ﻰــﻟﺍ
(0.1MN/m
2
)
.
ﻋﻠﻤﺎﹰ ﺃﻥ،ﺔﻤﺎﻌﻟﺍ ﺔﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭﺤﻟﺍﻭ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺏﺴﺤﺍ
:
Cv=0.718 kJ/kg.K
،
γ=1.4
)
5.81
(
ﺎـﻫﺭﻁﻗ ﺔﻠﻴﻭﻁ ﺔﻴﺩﻭﻤﻋ ﺔﻨﺍﻭﻁﺴﺍ
(600 mm)
ﻰـﻠﻋ ﻱﻭـﺘﺤﺘ
(0.085 m
3
)
ﻐﻁـﻀ ﺀﺍﻭـﻬﻟﺍ ﻥـﻤ
(1MN/m
2
)
ﻪـﺘﻠﺘﻜ ﻙﺎﻜﺘﺤﻻﺍ ﻡﻴﺩﻋ ﺱﺒﻜﻤﺒ ﺔﻨﺍﻭﻁﺴﻻﺍ ﻲﻓ ﺭﻭﺼﺤﻤ ﺀﺍﻭﻬﻟﺍﻭ
(90kg)
ﻪـﺘﻼﻔﻨﺍ ﺩـﻨﻋ
ﺍﺤﺴﺏ ﺴﺭﻋﺘﻪ ﻋﻨﺩ ﺇﺭﺘﻔﺎﻋﻪ ﻤﺴﺎﻓﺔ،ﻰﻠﻋﻻﺍ ﻰﻟﺍ ﹰﺎﻴﺩﻭﻤﻋ ﺱﺒﻜﻤﻟﺍ ﻙﺭﺤﺘﻴ
(1.2m)
ﻲـﻓ ﺀﺍﻭـﻬﻟﺍ ﻁﻐﻀﻭ
ﺍﻻﺴﻁﻭﺍﻨﺔ
.
ﻴﺘﻤﺩﺩ ﺍﻟﻬﻭﺍﺀ ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.35
=C.)
.
ﺎـﻬﻟﺎﻤﻫﺍ ﻥﻜﻤﻴ ﺀﺍﻭﻬﻟﺍ ﺔﻋﺭﺴ ﻥﺍﻭ
.
ﻀﻐﻁـﻟﺍﻭ
ﺍﻟﺠﻭﻱ ﻓﻭﻕ ﺍﻟﻤﻜﺒﺱ ﻫﻭ
(0.103 MN/m
2
)
.
kJ/kg.K
239
.
0
1
3
.
1
3
.
1
4
.
1
718
.
0
1)
-
(n
n)
-
(
Cv
Cn
kJ
03
.
1
1
-
1.3
0.0176
0.1
-
0.003
1
1
-
1.4
1.3
-
1.4
1
n
V
P
V
P
1
n
W
1
n
Q
m
0176
.
0
1
.
0
1
003
.
0
P
P
V
V
2
2
1
1
3
3
.
1
1
n
1
2
1
1
2
=
−
−
=
γ
=
=
×
×
×
=
−
−
×
−
γ
−
γ
=
×
−
γ
−
γ
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
J
1060
1.2
9.81
90
mgz
PE
MJ
1049
.
0
1
-
1.35
0.424
0.114
-
0.085
1
1
n
V
P
V
P
W
MN/m
114
.
0
424
.
0
085
.
0
1
V
V
P
P
2
2
1
1
2
35
.
1
35
.
1
2
1
1
2
=
×
×
=
=
∆
=
×
×
=
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
m/s
3
.
39
1545
90
2.69540
C
J
69540
J
10
10
1060
0343
.
0
1049
.
0
2
mc
MJ
0343
.
0
2
.
1
4
0.6
0.103
L
.
4
D
.
.
P
L
.
A
.
P
V
.
P
W
6
6
2
2
2
atm
atm
atm
=
=
=
∴
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
=
×
×
π
=
π
=
=
=
3
2
1
2
1
2
m
424
.
0
085
.
0
2
.
1
4
6
.
0
V
L
.
4
D
.
V
L
.
A
V
=
+
×
×
π
=
+
π
=
+
=

)
150
(
)
5.82
(
ﺍﺴﻁﻭﺍﻨﺔ ﺘﺤﺘﻭﻱ ﻋﻠﻰ
(0.085 m
3
)
ﻤﻥ ﻏﺎﺯ ﻀﻐﻁﻪ
(1.032 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(38
°C)
ﻴﻀﻐﻁ،
ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.3
=C
.
)
ﺍﻟﻰ
(5.5 bar)
.
ﻋﻠﻤﺎﹰ ﺃﻥ،ﺔﻠﻘﺘﻨﻤﻟﺍ ﺔﻴﺭﺍﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ ﺩﺠﻭﺃ
:
R=0.287 kJ/kg.K
،
Cv=0.75 kJ/kg.K
)
5.83
(
ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(0.013 kg)
ﻤﻭﺠﻭﺩ ﺩﺍﺨل ﺍﺴﻁﻭﺍﻨﺔ ﻨﺴﺒﺔ ﺇﻨﻀﻐﺎﻁﻬﺎ
(14/1)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘ
ﺎـﻬ
(100
°C)
ﻋﻨﺩﻤﺎ ﺘﻜﻭﻥ ﺍﻟﻌﻤﻠﻴﺔ ﺒﻭﻟﺘﺭﻭﺒﻴﺔ ﻭﺘﺨﻀﻊ ﻟﻠﻘﺎﻨﻭﻥ
(PV
1.3
=C.)
.
ﺍﺤﺴﺏ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp=0.72 kJ/kg.K
،
R=0.28 kJ/kg.K
kJ
35
.
10
311)
-
(458
0.715
0985
.
0
)
T
mCv(T
U
kg
0985
.
0
311
0.287
0.085
5
.
103
RT
V
P
m
K
458
032
.
1
5
.
5
311
P
P
T
T
1
2
1
1
1
3
.
1
1
3
.
1
n
1
n
1
2
1
2
=
×
=
−
=
∆
=
×
×
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−
kJ
-3.5
(-13.85)
10.35
W
U
Q
kJ
-13.85
1
-
1.3
458)
-
(311
0.287
0.0985
1
n
)
T
T
(
mR
W
2
1
=
+
=
+
∆
=
=
×
=
−
−
=
kJ
-5.463
1
-
1.3
823.28)
-
(373
0.28
013
.
0
1
n
)
T
T
(
mR
W
K
28
.
823
)
14
(
373
V
V
T
T
1.636
0.72/0.44
Cp/Cv
kJ/kg.K
44
.
0
28
.
0
72
.
0
R
Cp
Cv
2
1
3
.
0
1
n
2
1
1
2
=
×
=
−
−
=
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
γ
=
−
=
−
=
−
kJ
-2.886
1
636
.
1
3
.
1
636
.
1
)
463
.
5
(
1
n
W
Q
=
−
−
×
−
=
−
γ
−
γ
=

)
151
(
)
5.84
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.14m
3
)
ﻭﻀﻐﻁﻪ
(1.38 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(38
°C)
ﺴﺏـﺤﻭ ﹰﺎـﻴﺒﻭﺭﺘﻟﻭﺒ ﻁﻐﻀﻴ
ﺍﻟﻌﻼﻗﺔ
(PV
1.35
=C.)
ﺍﻟﻰ
(8.7bar)
.
ﺍﺤﺴﺏ
)
1
(
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
)
2
(
ﺔـﻗﺎﻁﻟﺍ ﻲـﻓ ﺭﻴﻐﺘﻟﺍ
ﺍﻟﺩﺍﺨﻠﻴﺔ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R=0.264 kJ/kg.K
،
γ=1.4
)
5.85
(
ﺍﺴﻁﻭﺍﻨﺔ ﺘﺤﺘﻭﻱ ﻋﻠﻰ
(0.07 kg)
ﻤﻥ ﻤﺎﺌﻊ ﻀﻐﻁﻪ
(1 bar)
ﻭﺤﺠﻤﻪ
(0.06 m
3
)
ﻭﻁﺎﻗﺔ ﺩﺍﺨﻠﻴﺔ ﻨﻭﻋﻴﺔ
(200 kJ/kg)
.
ﻀﻐﻁ ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
n
=C.)
ﻐﻁﻪـﻀ ﺢﺒﺼﺍ ﻰﺘﺤ
(9 bar)
ﻪـﻤﺠﺤﻭ
(0.0111
m
3
)
ﻭﻁﺎﻗﺔ ﺩﺍﺨﻠﻴﺔ ﻨﻭﻋﻴﺔ
(370 kJ/kg)
.
؟ﺍﺤﺴﺏ ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
kJ
-33.788
1
35
.
1
0358
.
0
870
14
.
0
138
1
n
V
P
V
P
W
m
0358
.
0
870
138
14
.
0
P
P
V
V
2
2
1
1
12
3
35
.
1
1
n
1
2
1
1
2
=
−
×
−
×
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
kJ
564
.
29
33.788
-4.223
W
-
Q
U
kJ
-4.223
1
4
.
1
35
.
1
4
.
1
788
.
33
1
n
W
Q
12
12
=
+
=
=
∆
=
−
−
=
−
γ
−
γ
×
=
kJ
2
.
13
1
-
1.302
0.011
900
-
0.06
100
1
n
V
P
V
P
W
302
.
1
n
0.06
0.0111
n
L
n
9
1
Ln
06
.
0
0111
.
0
9
1
V
V
P
P
2
2
1
1
n
n
1
2
2
1
−
=
×
×
=
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
kJ
-1.3
(-13.2)
11.9
W
U
Q
kJ
9
.
11
)
200
370
(
07
.
0
m
U
=
+
=
+
∆
=
=
−
=
µ
∆
=
∆

)
152
(
)
5.86
(
ﺍﺜﺒﺕ ﺍﻥ،ﻲﺘﺎﺒﺎﻴﺩﻻﺍ ﺀﺍﺭﺠﻻﺍ ﻲﻓ
)
Cv
Cp
=
γ
.(
Cv
Cp
Cv
Cv
Cv
Cp
1
Cv
Cv
Cp
1
Cv
R
Cv
R
1
=
γ
+
−
=
+
−
=
+
=
γ
=
−
γ
Cv
1
R
)
T
T
(
Cv
1
)
T
T
(
R
w
w
q
1
2
1
2
=
−
γ
−
=
−
γ
−
µ
∆
=
−
µ
∆
=
−
)
5.87
(
ﻓﻲ ﺍﺠﺭﺍﺀ ﺍﺩﻴﺒﺎﺘﻲ
.
ﺍﺫﺍ ﻜﺎﻥ
)
U
H
H
(
1
2
γ
=
−
.
ﺍﺜﺒﺕ ﺍﻥ
)
Cp=Cp
(
Cp
Cp
Cp
Cv
Cp
Cv
T
mCp
T
mR
T
mCv
)
T
T
(
mCp
)
T
T
(
mR
U
)
T
T
(
mCv
Cv
Cp
)
V
P
U
(
)
V
P
U
(
U
H
H
1
2
1
2
1
2
1
1
1
2
2
2
1
2
=
∴
=
−
+
∆
=
∆
+
∆
=
+
∆
−
=
+
−
+
γ
=
−
−
−
)
5.88
(
ﻓﻲ ﺍﺠﺭﺍﺀ ﺍﺩﻴﺒﺎﺘﻲ
.
ﺍﺜﺒﺕ ﺍﻥ
)
R=Cp-Cv
(
Cv
Cp
R
)
Cv
Cv
Cp
(
Cv
)
1
Cv
Cp
(
Cv
)
1
(
Cv
R
−
=
−
=
−
=
−
γ
=
T
mCv
1
T
mR
U
1
V
P
V
P
U
W
U
W
Q
1
1
2
2
∆
=
−
γ
∆
∆
=
−
γ
−
∆
=
−
∆
=
−

)
153
(
ﻤﺴﺎﺌل
)
5.11
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(1 kg)
ﻤﻭﺠﻭﺩ ﺘﺤﺕ ﻀﻐﻁ
(1 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺓ
(20
°C)
ﻀﻐﻁ ﺍﻟﻐﺎﺯ ﺍﻟﻰ
)
4
1
(
ﺤﺠﻤﻪ
ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﺭﺍﺀـﺠﺍ ﻲﻓ ﻁﺎﻐﻀﻨﻻﺍ ﻡﺘ ﺍﺫﺇ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ ﻡﺠﺤﻭ ﻁﻐﻀ ﻥﻤ ﺔﻴﺌﺎﻬﻨﻟﺍ ﺀﺍﻭﻬﻟﺍ ﺔﻟﺎﺤ ﺏﺴﺤﺍ
)ﺃ
(
ﺍﻴﺯﻭﺜﺭﻤﻠﻲ
)
ﺏ
(
ﺒﻭﻟﺘﺭﻭﺒﻲ ﻭﺒﻘﻴﻤﺔ ﺒﻭﻟﺘﺭﻭﺒﻴﺔ ﻤﻘﺩﺍﺭﻫﺎ
)
1.25
.(
ﺔـﻤﻴﻗ لﻗﺍ لﻐﺸﻠﻟ ﻥﻭﻜﻴﺴ ﺀﺍﺭﺠﺍ ﻱﺃ ﻲﻓ
.
ﻗﺎﺭﻥ ﺫﻟﻙ ﻤﻊ ﺍﻟﺭﺴﻡ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp=1 kJ/kg.K
، Cv=0.71 kJ/kg.K
ﺝ
:
)
0.85 m
2
،
0.2124 m
3
،
4 bar
،
-117.8 kJ
،
5.657 bar
،
414.36 K
،
-140.78 kJ
(
)
5.12
(
ﻜﻤﻴﺔ ﻤﻥ ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(1 kg)
ﻭﺤﺠﻤﻪ
(0.1 m
3
)
ﻓﻲ ﻨﻅﺎ ﻤﻐﻠﻕ
.
ﻰـﺘﺤ ﺕﺒﺎﺜ ﻁﻐﻀ ﺕﺤﺘ ﻪﻨﻴﺨﺴﺘﺒ ﺩﺩﻤﺘ
ﺍﺯﺩﺍﺩﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺒﻤﻘﺩﺍﺭ
(50
°C)
ﻭﺘﻀﺎﻋﻑ ﺤﺠﻤﻪ
.
ﻭﻜﺎﻨﺕ ﻗﺭﺍﺀﺓ ﺍﻟﻤﺎﻨﻭﻤﺘﺭ ﺍﻟﻤﺭ
ﺎﻡـﻅﻨﻟﺍ ﻲﻓ ﻁﻭﺒ
(20 cmHg)
.
ﻭﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻻﺠﺭﺍﺀ ﻜﺎﻨﺕ ﻗﺭﺍﺀﺓ ﺍﻟﺒﺎﺭﻭﻤﻴﺘﺭ
(1.01 bar)
.
ﻲـﻓ ﺭـﻴﻐﺘﻟﺍ ﺭﺍﺩـﻘﻤ ﺏﺴﺤﺍ
ﺍﻻﻨﺜﺎﻟﺒﻲ ﻟﻬﺫﺍ ﺍﻻﺠﺭﺍﺀ ﻭﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
δHg = 13600 kg/m
3
، Cv=0.7 kJ/kg.K
ﺝ
:)
37 kJ
،
12.77 kJ
(
)
5.13
(
ﺍﺴﻁﻭﺍﻨﺔ ﻤﺤﺭﻙ ﺩﻴﺯل
.
ﻀﻐﻁﻬﺎ
(0.95 bar)
ﻭﺤﺠﻤﻬﺎ
(14L)
ﺎـﻬﺘﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ
(100
°C)
.
ﺴﺒﺔـﻨﻟﺍ
ﺍﻟﺤﺠﻤﻴﺔ ﻟﻸﻨﻀﻐﺎﻁ
)
1
14
(
.
ﺍﺤﺴﺏ
:
)
1
(
ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ
)
2
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
)
3
(
ﻀﻐﺎﻁـﻨﺍ ﺔـﻴﻠﻤﻋ ﺀﺎـﻨﺜﺍ ،ﺔـﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭـﺤﻟﺍ
ﻋﻠﻤﺎﹰ ﺃﻥ،ﺔﻴﺒﻭﺭﺘﻟﻭﺒ
:
n=1.3
، Cp=0.72 kJ/kg.K ، R=0.28 kJ/kg.K
ﺝ
:
)
-5.352 kJ
،
2.516 kJ
،
-2.818 kJ
(

)
154
(
)
5.14
(
ﻫﻭﺍﺀ ﻀﻐﻁﻪ
(1.2 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C))
ﻪـﻤﺠﺤ ﺢﺒـﺼﺍ ﺙـﻴﺤﺒ ﻁﻐﻀـﻟﺍ ﺕﻭﺒﺜﺒ ﻥﺨﺴ
(0.4 m
3
)
.
ﺜﻡ ﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺤﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(35
°C))
.
ﻲـﻓ لـﻘﺘﻨﻤﻟﺍ لﻐﺸـﻟﺍ ﻥﺎﻜﻭ
ﺍﻻﺠﺭﺍﺌﻴﻥ ﻤﺘﺴﺎﻭﻱ ﻓﺈﺫﺍ ﻋﻠﻤﺕ ﺃﻥ
:
Cv=0.717 kJ/kg.K
،
Cp=1.005 kJ/kg.K
.
ﺍﺤﺴﺏ
) :
1
(
ﺤﺠﻡ ﺍﻟﻐﺎﺯ ﻓﻲ ﺍﻟﺒﺩﺍﻴﺔ
)
2
(
ﻜﻤﻴﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻟﻸﺠﺭﺍﺀﻴﻥ
)
3
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
ﻟﻸﺠﺭﺍﺀﻴﻥ
.
ﺝ
:
)
0.368 m
3
،
13.2 kJ
،
9.42 kJ
،
-3.77 kJ
(
)
5.15
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(0.2 kg)
ﻭﻀﻐﻁﻪ
(1.5 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(17
°C))
.
ﺴﺏـﺤﻭ ﹰﺎـﻴﺒﻭﺭﺘﻟﻭﺒ ﻁﻐـﻀ
ﺍﻟﻌﻼﻗﺔ
(PV
1.25
=C.)
ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺢ ﻀﻐﻁﻪ ﻀﻌﻑ ﻤﺎ ﻜﺎﻥ ﻋﻠﻴﻪ ﻓﻲ ﺍﻟﺒﺩﺍﻴﺔ
.
ﺭﺍﺀـﺠﺇ ﻲﻓ ﺩﺩﻤﺘ ﻙﻟﺫ ﺩﻌﺒ
ﺍﻴﺯﻭﺜﺭﻤﻠﻲ ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺢ ﺤﺠﻤﻪ
(0.13 m
3
)
.
ﺍﺤﺴﺏ
)
1
(
ﻀﻐﺎﻁـﻨﻻﺍ ﺩﻌﺒ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ
)
2
(
ﺸﻐلـﻟﺍ
ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ ﻋﻨﺩ ﺍﻻﻨﻀﻐﺎﻁ
)
3
(
ﻀﻐﻁ ﺍﻟﻐﺎﺯ ﺒﻌﺩ ﺍﻟﺘﻤﺩﺩ
)
4
(
ﺩﺩـﻤﺘﻟﺍ ﺩـﻨﻋ ﺔـﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭـﺤﻟﺍ
ﻭﺍﺘﺠﺎﻫﻬﺎ
.
ﻋﻠ
ﻤﺎﹰ ﺃﻥ
:
Cv = 0.717 kJ/kg.K
، Cp = 1.005 kJ/kg.K
ﺝ
:
331 K)
،
-9.9 kJ
،
-3.71 kJ
،
1.47 bar
،
13.64 kJ
(
)
5.16
(
ﻏﺎﺯ ﻜﺘﻠﺘﻪ
(0.5 kg)
ﻤﻭﺠﻭﺩ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ
.
ﻐﻁـﻀ ﻥـﻤ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﺩﺩﻤﺘ
(5 bar)
ﺭﺍﺭﺓـﺤ ﺔـﺠﺭﺩﻭ
(100
°C)
ﺍﻟﻰ ﻀﻐﻁ
(1.89 bar)
ﺒﺤﻴﺙ ﺍﺼﺒﺢ ﺤﺠﻤﻪ ﻀﻌﻑ ﻤﺎ ﻜﺎﻥ ﻋﻠﻴﻪ،
ﺩﺩـﻤﺘ ﻡـﺜ ،ﺔـﻴﺍﺩﺒﻟﺍ ﻲﻓ
ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ ﺍﻟﻰ
(1 bar)
.
ﻓﺄﺫﺍ ﻜﺎﻨﺕ
(Cv=0.71 kJ/kg.K)
.
ﻲـﻁﻁﺨﻤ ﻰـﻠﻋ ﺕﺍﺀﺍﺭـﺠﻻﺍ ﻡـﺴﺭﺍ
(P-V)
ﻭ
(T-S)
ﻭﺍﺤﺴﺏ
)
1
(
ﺤﺠﻡ ﺍﻟﻐﺎﺯ ﻓﻲ ﺒﺩﺍﻴﺔ ﻭﻨﻬﺎﻴﺔ ﺍﻻﺠﺭﺍﺀ ﺍﻻﺩﻴﺎﺒﺎﺘﻲ
)
2
(
ﺭﺍﺭﺓـﺤﻟﺍﻭ لﻐﺸﻟﺍ
ﺍﻟﻤﻨﺘﻘﻠﻴﻥ ﻓﻲ ﺍﻻﺠﺭﺍﺀﻴﻥ
)
3
(
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻸﺠﺭﺍﺀﻴﻥ
.
ﺝ
:
)
0.107 m
3
،
0.213 m
3
،
32.57 kJ
،
25.63 kJ
،
-32.33 kJ
،
0
(
)
5.17
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.03 m
3
)
ﻭﻀﻐﻁﻪ
(1 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
ﻴﻀﻐﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺍﻟﻰ
( )
4
1
ـ ﺤﺠﻤ
ﻪ
ﺍﻻﻭل
.
ﺜﻡ ﻴﺒﺭﺩ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﺍﻟﻰ ﺍﻥ ﺘﻌﻭﺩ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
.
ﺜﻡ ﻴﺘﻤﺩﺩ ﻓﻲ ﺍﺠﺭﺍﺀ ﺍﺩﻴﺎﺒﺎﺘﻲ ﺍ
ﻰـﻟ
ﻀﻐﻁ
(1 bar)
.
ﻓﺈﺫﺍ ﻋﻠﻤﺕ ﺍﻥ
(
γ=1.4)
.
ﺍﺭﺴﻡ ﺍﻻﺠﺭﺍﺀﺍﺕ ﻋﻠﻰ ﻤﺨﻁﻁﻲ
(P-V)
ﻭ
(T-S)
ﻭﺍﺤﺴﺏ
:
)
1
(
ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺤﺠﻡ ﻓﻲ ﻨﻬﺎﻴﺔ ﺍﻟﺘﻤﺩﺩ
)
2
(
ﺼﺎﻓﻲ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل ﻓﻲ ﺍﻻﺠﺭﺍﺀﺍﺕ
.
ﺝ
:
165.4 K)
،
0.01723 m
3
،
-4.75 kJ
(

)
155
(
)
5.18
(
ﺍﺴﻁﻭﺍﻨﺔ ﺘﺤﺘﻭﻱ ﻋﻠﻰ ﻏﺎﺯ ﻀﻐﻁﻪ
(1 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(27
°C))
:
) ﺃ
(
ﺍﺜﻨﺎﺀ ﺍﻟﻌﻤﻠﻴﺔ
A
ﻭﺕـﺒﺜﺒ ﺩﺩـﻤﺘﻴ ﻙـﻟﺫ ﺩﻌﺒﻭ ﻁﻐﻀﻟﺍ ﻑﻋﺎﻀﺘﻴ ﻰﺘﺤ ﻡﺠﺤﻟﺍ ﻭﺕﺒﺜﺒ ﺓﺭﺍﺭﺤ ﻑﺎﻀﺘ
ﺍﻟﻀﻐﻁ ﺤﺘﻰ ﻴﺼﺒﺢ ﺍﻟﺤﺠﻡ
)
3
(
ﺍﻀﻌﺎﻓﻪ
.
)
ﺏ
(
ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻟﻌﻤﻠﻴﺔ
B
ﻡـﺠﺤﻟﺍ ﺢﺒﺼـﻴ ﻰـﺘﺤ ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ ﺩﺩﻤﺘﻴ ﺎﻬﺴﻔﻨ ﺔﻟﺎﺤﻟﺎﺒﻭ ﺯﺎﻐﻟﺍ ﺱﻔﻨ
)
3
(
ﺒﻌﺩ ﺫﻟﻙ ﺘﻀﺎﻑ ﺤﺭﺍﺭﺓ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺤﺘﻰ ﻴﻠﺘﻘﻲ ﻤﻊ ﺍﻟﺤﺎﻟﺔ،ﻑﺎﻌﻀﺍ
ﺔـﻴﻠﻤﻌﻠﻟ ﺔﻴﺌﺎﻬﻨﻟﺍ
A
.
ﺴﺏـﺤﺍ
ﻟﻠﻜﻴﻠﻭﻏﺭﺍﻡ ﺍﻟﻭﺍﺤﺩ ﻭﻟﻜﻼ ﺍﻟﻌﻤﻠﻴﺘﻴﻥ
) :
1
(
ﺼﺎﻓﻲ ﺍﻟﺤﺭﺍﺭﺓ
)
2
(
ﺼﺎﻓﻲ ﺍﻟﺸﻐل
)
3
(
ﺔـﻗﺎﻁﻟﺍ ﻲﻓ ﺭﻴﻐﺘﻟﺍ
ﺍﻟﺩﺍﺨﻠﻴ
ﻪ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cv = 0.744 kJ/kg.K
، R = 0.297 kJ/kg.K
ﺝ
:
)1472.4kJ/kg
، 356.4kJ/kg
، 1116kJ/kg
، 1294.2kJ/k.g, 178.2kJ/kg
، 1116 kJ/kg (
)
5.19
(
ﻫﻭﺍﺀ ﻜﺘﻠﺘﻪ
(0.5 kg)
ﻭﻀﻐﻁﻪ
(1.2 bar)
ﻭﺤﺠﻤﻪ
(0.4 m
3
)
.
ﺜﻡ ﻴﻀﻐﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ،ﹰﺎﻴﻠﻤﺭﺜﻭﺯﻴﺍ ﻁﻐﻀﻴ
ﺒﺤﻴﺙ ﺘﺼﺒﺢ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(200
°C)
.
ﺍﺤﺴﺏ ﺤﺠﻡ ﺍﻟﻬﻭﺍﺀ ﻓﻲ ﻨﻬﺎﻴﺔ ﻜل ﻤﻥ ﺍﻻﺠﺭﺍﺀﻴﻥ ﺍﺫﺍ ﻜﺎﻥ ﺍﻟﺸﻐل
ﻓﻲ ﺍﻻﺠﺭ
ﺍﺌ
ﻴﻥ
ﻤﺘﺴﺎﻭﻱ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
R=0.287 kJ/kg.K
ﺝ
:
)
0.142 m
3
،
0.06 m
3
(
)
5.20
(
ﻏﺎﺯ ﺤﺠﻤﻪ
(0.3m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(20
°C)
ﻭﻀﻐﻁﻪ
(1bar)
.
ﺭﺍﺭﺓـﺤﻟﺍ ﻥـﻤ ﺔﻴﻤﻜ ﻪﻴﻟﺍ ﺕﻔﻴﻀﺃ
ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺤﺕ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(100
°C)
.
ﺩﺍﺭﻫﺎـﻘﻤ ﻁﻐﻀـﻟﺍ ﺕﻭﺒﺜﺒ ﺓﺭﺍﺭﺤ ﺕﺤﺭﻁ ﻡﺜ
ﻨﺼﻑ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ ﺍﻟﺘﻲ ﺍﻀﻴﻔﺕ ﻓﻲ ﺍﻻﺠﺭﺍﺀ ﺍﻻﻭل
.
ﻓﺎﺫﺍ ﻋﻠﻤﺕ ﺍﻥ
(
γ=1.4)
.
ﺭﺍﺀﺍﺕـﺠﻻﺍ ﺢﻀﻭ
ﻋﻠﻰ
ﻤﺨﻁﻁﻲ
(P-V)
ﻭ
(T-S)
.
لـﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍ ﺭﺍﺩﻘﻤﻭ ﺯﺎﻐﻠﻟ ﻲﺌﺎﻬﻨﻟﺍ ﻡﺠﺤﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺏﺴﺤﺍﻭ
ﺨﻼل ﻜل ﺇﺠﺭﺍﺀ
.
ﺝ
:
)
344.3 K
،
0.277 m
3
،
-29.37 kJ
(

)
156
(
)
5.21
(
(1kg)
ﻤﻥ ﺍﻟﻬﻭﺍﺀ ﺩﺍﺨل ﺍﺴﻁﻭﺍﻨﺔ ﻀﻐﻁﻪ ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(1 bar)
ﻭ
(15
°C)
ﻋﻠﻰ ﺍﻟﺘﻭﺍﻟﻲ
.
ﻀﻐﻁـﻴ
ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺍﻟﻰ
( )
4
1
ﺤﺠﻤﻪ ﺍﻻﻭل
.
ﻓﺈﺫﺍ ﻜﺎﻥ ﺍﻻﻨﻀﻐﺎﻁ
)
1
(
ﺔـﻗﻼﻌﻟﺍ ﻕـﻓﻭ ﹰﺎﻴـﺴﺎﻜﻌﻨﺇ
(PV
γ
=C
1
)
)
2
(
ﻻ
ﺍﻨﻌﻜﺎﺴﻴﺎﹰ ﺒﺤﻴﺙ ﺍﺼﺒﺤﺕ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻨﻬﺎﺌﻴﺔ ﻓﻲ ﻫﺫﻩ ﺍﻟﺤﺎﻟﺔ ﺍﻜﺒﺭ ﺒﻤﻘﺩﺍﺭ
(6.6
°C)
ﺔـﻟﺎﺤﻟﺍ ﻥﻋ
)
1
.(
ﺍﻭﺠﺩ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﻤﻘﺩﺍﺭ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺘﻘل ﻭﺍﻻﻨﺘﺭﻭﺒﻲ ﻓﻲ ﺍﻟﺤﺎﻟﺘﻴﻥ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
γ=1.4 ، R=0.29 kJ/kg.K
ﺝ
:
)
-154.5 kJ
،
-159.3 kJ
،
0.0095 kJ/K
(
)
5.22
(
(0.5 kg)
ﻤﻥ ﻏﺎﺯ ﻀﻐﻁﻪ
(1.5 bar)
ﻭﺤﺠﻤﻪ
(280L)
.
ﻪـﻤﺠﺤ ﺢﺒـﺼﺍ ﻥﺍ ﻰـﻟﺍ ﹰﺎﻴﺒﻭﺭﺘﻟﻭﺒ ﻁﻐُﻀ
(100L)
ﺘﺒﻌﺎﹰ ﻟﻠﻌﻼﻗﺔ
(PV
1.2
=C.)
ﻭﺍﻋﻴﺩ ﺍﻟﻰ ﺤﺠﻤﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ ﺒﺈﺠﺭﺍﺀ ﺍﻴﺯﻭﺜﺭﻤﻠﻲ
.
ﺭﺍﺀﺍﺕـﺠﻻﺍ ﻡﺴﺭﺍ
ﻋﻠﻰ ﻤﺨﻁﻁﻲ
(P-V)
ﻭ
(T-S)
ﻭﺍﺤﺴﺏ
:
)
1
(
ﺍﻟﻀﻐﻁ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ ﻨﻬﺎﻴﺔ ﻜل ﺇﺠﺭﺍﺀ
)
2
(
لـﻜ لﻼـﺨ ﺔـﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍﻭ لﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍ
ﺍﺠﺭﺍﺀ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cv = 0.724 kJ/kg.K
، Cp = 1.02 kJ/kg.K
ﺝ
:
5.16 bar)
،
360.88 K
،
1.84 bar
،
-57.054 kJ
،
54.99 kJ
(
)
5.23
(
ﻫﻭﺍﺀ ﺒﺩﺍﺨل ﺍﺴﻁﻭﺍﻨﺔ
.
ﺍﻟﻨﺴﺒﺔ ﺍﻟﺤﺠﻤﻴﺔ
( )
1
17
.
ﺎﻟﺘﻴﻥـﺤ ﻲﻓ ﺔﻬﺒﺎﺸﺘﻤ ﻑﻭﺭﻅﺒ ﻁﻐﻀﻴ
) :
1
(
ﺎﹰـﻴﻠﻤﺭﺜﻭﺯﻴﺍ
.
)
2
(
ﺒﻭﻟﺘﺭﻭﺒﻴﺎﹰ ﻭﻓﻕ ﺍﻟﻘﺎﻨﻭﻥ
(PV
1.3
=C.)
ﺍﺤﺴﺏ ﺍﻟﻨﺴﺒﺔ ﺒﻴﻥ ﺍﻟﺤﺎﻟﺘﻴﻥ ﻟﻜل ﻤﻥ ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
ﻭﺍﻟﻀﻐﻁ ﺍﻟﻨﻬﺎﺌﻲ
.
ﺝ
:
)
0.634
،
10.85
،
0.425
(
)
5.24
(
ﺍﻭﻜﺴﺠﻴﻥ ﺤﺠﻤﻪ
(2L)
ﻭﻀﻐﻁﻪ
(2 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(40
°C)
ﻭﺕـﺒﺜﺒ ﻕـﻠﻐﻤ ﻡﺎـﻅﻨ ﻲـﻓ ﺩﺩﻤﺘ
ﺍﻟﻀﻐﻁ ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺢ ﺤﺠﻤﻪ ﻀﻌﻑ ﺤﺠﻤﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﻪـﻤﺠﺤ ﻰـﻟﺍ ﺩﺎـﻋ ﻥﺍ ﻰـﻟﺍ ﹰﺎﻴﻠﻤﺭﺜﻭﺯﻴﺍ ﻁﻐﻀ
ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﺜﻡ ﺘﻤﺩﺩ ﻤﺭﺓ ﺍﺨﺭﻯ ﺒﻭﻟﺘﺭﻭﺒﻴﺎﹰ ﻭﻓﻕ ﺍﻟﻘﺎﻨﻭﻥ
(PV
1.3
=C.)
ﻪـﻤﺠﺤ ﻑﻌﻀ ﻪﻤﺠﺤ ﺢﺒﺼﺍ ﺙﻴﺤﺒ
ﺍﻻﺒﺘﺩﺍﺌﻲ ﺜﺎﻨﻴﺔ
.
ﺍﺭﺴﻡ ﺍﻻﺠﺭﺍﺀﺍﺕ ﻋﻠﻰ ﻤﺨﻁﻁﻲ
(P-V)
ﻭ
(T-S)
ـ ﻭﺍﺤ
ﺴﺏ
)
1
(
ﺭﺍﺭﺓـﺤﻟﺍﻭ لﻐﺸـﻟﺍ
ﺍﻟﻤﻨﺘﻘﻠﻴﻥ
)
2
(
ﻤﻘﺩﺍﺭ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻜل ﺇﺠﺭﺍﺀ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cv = 0.62 kJ/kg.K
، Cp = 0.92 kJ/kg.K
ﺝ
:
)
0.4 kJ
،
0.482 kJ
،
1.44 kJ
،
-0.534 kJ
،
0.0945 kJ
،
1.04 kJ
،
0
،
-0.389 kJ
.(

)
157
(
)
5.25
(
ﻜﺘﻠﺔ ﻤﻥ ﺍﻟﻬﻭﺍﺀ ﻤﻭﺠﻭﺩﺓ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ
ﺘﻤﺩﺩﺕ ﺒﺸﻜل ﻟﺤﻅﻲ
)
ﻴﻤﻜﻥ ﺍﻋﺘﺒﺎﺭﻩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ
(
ﻤﻥ ﻀﻐﻁ ﻤﻘﺩﺍﺭﻩ
(6 bar)
ﺍﻟﻰ
(1.48 bar)
.
ﻭﺕـﺒﺜﺒ ﺔﻴﺍﺩﺒﻟﺍ ﻲﻓ ﻪﻴﻠﻋ ﺕﻨﺎﻜ ﺎﻤ ﻰﻟﺍ ﻪﺘﺭﺍﺭﺤ ﺔﺠﺭﺩ ﺕﺩﺎﻋ ﻥﺍ ﻰﻟﺍ ﻙﺭﺘ ﻡﺜ
ﺤﺠﻤﻪ ﻓﺎﺭﺘﻔﻊ ﻀﻐﻁﻪ ﻨﺘﻴﺠﺔ ﻟﺫﻟﻙ ﺍﻟﻰ
(2.21 bar)
.
ﺍﻭﺠﺩ ﻗﻴﻤﺔ
(R)
ﻭﺍﺭﺴ
ﻡ
ﻤﺨﻁﻁ
(P-V)
ﻋﻠﻤﺎﹰ ﺃﻥ
:
Cp = 1.005 kJ/kg.K
ﺝ
:
)
0.287 kJ/kg.K
(
)
5.26
(
ﻫﻭﺍﺀ ﻤﻭﺠﻭﺩ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻨﺴﺒﺘﻪ ﺍﻟﺤﺠﻤﻴﺔ
)
17
.(
ﺭﺍﺌﻴﻥ ﺍﻻﻭلـﺠﺇ ﻲـﻓ ﺓﺩـﺤﺍﻭ ﺔـﻁﻘﻨ ﻥـﻤ ﻁﻐﻀﻴ
ﺍﻴﺯﻭﺜﺭﻤﻠﻲ ﻭﺍﻟﺜﺎﻨﻲ ﺒﻭﻟﺘﺭﻭﺒﻲ ﻴﺨﻀﻊ ﻟﻠﻌﻼﻗﺔ
(PV
1.3
=C.)
.
ﻥـﻤ لـﻜﻟ لﻐﺸـﻟﺍ ﻥﻴـﺒ ﺔﺒﺴـﻨﻟﺍ ﺏﺴﺤﺍ
ﺍﻻﺠﺭﺍﺌﻴﻥ ﻭﻜﺫﻟﻙ ﺍﻟﻨﺴﺒﺔ ﺒﻴﻥ ﺍﻟﻀﻐﻁ ﺍﻟﻨﻬﺎﺌﻲ ﻟﻜل ﻤﻥ ﺍﻻﺠﺭﺍﺀﻴﻥ
.
ﺝ
:
)
0.634
،
0.425
(
)
5.27
(
ﻏﺎﺯ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻴﺘﻤﺩﺩ ﺍﻴﺯﻭﺜﺭﻤﻠﻴﺎﹰ ﺍﻟﻰ
( )
6
1
ﺎﹰـﻴﺘﺎﺒﺎﻴﺩﺍ ﺩﺩـﻤﺘﻴ ﺔﻁﻘﻨﻟﺍ ﺱﻔﻨ ﻥﻤﻭ ﻲﺌﺍﺩﺘﺒﻻﺍ ﻪﻁﻐﻀ ﻥﻤ
ﺤﺴﺏ ﺍﻟﻌﻼﻗﺔ
(PV
1.36
=C.)
ﺍﻟﻰ
( )
6
1
ﻤﻥ
ﻀﺎﹰـﻴﺍ ﻲﺌﺍﺩﺘﺒﻻﺍ ﻪﻁﻐﻀ
.
ﺸﻐلـﻟﺍ ﻥﻴـﺒ ﺔﺒﺴـﻨﻟﺍ ﺏﺴـﺤﺍ
ﺍﻻﻴﺯﻭﺜﺭﻤﻠﻲ ﻭﺍﻟﺸﻐل ﺍﻻﺩﻴﺎﺒﺎﺘﻲ
.
ﺝ
:
)
1.72
(
)
5.28
(
ﺭﺍﺀﻴﻥ ﺍﻻﻭلـﺠﺍ ﻲـﻓ ﺔﻬﺒﺎﺸـﺘﻤ ﻑﻭﺭـﻅ ﻲـﻓ ﺩﺩﻤﺘ ﻲﻟﺎﺜﻤ ﺯﺎﻏ ﻰﻠﻋ ﻱﻭﺘﺤﺘ ﺱﺒﻜﻤﺒ ﺔﻘﻠﻐﻤ ﺔﻨﺍﻭﻁﺴﺍ
ﺍﻴﺯﻭﺜﺭﻤﻠﻲ ﻭﺍﻟﺜﺎﻨﻲ ﺒﻭﻟﺘﺭﻭﺒﻲ ﻴﺨﻀﻊ ﻟﻠﻌﻼﻗﺔ
(PV
1.3
=C.)
.
ﻭﻜﺎﻨﺕ ﺍﻟﻨﺴﺒﺔ ﺒﻴﻥ ﺍﻟﺤﺠﻡ ﺍﻻﺒﺘﺩﺍﺌﻲ ﻭﺍﻟﺤﺠﻡ
ﺍﻟﻨﻬﺎﺌﻲ
( )
17
1
.
ﺍﺤﺴﺏ ﺍﻟﻨﺴﺒﺔ ﺒﻴﻥ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﺔ ﻟﻜ
ل ﻤﻥ ﺍﻻﺠﺭﺍﺀﻴﻥ
.
ﻋﻠﻤﺎﹰ ﺃﻥ
:
γ = 1.4
، R = 0.293 kJ/kg.K
ﺝ
:
)
5.97
(
)
5.29
(
ﻏﺎﺯ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﺤﺠﻤﻪ
(0.106m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(100
°C)
ﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﺒﺤﻴﺙ ﺍﺼﺒﺢ ﻀﻐﻁﻪ
( )
3
1
ﻤﺎ ﻜﺎﻥ ﻋﻠﻴﻪ ﻓﻲ ﺍﻟﺒﺩﺍﻴﺔ
.
ﻭﺍﺼﺒﺢ ﺤﺠﻤﻪ ﻀﻌﻑ ﻤﺎ ﻜﺎﻥ ﻋﻠﻴﻪ ﻓﻲ ﺍﻟﺒﺩﺍﻴﺔ
.
ﺜﻡ ﺘﻤﺩﺩ ﺍﻴﺯ
ﻭﺜﺭﻤﻠﻴﺎﹰ ﺒﺤﻴﺙ
ﻜﺎﻥ ﺍﻟﺸﻐل ﺍﻟﻤﻨﺠﺯ ﻓﻲ ﺍﻻﺠﺭﺍﺀﻴﻥ ﻤﺘﺴﺎﻭﻱ
.
ﺍﺤﺴﺏ ﺤﺠﻡ ﺍﻟﻐﺎﺯ ﻓﻲ ﻨﻬﺎﻴﺔ ﺍﻻﺠﺭﺍﺀ ﺍﻻﻴﺯﻭﺜﺭﻤﻠﻲ
.
ﺝ
:
)
0.5 m
3
(

)
158
(
)
5.30
(
ﺩﺍﺭﻩـﻘﻤ ﻁﻐـﻀ ﺕﺤﺘ ﻕﻠﻐﻤ ﻡﺎﻅﻨ ﻲﻓ ﺩﻭﺠﻭﻤ ﻥﻴﺠﻭﺭﺘﻨ ﺯﺎﻏ
(100bar)
ﺩﺍﺭﻫﺎـﻘﻤ ﺓﺭﺍﺭـﺤ ﺔـﺠﺭﺩﻭ
(600
°C)
.
ﺩﺍﺭﻩــﻘﻤ ﹰﺎــﻤﺠﺤ لﻐﺸــﻴﻭ
(1.31 L)
.
ﻐﻼﹰــﺸ ﺞﺘــﻨﺃﻭ ﹰﺎــﻴﺒﻭﺭﺘﻟﻭﺒ ﺩﺩــﻤﺘ
ﺩﺍﺭﻩــﻘﻤ
(28.65kJ)
.
ﻓﺈﺫﺍ ﻋﻠﻤﺕ ﺍﻥ ﺍﻻﺱ ﺍﻟﺒﻭﻟﺘﺭﻭﺒﻲ
(n=1.3)
ﻲـﻓ ﻡـﺠﺤﻟﺍﻭ ﻁﻐﻀﻟﺍﻭ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﺩﺠﻭﺍ
ﻨﻬﺎﻴﺔ ﺍﻻﺠﺭﺍﺀ
.
ﺝ
:
)
27
°C
،
0.978 bar
،
46 L
(
)
5.31
(
ﻫﻭﺍﺀ ﻀﻐﻁﻪ
(1.02 bar)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(268
°C)
.
ﻰ ﺍﻥـﻟﺍ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﻁﻐﻀ ﻡﺜ ،ﹰﺎﻴﻠﻤﺭﺜﻭﺯﻴﺍ ﻁﻐﻀ
ﺍﺼﺒﺢ ﻀﻐﻁﻪ
(51 bar)
ﻭﺤﺠﻤ
ﻪ
(0.032 m
3
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(1000
°C)
.
ﻰـﻠﻋ ﺕﺍﺀﺍﺭﺠﻻﺍ ﻡﺴﺭﺍ
ﻤﺨﻁﻁ
(P-V)
ﻭﺍﺤﺴﺏ
) :
1
(
ﻲـﻠﻤﺭﺜﻭﺯﻴﻻﺍ ﻁﺎﻐﻀﻨﻻﺍ ﺩﻌﺒﻭ لﺒﻗ ﺀﺍﻭﻬﻟﺍ ﻡﺠﺤ
) .
2
(
ﺭﺍﺭﺓـﺤﻟﺍ ﻲﻓﺎـﺼ
ﻋﻠﻤﺎﹰ ﺃﻥ،ﻥﻴﻠﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍﻭ
:
γ =1.4
،
R = 0.287 kJ/kg.K
ﺝ
:
)
0.681 m
3
،
0.272 m
3
،
-63.72 kJ
،
-157.5 kJ
(
)
5.32
(
ﺍﺴﻁﻭﺍﻨﺔ
ﺤﺠﻤﻬﺎ
(300 L)
ﺘﺤﺘﻭﻱ ﻋﻠﻰ ﺍﻭﻜﺴﺠﻴﻥ ﻀﻐﻁﻪ
(3.1 MN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(18
°C)
.
ﻓﺘﺢ ﺍﻟﺼﻤﺎﻡ ﻭﺍﺴﺘﻌﻤل ﻗﺴﻡ ﻤﻥ ﺍﻟﻐﺎﺯ ﻓﺄﺼﺒﺢ ﻀﻐﻁ ﺍﻻﻭﻜﺴﺠﻴﻥ ﺍﻟﻤﺘﺒﻘﻲ ﻓﻲ ﺍﻻﺴﻁﻭﺍﻨﺔ
(1.7 MN/m
2
)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(15
°C)
.
ﺒﻌﺩ ﺇﻋﺎﺩﺓ ﺇﻏﻼﻕ ﺍﻟﺼﻤﺎﻡ ﺇﻨﺘﻘﻠﺕ ﺤﺭﺍﺭﺓ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﺒﺤﻴﺙ ﻋﺎﺩ ﺍﻻﻭﻜﺴﺠﻴﻥ
ﺍﻟﻤﺘﺒﻘﻲ ﺍﻟﻰ
ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
.
ﻓﺈﺫﺍ ﻋﻠﻤﺕ ﺍﻥ
(
γ=1.4)
،
(Cp=0.91 kJ/kg.K)
ﺴﺠﻴﻥـﻜﻭﻸﻟ
.
ﺍﺤﺴﺏ
:
)
ﺃ
(
ﻜﺘﻠﺔ ﺍﻻﻭﻜﺴﺠﻴﻥ ﺍﻟﻤﺴﺘﻌﻤل
)
ﺏ
(
ﺴﺠﻴﻥـﻜﻭﻻﺍ ﻰﻟﺍ ﺔﻨﺍﻭﻁﺴﻻﺍ ﻥﺍﺭﺩﺠ لﻼﺨ ﺔﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺭﺍﺩﻘﻤ
ﺒﻌﺩ ﻏﻠﻕ ﺍﻟﺼﻤﺎﻡ
)
ﺝ
(
ﻀﻐﻁ ﺍﻻﻭﻜﺴﺠﻴﻥ ﺍﻟﻨﻬﺎﺌﻲ
.
ﺝ
:
)
5.5 kg
،
10.725 kJ
،
1.72 MN/m
2
(
)
5.33
(
ﻏﺎﺯ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻜﺘﻠﺘﻪ
(0.75 kg)
ﻭﻀﻐﻁﻪ
(1 bar)
ﻪـﺘﺭﺍﺭﺤ ﺔﺠﺭﺩﻭ
(20
°C)
ﺈﺠﺭﺍﺀـﺒ ﻁﻐـﻀ
ﺴﺏـﺤ ﻲﺒﻭﺭﺘﻟﻭـﺒ ﺀﺍﺭﺠﺈـﺒ ﻁﻐﻀ ﻙﻟﺫ ﺩﻌﺒﻭ ﻲﺌﺍﺩﺘﺒﻻﺍ ﻪﻤﺠﺤ ﻑﺼﻨ ﻪﻤﺠﺤ ﺢﺒﺼﺍ ﻥﺍ ﻰﻟﺍ ﻲﻠﻤﺭﺜﻭﺯﻴﺍ
ﺍﻟﻌﻼﻗﺔ
(PV
1.3
=C.)
ﺍﻟﻰ ﺍﻥ ﺍﺼﺒﺢ ﺤﺠﻤﻪ ﺭﺒﻊ ﺤﺠﻤﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﻁـﻁﺨﻤ ﻰـﻠﻋ ﻥﻴﺀﺍﺭﺠﻻﺍ ﻡﺴﺭﺍ
(P-
V)
ﺇﺫﺍ ﻋﻠﻤﺕ،
ﺃﻥ
:
(Cv=0.718 kJ/kg.K
ﻭ
(Cp=1 kJ/kg.K)
.
ﺍﺤﺴﺏ ﻤﺎ ﻴﻠﻲ
:
ﺃ
-
ﺍﻟﺤﺠﻡ ﻭﺍﻟﻀﻐﻁ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻓﻲ ﻨﻬﺎﻴﺔ ﻜل ﺇﺠﺭﺍﺀ
.
ﺏ
-
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﺘﺒﺎﺩﻟﺔ ﺒﻴﻥ ﺍﻟﻨﻅﺎﻡ ﻭﺍﻟﻤﺤﻴﻁ ﻓﻲ ﻜل ﺇﺠﺭﺍﺀ
.
ـﺠ
-
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻜل ﺇﺠﺭﺍﺀ
.
ﺝ
:
)
0.6197m
3
،
0.3098m3
،
0.1549m3
،
2bar
،
5bar
،
360.7K
،
-43 kJ
،
47.73 kJ
،
11.3 kJ
،
36.46 kJ
(

)
159
(
)
5.34
(
ﻏﺎﺯ ﻤﺜﺎﻟﻲ ﻤﻭﺠﻭﺩ ﻓﻲ ﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻴﻤﺭ ﻓﻲ ﺍﻻﺠﺭﺍﺀﺍﺕ ﺍﻟﺘﺎﻟﻴﺔ
:
)
1
(
ﺍﻀﺎﻓﺔ ﺤﺭﺍﺭﺓ ﺒﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ ﻟﻴﺭﺘﻔﻊ ﻀﻐﻁﻪ ﻤﻥ
(2 bar)
ﺍﻟﻰ
(7 bar)
.
)
2
(
ﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻲ
.
)
3
(
ﺇﻨﻀﻐﺎﻁ ﺍﻴﺯﻭﺜﺭﻤﻠﻲ ﻟﻴﻌﻭﺩ ﺍﻟﻐﺎﺯ ﺍﻟﻰ ﺤﺎﻟﺘﻪ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
.
ﻓﺈﺫﺍ ﻜﺎﻥ
(Q
o
)
ﺘﻤﺜل ﺍﻟﺤﺭ
ﺕـﻨﺎﻜﻭ ،ﻲـﻠﻤﺭﺜﻭﺯﻴﻻﺍ ﺀﺍﺭﺠﻻﺍ ﻲﻓ ﺔﺤﻭﺭﻁﻤﻟﺍ ﺓﺭﺍ
(Q
in
)
ﺭﺍﺭﺓـﺤﻟﺍ لـﺜﻤﺘ
ﺍﻟﻤﻀﺎﻓﺔ ﻓﻲ ﺍﺠﺭﺍﺀ ﺜﺒﻭﺕ ﺍﻟﺤﺠﻡ
.
ﺍﺤﺴﺏ ﻗﻴﻤﺔ
( )
in
o
Q
Q
ﻭﺍﺭﺴﻡ ﺍﻻﺠﺭﺍﺀﺍﺕ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-V)
.
ﺝ
:
)
0.5
.(

)
160
(
ﺍﻟﻔﺼﻞ ﺍﻟﺴﺎﺩﺱ
–
ﺍﻷﻧﻈﻤﺔ ﺍﻟﻤﻔﺘﻮﺣﺔ
)
6.1
(
-
ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
The Open Systems
ﺍﻥ ﺍﻻﺠﺭﺍﺀﺍﺕ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺘﺨﻀﻊ ﻟﻠﻤﺨﻁﻁ ﺍﻟﺘﺎﻟﻲ
:
ﺴﺒﻕ ﺍﻥ ﺘﻤﺕ ﻤﻨﺎﻗﺸﺔ ﺍﺠﺭﺍﺀﺍﺕ ﻋﺩﻡ ﺍﻟﺘﺩﻓﻕ
(Non-Flow)
ﺔـﻟﺩﺎﻌﻤ ﺯﻤﺭﻭ ﺔﻘﻠﻐﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﻭﺍ
ﺍﻟﻁﺎﻗﺔ ﻓﻴﻬﺎ
(NFEE)
.
ﺭﺍﺀﺍﺕـﺠﺍ ﺵﻗﺎﻨﻨـﺴ لﺼﻔﻟﺍ ﺍﺫﻫ ﻲﻓﻭ
ﺩﻓﻕـﺘﻟﺍ
(Flow Process)
ﺔـﻤﻅﻨﻻﺍﻭ
ﻭﺍﻟﺘﻲ ﻤﻥ ﺍﻟﻤﻤﻜﻥ ﺍﻥ ﺘﻜﻭﻥ ﺘﺩﻓﻘﺎﹰ ﻏﻴﺭ ﻤﻨﺘﻅﻡ،ﺔﺤﻭﺘﻔﻤﻟﺍ
(Non-Steady)
ﺍﻭ ﺘﺩﻓﻘﺎﹰ ﻤﻨﺘﻅﻤﺎﹰ،
(Steady)
.
ـﻴﺭﻤﺯ ﻟﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻓﻲ ﺍﻟﺘﺩﻓﻕ ﺍﻟﻤﻨﺘﻅﻡ ﺒ
(SFEE)
ﻭﻴﺘﻤﻴﺯ ﺒﻤﺎ ﻴﺄﺘﻲ،
:
1
-
ﻴﻜﻭﻥ ﻤﻌﺩل ﺍﻟﺘﺩﻓﻕ ﺍﻟﻜﺘﻠﻲ ﺜﺎﺒﺘﺎﹰ ﻭﻤﺘﺴﺎﻭﻴﺎﹰ ﻋﻨﺩ ﺍﻟﻤﺩﺨل ﻭﺍﻟﻤﺨ
ﺭﺝ
.
2
-
ﺘﺩﻓﻕ ﺍﻟﻤﺎﺌﻊ ﻭﺍﻨﺘﻘﺎل ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﻴﻜﻭﻥ ﺒﻤﻌﺩل ﺯﻤﻨﻲ ﻤﻨﺘﻅﻡ
.
3
-
ﻻ ﺘﺘﻐﻴﺭ ﺨﻭﺍﺹ ﺍﻟﻤﺎﺌﻊ ﻋﻨﺩ ﺍﻴﺔ ﻨﻘﻁﺔ ﻓﻲ ﺍﻟﻨﻅﺎﻡ ﻋﻨﺩ ﺘﻐﻴﺭ ﺍﻟﺯﻤﻥ
.
4
-
ـ ﻋﻨﺩ ﺍﻴﺔ ﻨﻘﻁﺔ ﻓﻲ ﺍﻟﻨﻅﺎﻡ ﻴﻜﻭﻥ ﻟﻠﻤﺎﺌﻊ ﺨﺎﺼﻴﺔ ﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﻴﺔ ﻜﺎﻟ
)
P
،
T
،
ν
(
ﺔـﻴﻜﻴﻨﺎﻜﻴﻤ ﺔﻴﺼﺎﺨﻭ
ﺤﻴﺙ ﺘﺸﻤل ﺴﺭﻋﺔ ﺍﻟﻤﺎﺌﻊ ﻭﺍﺭﺘﻔﺎﻋﻪ ﻓﻭﻕ ﺨﻁ ﻗ
ﺎﻋﺩﺓ ﻤﻌﻴﻥ
.
ﻲـﻓ ﻥﺍﺭﺜﺅﺘ ﺩﻗﻭ ،ﻥﺎﺘﻴﺼﺎﺨﻟﺍ ﻥﺎﺘﺎﻫ ﺭﻴﻐﺘﺘ ﺩﻗ
ﺍﻟﺸﻐل ﻭﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﻨﺘﻘﻠﻴﻥ ﻋﺒﺭ ﺍﻟﺤﺩﻭﺩ
.
ﺎﺀـﻤﻟﺍ ،ﻥﻴﺒﺭﻭـﺘ ﺭﺒﻋ ﻕﻓﺩﺘﻴ ﺭﺎﺨﺒ ،ﺔﻫﻭﻓ ﺭﺒﻋ ﺯﺎﻏ ﺩﺩﻤﺘ ،ﺔﺤﻭﺘﻔﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﻰﻠﻋ ﺔﻠﺜﻤﻻﺍ ﻥﻤﻭ
ﻏﺎﺯ ﻴﻀﻐﻁ ﻓﻲ ﻀﺎﻏﻁ،ﺭﺎﺨﺒﻜ ﻪﻜﺭﺘﻴ ﻱﺫﻟﺍﻭ لﺠﺭﻤ ﻰﻟﺍ لﺨﺍﺩﻟﺍ
…
ﺍﻟﺦ
.
ﺇﻥ ﺸﻜل
(6.3-b)
ﺍﻟﺫﻱ ﺴﻴﺭﺩ ﺫﻜ
ﻴﻭﻀﺢ ﺘﺩﻓﻕ ﺍﻟﻤﺎﺌﻊ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ،ﺩﻌﺒ ﺎﻤﻴﻓ ﻩﺭ
.
)
6.2
(
-
ﺍﻟﺸﻐل ﺍﻟﺼﺎﻓﻲ
Net Work
،ﺎﻥـﻴﺭﺠﻟﺍ لﻐـﺸﻭ ﺓﺭﺍﺩﻻﺍ ﺩﻭـﻤﻋ لﻐـﺸ ﺎﻤﻫ لﻐﺸﻟﺍ ﻥﻤ ﺎﻥﻋﻭﻨ ﻙﺎﻨﻫ ﺔﺤﻭﺘﻔﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﻲﻓ
ﻤﻭﻀﺤﺎﻥ ﻓﻲ ﺍﻟﻔﻘﺭﺍﺕ ﺍﻵﺘﻴﺔ
:
( )
m
&
Process
Non-Flow
Flow
Non-Steady
Steady
(NFEE)
(SFEE)
(NSFEE)
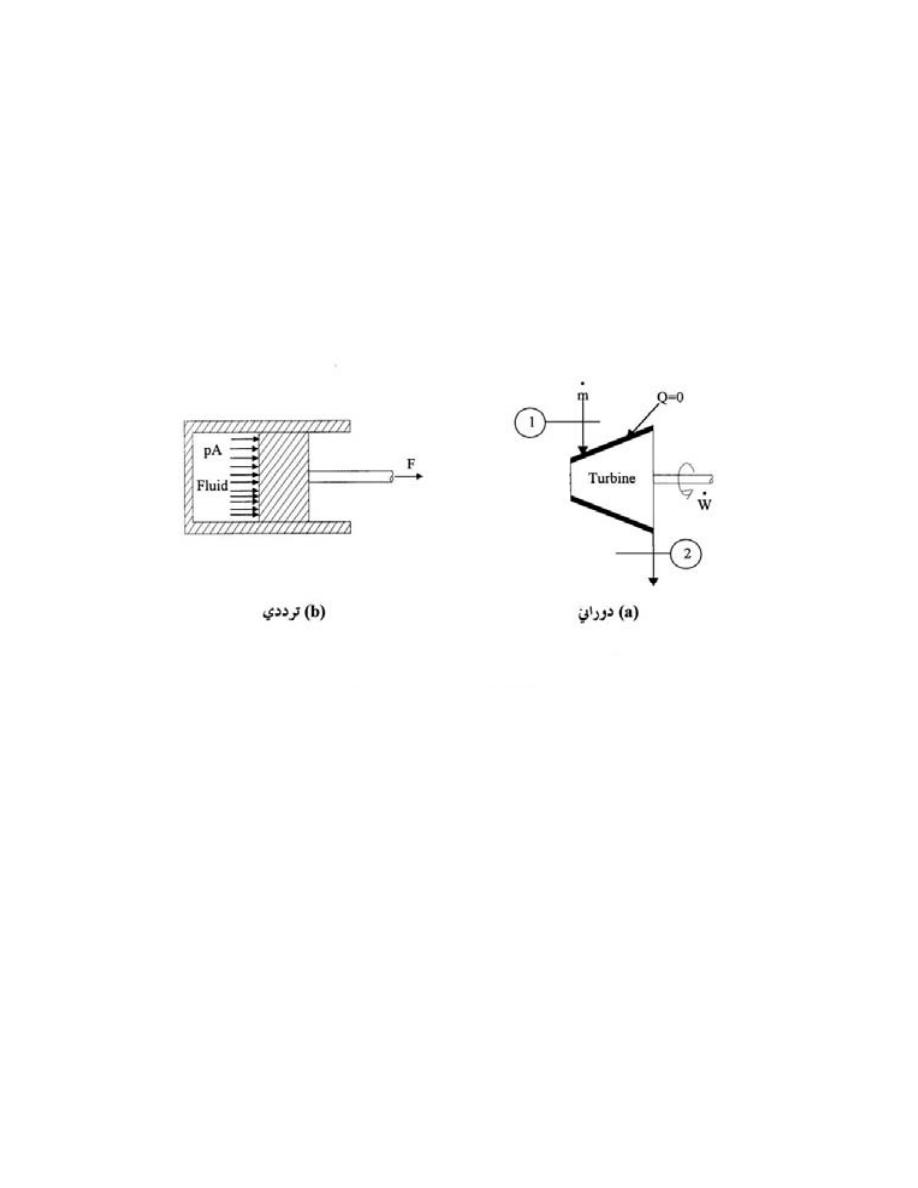
)
161
(
)
6.2.1
(
-
ﺸﻐل ﻋﻤﻭﺩ ﺍﻻﺩﺍﺭﺓ
Shaft Work
ﺭﻤﺯﻩ
(Ws)
.
ﺭﺒﻤﺎ ﻴﺘﺒﺎﺩﺭ ﺍﻟﻰ ﺍﻻﺫﻫﺎﻥ
ﺍﻥ ﺍﻟﺸﻐل
(W)
ﻐلـﺸ ﺩﺭـﺠﻤ ﻭـﻫ ﺔﻗﺎﻁﻟﺍ ﺔﻟﺩﺎﻌﻤ ﻲﻓ
ﺍﻟﻌﻤﻭﺩ
(Ws)
.
ﺍﻻ ﺍﻥ ﺫﻟﻙ ﻏﻴﺭ ﺼﺤﻴﺢ
.
ﺎﺭﺠﻲـﺨﻟﺍ لﻐﺸﻟﺍ ﻰﻠﻋ ﺔﻟﻻﺩﻠﻟ لﻤﻌﺘﺴﻴ ﺩﻭﻤﻌﻟﺍ لﻐﺸ ﺢﻠﻁﺼﻤﻓ
ﺍﻟﻤﻨﺘﻘل ﻤﻥ ﺍﻭ ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ
(External Work Done)
ﺫﻱـﻟﺍﻭ ﺎﻤ ﺯﺎﻬﺠ لﻼﺨ ﻊﺌﺎﻤﻟﺍ ﻥﺎﻴﺭﺠ ﺀﺎﻨﺜﺍ ﻲﻓ
ﺸﻜل،ﺯﺎﻬﺠﻟﺍ ﻥﻤ ﺯﺭﺒﻴ ﺩﻭﻤﻋ ﺔﻁﺎﺴﻭﺒ لﻘﻨﻴ
)
6.1
(
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل،ﹰﺎﻴﻨﺍﺭﻭﺩ ﻙﺭﺤﺘﻴ ،
(6.1-a)
، ﺍﻭ ﺘﺭﺩﺩﻴﺎﹰ
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل
(6.1-b)
.
)
6.2.2
(
-
ﺸﻐل ﺍﻭ ﻁﺎﻗﺔ ﺍﻟﺠﺭﻴﺎﻥ
Flow Work
ﻫﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻭ ﺍﻟﺸﻐل ﺍﻟﻨﺎﺘﺞ ﺒﺴﺒﺏ ﺠﺭﻴﺎﻥ ﺍﻟﻤﺎﺌﻊ
.
ﻥ ﺍﻭـﻤ ﺝﺭﺨﻴ ﻭﺍ لﺨﺩﻴ ﻊﺌﺎﻤ ﻥﻤ ﻡﺠﺤ ﻱﺃ ﻥﺇ
ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ ﻴﺠﺏ ﺍﻥ ﻴﺯﻴﺢ ﺤﺠﻤﺎﹰ ﻤﺴﺎﻭﻴﺎﹰ ﻟﻪ ﻟﻴﺘﺴﻨﻰ ﻟﻪ ﺍﻟﺩﺨﻭل ﺍﻭ
ﺍﻟﺨﺭﻭﺝ
.
ﻴﻜﻭﻥ ﺍﻟﺠﺭﻴﺎﻥ ﻤﺴﺘﻘﺭﺍﹰٍﺫﺌﺩﻨﻋ
ﺎﻥـﻴﺭﺠﻟﺍ لﻐﺸـﺒ ﻰﻤﺴﻴ ،ﺔﺤﺍﺯﻤﻟﺍ ﺔﻠﺘﻜﻟﺍ ﻰﻠﻋ ﹰﻼﻐﺸ ﺯﺠﻨﺘ ﻥﺍ ﺏﺠﻴ ﺔﺤﻴﺯﻤﻟﺍ ﺔﻠﺘﻜﻟﺍﻭ
(Flow Work)
،
ﺭﻤﺯﻩ
(W
Flow
)
.
ﻜلـﺸ ﻲﻓ ﺎﻤﻜ ،ﺡﻭﺘﻔﻤ ﻡﺎﻅﻨ ﻥﻤﻀ ﻡﺎﻅﺘﻨﺄﺒ ﻕﻓﺩﺘﻴ ﻊﺌﺎﻤﻟﺍ ﻥﺍ ﺽﺭﺘﻔﻨ
(6.2-a)
ﺩﺨلـﻴ ﺙـﻴﺤ ،
ﻭﻴﺨﺭﺝ ﺒﻨﻔﺱ ﺍﻟﻤﻌﺩل
.
ﻭﺍﻥ ﺸﺭﻭﻁ ﺍﻟﻤﺎﺌﻊ
ﻋﻨﺩ ﺍﻟﺩﺨﻭل
(P
1
)
،ﻀﻐﻁـﻟﺍ لﺜﻤﺘ
ﺎﺌﻊـﻤﻟﺍ ﻡـﺠﺤ
ﺍﻟﻤﺘﺩﻓﻕ ﻓﻲ ﺍﻟﺜﺎﻨﻴﺔ ﺍﻟﻭﺍﺤﺩﺓ
.
ﻭﺸﺭﻭﻁﻪ ﻋﻨﺩ ﺍﻟﺨﺭﻭﺝ
)
m
(
&
)
V
(
1
&
)
P
,
V
(
2
2
&
ﺸﻜل
)
6.1
(
-
ﺸﻐل ﺍﻟﻌﻤﻭﺩ
)
W
s
(
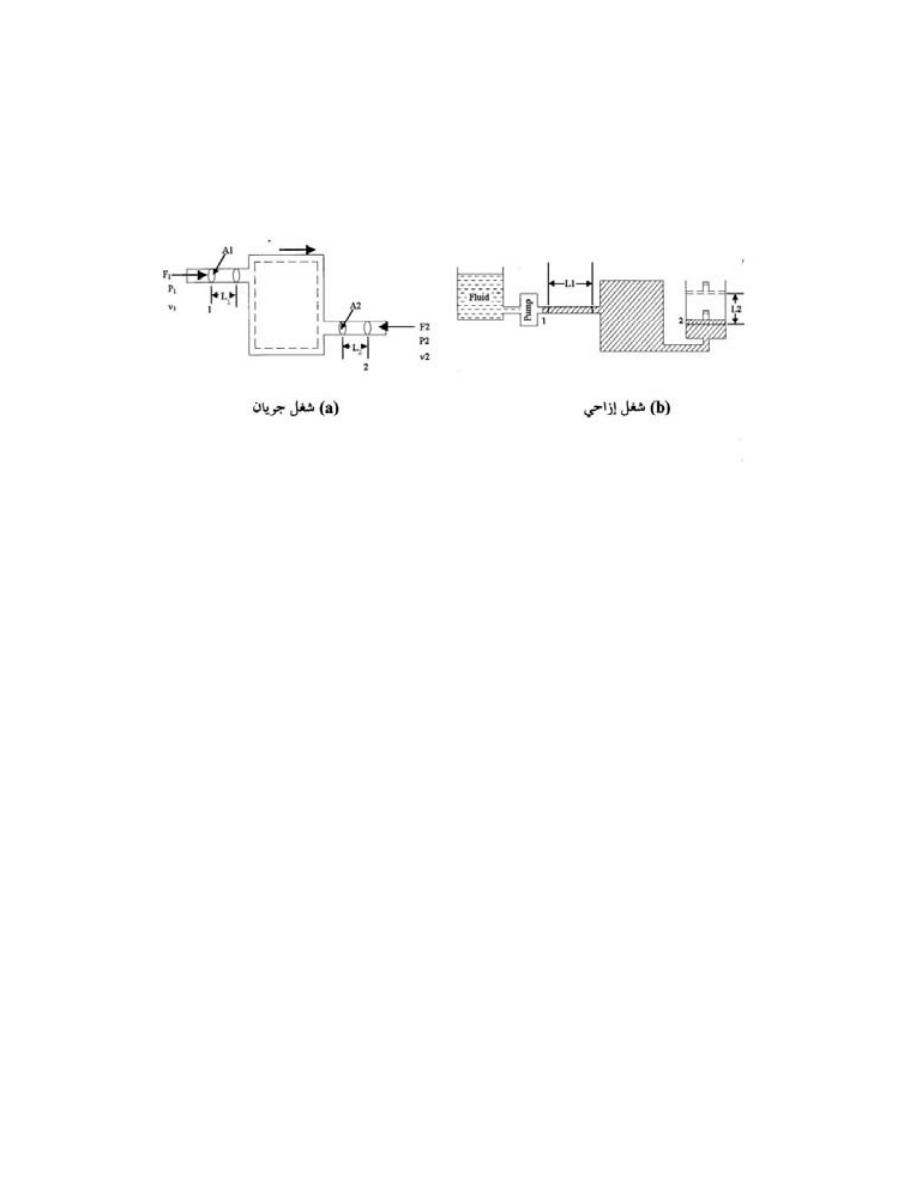
)
162
(
ﻭﻋﻨﺩﻤﺎ ﻴﺠﺭﻱ ﺍﻟﻤﺎﺌﻊ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻴﻜﻭﻥ ﻋﻠﻰ ﺸﻜل ﺍﺴﻁﻭﺍﻨﺔ ﻤﺴﺎﺤﺔ ﻤﻘﻁﻌﻬﺎ
(A)
ﺘﺘﻘﻠﺹ،
ﺍﻭ ﺘﺘﻤﺩﺩ ﺘﺒﻌﺎﹰ ﻟﺘﻐﻴﺭ ﻤﺴﺎﺤﺔ ﺍﻟﻤﻘﻁﻊ ﻭﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﻀﻐﻁ
.
ـﻰ ﻁـﻠﻋ ﻥﻭﻜﺘﺴ ﻊﺌﺎﻤﻟﺍ ﺔﻨﺍﻭﻁﺴﺍ ﻥﺇ
ﻭل
ﺍﻟﻤﺴﺎﺭ ﺘﺤﺕ ﺘﺄﺜﻴﺭ ﻗﻭﺘﻴﻥ ﺍﻭ ﻨﻭﻋﻴﻥ ﻤﻥ ﺍﻟﺸﻐل ﺍﻟﺠﺭﻴﺎﻨﻲ ﻫﻤﺎ
:
-
1
-
ﺍﻟﺸﻐل ﺍﻟﺩﺍﺨل
(W
Flow
)
in
:
ﻫﻭ ﺍﻟﻘﻭﺓ ﺍﻟﻤﺅﺜﺭﺓ ﻓﻲ ﺍﺴﻁﻭﺍﻨﺔ ﺍﻟﻤﺎﺌﻊ ﺒﺄﺘﺠﺎﻩ ﺍﻟﺠﺭﻴﺎﻥ
.
ﻼﺯﻡـﻟﺍ لﻐﺸﻟﺍ ﻱﺃ
ﻟﺩﻓﻊ ﻜﻴﻠﻭ ﻏﺭﺍﻡ ﻭﺍﺤﺩ ﻤﻥ ﺍﻟﻤﺎﺌﻊ ﻓﻲ ﺍﻟﺜﺎﻨﻴﺔ ﺍﻟﻭﺍﺤﺩﺓ ﺍﻟﻰ ﺩﺍﺨل ﺍﻟﻨﻅﺎﻡ ﻟﻤﺴﺎﻓﺔ
(L
1
)
ﻭﻴﺴﺎﻭﻱ
:
ﻭﺍﺫﺍ ﻜ
ﺎﻨﺕ
(
ν)
ﺃﻱ ﻟﻜل،ﻲﻋﻭﻨﻟﺍ لﻐﺸﻟﺍ ﻥﻭﻜﻴﺴﻓ ﻲﻋﻭﻨﻟﺍ ﻡﺠﺤﻟﺍ لﺜﻤﺘ
(1kg/s)
ﻴﺴﺎﻭﻱ
:
2
-
ﺍﻟﺸﻐل ﺍﻟﺨﺎﺭﺝ
(W
Flow
)
out
:
ﻫﻭ ﺍﻟﻘﻭﺓ ﺍﻟﻤﺅﺜﺭﺓ ﺒﺎﻻﺘﺠﺎﻩ ﺍﻟﻤﻌﺎﻜﺱ ﻟﺠﺭﻴﺎﻥ ﺍﺴﻁﻭﺍﻨﺔ ﺍﻟﻤﺎﺌﻊ
(F
2
)
.
ﺃﻱ
ﺍﻟﺸﻐل ﺍﻟﻼﺯﻡ ﻟﺩﻓﻊ ﻜﻴﻠﻭ ﻏﺭﺍﻡ ﻭﺍﺤﺩ ﻤﻥ ﺍﻟﻤﺎﺌﻊ ﻓﻲ ﺍﻟﺜﺎﻨﻴﺔ ﺍﻟﻭﺍ
ﺤﺩﺓ
ﺴـﻤﻟ ﻡﺎﻅﻨﻟﺍ ﺝﺭﺎﺨ ﻰﻟﺍ
ﺎﻓﺔ
2
L
ﻭﻴﺴﺎﻭﻱ
:
ﻭﺍﻟﺸﻐل ﺍﻟﻨﻭﻋﻲ ﻴﻜﻭﻥ
:
ﻭﻋﻠﻴﻪ ﻓﺄﻥ ﻤﻘﺩﺍﺭ ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﻁﺎﻗﺔ ﺍﻭ ﺸﻐل ﺍﻟﺠﺭﻴﺎﻥ ﺍﻟﻨﻭﻋﻲ ﻴﺴﺎﻭﻱ
:
-
∆w
Flow
= (w
Flow
)
out
– (w
Flow
)
in
……. (6.5)
∆w
Flow
= P
2
ν
2
- P
2
ν
2
=
∆Pν ……..
(6.6)
(6.1)
.......
m
P
V
P
L
A
P
L
F
)
W
(
1
1
1
1
1
1
1
1
1
in
Flow
&
&
ν
=
=
=
=
(
)
(6.2)
.......
P
w
1
1
in
Flow
ν
=
)
m
(
&
(6.3)
.......
m
P
V
P
L
A
P
L
F
)
W
(
2
2
2
2
2
2
2
2
2
out
Flow
&
&
ν
=
=
=
=
(
)
(6.4)
.......
P
w
2
2
out
Flow
ν
=
)
m
(
&
ﺸﻜل
)
6.2
(
-
ﺍﻨﻭﺍﻉ ﺍﻟﺸﻐل

)
163
(
ﻭﻫﻜﺫﺍ ﺴﻴﻜﻭﻥ ﺍﻟﺸﻐل ﺍﻟﻨﻭﻋﻲ
(w)
ﻓﻲ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻫﻭ ﺍﻟﻤﺠﻤﻭﻉ ﺍﻟﺠﺒﺭﻱ ﻟﻠﺸﻐل ﺍ
ﺃﻱ،لـﻘﺘﻨﻤﻟ
ﺍﻟﺸﻐل ﺍﻟﻨﻭﻋﻲ ﺍﻟﺼﺎﻓﻲ
(w
net
)
ﻭﻴﺴﺎﻭﻱ
:
w
net
= ws +
∆w
Flow
= ws +
∆Pν
………. (6.7)
or
W
net
= Ws +
∆PV
………..
(6.8)
ﻰـﻠﻋ ﹰﻼﻐـﺸ ﺯﺠﻨﺘ ﺔﺤﻴﺯﻤﻟﺍ ﺔﻠﺘﻜﻟﺍﻭ ﻊﺌﺎﻤﻟﺍ ﺔﺤﺍﺯﺇ ﺏﺒﺴﺒ ﺞﺘﺎﻨﻟﺍ لﻐﺸﻟﺍ ﻭﻬﻓ ﻲﺤﺍﺯﻻﺍ لﻐﺸﻟﺍ ﺎﻤﺍ
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﺔﺤﺍﺯﻤﻟﺍ ﺔﻠﺘﻜﻟﺍ
(6.2-b)
ﻟﺘﺯﻴﺢ ﻤﻜﺒﺴ
ﺍﻟﺸﻐل ﺍﻻﺯﺍﺤﻲ ﻭﺭﻤﺯﻩ،ﺭﺨﻵ ﻊﻗﻭﻤ ﻥﻤ ﹰﺎ
(Wdis.)
ﻴﺴﺘﺨﺭﺝ ﺒﺎﻟﻁﺭﻴﻘﺔ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ
.
∆w
net
=
∆w
Disp.
= P
2
ν
2
– P
1
ν
2
=
∆Pν
……….
(6.9)
or
W
net
=
∆PV
………. (6.10)
)
6.3
(
-
ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
Energy Equation for Open System
ﺘﻨﺘﻘل ﺍﻟﻁﺎﻗﺔ ﻓﻲ ﻫﺫﻩ ﺍﻻﻨﻅﻤﺔ ﺒﺄﺸﻜﺎﻟﻬﺎ ﺍﻟﻤﺨﺘﻠﻔﺔ ﻭﻜﺫﻟﻙ ﺍﻟﻜﺘﻠﺔ ﻋﺒﺭ ﺍﻟﺤﺩﻭﺩ
.
ﻭﺍﺹـﺨﻟﺍ ﺕﻨﺎﻜ ﺍﺫﺈﻓ
ﺭﺓ ﺃﻱـﻴﻐﺘﻤ ﺔﻠﺘﻜﻟﺍﻭ
ﺴﺘﻘﺭـﻤﻟﺍ ﺭـﻴﻏ ﻥﺎـﻴﺭﺠﻠﻟ ﺔـﻗﺎﻁﻟﺍ ﺔـﻟﺩﺎﻌﻤﺒ ﺓﺍﺩﺎـﻌﻤﻟﺍ ﻰﻤﺴـﺘﻓ
(Unsteady Flow Energy Equation)
.
ﻴﺭﻤﺯ ﻟﻬﺎ ﺇﺨﺘﺼﺎﺭﺍﹰ
(USFEE)
.
ﺫﺍ ﺍﻟـﻫ ﻥﺇ
ﻥـﻤ ﻉﻭـﻨ
ﺸﻜل،ﹰﺍﺭﻴﺜﻜ ﺎﻨﻤﻬﻴ ﻻ ﻥﺎﻴﺭﺠﻟﺍ
(6.3-a)
.
ﺍﻤﺎ ﺍﻟﻨﻭﻉ ﺍﻵﺨﺭ ﻭﺍﻟﻤﻬﻡ ﻤﻥ ﺍﻟﺠﺭﻴﺎﻥ ﻫﻭ ﺍﻟﺠﺭﻴﺎﻥ ﺍﻟﻤﺴﺘﻘﺭ
(Steady Flow)
ﺼﺎﺩﻓﻨﺎـﻴ ﻱﺫﻟﺍﻭ ،
ﻙﻟﺫﻟ ،ﺭﻘﺘﺴﻤ لﻜﺸﺒ لﻘﺘﻨﺘ ﺔﻗﺎﻁﻟﺍ ﻙﻟﺫﻜﻭ ،لﺩﻌﻤﻟﺍ ﺱﻔﻨﺒ ﺔﻠﺘﻜﻟﺍ ﺝﺭﺨﺘﻭ لﺨﺩﺘ ﺙﻴﺤ ﺔﻴﺴﺩﻨﻬﻟﺍ ﺕﺎﻘﻴﺒﻁﺘﻟﺍ ﻲﻓ
ﺘﺴﻤﻰ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﺒﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻟﻠ
ﺠﺭﻴﺎﻥ ﺍﻟﻤﺴﺘﻘﺭ
(Steady Flow Energy Equation)
ﻴﺭﻤﺯ ﻟﻬﺎ
ـﺇﺨﺘﺼﺎﺭﺍﹰ ﺒ
(SFEE)
ﺸﻜل،
(6.3-b)
.
ﻭﻥـﻜﺘ ﻥﺍ ﺏـﺠﻴ ﻡﺎﻅﻨﻟﺍ ﻲﻓ ﻊﻁﻘﻤ ﻱﺃ ﻲﻓ ﻕﻓﺩﺘﻤﻟﺍ ﻊﺌﺎﻤﻟﺍ ﺹﺍﻭﺨ ﻥﺍ ﻲﻨﻌﻴ ﺭﻘﺘﺴﻤﻟﺍ ﻥﺎﻴﺭﺠﻟﺍ ﻥﺇ
ﺜﺎﺒﺘﺔ ﻭﻻ ﺘﺘﻐﻴﺭ ﻤﻊ ﺘﻐﻴﺭ ﺍﻟﺯﻤﻥ
.
ﺃﻱ ﺍﻥ
:
1
.
ﻜﺘﻠﺔ ﺍﻟﻤﺎﺌﻊ ﺍﻟﻤﺘﺩﻓﻕ ﻓﻲ ﻭﺤﺩﺓ ﺍﻟﺯﻤﻥ ﻭﻤﻌﺩل ﺍ
ﻟﺘﺩﻓﻕ
(Flow Rate)
ﺎﻡـﻅﻨﻟﺍ ﻲﻓ ﻊﻁﻘﻤ ﻱﺃ ﺭﺒﻋ
ﺜﺎﺒﺘﺔ
.
2
.
ﺃﻱ ﺍﻥ ﻤﻌﺩل ﺍﻻﻨﺘﻘﺎل ﻴﻜﻭﻥ ﺜﺎﺒﺘﺎﹰ ﻜﻤﺎ ﻓﻲ،ﻡﻅﺘﻨﻤ ﻲﻨﻤﺯ لﺩﻌﻤﺒ ﻡﺘﻴ ﻥﺍ ﺏﺠﻴ ﺓﺭﺍﺭﺤﻟﺍ ﻭﺍ لﻐﺸﻟﺍ لﺎﻘﺘﻨﺇ
ﺍﻟﻤﺤﺭﻜﺎﺕ ﺍﻟﺒﺨﺎﺭﻴﺔ ﻭﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ ﻭﺍﻟﺜﻼﺠﺎﺕ ﻭﺍﻟﻀﻭﺍﻏﻁ ﻭﻏﻴﺭﻫﺎ
.
)
m
m
(
out
in
&
&
≠
)
m
(
&

)
164
(
ﺸﻜل،ﺡﻭﺘﻔﻤ ﻡﺎﻅﻨ ﺩﻭﺠﻭ ﺽﺭﺘﻔﻨ
(6.3-b)
ـﺎﺌﻊ ﺸـﻤﻟﺍ ﻪـﻟﻼﺨ ﻱﺭﺠﻴ
ﺩﺨﻭلـﻟﺍ ﺩـﻨﻋ ﻪﻁﻭﺭ
)
P
1
،
ν
1
،
µ
1
،
C
1
(
ﻭﻋﻨﺩ ﺍﻟﺨﺭﻭﺝ
)
P
2
،
ν
2
،
µ
2
،
C
2
.(
ﺇﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻠﻴﺔ ﻟﻠﻨﻅﺎﻡ ﻭﻟﻜل
(1kg)
ﺘﺸﻤل
:
1
-
ﻁﺎﻗﺔ ﺍﻭ ﺸﻐل ﺍﻟﺠﺭﻴﺎﻥ
(P
ν)
.
2
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ
(
µ)
.
3
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ
.
4
-
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ
(gz)
.
ﻓﻠﻭ ﺍﻀﻴﻔﺕ ﻜﻤﻴﺔ ﻤﻥ ﺍﻟﺤﺭﺍﺭﺓ
(q)
ﺍﻟﻰ ﺍﻟﻨﻅﺎﻡ ﻓﺴﻴﺘﺤﻭل ﺠﺯﺀ ﻤﻨﻬﺎ
ﺍﻟﻰ ﺸﻐل ﻭﺍﻟﺠﺯﺀ ﺍﻵﺨﺭ ﺍﻟﻰ
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻠﻴﺔ
.
ﻭﺇﺴﺘﻨﺎﺩﺍﹰ ﺍﻟﻰ ﻗﺎﻨﻭﻥ ﺤﻔﻅ ﺍﻟﻁﺎﻗﺔ ﻓﺈﻥ
:
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺨﺎﺭﺠﺔ
(E
out
)
=
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﺔ
(E
in
)
ﺍﻭ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻠﻴﺔ ﺍﻟﻨﻬﺎﺌﻴﺔ
+
ﺸﻐل ﺍﻟﻌﻤﻭﺩ
(ws)
=
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻠﻴﺔ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
+
q
ﻫﺫﻩ ﺍﻟﻤﻌﺎﺩﻟﺔ ﻋﺎﻤﺔ
.
ﻓﺈﺫﺍ ﻜﺎﻥ ﺍﻟﻨﻅﺎﻡ ﻤﻐﻠﻕ ﻭﺒ
ﺎـﻫﺯﻤﺭ ﺔـﻟﺩﺎﻌﻤ ﺞﺘـﻨﻴﻓ ﺔﻨﻤﺎﻜﻟﺍﻭ ﺔﻴﻜﺭﺤﻟﺍ ﻥﻴﺘﻗﺎﻁﻟﺍ لﺎﻤﻫﺈ
(NFEE)
ﻭﺘﻌﺒﻴﺭﻫﺎ ﺍﻟﺭﻴﺎﻀﻲ
:
q – (
∆Pν + w
s
) =
∆µ …………
(6.11)
∴ q – w
net
=
∆µ
………… (6.12)
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
2
C
2
(
)
s
s
12
2
1
2
2
1
2
2
2
2
2
2
2
s
1
2
1
1
1
1
w
P
PE
KE
q
w
P
z
g
2
C
C
q
gz
2
C
P
w
gz
2
C
P
q
+
ν
∆
+
∆
+
∆
+
µ
∆
=
+
ν
∆
+
∆
+
−
+
µ
−
µ
=
+
+
µ
+
ν
+
=
+
+
µ
+
ν
+
ﺸﻜل
)
6.3
(
-
ﺠﺭﻴﺎﻥ ﺍﻟﻤﻭﺍﺌ
ﻊ
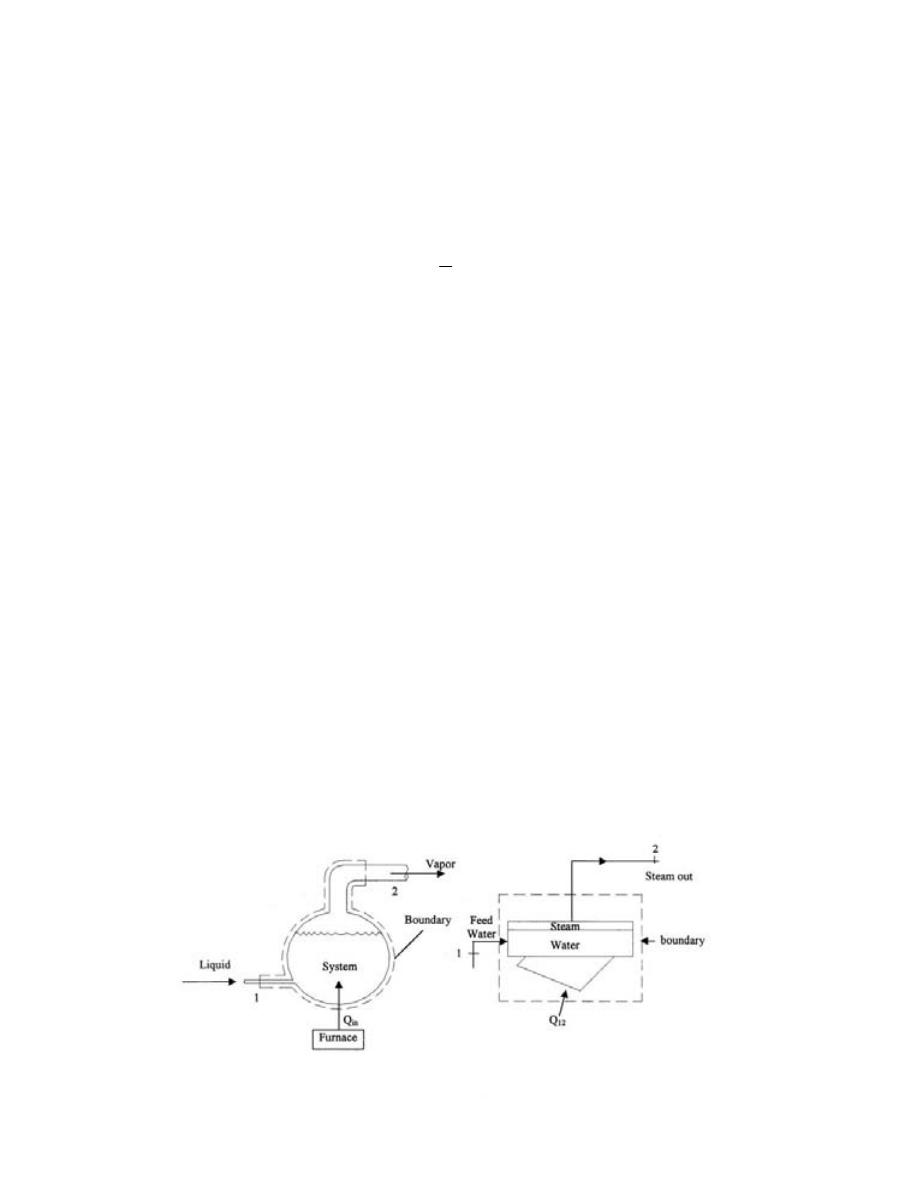
)
165
(
ﻭﺇﺫﺍ ﻜﺎﻥ ﺍﻟﻨﻅﺎﻡ ﻤﻔﺘﻭﺡ ﻓﻴﻨﺘﺞ ﻤﻌﺎﺩﻟﺔ ﺭﻤﺯﻫﺎ
(SFEE)
ﻭﺘﻌﺒﻴﺭﻫﺎ ﺍﻟﺭﻴﺎﻀﻲ
:
q –w
s
=
∆µ + ∆Pν = ∆ (µ + Pν)
..……… (6.13)
∴ q – w
s
=
∆h
………… (6.14)
ـﺇﻥ ﻤﻌﺎﺩﻻﺕ ﺍﻟ
(NFEE)
ـ ﻭﺍﻟ
(SFEE)
ﺘﺩﻋﻰ ﺍﺤﻴﺎﻨﺎﹰ ﺒﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺒﺴﻴﻁﺔ
.
ﻭلــﺠ ﺎﻤﻬﺘﺍﺩــﺤﻭ ﺔــﻗﺎﻁ ﺎــﻤﻫ ﺓﺭﺍﺭــﺤﻟﺍﻭ لﻐﺸــﻟﺍ ﻥﺇ
(J)
.
ﺸﻐل ﺍﻭــﻟﺍ لﺩــﻌﻤ ﺎــﻤﺍ
ﻭﺍﻁـﻟﺍ ﺎﻤﻬﺘﺍﺩﺤﻭ ﺓﺭﺩﻗ ﺎﻤﻬﻓ ﻥﻴﻠﻘﺘﻨﻤﻟﺍ ﺓﺭﺍﺭﺤﻟﺍ
.
ﻓ
ﺎﺩـﺠﻴﺍ ﺩـﻌﺒ
(w
s
)
ﺍﻭ
(q)
ﺴﺏـﺤﺒ
ﺍﻟﻤﻌﺎﺩﻻﺕ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ ﻓﺘﺤﺴﺏ ﺍﻟﻘﺩﺭﺓ ﻜﺎﻟﺘﺎﻟﻲ
:
ﺤﻴﺙ ﺍﻥ ﺘﻤﺜل ﻤﻌﺩل ﺘﺩﻓﻕ ﺍﻟﻤﺎﺌﻊ ﺒﻭﺤﺩﺍﺕ
(kg/s)
.
ﻭﻴﻤﻜﻥ ﻜﺘﺎﺒﺔ
(w
s
)
ﺭـﻜﺫ ﻥﻭﺩﺒ
(s)
ﺃﻱ
(w)
ﻓﻘﻁ
.
)
6.4
(
-
ﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻋﻠﻰ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
Application of the First Law of Thermodynamics on the Open System
ﺔـﺤﻭﺘﻔﻤﻟﺍ ﺔﻤﻅﻨﻸﻟ ﺔﻗﺎﻁﻟﺍ ﺔﻟﺩﺎﻌﻤ ﺎﻬﻴﻠﻋ ﻕﺒﻁﻨﺘ ﻲﺘﻟﺍ ﻕﻓﺩﺘﻟﺍ ﺕﺎﻴﻠﻤﻋ ﻥﺇ
(Energy Equation
for Open System)
ﺘﻜﻭﻥ ﻋﻠﻰ ﻨﻭﻋﻴﻥ
:
ﺴﺘﻘﺭـﻤﻟﺍ ﺭـﻴﻏ ﻕﻓﺩﺘﻟﺍ ﺔﻴﻠﻤﻌﺒ ﻰﻤﺴﻴﻭ لﻭﻻﺍ
(Unsteady
Flow Process)
ﻭﺍﻟﺜﺎﻨﻲ ﻭﻫﻭ ﺍﻟﻤﻬﻡ ﻭﻴﺴﻤﻰ ﺒﻌﻤﻠﻴﺎﺕ ﺍﻟﺘﺩﻓﻕ ﺍﻟﻤﺴﺘﻘﺭ
(Steady Flow Process)
.
ﻭﻫﻨﺎﻙ ﺍﻤﺜﻠﺔ ﻜﺜﻴﺭﺓ ﻋﻠﻰ ﻋﻤﻠﻴﺎﺕ ﺍﻟﺘﺩﻓﻕ ﺍﻟﻤﺴﺘﻘﺭ ﻤﺜل
:
،ﻭﺭﺒﻴﻥـﺘﻟﺍ ،ﻁﻏﺎﻀﻟﺍ ،ﻑﺜﻜﻤﻟﺍ ،لﺠﺭﻤﻟﺍ
ﺼﻤﺎﻡ ﺍﻟﺨﺎﻨﻕ،ﺙﻔﻨﻤﻟﺍ
…
ﺍﻟﺦ
.
ﻭﺴﻨﺘﻨﺎﻭل ﻫﺫﻩ ﺍﻟﻌﻤﻠﻴﺎﺕ ﺒﺸﻜل ﺘﻔﺼﻴﻠﻲ ﻭﻜﻤﺎ ﻴﺄﺘﻲ
:
)
6.4.1
(
-
ﺍﻟﻤﺭﺠل ﻭﺍﻟﻤﻜﺜﻔﺎﺕ ﺍﻟﺒﺨﺎﺭﻴﺔ
Boiler & Steam Condenser
ﻴﺘﻡ ﻓﻲ ﺍﻟﻤﺭﺠل ﺍ
ﺭﺘﻔﻌﻴﻥـﻤ ﻁﻐﻀﻭ ﺓﺭﺍﺭﺤ ﺔﺠﺭﺩﺒ ﺭﺎﺨﺒ ﻰﻟﺍ ﺀﺎﻤﻟﺍ لﻴﻭﺤﺘ ﻱﺭﺎﺨﺒﻟ
.
ﺭﺽـﻐﻟﻭ
ﻲﻨﻤﺯﻟﺍ لﺩﻌﻤﻟﺍ ﻱﻭﺎﺴﻴ ﻲﻨﻤﺯ لﺩﻌﻤﺒ ﺀﺎﻤ ﺔﻴﺫﻐﺘﻟﺍ ﺔﺨﻀﻤ ﺯﻬﺠﺘ لﺠﺭﻤﻟﺍ ﻲﻓ ﺀﺎﻤﻟﺍ ﻯﻭﺘﺴﻤ ﻰﻠﻋ ﺔﻅﻓﺎﺤﻤﻟﺍ
ﺸﻜل،لﺠﺭﻤﻟﺍ ﻥﻤ ﺭﺎﺨﺒﻟﺍ ﻕﻓﺩﺘﻟ
)
6.4
.(
ﻭﻴﺠﺏ ﺘﺠﻬﻴﺯ ﺍﻟﻔﺭﻕ ﺒﺎﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ ﺒﻤﻌﺩل ﺯﻤﻨﻲ ﻤﻨﺘﻅﻡ ﻟﻜﻲ
)
Q
( &
)
s
J
W
(
=
(6.15)
.........
w
.
m
W
s
&
& =
(6.16)
.
..........
q
.
m
Q
&
& =
)
W
( &
)
m
(
&
ﺸﻜل
)
6.4
(
-
ﺍﻟﻤﺭﺠل
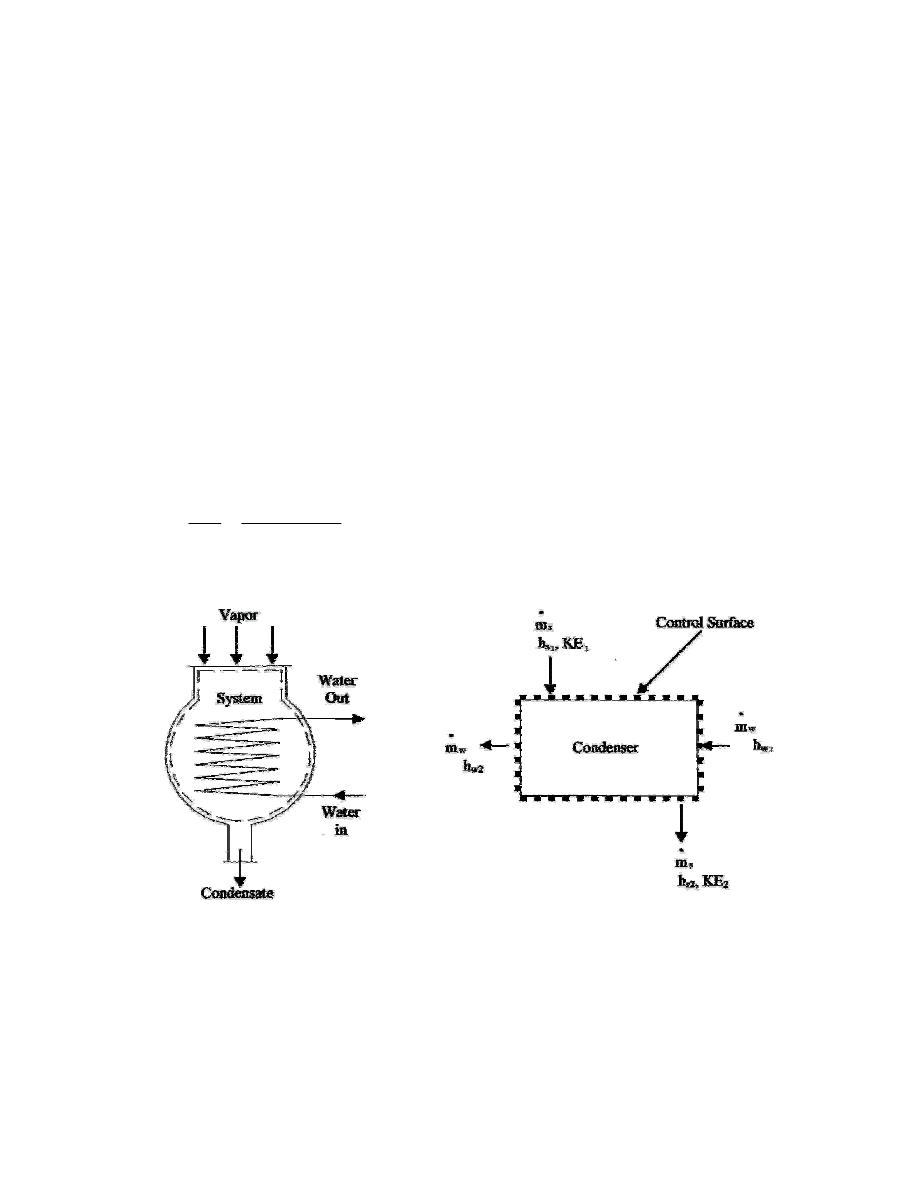
)
166
(
ﻴﺴﺘﻤﺭ ﺇﻨﺘﺎﺝ ﺍﻟﺒﺨﺎ
ﺭ ﺒﻬﺫﺍ ﺍﻟﻤﻌﺩل ﻭﺒﻀﻐﻁ ﻤﻨﺘﻅﻡ
.
ﻊـﻁﻘﻤ ﻱﺃ ﻲﻓ ﻊﺌﺎﻤﻟﺍ ﺹﺍﻭﺨ ﺕﺒﺜﺘ ﻁﻭﺭﺸﻟﺍ ﻩﺫﻫ ﺕﺤﺘ
ﻀﻤﻥ ﺍﻟﻨﻅﺎﻡ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﺯﻤﻥ
.
ﺯـﻴﻤﺘﺘ ﹰﺎﻘﺤﻻ ﻪﻨﻋ ﺙﺩﺤﺘﻨﺴ ﻱﺫﻟﺍ ﻑﺜﻜﻤﻟﺍﻭ لﺠﺭﻤﻟﺍ ﻲﻓ ﻕﻓﺩﺘﻟﺍ ﺕﺍﺀﺍﺭﺠﺇ ﻥﺇ
ﺒﻤﺎ ﻴﻠﻲ
:
1
-
ﻟﺫﺍ ﻴﻤﻜﻥ ﺍﻫﻤﺎل ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ،ﺭﻴﻐﺼ ﻊﺌﺎﻤﻠﻟ ﺝﻭﺭﺨﻟﺍﻭ لﻭﺨﺩﻟﺍ ﻲﺘﻋﺭﺴ ﻥﻴﺒ ﻕﺭﻔﻟﺍ
.
2
-
ﺴﺭﻋﺔ ﺍﻟﻤﺎﺌﻊ
ﺎﻙـﻜﺘﺤﺇ ﺭﻴﺜﺄـﺘ لـﻤﻬﻴ ﺍﺫـﻟ ،ﺝﺭﺨﻤﻟﺍﻭ لﺨﺩﻤﻟﺍ ﺩﻨﻋ ﻪﺘﻋﺭﺴ ﻥﻤ ﺭﻐﺼﺍ ﻡﺎﻅﻨﻟﺍ لﺨﺍﺩ
ﺍﻟﻠﺯﻭﺠﺔ
.
3
-
ﻓﺴﻴﻜﻭﻥ ﺍﻟﻀﻐﻁ ﺜﺎﺒﺕ ﻋﺒﺭ ﻜﺎﻤل ﺍﻟﺠﻬﺎﺯ،ﻙﺎﻜﺘﺤﺇ ﺩﻭﺠﻭ ﻡﺩﻋ ﺽﺍﺭﺘﻓﺇ ﺩﻨﻋ
.
4
-
ﺍﻻﺭﺘﻔﺎﻋﺎﺕ ﺍﻟﺭﺃﺴﻴﺔ ﻟﻔﺘﺤﺔ ﺍﻟﺩﺨﻭل ﻭﺍﻟﺨﺭﻭﺝ ﻤﺘﻘﺎﺭﺒﺔ ﻓﺘﻬﻤل ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ
.
ﺔـﻟﺩﺎﻌﻤ ﺢﺒﺼـﺘ ﻪﻴﻠﻋ
ﺍﻟﻁﺎﻗﺔ ﻜﻤﺎ ﻴﺄﺘﻲ
:
ﺃﻥ ﺍﻟ
ﻲـﺘﻟﺍ ﺓﺭﺍﺭـﺤﻟﺍ ﻥـﻤ ﺭﺒﻜﺃ ﺩﻭﻗﻭﻟﺍ ﻕﺭﺤ ﻥﻤ ﺔﺠﺘﺎﻨﻟﺍﻭ لﺠﺭﻤﻟﺍ ﻰﻟﺍ ﺔﻓﺎﻀﻤﻟﺍ ﺓﺭﺍﺭﺤ
ﺘﺤﻭل ﺍﻟﻤﺎﺀ ﺍﻟﻰ ﺍﻟﺒﺨﺎﺭ ﻟﺫﺍ ﻓﺈﻥ ﻜﻔﺎﺀﺓ ﺍﻟﻤﺭﺠل ﺍﻟﺤﺭﺍﺭﻴﺔ ﺘﻌﺭﻑ ﺒﺎﻟﻤﻌﺎﺩﻟﺔ ﺍﻵﺘﻴﺔ
:
ﺤﻴﺙ ﺍﻥ
)
s
m
&
(
ـﻜﺘﻠﺔ ﺍﻟﺒﺨﺎﺭ ﺍﻟﻤﺘﺩﻓﻕ ﺒﺎﻟ
(kg/s)
،
)
f
m
&
(
ــﺔ ﺒﺎﻟـﻗﺭﺘﺤﻤﻟﺍ ﺩﻭـﻗﻭﻟﺍ ﺔﻠﺘﻜ
(kg/s)
،
(LCV)
ـ ﺍﻟﻘﻴﻤﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ ﻟﻠﻭﻗﻭﺩ ﺒﺎﻟ
(kJ/kg)
.
ﺍﻤﺎ ﺍﻟﻤﻜﺜﻔﺎﺕ ﺍﻟﺒﺨﺎﺭﻴﺔ ﻓﻤﺒﺩﺃ ﻋﻤﻠﻬﺎ ﻋﻜﺱ ﻋﻤل ﺍﻟﻤﺭﺠل ﺍﻟﺒﺨﺎﺭﻱ
.
ﺎـﻤﻜ ﻱﺭﺎـﺨﺒﻟﺍ لﺠﺭﻤﻟﺍ ﻲﻔﻓ
ﺍﻭﻀﺤﻨﺎ ﻫﻨﺎﻙ ﻁﺎﻗﺔ ﺤﺭﺍﺭﻴﺔ ﺘﺠﻬﺯ ﻟﺘﺤﻭﻴل ﺍﻟﺴﺎﺌل ﺍﻟﻰ ﺒﺨﺎﺭ
.
ﺔـﻗﺎﻁﻟﺍ ﻉﺍﺯـﺘﻨﺇ ﺔﻤﻬﻤﺒ ﻡﻭﻘﻴﻓ ﻑﺜﻜﻤﻟﺍ ﺎﻤﺍ
(6.17)
...
..........
)
T
-
(T
.Cp
m
)
h
h
(
m
H
Q
1
2
1
2
s
12
12
&
&
&
&
=
−
=
∆
=
)
Q
(
in
&
(6.18)
...
..........
LCV
.
m
)
h
h
(
m
Q
Q
f
1
2
s
in
12
th
&
&
&
&
−
=
=
η
)
Q
(
12
&
ﺸﻜل
)
6.5
(
-
ﺍﻟﻤﻜﺜﻑ
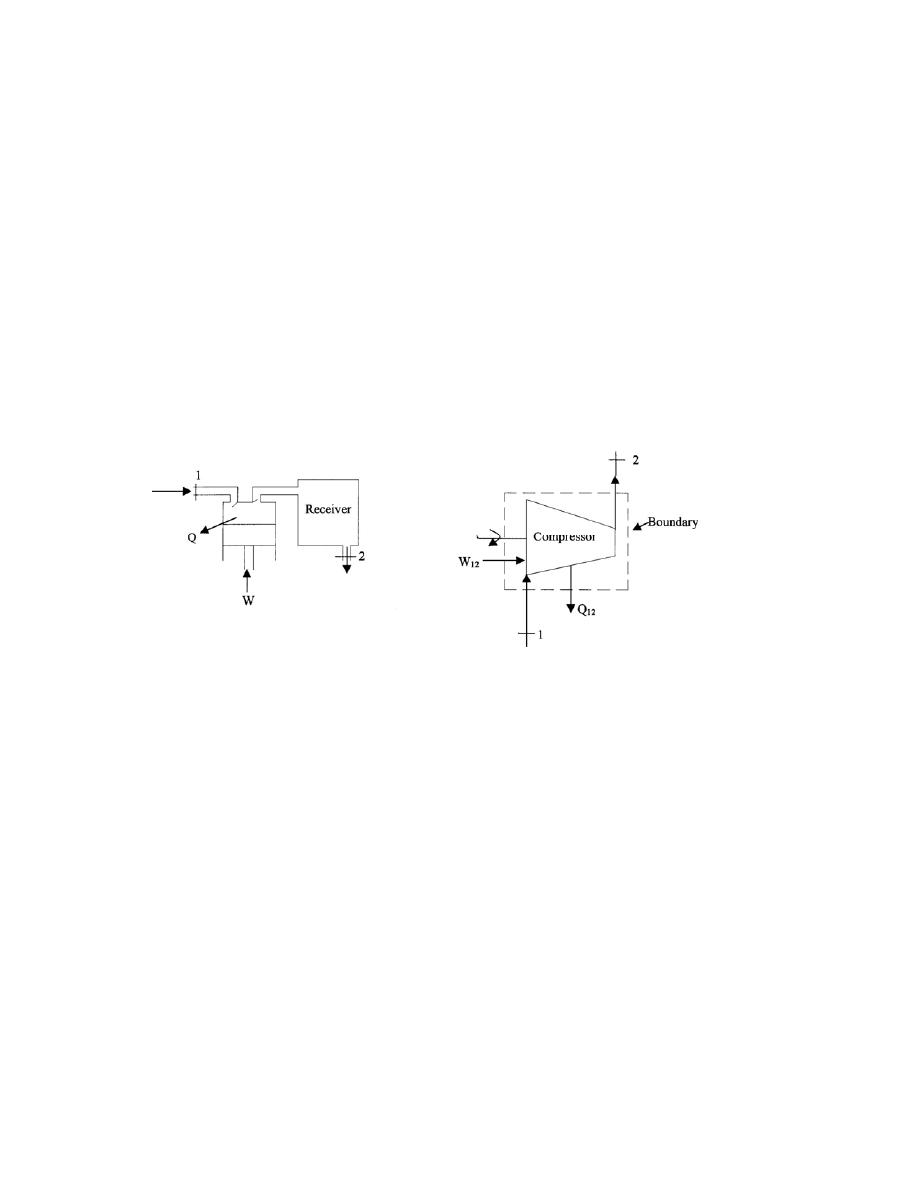
)
167
(
ﺍﻟﺤﺭ
ﺍﺭﻴﺔ ﻤﻥ ﺍﻟﺒﺨﺎﺭ ﻟﺘﺤﻭﻴﻠﻪ ﺍﻟﻰ ﺴﺎﺌل
.
ﺩﻋﻰـﺘ ﻲـﺘﻟﺍ ﻑﺜﻜﻤﻟﺍ لﺌﺎﺴﻟﺍ ﺔﻴﻤﻜ ﻥﻭﻜﺘ ﺭﺍﺭﻘﺘﺴﻻﺍ ﺔﻟﺎﺤ ﻲﻓﻭ
ﺸﻜل،ﻑﻴﺜﻜﺘﻟﺍ ﺞﺘﺎﻨﺒ
)
6.5
(
ﻭﺍﻟﺨﺎﺭﺠﺔ ﻤﻥ ﺍﻟﻤﻜﺜﻑ ﻤﺴﺎﻭﻴﺔ ﻟﻜﺘﻠﺔ ﺍﻟﺒﺨﺎﺭ ﺍﻟﺩﺍﺨﻠﺔ ﺍﻟﻴﻪ
.
ﻓﻌﻨﺩ ﺇﻫﻤﺎل ﺍﻟﺸﻐل
ﻭﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ ﻭﺍﻟﻜﺎﻤﻨﺔ ﻓﺴﻴﻨﺘﺞ ﻤﻥ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﺍﻥ ﻤﻌﺩل ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﺘﻲ ﻴﻨﺘﺯﻋ
ﺎﻓﺊـﻜﺘ ﺩﻴﺭﺒﺘﻟﺍ ﺀﺎﻤ ﺎﻬ
ﺃﻱ،ﺔﻟﺎﻐﺸﻟﺍ ﺓﺩﺎﻤﻠﻟ ﻲﻠﻜﻟﺍ ﻲﺒﻟﺎﺜﻨﻻﺍ ﻲﻓ ﻥﺎﺼﻘﻨﻟﺍ
:
ﻭﺒﻤﺎ ﺃﻥ
h
1
> h
2
ﺃﻱ ﻤﻔﻘﻭﺩﺓ،ﺔﺒﻟﺎﺴ ﺓﺭﺍﺭﺤﻟﺍ ﺓﺭﺎﺸﺇ ﻥﻭﻜﺘ ﺍﺫﻟ ،
.
)
6.4.2
(
-
ﺍﻟﻀﺎﻏﻁ ﻭﺍﻟﺘﻭﺭﺒﻴﻥ
Compressor & Turbine
ﻴﺴﺘﻌﻤل ﺍﻟﻀﺎﻏﻁ ﺠﺯﺀﺍﹰ ﻤﻥ ﺍﻟﺸﻐل ﺍﻟﻤﺠﻬﺯ ﻤﻥ ﻤﺼﺩﺭ ﺨﺎﺭﺠﻲ ﻟﺭﻓﻊ ﻀﻐﻁ ﺍﻟﻐﺎﺯﺍﺕ
.
ﺍﻤﺎ ﺍﻟﺠﺯﺀ
ﺍﻵﺨﺭ ﻓﻴﺘﺤﻭل ﺍﻟﻰ ﺤﺭﺍﺭﺓ ﺘﻨﺘﻘل ﺍﻟﻰ ﺍﻟﻭﺴﻁ ﺍﻟﻤﺤﻴﻁ ﻜﻤﺎ ﻤﻭﻀﺢ ﻓﻲ ﺸﻜل
(6.6)
.
ﺍﻥ ﺍﻟﺘﻭﺭﺒﻴﻥ ﺍﻟﺒﺨﺎﺭﻱ ﺍﻭ ﺍﻟﻐﺎﺯﻱ ﻤﺜل ﺍﻟﻤﺤﺭﻙ ﺍﻟﺘﺭﺩﺩﻱ ﺘﺘﺤﻭل ﻓﻴﻪ ﺒﻌﺽ ﻁﺎﻗﺔ ﺍﻟﻤﺎﺌﻊ ﺍﻟﻰ ﺸﻐل
ﻤﻴﻜﺎﻨﻴﻜﻲ ﻤﻭﺠﺏ ﺒﺼﻔﺔ ﺩﺍﺌﻤﺔ
.
ﻕ ﻻـﻠﻐﻤ ﻡﺎﻅﻨ ﻲﻓ ﻱﺩﺩﺭﺘﻟﺍ ﻙﺭﺤﻤﻟﺍ ﻲﻓ ﻊﺌﺎﻤﻟﺍ ﺩﺩﻤﺘ ﻡﺘﻴ ﻥﻴﺤ ﻲﻓ ﻪﻨﺍ ﻻﺍ
ﻓﺈﻨ،ﻲﻨﺎﻴﺭﺠ
ﻪ ﻓﻲ ﺍﻟﺘﻭﺭﺒﻴﻥ ﻴﻜﻭﻥ ﻜﻨﻅﺎﻡ ﻤﻔﺘﻭﺡ ﺫﻱ ﺍﻟﺠﺭﻴﺎﻥ ﺍﻟﻤﺴﺘﻘﺭ
.
ﻋﻤل ﺍﻟﺘﻭﺭﺒﻴﻥ ﻋﻜﺱ ﻋﻤل ﺍﻟﻀﺎﻏﻁ ﺤﻴﺙ ﻴﺘﺩﻓﻕ ﺍﻟﻤﺎﺌﻊ ﻭﻴﺘﻤﺩﺩ ﺴﺭﻴﻌﺎﹰ ﻓﻲ ﺍﻟﺘﻭﺭﺒﻴﻥ ﻤﺴﺒﺒﺎﹰ ﺩﻭﺭﺍﻥ
ﺍﻟﺯﻋﺎﻨﻑ ﻭﺘﺩﻭﻴﺭ ﻋﻤﻭﺩ ﺍﻟﺘﻭﺭﺒﻴﻥ ﺍﻟﺫﻱ ﻴﺴﺘﻐل ﻟﺘﺩﻭﻴﺭ ﺤﻤل ﺨﺎﺭﺠﻲ ﻜﻤﻭﻟﺩﺓ ﻜﻬﺭﺒﺎﺌﻴﺔ ﻤﺜﻼﹰ ﺸﻜل
)
6.7
.(
(6.19)
.......
..........
)
T
-
(T
.Cp
m
)
h
(h
m
H
Q
1
2
w
w
1
2
w
12
12
&
&
&
&
=
−
=
∆
=
ﺸﻜل
)
6.6
(
-
ﺍﻟﻀﺎﻏﻁ
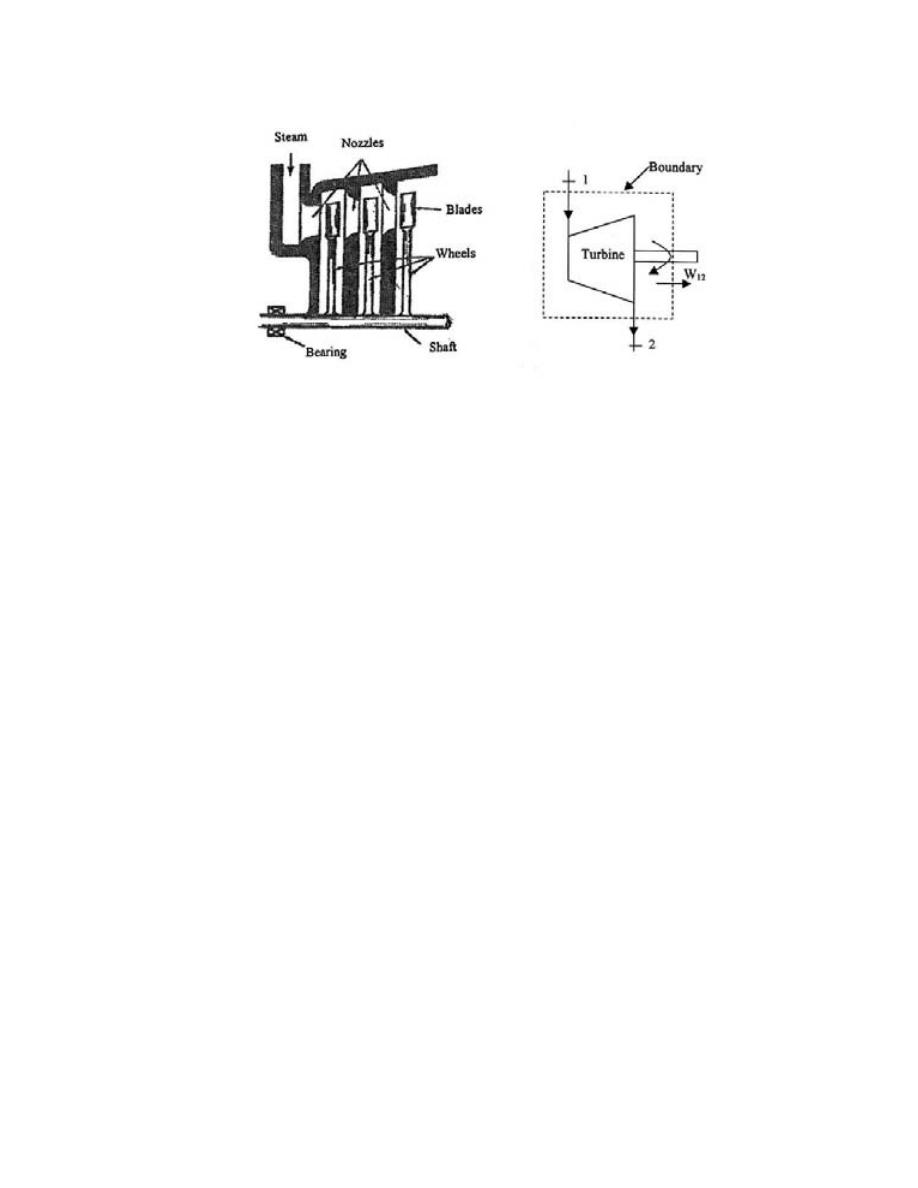
)
168
(
ﺇﻥ ﺇﺠﺭﺍﺀﺍﺕ ﺍﻟﺘﺩﻓﻕ ﻓﻲ ﺍﻟﻀﺎ
ﻏﻁ ﻭﺍﻟﺘﻭﺭﺒﻴﻥ ﺘﺘﻤﻴﺯ ﺒﻤﺎ ﻴﺄﺘﻲ
:
1
-
ﺃﻱ ﺍﻥ،ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﺀﺍﺭﺠﻻﺍ لﻌﺠﻴ ﺎﻤﻤ ،ﻱﺭﺍﺭﺤﻟﺍ لﺩﺎﺒﺘﻠﻟ ﻲﻓﺎﻜﻟﺍ ﺕﻗﻭﻟﺍ ﺭﻓﻭﺘ ﻡﺩﻋﻭ ﻊﺌﺎﻤﻟﺍ ﻕﻓﺩﺘ ﺔﻋﺭﺴ
(Q=0)
.
2
-
ﻋﺩﻡ ﻭﺠﻭﺩ ﻓﺭﻕ ﻜﺒﻴﺭ ﺒﻴﻥ ﺴﺭﻋﺘﻲ ﺍﻟﺩﺨﻭل ﻭﺍﻟﺨﺭﻭﺝ ﻟﻠﻤﺎﺌﻊ ﻓﺘﻬﻤل ﺍﻟﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ
.
3
-
ﺘﻘﺎﺭﺏ ﺍﻻﺭﺘﻔﺎﻋﺎﺕ ﺍﻟﺭﺃﺴﻴﺔ ﻟﻔﺘﺤﺘﻲ ﺍﻟﺩﺨﻭل ﻭﺍﻟﺨﺭﻭﺝ ﻟﺫﺍ ﺘﻬﻤل
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ
.
ﺔـﻟﺩﺎﻌﻤ ﺢﺒﺼﺘ ﻪﻴﻠﻋ
ﺍﻟﻁﺎﻗﺔ ﻜﻤﺎ ﻴﺄﺘﻲ
:
ﻴﻤﺜل ﻤﻌﺩل ﺸﻐل ﺍﻟﻌﻤﻭﺩ ﺍﻟﻤﻨﺘﻘل ﻋﺒﺭ ﺤﺩﻭﺩ ﺍﻟﻨﻅﺎﻡـﻟﺍ ﻥﺇ
.
)
6.4.3
(
-
ﺘﺴﻠﺴل ﺍﻟﻌﻤﻠﻴﺎﺕ ﻓﻲ ﺍﻟﻀﺎﻏﻁ ﻭﺍﻟﺘﻭﺭﺒﻴﻥ
Theoretical Sequence of Processes
ﺍﺘﻀﺢ ﻟﻨﺎ ﺍﻥ،ﺔﻘﻠﻐﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﻲﻓ ﻲﺤﺍﺯﻻﺍ لﻐﺸﻠﻟ ﺎﻨﺘﺴﺍﺭﺩ ﺩﻨﻋ
ﺍﻟﻤﺴﺎﺤﺔ ﺍﻟﻤﻭﺠﻭﺩﺓ ﺘﺤﺕ ﻤﻨﺤﻨﻲ
ﺍﻻﺠﺭﺍﺀ ﻋﻠﻰ ﻤﺨﻁﻁ
(P-
ν)
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل،لﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍ لﺜﻤﻴ
(6.8-a)
.
ﺔـﻟﺩﺎﻌﻤﻠﻟ ﻊﻀـﺨﻴ ﻪﺒﺎﺴﺤﻭ
ﺍﻟﺘﻜﺎﻤﻠﻴﺔ ﻟﺘﻔﺎﻀل ﺩﺍﻟﺔ ﺍﻟﺤﺎﻟﺔ
(d
ν)
ﺃﻱ،
:
∫
ν
=
2
1
Pd
w
(6.20)
.......
)
T
-
.Cp.(T
m
)
h
(h
m
H
W
2
1
1
2
12
s
&
&
&
&
=
−
=
∆
=
−
( )
s
W
&
ﺸﻜل
)
6.7
-(
ﺍﻟﺘﻭﺭﺒﻴﻥ
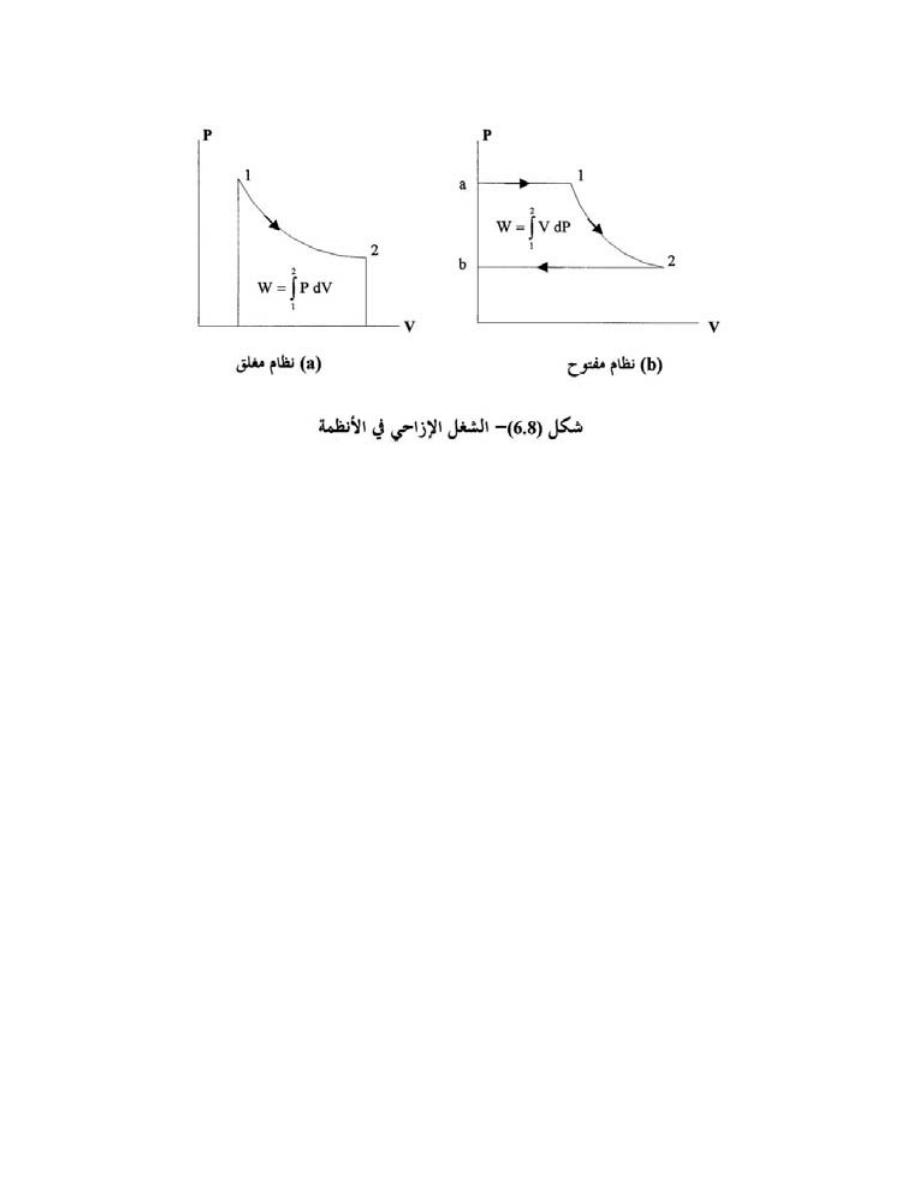
)
169
(
ﺍﻤﺎ ﺒﺎﻟﻨﺴﺒﺔ ﻟﻸﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ ﻓﺈﻥ ﺍﻟﺸﻐل ﻴﻤﺜل ﺍﻟﻤﺴﺎﺤﺔ ﺍﻟﻤﺤﺼﻭﺭﺓ ﺒﺘﺴﻠﺴل ﺍﻟﻌﻤﻠﻴ
ﺎﺕ ﺍﻟﺘﻲ ﻴﻜﻭﻥ
ﺠﺯﺀ ﻤﻨﻬﺎ ﺠﺭﻴﺎﻨﻲ ﻤﻥ
(a)
ﺍﻟﻰ
)
1
(
ﺍﻭ ﻤﻥ
)
2
(
ﺍﻟﻰ
(b)
ﻭﺍﻟﺠﺯﺀ ﺍﻻﺨﺭ ﻻ ﺠﺭﻴﺎﻨﻲ ﻤﻥ،
)
1
(
ﻰـﻟﺍ
)
2
(
ﻜﻤﺎ ﻓﻲ ﺸﻜل
(6.8-b)
.
ﻭﺤﺴﺎﺒﺎﺕ ﺍﻟﺸﻐل ﻴﺨﻀﻊ ﻟﻠﻤﻌﺎﺩﻟﺔ ﺍﻟﺘﻜﺎﻤﻠﻴﺔ ﻟﺘﻔﺎﻀل ﺩﺍﻟﺔ ﺍﻟﺤﺎﻟﺔ
(dP)
ﺃﻱ،
:
ﻴﺘﻜﻭﻥ ﺍﻟﺘﺴﻠﺴل ﺍﻟﻨﻅﺭﻱ ﻟﻠﻌﻤﻠﻴﺎﺕ ﻓﻲ ﺍﻟﻀﺎﻏﻁ ﻤﻥ
)
3
(
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﺕﺎﻴﻠﻤﻋ
)
6.9
(
ﺎـﻫﺯﺠﻭﻨ
ﻜﻤﺎ ﻴﺄﺘﻲ
:
1
-
ﻋﻤﻠﻴﺔ ﺴﺤﺏ ﻤﻥ
(a)
ﺍﻟﻰ
)
1
(
ﺤﻴﺙ ﻴﺘﺩﻓﻕ ﺍﻟﻐﺎﺯ ﺍﻟﻰ ﺍﻟﻀﺎﻏﻁ ﻭﺍﻟﺫﻱ ﻴﻤﻜﻥ ﺘﺼﻭﺭﻩ،ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ
ﻋﺒﺎﺭﺓ ﻋﻥ ﻤﻜﺒﺱ ﻭﺍﺴﻁﻭﺍﻨﺔ
.
ﻭﺒﻤﺎ ﺍﻥ
(Va=0)
ﻓﺴﻴﻜﻭﻥ
:
2
-
ﺇﻨﻀﻐﺎﻁ ﺍﺩﻴﺒﺎﺘﻲ ﻤﻥ
)
1
(
ﺍﻟﻰ
)
2
(
ﻭﻴﻜﻭﻥ
:
(6.21)
..........
dP
Pd
dP
w
2
1
T
∫
ν
+
ν
=
ν
=
(6.22)
.
..........
P
)
(
P
P
w
1
1
a
1
1
ai
ν
=
ν
−
ν
=
ν
∆
=
(6.23)
...
..........
w
w
q
2
1
1
2
0
µ
−
µ
=
µ
−
µ
=
µ
∆
=
−
/
=
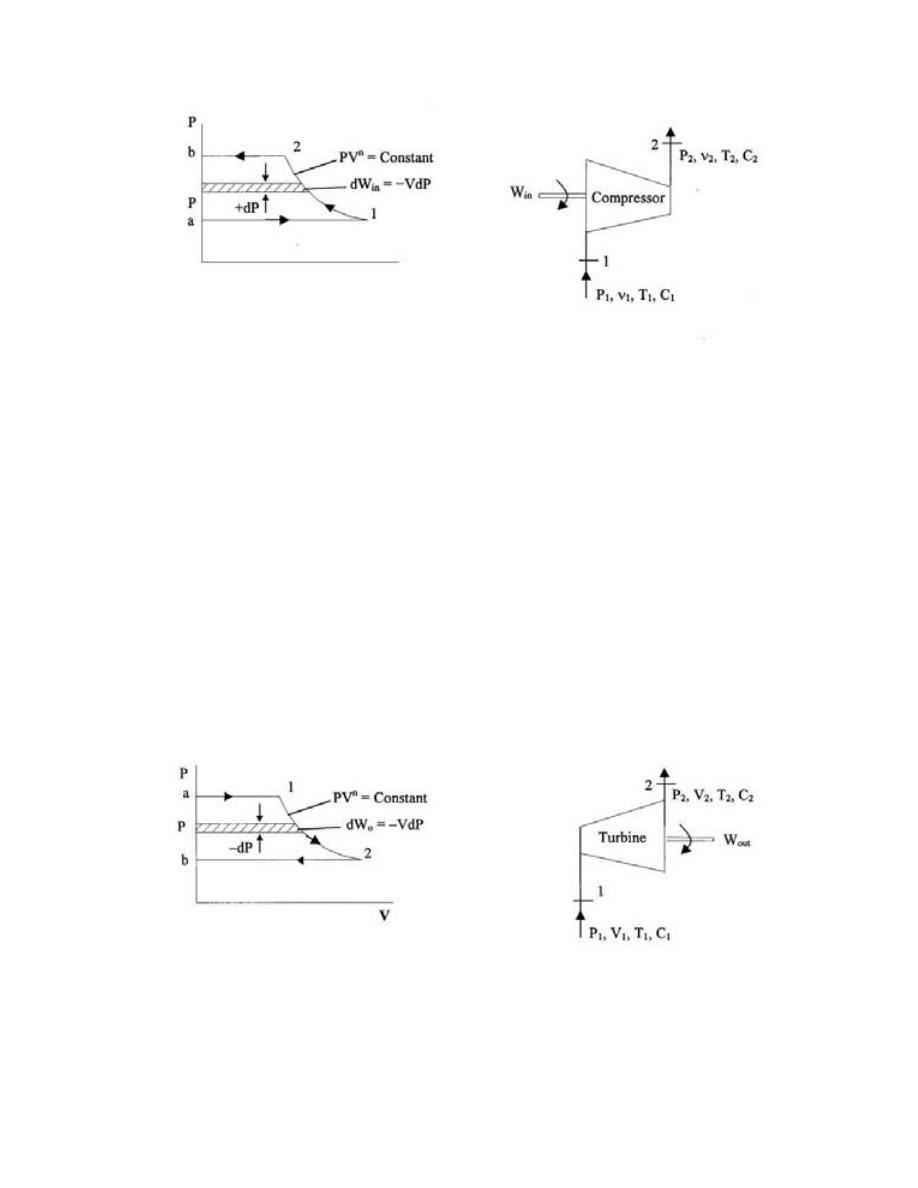
)
170
(
3
-
ﻋﻤﻠﻴﺔ ﺩﻓﻊ ﻤﻥ
)
2
(
ﺍﻟﻰ
(b)
ﺤﻴﺙ ﻴﻨﺩﻓﻊ ﺍﻟﻐﺎ،ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ
ﺎﺭﺝـﺨﻟﺍ ﻰـﻟﺍ ﺯ
.
ﺎ ﺇﻥـﻤﺒﻭ
(V
b
=0)
ﻓﺴﻴﻜﻭﻥ
:
w
2b
= P
∆ν = P
2
(
ν
b
-
ν
2
) = - P
2
ν
2
……… (6.24)
ﺃﻱ،ﺙﻼﺜﻟﺍ ﺕﺎﻴﻠﻤﻌﻟﺍ لﻼﺨ لﻘﺘﻨﻤﻟﺍ لﻐﺸﻟﺍ ﻉﻭﻤﺠﻤ ﻭﻫ لﻘﺘﻨﻤﻟﺍ ﻲﻠﻜﻟﺍ لﻐﺸﻟﺍﻭ
:
w
T
= P
1
ν
1
+ (
µ
1
-
µ
2
) + (-P
2
ν
2
)
= (P
1
ν
1
+
µ
1
) – (P
2
ν
2
+
µ
2
)
= h
1
– h
2
………
(6.25)
ﺇﻥ
ﻜﻤﺎ ﻤﻭﻀﺤﺔ ﻓﻲ ﺍﻟﺸﻜل،ﻥﻴﺒﺭﻭﺘﻟﺍ ﺱﻜﻋ ﻁﻏﺎﻀﻟﺍ ﺕﺎﻴﻠﻤﻋ
)
6.10
.(
ﺸﻜل
)
6.9
(
-
ﺍﻟﺘﺴﻠﺴل ﺍﻟﻨﻅﺭﻱ ﻟﻠﻌﻤﻠﻴﺎﺕ ﻓﻲ ﺍﻟﻀﺎﻏﻁ
ﺸﻜل
)
6.10
(
-
ﺍﻟﺘﺴﻠﺴل ﺍﻟﻨﻅﺭﻱ ﻟﻠﻌﻤﻠﻴﺎﺕ ﻓﻲ ﺍﻟﺘﻭﺭﺒ
ﻴﻥ
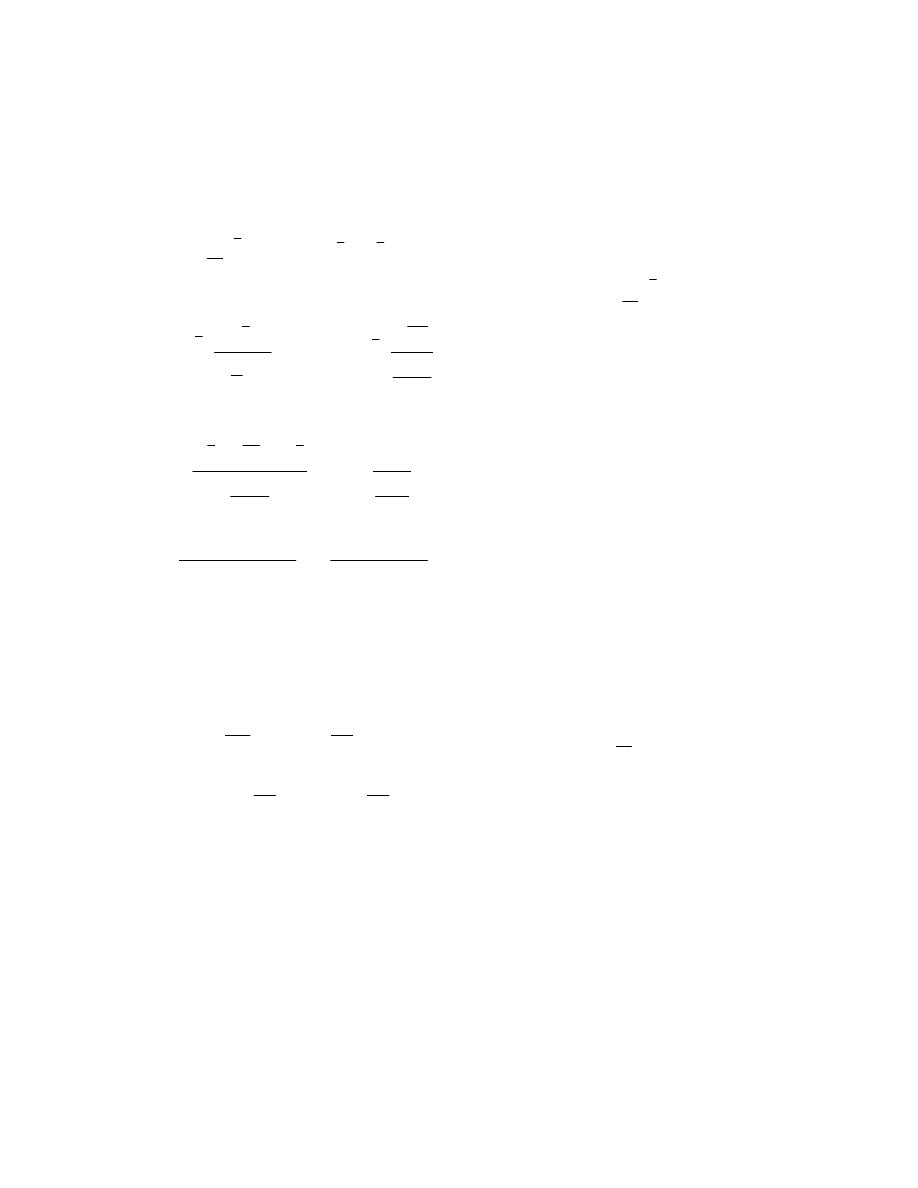
)
171
(
ﺇﺸﺘﻘﺎﻕ ﻤﻌﺎﺩﻟﺔ ﺍﻟﺸﻐل ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
)
ﻀﺎﻏﻁ
(
1- Adiabatic Process
2- Isothermal Process
( )
(6.27)
.
..........
1
)
T
T
(
R
1
)
P
(P
-
1
-
.
P
1
.
P
.
P
-
1
P
P
1
1
P
C
-
dP
.
P
.
C
dP
.
P
C
(6.26)
..
..........
dP
w
1
2
1
1
2
2
P
P
P
P
1
.
1
-
1
P
P
1
1
P
P
1
1
1
2
1
2
1
1
-
1
1
2
1
12
2
1
2
1
2
1
2
1
−
γ
−
γ
−
=
−
γ
ν
−
ν
γ
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
γ
γ
ν
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
γ
−
γ
ν
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
γ
−
γ
ν
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
γ
−
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
ν
−
=
γ
γ
γ
γ
γ
γ
−
γ
γ
γ
+
γ
−
γ
γ
γ
γ
∫
∫
∫
γ
γ
⎟
⎠
⎞
⎜
⎝
⎛
=
ν
∴
=
ν
1
P
C
.
C
P
Q
(6.29)
..
..........
P
P
n
L
RT
P
P
n
L
P
-
P
P
Ln
C
P
dP
C
-
(6.28)
.........
dP
w
1
2
1
2
1
2
2
1
2
1
12
−
=
ν
=
−
=
=
ν
−
=
∫
∫
P
C
.
C
P
=
ν
∴
=
ν
Q
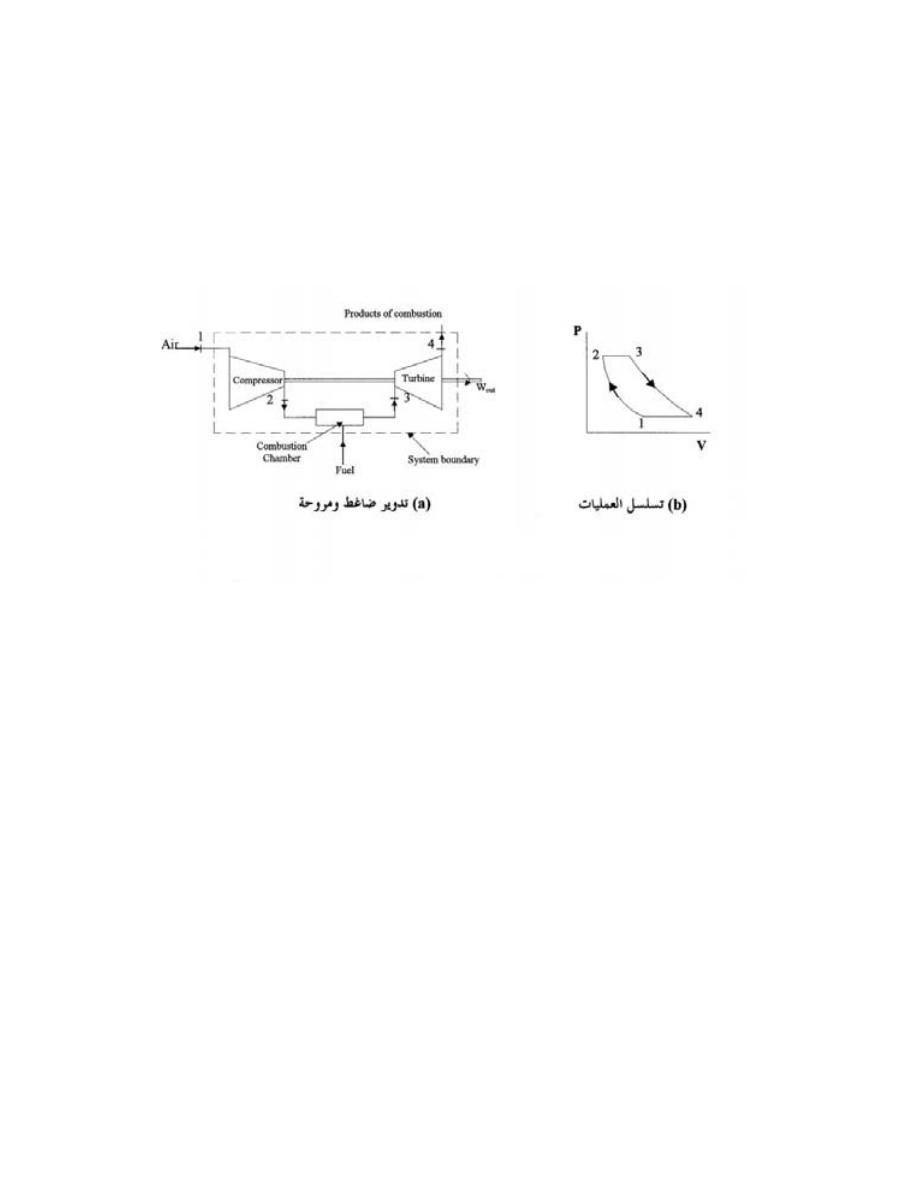
)
172
(
)
6.4.4
(
-
ﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ ﺍﻟﻐﺎﺯﻴﺔ
Gas Turbines
ﺘﺘﻤﻴﺯ ﺍﻟﺘﻭﺭﺒﻴﻨﺎﺕ ﺍﻟﻐﺎﺯﻴﺔ ﺒﺒﺴﺎﻁﺘﻬﺎ ﻓﻲ
ﺩﻡـﻋﻭ ﺩﻭﻗﻭﻟﺍ ﻥﻤ ﺔﺼﻴﺨﺭ ﻉﺍﻭﻨﺍ ﺎﻬﻟﺎﻤﻌﺘﺴﺍﻭ ،ﺏﻴﻜﺭﺘﻟﺍ
ﺤﺎﺠﺘﻬﺎ ﺍﻟﻰ ﻤﺎﺀ ﺘﺒﺭﻴﺩ
.
ﻭﻤﻨﻅﻭﻤﺎﺕ،ﺕﺍﺭﺎﻴﺴﻟﺍ ،ﻥﻔﺴﻟﺍ ،ﺕﺍﺭﻁﺎﻘﻟﺍ ،ﺔﻗﺎﻁﻟﺍ ﺩﻴﻟﻭﺘ ﺕﺎﻁﺤﻤ ﻲﻓ ﻡﺩﺨﺘﺴﺘ ﺍﺫﻟ
ﺩﻓﻊ ﻟﻠﻁﺎﺌﺭﺍﺕ ﺍﻟﻤﺘﻭﺴﻁﺔ ﺍﻟﺴﺭﻋﺔ ﻭﺍﻟﻁﺎﺌﺭﺍﺕ ﺍﻟﻌﻤﻭﺩﻴﺔ
.
ـﺩﺭﺓ ﻓـﻘﻟﺍ ﺔﻴﻘﺒ ﻡﺩﺨﺘﺴﻴﻭ ﺀﺍﻭﻬﻟﺍ ﻁﻏﺎﻀ لﻴﻐﺸﺘﺒ ﻥﻴﺒﺭﻭﺘﻟﺍ ﻡﻭﻘﻴ ﺕﺍﺭﺌﺎﻁﻟﺍ ﻲﻓ
ﺔـﺤﻭﺭﻤ ﺓﺭﺍﺩﺇ ﻲ
ﺤﻴﺙ ﻴﺭﻜﺏ ﺍﻟﺘﻭﺭﺒﻴﻥ ﻭﺍﻟﻀﺎﻏﻁ،ﻲﻨﻴﺒﺭﻭﺘﻟﺍ ﻲﺤﻭﺭﻤﻟﺍ ﻙﺭﺤﻤﻟﺎﺒ ﻙﺭﺤﻤﻟﺍ ﺍﺫﻫ ﻰﻤﺴﻴ ﺍﺫﻟ ،ﺔﻴﻌﻓﺩﻟﺍ ﺓﺭﺌﺎﻁﻟﺍ
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﺔﺤﻭﺭﻤﻟﺍ ﺭﻴﻭﺩﺘ ﺩﻭﻤﻋ ﺱﻔﻨ ﻰﻠﻋ
(6.11-a)
.
ﺔـﻴﻟﺎﺜﻤﻟﺍ ﺀﺍﻭﻬﻟﺍ ﺓﺭﻭﺩﻟ ﺕﺎﻴﻠﻤﻌﻟﺍ لﺴﻠﺴﺘ ﺎﻤﺍ
ﻭﺍﻟﻤﻭﻀﺤﺔ ﻓﻲ ﺸﻜل
(6.11-b)
ﺘﻜﻭﻥ ﻜﻤﺎ ﻴﺄﺘﻲ
:
1
-
ﻴﻀﻐﻁ ﺍﻟﻬﻭﺍﺀ ﺍﺩﻴﺎﺒﺎﺘﻴ
ﺎﹰ ﻓﻲ ﺍﻟﻀﺎﻏﻁ
(1
→2)
.
2
-
ﺘﻀﺎﻑ ﺤﺭﺍﺭﺓ
(2
→3)
ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
.
3
-
ﻴﺘﻤﺩﺩ ﺍﻟﻬﻭﺍﺀ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﻓﻲ ﺍﻟﺘﻭﺭﺒﻴﻥ
(3
→4)
ﻓﻴﻘﻭﻡ ﺒﺘﺸﻐﻴل ﺍﻟﻀﺎﻏﻁ ﻭﺇﻨﺘﺎﺝ ﻗﺩﺭﺓ ﻓﺎﺌﻀﺔ،
(W
out
)
.
4
-
ﻁﺭﺩ ﺤﺭﺍﺭﺓ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
(4
→1)
ﺤﺘﻰ ﻴﻌﻭﺩ ﺍﻟﻬﻭﺍﺀ ﺍﻟﻰ ﺤﺎﻟﺘﻪ ﺍﻻﺼﻠﻴﺔ
.
ﺢـﻀﻭﻴ ﻲﻟﺎﺘﻟﺍ لﺎﺜﻤﻟﺍﻭ
ﺍﻟﻤﻨﺎﻗﺸﺔ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ
.
ﺸﻜل
)
6.11
(
-
ﺍﻟﺘﻭﺭﺒﻴﻥ ﺍﻟﻐﺎﺯﻱ ﻓﻲ ﻁﺎﺌﺭﺓ
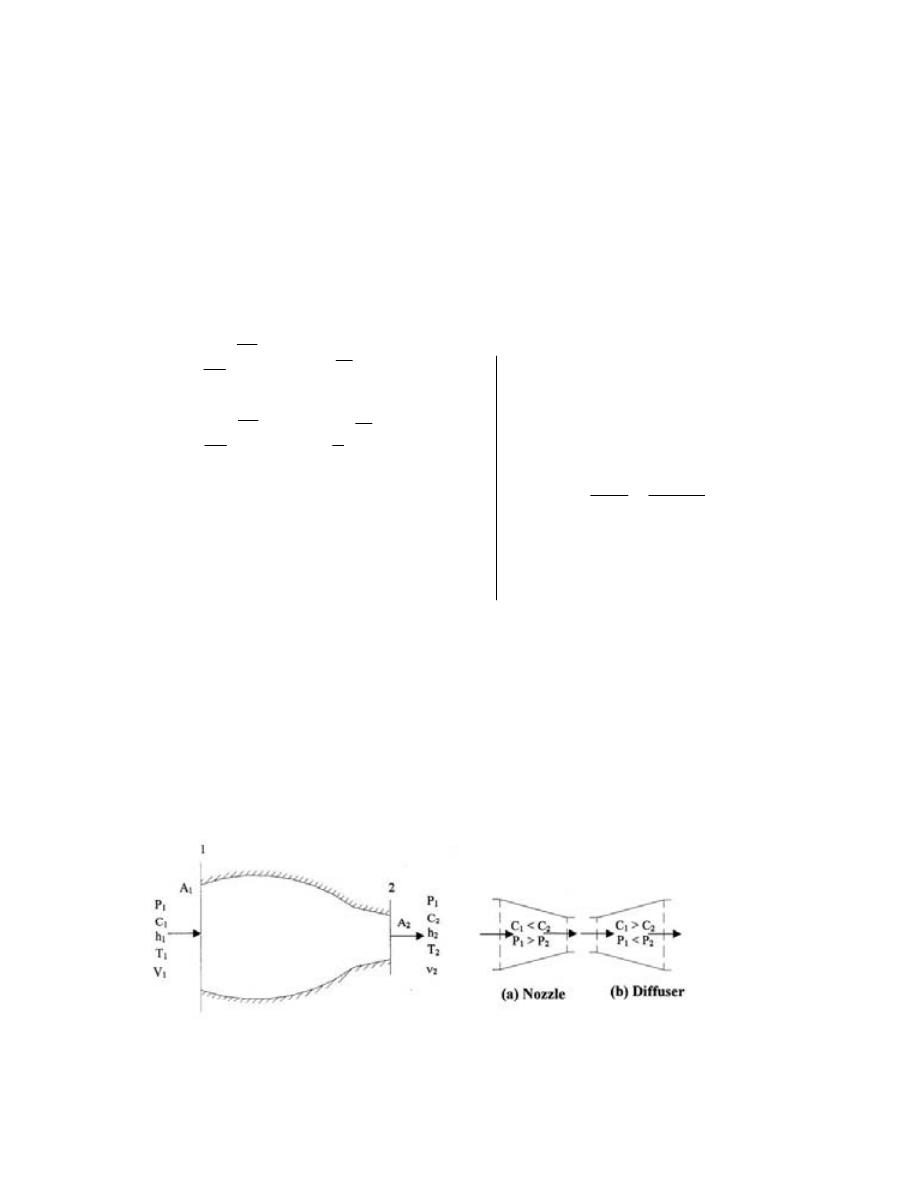
)
173
(
ﻤﺜﺎل
)
6.1
(
ﻫﻭﺍﺀ ﻀﻐﻁﻪ
(101 kPa)
ﻭﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(27
°C)
.
ﺴﺒﺔـﻨ ﻥﻭـﻜﺘ ﺙﻴﺤﺒ ﻁﻏﺎﻀ ﻲﻓ ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﻁﻐﻀﻴ
ﺍﻟﻀﻐﻁ
)
1
/
5
(
ﻪـﺘﺭﺍﺭﺤ ﺔـﺠﺭﺩ ﺢﺒﺼـﺘ ﺙﻴﺤﺒ ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ ﻱﺭﺍﺭﺤ لﺩﺎﺒﻤ ﻲﻓ ﺓﺭﺍﺭﺤ ﺏﺴﺘﻜﻴ ﻡﺜ ،
(1050
°C)
ﻭﺩـﻌﻴﻭ ﺔﻀﺌﺎﻓ ﺔﻗﺎﻁ ﺝﺎﺘﻨﺍ ﻊﻤ ﻁﻏﺎﻀﻟﺍ لﻴﻐﺸﺘﺒ ﻡﻭﻘﻴﻭ ﺩﺩﻤﺘﻴﻟ ﻥﻴﺒﺭﻭﺘ ﻰﻟﺍ ﺀﺍﻭﻬﻟﺍ لﺨﺩﻴ ﻡﺜ
ﺍﻟﻰ ﻀﻐﻁﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﺍﻭﺠﺩ ﻟﻜل
(1kg)
ﻤﻥ ﺍﻟﻬﻭﺍﺀ
) :
ﺃ
(
ﺍﻟﺸﻐل ﺍﻟﺼﺎﻓﻲ
) .
ﺏ
(
ﻜﻔﺎﺀﺓ ﺍﻟﻤﻨﻅﻭﻤﺔ
.
ﺎﹰـﻤﻠﻋ
ﺃﻥ
:
γ=1,4
،
Cp=1,004 kJ/kg.K
-
ﺇﺴﺘﻨﺎﺩﺍﹰ ﺍﻟﻰ ﺸﻜل
)
6.11
(
ﻓﺴﻴﻜﻭﻥ
:
q
in
= C
p
(T
3
– T
2
)
= 1
.004 (1323–475.37)
= 851.17kJ/kg
w
T
= C
p
(T
3
-T
4
) = 1.004 (1323-835.4)
= 489.67 kJ/kg
w
c
= C
p
(T
1
– T
2
)
= 1.004 (300-475.4) = -175.92 kJ/kg
w
net
= w
T
+ w
c
= 489.67 + (-175.92) = 313.75 kJ/kg
6.4.5
ﺍﻟﻤﻨﻔﺙ
)
ﺍﻟﺒﻭﻕ
(
ﻭﺍﻟﻨﺎﺸﺭ
)
ﺍﻟﻤﺒﺩﺩ
(
Nozzle & Diffuser
ﻫﻲ ﻋﺒﺎﺭﺓ ﻋﻥ ﺍﻨﺎﺒﻴﺏ ﺩﺍﺌﺭﻴﺔ ﻤﺴﺎﺤﺔ ﻤﻘﻁﻌﻲ ﺍﻟﺩﺨﻭل ﻭﺍﻟﺨﺭﻭﺝ ﻓﻴﻬﺎ ﻤﺘﻐﻴﺭﺓ
.
ﻜلـﺸ ،ﺙـﻔﻨﻤﻟﺎﻓ
(6.12-a)
ﺴﺎﺭﻉـﺘ ﻰـﻟﺍ ﻱﺩﺅﻴ ﺎﻤﻤ ﺝﺭﺨﻤﻟﺍ ﻰﻟﺍ لﺨﺩﻤﻟﺍ ﻥﻤ ﻁﻐﻀﻟﺍ ﺽﺎﻔﺨﻨﺍ ﻪﻨﻋ ﺞﺘﻨﻴ ﺙﻴﺤﺒ ﻡﻤﺼﻤ ،
ﺘﺩﻓﻕ ﺍﻟﻤﺎﺌﻊ
.
ﺸﻜل،ﺭﺸﺎﻨﻟﺍ ﺎﻤﺍ
(6.12-b)
ﻀﻐﻁـﻟﺍ ﺩﺎﻴﺩﺯﺇ ﻪﻨﻋ ﺞﺘﻨﻴ ﺙﻴﺤﺒ ﻡﻤﺼﻤ ﻭﻬﻓ ،ﺙﻔﻨﻤﻟﺍ ﺱﻜﻋ ،
ﺃﻱ ﺍﻟﺤﺼﻭل ﻋﻠﻰ ﺍﻗﺼﻰ،ﻕﻓﺩﺘﻟﺍ ﺔﻋﺭﺴ ﺽﺎﻔﺨﻨﺇ ﻰﻟﺍ ﻱﺩﺅﻴ ﺎﻤﻤ ،ﺝﺭﺨﻤﻟﺍ ﻰﻟﺍ لﺨﺩﻤﻟﺍ ﻥﻤ
ﻗﻴﻤﺔ ﻟﻠﻀﻐﻁ
369
.
0
17
.
851
75
.
313
q
w
in
net
=
=
=
η
( )
K
4
.
835
5
1
1323
P
P
.
T
T
K
4
.
475
5
300
P
P
.
T
T
4
.
1
4
.
0
1
3
4
3
4
4
.
1
4
.
0
1
1
2
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
γ
−
γ
γ
−
γ
ﺸﻜل
)
6.3
(
-
ﺍﻟﻤﻨﺎﻓﺙ ﺃﻭ ﺍﻟﻨﻭﺯﻻﺕ
)
ﺍﻟﺒﻭﻕ
(

)
174
(
ﻋﻠﻰ ﺤﺴﺎﺏ ﺍﻨﺨﻔﺎﺽ ﺍﻟﺴﺭﻋﺔ
.
ﺎﺕـﺒﻜﺭﻤﻟﺍﻭ ﺕﺍﺭﺌﺎـﻁﻟﺍ ﺫﺨﺂﻤﻟ ﻊﻓﺩ ﺓﻭﻗ ﺩﻴﻟﻭﺘ ﻲﻓ ﺓﺭﻴﺒﻜ ﺔﻴﻤﻫﺍ ﺙﻓﺎﻨﻤﻠﻟﻭ
ﺓﺭﻴﻐـﺼ ﺔﻋﺭﺴﺒ لﺠﺭﻤﻟﺍ ﻥﻤ ﺝﺭﺎﺨﻟﺍ ﺭﺎﺨﺒﻟﺍ ﹰﻼﺜﻤﻓ ،ﺔﻴﺭﺎﺨﺒﻟﺍ ﺎﺕﻨﻴﺒﺭﻭﺘﻟﺍ لﻴﻐﺸﺘ ﻲﻓ ﻙﻟﺫﻜﻭ ﺦﻴﺭﺍﻭﺼﻟﺍﻭ
ﻭﻫﺫﺍ ﻴﻌﻨﻲ،ﻥﻴﺒﺭﻭﺘﻟﺍ ﺵﻴﺭﺒ ﻪﻤﺍﺩﻁﺼﺇ لﺒﻗ ﺙﻔﻨﻤﻟﺍ لﻼﺨ ﻪﻘﻓﺩﺘﺒ ﻪﺘﻋﺭﺴ ﺩﺍﺩﺯﺘ
ﺍﻥ ﻓﺘﺭﺓ ﺘﻭﺍﺠﺩ ﺍﻟﻤﺎﺌﻊ ﻓﻲ
ﺩﺩـﻤﺘﻟﺍ ﺩـﻌﻴ ﻙﻟﺫـﻟ ،ﻁﻴﺤﻤﻟﺍﻭ ﻡﺎﻅﻨﻟﺍ ﻥﻴﺒ ﻱﺭﺍﺭﺤﻟﺍ لﺩﺎﺒﺘﻠﻟ ﻲﻓﺎﻜﻟﺍ ﺕﻗﻭﻟﺍ ﺭﻓﻭﺘﻴ ﻻ ﺍﺫﻟ ،ﺓﺭﻴﺼﻗ ﺙﻔﻨﻤﻟﺍ
ﺃﻱ،ﻲﺘﺎﺒﺎﻴﺩﺍ
(q=0)
.
ﺃﻱ،لﻐـﺸ لﺎـﻘﺘﻨﺇ لﺼﺤﻴ ﻼﻓ ﺔﻜﺭﺤﺘﻤ ﺀﺍﺯﺠﺃ ﻰﻠﻋ ﺙﻔﻨﻤﻟﺍ ﻱﻭﺘﺤﻴ ﻻ
(w=0)
.
ﺃﻱ،ﺓﺭﻴﻐﺼ ﺔﻴﺴﺃﺭﻟﺍ ﺕﺎﻋﺎﻔﺘﺭﻻﺍ ﻥﻴﺒ ﻑﻼﺘﺨﻻﺍﻭ
(
∆PE=0)
.
ﺍﻤﺎ
ﺍﻟﺴﺭﻋﺔ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
(C
1
)
ﻴﻤﻜﻥ ﺇﻫﻤﺎﻟﻬﺎ
ﻟﻜﻭﻨﻬﺎ ﺼﻐﻴﺭﺓ ﻤﻘﺎﺭﻨﺔﹰ ﺒﺎﻟﺴﺭﻋﺔ ﺍﻟﻨﻬﺎﺌﻴﺔ
(C
2
)
.
ﻟﺫﺍ ﺘﺼﺒﺢ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻟﻠﻤﻨﻔﺙ ﺍﻭ ﺍﻟﻨﺎﺸﺭ ﻜﻤﺎ ﻴﺄﺘﻲ
:
ﻭﻜﻤﺎ ﻤﺭ ﺒﻨﺎ ﺴﺎﺒﻘﺎﹰ ﻋﻨﺩ ﺩﺭﺍﺴﺘﻨﺎ ﻟﻠﻁﺎﻗﺔ ﺍﻟﺤﺭﻜﻴﺔ ﻓﺈﻥ
ﺕـﻨﺎﻜ ﺍﺫﺇﻭ ،
ـﺍﻟ
(
∆h)
ﺒﻭﺤﺩﺍﺕ
(kJ/kg)
ﻓﺴﺘﻜ
ﻭﻥ ﺍﻟﻤﻌﺎﺩﻟﺔ
)
6.31
(
ﻜﺎﻟﺘﺎﻟﻲ
:
ﻭﺒﺎﻟﺘﺎﻟﻲ ﻓﺈﻥ ﺍﻟﺴﺭﻋﺔ
(C)
ﺴﺘﻜﻭﻥ ﺒﻭﺤﺩﺍﺕ
.
ﻤﺜﺎل
)
6.2
(
1
-
ﻫﻭﺍﺀ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(35
°C)
ﻴﺩﺨل ﻤﻨﻔﺙ ﺒﺴﺭﻋﺔ
)
0.7m/s
(
ﺭﺍﺭﺓـﺤ ﺔﺠﺭﺩﺒ ﺝﺭﺨﻴﻭ
(10
°C)
.
ﺇﺫﺍ ﻜﺎﻥ،ﺝﻭﺭﺨﻟﺍ ﺔﻋﺭﺴ ﺏﺴﺤﺍ
Cp = 1.005 kJ / kg . K
2
-
ﻋﻨﺩ ﺇﻓﺘﺭﺍﺽ ﺍﻥ ﺍﻟﺴﺭﻋﺔ ﺍﻻﺒﺘﺩﺍﺌﻴﺔ
ﺼﻔﺭ ﻓﻲ ﺍﻟﺴﺅﺍل ﺍﻟﺴﺎﺒﻕ
.
ﺍﺤﺴﺏ ﺍﻟﺴﺭﻋﺔ ﺍﻟﻨﻬﺎﺌﻴﺔ
.
(6.31)
..........
h
2
C
C
2
C
C
h
(6.30)
.........
KE
h
0
12
2
1
2
2
2
1
2
2
12
12
12
∆
−
=
∴
−
+
∆
=
∆
+
∆
=
)
s
/
m
10
kg
/
kJ
(
2
2
3
=
(6.32)
..........
h
10
2
C
C
s
m
10
2
s
m
kg
/
kJ
s
/
m
10
.
kg
/
kJ
2
s
m
h
2
C
C
12
3
2
1
2
2
2
2
3
2
2
2
2
3
2
2
12
2
1
2
2
∆
×
−
=
∴
×
−
⇒
−
⇒
∆
−
=
)
s
m
(
s
m
166
.
224
)
50250
(
49
.
0
(-25.125)
2000
)
7
.
0
(
h
2000
C
C
kg
kJ
-25.125
35)
-
(10
005
.
1
)
T
T
(
C
h
2
12
2
1
2
1
2
p
12
=
+
=
×
−
=
∆
−
=
=
=
−
=
∆
s
m
165
.
224
50250
)
125
.
25
(
2000
0
h
2000
0
C
12
2
=
=
=
−
−
=
∆
−
=
t
1
=35
o
C
t
2
=10
o
C
C
2
=?
C
1
=0.7m/s
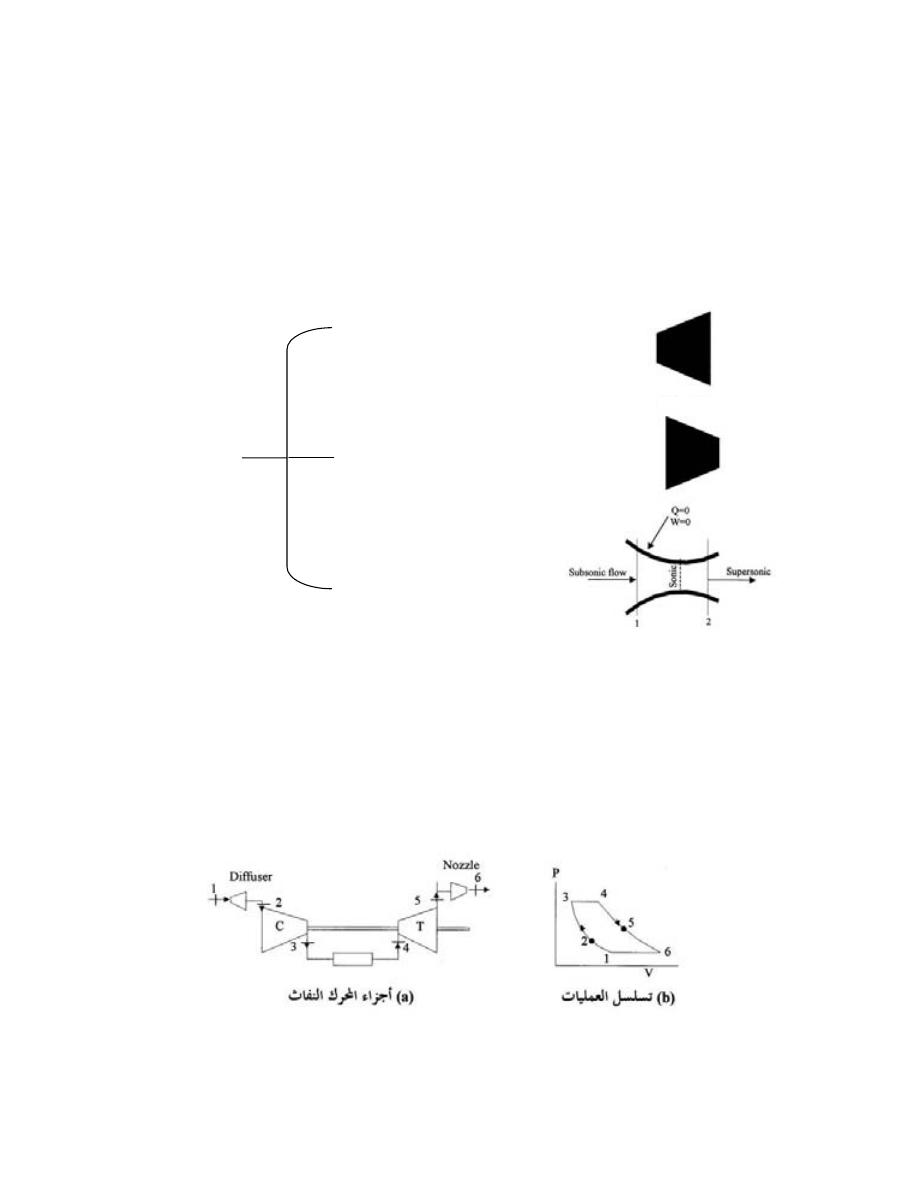
)
175
(
ﺴﺎﺏـﺤ ﻡﺘـﻴﻭ ،ﻲﻟﺎﺜﻤﻟﺍ ﺯﺎﻐﻟﺍ ﻥﻴﻨﺍﻭﻗ ﻕﻴﺒﻁﺘ ﻥﻜﻤﻴ ﻻ ،ﺓﺭﺨﺒﻻﺍﻭ ﺔﻴﻘﻴﻘﺤﻟﺍ ﺕﺍﺯﺎﻐﻠﻟ ﺔﺒﺴﻨﻟﺎﺒ
(
∆h)
ﺒﺎﻟﺭﺠﻭﻉ ﺍﻟﻰ ﺠﺩﺍﻭل ﺍﻟﺨﻭﺍﺹ
.
ﻀﻊـﺨﻴ ،ﻲﺘﺎـﺒﺎﻴﺩﺍ ﺙﻔﻨﻤﻟﺍ ﻲﻓ ﺩﺩﻤﺘﻟﺍ ﻥﺈﻓ ﺔﻴﻟﺎﺜﻤﻟﺍ ﺕﺍﺯﺎﻐﻠﻟ ﺔﺒﺴﻨﻟﺎﺒ ﺎﻤﺍ
ﻟﻠﻌﻼﻗﺔ
).
C
PV
=
γ
(.
ﻭﺍﻟﻤﺨﻁﻁ ﺍﻟﺘﺎﻟﻲ ﻴﺒﻴﻥ ﺍﻻﻨﻭﺍﻉ ﺍﻟﻤﺨﺘﻠﻔﺔ ﻟﻠﻤﻨﺎﻓﺙ ﻭﺍﻟﻨﺎﺸﺭﺍﺕ
)
6.4.6
(
-
ﻤﺤﺭﻙ ﺍﻟﻁﺎﺌﺭﺓ ﺍﻟﺩﻓﻌﻲ
)
ﺍﻟﻨﻔﺎﺙ
(
Air Craft Propulsion
ﻰـﻠﻋ ﺎﻬﺘﻋﺭـﺴ ﺩـﻴﺯﺘ ﻲـﺘﻟﺍ ،ﺔﻴﻟﺎﻌﻟﺍ ﺕﺎﻋﺭﺴﻟﺍ ﺕﺍﺫ ﺕﺍﺭﺌﺎﻁﻟﺍ ﻲﻓ
(800Km/h)
ﺴﺘﺨﺩﻡـﺘ ،
ﺍﻟﻤﺤﺭﻜﺎﺕ ﺍﻟﺘﻭﺭﺒﻴﻨﻴﺔ ﺍﻟﺩﻓﻌﻴﺔ ﻟﻠﺤﺼﻭل ﻋﻠﻰ ﻗﻭﺓ ﺍﻟﺩﻓﻊ ﺘﺴ
ﻲـﻓ ﺎﻫﺀﺍﺯﺠﺍ ﺔﺤﻀﻭﻤﻟﺍ ﺔﺜﺎﻔﻨﻟﺍ ﺕﺎﻜﺭﺤﻤﻟﺎﺒ ﻰﻤ
ﺍﻟﺸﻜل
(6.13-a)
.
ﻭﺘﺴﻠﺴل ﻋﻤﻠﻴﺎﺘﻬﺎ ﻤﻭﻀﺤﺔ ﻓﻲ ﺸﻜل
(6.13-b)
ﻭﻫﻲ ﻜﺎﻟﺘﺎﻟﻲ،
:
1
-
ﻴﺩﺨل ﺍﻟﻬﻭﺍﺀ ﺍﻟﻨﺎﺸﺭﺓ ﺒﺴﺭﻋﺔ ﻋﺎﻟﻴﺔ
.
ﻰـﻟﺍ ﻱﺩﺅﻴ ﻱﺭﺍﺭﺤ ﻯﻭﺘﺤﻤ ﻰﻟﺍ ﺀﺍﻭﻬﻠﻟ ﺔﻴﻜﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍ لﻭﺤﺘﺘ
ﺯﻴﺎﺩﺓ ﻓﻲ ﺍﻟﻀﻐﻁ
(1
→2)
.
ﻴﻀﺎﻑ ﺍﻟﻰ ﻀﻐﻁ ﺍﻟﻀﺎﻏﻁ
(2
→3)
ﻀﻐﺎـﻨﺇ ﺔـﻴﻠﻤﻋ ﻲـﻓ
ﺴﻤﻰـﺘ ﻁ
ﻀﺎﻏﻁﻲــﺘﻟﺍ ﻁﺎﻐﻀــﻨﻻﺎﺒ
(Ram Compression)
ﺴﻥ ﺍﻻﺩﺍﺀــﺤﺘ ﻰــﻟﺍ ﻱﺩﺅــﻴ
.
ﺭﺍﺀــﺠﻻﺍ ﻥﺇ
(1
→2→3)
ﺃﺩﻴﺎﺒﺎﺘﻴﺎﹰ
.
Nozzle
Convergent Nozzle
ﻓﻭﻫﺔ ﻤﻠﺘﻤﺔ ﺍﻭ ﻤﺘﻀﻴﻘﺔ
)
ﺍﻟﻤﻨﻔﺙ
(
Divergent Nozzle
ﻓﻭﻫﺔ ﻤﻨﻔﺭﺠﺔ
)
ﺍﻟﻨﺎﺸﺭﺓ
(
(Diffuser)
Convergent - Divergent
Nozzle
ﺍﻟﻔﻭﻫﺔ ﺍﻟﻤﻠﺘﻤﺔ ﺍﻟﻤﻨﻔﺭﺠﺔ ﺍﻭ ﺍﻟﻤﺘﻀﻴﻘﺔ
ﺍﻟﻤﺘﻭﺴﻌﺔ
)
ﺍﻟﻨﺎﺸﺭﺓ
(
(Diffuser)
ﺸﻜل
)
6.13
(
-
ﺍﻟﻤﺤﺭﻙ ﺍﻟﺘﻭﺭﺒﻴﻨﻲ ﺍﻟﺩﻓﻌﻲ
)
ﺍﻟﻨﻔﺎﺙ
(

)
176
(
2
-
ﻴﺤﺘﺭﻕ ﺍﻟﻭﻗﻭﺩ ﻓﻲ ﻏﺭﻑ ﺍﻻﺤﺘﺭﺍﻕ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ
(P
3
=P
4
)
ﺤﻴﺙ ﻴﺯﺩﺍﺩ ﺤﺠﻡ ﺍﻟﻐﺎﺯﺍﺕ
(3
→4)
.
3
-
ﺘﺘﻤﺩﺩ ﺍﻟﻐﺎﺯﺍﺕ ﻓﻲ ﺍﻟﺘﻭﺭﺒﻴﻥ ﻓﻴﻘﻭﻡ ﺒﺘﺸﻐﻴل ﺍﻟﻀﺎﻏﻁ ﻓﻘﻁ
(4
→5)
.
ﺍﻤﺎ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻤﺘﺒﻘﻴﺔ
ﻟﻬﺫﻩ ﺍﻟﻐﺎﺯﺍﺕ
ﻓﺘﺘﻤﺩﺩ ﻓﻲ ﺍﻟﻤﻨﻔﺙ
(5
→6)
ﻊـﻓﺩ ﻰـﻠﻋ لـﻤﻌﺘ ﺔﻴﺭﻭﺤﻤ ﻊﻓﺩ ﺓﻭﻗ ﺔﺒﺒﺴﻤ ﹰﺍﺩﺠ ﺔﻴﻟﺎﻋ ﺔﻋﺭﺴﺒ ﺝﺭﺨﺘﻭ
ﺍﻟﻁﺎﺌﺭﺓ
.
ﺇﻥ ﺍﻻﺠﺭﺍﺀ
(4
→5→6)
ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ
.
ﻓﻴﻘﺎل ﺍﻥ ﺍﻟﻁﺎﺌﺭﺓ،ﻪﺴﻔﻨ ﺙﻔﻨﻤﻟﺍ ﻥﻤ ﻡﻠﺘﺴﺘ ﻊﻓﺩﻟﺍ ﺓﻭﻗ ﻥﺇ
ﺫﺍﺕ ﺩﻓﻊ ﻨﻔﺎﺙ
.
ﻴﺴﺘﻌﻤل ﻓﻴﻪ ﺍﻟﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ ﻭﻴﻬ،ﻲﻟﺎﺜﻤ ﹰﺎﻔﻨﺁ ﺭﻭﻜﺫﻤﻟﺍ لﻴﻠﺤﺘﻟﺍ
ﺔـﻴﻋﻭﻨﻟﺍ ﺓﺭﺍﺭـﺤﻟﺍ ﻲـﻓ ﺭﻴﻐﺘﻟﺍ لﻤ
ﻭﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻜﺘﻠﺔ ﺨﻼل ﺍﻻﺤﺘﺭﺍﻕ
.
ﻭﺍﺀـﻬﻟﺍ لﻼﺨ ﻙﺭﺤﺘﺘ ﺓﺭﺌﺎﻁﻟﺍ ﺕﻨﺎﻜ ﺍﺫﺇ ﻕﺭﻓ ﺩﺠﻭﻴ ﻻ لﻴﻠﺤﺘﻟﺍ ﻲﻓﻭ
ﺍﻟﺴﺎﻜﻥ ﺒﺴﺭﻋﺔ
(200m/s)
ﺍﻭ ﺍﻟﻤﺤﺭﻙ ﺜﺎﺒﺕ ﻭﻴﺩﺨل ﺍﻟﻴﻪ ﺍﻟﻬﻭﺍﺀ ﺒﺴﺭﻋﺔ
(200m/s)
ﻜﺤﺭﻜﺔ ﻨﺴﺒﻴﺔ
.
ﺇﻥ ﺍﻟﻬﻭﺍﺀ ﻴﺩﺨل ﺍﻟﻨﺎﺸﺭﺓ ﻭﻴﺨﺭﺝ ﻤﻥ ﺍﻟﻤﻨﻔﺙ ﺒﺴﺭﻋﺔ ﻋﺎﻟﻴﺔ ﺠ
ﺩﺍﹰ
.
ﺭﺓـﺸﺎﻨﻟﺍ ﻥﻤ ﺝﺭﺎﺨﻟﺍ ﺀﺍﻭﻬﻟﺍ ﺎﻤﺍ
ﻭﺍﻟﺩﺍﺨل ﺍﻟﻰ ﺍﻟﻤﻨﻔﺙ ﻓﺴﺭﻋﺘﻪ ﻤﻨﺨﻔﻀﺔ ﻴﻤﻜﻥ ﺇﻫﻤﺎﻟﻬﺎ ﻟﺘﺴﻬﻴل ﺍﻟﺤﺴﺎﺒﺎﺕ
.
ﻴﻥـﺒ ﻕﺭـﻔﻟﺍ ﻥﺈﻓ ﺍﺫﻟ
(C
6
)
ﻭ
(C
1
)
ﺸﻜل،
(6.13-a)
ﺴﻴﺘﺤﻭل ﺍﻟﻰ ﻗﻭﺓ ﺩﻓﻊ ﻟﻠﻁﺎﺌﺭﺓ،
(F)
.
ﻓﺈﺫﺍ ﻜﺎﻥ
(a)
ﺘﻤﺜل ﺍﻟﺘﻌﺠﻴل ﻓﺴﻴﻜﻭﻥ
:
ﻫﺫﻩ ﺍﻟﻤﻌﺎﺩﻟﺔ ﺘﻁﺒﻕ ﻋﻨﺩﻤﺎ ﻴﻜﻭﻥ ﺍﻟﺘﻤﺩﺩ ﻜﺎﻤل
.
ﻭﺍﻟﻤﺜ
ﺎل ﺍﻟﺘﺎﻟﻲ ﻴﻭﻀﺢ ﺍﻟﻤﻨﺎﻗﺸﺔ ﺍﻟﻤﺫﻜﻭﺭﺓ ﺁﻨﻔﺎﹰ
.
(6.34)
.
..........
)
C
(C
m
)
C
C
(
t
m
a
.
m
F
(6.33)
.......
t
C
C
a
1
6
1
6
1
6
−
=
−
=
=
−
=
&

)
177
(
ﻤﺜﺎل
)
6.3
(
ﻁﺎﺌﺭﺓ ﺘﻁﻴﺭ ﺒﺴﺭﻋﺔ
(800Km/h)
.
ﺭﺍﺭﺓـﺤ ﺔـﺠﺭﺩﺒ ﺓﺭـﺸﺎﻨﻟﺍ ﺀﺍﻭـﻬﻟﺍ لﺨﺩﻴ
(-24,6
°C)
ﻐﻁـﻀﻭ
(46.6kPa)
.
ﺜﻡ ﻴﻀﻐﻁ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﻓﻲ ﻀﺎﻏﻁ ﺍﻟﻰ
(280kPa)
.
ﺴﺏـﺘﻜﻴﻟ ﻱﺭﺍﺭﺤ لﺩﺎﺒﻤ لﺨﺩﻴ ﻙﻟﺫ ﺩﻌﺒ
ﺤﺭﺍﺭﺓ ﺒﺜﺒﻭﺕ ﺍﻟﻀﻐﻁ ﻭﻟﺘﺼﺒﺢ ﺩﺭﺠﺔ ﺤﺭﺍﺭﺘﻪ
(1090
°C)
.
ﺜﻡ ﻴﺘﻤﺩﺩ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﻓﻲ ﺘﻭﺭﺒﻴﻥ ﻓﻴﻘﻭﻡ ﺒﺘﺸﻐﻴل
ﺍﻟﻀﺎﻏﻁ
.
ﻭﻴﺩﺨل ﺍﻟﻰ ﻤﻨﻔﺙ ﻟﻴﺘﻤﺩﺩ ﻭﻴﻌﻭﺩ ﺍﻟﻰ ﻀﻐﻁﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﺔـﻤﻭﻅﻨﻤﻟﺍ ﻲﻓ ﻁﺎﻐﻀﻨﻻﺍﻭ ﺩﺩﻤﺘﻟﺍ ﻥﺎﻜ
ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ
.
ﺍﻫﻤل ﺴﺭﻋﺔ ﺍﻟﻬﻭﺍﺀ ﻋﻨﺩ ﻤﺨﺭﺝ ﺍﻟﻨﺎﺸﺭﺓ ﻭﻤﺩﺨل ﺍﻟﻤﻨﻔﺙ
.
ﺍﻫﻤل ﻁﺎﻗﺔ ﺍﻟﻭﻀﻊ ﻓﻲ ﺍﻟﻤﻨﻅﻭﻤﺔ
.
ﻓﺈﺫﺍ
ﻜﺎﻥ ﻤﻌﺩل ﺠﺭﻴﺎﻥ ﺍﻟﻬﻭﺍﺀ
(95 kg/s)
.
ﺍﺤﺴﺏ
:
)
1
(
ﺴﺭﻋﺔ ﺍﻟﻬﻭﺍﺀ ﻋﻨﺩ ﺍﻟﺨﺭﻭﺝ ﻤﻥ ﺍﻟﻤﻨﻔﺙ
) .
2
(
ﻗﻭﺓ ﺍﻟﺩﻓﻊ
.
ﻋﻠﻤﺎﹰ ﺒﺄﻥ
:
Cp = 1
.004 kJ/kg.K
γ = 1.4
ﺍﻨﻅﺭ ﺸﻜل
)
6.13
(
ﺍﻟﻔﺭﻕ ﺒﻴﻥ
)
C
6
،
C
1
(
ﺃﻱ،ﻊﻓﺩ ﺓﻭﻗ ﻰﻟﺍ لﻭﺤﺘﻴ
:
m/s
6
.
901
1221.36)
-
(816.52
1.004
2000
)
T
T
(
Cp
2000
C
K
52
.
816
64
.
190
6
.
46
36
.
1221
P
P
T
T
kPa
64
.
190
1336
36
,
1221
280
T
T
P
P
K
36
.
1221
T
)
T
1336
(
004
.
1
36
.
142
)
T
T
(
Cp
w
5
6
6
4
.
1
4
.
0
1
5
1
5
6
4
.
0
4
.
1
1
4
5
4
5
5
5
5
4
T
=
×
=
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
−
=
⇒
−
=
−
γ
γ
−
γ
γ
N
64.54
222.2)
-
(901.6
95
)
C
(C
m
F
1
6
=
=
−
= &
kg
kJ
36
.
142
)
273
94
.
414
(
004
.
1
)
T
T
(
Cp
w
w
K
94
.
414
8
.
64
280
273
P
P
T
T
kPa
8
.
64
6
.
248
273
6
.
46
T
T
P
P
C
0
)
6
.
24
(
6
.
24
t
t
t
t
t
C
6
.
24
1.004
2000
)
2
,
222
(
Cp
2000
C
t
t
Cp
2000
h
2000
C
m/s
2
.
222
3600
100
800
C
2
3
C
T
4
.
1
4
.
0
1
2
3
2
3
4
.
0
4
.
1
1
1
2
1
2
1
12
2
1
2
2
2
1
12
12
12
2
1
2
1
=
−
=
−
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
−
+
=
+
∆
=
−
=
=
×
=
=
∆
∆
=
∆
=
=
×
=
γ
−
γ
−
γ
γ
o
o

)
178
(
ﻤﺜﺎل
)
6.4
(
ﻁﺎﺌﺭﺓ ﺘﻁﻴﺭ ﺒﺴﺭﻋﺔ
(200 m/s)
.
ﻴﺩﺨل ﺍﻟﻬﻭﺍﺀ ﺍﻟﻨﺎﺸﺭﺓ ﺒﺩﺭﺠﺔ
ﺭﺍﺭﺓـﺤ
(-33
°C)
ﻊـﻁﻘﻤ ﺔﺤﺎﺴـﻤﻭ
ﺍﻟﺩﺨﻭل
(0.6m
2
)
.
ﻴﻀﻐﻁ ﺍﻟﻬﻭﺍﺀ ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ ﻓﻲ ﻀﺎﻏﻁ ﺍﻟﻰ
)
9
(
ﺍﻀﻌﺎﻑ ﻀﻐﻁﻪ ﺍﻻﺨﻴﺭ
.
ﻰـﻟﺍ لﺨﺩﻴ ﻡﺜ
ﺭﺍﺭﺓـﺤ ﺔﺠﺭﺩﺒ ﺝﺭﺨﻴﻟ ﺙﻔﻨﻤ ﻲﻓ ﺩﺩﻤﺘﻴ ﻡﺜ ،ﻥﻴﺒﺭﻭﺘ ﻲﻓ ﺩﺩﻤﺘﻴﻭ ﻕﺍﺭﺘﺤﻻﺍ ﺔﻓﺭﻏ
(558K)
ﺔـﻫﻭﻓ ﻥـﻤ
ﻤﺴﺎﺤﺔ ﻤﻘﻁﻌﻬﺎ
(0.4m
3
)
ﻟﻴﻌﻭﺩ ﺍﻟﻰ ﻀﻐﻁﻪ ﺍﻻﺒﺘﺩﺍﺌﻲ
.
ﻀـﻨﻻﺍ ﻥﺎﻜ ﺍﺫﺈﻓ
ﺭﻙـﺤﻤﻟﺍ ﻲـﻓ ﺩﺩـﻤﺘﻟﺍﻭ ﻁﺎﻐ
)
ﺍﻟﻤﻨﻅﻭﻤﺔ
(
ﺍﺩﻴﺎﺒﺎﺘﻴﺎﹰ
.
ﺍﻫﻤل ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﺎﻤﻨﺔ ﻭﺍﺤﺴﺏ
:
)
1
(
ﻜﺘﻠﺔ ﺍﻟﻬﻭﺍﺀ ﺍﻟﻤﺘﺩﻓﻘﺔ
)
2
(
ﺸﻐل ﺍﻟﺘﻭﺭﺒﻴﻥ
)
3
(
ﻗﻭﺓ ﺍﻟﺩﻓﻊ
)
4
(
ﻜﻔﺎﺀﺓ ﺍﻟﻤﻨﻅﻭﻤﺔ ﺍﻟﺤﺭﺍﺭﻴﺔ
.
Cp = 1
.004 kJ/kg.K
γ = 1.4
ﺍﻻﺴﺘﻌﺎﻨﺔ ﺒﺸﻜل
)
6.13
(
kg
kJ
227.9
260)
-
(487
004
.
1
)
T
(T
Cp
w
w
2
3
C
T
=
=
−
=
=
ﺍﻟﻔﺭﻕ ﺒﻴﻥ
C
6
,C
1
ﻴﺘﺤﻭل
ﺃﻱ،ﻊﻓﺩ ﺓﻭﻗ ﻰﻟﺍ
:
-
N
43.3
200)
-
(697.5
11
.
87
)
C
(C
m
F
1
6
=
=
−
= &
%
18
10
8
.
4
10
66
.
8
kW
10
4.8
2000
200
5
.
697
)
240
558
(
004
.
1
11
.
87
2000
C
C
)
T
T
(
Cp
m
W
Q
W
10
8.66
200
3
.
43
P
C
.
F
t
a
P
4
3
th
4
2
2
2
1
2
6
1
6
16
16
6
=
×
×
=
η
×
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
−
+
=
×
=
×
=
=
=
&
&
&
K
487
)
9
(
260
P
P
T
T
K
260
T
C
13
)
33
(
9
.
19
t
t
t
9
.
19
2008
200
Cp
2000
C
t
m/s
5
.
697
C
C
4
.
0
558
287
.
0
50
C
A
RT
P
11
.
87
m
m
s
kg
87.11
200
0.6
240
287
.
0
50
C
A
RT
P
C
A
m
286
.
0
1
2
3
2
3
2
12
2
2
2
1
12
6
6
6
6
6
6
6
1
1
1
1
1
1
1
1
1
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
⇒
−
=
−
+
=
+
∆
=
=
=
=
∆
=
×
×
×
=
×
=
=
=
=
×
×
×
=
×
=
ρ
=
γ
−
γ
o
&
&
&
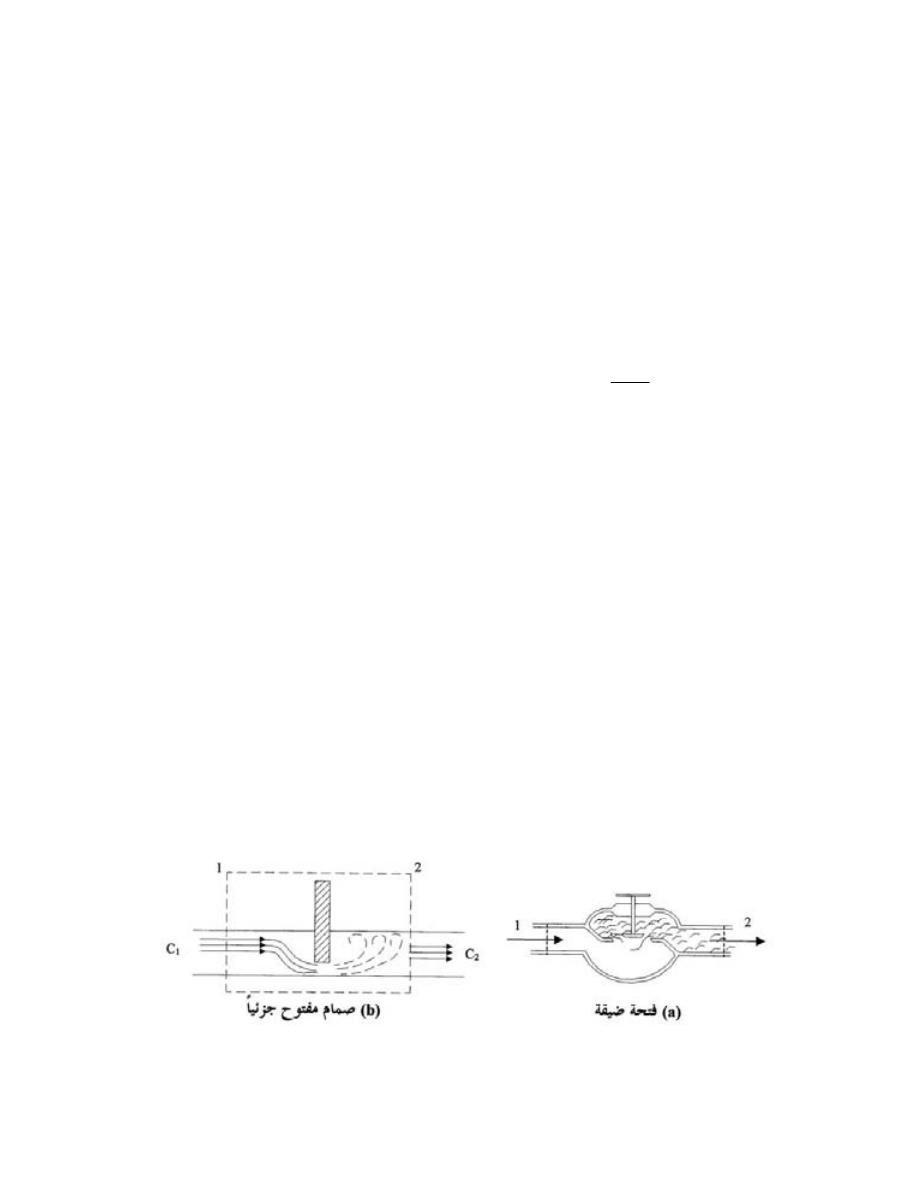
)
179
(
)
6.4.7
(
-
ﻤﻌﺎﺩﻟﺔ ﺍﻻﺴﺘﻤﺭﺍﺭﻴﺔ
Continuity Equation
ﻲـﻫﻭ ،ﻡﻅﺘﻨﻤﻟﺍ ﻕﻓﺩﺘﻟﺍ ﻲﻓ ﺔﻠﺘﻜﻟﺍ ﻅﻔﺤ ﺃﺩﺒﻤ ﻥﻋ ﺭﺒﻌﺘ ،ﻊﺌﺍﻭﻤﻟﺍ ﻕﻓﺩﺘ ﺕﻻﺎﺠﻤ ﻲﻓ ﺓﺭﺜﻜﺒ ﻡﺩﺨﺘﺴﺘ
ﺇﺫ ﺍﻨﻬﺎ ﻤ،ﺭﻴﻐﺘﺘ ﻻ ﻡﻭﻠﻌﻤ ﻥﻤﺯ لﻼﺨ ﻊﻁﻘﻤ ﻱﺃ ﺭﺒﻋ ﻕﻓﺩﺘﻤﻟﺍ ﻊﺌﺎﻤﻟﺍ ﺔﻠﺘﻜ ﻥﺍ ﺱﺎﺴﺍ ﻰﻠﻋ ﺔﻴﻨﺒﻤ
ﻰـﻠﻋ ﺔﻴﻨﺒ
ﺍﻻﻓﺘﺭﺍﻀﺎﺕ ﺍﻵﺘﻴﺔ
:
1
-
ﺎلـﻘﺘﻨﺍ ﺏﺒﺴـﺒ ﺝﺭﺨﻤﻟﺍ ﺩﻨﻋﻭ ،ﻡﺎﻅﻨﻟﺍ لﺨﺍﺩ ﺔﻁﻘﻨ ﻱﺃ ﻲﻓﻭ ،لﺨﺩﻤﻟﺍ ﺩﻨﻋ ﺔﺘﺒﺎﺜ ﻊﺌﺎﻤﻟﺍ ﺹﺍﻭﺨ ﻰﻘﺒﺘ
ﺍﻟﺤﺭﺍﺭﺓ ﻭﺍﻟﺸﻐل ﻋﺒﺭ ﺍﻟﺤﺩﻭﺩ ﺒﻤﻌﺩل ﺜﺎﺒﺕ
.
2
-
ﺘﺴﺎﻭﻱ ﻤﻌﺩل ﺍﻟﺘﺩﻓﻕ ﺍﻟﻜﺘﻠﻲ
(Mass Flow Rate)
ﻜلـﺸ ﻰﻟﺍ ﺓﺭﺎﺸﺇ ﺝﻭﺭﺨﻟﺍﻭ لﻭﺨﺩﻟﺍ ﺩﻨﻋ
)
6.12
.(
ﻓﺈﻥ ﺒﻭﺤ
ﺩﺍﺕ
(kg/s)
ﺘﻜﻭﻥ ﺜﺎﺒﺘﺔ ﻋﺒﺭ ﺃﻱ ﻤﻘﻁﻊ ﻓﻲ ﺍﻟﻤﻨﻔﺙ
.
ﺎﻥـﻜ ﺍﺫﺈﻓ
(A)
لـﺜﻤﺘ
ـﻤﺴﺎﺤﺔ ﺍﻟﻤﻘﻁﻊ ﺒﺎﻟ
(m
2
)
ﻭﺍﻥ،
(D)
ــﺔ ﺒﺎﻟـﻫﻭﻔﻟﺍ ﺭﻁﻗ
(m)
ﻭ،
(C)
ﺴﺭﻋﺔـﻟﺍ
ﺒﻭﺤﺩﺍﺕ
(m/s)
ﻭ
(ρ)
ـ ﻜﺜﺎﻓﺔ ﺍﻟﻤﺎﺌﻊ ﺒﺎﻟ
(kg/m
3
)
ﻓﺴﻴﻜﻭﻥ
:
)
6.4.8
(
-
ﺍﻨﻭﺍﻉ ﺍﺨﺭﻯ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
1
-
ﺼﻤﺎﻡ ﺍﻟﺨﺎﻨ
ﻕ
)
ﺍﻟﺨﻨﻕ
(
Throttle Valve (Throttling)
ﻜﻤﺎ ﻓﻲ ﺸﻜل،ﺔﻘﻴﻀ ﺔﺤﺘﻓ لﻼﺨ ﻊﺌﺎﻤ ﻥﺎﻴﺭﺠ ﺩﻨﻋ
(6.15-a)
،ﺎﹰـﻴﺌﺯﺠ ﺡﻭـﺘﻔﻤ ﻡﺎﻤﺼ لﻼﺨ ﻭﺍ
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل
(6.15-b)
ﻭﺒﺴﺒﺏ ﺍﺤﺘﻜﺎ،ﻪﻁﻐﻀ ﺹﻘﻨﻴ ﻑﻭﺴ ﻙﻟﺫﻟ ،ﻕﻨﺨ ﺩﻗ ﻊﺌﺎﻤﻟﺍ ﻥﺄﺒ لﺎﻘﻴ ٍﺫﺌﺩﻨﻋ ،
ﻙ
ﻟﻜﻥ ﻫﺫﻩ ﺍﻟﺤﺭ،ﺓﺭﺍﺭﺤ ﺩﻟﻭﺘﺘ ﺭﻭﺒﻌﻟﺍ ﺭﻤﻤ ﺔﻓﺎﺤ ﻊﻤ ﻊﺌﺎﻤﻟﺍ
ﺍﺭﺓ ﺼﻐﻴﺭﺓ ﻴﻤﻜﻥ ﺇﻫﻤﺎﻟﻬﺎ ﺒﺴﺒﺏ ﺍﻟﺘﺩﻓﻕ ﺍﻟﺴﺭﻴﻊ
ﻙﻟﺫـﻟ ،ﺓﺭﺍﺭﺤﻟﺍ لﺎﻘﺘﻨﻷ ﺔﻴﻓﺎﻜ ﺔﺤﺎﺴﻤ ﻻﻭ ﻑﺎﻜ ﺕﻗﻭ ﻙﺎﻨﻫ ﻥﻭﻜﻴ ﻻ ﺙﻴﺤﺒ ﺓﺭﻴﺼﻗ ﺔﻓﺎﺴﻤ لﻼﺨﻭ ،ﻊﺌﺎﻤﻠﻟ
ﺃﻱ،ﹰﺎﻴﺘﺎﺒﺎﻴﺩﺍ ﺀﺍﺭﺠﺍ ﻕﻨﺨﻟﺍ ﺩﻌﻴ
(q=0)
.
ﻥ ﺩﻭﻥـﻤ ﻡﺘﻴـﺴ ﺩﺩﻤﺘﻟﺍ ﻥﺈﻓ ﺔﻜﺭﺤﺘﻤ ﺀﺍﺯﺠﺍ ﺩﻭﺠﻭ ﻡﺩﻋ ﺏﺒﺴﺒﻭ
ﻤﻘﺎﻭﻤﺔ ﻟﺫﻟﻙ ﻓﺎﻥ
(w=0)
.
ﻭﻜﺫﻟﻙ ﻓﺈﻥ ﺍ
ﻟﻔﺭﻕ ﺒﻴﻥ
(C
1
)
ﻭ
(C
2
)
ﺼﻐﻴﺭﺍﹰ ﺨﺎﺼﺔﹰ ﺇﺫﺍ ﻜﺎﻥ ﺍﻟﻤﻘﻁﻌﻴﻥ
)
m
(
&
)
m
(
&
)
4
D
A
(
2
π
=
(6.36)
..........
.
Const
AC
C
A
C
A
(6.35)
.........
.
Const
m
m
2
2
2
1
1
1
2
1
=
ρ
=
ρ
=
ρ
=
= &
&
ﺸﻜل
)
6.15
(
-
ﺼﻤﺎﻡ ﺍﻟﺨﺎﻨﻕ
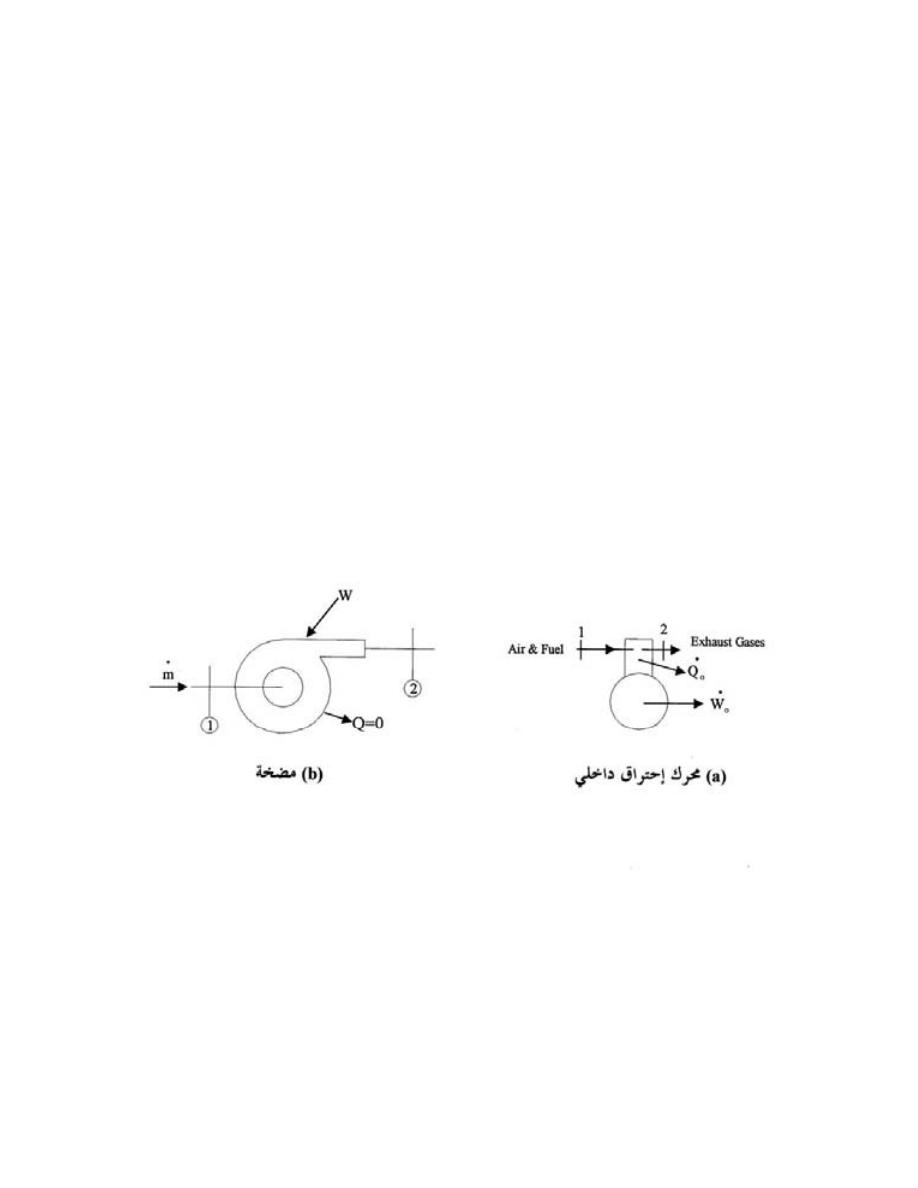
)
180
(
ﺔـﻐﻟﺎﺒﻟﺍ ﺔﻋﺭﺴـﻟﺍ ﻥﺍ ﺎـﻤﻟﺎﻁ ،ﺔـﻴﻜﺭﺤﻟﺍ ﺔـﻗﺎﻁﻟﺍ لـﻤﻬﺘ ﻙﻟﺫﻟ ،ﺔﺤﺎﺴﻤﻟﺍ ﺎﻴﻭﺎﺴﺘﻤ
(30 m/s)
ﺎﻓﺊـﻜﺘ
(0.5 kJ/kg)
ﻤﻘﺎﺭﻨﺔﹰ ﺒﻘﻴﻤﺔ ﺍﻟﻤﺤﺘﻭﻯ ﺍﻟﺤﺭﺍﺭﻱ ﺫﻱ ﺍﻟﻘﻴﻤﺔ
(2500 kJ/kg)
ﺎﺭـﺨﺒﻟﺍ ﻭﻫ ﻊﺌﺎﻤﻟﺍ ﻥﺎﻜ ﺍﺫﺍ
ﻤﺜﻼﹰ
.
ﻭﻋﻠﻴﻪ ﻓﺈﻥ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ
:
h
1
= h
2
……….. (6.37)
ﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ ﻴﻜﻭﻥ ﺍﻟﻤﺤﺘﻭﻯ ﺍﻟﺤﺭﺍﺭﻱ
(h=CpT)
ﻭﺒﻤﺎ ﺍﻥ،
(Cp=Const.)
ﻋﻠﻴﻪ ﻓﻠﻥ،
ﻴﻜﻭﻥ ﻫﻨﺎﻟﻙ ﺘﻐﻴﺭ ﻓﻲ ﺩﺭﺠﺎﺕ ﺍﻟﺤﺭﺍﺭﺓ ﻋﻨﺩ ﺨﻨﻕ ﺍﻟﻐﺎﺯ ﺍﻟﻤﺜﺎﻟﻲ
.
ﺍﻤﺎ ﻋﻨﺩ ﺨﻨﻕ ﻏﺎﺯ ﺤﻘﻴﻘﻲ ﻓﺴﻴﻜﻭﻥ ﻫﻨﺎﻙ
ﺒﺼﻭﺭﺓ ﻋﺎﻤﺔ ﻫﺒﻭﻁ ﻓﻲ ﺩﺭﺠﺔ ﺍﻟﺤﺭﺍﺭﺓ
.
2
-
ﻤﺤﺭﻙ ﺍﻻﺤﺘﺭﺍﻕ ﺍﻟﺩﺍﺨﻠﻲ
Internal Combustion Engine
ﻴﻘﻭﻡ ﺒﺈﻨﺘﺎﺝ ﺸﻐل ﻤﻴﻜﺎﻨﻴﻜﻲ ﻤﻭﺠﺏ ﺒﺼﻔﺔ ﺩﺍﺌﻤﺔ
.
ﺃﻱ ﺍﻥ ﺠﺯﺀ ﻤﻥ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻴﻤﻴﺎﺌﻴﺔ ﻟﻠﻭﻗﻭﺩ ﻴﺘﺤﻭل
ﺍﻟﻰ ﺸﻐل ﻤﻴﻜﺎﻨﻴﻜﻲ
.
ﺔـﺤﻭﺘﻔﻤ ﺓﺭﻭﺩ ﺕﺍﺫ ﺔـﻟﺁ ﻲﻠﺨﺍﺩﻟﺍ ﻕﺍﺭﺘﺤﻻﺍ ﻙﺭﺤﻤ ﻥﺍ
)
Open Circuit
(
ﻭﺫﺍﺕ،
ﺠﺭﻴﺎﻥ ﺸﺒﻪ ﻤﺴﺘﻘﺭ
)
quasi-steady Flow
(
ـﻟﻜﻥ ﻴﻌﺎﻤل ﻜﺂﻟﺔ ﺫﺍﺕ ﺠﺭﻴ
ﺴﺘﻘﺭـﻤ ﻥﺎ
)
Steady Flow
(
ﻁﺔـﺴﺍﻭﺒ ﺏﺤﺴﻟﺍ ﻁﻭﺸ لﻼﺨ ﺩﻤﺨﺘ ﻥﺎﻴﺭﺠﻟﺍ ﺕﺎﻀﺒﻨ ﻥﺍﻭ ، ﺕﺎﻨﺍﻭﻁﺴﻻﺍ ﺓﺩﺩﻌﺘﻤ ﺕﺎﻜﺭﺤﻤﻟﺍ ﻡﻅﻌﻤ ﻪﻨﻻ
ﻤﺭﺸﺤﺎﺕ ﺍﻟﻬﻭﺍﺀ
)
Air Filters
(
ﻭﺨﻼل ﺸﻭﻁ ﺍﻟﻌﺎﺩﻡ ﺒﻭﺍﺴﻁﺔ ﻤﺨﻤﺩﺍﺕ ﺍﻟﺼﻭﺕ
)
Silencers
.(
ﻤﺤﺭﻙ ﺍﻻﺤﺘﺭﺍﻕ ﺍﻟﺩﺍﺨﻠﻲ ﻴﻘﻭﻡ ﺒﺄﻨﺘﺎﺝ ﺸﻐل ﻤﻴﻜﺎﻨﻴﻜﻲ ﻤﻭﺠﺏ ﺒﺼﻔﺔ ﺩﺍﺌﻤﺔ
.
ﺃﻱ ﺍﻥ
ﻥـﻤ ﺀﺯـﺠ
ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻴﻤﻴﺎﺌﻴﺔ ﻟﻠﻭﻗﻭﺩ ﻴﺘﺤﻭل ﺍﻟﻰ ﺸﻐل ﻤﻴﻜﺎﻨﻴﻜﻲ
.
ﻭﻜﻤﺎ ﻓﻲ ﺸﻜل
(6.16-a)
ﻁـﺴﻭﻟﺍ ﻰﻟﺍ ﺩﺭﻁﻴ ﺀﺯﺠﻭ
ﺃﻱ ﺍﻥ،ﺔﻟﺎﻐﺸﻟﺍ ﺓﺩﺎﻤﻠﻟ ﻲﻠﻜﻟﺍ ﻲﺒﻟﺎﺜﻨﻻﺍ ﺓﺩﺎﻴﺯ ﻰﻠﻋ لﻤﻌﻴ ﻲﻗﺎﺒﻟﺍﻭ ﺓﺭﺍﺭﺤ ﺔﺌﻴﻫ ﻰﻠﻋ ﻙﺭﺤﻤﻠﻟ ﻁﻴﺤﻤﻟﺍ
:
ﻭﺘﺼﺒﺢ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ
:
(6.38)
........
H
Q
W
Q
Q
o
o
in
F
∆
+
+
=
=
&
&
&
&
(6.39)
..........
H
)
Q
W
(
Q
o
o
in
∆
=
+
−
&
&
&
ﺸﻜل
)
6.16
(
-
ﻤﺤﺭﻙ ﻭ ﻤﻀﺨﺔ
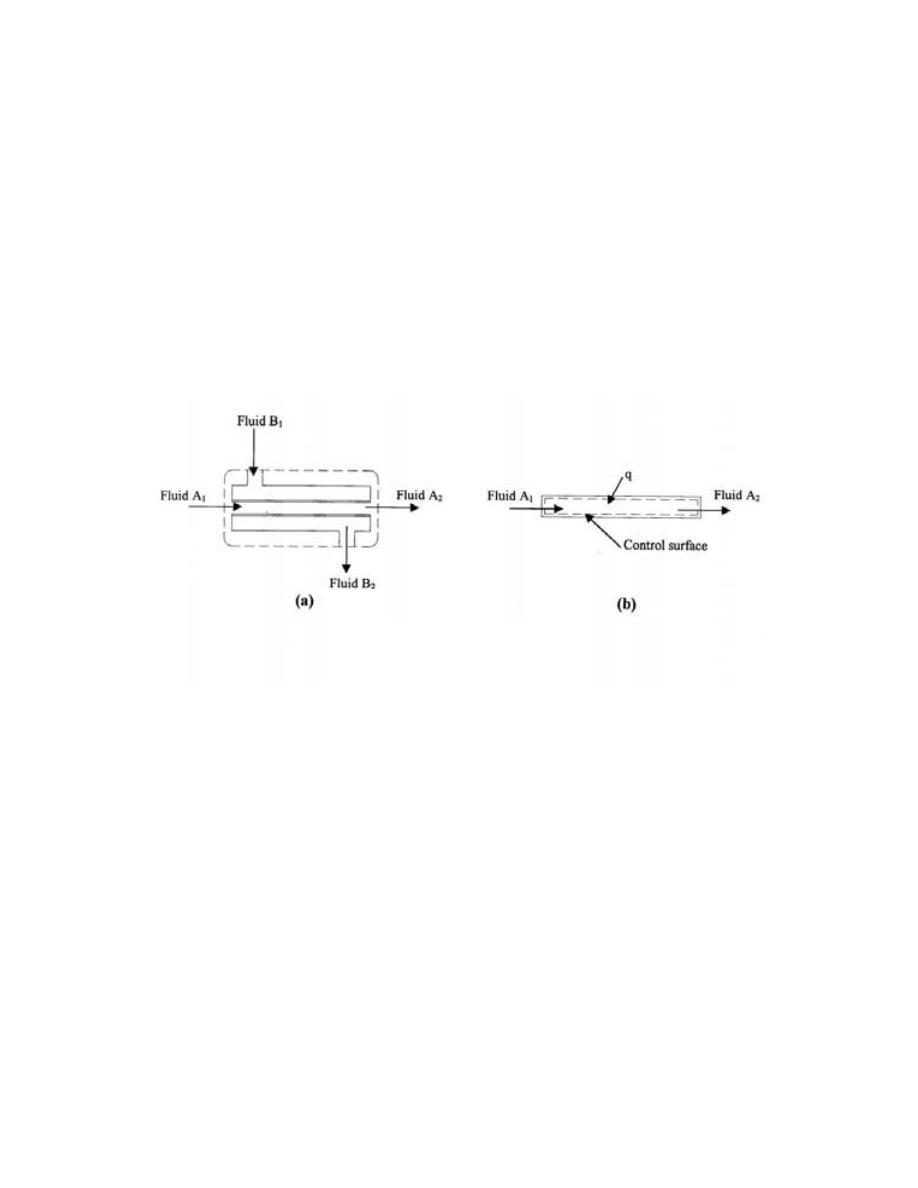
)
181
(
3
-
ﺍﻟﻤﻀﺨﺔ
Pump
ﺸﻜ،لﺌﺍﻭﺴﻟﺍ ﻁﻐﻀ ﺓﺩﺎﻴﺯﺒ ﻡﻭﻘﺘ
ل
(6.16-b)
ﺃﻱ ﺍﻥ ﻤﻌﺩل ﺍﻟﺸﻐل ﺍﻟﺫﻱ ﺘﺄﺨﺫﻩ ﺍﻟﻤﻀﺨﺔ ﻴﺴﺎﻭﻱ،
ﺍﻟﺯﻴﺎﺩﺓ ﺍﻟﻜﻠﻴﺔ ﻷﻨﺜﺎﻟﺒﻲ ﺍﻟﻤﺎﺩﺓ ﺍﻟﺸﻐﺎﻟﺔ
.
ﻭﺘﻜﻭﻥ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ
:
4
-
ﺍﻟﻤﺒﺎﺩل ﺍﻟﺤﺭﺍﺭﻱ
Heat Exchanger
لـﻤﻋ ﻲﺘﺩﺎﻤ ﻥﻴﺒ ﻱﺭﺍﺭﺤﻟﺍ لﺩﺎﺒﺘﻟﺍ ﺎﻬﻴﻓ ﻡﺘﻴ ﺭﻘﺘﺴﻤ ﻥﺎﻴﺭﺠ ﺕﺍﺫ ﺔﺤﻭﺘﻔﻤ ﺔﻤﻅﻨﺍ ﻲﻫ
(A)
ﻭ
(B)
ﻜﻤﺎ ﻓﻲ ﺍﻟﺸﻜل
(6.17)
.
ﻴﻤﻜ
ﻥ ﺍﻥ ﺘﻜﻭﻥ ﻤﻥ ﻨﻭﻉ ﻭﺍﺤﺩ ﺍﻭ ﻤﺨﺘﻠﻔﺔ
.
ﺭ ﺃﻱـﺸﺎﺒﻤ ﺱﺎـﻤﺘﺒ ﺙﺩـﺤﻴ لﺩﺎﺒﺘﻟﺍ
ﺍﻭ ﺒﺘﻤﺎﺱ ﻏﻴﺭ ﻤﺒﺎﺸﺭ ﺃﻱ ﺒﻀﻐﻁ ﻤﺨﺘﻠﻑ،ﻁﻐﻀﻟﺍ ﺕﻭﺒﺜﺒ
.
ﺔـﻨﻤﺎﻜﻟﺍﻭ ﺔﻴﻜﺭﺤﻟﺍ ﺔﻗﺎﻁﻟﺍﻭ لﻐﺸﻟﺍ لﺎﻤﻫﺈﺒﻭ
ﺘﺼﺒﺢ ﻤﻌﺎﺩﻟﺔ ﺍﻟﻁﺎﻗﺔ ﻟﻜل ﻤﺎﺩﺓ ﻋﻤل
:
Q
12
=
∆H
12
ﻓﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻤﺎﺩﺓ
(A)
ﻴﻜﻭﻥ
:
(Q
12
)
A
= (
∆H
12
)
A
ﻭﺒﺎﻟﻨﺴﺒﺔ ﻟﻠﻤﺎﺩﺓ
(B)
ﻴ
ﻜﻭﻥ
:
(Q
12
)
B
= (
∆H
12
)
B
ﻭﻷﻥ ﺍﻟﺤﺭﺍﺭﺓ ﺍﻟﻤﺘﺒﺎﺩﻟﺔ ﺒﻴﻥ
(A)
ﻭ
(B)
ﻤﺘﺴﺎﻭﻴﺔ
.
ﻭﺍﻻﺸﺎﺭﺓ
)
-
(
ﺭﻯـﺨﻻﺍﻭ ﺓﺩﻭـﻘﻔﻤ ﺎﻫﺩـﺤﺍ ﻥﺍ ﻲﻨﻌﺘ
ﻤﻜﺘﺴﺒﺔ ﻓﺴﻴﻜﻭﻥ
:
(Q
12
)
A
=
− (Q
12
)
B
m
A
C
A
(T
2
– T
1
) = m
B
C
B
(T
1
– T
2
)
………. (6.41)
(6.40)
........
H
W
&
&
∆
=
ﺸﻜل
)
6.17
(
-
ﻤﺒﺎﺩل ﺤﺭﺍﺭﻱ

)
182
(
ﻤﺜﺎل
)
6.5
(
ﻤﺒﺎﺩل ﺤﺭﺍﺭﻱ ﻴﺴﺘﻌﻤل ﻟﺘﺒﺭﻴﺩ ﺍﻟﻤﺎﺀ ﺒﻭﺴﺎﻁﺔ ﺍﻟﻬﻭﺍﺀ
.
ﻴﺩﺨل
ﺔـﺠﺭﺩﺒ لﺩﺎـﺒﻤﻠﻟ ﺀﺍﻭـﻬﻟﺍ
(25
°C)
ﻭﻴﺨﺭﺝ ﺒﺩﺭﺠﺔ
(40
°C)
.
ﺍﻟﻤﺎﺀ ﻴﺩﺨل ﺒﺩﺭﺠﺔ
(80
°C)
ﻭﻴﺨﺭﺝ ﺒﺩﺭﺠﺔ
(40
°C)
.
ﻓﺈﺫﺍ ﻜﺎﻨﺕ
:
Cw = 4.2 kJ/kg.K
Cpa = 1.005 kJ/kg.K
ﺍﻭﺠﺩ ﺍﻟﻨﺴﺒﺔ ﺒﻴﻥ ﻜﺘﻠﺘﻲ ﺍﻟﻬﻭﺍﺀ ﻭﺍﻟﻤﺎﺀ
.
ﺇﻥ ﺘﻁﺒﻴﻘﺎﺕ ﺍﻟﻘﺎﻨﻭﻥ ﺍﻻﻭل ﻟﻠﺜﺭﻤﻭﺩﻴﻨﺎﻤﻴﻜﺎ ﻋﻠﻰ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ ﻭﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔ
ﺘﻭﺤﺔ ﻤﻭﻀﺤﺔ ﻓﻲ
ﺠﺩﻭل ﺭﻗﻡ
)
6.2
.(
ﺨﻼﺼﺔ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
Summary of Open Systems
ﻲـﻓ ﺢـﻀﻭﻤ ﺎﻤ ﺏﺴﺤﻭ ﺔﺤﻭﺘﻔﻤﻟﺍ ﺔﻤﻅﻨﻻﺎﺒ ﺔﺼﺎﺨﻟﺍ ﺕﺎﻴﻠﻤﻌﻟﺍ ﺹﻴﺨﻠﺘ ﻥﻜﻤﻴ ﺩﺭﻭ ﺎﻤ لﻼﺨ ﻥﻤ
ﺠﺩﻭل ﺭﻗﻡ
)
6.1
(
ﻡـﻗﺭ لﻭﺩـﺠ ﻲـﻓ ﺢﻀﻭﻤﺎﻤ ﺏﺴﺤﻭ ﺔﺤﻭﺘﻔﻤﻟﺍﻭ ﺔﻘﻠﻐﻤﻟﺍ ﺔﻤﻅﻨﻻﺍ ﺹﻴﺨﻠﺘ ﻥﻜﻤﻴﻭﺎﻤﻜ ،
)
6.2
.(
14
.
11
)
25
40
(
005
.
1
)
40
80
(
2
.
4
)
T
T
(
C
)
T
T
(
C
m
m
a
1
2
Pa
w
2
1
w
w
a
=
−
−
=
−
−
=
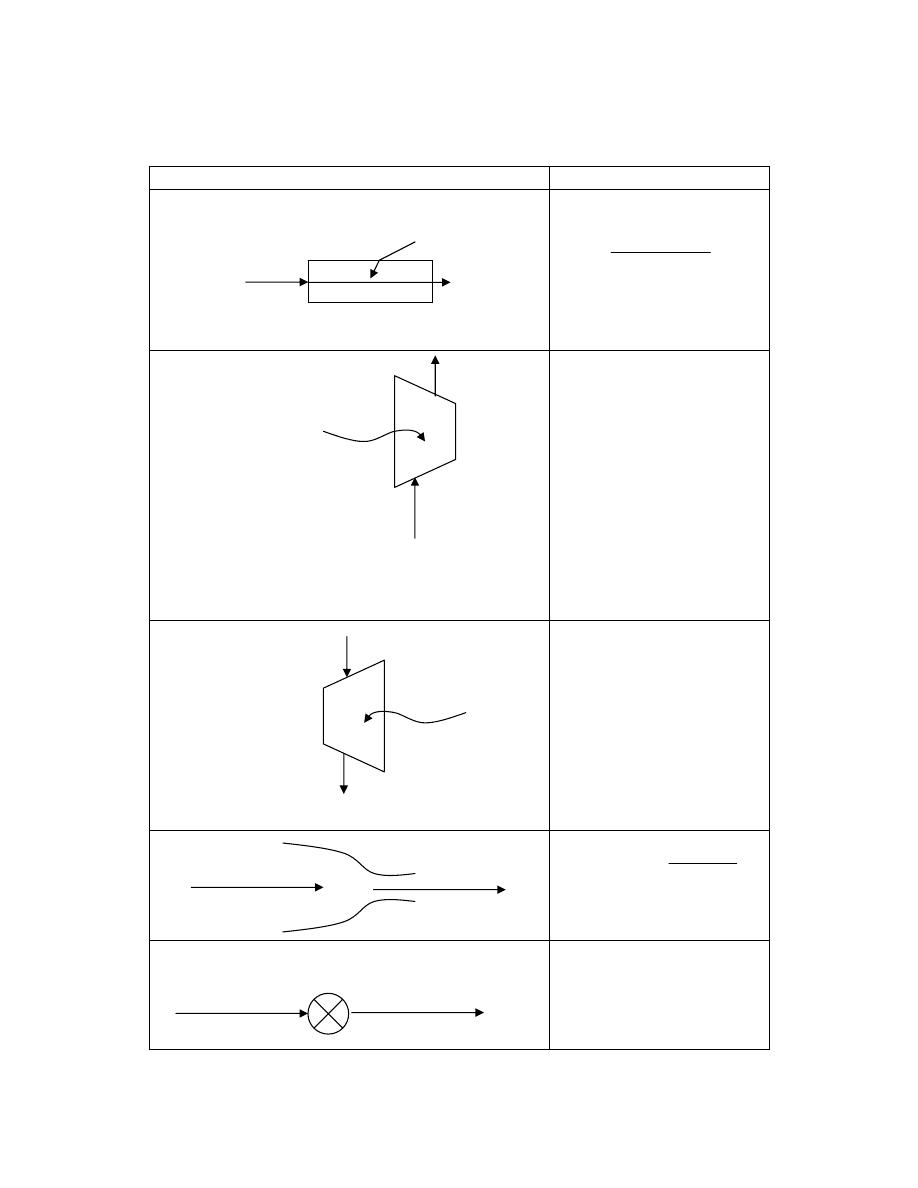
)
183
(
ﺠﺩﻭل
)
6.1
(
ﺍ
ﻟﻌﻤﻠﻴﺎﺕ ﻓﻲ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻔﺘﻭﺤﺔ
System Energy
1. Boiler
2. Compressor or Pump
3. Turbine
4. Nozzle
5. Throttle Valve
CV
.
m
)
h
h
(
m
)
h
h
(
m
H
Q
f
1
2
s
b
1
2
&
&
&
&
&
−
=
η
−
=
∆
=
)
h
h
(
m
H
W
1
2
−
=
∆
=
−
&
&
&
)
h
h
(
m
W
2
1
−
= &
&
12
2
1
2
2
2
1
2
2
12
h
2
C
C
2
C
C
h
O
∆
−
=
−
+
∆
=
1
2
h
h
=
.
m
.
Q
1
2
2
1
.
m
.
W
s
2
1
.
W
s
C
2
<C
1
C
1
1
2
1
2
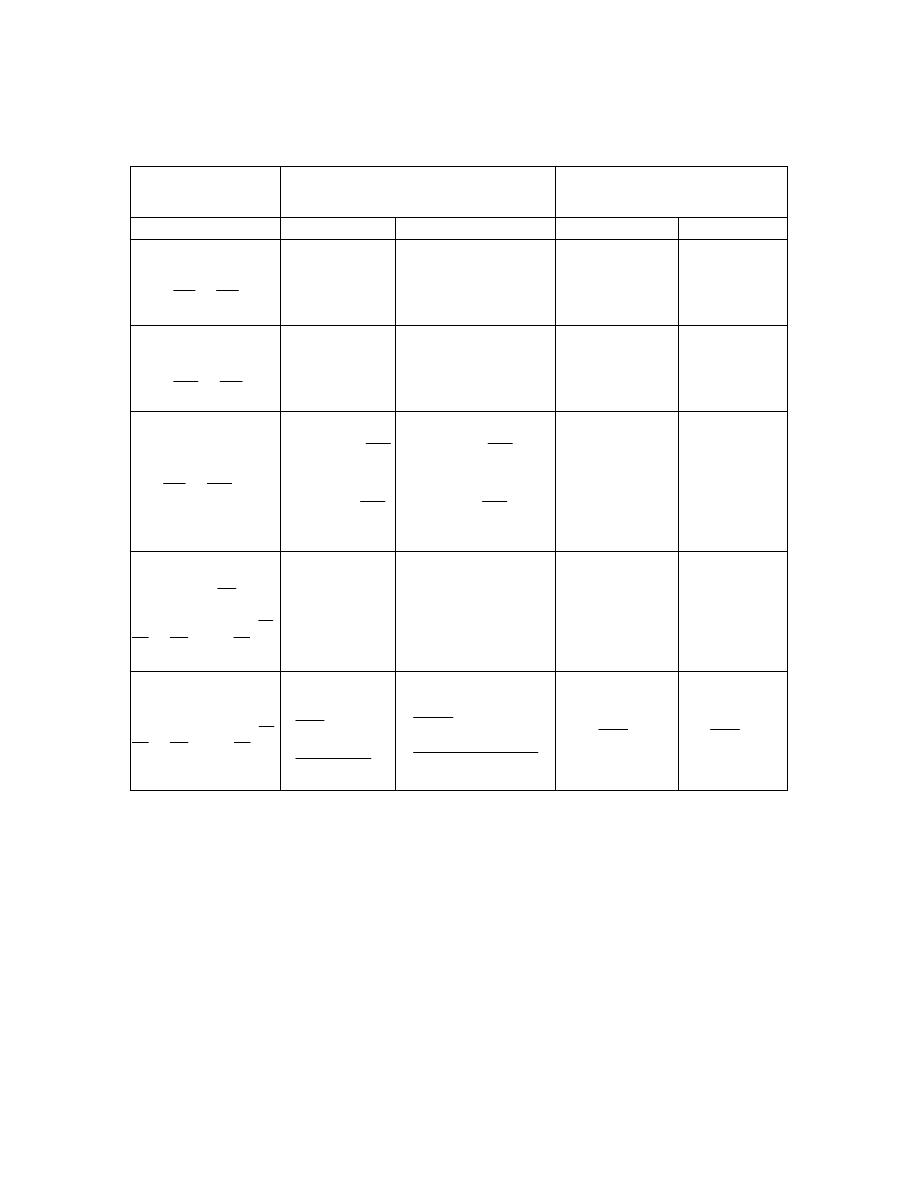
)
184
(
ﺠﺩﻭل
)
6.2
(
ﺨﻼﺼﺔ ﺍﻻﻨﻅﻤﺔ ﺍﻟﻤﻐﻠﻘﺔ ﻭﺍﻟﻤﻔﺘﻭﺤﺔ
Process PV
n
=C
ﺍﻟﺤﺎﻟﺔ
W
ﺍﻟﺸﻐل
Q
ﺍﻟﺤﺭﺍﺭﺓ
Closed = Pd
ν
Open = -∫
νdP
Closed=W+
∆U Open=W+∆H
V = C
.
. n =
∞
Zero
=-
ν(P
2
-P
1
)
=
ν (P
1
-P
2
)
= R (T
1
-T
2
)
=Cv dt
=Cv dt
p = C
.
. n = 0
= R (T2-T1)
= P (V2-V1)
Zero
= Cp dt
= Cp dt
T = C
.
. n = 1
Q=W
Q=W
= -
∆U
=Cv (T
1
-T
2
)
= -
∆H
=Cp (T
1
-T
2
)
Zero Zero
1
2
1
2
T
T
P
P =
1
2
1
2
T
T
V
V =
2
1
1
2
V
V
P
P =
1
2
1
1
2
1
1
V
V
Ln
RT
V
V
Ln
V
P
=
=
1
2
1
1
2
1
1
V
V
Ln
RT
V
V
Ln
V
P
=
=
γ
−
γ
−
γ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
γ
=
=
1
1
2
1
2
1
1
2
P
P
V
V
T
T
Cv
Cp
n
,
.
C
S
n
1
n
1
2
1
n
2
1
1
2
n
P
P
V
V
T
T
.
C
PV
−
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
1
n
V
P
V
P
)
T
T
(
1
n
R
2
2
1
1
2
1
−
−
=
−
−
=
1
n
)
V
P
V
P
(
n
)
T
T
(
1
n
nR
2
2
1
1
2
1
−
−
=
−
−
=
dt
Cn
dt
1
n
n
Cv
=
−
−
=
γ
dt
Cn
dt
1
n
n
Cv
=
−
−
=
γ

)
185
(
ﺍﻤﺜﻠﺔ ﻤﺤﻠﻭﻟ
ﺔ
)
6.6
(
ﻴﻬﺒﻁ ﺴﺎﺌﻕ ﺒﺴﻴﺎﺭﺓ ﻜﺘﻠﺘﻬﺎ
(1350 kg)
ﻤﻥ ﺴﻁﺢ ﺘل
.
ﻭﻴﺸﺎﻫﺩ ﻋﻨﺩ ﺍﻟﻘﺎﻋﺩﺓ ﻀﻭﺀﺍﹰ ﺍﺤﻤﺭ ﻴﺠﺏ ﺍﻥ ﻴﺘﻭﻗﻑ
ﻋﻨﺩﻩ
.
ﺩﺭﻫﺎـﻗ ﺔﻋﺭﺴـﺒ ﻙﺭﺤﺘﺘ ﺓﺭﺎﻴﺴﻟﺍ ﺕﻨﺎﻜ لﻤﺍﺭﻔﻟﺍ ﻰﻠﻋ ﻁﻐﻀﻟﺍ ﻲﻓ ﻕﺌﺎﺴﻟﺍ ﺀﺩﺒ ﺎﻤﺩﻨﻋﻭ
(28m/s)
.
ﻭﻜﺎﻥ ﻋﻠﻰ ﺇﺭﺘﻔﺎﻉ ﺭﺃﺴﻲ ﻗﺩﺭﻩ
(30m)
ﻓﻭﻕ ﻗﺎﻋﺩﺓ ﺍﻟﺘل
.
ﻤﺎ ﻫﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺘﻲ ﺘﺘﺒﺩﺩ ﻜﺤﺭ
لـﻤﺍﺭﻔﻟﺍ ﻲﻓ ﺓﺭﺍ
ﺒﻔﺭﺽ ﺇﻫﻤﺎل ﺘﺄﺜﻴﺭ ﺍﻟﺭﻴﺎﺡ ﻭﻋﻭﺍﻤل ﺍﻻﺤﺘﻜﺎﻙ ﺍﻟﻤﺨﺘﻠﻔﺔ ﻋﻠﻰ ﺍﻟﻌﻤﻠﻴﺔ
) .
ﺍﻋﺘﺒﺭ ﺍﻟﺴﻴﺎﺭﺓ ﻜﻨﻅﺎﻡ
(
ﺍﻟﺤﺭﺍﺭﺓ ﺨﺎﺭﺠﺔ ﻤﻥ ﺍﻟﻨﻅﺎﻡ
)
-
(
)
6.7
(
ﻏﺎﺯ ﻴﺠﺭﻱ ﻓﻲ ﺍﻨﺒﻭﺏ ﺇﺭﺘﻔﺎﻋﻪ
(60.96m)
ﻓﻭﻕ ﺴﻁﺢ ﺍﻟﺒﺤﺭ ﺒﺴﺭﻋﺔ
(6.096 m/s)
ﺭﺍﺭﺓـﺤ ﺔﺠﺭﺩﻭ
(148.9
°C)
.
ﺍﺤﺴﺏ ﺍﻟﻁﺎﻗﺔ ﺍﻟﻜﻠﻴﺔ ﻟﻠﻐﺎﺯ ﻭﺍ
ﻲـﻓ ﺱﺎـﺴﻻﺍ ﺓﺭﺍﺭﺤﻟﺍ ﺔﺠﺭﺩ ﻲﻫ ﻱﻭﺌﻤﻟﺍ ﺭﻔﺼﻟﺍ ﻥﺍ ﺭﺒﺘﻋ
ﻗﻴﺎﺱ ﺍﻟﻁﺎﻗﺔ
.
ﻭﺍﻥ
:
Cv=0.6741 kJ/kg.K
)
6.8
(
ﻤﺭﻭﺤﺔ ﻓﻲ ﻏﺭﻓﺔ ﻤﻐﻠﻘﺔ ﻁﺎﻗﺘﻬﺎ ﺍﻟﺤﺭﻜﻴﺔ
(678kJ)
.
ﻗﻁﻊ ﺘﺠﻬﻴﺯ ﺍﻟﻘﺩﺭﺓ ﻋﻨﻬﺎ ﻭﻭﺼﻠﺕ ﺘﺩﺭﻴﺠﻴﺎﹰ ﺍﻟﻰ ﺤﺎﻟﺔ
ﺍﻟﺴﻜﻭﻥ
.
ﺇﺫﺍ ﻋﻠﻤﺕ ﺍﻥ ﺍﻟﻔﻘﺩﺍﻥ ﺍﻟﺤﺭﺍﺭﻱ ﻤﻥ ﺠﺩﺭﺍﻥ ﺍﻟﻐﺭﻓﺔ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻟﺘﺒﺎﻁﺅ ﻴﻘﺩ
ـﺭ ﺒ
(50kJ)
.
ﺍﺤﺴﺏ
ﺍﻟﺘﻐﻴﺭ ﻓﻲ ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﻟﻤﺤﺘﻭﻴﺎﺕ ﺍﻟﻐﺭﻓﺔ
.
Q – W =
∆U
12
+
∆KE + ∆PE
-50 =
∆U
12
+ (0 – 678)
∆U
12
= 628 kJ
)
6.9
(
ﻤﺭﻭﺤﺔ ﻓﻲ ﻏﺭﻓﺔ ﻤﻐﻠﻘﺔ ﺘﺩﻭﺭ ﺒﺴﺭﻋﺔ
(1164m/s)
ﻗﻁﻊ ﻋﻨﻬﺎ ﺘﺠﻬﻴﺯ ﺍﻟﻘﺩﺭﺓ ﻭﻭﺼﻠﺕ ﺘﺩﺭﻴﺠﻴﺎﹰ ﺍﻟﻰ ﺤﺎﻟﺔ
ﺍﻟﺴﻜﻭﻥ
.
ﺇﺫﺍ ﻋﻠﻤﺕ ﺍﻥ ﺍﻟﻔﻘﺩ ﺍﻟﺤﺭﺍﺭﻱ ﻤﻥ ﺠﺩ
ﺭﺍﻥ ﺍﻟﻐﺭﻓﺔ ﻓﻲ ﺍﺜﻨﺎﺀ ﺍﻟﺘﺒﺎﻁﺅ
(50kJ/kg)
.
ﺍﻭﺠﺩ ﺍﻟﺘﻐﻴﺭ ﻓﻲ
ﺍﻟﻁﺎﻗﺔ ﺍﻟﺩﺍﺨﻠﻴﺔ ﺍﻟﻨﻭﻋﻴﺔ ﻟﻤﺤﺘﻭﻴﺎﺕ ﺍﻟﻐﺭﻓﺔ
.
kJ
-926.367
J
-926367
)
30
0
(
81
.
9
2
28
0
1350
)
z
z
(
g
2
C
C
m
PE
KE
Q
2
2
1
2
2
1
2
2
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
×
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
−
=
∆
+
∆
=
kJ/kg
99
.
100
96
.
60
81
.
9
1
2
)
096
.
6
(
1
)
0
148
(
6741
.
0
1
mgz
2
mC
T
mCv
PE
KE
U
Q
2
2
=
×
×
+
×
+
−
×
=
+
+
∆
=
∆
+
∆
+
∆
=
2000
C
C
q
PE
KE
w
q
2
1
2
2
12
12
12
12
12
12
12
−
+
µ
∆
=
∆
+
∆
+
µ
∆
=
−
kJ/kg
628
2000
)
1164
(
0
50
12
2
12
=
µ
∆
−
+
µ
∆
=
−
