Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٥٨
-
2-) Thevenin's Theorems:-
ﺗﺳﺗﺧدم ﻓﻲ اﻏﻠب اﻻﺣﯾﺎن اذا ﻛﺎن اﻟﻣطﻠوب اﯾﺟﺎد اﻟﺗﯾﺎر او اﻟﻔوﻟﺗﯾﺔ ﻓﻲ ﻣﻘﺎوﻣﺔ ﻣﺣددة ﻓﻲ اﻟداﺋرة
.
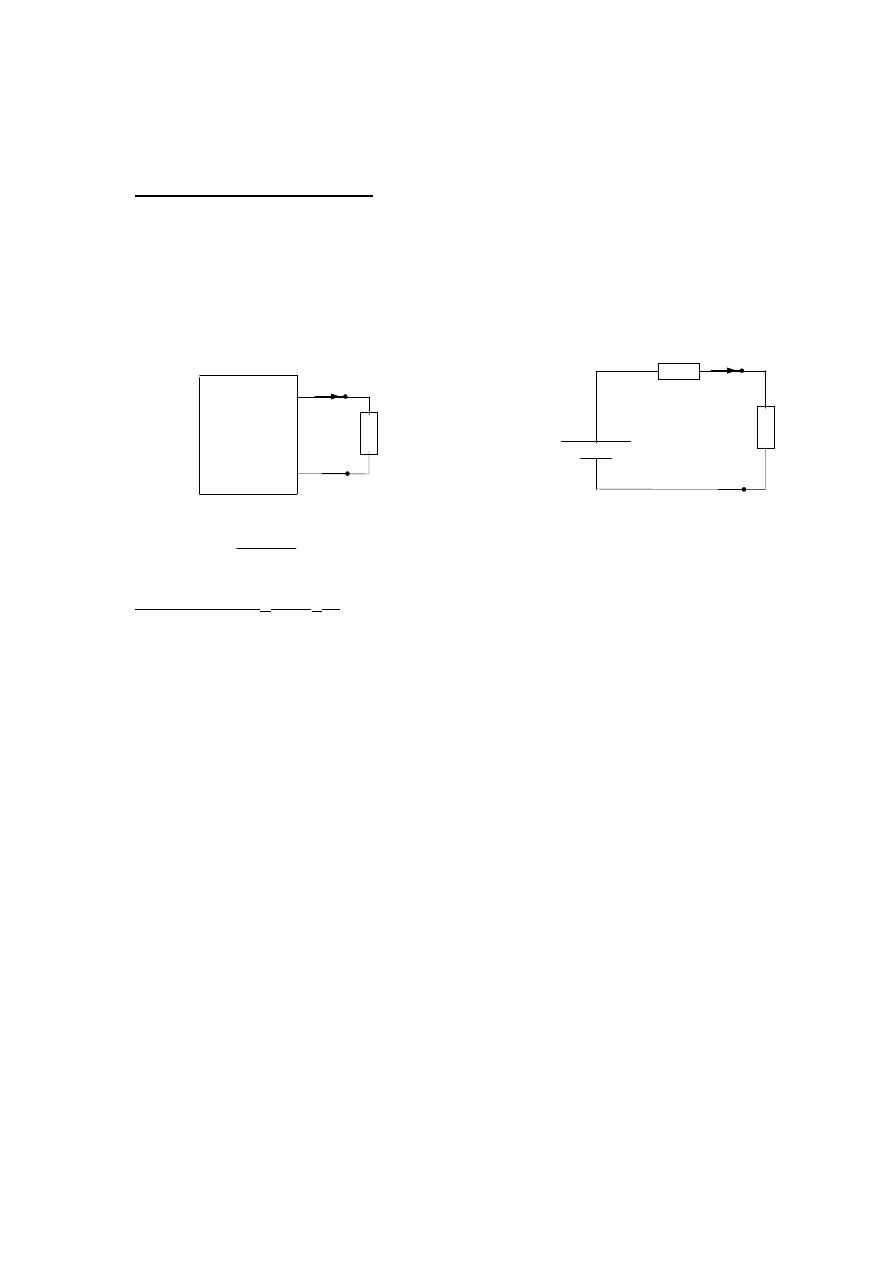
Any two terminal linear network can be replaced by an equivalent circuit
of a voltage source ( E
th
) and a series resistor ( R
th
); as shown in figure below:-
R
th
R
L
E
th
a
b
R
L
Complex
network
a
b
I
I
Hence;
L
th
th
R
R
E
I
Steps to find E
th
& R
th
:-
1. Remove that portion of the network across which the Thevenins
equivalent circuit is to be find.
2. Mark the terminals of the remaining two
– terminal network.
3. Calculate R
th
by first setting all sources to zero ( voltage sources are
replaced by short circuits and current sources are replaced by open
circuit ), and finding the resultant resistance between the two marked
terminals.
4. Calculate E
th
by first returning all sources to their origin positions and
finding the open circuit voltage between the marked terminals.
5. Draw the Thevenins equivalent circuit with the portion of the circuit
previously removed replaced between the terminals of the equivalent
circuit.
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٦٨
-
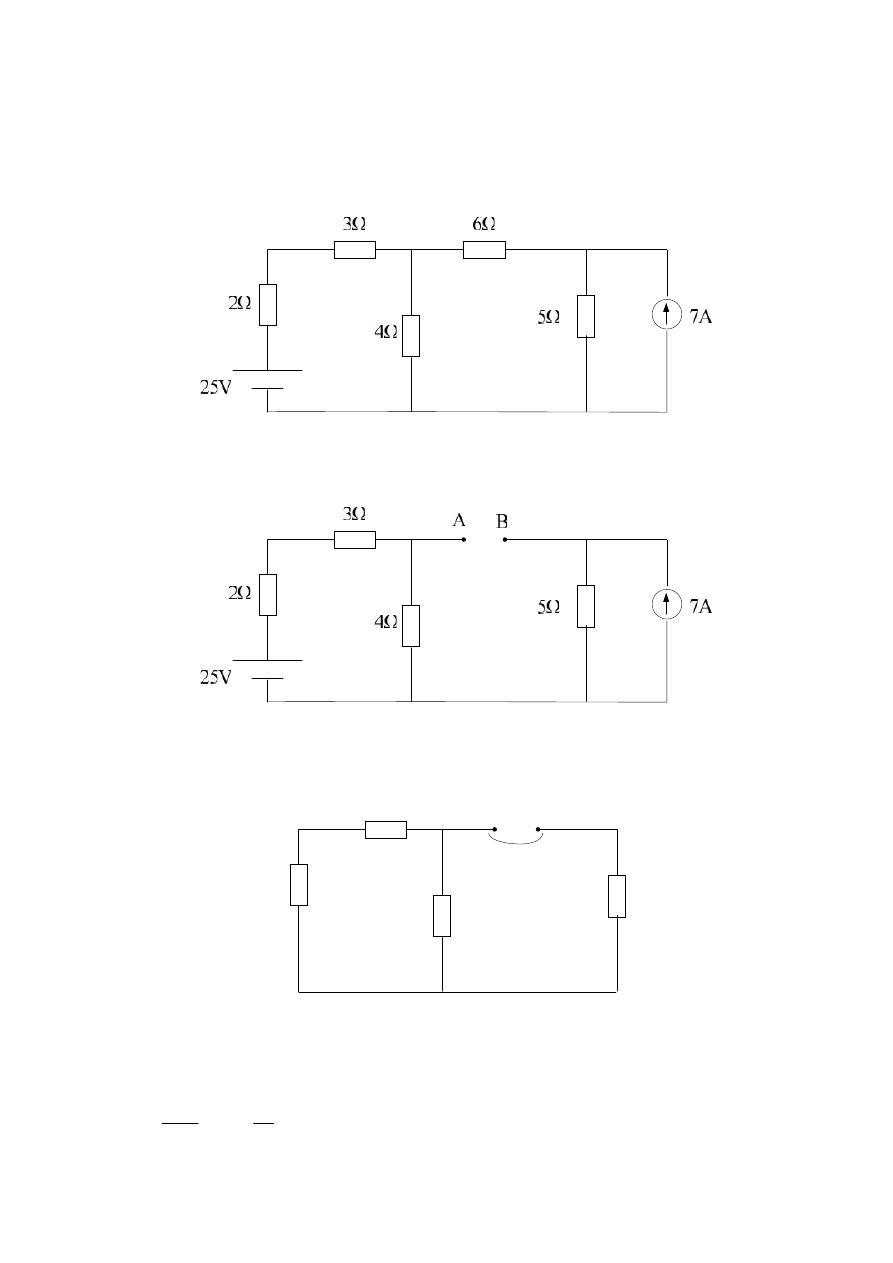
Example 1:- For the following circuit diagram, find the current in ( 6
Ω )
resistor?
Solution:-
1.) Find R
th
:
5Ω
4Ω
2Ω
3Ω
A
B
R
th
22
.
7
5
9
20
5
4
5
4
*
5
5
4
//
3
2
th
R
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٧٨
-
2.) Find E
th
:
5Ω
4Ω
2Ω
25V
3Ω
7A
A
B
V
oc
V
1
V
2
7A
A
9
25
V
E
V
V
V
V
V
V
th
oc
oc
oc
89
.
23
89
.
23
35
9
100
0
5
*
7
9
25
*
4
0
2
1
6Ω
R
th
= 7.22 Ω
E
th
= 23.89 V
A
B
I
A
R
R
E
I
L
th
th
8
.
1
6
22
.
7
89
.
23
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٨٨
-
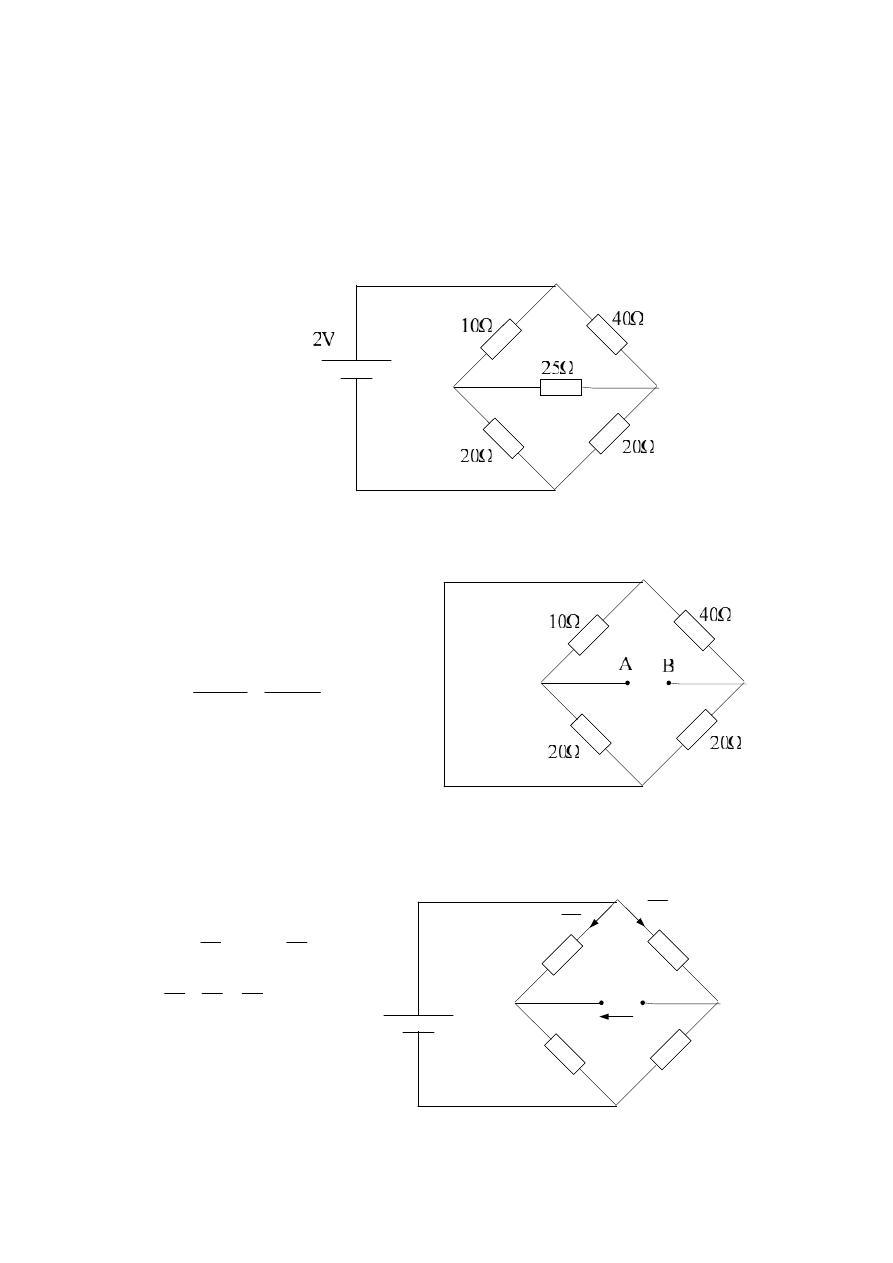
Example 2:-
Find the current in the 25Ω resistor for the following circuit
network?
Solution:-
1.) Find R
th
:
2.) Find E
th
:
10Ω
40Ω
20Ω
20Ω
A
B
2V
V
oc
A
60
2
A
30
2
20
20
40
20
*
40
20
10
20
*
10
20
//
40
20
//
10
th
th
R
R
V
E
V
V
V
th
oc
oc
67
.
0
67
.
0
60
40
30
20
60
80
0
60
2
*
40
30
2
*
10
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٩٨
-
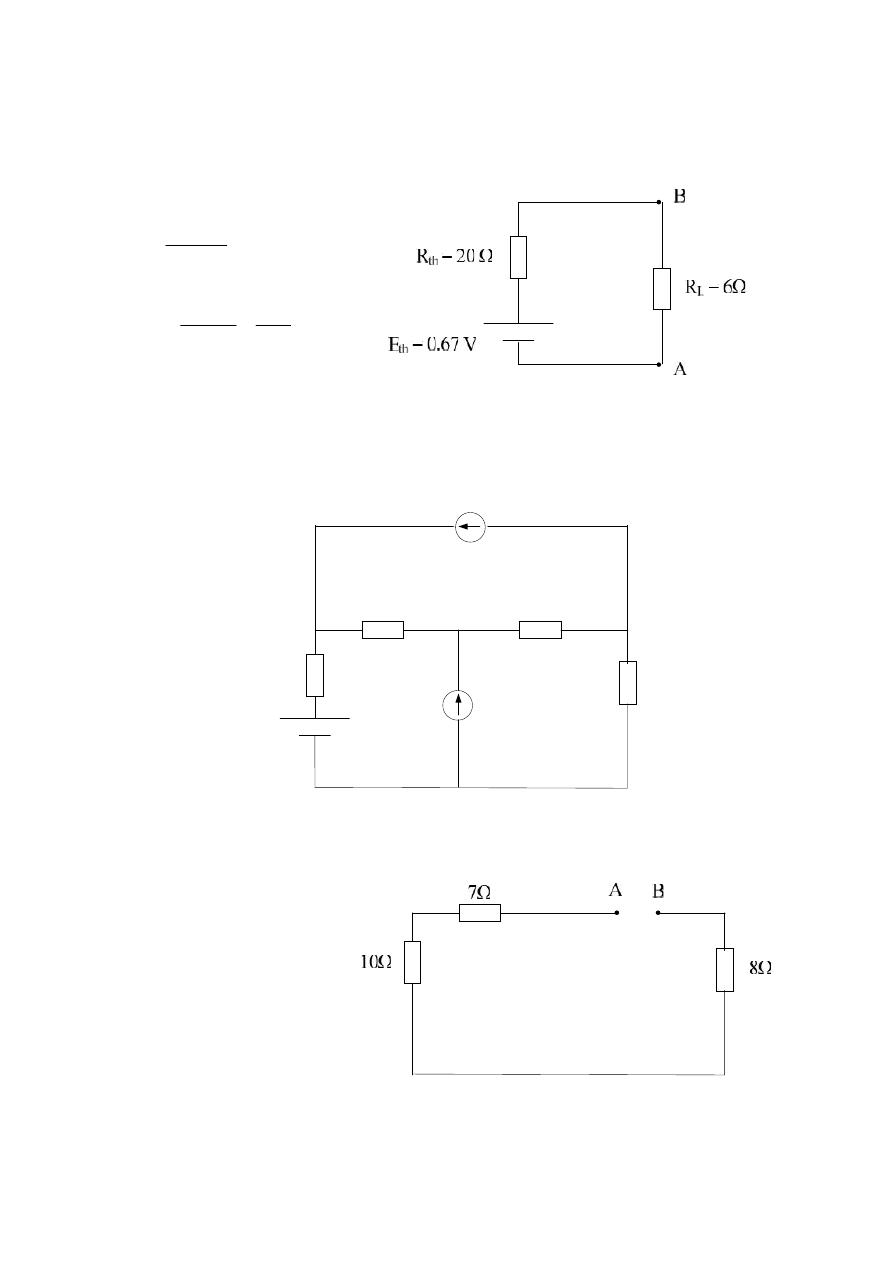
Example 3:-
Find I in the ( 9Ω ) resistor for the following cct. diagram?
9Ω
8Ω
7Ω
6A
4A
10Ω
25V
Solution :-
25
8
10
7
th
R
A
I
R
R
E
I
L
th
th
45
67
.
0
25
20
67
.
0
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٠٩
-
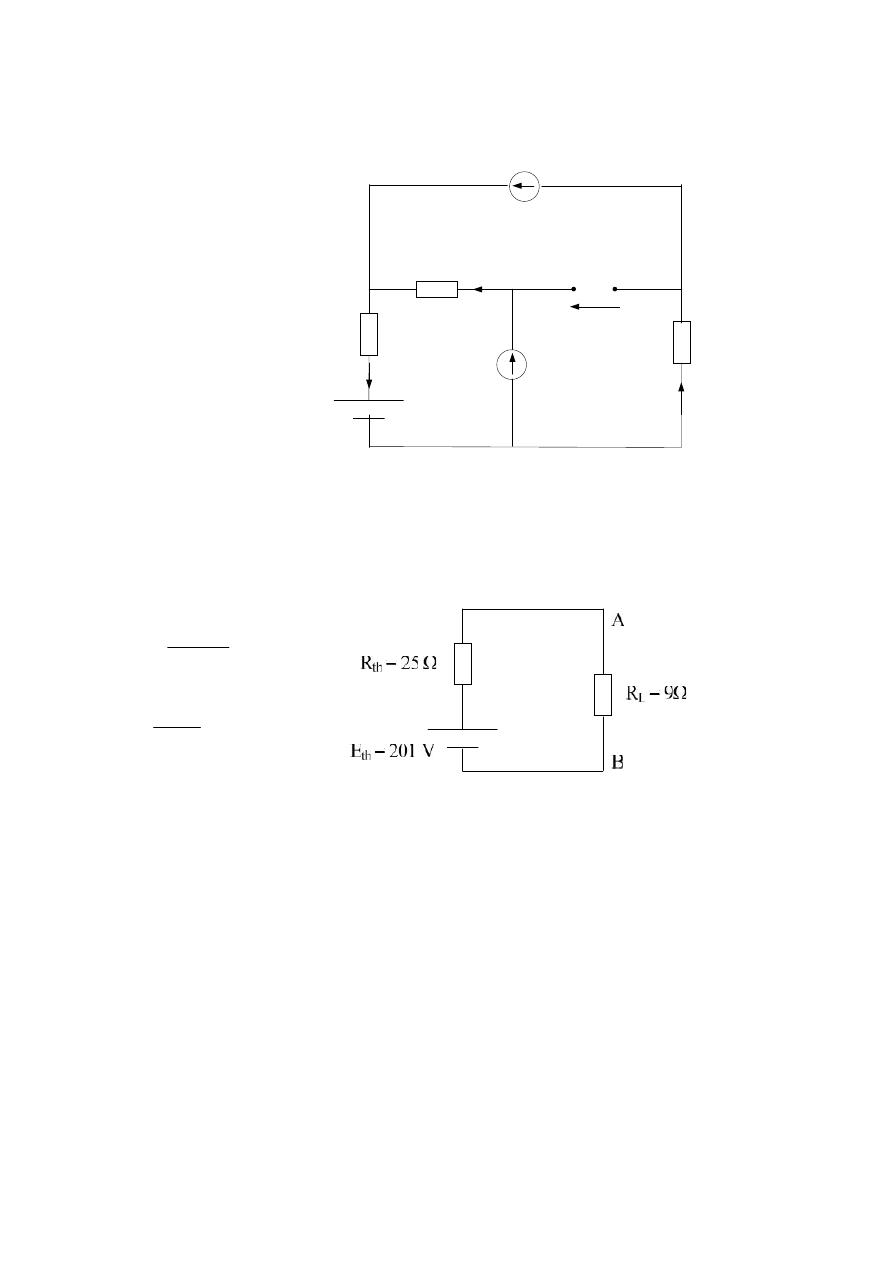
8Ω
7Ω
6A
4A
10Ω
25V
A
B
V
oc
6A
4A
10A
V
V
V
oc
oc
201
0
6
*
8
25
10
*
10
7
*
4
A
R
R
E
I
L
th
th
91
.
5
9
25
201
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
١٩
-
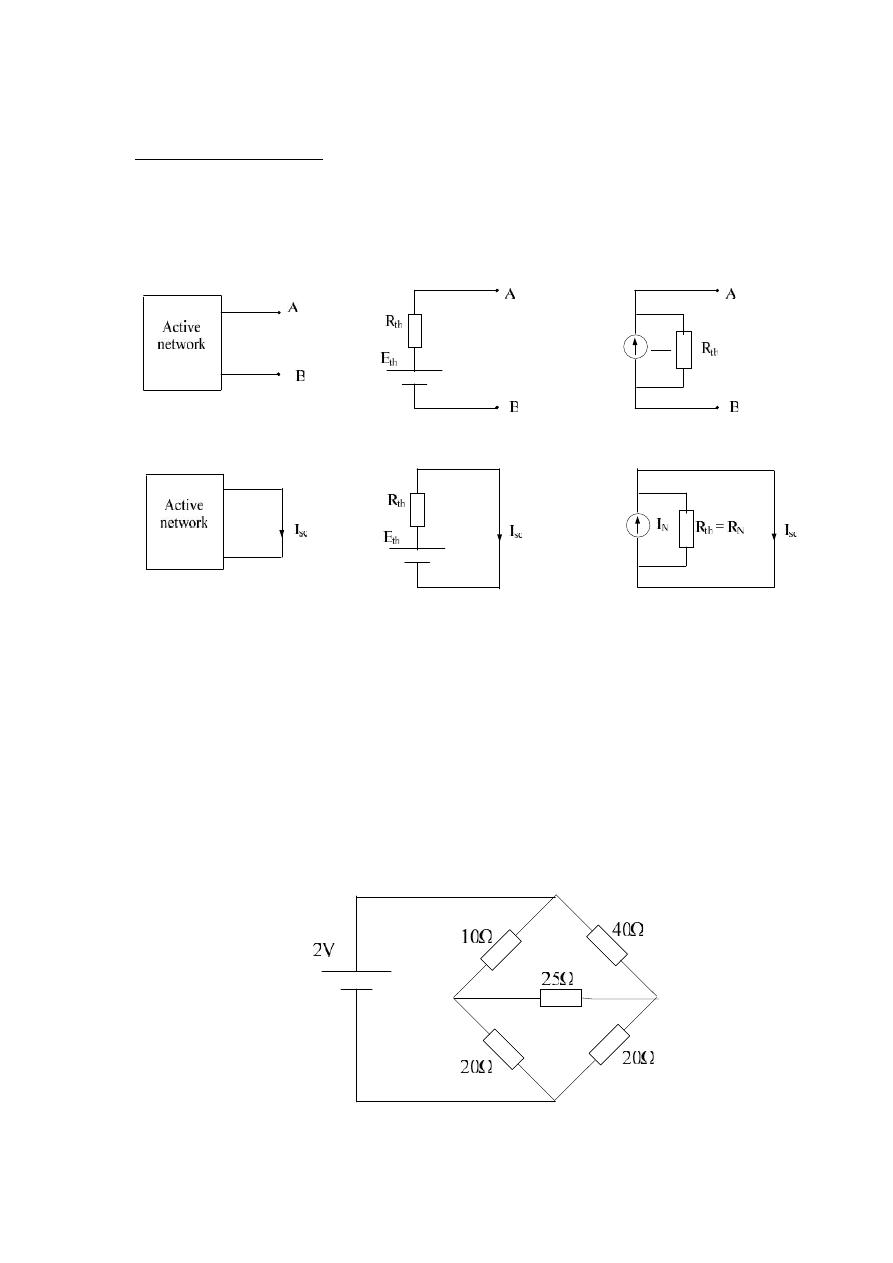
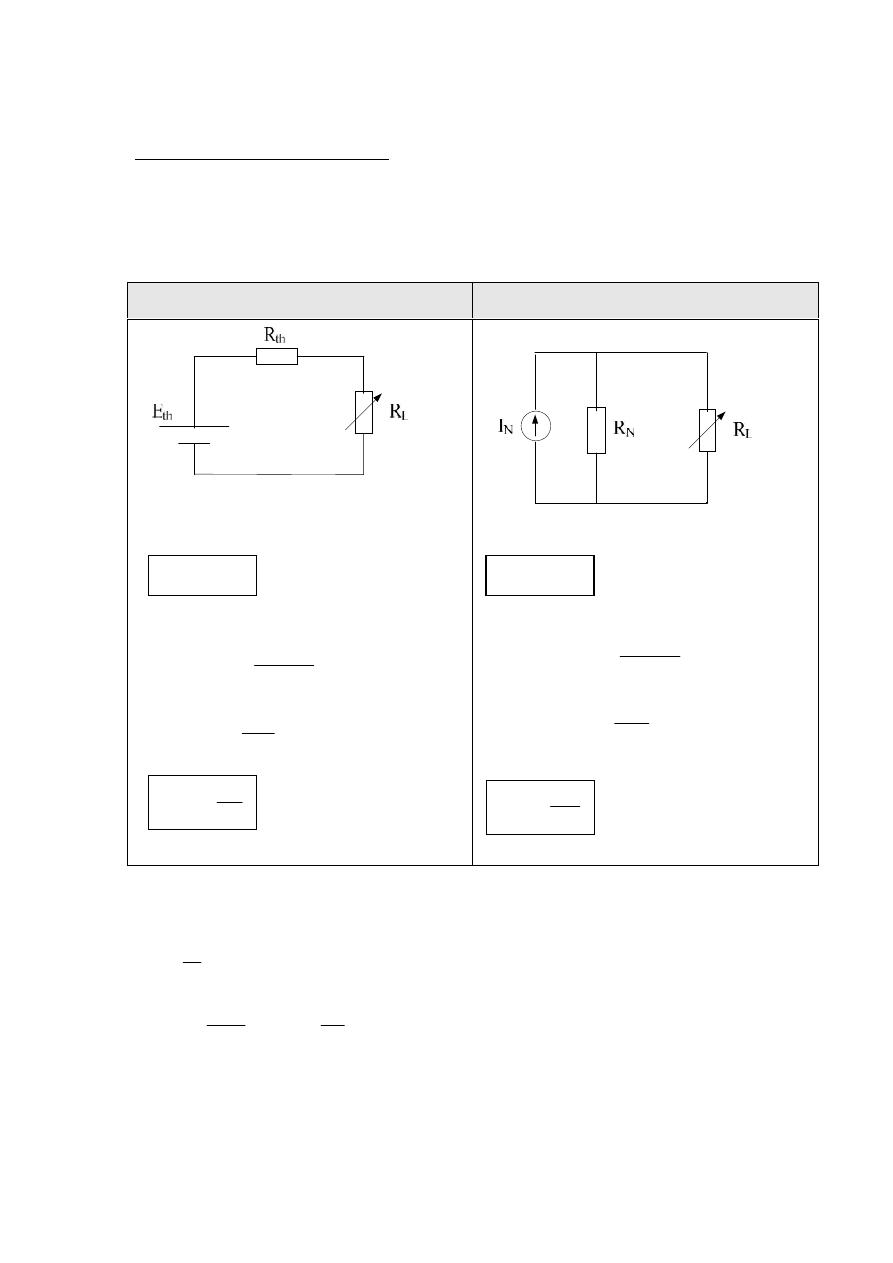
Norton's Theorems:-
Any two terminal linear network can be replaced by an equivalent circuit
consisting of a current source and a parallel resistor.
th
th
R
E
R
N
= R
th
as before .
I
N
= I
sc
= short circuit current between the two terminals of the active network.
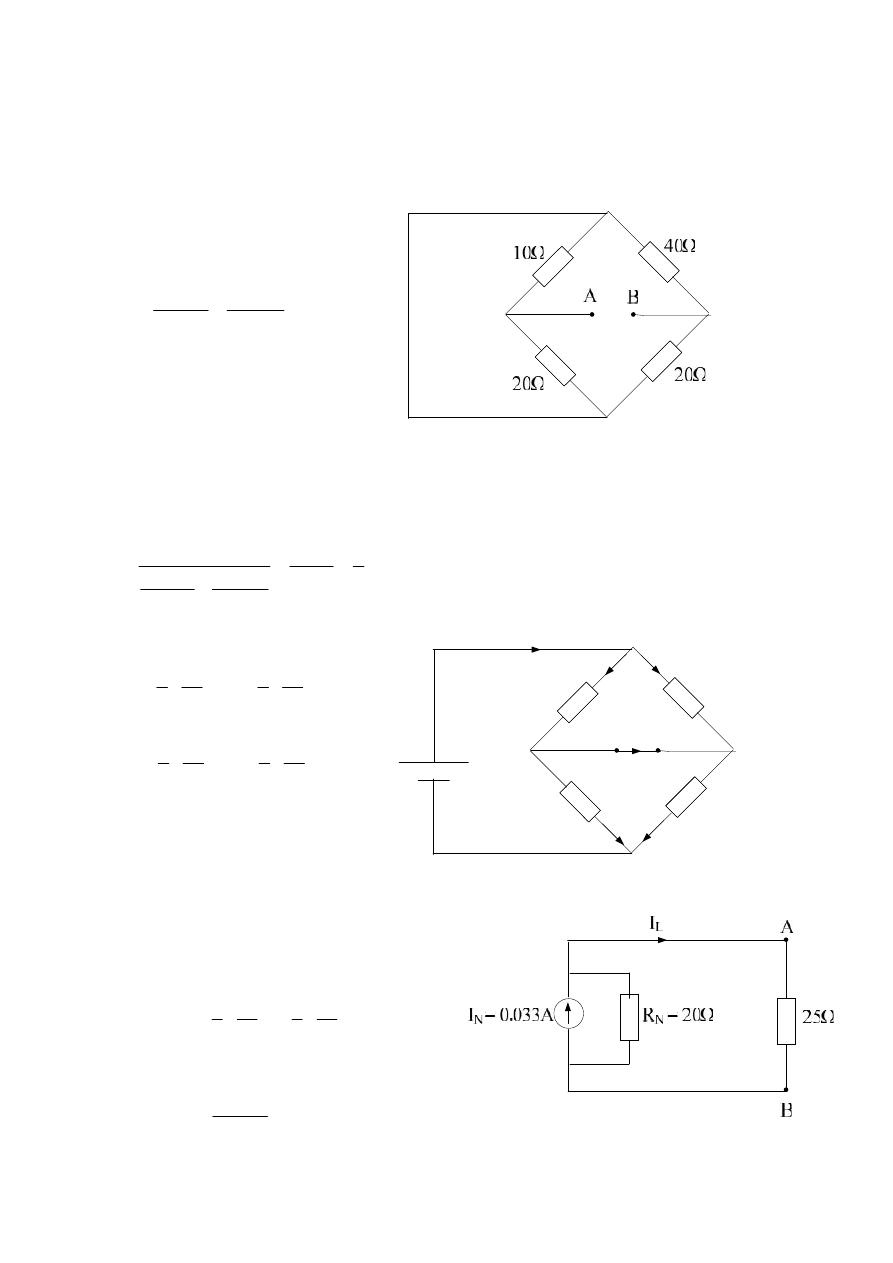
Example 1:-
Find the current in 25Ω resistor for the following circuit network
using Norton's Theorem?
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٢٩
-
Solution:-
First find R
N
:-
Second find I
N
:-
10Ω
40Ω
20Ω
20Ω
A
B
2V
I
N
I
1
I
2
I
4
I
3
I
20
20
40
20
*
40
20
10
20
*
10
20
//
40
20
//
10
N
R
A
I
9
1
10
8
2
20
20
20
*
20
40
10
40
*
10
2
40
20
*
9
1
&
40
20
*
9
1
50
10
*
9
1
&
50
40
*
9
1
4
3
2
1
I
I
I
I
KCL at A
I
1
– I
N
– I
3
= 0
I
N
= I
1
– I
3
A
033
.
0
40
20
*
9
1
50
40
*
9
1
A
I
L
0147
.
0
25
20
20
*
033
.
0
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٣٩
-
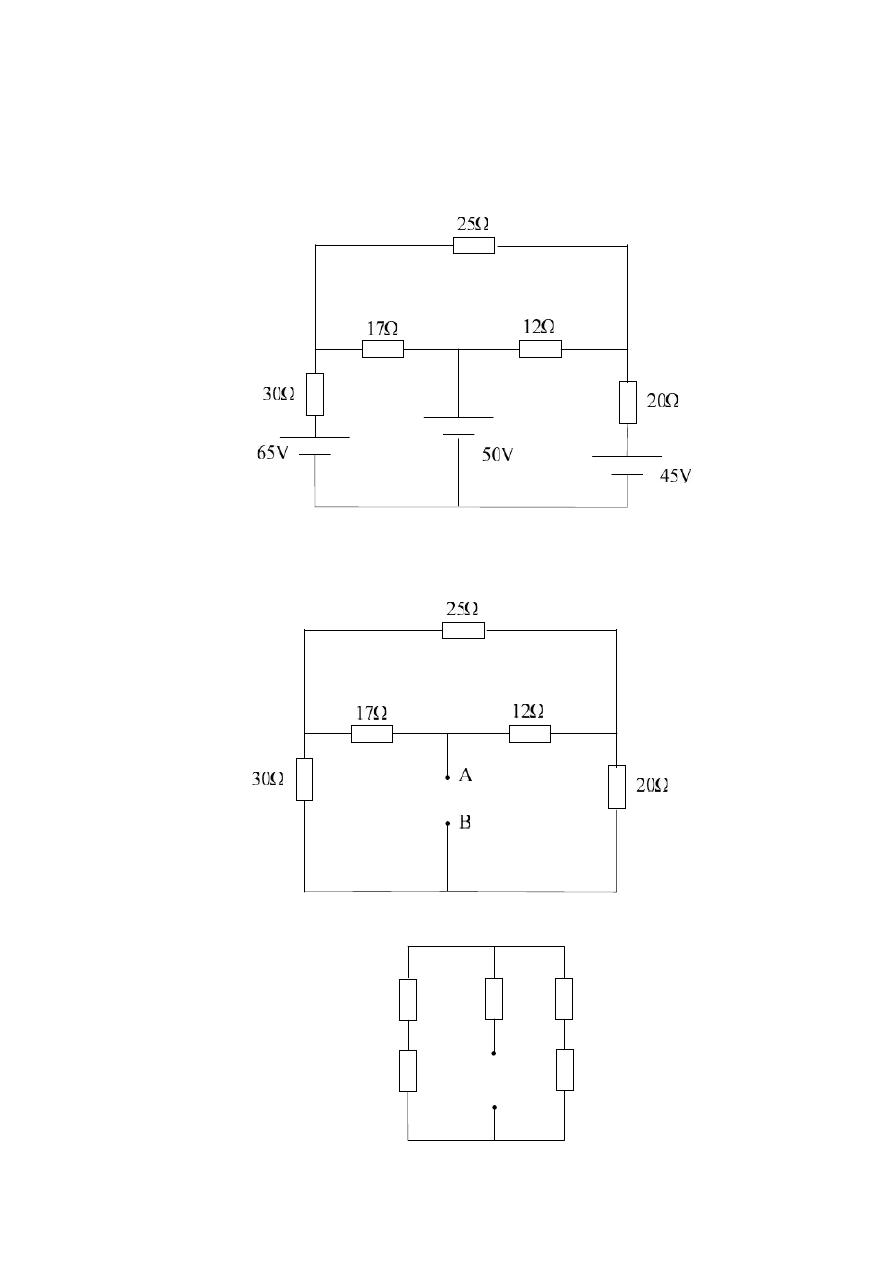
Example 2:- Find I in 50v voltage source, for the following circuit using
Norton's Theorem?
Solution:-
1.) Find R
N
:-
R
1
R
2
R
3
30Ω
20Ω
A
B
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٤٩
-
8
.
7
54
25
*
17
1
R
,
78
.
3
54
17
*
12
2
R
,
56
.
5
54
12
*
25
3
R
19
78
.
3
56
.
25
//
8
.
37
20
//
30
2
3
1
R
R
R
R
N
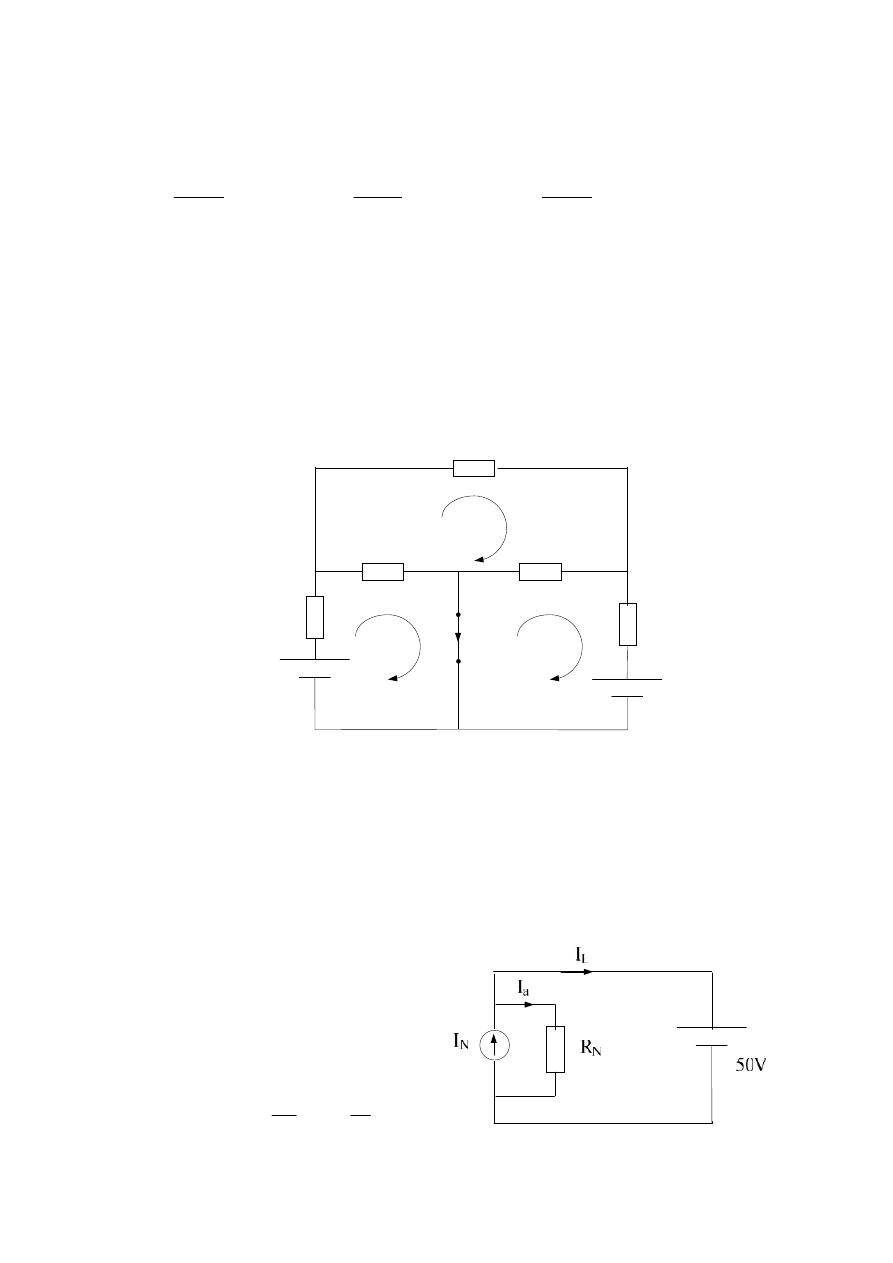
2.) Find I
N
:-
12Ω
20Ω
17Ω
30Ω
65V
25Ω
45V
A
B
I
N
I
b
I
c
I
a
-47I
a
+ 17I
c
+ 65 = 0
-32I
b
+ 12I
c
- 45 = 0
-54I
c
+ 17I
a
+ 12I
b
= 0
After find I
a
, I
b
, I
c
I
N
= I
a
– I
b
19
50
50
I
-
I
I
0
I
-
I
-
I
a
N
L
L
a
N
N
N
N
I
R
I
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٥٩
-
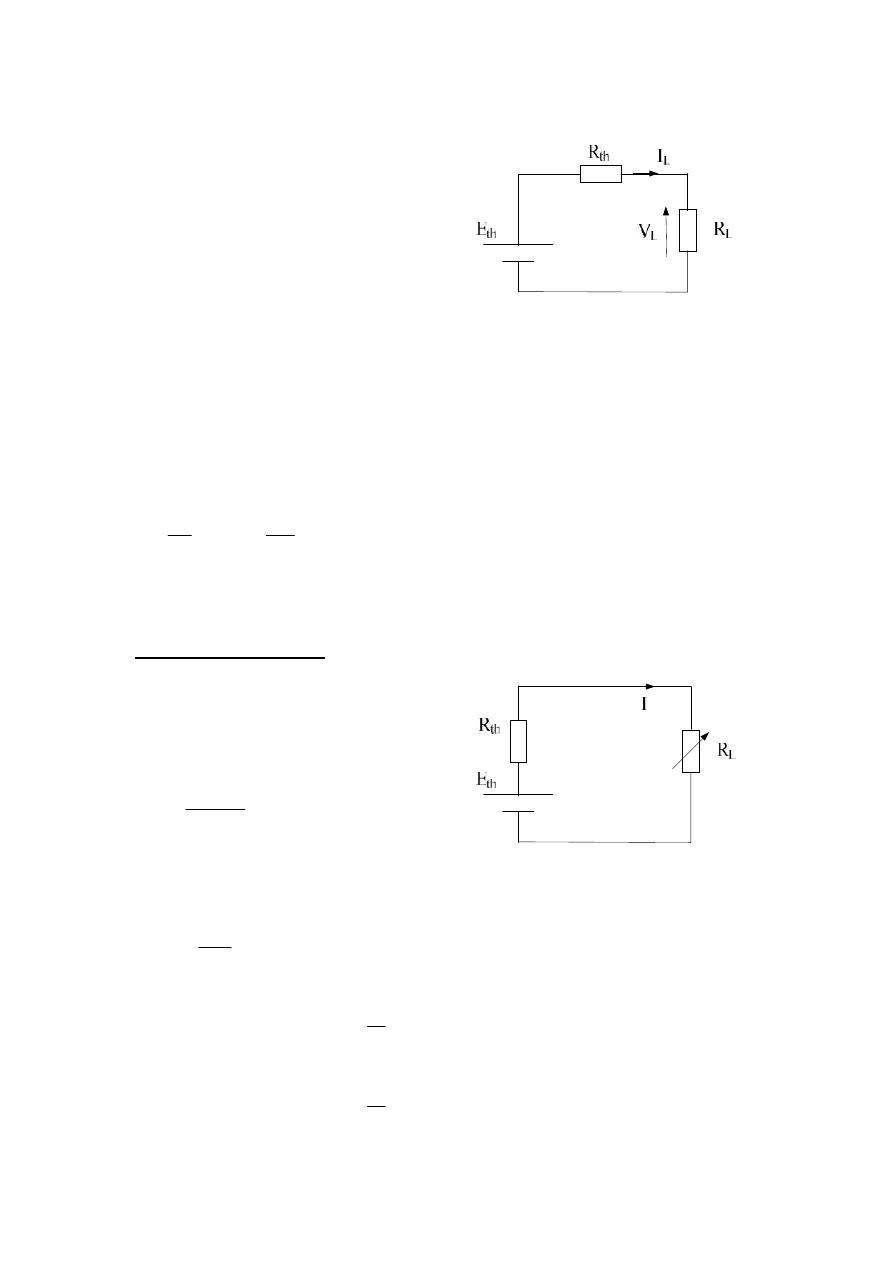
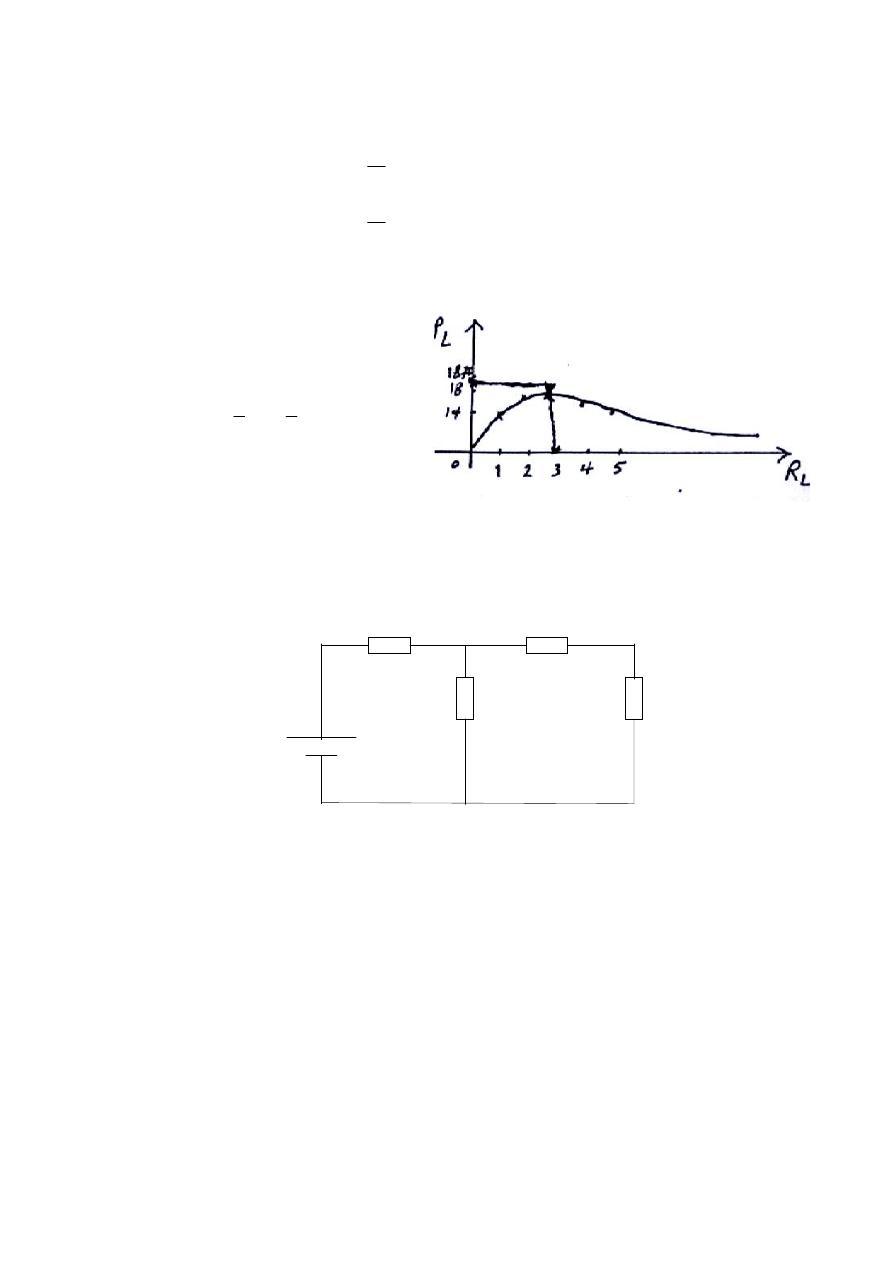
Maximum Power Transfer:-
A load will receive maximum power from a d.c. network when its total
resistive value is exactly equal to the Thevenin resistance of the network.
For Thevenin cct.
Nortan cct.
For Max. power
L
L
th
th
L
L
L
R
R
R
E
R
I
P
*
2
2
.
max
th
th
th
R
R
E
*
4
2
2
L
L
N
N
N
L
L
L
R
R
R
R
I
R
I
P
*
2
2
.
max
N
N
N
N
R
R
R
I
*
4
2
2
2
Under Max. Power transfer conditions, the efficiency is:-
%
100
*
%
i
o
P
P
%
100
*
L
th
L
L
I
E
I
V
%
100
*
th
L
E
V
R
L
= R
th
R
L
= R
N
th
th
L
R
E
P
4
2
.
max
4
2
.
max
N
N
L
R
I
P
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٦٩
-
E
th
= V
L
+ R
th
I
th
R
th
= R
L
( for max. power transfer )
E
th
= V
L
+ R
L
I
L
= V
L
+ V
L
= 2V
L
%
50
%
100
*
2
%
100
*
L
L
th
L
V
V
E
V
The efficiency will always be 50% under max. power transfer conditions .
* Practical example:-
Let
R
th
= 3
Ω & R
L
= 1Ω & E
th
= 15 V
W
P
L
14
1
*
1
3
15
2
For R
L
= 2Ω
W
P
L
18
2
*
5
15
2
For R
L
= 3Ω
W
P
L
75
.
18
3
*
6
15
2
L
L
th
L
L
R
R
R
E
R
I
P
*
2
2
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٧٩
-
For R
L
= 4Ω
W
P
L
36
.
18
4
*
7
15
2
For R
L
= 5Ω
W
P
L
57
.
17
5
*
8
15
2
Note that when R
L
= R
th
, we
get the max. power of P
L
.
Hence
EI
P
P
in
L
2
1
2
1
or P
in
= 2 P
L
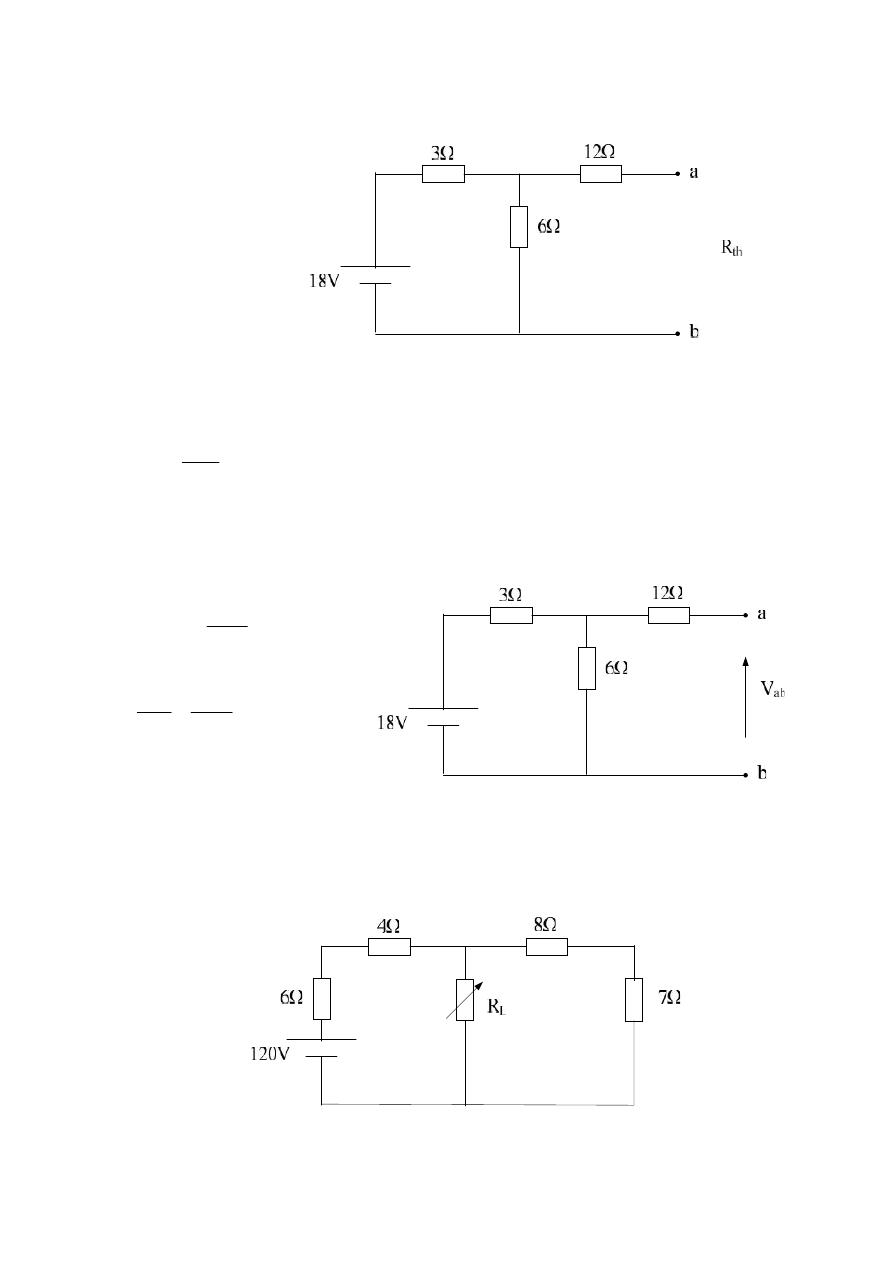
Example 1:- Find the value of R
L
for maximum power transfer to R
L
, and
determine the power delivered under these conditions ?
12Ω
R
L
6Ω
3Ω
18V
Solution:-
First remove R
L
, and find the equivalent resistance ( R
th
)
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٨٩
-
For Max. power R
L
= R
th
14
L
R
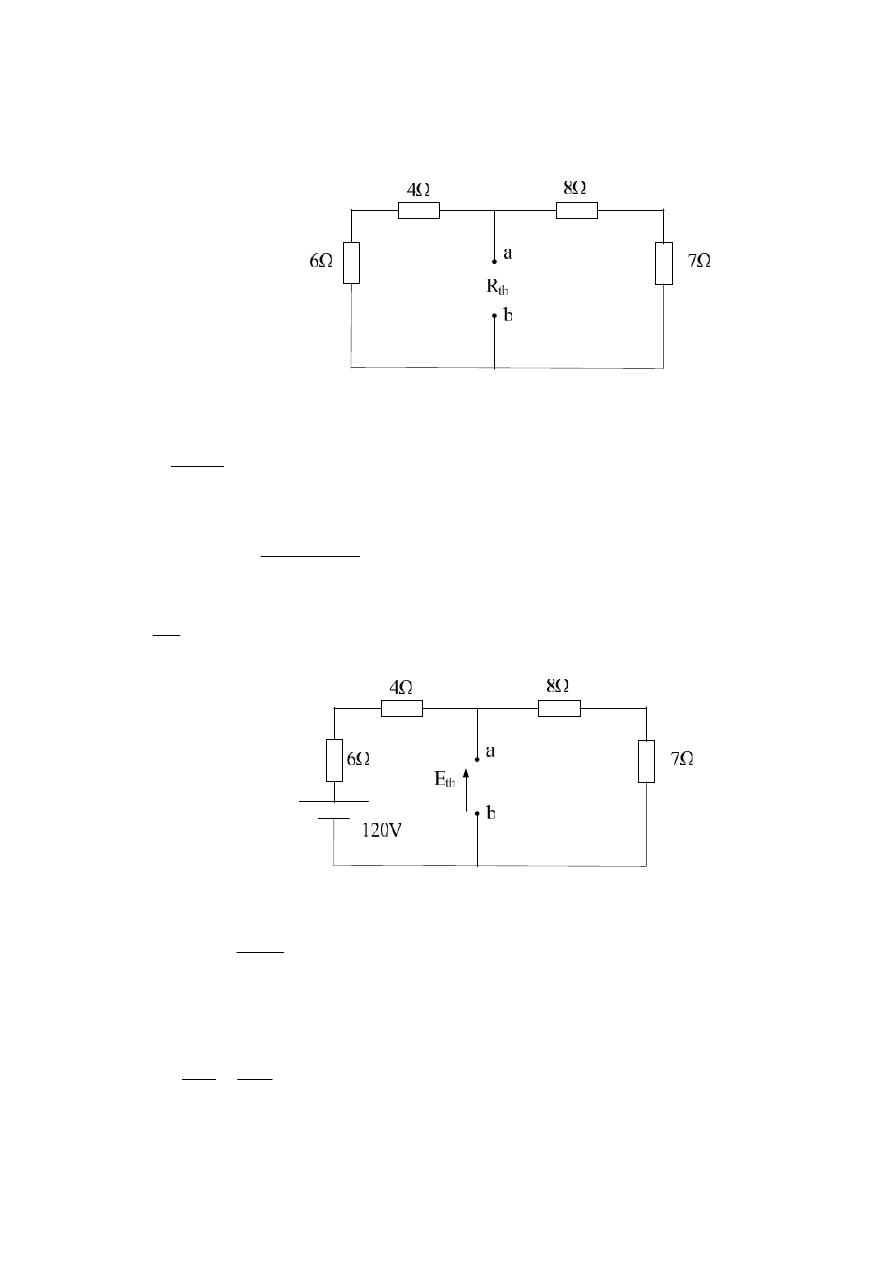
Example 2:- Find the value of R
L
for the following cct. for max. power transfer,
and find P
L
?
14
12
6
3
6
*
3
12
6
//
3
th
th
R
R
V
V
E
ab
th
12
3
6
6
*
18
W
R
E
P
th
th
57
.
2
14
*
4
12
4
2
2
.
max
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٩٩
-
Solution:-
V
E
V
V
th
ab
oc
72
15
*
25
120
7
8
*
7
8
4
6
120
W
R
I
P
L
L
216
6
*
6
6
72
2
2
or
L
th
eq
R
R
R
6
10
15
10
*
15
4
6
//
7
8
.
W
R
E
P
th
th
L
216
6
*
4
7
4
2
2
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٠٠١
-
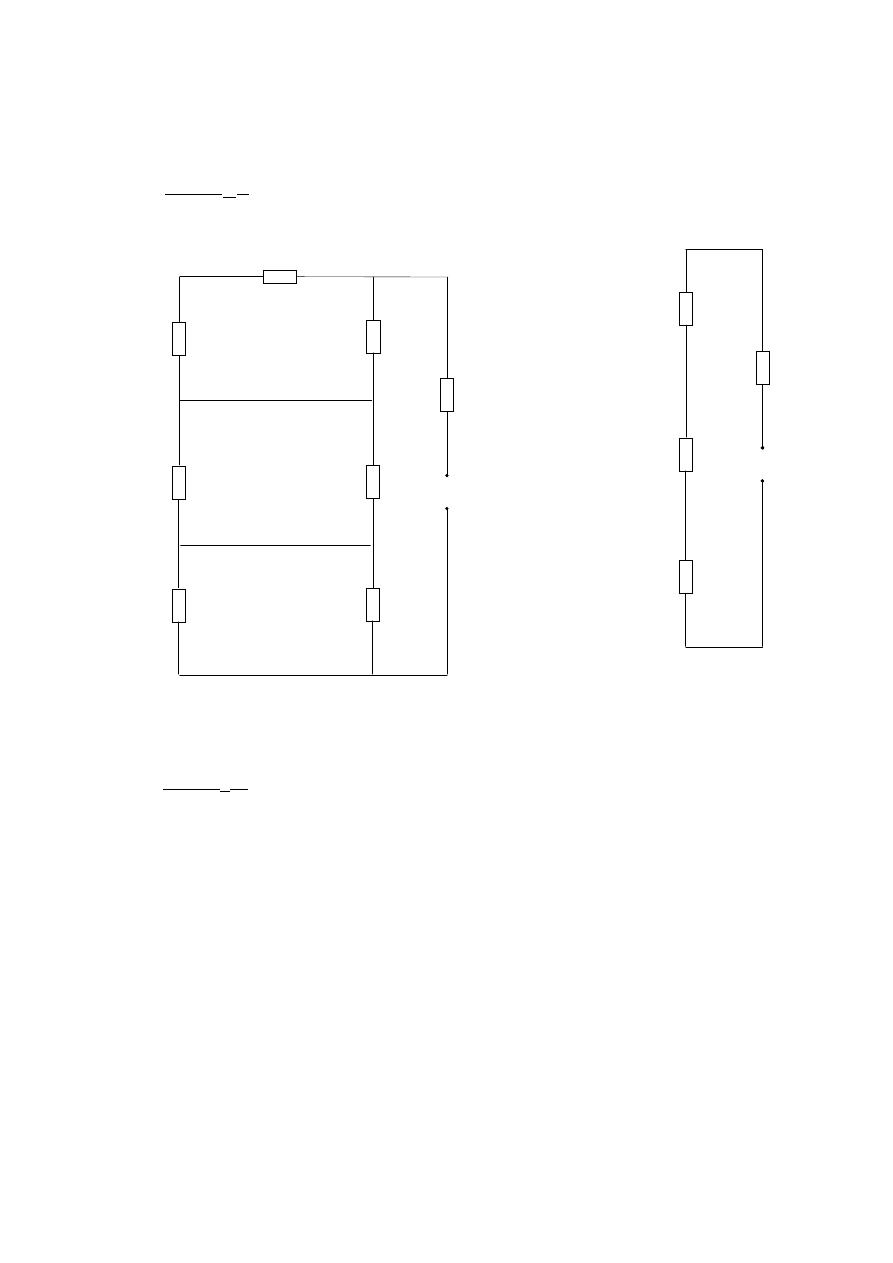
Example 3 (sheet 5, fig. 20):- Find the maximum power in ( R ), for the
following cct. diagram?
1Ω
1Ω
2Ω
6Ω
6Ω
2A
4Ω
10V
6V
2Ω
2Ω
4Ω
R
6V
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
١٠١
-
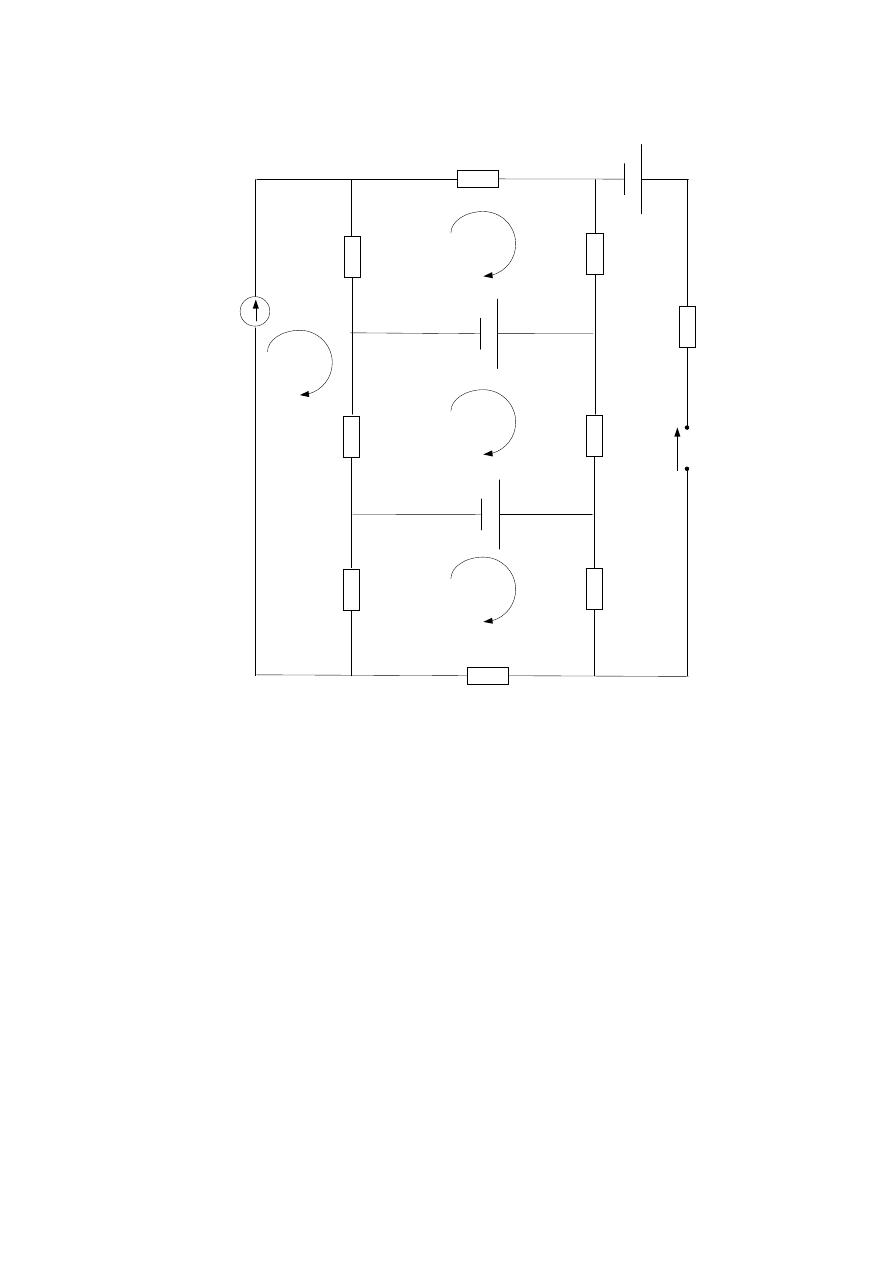
Solution:-
1-) Find R
th.
:-
1Ω
1Ω
2Ω
6Ω
6Ω
4Ω
4Ω
4Ω
A
B
1Ω
3Ω
4Ω
2Ω
A
B
R
R
R
th
eq
10
2
3
1
4
.
2.) Find E
th
:-
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٢٠١
-
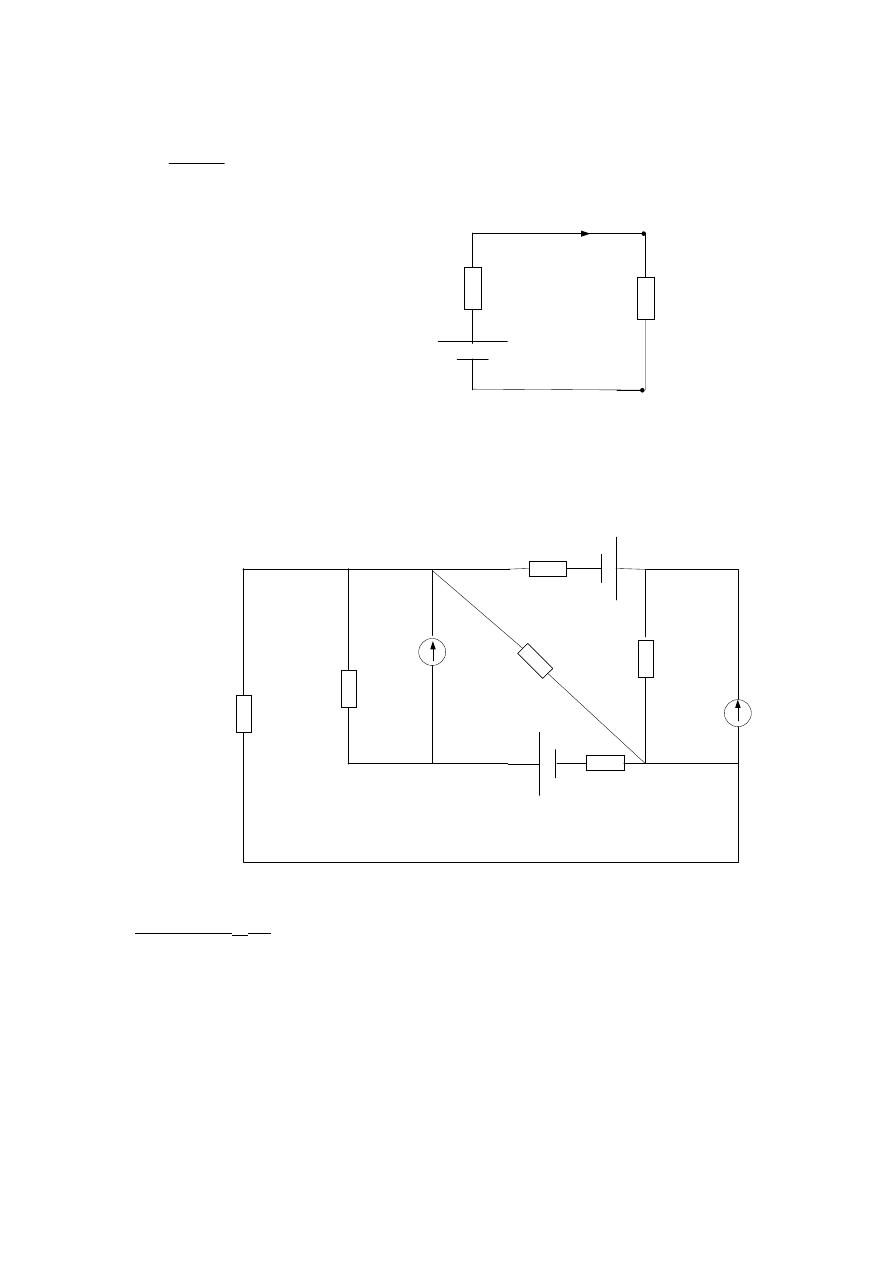
1Ω
1Ω
2Ω
6Ω
6Ω
2A
4Ω
10V
6V
2Ω
2Ω
4Ω
6V
A
B
I
Y
I
X
I
Z
2A
V
oc
A
I
I
A
I
I
A
I
I
z
z
y
y
x
x
25
.
1
0
2
*
2
6
8
33
.
1
0
6
*
2
6
10
12
2
0
2
*
1
10
4
From KVL
V
V
V
oc
oc
15
4
8
5
6
0
2
*
2
33
.
1
*
6
25
.
1
*
4
6
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٣٠١
-
A
I
75
.
0
10
10
15
R
L
= 10Ω
E
th
= 15 V
R
th
= 10Ω
B
A
I
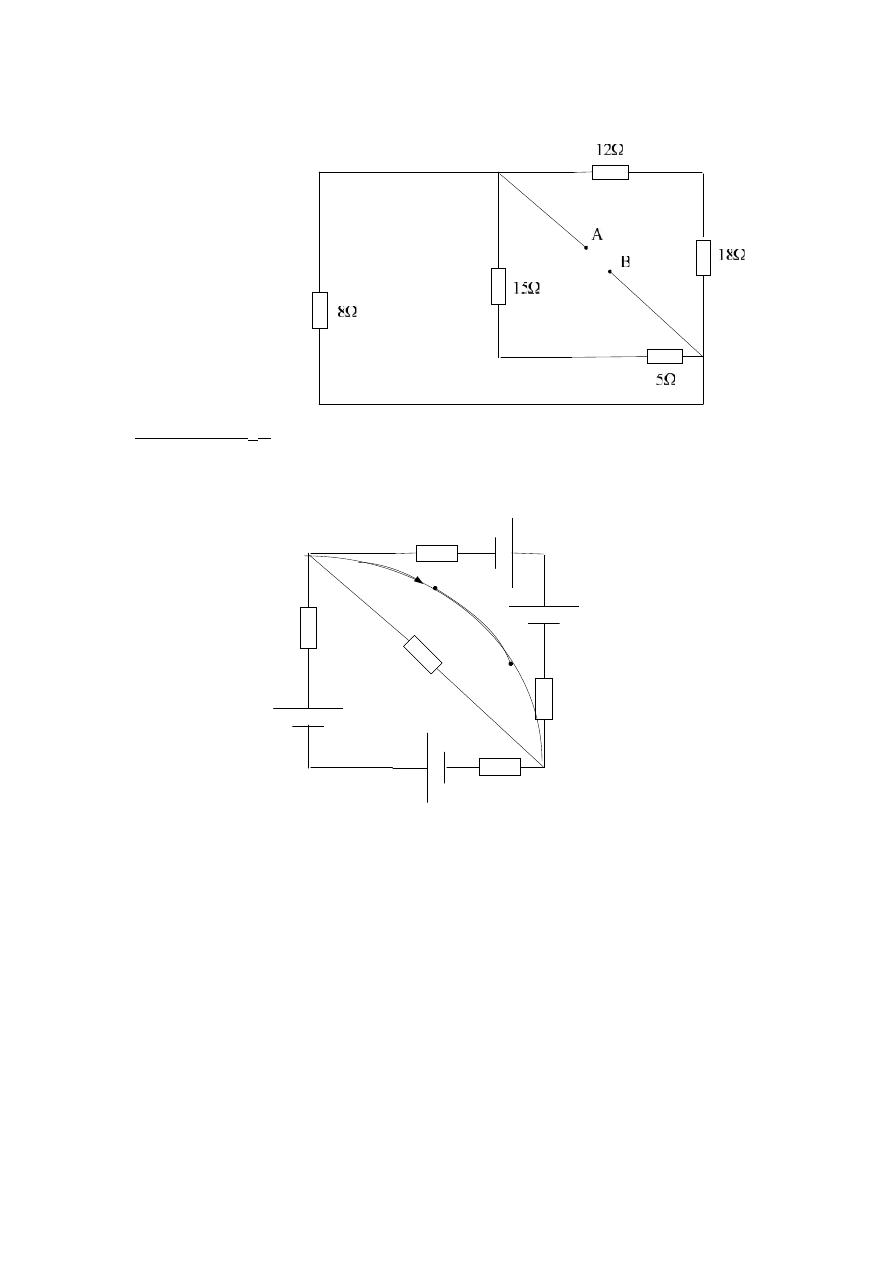
Example 4 (sheet 5, fig. 21):- Find the maximum power in ( R ), for the
following cct. diagram?
80mA
18Ω
5Ω
12Ω
R
15Ω
0.86V
0.3V
8Ω
20mA
Solution:-
First find R
eq.
:-
)
18
12
(
.
eq
R
//
)
5
15
(
//8 = 4.8
Ω
W
R
I
P
625
.
5
10
*
75
.
0
2
2
.
max
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٤٠١
-
Second find I
N
:-
18Ω
5Ω
12Ω
15Ω
0.86V
0.3V
0.36V
1.2V
8Ω
I
sc
A
B
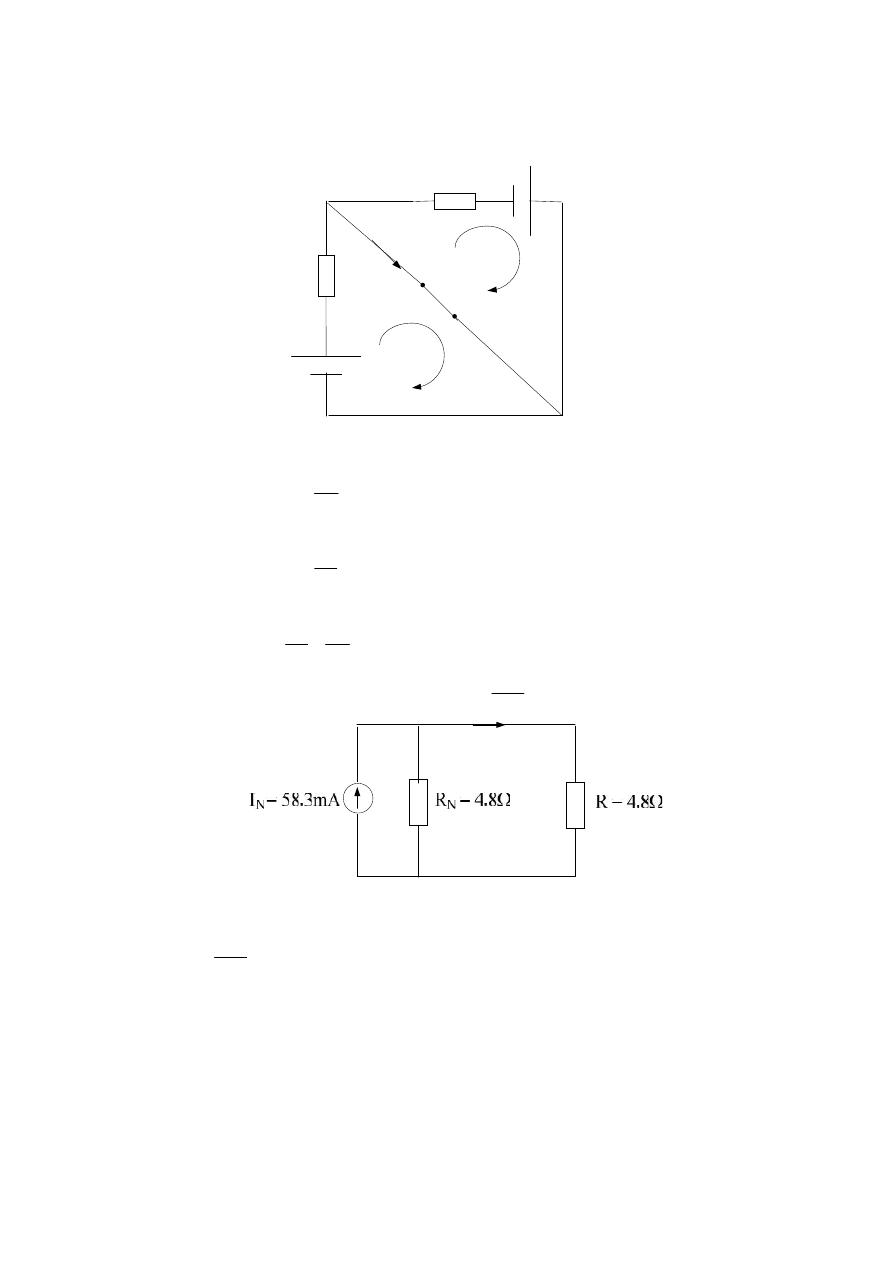
Dr. Sameir Abd Alkhalik Aziez
University of Technology ( Lecture (10))
-
٥٠١
-
30Ω
20Ω
0.5V
1.5V
A
B
I
sc
I
Y
I
X
mA
I
I
I
I
I
I
I
I
x
y
sc
N
y
y
x
x
3
.
58
30
5
.
0
20
5
.
1
20
5
.
1
0
5
.
1
20
30
5
.
0
0
5
.
0
30
A
2
3
.
58
mW
P
1
.
4
8
.
4
*
10
*
2
3
.
58
2
3
.
max
