Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٧٦
-
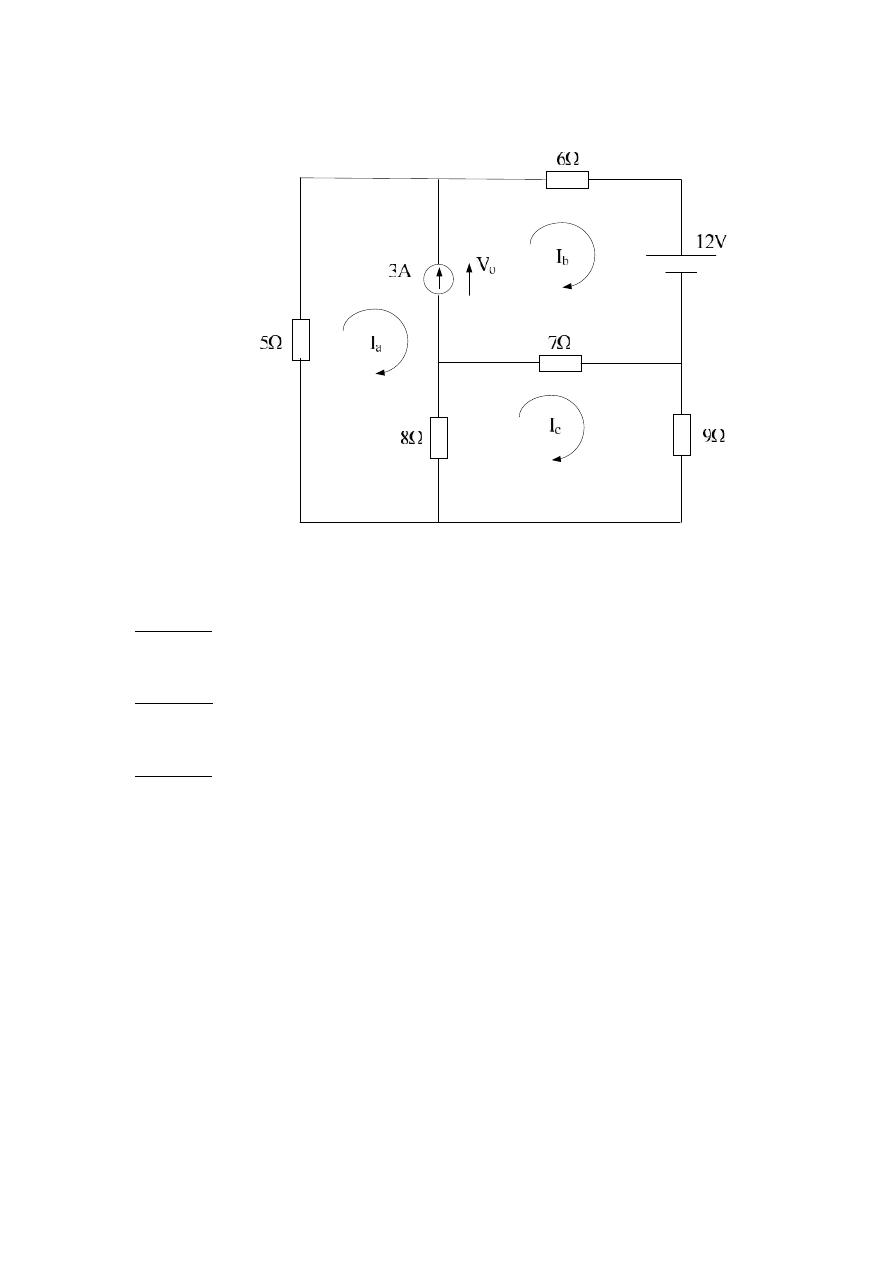
Example ( 7 ) : Solve the following circuit , using loop current method :-
Solution:
Loop a :-
-( 5+8 )I
a
+ 8I
c
- V
o
= 0
Loop b :-
-( 6+7 )I
b
+ 7I
c
+ V
o
– 12 = 0
Loop c :-
-( 8+7+9 )I
c
+ 8I
a
+ 7I
b
= 0
I
b
– I
a
= 3
ﻣﻼ
ﺔـــظﺣ
:
-
ﻰـــﻠﻋ يوـــﺗﺣﺗ ﻲـــﺗﻟا ﺔﻠﺋـــﺳﻻا ﻩذـــﻫ لـــﺛﻣ ﻲـــﻓ
V
o
رحـــط وا ﻊـــﻣﺟ تﺎـــﯾﻠﻣﻋ يرـــﺟﻧ ،
اﻟﻣﻌﺎدﻻت اﻟﺗﻲ ﺗﺣﺗوي ﻋﻠﻰ
V
o
ﻟﻠﺗﺧﻠص ﻣﻧﻬﺎ و ﻧﺑﺳط اﻟﺣل
.
ﺎدــــﺟﯾا بوــــﻠطﻣﻟا نﺎــــﻛ اذا ﺎــــﻣأ
V
o
ﺎﻟﺗﺧﻠصــــﺑ موــــﻘﻧ ﺎــــﺿﯾﺎﻓ ،
ﻣ
ﺎ اوﻻــــﻬﻧ
)
رحــــط وا ﻊــــﻣﺟ قــــﯾرط نــــﻋ
اﻟﻣﻌﺎدﻻت
اﻟﺗﻲ ﺗﺣﺗوي ﻋﻠﻰ
V
o
(
ﺛم ﺑﻌد اﯾﺟﺎد اﻟﺗﯾﺎ
ﻰـﻠﻋ يوـﺗﺣﺗ ﻲـﺗﻟا ﺔﻟدﺎﻌﻣﻟا ﻲﻓ ﺎﻬﺿوﻌﻧ تار
V
o
وﻧﺟدﻫﺎ
.
-------------------
( 1 )
-------------------
( 2 )
-------------------
( 3 )
-------------------
( 4 )

Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٨٦
-
Loop a+b :
-13I
a
- 13I
b
+ 15I
c
– 12 = 0
Loop c :-
-24I
c
+ 8I
a
+ 7I
b
= 0
I
b
– I
a
= 3
Rearrange Eq.s :-
-13I
a
- 13I
b
+ 15I
c
= 12
8I
a
+ 7I
b
-24I
c
= 0
- I
a
+ I
b
= 3
A
D
D
I
a
862
.
1
1402
2610
0
1
1
24
7
8
15
13
13
0
1
3
24
7
0
15
13
12
1
D
D
I
b
2
D
D
I
c
3
أﻛﻣل اﻟﺣل
-------------------
(
1
)
-------------------
(
2
)
-------------------
(
3
)
-------------------
(
3
)
-------------------
(
1
)
-------------------
(
2
)
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٩٦
-
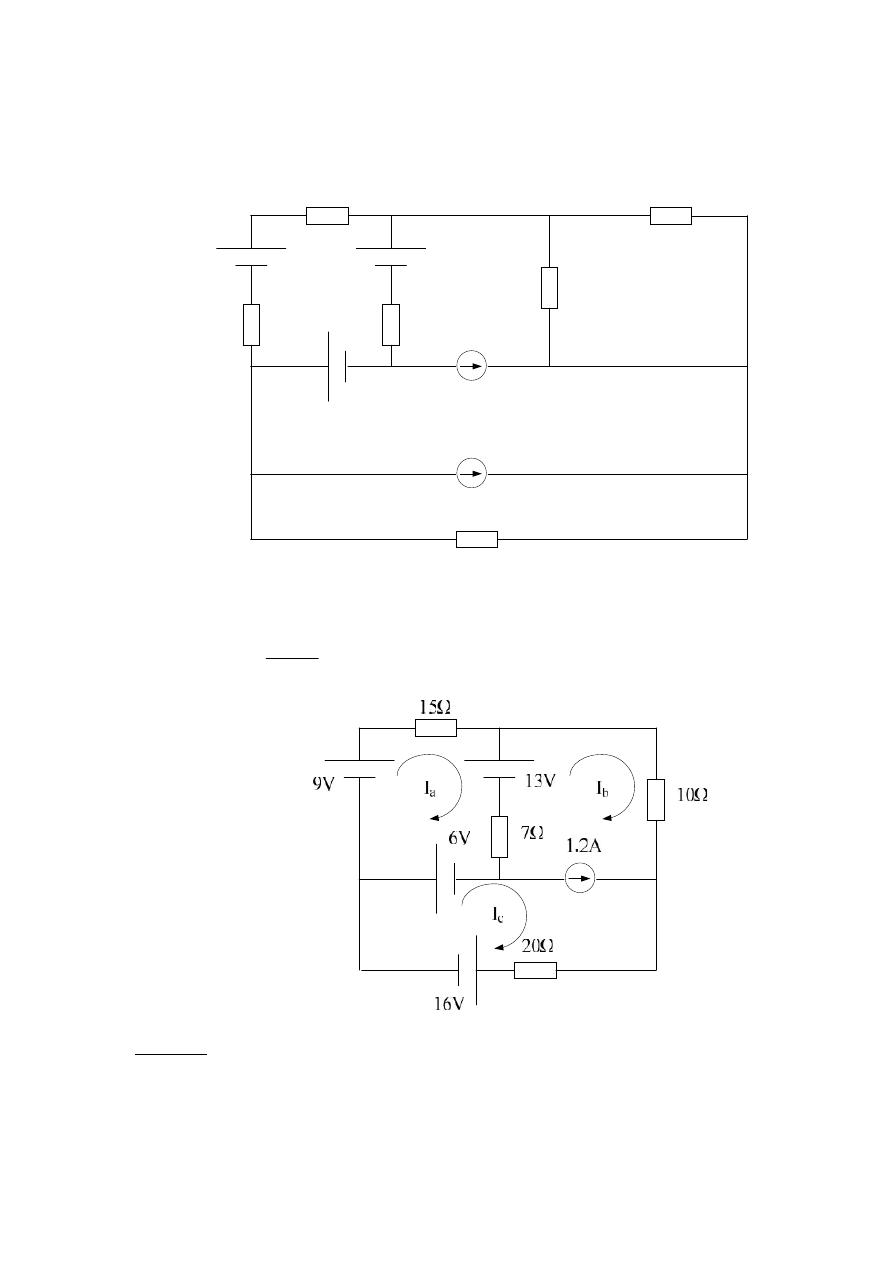
Example, (Sheet 4 – Q. 25): Solve the following circuit diagram using loop
current:
30Ω
15Ω
13V
7Ω
9V
3Ω
12Ω
1.2A
0.8A
20Ω
6V
Solution:-
15 Ω // 30 Ω =
10
30
15
30
*
15
; 12 + 3 = 15 Ω
Loop a:-
-( 15+7 )I
a
+ 6 + 9 + 7I
b
- 13 = 0
-------------------
( 1 )
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٠٧
-
Loop b:-
-( 7+10 )I
b
- V
o
+ 13 + 7I
a
= 0
Loop c:-
-20I
c
– 16 – 6 + V
o
= 0
I
c
– I
b
= 1.2
Loop b+c:
-17I
b
- 20I
c
+ 7I
a
– 9 = 0
Rearrange Eq.s :-
Loop a:
-22I
a
+ 7I
b
= -2
Loop b+c:
7I
a
- 17I
b
-20I
c
= 9
I
b
– I
c
= -1.2
أﻛﻣل اﻟﺣل
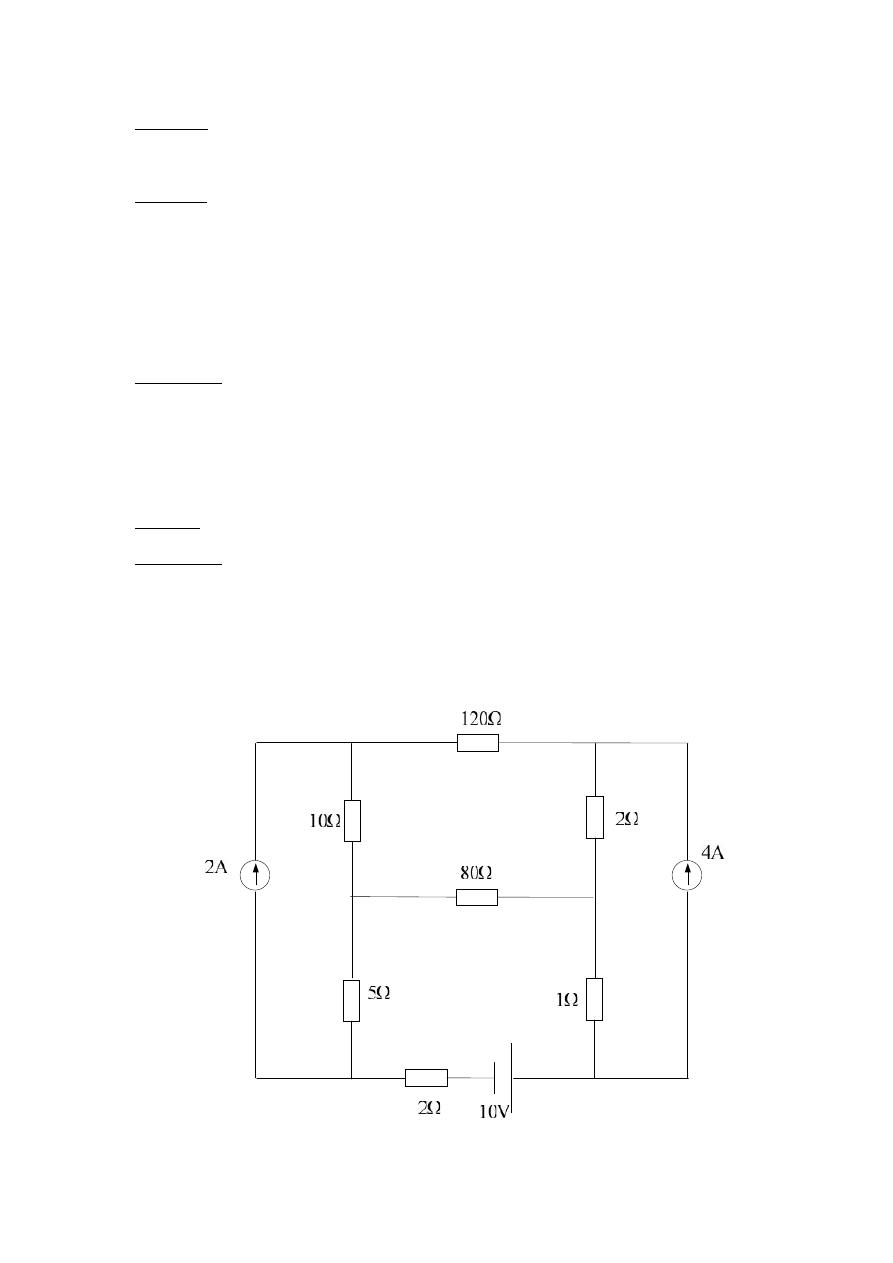
Example, (Sheet 4 – Q. 7): Solve the following circuit diagram:
-------------------
( 2 )
-------------------
( 3 )
-------------------
( 4 )
-------------------
( 3 )
-------------------
( 1 )
-------------------
( 2 )
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
١٧
-
Solution:
120Ω
80Ω
5Ω
2Ω
10V
1Ω
10Ω
2Ω
8V
20V
4V
10V
I
b
I
a
Loop a :-
-( 10+120+2+80 )I
a
+ 80I
b
- 8 + 20 = 0
Loop b :-
-( 2+5+80+1 )I
b
+ 80I
a
- 4 - 10 + 10 = 0
Rearrange Eq.s :-
-212I
a
+ 80I
b
= -12
80I
a
- 88I
b
= 4
أﻛﻣل اﻟﺣل
Nodal voltage:-
-------------------
( 1 )
-------------------
( 2 )
-------------------
( 1 )
-------------------
( 2 )
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٢٧
-
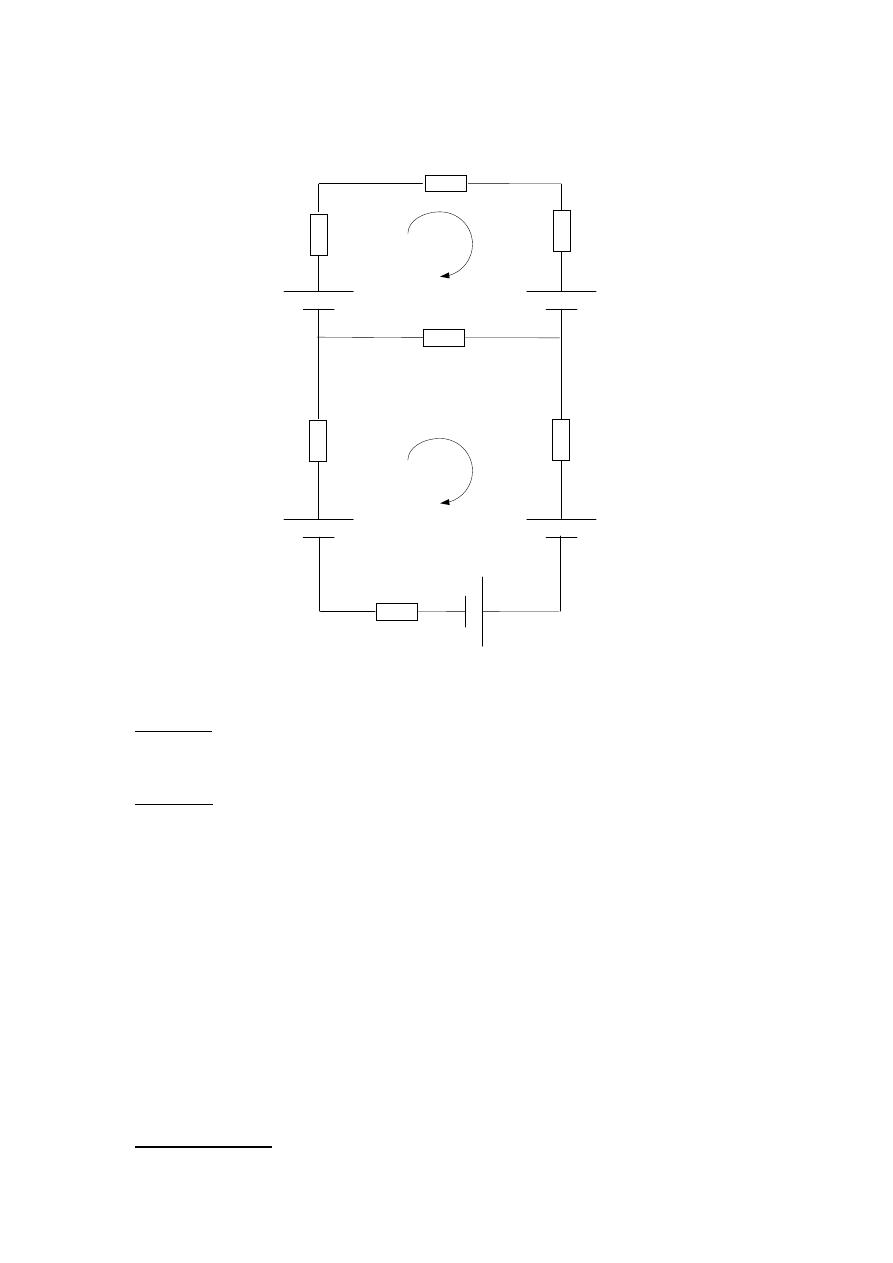
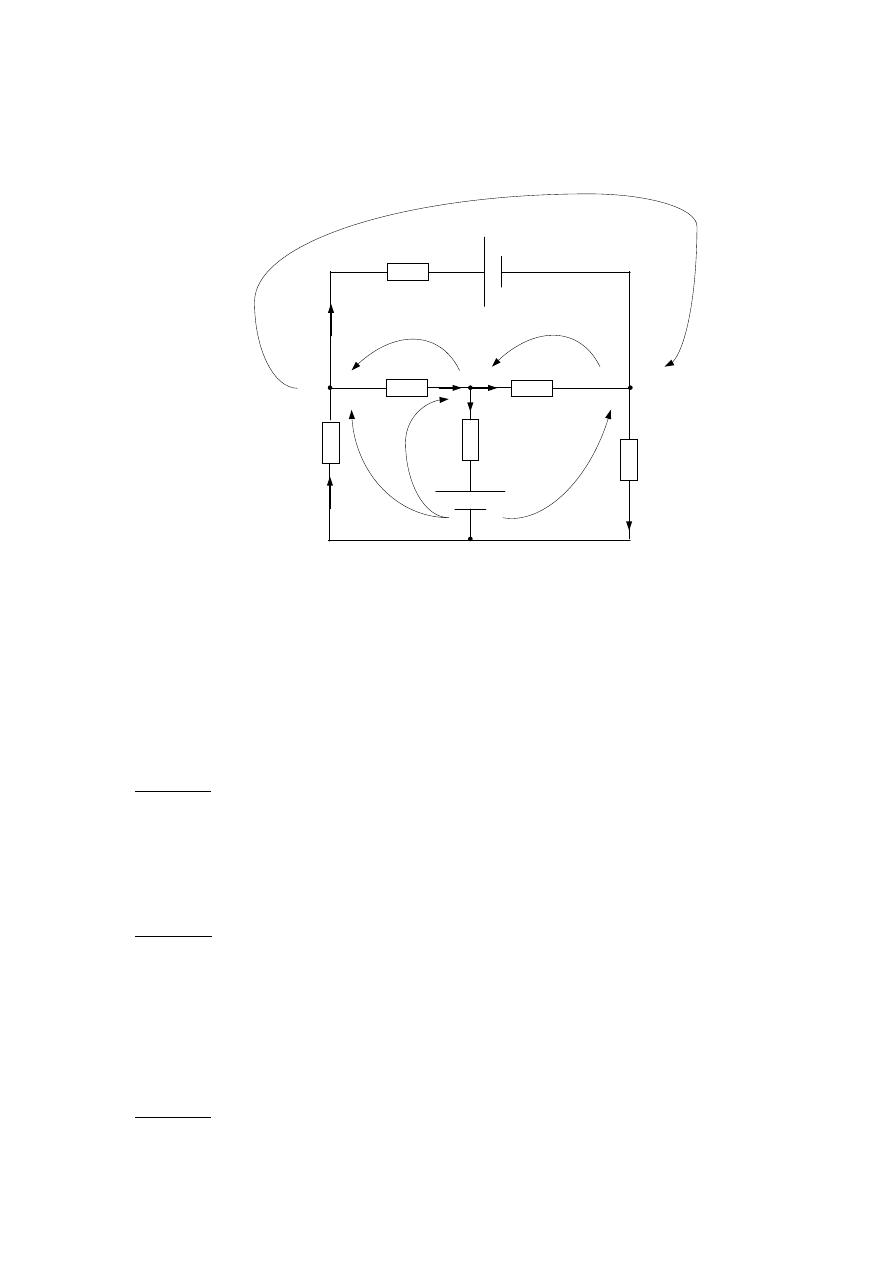
Example 1 :- Solve the following circuit using the nodal voltage method:
R
4
R
1
E
2
R
2
R
3
R
5
R
6
E
1
V
B
- V
C
V
A
- V
B
V
C
V
A
V
B
A
C
D
B
V
C
- V
A
I
1
I
4
I
6
I
5
I
3
I
2
Solution :-
Choose reference point
N = 4
Let D be a reference point
I
N
= N-1 = 3
Kcl at B:
I
5
– I
2
– I
6
= 0
(V
A
– V
B
) G
5
– ( V
B
– E
2
) G
2
– ( V
B
– V
C
) G
6
= 0
Kcl at A:
I
3
– I
5
– I
1
= 0
-V
A
G
3
– ( V
A
– V
B
) G
5
– [( V
A
– V
C
)- E
1
] G
1
= 0
Kcl at C:
ﻧﻘﺎط اﻟﺗﻔرع
ﻋدد اﻟﻣﻌﺎدﻻت
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٣٧
-
I
6
+ I
1
– I
4
= 0
( V
B
– V
C
) G
6
+ [( V
A
– V
C
)- E
1
] G
1
– V
C
G
4
= 0
Rearrange:
A :
( V
B
– V
A
) G
5
-V
A
G
3
+ ( V
C
– V
A
) G
1
- E
1
G
1
= 0
B :
(V
A
– V
B
) G
5
+ ( V
C
– V
B
) G
6
- V
B
G
2
+ E
2
G
2
= 0
C :
( V
B
– V
C
) G
6
– V
C
G
4
+ ( V
A
– V
C
) G
1
- E
1
G
1
= 0
Hence, we can arrange the above equations in the following form:-
A :
- V
A
( G
1
+ G
3
+ G
5
) + V
B
G
5
+ V
C
G
1
+ E
1
G
1
= 0
B :
- V
B
( G
2
+ G
5
+ G
6
) + V
A
G
5
+ V
C
G
6
+ E
2
G
2
= 0
C :
- V
C
( G
1
+ G
4
+ G
6
) + V
A
G
1
+ V
B
G
6
- E
1
G
1
= 0
Then, we can find V
A
, V
B
, V
C
by the determinate method .
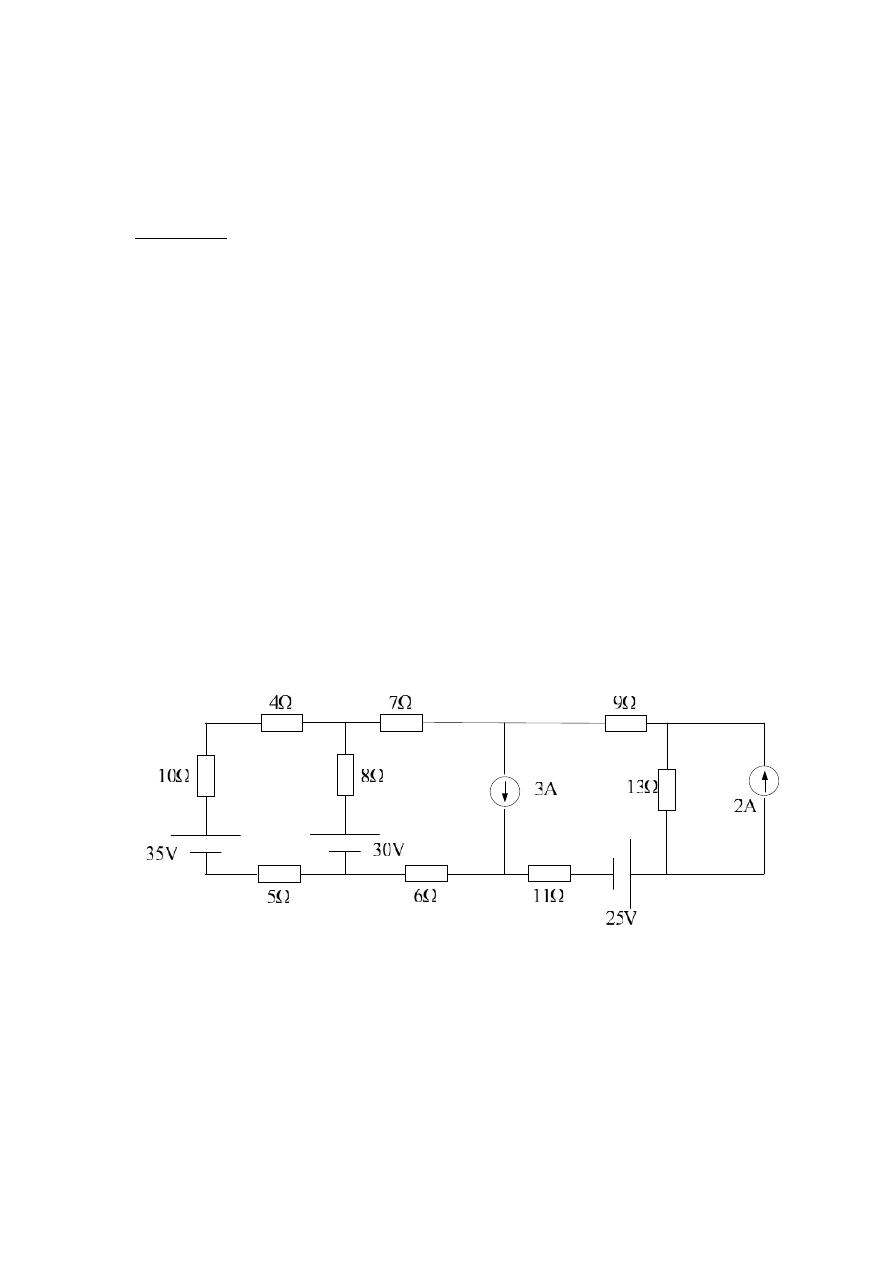
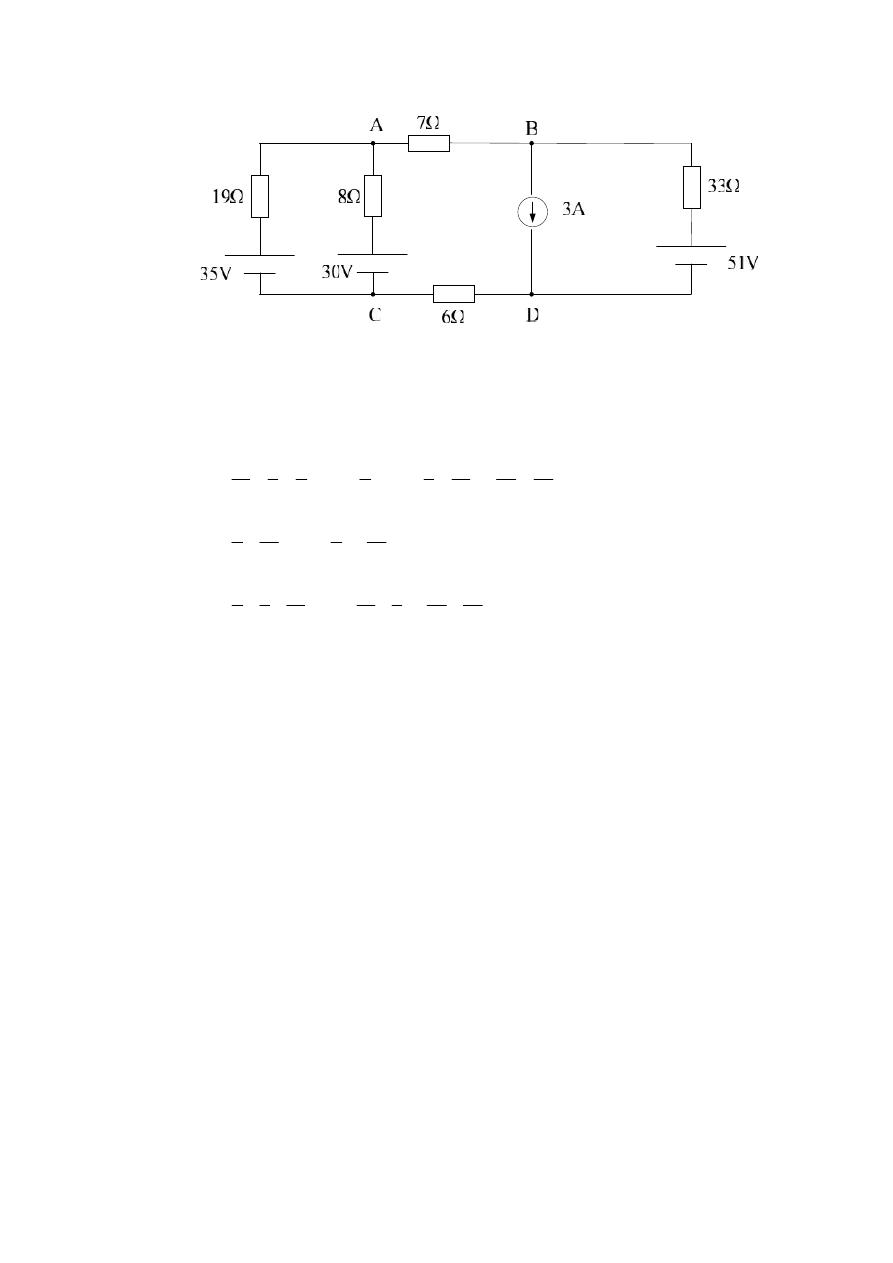
Example 2 :- Solve the following circuit diagram using nodal voltage .
Solution:
First we simplify the circuit and make a less nodal point.
-----------
( 1 )
-----------
( 2 )
-----------
( 3 )
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٤٧
-
N = 4 ; I
N
= 4
– 1 = 3
Let D be a reference point
A :
0
19
35
8
30
19
1
8
1
7
1
7
1
8
1
19
1
C
B
A
V
V
V
B :
0
3
33
51
7
1
33
1
7
1
A
B
V
V
C :
0
19
35
8
30
8
1
19
1
19
1
8
1
6
1
A
C
V
V
Rearrange
-0.321 V
A
+ 0.143 V
B
+ 0.178 V
C
= -5.592
0.143 V
A
- 0.174 V
B
= 1.455
0.178 V
A
- 0.344 V
C
= 5.592
اﻛﻤﻞ اﻟﺤﻞ ﺟﺪ
V
A
, V
B
, V
C
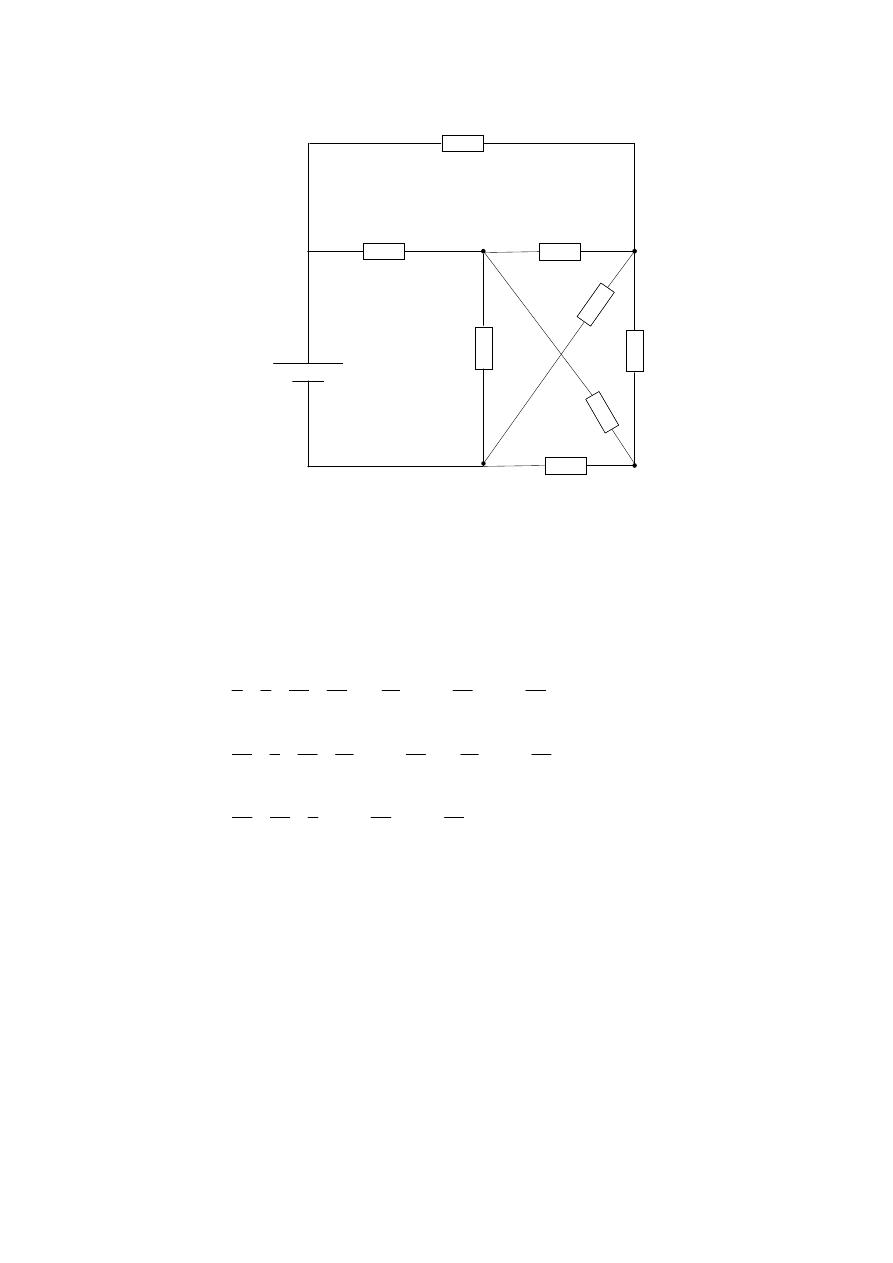
Example 3 :- Solve the following circuit using nodal voltage method:
-----------
( 1 )
-----------
( 3 )
-----------
( 2 )
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٥٧
-
9Ω
50Ω
5Ω
30Ω
15Ω
20Ω
6Ω
15V
3Ω
A
C
D
B
E
Solution:
Let D reference
V
A
= 15 V
B :
0
20
1
30
1
6
15
20
1
30
1
9
1
6
1
E
C
B
V
V
V
C :
0
50
1
3
15
30
1
15
1
50
1
3
1
30
1
E
B
C
V
V
V
D :
0
50
1
20
1
5
1
50
1
20
1
C
B
E
V
V
V
Then rearrange the above equations and find V
B
, V
C
, V
E
.
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٦٧
-
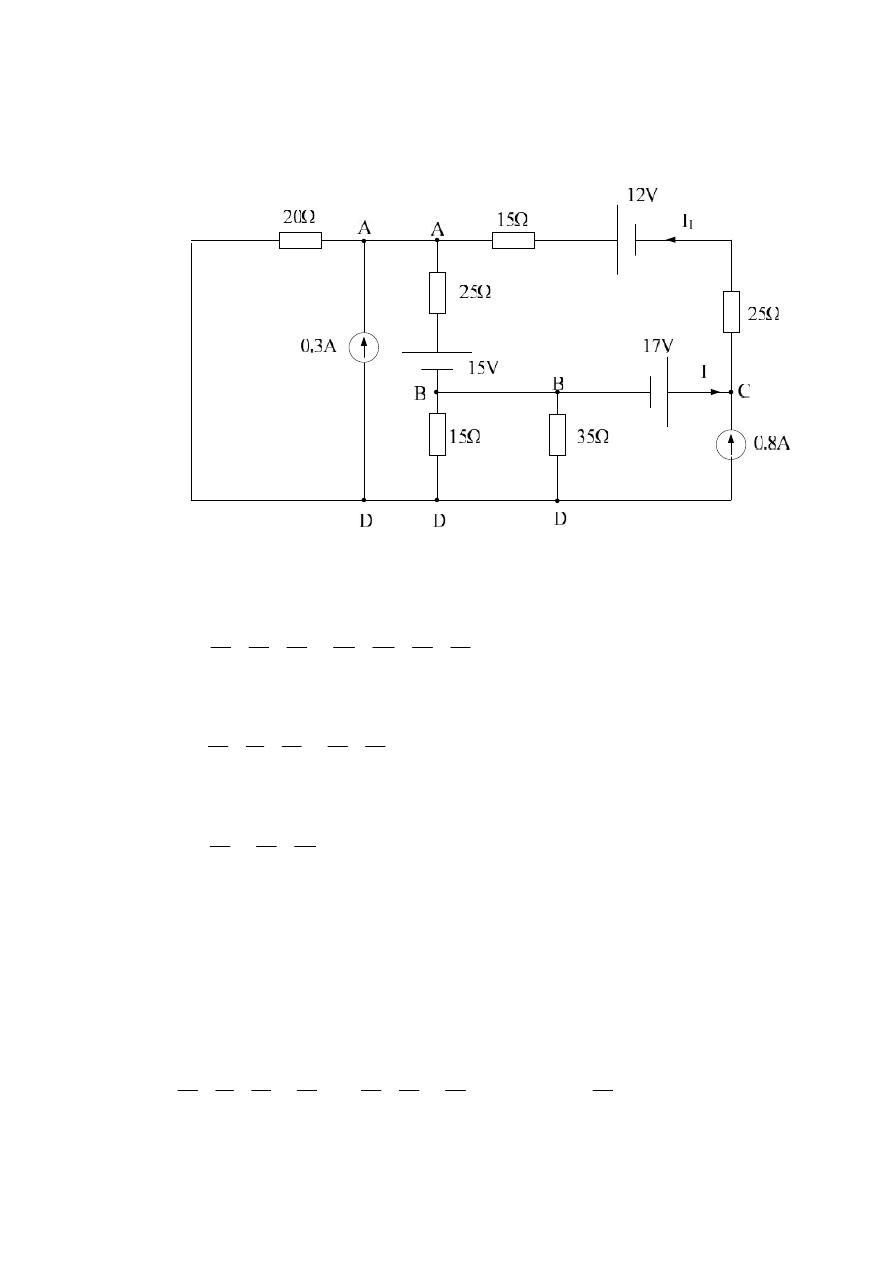
Example, (Sheet 4 – Q. 24): For the following circuit diagram, find I & I
1
,
using nodal voltage method:
Solution:
First; let D reference:-
A :
0
3
.
0
25
15
40
12
40
25
20
1
25
1
40
1
C
B
A
V
V
V
B :
0
25
15
25
35
1
15
1
25
1
I
V
V
A
B
C :
0
8
.
0
40
40
12
40
1
I
V
V
A
C
V
B
+ 17 = V
C
Then the above equations can be minimized to:-
B + C:
0
40
1
17
8
.
0
40
12
40
1
25
1
25
15
35
1
15
1
25
1
B
A
B
V
V
V
A :
-----------
( 1 )
-----------
( 3 )
-----------
( 2 )
-----------
( 4 )
-----------
( 1 )

Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (8))
-
٧٧
-
0
3
.
0
25
15
40
12
40
17
25
20
1
25
1
40
1
B
B
A
V
V
V
Then solve to find V
A
& V
B
; hence we can find V
C
from eq. ( 4 ); to find I sub.
V
A
& V
B
in eq. ( 2 ); and to find I
1
; then I
1
= I + 0.8
Second solution; let B reference
Hence V
C
= 17 V
A :
0
3
.
0
25
15
20
40
17
40
12
20
1
25
1
40
1
D
A
V
V
D :
0
8
.
0
3
.
0
20
20
1
35
1
15
1
A
D
V
V
Then find V
A
& V
D
from the above equations; hence to find I;
C :
0
40
12
8
.
0
40
40
17
I
V
A
And to find I
1
; I
1
= I + 0.8
-----------
( 2 )
-----------
( 2 )
-----------
( 1 )
