
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
١٥
-
Matrices :-
Second order determinate
Col. 1
Col. 2
1
2
2
1
2
2
1
1
b
a
b
a
b
a
b
a
D
Col. 1
Col. 2
Col. 3
a
1
x
b
1
y
=
c
1
a
2
x
b
2
y
=
c
2
2
1
2
2
1
1
c
c
y
x
b
a
b
a
2
1
2
1
2
1
2
1
2
2
1
1
2
2
1
1
1
a
b
b
a
c
b
b
c
b
a
b
a
b
c
b
c
D
D
x
2
1
2
1
2
1
2
1
2
2
1
1
2
2
1
1
2
a
b
b
a
a
c
c
a
b
a
b
a
c
a
c
a
D
D
y
Example :- Find the value of D
2
6
1
4
D
Solution :-
14
6
8
6
*
1
2
*
4
2
6
1
4
D
-
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٢٥
-
Example :- Solving the equations below by determinates
4I
1
– 6 I
2
= 8
2I
1
+ 4 I
2
= 20
Solution :-
20
8
4
2
6
4
2
1
I
I
A
D
D
I
428
.
5
12
16
120
32
2
*
6
4
*
4
20
*
6
4
*
8
4
2
6
4
4
20
6
8
1
1
A
D
D
I
28
.
2
28
2
*
8
20
*
4
28
20
2
8
4
1
1
Third – order determinant :-
3
2
1
3
2
1
3
3
3
2
2
2
1
1
1
b
b
b
a
a
a
c
b
a
c
b
a
c
b
a
D
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
c
a
b
b
c
a
a
b
c
b
a
c
a
c
a
c
b
a
D
Example :- Find the value of D
2
4
0
0
1
2
3
2
1
D

Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٣٥
-
Solution :-
4
1
2
0
2
1
2
4
0
0
1
2
3
2
1
D
14
8
22
8
0
0
24
0
2
2
*
2
*
2
1
*
0
*
4
3
*
1
*
0
4
*
2
*
3
0
*
0
*
2
2
*
1
*
1
D
D
Example :- Find V
1
, V
2
, V
3
from the following equations :-
2V
1
+ 4V
2
+2V
3
= 8
5V
1
– 2V
2
– 10V
3
= 18
V
1
+ 8V
2
– 20V
3
= -8
Solution :-
8
18
8
20
8
1
10
2
5
2
4
2
3
2
1
V
V
V
8
2
4
1
5
2
20
8
1
10
2
5
2
4
2
8
2
4
8
18
8
20
8
8
10
2
18
2
4
8
1
1
D
D
V
4
*
5
*
20
2
*
10
*
8
2
*
2
*
1
8
*
5
*
2
1
*
10
*
4
20
*
2
*
2
4
*
18
*
20
8
*
10
*
8
2
*
2
*
8
8
*
18
*
2
8
*
10
*
4
20
*
2
*
8
1
V
V
V
35
.
4
684
2976
1
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٤٥
-
684
8
18
8
1
5
2
20
8
1
10
18
5
2
8
2
2
2
D
D
V
684
8
2
4
1
5
2
8
8
1
18
2
5
8
4
2
3
3
D
D
V
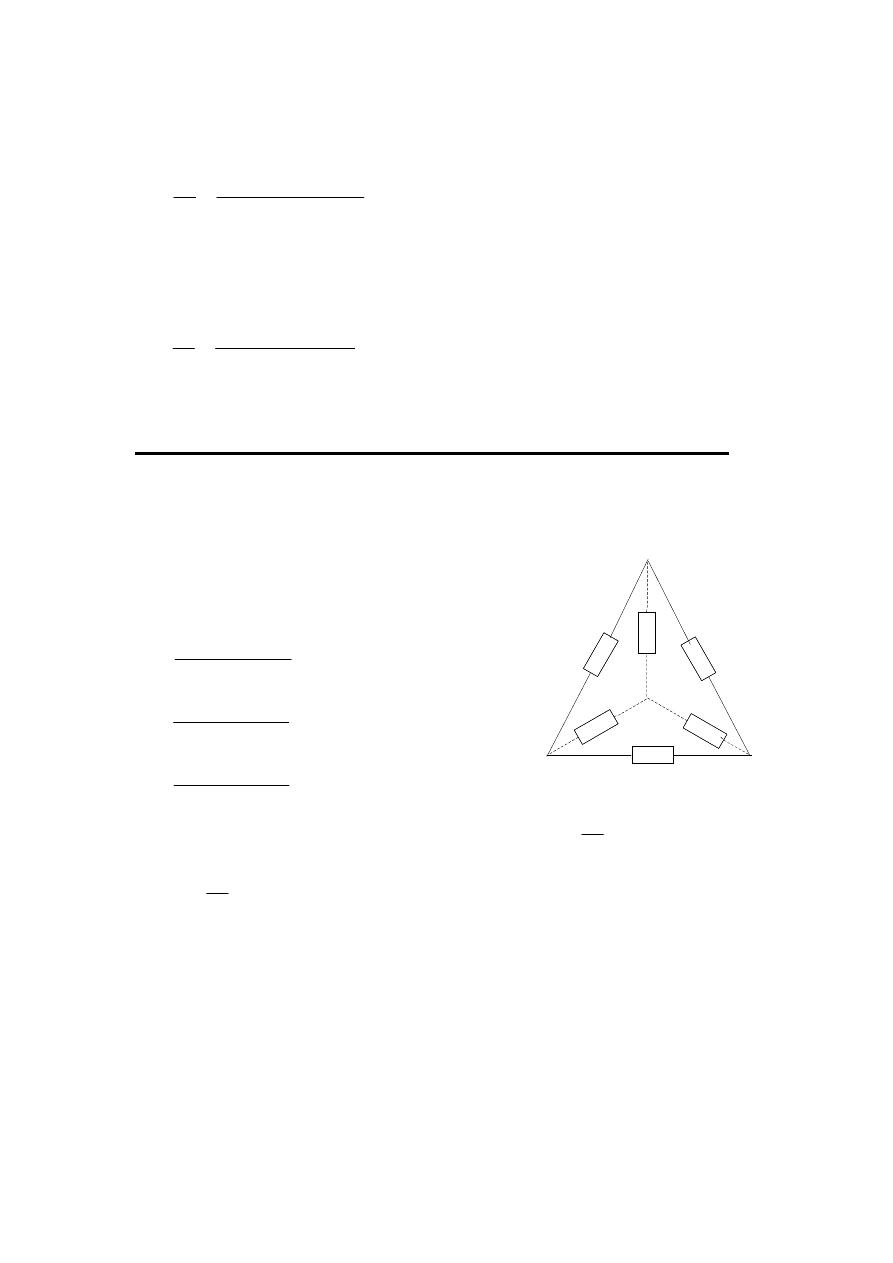
Star – Delta (
) and Delta – Star (
) transformation :-
1. ) Delta
– Star (
) transformation :-
B
A
C
R
B
R
A
R
C
R
BC
R
AB
R
CA
If R
Ab
= R
BC
= R
CA
= R
∆
, in this case
R
R
R
R
R
C
B
A
3
or
3
R
R
If the value of R
AB
, R
CA
, R
BC
are
known, and we need to get the values
of R
A
, R
B
, R
C
; then :-
BC
CA
AB
CA
AB
A
R
R
R
R
R
R
BC
CA
AB
BC
AB
B
R
R
R
R
R
R
BC
CA
AB
BC
CA
C
R
R
R
R
R
R
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٥٥
-
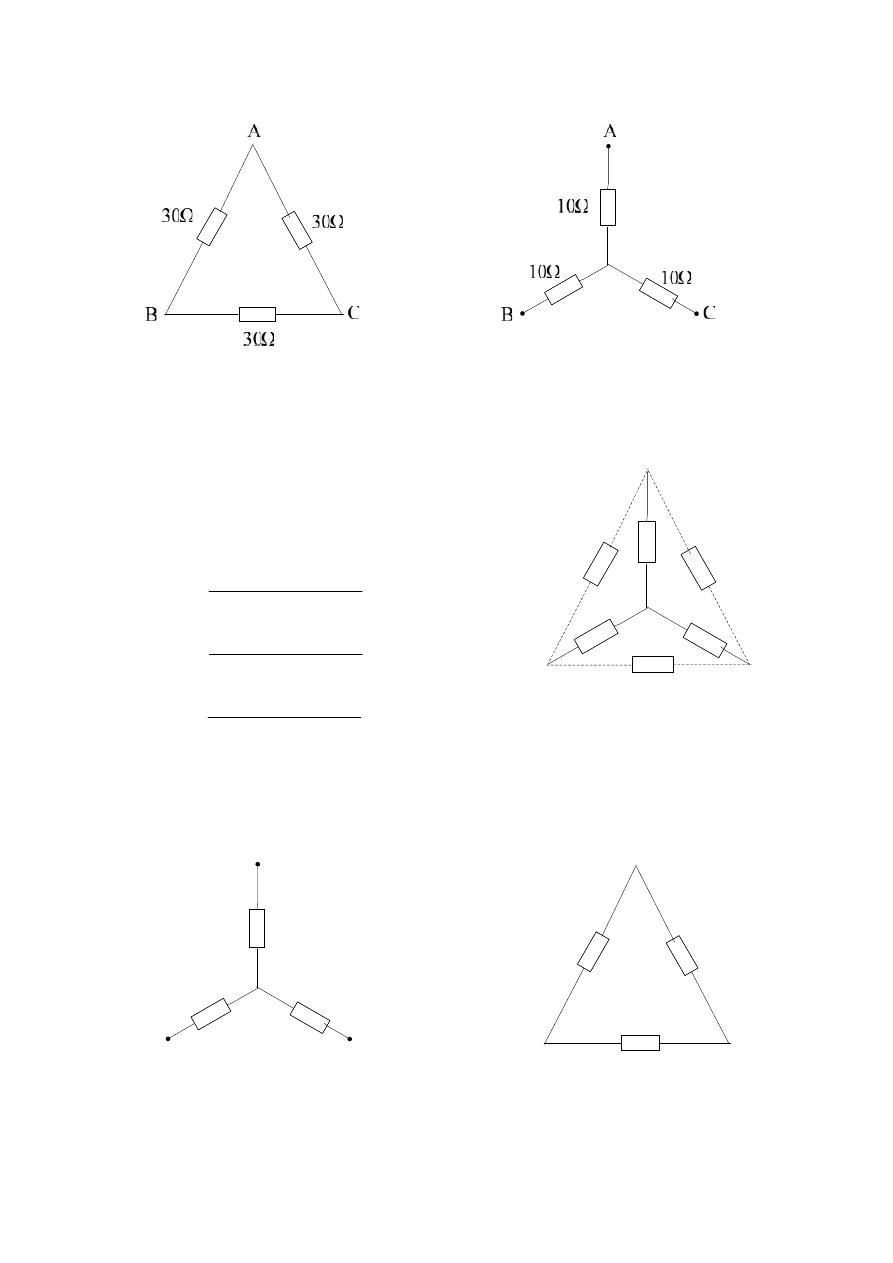
2. ) Star
– Delta (
) transformation :-
B
A
C
R
B
R
A
R
C
R
BC
R
AB
R
CA
If
R
R
R
R
C
B
A
, in this case R
AB
= R
CA
= R
BC
= R
∆
= 3 R
Y
B
A
C
4Ω
4Ω
4Ω
B
A
C
12Ω
12Ω
12Ω
If the value of R
A
, R
B
, R
C
are known ,
and we need to get the values of R
AB
,
R
CA
, R
BC
; as follows :-
C
C
A
C
B
B
A
AB
R
R
R
R
R
R
R
R
A
C
A
C
B
B
A
BC
R
R
R
R
R
R
R
R
B
C
A
C
B
B
A
CA
R
R
R
R
R
R
R
R
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٦٥
-
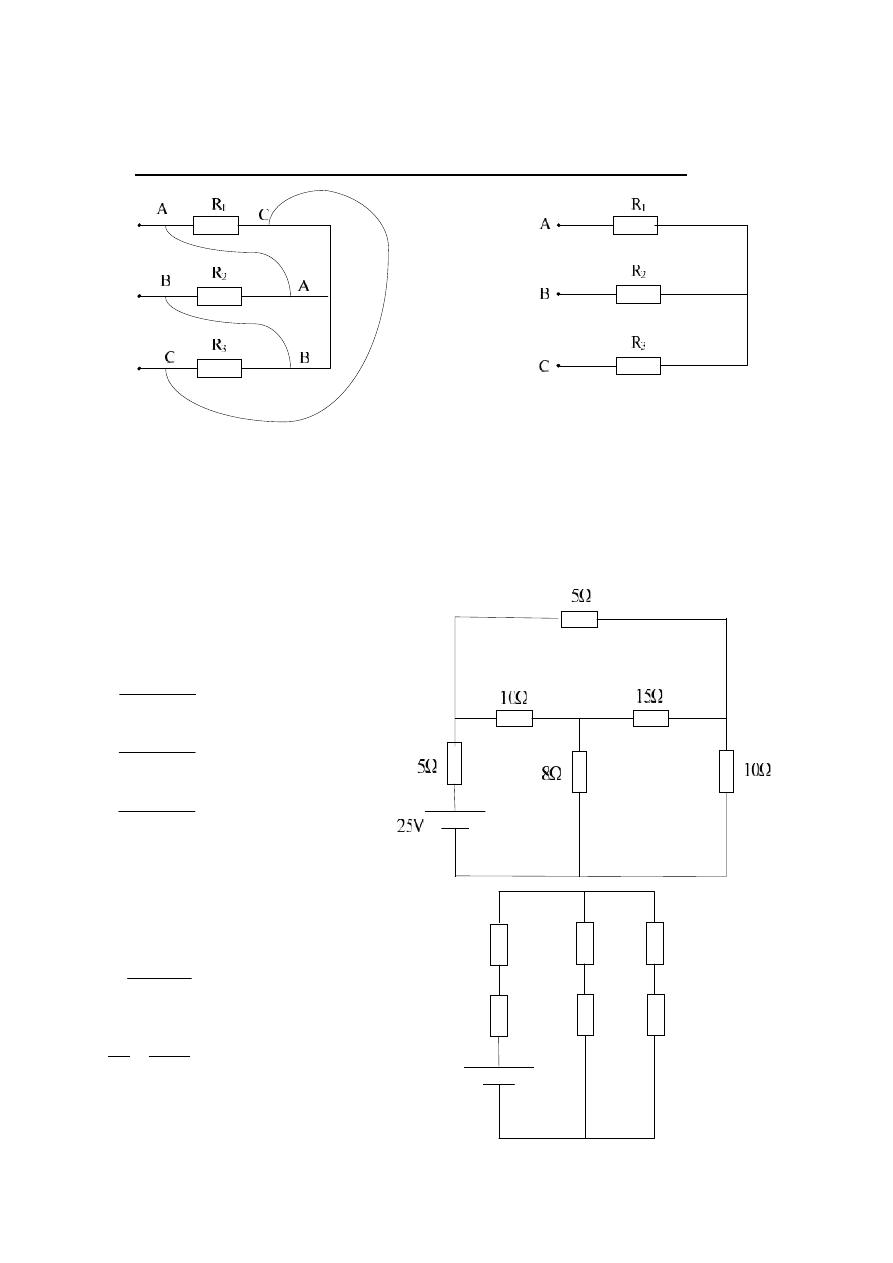
Examples of star and delta connections and transformation :-
Example :- Find the current flow in the 25 V source for the following circuit :-
Solution :-
25 V
R
c
R
b
R
a
5Ω
8Ω
10Ω
Delta connection
Star connection
5
.
2
15
10
5
15
*
5
a
R
5
15
10
5
15
*
10
b
R
67
.
1
15
10
5
10
*
5
c
R
A
R
E
I
R
R
R
R
R
R
R
R
T
T
T
T
T
c
b
a
T
92
.
1
04
.
13
25
04
.
13
67
.
6
37
.
6
67
.
6
13
5
.
12
13
*
5
.
12
67
.
6
13
//
5
.
12
5
67
.
1
8
5
//
10
5
.
2
5
8
//
10
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٧٥
-
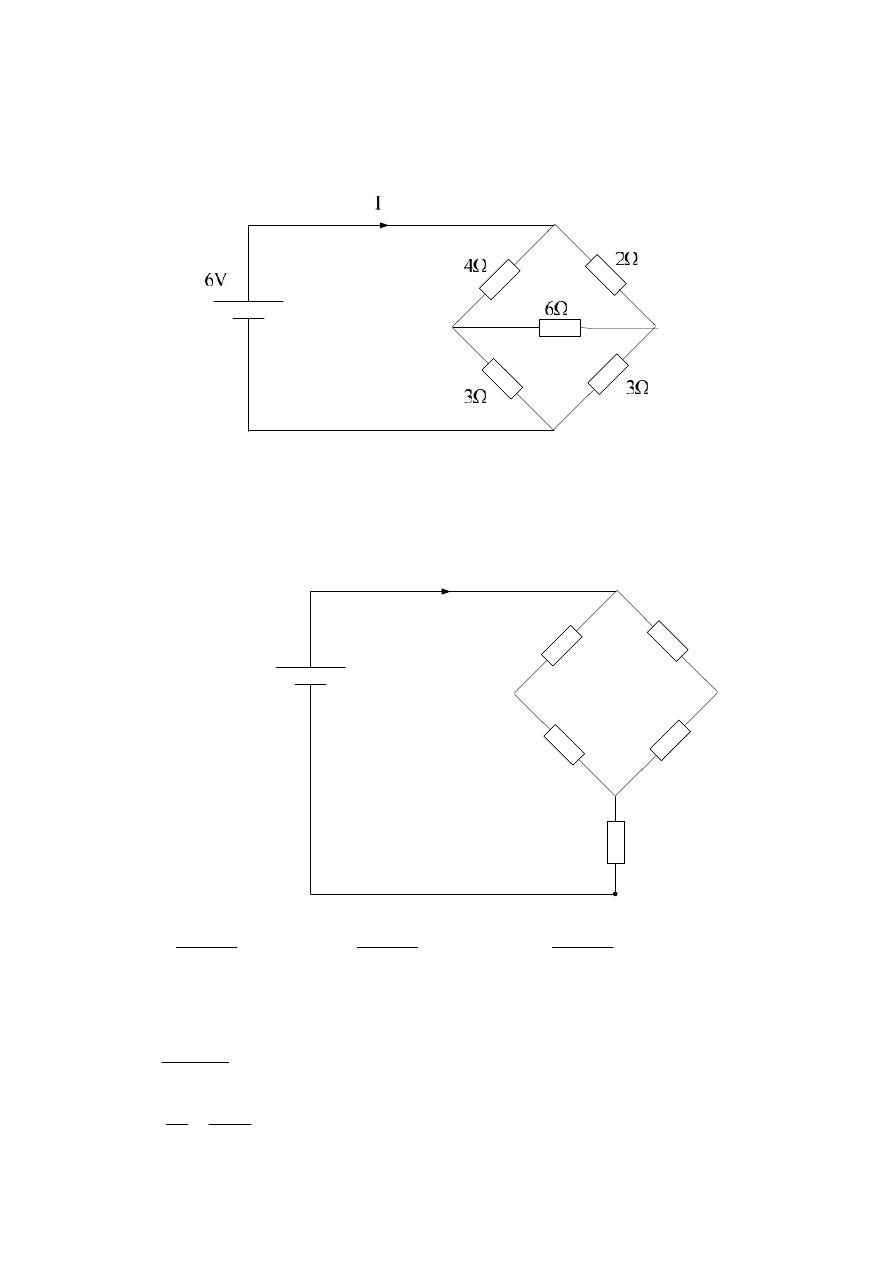
Example :- For the following network , find I ?
Solution :- The resistances ( 6 , 3 , 3 ) are delta , can convert to star connection
as follows:
a
b
c
6V
4Ω
2Ω
R
a
R
b
R
c
I
5
.
1
3
3
6
3
*
6
a
R
,
5
.
1
3
3
6
3
*
6
b
R
,
75
.
0
3
3
6
3
*
3
c
R
75
.
0
5
.
3
5
.
5
5
.
3
*
5
.
5
5
.
3
//
5
.
5
2
//
4
c
c
b
a
T
R
R
R
R
R
A
R
E
I
T
077
.
2
889
.
2
6
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٨٥
-
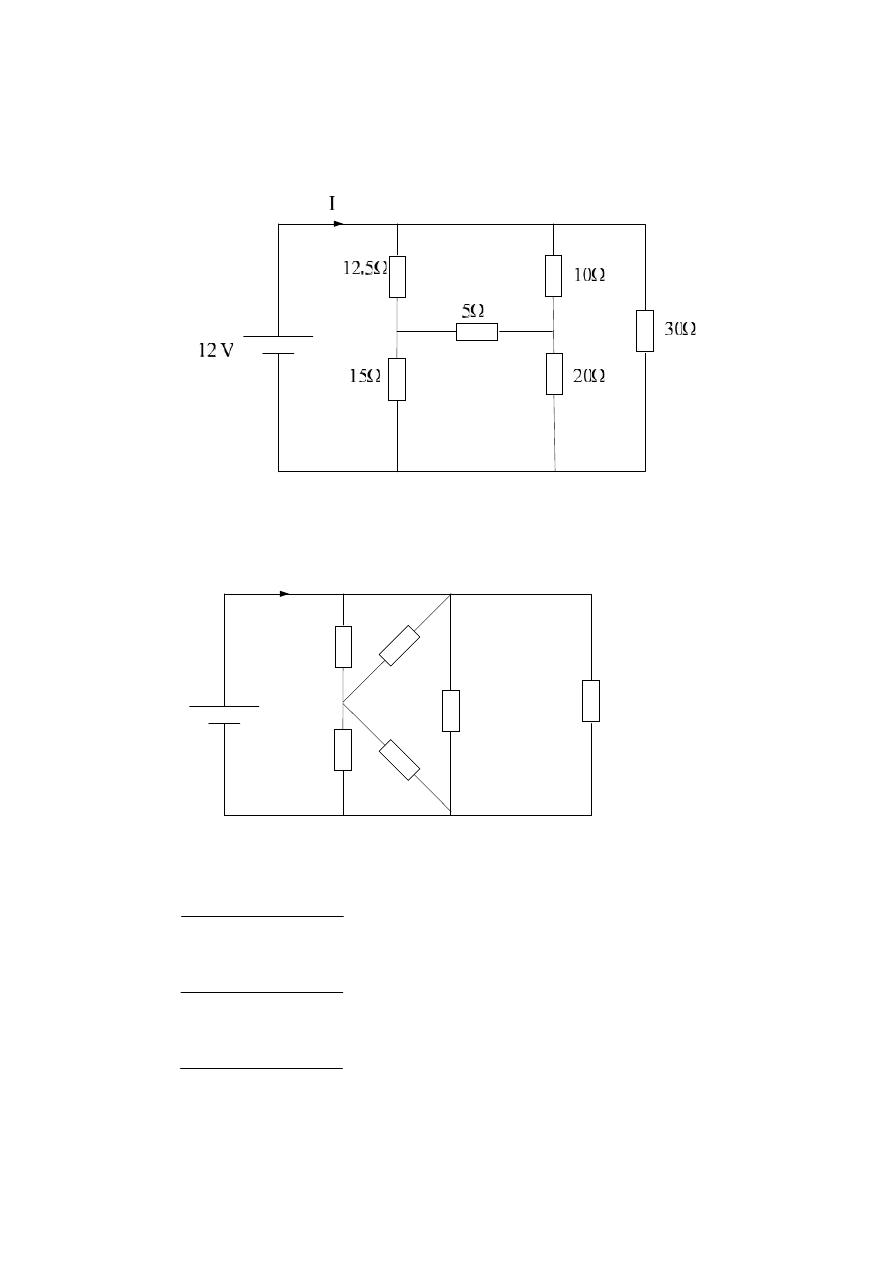
Example :- Find I for the following cct. network :-
Solution :- Th
e resistors ( 5Ω , 10Ω , 20Ω ) are star convert to delta
12 V
15Ω
12.5Ω
30Ω
I
b
a
c
R
bc
R
ab
R
ac
35
10
20
*
5
5
*
10
20
*
10
5
.
17
20
20
*
5
5
*
10
20
*
10
70
5
20
*
5
5
*
10
20
*
10
bc
ac
ab
R
R
R
Dr. Sameir Abd Alkhalik Aziez
University of Technology Lecture (6))
-
٩٥
-
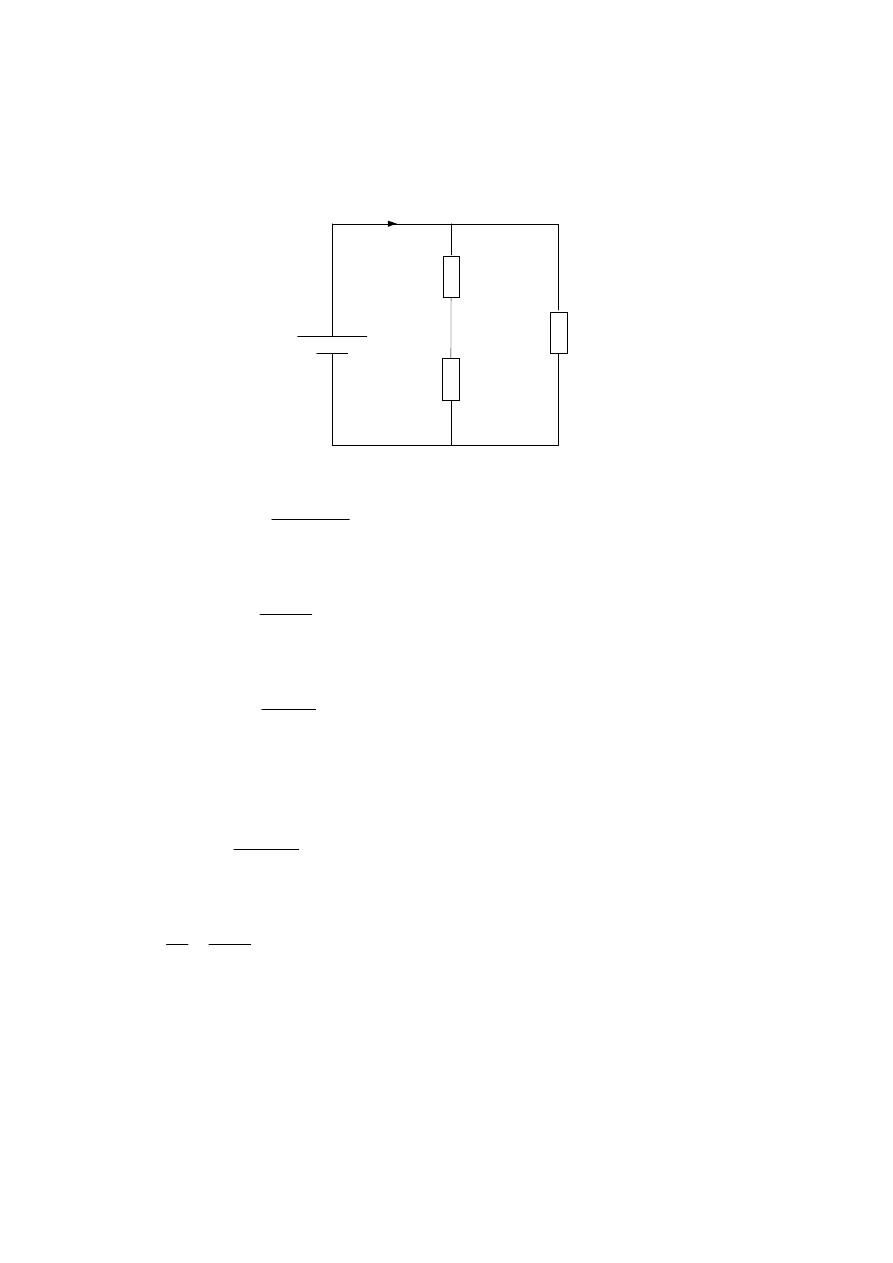
It is clear that ( 12.5 Ω // R
ac
) and (1
5 Ω // R
bc
) and (30 Ω // R
ab
) , hence the
circuit can be reduce to the following network :-
12 V
R
3
I
R
1
R
2
3
.
7
5
.
17
5
.
12
5
.
17
*
5
.
12
//
5
.
12
1
ac
R
R
5
.
10
35
15
35
*
15
//
15
2
bc
R
R
21
70
30
70
*
30
//
30
3
ab
R
R
634
.
9
21
8
.
17
21
*
8
.
17
21
//
8
.
17
21
//
5
.
10
3
.
7
//
3
2
1
R
R
R
R
T
A
R
E
I
T
246
.
1
634
.
9
12
